|
|
|
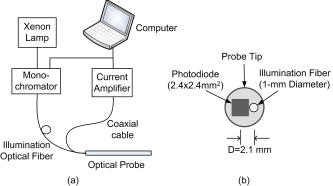
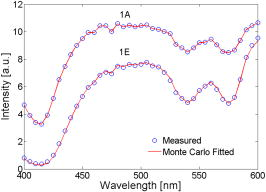
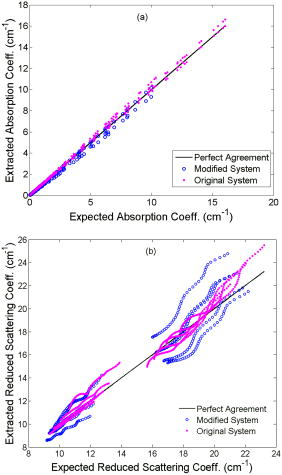
UV-visible diffuse reflectance spectroscopy (UV-VIS DRS) is sensitive to the absorption and scattering properties of biological molecules in tissue and thus can be used as a tool for quantitative tissue physiology in vivo. One major absorber of light in mucosal tissue in the visible range is hemoglobin (Hb), which shows distinctive, wavelength-dependent absorbance characteristics depending on its concentration and oxygenation. Tissue scattering is sensitive to the size and density of cellular structures such as nuclei and mitochondria. Thus, DRS of tissues can quantify changes in oxygenation, blood volume and alterations in cellular density and morphology. Some potential clinical applications of UV-VIS DRS include monitoring of tissue oxygenation,1 precancer and cancer detection,2, 3 intraoperative tumor margin assessment,4 and assessing tumor response to cancer therapy.1 Our group has developed a fiber optic DRS system5 and a fast inverse Monte Carlo (MC) model of reflectance6 to nondestructively and rapidly quantify tissue absorption and scattering properties. The system consists of a xenon lamp, a monochromator, a fiber optic probe, an imaging spectrograph, and a CCD camera. Previously published studies by our group7 show that this technology is capable of quantifying breast tissue physiological and morphological properties, and that these quantities can be used to discern between malignant and non-malignant tissues with sensitivities and specificities exceeding 80%. Although this technology coupled with the MC model is a robust toolbox for quantifying tissue optical properties, this system suffers from several drawbacks similar to other spectrometers. First, optical fibers when used for detection, collect a relatively small portion of the remitted signal, thus high-quantum-efficiency, low-noise detectors are required to detect the signal, particularly in the UV-blue spectral region. Optical-fiber-based detection, while reasonable for single-point sampling, is unwieldy and expensive when expanded for use in imaging applications. Thus, a simpler, low-cost, and more portable reflectance spectrometer, capable of making fast measurements and easily extendable into a spectral imaging platform for mapping tissue optical properties is desirable for clinical applications. Previous studies have attempted to develop a portable DRS probe for cancer detection. Cerussi 8 developed a handheld laser breast scanner (LBS) based on frequency-domain near-infrared spectroscopy for breast cancer detection. The LBS probe consists of a fiber bundle for illumination and an avalanche photodiode module placed from the fiber bundle for detection. Feather 9 reported a portable diffuse reflectometer that uses nine LEDs at three visible wavelengths to illuminate skin and a photodiode to collect diffusely reflected light, through a aperture. The LBS has a sensing depth over , but is difficult to multiplex into a spectral imaging device because of the size of the device. The LED-photodiode-based reflectometer is extendable to imaging, but measurements based on this device does not provide quantitative endpoints such as absorption and scattering, which relate to the underlying biology of the tissue. Our long-term goal is to develop a cost-effective, miniature spectral imaging device for quantifying tumor physiology and morphology with performance comparable to its benchtop counterpart. In this letter, we describe a single-point hybrid optical probe that consists of a multimode illumination fiber and a silicon photodiode as a first step toward the long-term goal. We demonstrate that diffuse reflectance (DR) spectra measured with the hybrid system coupled with our inverse MC model provides quantitative measures of tissue absorption and scattering with accuracy that is comparable to that of the original benchtop system. The hybrid system, shown in Fig. 1a , consists of a xenon lamp and monochromator (JY Horiba, Edison, New Jersey), a illumination optical fiber [numerical aperture ], a silicon photodiode (S1226, Hamamatsu, Japan) with a low-noise current amplifier (PDA-750, Terahertz Technologies Inc., Oriskany, New York), and a laptop computer. The hybrid system uses the same light source and monochromator and an illumination fiber with similar diameter and NA as the original system. The primary difference between the two systems is that the photodiode and current amplifier in the new system replace the collection fibers, spectrograph, and CCD camera in the original system. At the distal end of the probe [Fig. 1b] the edge of the photodiode was trimmed to the active area and transparent epoxy was used to bond the cleaved fiber adjacent to the photodiode, such that the center-to-center distance between the fiber and the photodiode is . The overall diameter of the probe tip is . The maximum power out of the illumination fiber was at , and the minimum power was at . This system has significantly lower cost and better collection efficiency than the original system because of the larger NA of the silicon photodiode and its direct contact with the sample. It can also be easily multiplexed into a spectral imaging device by interfacing a bundle of optical fibers to the exit slit of the monochromator and separating the fibers at the distal end, such that each fiber is coupled to a discrete photodiode within a large matrix of photodiodes. To evaluate the performance of the modified system, a series of experiments were conducted on homogeneous tissue phantoms. Prior to the phantom experiments, the long-term drift and signal-to-noise ratio (SNR) of the system were characterized. We determined that the drift of the system was less than over with the lamp on and the probe tip in contact with the surface of a liquid phantom. By taking three consecutive DR spectra from in the darkest phantom among the 10 phantoms described in the following, we calculated an average SNR of over all wavelengths and a minimum SNR of at , which is close to the Soret band of oxy-Hb. Phantoms with absorption coefficient and reduced scattering coefficient representative of human breast tissues in the wavelength range6 were created with the scatterer, -diam polystyrene spheres (07310-15, Polysciences, Inc., Warrington, Pennsylvania) and variable concentrations of the absorber, Hb (H0267, Sigma Co., St. Louis, Missouri). Two sets of liquid phantoms were created by titrating the absorber at two scattering levels, and all DR measurements were made the day the phantoms were prepared. The first set of phantoms (1A to 1E) consisted of five low-scattering phantoms (wavelength-averaged ) with wavelength-averaged of 0.49, 0.88, 1.28, 1.58, and over the range. The second set (2A to 2E) consisted of five high-scattering phantoms (wavelength-averaged ) with the same values as the first set. A complete DR spectrum was collected from each phantom by scanning the bandpass of the monochromator from at increments of . Then, a DR spectrum was also obtained from a Spectralon 99% diffuse reflectance puck (SRS-99-010, Labsphere, Inc., North Sutton, New Hampshire) with the probe in contact with the puck immediately after the phantom measurements with the same instrument settings. An inverse MC model6 was used to extract the and of the liquid phantoms. The model was validated in both phantom6, 10 and clinical studies.7 The MC forward model assumes a set of absorbers (oxy-Hb with known extinction coefficients measured using a spectrophotometer in this case) are present in the medium. The scatterer (polystyrene microsphere in this study) is assumed to be single-sized, spherically shaped, and uniformly distributed. The of the medium are calculated from the concentration of each absorber and the corresponding extinction coefficients using Beer’s law. The and anisotropy factor are calculated using Mie theory.11 The and are then input into a scalable MC model of light transport to obtain a modeled DRs spectrum. In the inverse model, the modeled DR is adaptively fitted to the measured tissue DR. When the sum of square error between the modeled and measured DR is minimized, the concentrations of absorber, from which can be derived, and are extracted. To experimentally compare measured phantom spectra to MC simulated phantom spectra for the fitting process, the “calibrated” DR spectrum of the target phantom for which the optical properties are to be quantified, was divided point by point by the “calibrated” DR spectrum of a reference phantom with known optical properties. The term “calibrated” in both cases refers to the normalization of the DR spectrum to that measured from the Spectralon puck for correction of the wavelength-dependent response of the instrument. In this phantom study, phantom 1C (wavelength-averaged , wavelength-averaged ) was selected as a reference phantom and the remaining nine phantoms were used as targets. Bender previously provided guidelines for the selection of a reference phantom.10 Figure 2 shows the Spectralon puck-calibrated reflectance spectra for two phantoms 1A and 1E and the corresponding fits to the MC model. The three valleys at 415, 540, and on the spectra for both phantoms are the Soret band , band , and band of oxygenated Hb, respectively. There is excellent agreement between the measured spectra and the fits. Figures 3a and 3b show the extracted versus expected and for all wavelengths over the range quantified with the modified and original systems for the similar range of optical properties. The 10 phantoms tested with the modified system have an overall range of and a range of , while that tested with the original system have overall and ranges of and , respectively. The reference phantom used for measurements made with the original system had a wavelength-averaged and . The correlation coefficients for and are 0.9981 and 0.9588, respectively, for optical properties quantified with the modified system. An overall error of was calculated for and for for the modified system. For the purposes of comparison, the original system had a overall errors and for extracting and , respectively. The modified system can quantify absorption from phantoms with modest absorption coefficients (up to ). Compared to the original system, the modified system has higher errors in extraction of scattering coefficient due to its lower SNR for high scattering. The dynamic range of the system may be improved by decreasing the center-to-center distance between the source and detector as well as by increasing the area of the photodiode. We believe that the modified system combined with our MC model can be extended into an optical spectral imaging system to map out the concentrations of absorbers and the bulk tissue scattering properties of subsurface tissue volumes, which are on a length scale of several millimeters. There are a number of applications for which this technology would be ideally suited, including epithelial precancer and cancer detection (such as those of the skin, oral cavity, and cervix), intraoperative tumor margin assessment, and the monitoring of tumor response to therapy in organ sites such as the head and neck and cervix. More importantly, placing the detector directly at the tissue surface will improve collection efficiency and will significantly reduce the cost associated with expensive and sophisticated CCDs. AcknowledgmentsThis work has been funded by a Department of Defense Breast Cancer Research Program (DOD BRCP) Era of Hope Scholar award to Dr. Nirmala Ramanujam. ReferencesI. J. Bigio and
S. G. Bown,
“Spectroscopic sensing of cancer and cancer therapy, current status of translational research,”
Cancer Biother, 3
(3), 259
–267
(2004). 1062-8401 Google Scholar
G. Zonios,
L. T. Perelman,
V. Backman,
R. Manoharan, M. Fitzmaurice, J. Van Dam, and
M. S. Feld,
“Diffuse reflectance spectroscopy of human adenomatous colon polyps in vivo,”
Appl. Opt., 38
(31), 6628
–6637
(1999). https://doi.org/10.1364/AO.38.006628 0003-6935 Google Scholar
Y. N. Mirabal,
S. K. Chang,
E. N. Atkinson,
A. Malpica,
M. Follen, and
R. Richards-Kortum,
“Reflectance spectroscopy for in vivo detection of cervical precancer,”
J. Biomed. Opt., 7
(4), 587
–594
(2002). https://doi.org/10.1117/1.1502675 1083-3668 Google Scholar
W. C. Lin,
S. A. Toms,
M. Johnson,
E. D. Jansen, and
A. Mahadevan-Jansen,
“In vivo brain tumor demarcation using optical spectroscopy,”
Photochem. Photobiol., 73
(4), 396
–402
(2001). https://doi.org/10.1562/0031-8655(2001)073<0396:IVBTDU>2.0.CO;2 0031-8655 Google Scholar
C. Zhu,
G. M. Palmer,
T. M. Breslin,
F. Xu, and
N. Ramanujam,
“Use of a multiseparation fiber optic probe for the optical diagnosis of breast cancer,”
J. Biomed. Opt., 10
(2), 024032
(2005). https://doi.org/10.1117/1.1897398 1083-3668 Google Scholar
G. M. Palmer and
N. Ramanujam,
“Monte Carlo-based inverse model for calculating tissue optical properties. Part I, Theory and validation on synthetic phantoms,”
Appl. Opt., 45
(5), 1062
–1071
(2006). https://doi.org/10.1364/AO.45.001062 0003-6935 Google Scholar
C. Zhu,
G. M. Palmer,
T. M. Breslin,
J. Harter, and
N. Ramanujam,
“Diagnosis of breast cancer using diffuse reflectance spectroscopy: comparison of a Monte Carlo versus partial least squares analysis based feature extraction technique,”
Lasers Surg. Med., 38
(7), 714
–724
(2006). https://doi.org/10.1002/lsm.20356 0196-8092 Google Scholar
A. Cerussi,
N. Shah,
D. Hsiang,
A. Durkin,
J. Butler, B. J. Tromberg,
“In vivo absorption, scattering, and physiologic properties of 58 malignant breast tumors determined by broadband diffuse optical spectroscopy,”
J. Biomed. Opt., 11
(4), 044005
(2006). https://doi.org/10.1117/1.2337546 1083-3668 Google Scholar
J. W. Feather,
D. J. Ellis, and
G. Leslie,
“A portable reflectometer for the rapid quantification of cutaneous haemoglobin and melanin,”
Phys. Med. Biol., 33
(6), 711
–722
(1988). 0031-9155 Google Scholar
J. E. Bender,
K. Vishwanath,
L. K. Moore,
J. Q. Brown,
V. Chang,
G. M. Palmer, and
N. Ramanujam,
“A robust Monte Carlo model for the extraction of biological absorption and scattering in vivo,”
IEEE Trans. Biomed. Eng.,
(0018-9294) Google Scholar
B. C. F. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York
(1998). Google Scholar
|