|
|
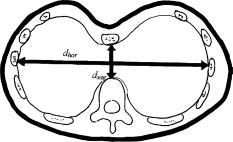
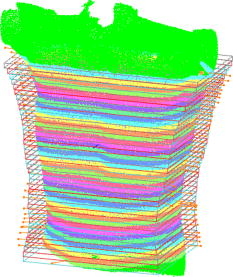
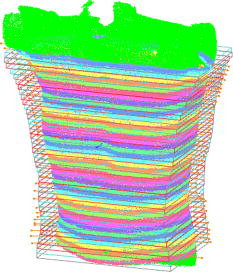
1.IntroductionPectus excavatum is the most common congenital deformity of the chest wall, with a variable reported incidence from 0.23 to 1%.1, 2, 3 The deformity of pectus excavatum is characterized by an inward depression of the sternum. In moderate-to-severe cases, exercise intolerance and, rarely, chest pain may associate the deformity. Profound psychological inacceptance of an altered body image can become a more important problem for adolescent and young adult patients. Psychological and cosmetic indications for surgical treatment gained more importance due to introduction of minimally invasive and cosmetic surgical methods. Physical examination, charts, preoperative photographs, and computed tomography (CT) scans are used to identify pectus excavatum cases. Physical examination should pay attention to asymmetry index, relative length of depression to the sternum, fraction of sternum affected, degree of sternal torsion, and localized versus diffuse morphology.4 Preoperative photographs are used to document the deepest point of the pectus, the length of the pectus relative to the sternum, the relative amount of the sternum affected, symmetry of the pectus, localized or diffuse (cup or saucer) morphology, and the presence of flaring of the lower costal margin. Standard photography is not sufficient to document 3-D components of the deformity. However, preoperative photographs can be used to determine chest lines, the area affected by the depression, the vertical length of the deformity, and the length of the sternum affected. Clinical evaluation and outcome assessment influence the treatment option strongly. Physical examination of patients, measurement of the chest circumference with a metric tape, and anthropometric measurement called chest cyrtometry are performed for basic documentation.5, 6 The anthropometric index is a simple method to assess the deformity. It is defined as a maximum anteroposterior measurement in the region of greatest deformity divided by measurement of greatest depth of the defect. Charts, preoperative photographs, and CT scans are usually used to identify pectus excavatum cases. Radiological examination sometimes may additionally define the orientation and relationships of the ribs, costal cartilages, and sternum for preoperative planning. However, plain photographs cannot become concurrent to CT assessment and Haller index (HI) calculation,7, 8 which remains a gold standard for preoperative planning and decision making. The Haller index calculated from CT scans was developed to provide an objective measure of the depth of the deformity for determining surgical eligibility.9 Kim 10 developed additionally indices that can automatically be extracted by computerized image to describe the depression and asymmetry of the chest wall, and the eccentricity, flatness, and circularity index, to present the deformation of the chest wall in detail. Despite several reported pectus excavatum severity classifications, the Haller index remains the most commonly used. Haller index (Fig. 1 ) greater than 3.2 is used as one of the criteria for surgical correction. The proposed value was accepted as the cutoff between mild and moderate pectus excavatum. Single-level HI may not supply sufficient information about chest-wall deformity in all cases. Multiple-level slice examination may supplement an assessment for more accurate diagnosis and preoperative planning.11 Due to current trends to reduce overall yearly exposition to ionizing radiation, new methods of pectus excavatum assessment are developed, particularly for repeated monitoring. 2.Relevant WorkAlthough anthropometric index measurement is a very simple method, the human factor may cause a relatively wide range of measurement dispersion.5, 6 Moiré phototopography12 was found in the early 1980’s as the method suitable for 3-D chest assessment. Fortin used a structured light projection system to reconstruct a 3-D surface of a patient’s trunk to design a customized spinal brace.13 Single directional assessment of back curvature screening has been elaborated in previous studies.14 Poncet reported that thoracic outline cross sections can be measured based on 3-D data representing a patient’s body surface captured with an optical measurement system.15 However, the analysis method presented by them requires an operator’s interaction and may imply human factor errors that depend on experience in 3-D measurement data analysis and also clinical knowledge about pectus excavatum assessment. 3.Aim of the StudyPromising results of our experiments on 3-D body measurement as well as those described by other researchers caused us to make an attempt to develop an optical 3-D chest measurement system and automatic data processing algorithms to assess the shape and severity of deformity in pectus excavatum cases. This work presents a high-accuracy optical markerless 3-D measurement system for noninvasive, quick, and relatively inexpensive assessment of pectus excavatum deformity. The system facilitates automatic measurement and data processing software for analysis of the deformity. The process is fully automatic and does not require the operator to interact with the measurement system and data analysis software, which would effect an objective evaluation of the results. To fully automate the whole process, we have developed a new 3-D scan index that is calculated from a measured chest surface outline. The index shows correlation with the CT Haller index. Worth stressing is that the measurement method is not based on ionizing radiation, and the measurement process may be repeated frequently without any harm to the patient’s health. 4.Measurement SystemThe measurement system built utilizes four modules that measure a patient from four directions (Fig. 2 ). Directional sensors are optical markerless 3-D measurement systems based on a structured light projection method.16 The metrological properties of the system allow for accurate and repeatable measurements, which may be regarded as a good basis for medical examination. Fig. 2A visualization of a patient (a) being measured in the system. Each measurement module consists of (b) a CCD camera and (c) a DLP projector (d) fixed to a stand and (e) is controlled by a computer. 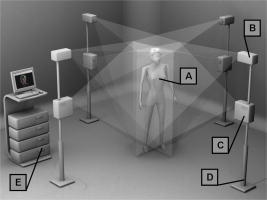 Each module [Fig. 3a ] consists of a projection unit, which is a digital light processing (DLP) projector (TDP-MT700 by Toshiba Corporation), and a detection unit, which is a charge coupled device (CCD) camera (Flea B&W by Point Grey Research Incorporated), During the measurement, certain patterns (sinusoidal fringes and modified binary Grey codes) are projected onto the patient who is standing still inside a calibrated measurement volume. Fig. 3The measurement setup in the laboratory at the Institute of Micromechanics and Photonics: (a) a directional measurement module fixed to a stand, (b) a healthy individual lighted with a fringe pattern from the module in (a), (c) the two front ( and ) out of four directional point clouds representing the patient’s upper body surface, and (d) the front clouds merged automatically based on the global coordinate set calibration. 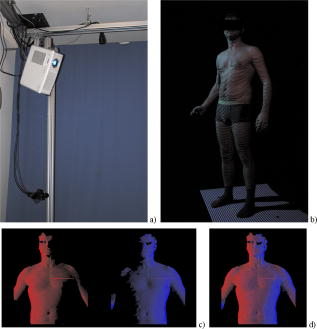 The shape of the body surface is calculated based on raster deformation [Fig. 3b]. To avoid detecting patterns projected by another unit, the adjacent modules are spectrally separated [Fig. 3c]. As the directional modules are calibrated in the same global coordinate set, the resulting clouds are merged automatically [Fig. 3d]. The dataset produced by the measurement system is in the form of a set of ( , , ) points that represent the surface of a patient’s body. All four directional modules measure in the same global coordinates set. An exemplary result of combined measurement from four directions is shown in Fig. 4 . The metrological values of the measurement system are as follows:
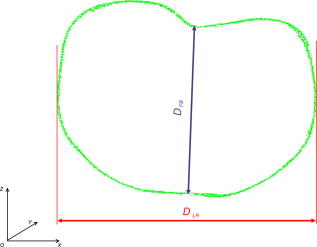
Fig. 4A 3-D point cloud representing the patient’s thoraco-abdominal region measured by the four-directional measurement system.  Stability of the patient during raster projection is essential for the successful measurement, as body movement greater than results in the need for repeating the measurement. Although the projection time is shorter than , for some patients it may be difficult to remain still. For these patients, additional support, i.e., handrails, may be used. 5.Automatic Analysis of Chest SurfaceThe developed method aims at calculating a 3-D scan index describing the deformity of the chest in the area where the deformity represents the highest chest depression. The proposed index is calculated based on a transverse slice of the trunk in a way similar to the Haller index to allow for a comparison with the latter. However, it is calculated based on external surfaces. is defined as the distance from the most depressed portion of the front chest wall to the surface of the back thoracic wall in the midline, divided by the external surface width of the chest at the same level (in the same slice). The formula is presented below as: where is the calculated index, is the length of the slice along the transversal axis, and is the distance from the most depressed point of the front chest wall to the back chest wall (Fig. 5 ).The main steps of the analysis path are as follows. First, the point cloud is divided into preliminary transverse slices. Based on them, the orientation of the torso model is adjusted to match the normalized coordinate set of the system (see Sec. 5.2). Then the point cloud is sliced again in the proper transverse direction. Next, for all closed slices, values of auxiliary are calculated and all auxiliary values are compared. The slice for which reaches its lowest value for the patient is regarded as the most depressed slice, and its auxiliary index is presented as the index value representative for the examined patient. The following paragraphs present a more detailed description of the developed algorithm. 5.1.Preliminary SlicesThe index is calculated for slices parallel to transverse planes of the body. In consequence, the correct patient orientation in the coordinate system is crucial for further processing. As the point cloud resulting from the measurement may be inaccurately positioned in the measurement volume, an automatic initial adjustment of its orientation is required. To achieve this, the torso model is cut into preliminary slices with planes horizontal in the coordinate set of the measurement system (Fig. 6 ). The height of the slices and their resulting their number depends on the density of the point cloud. The number of points in one slice has to be big enough for the points to create a solid contour. On the other hand, too-thick slices cause miscalculations of the index and extension of the processing time. The experiments showed that a slice height is optimal for the hardware setup used. The algorithm requires at least ten closed slices to be found. Slices recognized as open are regarded as incomplete and neglected. Then for each remaining slice its center of mass (CoM) and a long axis are calculated. The long axis is calculated for each slice by minimum root mean square (rms) line fitting for all its points. The resultant line formula defines the position and orientation of this axis. 5.2.Normalization of Created Model OrientationThe CoMs of all preliminary slices form a curve that is regarded as an approximation of the model’s vertical axis. The orientation of the torso model is adjusted in such a way that the model’s vertical axis matches the vertical axis of the coordinate set of the system. Also, the average long axis of the slices is adjusted to match the horizontal axis of the system. 5.3.Accurate Transverse SlicesWhen the orientation of the model has been corrected, the point cloud is sliced again with horizontal planes transverse to the patient’s torso (Fig. 7 ). Each slice is checked again as to whether it is a closed or open curve. 5.4.Calculation of Auxiliary IndexesThe auxiliary index is calculated for each closed slice. The index is a quotient of two distances. The first (placed in the nominator) is the distance from the most depressed point of the front chest wall to the back chest wall. More specifically, it is the shortest distance between two points where normal vectors form an angle exceeding . The denominator is the width of the slice, which is defined as the size of the slice along the transversal axis. The slice for which its index reaches its minimum is regarded as the most representative slice for the patient (Fig. 8 ), and its value is regarded as the index value representative of the patient. Fig. 8The slice recognized as the most representative for the examined patient. The characteristic distances used to calculate the value are also presented. 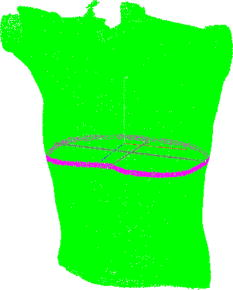 It is worth repeating that the presented method is fully automatic and does not require any user input. In particular, there are no markers attached to patient’s skin and no pointing of the deformation extreme with a mouse is required. 6.Clinical ExaminationsA prospective study was conducted from November 2007 to December 2008 at a diagnostic laboratory OGX (http://ogx.mchtr.pw.edu.pl) of the Institute of Micromechanics and Photonics. 12 patients with pectus excavatum (PE) were studied. The preliminary series consisted of white adolescent and young adult males an average age of and . The PE cases were documented through a paired examination of patient 3-D images and CT scans. The CT Haller index was calculated for all cases by an experienced orthopedist. Thorax shapes were measured with the use of the presented measurement system and analyzed according to the presented method. The CT Haller index ranged from 3.58 to 4.22 (average value 3.82). The following figures present the comparison of slices acquired by means of CT and 3-D optical scanner for patient 1 (Fig. 9 ) and patient 2 (Fig. 10 ). The body contour measured with the 3-D scanner is shown in green. There are two contours in Fig 10. The green color represents the contour before the surgery, while the blue color represents the contour after surgery. Fig. 9The CT image and body contour captured with the 3-D optical measurement system (patient 1). (Color online only.) 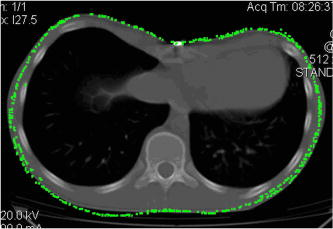 Fig. 10The CT image and body contour captured with the 3-D optical measurement system (patient 2). The green color represents the contour before the surgical operation, and the blue color represents the contour after the operation. (Color online only.) 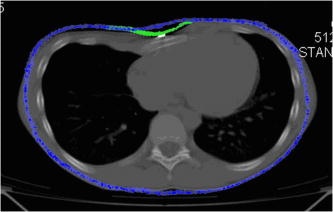 There are some differences in the contours of trunk slices imaged with the two modalities. These are caused by different positions of patient bodies during the CT examination where the patient is supine, and during the 3-D optical scanning procedure where the patient is standing. Table 1 presents a comparison of values of CT Haller index (CT HI), 3-D scan index calculated based on CT images (CT ), and of 3-D scan index calculated based on a 3-D scan . Table 1Table of measured values of (CT HI). (CT I3ds ), and (I3ds) indexes for examined patients.
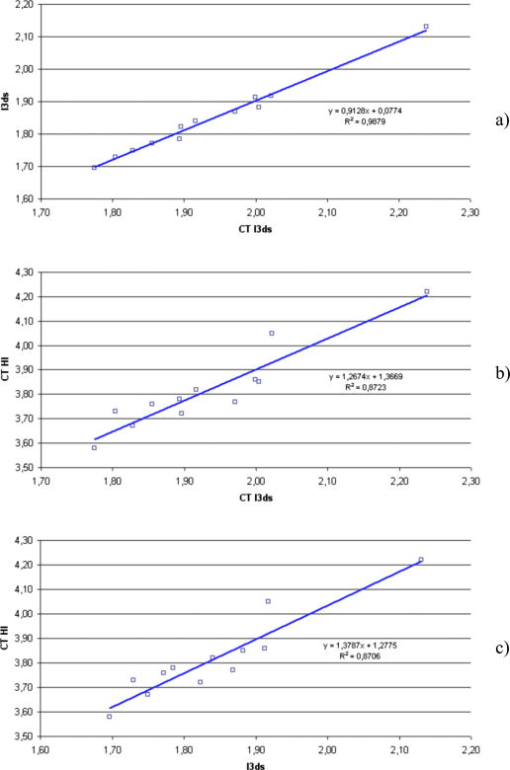
6.1.Correlation between Computed Tomography , , and Computed Tomography Haller IndexNull hypothesis was formulated as a lack of correlation between variables (CT ) and . This correlation was tested with Pearson’s correlation coefficient at the significance level and . A positive correlation between presented variables is present [Fig. 11a ]. Similarly correlations were tested between CT and the Haller index, and also between and the Haller index. For (CT ) and the Haller index, null hypothesis was formulated that no correlation is present. For preconditioned normal distribution of variables, the hypothesis was tested utilizing Pearson’s test of correlation coefficient. The hypothesis was verified at the significance level and Pearsons correlation coefficient . Due to lower value of P- than the significance level, the null hypothesis was rejected. The positive correlation between variables is seen in Fig. 11b. and HI correlations were tested utilizing Pearson’s correlation coefficient. Null hypothesis was set as no correlation was present . Considering the normal distribution of variables, the previously mentioned hypothesis was verified at the significance level. The calculated Pearson’s correlation coefficient was . Since p-value (P- ) is lower than the significance level, null hypothesis was rejected. Positive correlation was confirmed between tested variables, as presented in Fig. 11c. The results of the presented statistical analysis confirm an existing correlation between analyzed variables. 7.ConclusionThe study presents a new method for pectus excavatum severity assessment. The deformity analysis is conducted on a 3-D point cloud representing the surface of a patient’s torso captured with a four-directional measurement system based on a structured light projection built by us. A new 3-D scan index is proposed as a quantitative measure of the deformation. A positive correlation between and the Haller index is confirmed. The presented method utilizes a fully automatic markerless measurement. Also, the developed data processing path does not need any operator’s attention during the analysis process. These two facts make the presented method an objective one. Contrary to CT scanning, during a measurement based on white light projection, a patient is not exposed to harmful radiation, and there are no contraindications to frequent repetitions of the examination. 8.Future WorkIn the near future, we will conduct a clinical validation of the presented method on a larger number of patients, and the Haller index based on CT scans will be evaluated by a larger number of experts to avoid subjective assessment errors. Additionally, adaptation of the method to assess other chest wall anomalies, such as pectus carinatum, spinal curvature, and faulty posture in general, is planned. AcknowledgmentThe project is supported by grant number NR13-0020-04/2008 from the Polish Ministry of Science and Higher Education and statutory activity at the Institute of Micromechanics and Photonics, Warsaw University of Technology. The authors would like to express their gratitude to Dorota Kozioł for the statistical analyses used in this work. ReferencesA. M. Williams and D. C. G. Crabbe,
“Pectus deformities of the anterior chest wall,”
Paed. Resp. Rev., 4 237
–242
(2003). https://doi.org/10.1016/S1526-0542(03)00053-8 Google Scholar
C. S. Chung and N. C. Myrianthopoulos,
“Analysis of epidemiologic factors in congenital malformations,”
Birth Defects Orig Artic Ser., 11
(10), 1
–22
(1975). 0547-6844 Google Scholar
S. W. Daunt, J. H. Cohen, and S. F. Miller,
“Age-related normal ranges for the Haller index in children,”
Pediatr. Radiol., 34 326
–330
(2004). https://doi.org/10.1007/s00247-003-1116-1 0301-0449 Google Scholar
M. J. Cartoski, D. Nuss, M. J. Goretsky, V. K. Proudb, D. P. Croitoru, T. Gustin, K. Mitchell, E. Vasser, R. E. Kelly Jr.,
“Classification of the dysmorphology of pectus excavatum,”
J. Pediatr. Surg., 41 1573
–1581
(2006). https://doi.org/10.1016/j.jpedsurg.2006.05.055 0022-3468 Google Scholar
R. R. Brigato, J. R. Campos, F. B. Jatene, L. F. Moreira, and E. B. Rebeis,
“Pectus excavatum: evaluation of Nuss technique by objective methods,”
Interact. Cardiovasc. Thorac. Surg., 7
(6), 1084
–1088
(2008). https://doi.org/10.1510/icvts.2008.184580 Google Scholar
E. B. Rebeis, J. R. Campos, A. Fernandez, L. F. Moreira, and F. B. Jatene,
“Anthropometric index for pectus excavatum,”
Clinics, 62
(5), 599
–606
(2008). Google Scholar
J. A. Haller, S. S. Kramer, and S. A. Lietman,
“Use of CT scans in selection of patients for pectus excavatum surgery: a preliminary report,”
J. Pediatr. Surg., 22
(10), 904
–906
(1987). https://doi.org/10.1016/S0022-3468(87)80585-7 0022-3468 Google Scholar
J. A. Haller, D. W. Shermeta, J. J. Tepas,
“Correction of pectus excavatum without prostheses or splints: objective measurement of severity and management of asymmetrical deformities,”
Ann. Thorac. Surg., 26 73
–79
(1978). 0003-4975 Google Scholar
E. S. Pretorius, J. A. Haller, and E. K. Fishman,
“Spiral CT with 3D reconstruction in children requiring reoperation for failure of chest wall growth after pectus excavatum surgery. Preliminary observations,”
Clin. Imaging, 22
(2), 108
–116
(1998). https://doi.org/10.1016/S0899-7071(97)00073-9 0899-7071 Google Scholar
H. C. Kim, H. J. Park, S. Y. Ham, K. W. Nam, S. Y. Choi, J. S. Oh, H. Choi, G. S. Jeong, S. W. Park, M. G. Kim, and K. Sun,
“Development of automatized new indices for radiological assessment of chest-wall deformity and its quantitative evaluation,”
Med. Biol. Eng. Comput., 46 815
–823
(2008). https://doi.org/10.1007/s11517-008-0367-2 0140-0118 Google Scholar
M. L. Lawson, M. Barnes-Eley, B. L. Burke, K. Mitchell, M. E. Katz, Ch. L. Dory, S. F. Miller, D. Nuss, D. P. Croitoru, M. J. Goretsky, R. E. Kelly Jr.,
“Reliability of a standardized protocol to calculate cross-sectional chest area and severity indices to evaluate pectus excavatum,”
J. Pediatr. Surg., 41 1219
–1225
(2006). https://doi.org/10.1016/j.jpedsurg.2006.03.003 0022-3468 Google Scholar
S. J. Shochat, J. J. Csongradi, G. E. Hartman, and L. A. Rinsky,
“Moiré phototopography in the evaluation of anterior chest wall deformities,”
J. Pediatr. Surg., 16
(3), 353
–357
(1981). https://doi.org/10.1016/S0022-3468(81)80694-X 0022-3468 Google Scholar
D. Fortin,
“A 3-D visualization tool for the design and customization of spinal braces,”
Comput. Med. Imaging Graph., 31 614
–624
(2007). https://doi.org/10.1016/j.compmedimag.2007.07.006 0895-6111 Google Scholar
R. Sitnik, W. Glinkowski, M. Licau, W. Załuski, D. Kozioł, B. Glinkowska, and A. Górecki,
“Screening telediagnostics of spinal deformities based on optical 3D shape measurement system and automated data analysis—preliminary report,”
241
–245
(2006). Google Scholar
P. Poncet, D. Kravarusic, T. Richart, R. Evison, J. L. Ronsky, A. Alassiri, and D. Sigalet,
“Clinical impact of optical imaging with 3-D reconstruction of torso topography in common anterior chest wall anomalies,”
J. Pediatr. Surg., 42
(5), 898
–903
(2007). https://doi.org/10.1016/j.jpedsurg.2006.12.070 0022-3468 Google Scholar
R. Sitnik, M. Kujawińska, and J. Woźnicki,
“Digital fringe projection system for large-volume shape measurement,”
Opt. Eng., 41
(2), 443
–449
(2002). https://doi.org/10.1117/1.1430422 0091-3286 Google Scholar
|