|
|
1.IntroductionFluorescence diffuse optical tomography (FDOT) is capable of imaging fluorescent structures deep in the tissue, which enables whole-body imaging in small animals.1, 2, 3, 4 The development of noncontact light coupling (delivery and acquisition) and panoramic sampling techniques has greatly improved applicability of FDOT to practical experiments in small animal preclinical applications.5, 6, 7, 8 Free-space FDOT differs from traditional optical fiber-based methods by using a scanning laser, a CCD camera, and a rotation stage, without optical matching fluid. Using this configuration, the inverse problem is typically only moderately underdetermined. It can easily become overdetermined if one desires, as demonstrated in Ref. 9. Nonetheless, even using such a densely sampled data acquisition strategy, the quality of image reconstruction is still fundamentally limited by the highly ill-posed inverse problem due to the optical characteristics of biological tissue. A number of approaches have been reported to reconstruct fluorescence images in three dimensions, most of which use highly simplified geometries to model the forward problem that largely ignore the optical heterogeneity of the animal. For example, an infinite slab is a very frequently used geometry due to its mathematic simplicity, but it typically requires the animals to be immersed in optical matching fluid inside a parallel-plate imaging chamber.9, 10 It has been demonstrated that a priori information, particularly anatomical structures, improves image reconstruction significantly.11, 12, 13 However, the integration of a second imaging modality [typically x-ray computed tomography (CT) or magnetic resonance imaging (MRI)] significantly complicates experimental design for in vivo animal studies. Recently, several alternative methods have been proposed to provide structural information for diffuse optical image reconstruction, such as an all-optical dynamic contrast method for bioluminescence in the mouse, 14 incorporation of atlas structures for diffuse optical tomography (DOT) in the human brain,15 and the application of a spatially encoded light source to reconstruct the 3-D surface of the mouse for bioluminescence imaging16 and of the human breast17 for DOT. Although it has been demonstrated that optical heterogeneity of the medium can be obtained using DOT to assist FDOT reconstruction in the phantom and in the mouse,18, 19, 20, 21 conducting high-resolution DOT in the mouse that reveals anatomical details is challenging, which makes it a debatable choice whether one should use more detailed anatomical structural prior information or use more realistic optical properties measured in situ. In this paper, we demonstrate a hybrid method that incorporates an optically reconstructed surface of the actual animal with a generalized atlas mouse anatomy and use it as the structural priors for reconstruction. This method is a compromise between accuracy in reconstruction and simplicity in experimental design. 2.Methods2.1.Instrumentation2.1.1.FDOT systemThe FDOT system used in this study is based on our optical data acquisition platform described previously in Ref. 22 with slight modifications (Fig. 1 ). The main specifications of the constituents are recapitulated here for completeness. We use a continuous-wave laser diode (HL7851G, Opnext, Tokyo, Japan) housed inside a laser diode mounting module (TCLDM9, Thorlabs, Newton, New Jersey) with an integrated aspheric focusing lens. The mounting module is connected to a temperature controller and a laser diode driver (LDC205C and TED200C, Thorlabs, Newton, New Jersey). We implemented a scanning laser using a galvo scanner, which consists of a pair of perpendicularly positioned galvanometers each equipped with a high-reflectance mirror (6230H, Cambridge Technology, Lexington, Massachusetts) [Fig. 1b]. This galvo scanner directs the laser beam in a raster pattern in small steps and creates a discrete 2-D grid of illumination source positions across the surface of the animal. Fig. 1(a) Experimental setup and schematic drawings of (b) the galvo scanner and (c) the rotation stage: 1, the CCD camera; 2, the lens; 3, the white-light LED; 4, the filter wheel; 5, the rotation stage; 6, the galvo scanner; and 7, the laser diode assembly.  The photodetector is a CCD camera (Imager QE, LaVision, Goettingen, Germany) equipped with a large-aperture lens (AF Nikkor , Nikon, Melville, New York). The cooled CCD chip has an array of ( isotropic pixel size). A filter wheel is mounted in front of the camera, which houses 785- and bandpass interference filters with a passband (CVI Laser, Albuquerque, New Mexico). A white light-emitting diode (LED) light source equipped with a ground glass diffuser (LIU004 and DG20-120, Thorlabs, Newton, New Jersey) is mounted above the camera lens so that the exact surface of the animal can be reconstructed optically (algorithm detailed later). We developed a motorized rotation stage to vertically suspend the animal on the imaging platform [Fig. 1c], which uses two stepper motors to simultaneously rotate the upper and lower torso of the animal to achieve nonobstructed panoramic optical sampling. The stepper motors (Excitron, Boulder, Colorado) have a minimum step size of and an angular position error of . The laser and the camera are arranged in a transillumination configuration. The laser beam impinging the animal surface is from the optical axis of the camera lens to avoid glare (due to scattering and reflections) within the field of view (FOV) of the camera. The activation of the CCD camera, the actuation of the rotation stage and the galvo scanner is controlled using our own LabVIEW program (version 8.5, National Instruments, Austin, Texas) and auxiliary electronic devices. The entire FDOT system was shrouded by light blocking/absorbing material during optical data acquisition. 2.1.2.Micro-CT systemA dual-imaging-chain micro-CT system, consisting of two perpendicularly configured x-ray tube/detector pairs, as previously described in Ref. 23, is used to a acquire anatomical micro-CT data. The system has two Varian A197 x-ray tubes with dual focal spots (0.6 and ). The tubes are designed for angiographic studies with high instantaneous flux and total heat capacity, and are powered by two Epsilon High-Frequency X-ray generators (EMD Technologies, Quebec, Canada). The system has two identical XDI-VHR 2 detectors (Photonic Science, East Sussex, United Kingdom) using phosphor with a pixel size of , an input taper size of , and an image matrix of . Both detectors allow on-chip binning of up to and subarea readout, and subsequently can achieve a temporal resolution as high as . 2.2.Experimental Procedures2.2.1.Animal preparationAll animal studies were approved by the Duke University Institutional Animal Care and Use Committee. Animal experiments were conducted on nude mouse (Nu/Nu, , male) cadavers to limit the complexity of animal support. At before imaging, the animal received an injection of liposomal blood-pool contrast agent24 for micro-CT, delivered via the tail vein with a dose of . Before imaging began, the animal was euthanized by injecting a lethal dose of the mixture of sodium pentobarbital and butorphanol tartrate , after which a glass capillary ( in inner diameter and in length) was inserted into the chest cavity via a midline ventral incision on the neck, leaving approximately of the capillary outside. A fluorescent inclusion in the animal was created by filling this glass capillary with indocyanine green (ICG) solution (in deionized water). Care was taken to ensure that the glass capillary was between the heart and the spine to simulate the worst-case scenario in animal FDOT studies. Sutures were used on the incision to fix the capillary to the skin. After surgery, the animal was vertically positioned in the rotation stage by attaching its fore and hind limbs to the top and bottom bars mounted to the stepper motors, respectively [Fig. 1c]. The angular acceleration and deceleration of the stepper motors were empirically set to ensure smooth rotation without deforming the posture of the animal during the experiment. The ICG solution was prepared while the surgical procedures were being performed on the animal; it was kept in a dark container until the animal was positioned on the rotation stage; and was injected into the glass capillary just before optical data acquisition began. The time interval between solution preparation and the end of fluorescence acquisition is . 2.2.2.Optical data acquisitionIn this study, our region of interest (ROI) was set at the portion of the chest cavity around the heart, in which the fluorescent inclusion is surrounded by the heart, lungs, ribs, and spine. Note that the surgical procedures on the animal did not affect the optical measurement because the incision and the suture were outside the ROI (on the neck), and that we performed dissection on the animal after the experiment and found no blood clog in the chest. The focal plane of the camera was set at the midpoint between the rotation center and the proximal surface (with respect to the camera) of the animal. Panoramic data acquisition was achieved by incrementally rotating the animal . For each acquisition angle, the laser scanned vertically for 5 points spanning , along a line largely centered at the middle of the thoracic vertebrae. For each laser scanning position, the CCD camera was activated to acquire a fluorescence CCD image (with the filter) for an exposure time of . After the galvo scanner completed a scan and resumed its initial state, the animal was turned a small angle by the rotation stage, followed by another round of laser scan and data acquisition. This process was repeated until the phantom returned to its initial angular position. In this study, we used an angular step size of , resulting in a total of 40 acquisition angles. Afterward, the acquisition procedure detailed previously for the fluorescence data was repeated at the excitation wavelength (with the bandpass filter) to acquire the excitation data. Each of the fluorescence and excitation data acquisitions took approximately to finish. The number of detectors is 28 per angle per source position. As a result, the full dataset consists of 200 sources, 1120 detectors, and 5600 fluorescence measurements. To properly model the forward problem, the exact 3-D geometry of the animal surface is necessary. In this study, the surface was obtained using an optical method. After fluorescence and excitation data acquisition, we used the white LED light source to illuminate the animal surface and acquire a reflectance CCD image at each angular position without any filter (camera exposure time ). The last step in optical data acquisition was to calibrate the exact positions of the laser impinging on the animal surface. After the rotation stage was removed for micro-CT imaging, a planar translucent/attenuating calibration target made from Garolite (off the shelf) was placed in the focal plane of the camera lens. The surface of the target facing the camera was marked with evenly spaced horizontal and vertical lines with premeasured distances. The raster pattern of the laser was repeated, while the camera acquired an image at each scanning position, during which a neutral density filter was used to protect the CCD from excessive light. Together with the optically reconstructed animal surface, these optical calibration images were used to localize the exact illumination source positions in the forward model (algorithm described later). 2.2.3.Micro-CT imagingAfter acquiring the optical data, the rotation stage (with the animal still attached) and its peripherals were transported to the nearby x-ray laboratory for micro-CT imaging without disturbing the animal. In this study, only a single imaging chain was used for micro-CT imaging ( , , exposure, and 220 projections over of rotation). A geometric calibration procedure was performed afterward, which enabled computation of the projection matrices required for reconstruction using our lab-developed x-ray calibration phantom.25 A cone-beam reconstruction was applied on the projection images to form a matrix with an isotropic voxel size of . Reconstruction used a Feldkamp algorithm with Parker weighting,26, 27 which was implemented in a commercial software package Cobra EXXIM (EXXIM Computing, Livermore, California). Note that in our lab-developed micro-CT system, we typically use half-scan-angle reconstruction scanning, i.e., an arc of plus the fan angle ( for our system). This is preferred to a full rotation for in vivo studies because the tubes and wires carrying anesthesia gas and physiologic monitoring signals are coupled to the animal vertically from above or bottom and a half scan angle rotation creates less tension to the auxiliaries than a full rotation. Nonetheless, the half scan angle does not affect the image quality in micro-CT reconstruction, because of the specific algorithm used for reconstruction.27 2.3.Data Processing2.3.1.Optical surface reconstructionThe highly diffusive white LED light source is mounted just above the camera lens [shown in Fig. 1a] and is relatively far away from the animal compared to the dimensions of the animal within the camera FOV. As a result, we can consider the white-light CCD images as front-illuminated by a parallel light source. These white-light images are segmented using thresholding and are subsequently converted to binary images. These binary images contain the profiles of the animal at different acquisition angles and are equivalent to the back-illuminated parallel projection images. The relation between a 3-D volume and its 2-D projections is well modeled by the Radon transform.28 For computational efficiency, these binary images were downsampled by a factor of 4 before further processing, resulting in an isotropic in-plane resolution of . Because the rotation center of the animal does not necessarily coincide with the center of camera FOV, each binary image is corrected for its horizontal displacement. Such correction is achieved by comparing each pair of images acquired at the opposite angular positions and finding a displacement so that these two images closest mirror each other in terms of the smallest root mean square (rms) difference. For each horizontal line in this series of corrected binary images, we apply an inverse Radon transform followed by thresholding (at 95% level) to produce a binary 2-D axial slice containing the contour of the animal surface. The 3-D surface contour is obtained by stacking all axial slices ( 3-D isotropic resolution), as shown in Fig. 2 . The source and detector positions relative to the animal surface are also shown in Fig. 2 (marked by the double-arrow near the chest). This optically reconstructed animal surface is the geometrical basis for fluorescence image reconstruction and coregistration with anatomical micro-CT data. Fig. 2The 3-D surface contour of the animal (central) reconstructed from the white-light reflectance images from multiple acquisition angles (peripheral) using an inverse Radon transform. The area marked by a double-arrow on the surface contour represents the source and detector positions (shown as red and blue markers respectively), which define the ROI in reconstruction. (Color online only.) 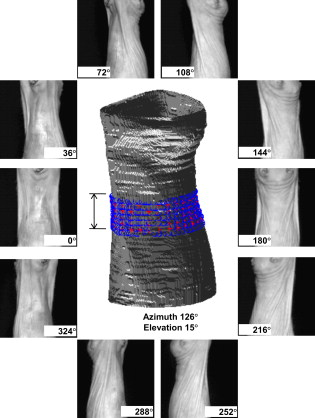 2.3.2.Source/detector localizationWith the 3-D surface contour and the optical calibration images available, the positions of the illumination sources on the animal surface can be computed from the origin and the direction of the impinging laser beam. The laser beam emitted from the laser diode is directed by the first reflector ( scan) and followed by the second reflector ( scan) before it impinges on the animal surface. The origin of the impinging laser beam is therefore located at the center of the scan reflector, and is known from geometrical measurement. The optical calibration images give an accurate position of the laser beam impinging the calibration target, from which the angle of each imaging laser beam is computed. The 3-D positions of the illumination sources are given by the intersection of the impinging lasers with the optically reconstructed animal surface. In this study, we used the FOV of the CCD camera to define the global coordinate system. The length unit of this coordinate system is the spatial resolution of the camera at the calibration target (i.e., in the camera focal plane), which is given by dividing the known grid spacing on the target by the number of voxels between corresponding lines on the grid. In our configuration, the spatial resolution of the CCD camera at its focal plane is (isotropic). Since the CCD is essentially a matrix of photodetectors, one can choose the specific locations on the CCD image as the detector positions after data acquisition. We specified a 2-D array of fixed locations in a CCD image ( points covering an area of horizontally and vertically, respectively) so that the ROI (the chest cavity around the heart) was adequately covered, which was applied to all acquisition angles. These detector positions chosen in the CCD images were mapped onto the animal surface using the same method as in localizing the source positions, except that the origin of the detector vector was set at the center of the surface of the camera lens. The measured fluorescence signal amplitude is the averaged intensity over a cluster of around a detector position, which corresponds to a rectangular area of in the focal plane. 2.3.3.Structural priorsIn this study, we used an atlas mouse anatomy to assist FDOT reconstruction because integration of a second imaging modality, such as CT or MRI, typically significantly increases the complexity of experimental designs for most animal studies. This atlas anatomy was derived from a time-gated high-resolution 4-D MRI data of mice,29 known as MOBY. In this paper, we refer to the anatomical structures derived from this digital atlas, which is a generalized representation of the mouse anatomy, as the MOBY anatomy. The MOBY anatomy has different resolution and orientation from those of our optical imaging. Another difference between the MOBY and the actual anatomy is the posture of the animal during imaging. In the MOBY anatomy, the animal was lying prone, while in our optical imaging, the animal was upright. Nonetheless, comparisons between our micro-CT and the MOBY images show that the differences are mostly in the curvature of the neck and the position of the head, which is out of our ROI. As a result, we take only the MOBY anatomy that contains the chest cavity and model the differences as a rigid coordinate system transformation and anisotropic scaling. Specifically, we first adjusted the orientation of the MOBY anatomy so that its principle axes coincided with those of the optically reconstructed 3-D surface. Second, we manually adjusted the origin of the MOBY anatomy in three dimensions and the scales of its three principle axes iteratively: for the axis (vertical) adjustment, the collarbones and the lower-end ribs in the MOBY anatomy matched the corresponding points in the optical surface, which were inherently registered to the highly visible landmarks in the white-light CCD image; and for the and axes (in the horizontal plane), the relative size of the MOBY anatomy to the optical surface matched that measured in the micro-CT images. Among all structures in the MOBY anatomy, we retained the following as a trade-off between anatomical accuracy and modeling simplicity: the muscle, bone (rib and spine), heart, lung, and liver. We adopted the method detailed in Ref. 30 to compute the absorption and diffusion coefficients of different types of tissue at the excitation and fluorescence wavelengths (785 and ). The specific values of the optical properties are listed in Table 1 . Table 1Optical properties, namely, the absorption coefficient μa , the reduced scattering coefficient μs′ and the index of refraction n , of each type of tissue at the excitation and the fluorescence wavelengths (785 and 830nm , respectively).
To evaluate the improvement of imaging quality as a result of the MOBY anatomy, we also created a homogeneous medium for comparison, which was a replica of the medium with MOBY anatomy, except that all types of tissue were assigned the same optical properties as that of the muscle. 2.3.4.Image reconstructionBecause of the large number of measurement channels, image reconstruction methods based on Monte Carlo simulations cannot be used without significant computing resources.31 And because of the complexity of the mouse anatomy, analytical methods are also not applicable. The finite element method (FEM) can be applied to an arbitrarily complex geometry and has proven to be effective in diffuse optical tomography, e.g., as demonstrated in Refs. 12, 32, 33, 34, 35. Therefore, image reconstruction in this study was carried out using an FEM software package for near-IR fluorescence and spectral tomography, known 36 as NIRFAST, which uses the diffusion equation in the frequency domain as the forward problem solver (modeling light propagation in the medium), and uses a Tikhonov regularization method to iteratively solve the inverse problem (obtaining the fluorescence yield). The Tikhonov regularization parameter is dynamically defined as the ratio of the variances of the measurement and optical properties. In addition, this software package was developed on the scientific programming platform MATLAB (The MathWorks, Natick, Massachusetts), which fits naturally with our existing data processing tools. Because a continuous-wave light source was used in this study, we specified a very low modulation frequency of in NIRFAST. The hybrid geometry of the animal created from the optical surface and the MOBY anatomy was downsampled to a resolution of and converted to a tetrahedral mesh using a MATLAB routine for the 3-D Delaunay triangulation method, which is based on the Quickhull algorithm.37 The mesh contains 10,220 nodes and 57,917 elements within a reconstruction boundary of . Using our lab-developed computer program, fluorescence/excitation signals, source/detector positions, along with the mesh data were subsequently converted from MATLAB internal data structures to formatted text files that could be read by NIRFAST. 2.3.5.Data coregistrationThe reconstruction result from the FDOT data (a 3-D matrix of fluorescence yield) must be coregistered with the anatomical micro-CT images to verify the reconstruction and compute the appropriate figures of merit. Coregistration of the FDOT and CT results was achieved via the optically reconstructed animal surface. The FDOT result from the FEM reconstruction software is represented in a 3-D mesh (tetrahedral grid with variable size), while the CT data are represented in a 3-D matrix (cubic grid with constant size). We took a series of nine axial slices with an interval of along the axis using a built-in interpolation tool of NIRFAST. These slices cover the entire ROI in our FDOT reconstruction, which is dictated by the coverage of the source/detector positions. This series of slices form a 3-D matrix (isotropic in-plane resolution but anisotropic in three dimensions), and will be referred to as the NIRFAST matrix in this paper. Each of these slices was subsequently thresholded at 50% of its maximum value to create a 2-D full width at half maximum (FWHM) plot, and normalized by its in-plane maximum for clearer visualization. These FWHM plots are hereafter referred to as the FWHM matrix. The coregistration of the FWHM matrix and micro-CT images was realized using a visualization software package Amira (version 5.2, Visage Imaging, Berlin, Germany). First, the NIRFAST matrix, which clearly shows the animal surface contour, was registered to the optically reconstructed surface by scaling the and axes of the former. The axis of the NIRFAST matrix was scaled by the inverse of the interslice distance in the micro-CT data. These two data sets match each other almost perfectly because the animal geometry used in reconstruction was based on the optical surface. The slight mismatch was the result of mesh generation and data interpolation. The FWHM matrix was registered to the optical surface using the same scaling parameters. Next, the optical surface was rotated, translated, and scaled to match the animal surface constructed from the micro-CT data. This transformation has of freedom (3 in translation, 2 in rotation, and 1 in scaling) because both data sets have isotropic resolution. The optical surface was matched to the micro-CT surface by manually adjusting the preceding six transformation parameters. The same transformation parameters found in the preceding were applied to the FWHM matrix, which had been registered to the optical surface, to achieve the final coregistration of the fluorescence reconstruction result ( resolution) and the high-resolution anatomical images from micro-CT ( resolution). 3.Results and DiscussionImage reconstruction by NIRFAST took (16 iterations) to meet the stopping criteria (projection error ) on a computer workstation (Precision T7400, Dell Computers, Round Rock, Texas) equipped with two quad-core processors (Xeon, Intel, Santa Clara, California) and of computer memory. Note that only one processor core and up to of memory were used during reconstruction. Coregistration of the optically reconstructed animal surface, the anatomical micro-CT data, and the FDOT reconstruction result is visualized in Fig. 3 . The optical surface (blue) [Fig. 3a] and the micro-CT data (yellow) [Fig. 3b] are registered well to each other, Fig. 3c. In Fig. 3d, the rendered FWHM matrix (appearing between the heart and spine in the chest cavity) shows good localization of the fluorophore with respect to the anatomical micro-CT data. Note that the oblique cylinder (marked by arrows) derived from the micro-CT data extending from neck to the abdomen is the glass capillary that contains the fluorophore. Fig. 3Rendering of (a) the optically reconstructed animal surface and (b) the anatomical micro-CT data show good registration with each other in (c). Using the same parameters of spatial transformation as in (c), the FDOT reconstruction result (the FWHM matrix, shown as red in the online color figure) is registered with the micro-CT data in (d). Also shown in (d) is the internal structures obtained from the micro-CT data, in which the two ends of the glass capillary containing the fluorophore are marked by arrows. 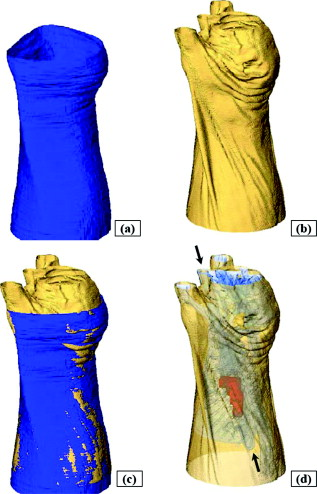 The FDOT result is further shown as the FWHM matrix overlaid onto the micro-CT data that covers the entire volume of our study (left panel of Fig. 4 ). The resolution of the FDOT data is and that of the micro-CT is . The axis increases as one advances from the heart at toward the liver at . The localization of the FDOT data can be judged by noting the alignment of the colored FDOT data with the glass capillary that is clearly displayed in the micro-CT data. The alignment is excellent in the central slices and still quite acceptable in the peripheral slices. The reconstruction result from the homogeneous medium (optically reconstructed surface with homogeneous internal optical properties) is shown in the right panel of Fig. 4, which does not show the fluorescent inclusion correctly. Fig. 4Normalized FDOT result (i.e., the FWHM matrix, shown in color) registered to anatomical micro-CT images within the ROI . In the anatomical images, the bright circle inside the chest cavity is the cross section of the glass capillary containing the fluorophore, which forms the fluorescent inclusion in the animal. The result on the left panel is reconstructed from the MOBY anatomy; that on the right is from the same animal surface but assuming homogeneity internally. 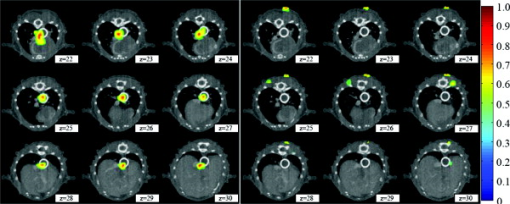 We define a figure of merit as the displacement of the centroid of a reconstructed structure in the FWHM matrix from that of the true fluorescent inclusion derived from the micro-CT data. The mean value of the displacement (i.e., localization error) over all slices is , with a standard deviation of . Another figure of merit is defined as the rms error of the FWHM matrix from the true location of the inclusion in each slice. The values of the rms error in all slices are normalized by their maximum amplitude. The localization error and the normalized rms error are plotted in Fig. 5 using a solid line and a dash-dotted line, respectively. Fig. 5Plots of the normalized maximum in-plane intensity (broken line), the normalized rms error (dash-dotted line), and the localization error (solid line) versus the slice position within the ROI . The dotted lines at the bottom are the ranges of coverage along the axis of the illumination sources and the detectors (shorter and longer lines, respectively), which define the ROI. Note that the image quality close to the central slices is better (smaller rms and localization errors) and gradually degrades as it approaches the boundaries of the ROI. 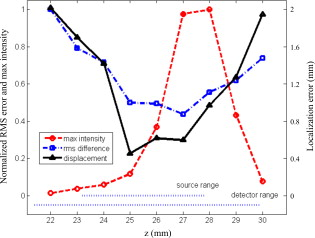 Note that the FWHM matrix is a normalized result of reconstruction. To better demonstrate the relative intensity of the reconstruction in three dimensions, the maximum in-plane amplitude of the reconstruction is also plotted in Fig. 5 (broken line). The dotted lines at the bottom of the figure are the ranges of coverage along the axis of the illumination sources and the detectors (shorter and longer lines, respectively). In conjunction with the coregistered images shown in Fig. 4, we theorize that the reason why the amplitude curve peaks at and is because this is the transitional area from the chest to the abdomen where the blockage of light due to the ribcage, the heart, and the lungs are significantly less compared to that in the chest . Beyond this area , the quick drop-off of the amplitude is contributed to the edge effect of the FOV. In other words, the reduced sensitivity in higher slices is due to highly absorbing and scattering organs within the chest cavity, and the sensitivity reduction in lower slices is because these slices are outside the area of source coverage although still within the detector coverage. The difference in the posture of the animal in prone and upright positions was found to be very small within the ROI by comparing the MOBY atlas anatomy and our experimental micro-CT data, as described previously. Although in principle the internal organs of the animal would have been shifted due to gravity, our hypothesis that such difference was insignificant for FDOT is validated by the reconstruction result, which shows that the fluorescent inclusion can be correctly localized with an error similar to the representative mesh size in reconstruction . Although the method presented here shows promising results, we note that there are limitations that must be addressed. The method discussed in this paper addresses mostly the qualitative aspect of reconstruction in terms of the localization accuracy. Because 3-D FDOT reconstruction is known to be highly nonlinear, depth- and algorithm-dependent, as reported in many studies, at this relatively early stage of methodology developed, we felt that it would be most appropriate to concentrate exclusively on the qualitative aspect of the method and leave the quantitative aspect to follow-up studies. For in vivo experiments, the attainable concentration of ICG is likely to be less than that of the fluorescent inclusion in this study, which would emit lower fluorescence signal and subsequently could result in longer integration time or fewer sampling points. In this case, more accurate optical and structural prior information (e.g., high-resolution in situ optical property mapping) might be necessary for successful reconstruction. The anatomic priors provided by the relatively simple MOBY phantom clearly aid the reconstruction. But those priors are not equivalent to the more detailed anatomy that the micro-CT can provide. At this point, the challenge is both algorithmic and computational. Larger and more detailed arrays should enable significantly improved reconstruction. But major computational resources will be required. The heterogeneous reconstruction result from a homogeneous fluorescent inclusion indicates that imaging artifacts exist. These too may well be addressed by additional computational resources enabling more extensive sampling and improved reconstruction algorithms. Further investigation on the causes and solutions is underway toward better reconstruction quality for quantitative imaging. 4.ConclusionsWe presented a method that can accurately localize a fluorescent inclusion deep in the chest cavity of a mouse in a free-space fluorescent imaging configuration. The reconstruction result registers well to the actual location and dimensions of the fluorescent inclusion revealed by micro-CT data. Compared with other reconstruction methods, the proposed method has two advantages. It uses a generalized atlas mouse anatomy to assist reconstruction and thus extends its application to the case where other anatomical imaging modalities, such as CT or MRI, are difficult or impossible to apply. The relatively simple model provides priors that can be accommodated with modest computational power. In this study, we confined our ROI within the chest due to computation efficiency considerations. In principle, this method can be applied to the entire torso of the animal as long as appropriate atlas is available. The second advantage is that the main resources used by this method (the MOBY anatomy and NIRFAST software package) are freely available to the public and thus make this method accessible to virtually any interested researcher. The work is a step toward a longer term goal where the simultaneous acquisition of optical data and accurate micro-CT data as priors in live animals will permit significant improvement in the spatial resolution for optical molecular imaging. Improvements are currently under way in both the hardware and algorithms. AcknowledgmentsThis study was funded by the National Institutes of Health/National Center for Research Resource (NIH/NCRR) Grant No. P41 RR005959 and National Cancer Institute (NCI) Small Animal Imaging Resource Program (SAIRP) Grant No. U24 CA092656. The authors are grateful to Yi Qi and Boma Fubara for their support in animal procedures, to Professor Laurence Hedlund for his assistance with the Institutional Animal Care and Use Committee (IACUC), and to Sally Zimney for her assistance in editing. The authors also would like to thank Professor Hamid Dehghani from the School of Computer Science, University of Birmingham, United Kingdom, for his help in using the NIRFAST software package. ReferencesA. P. Gibson, J. C. Hebden, and S. R. Arridge,
“Recent advances in diffuse optical imaging,”
Phys. Med. Biol., 50
(4), R1
–43
(2005). https://doi.org/10.1088/0031-9155/50/4/R01 0031-9155 Google Scholar
D. S. Kepshire, S. C. Davis, H. Dehghani, K. D. Paulsen, and B. W. Pogue,
“Subsurface diffuse optical tomography can localize absorber and fluorescent objects but recovered image sensitivity is nonlinear with depth,”
Appl. Opt., 46
(10), 1669
–1678
(2007). https://doi.org/10.1364/AO.46.001669 0003-6935 Google Scholar
A. B. Milstein, J. J. Stott, S. Oh, D. A. Boas, R. P. Millane, C. A. Bouman, and K. J. Webb,
“Fluorescence optical diffusion tomography using multiple-frequency data,”
J. Opt. Soc. Am. A, 21
(6), 1035
–1049
(2004). https://doi.org/10.1364/JOSAA.21.001035 0740-3232 Google Scholar
D. C. Comsa, T. J. Farrell, and M. S. Patterson,
“Quantitative fluorescence imaging of point-like sources in small animals,”
Phys. Med. Biol., 53
(20), 5797
–5814
(2008). https://doi.org/10.1088/0031-9155/53/20/016 0031-9155 Google Scholar
V. Ntziachristos, C. H. Tung, C. Bremer, and R. Weissleder,
“Fluorescence molecular tomography resolves protease activity in vivo,”
Nat. Med., 8
(7), 757
–760
(2002). https://doi.org/10.1038/nm729 1078-8956 Google Scholar
V. Ntziachristos, J. Ripoll, L. V. Wang, and R. Weissleder,
“Looking and listening to light: the evolution of whole-body photonic imaging,”
Nat. Biotechnol., 23
(3), 313
–320
(2005). https://doi.org/10.1038/nbt1074 1087-0156 Google Scholar
A. Garofalakis, G. Zacharakis, H. Meyer, E. N. Economou, C. Mamalaki, J. Papamatheakis, D. Kioussis, V. Ntziachristos, and J. Ripoll,
“Three-dimensional in vivo imaging of green fluorescent protein-expressing T cells in mice with noncontact fluorescence molecular tomography,”
Mol. Imaging, 6
(2), 96
–107
(2007). 1535-3508 Google Scholar
L. Herve, A. Koenig, A. Da Silva, M. Berger, J. Boutet, J. M. Dinten, P. Peltie, and P. Rizo,
“Noncontact fluorescence diffuse optical tomography of heterogeneous media,”
Appl. Opt., 46
(22), 4896
–4906
(2007). https://doi.org/10.1364/AO.46.004896 0003-6935 Google Scholar
E. E. Graves, J. Ripoll, R. Weissleder, and V. Ntziachristos,
“A submillimeter resolution fluorescence molecular imaging system for small animal imaging,”
Med. Phys., 30
(5), 901
–911
(2003). https://doi.org/10.1118/1.1568977 0094-2405 Google Scholar
S. Patwardhan, S. Bloch, S. Achilefu, and J. Culver,
“Time-dependent whole-body fluorescence tomography of probe bio-distributions in mice,”
Opt. Express, 13
(7), 2564
–2577
(2005). https://doi.org/10.1364/OPEX.13.002564 1094-4087 Google Scholar
L. Zhou, B. Yazici, and V. Ntziachristos,
“Fluorescence molecular-tomography reconstruction with a priori anatomical information,”
Proc. SPIE, 6868 68680O
(2008). https://doi.org/10.1117/12.763269 0277-786X Google Scholar
S. Srinivasan, B. W. Pogue, S. Davis, and F. Leblond,
“Improved quantification of fluorescence in 3-D in a realistic mouse phantom,”
Proc. SPIE, 6434 64340S
(2007). https://doi.org/10.1117/12.698636 0277-786X Google Scholar
D. E. Sosnovik, M. Nahrendorf, N. Deliolanis, M. Novikov, E. Aikawa, L. Josephson, A. Rosenzweig, R. Weissleder, and V. Ntziachristos,
“Fluorescence tomography and magnetic resonance imaging of myocardial macrophage infiltration in infarcted myocardium in vivo,”
Circulation, 115
(11), 1384
–1391
(2007). https://doi.org/10.1161/CIRCULATIONAHA.106.663351 0009-7322 Google Scholar
E. M. Hillman and A. Moore,
“All-optical anatomical co-registration for molecular imaging of small animals using dynamic contrast,”
Nature Photon., 1
(9), 526
–530
(2007). https://doi.org/10.1038/nphoton.2007.146 1749-4885 Google Scholar
A. Custo,
“Purely optical tomography: atlas-based reconstruction of brain activation,”
Massachusetts Institute of Technology,
(2008). Google Scholar
C. Kuo, O. Coquoz, T. L. Troy, H. Xu, and B. W. Rice,
“Three-dimensional reconstruction of in vivo bioluminescent sources based on multispectral imaging,”
J. Biomed. Opt., 12
(2), 024007
(2007). https://doi.org/10.1117/1.2717898 1083-3668 Google Scholar
H. Dehghani, M. M. Doyley, B. W. Pogue, S. Jiang, J. Geng, and K. D. Paulsen,
“Breast deformation modelling for image reconstruction in near infrared optical tomography,”
Phys. Med. Biol., 49
(7), 1131
–1145
(2004). https://doi.org/10.1088/0031-9155/49/7/004 0031-9155 Google Scholar
S. C. Davis, H. Dehghani, J. Wang, S. Jiang, B. W. Pogue, and K. D. Paulsen,
“Image-guided diffuse optical fluorescence tomography implemented with Laplacian-type regularization,”
Opt. Express, 15
(7), 4066
–4082
(2007). https://doi.org/10.1364/OE.15.004066 1094-4087 Google Scholar
Y. Tan and H. Jiang,
“DOT guided fluorescence molecular tomography of arbitrarily shaped objects,”
Med. Phys., 35
(12), 5703
–5707
(2008). https://doi.org/10.1118/1.3020594 0094-2405 Google Scholar
Y. Lin, H. Yan, O. Nalcioglu, and G. Gulsen,
“Quantitative fluorescence tomography with functional and structural a priori information,”
Appl. Opt., 48
(7), 1328
–1336
(2009). https://doi.org/10.1364/AO.48.001328 0003-6935 Google Scholar
A. Koenig, L. Herve, V. Josserand, M. Berger, J. Boutet, A. Da Silva, J. M. Dinten, P. Peltie, J. L. Coll, and P. Rizo,
“In vivo mice lung tumor follow-up with fluorescence diffuse optical tomography,”
J. Biomed. Opt., 13
(1), 011008
(2008). https://doi.org/10.1117/1.2884505 1083-3668 Google Scholar
X. Zhang, C. Badea, M. Jacob, and G. A. Johnson,
“Development of a noncontact 3-D fluorescence tomography system for small animal in vivo imaging,”
Proc. SPIE, 7191 71910D
(2009). https://doi.org/10.1117/12.808199 0277-786X Google Scholar
C. Badea, S. Johnston, B. Johnson, M. De Lin, L. W. Hedlund, and G. A. Johnson,
“A dual micro-CT system for small animal imaging,”
Proc. SPIE, 6913 691342
(2008). https://doi.org/10.1117/12.772303 0277-786X Google Scholar
S. Mukundan, K. Ghaghada, C. Badea, L. Hedlund, G. Johnson, J. Provenzale, R. Bellamkonda, and A. Annapragada,
“A nanoscale, liposomal contrast agent for preclincal microCT imaging of the mouse,”
Am. J. Roentgenol., 186
(2), 300
–307
(2006). https://doi.org/10.2214/AJR.05.0523 0092-5381 Google Scholar
S. Johnston, G. A. Johnson, and C. T. Badea,
“Geometric calibration for a dual tube/detector micro-CT system,”
Med. Phys., 35
(5), 1820
–1829
(2008). https://doi.org/10.1118/1.2900000 0094-2405 Google Scholar
L. A. Feldkamp, L. C. Davis, and J. W. Kress,
“Practical cone-beam algorithm,”
J. Opt. Soc. Am., 1
(6), 612
–619
(1984). https://doi.org/10.1364/JOSAA.1.000612 0030-3941 Google Scholar
D. L. Parker,
“Optimal short scan convolution reconstruction for fan beam CT,”
Med. Phys., 9
(2), 254
–257
(1982). https://doi.org/10.1118/1.595078 0094-2405 Google Scholar
A. C. Kak and M. Slaney, Principles of Computerized Tomographic Imaging,
(1988) Google Scholar
W. P. Segars, B. M. W. Tsui, E. C. Frey, G. A. Johnson, and S. S. Berr,
“Development of a 4-D digital mouse phantom for molecular imaging research,”
Mol. Imaging Biol., 6
(3), 149
–159
(2004). https://doi.org/10.1016/j.mibio.2004.03.002 1536-1632 Google Scholar
G. Alexandrakis, F. R. Rannou, and A. F. Chatziioannou,
“Tomographic bioluminescence imaging by use of a combined optical-PET (OPET) system: a computer simulation feasibility study,”
Phys. Med. Biol., 50
(17), 4225
–4241
(2005). https://doi.org/10.1088/0031-9155/50/17/021 0031-9155 Google Scholar
X. Zhang and C. Badea,
“Effects of sampling strategy on image quality in noncontact panoramic fluorescence diffuse optical tomography for small animal imaging,”
Opt. Express, 17
(7), 5125
–5138
(2009). https://doi.org/10.1364/OE.17.005125 1094-4087 Google Scholar
H. Jiang,
“Frequency-domain fluorescent diffusion tomography: a finite-element-based algorithm and simulations,”
Appl. Opt., 37
(22), 5337
–5343
(1998). https://doi.org/10.1364/AO.37.005337 0003-6935 Google Scholar
A. Joshi, W. Bangerth, K. Hwang, J. C. Rasmussen, and E. M. Sevick-Muraca,
“Fully adaptive FEM based fluorescence optical tomography from time-dependent measurements with area illumination and detection,”
Med. Phys., 33
(5), 1299
–1310
(2006). https://doi.org/10.1118/1.2190330 0094-2405 Google Scholar
S. R. Arridge, M. Schweiger, M. Hiraoka, and D. T. Delpy,
“A finite element approach for modeling photon transport in tissue,”
Med. Phys., 20
(2), 299
–309
(1993). https://doi.org/10.1118/1.597069 0094-2405 Google Scholar
H. Dehghani, B. W. Pogue, S. P. Poplack, and K. D. Paulsen,
“Multiwavelength three-dimensional near-infrared tomography of the breast: initial simulation, phantom, and clinical results,”
Appl. Opt., 42
(1), 135
–145
(2003). https://doi.org/10.1364/AO.42.000135 0003-6935 Google Scholar
H. Dehghani, M. E. Eames, P. K. Yalavarthy, S. C. Davis, S. Srinivasan, C. M. Carpenter, B. W. Pogue, and K. D. Paulsen,
“Near infrared optical tomography using NIRFAST: algorithms for numerical model and image reconstruction algorithms,”
Commun. Numer. Methods Eng., 25
(6), 711
–732
(2009). https://doi.org/10.1002/cnm.1162 1069-8299 Google Scholar
C. B. Barber, D. P. Dobkin, and H. T. Huhdanpaa,
“The quickhull algorithm for convex hulls,”
ACM Trans. Math. Softw., 22
(4), 469
–483
(1996). https://doi.org/10.1145/235815.235821 0098-3500 Google Scholar
|
||||||||||||||||||||||||||||||||||||||||


