|
|
1.IntroductionExisting clinical technologies used to characterize patient blood such as impedance counters and flow cytometers, though very effective in terms of throughput, offer limited information, are expensive, bulky, costly to maintain, and often require careful calibration. Though there have been reports of using high throughput cytometers to characterize red cell morphology,1 this approach is limited, as it only provides a general description of shape (e.g., ellipsoid versus spherical) and is unable to provide the resolution required for aiding in differential diagnosis. Automated counters are thus designed to produce accurate measurements of normal blood and to alert the technician with “flags” when numerical abnormalities exist, so that a smear can then be prepared and examined.2 Even though automated blood analyzers have reduced the number of samples that require smears to 15%, the examination of a smear is still an indispensible tool in providing differential diagnosis (commonly for anemias and thrombocytopenia), recommending further tests, speedy diagnosis of certain infections, and the identification of leukemia and lymphoma.3 Despite the ability of the automated instruments to measure volume and hemoglobin concentrations, they are unable to accurately measure morphologic abnormalities and variations in shape at the single cell level, and thus a pathologist is required to manually examine a smear. Other modern methods that can be used for accurately assessing red cell morphology, such as confocal microscopy, suffer from complicated procedures and the need for using specialized exogenous contrast agents. We employ an optical interferometry technique, diffraction phase cytometry (DPC), which is also designed to produce accurate measurements of normal blood, and in addition is capable of characterizing specific morphological abnormalities in diseased blood. The simplicity and versatility of the DPC technique have been previously demonstrated by combining it with CD-ROM technology for characterizing red blood cells (RBCs).4 By giving access to detailed 2-D and 3-D morphological parameters such as volume, surface area, sphericity, diameter, etc., DPC provides new information that is currently unavailable from commercial instruments. It is known that the distributions of these parameters and correlations between them reveal physiologically important information about a given blood sample.5 For example, the minimum cylindrical diameter (MCD) can be used to predict the minimum capillary diameter that a given cell can squeeze through.6 We present a comparison between the abilities of the DPC system and a state of the art clinical impedance counter to measure and characterize RBCs. It is shown that after taking the mean cell hemoglobin concentration (MCHC) into account, the DPC data correlates very well with the impedance counter. The advantages of using the DPC are also illustrated by an analysis of the volume and sphericity distributions obtained from two patients. DPC also has the advantage that it can be easily implemented as an add-on modality to a microscope without adding any additional preparatory steps to the laboratory workflow. The results shown here are from measurements on whole blood samples. This further illustrates the flexibility of the technology, as it can be applied to both perpherial blood smears or to samples stored according to clinical protocols. Considering the agreement with current techniques and the detailed morphological information provided by the DPC, it could prove to be both a powerful diagnostic tool and a way to improve blood testing efficiency by reducing the number of cases that require a manual smear analysis. 2.Materials and MethodsWhole blood is drawn from patients at a local community hospital via venepuncture by a certified phlebotamist and is stored in EDTA coated containers at room temperature. A complete blood count analysis (CBC) is then performed on each sample with the Coulter LH50 (Beckman-Coulter) impedance counter used for routine analysis in the hematology laboratory at the hospital. Each sample is marked with a unique identifier, and all unique personal patient information (name, identification number, etc.) is removed in compliance with HIPPA regulations and the University of Illinois Internal Review Board to maintain patient confidentiality. The whole blood is then diluted with the same Coulter LH series diluent (Beckman-Coulter) used by the impedance counter for a final concentration of 0.2% whole blood in solution. This concentration was chosen because it provides an adequate cell count for comparison with the CBC while being low enough to provide sufficient distribution of the cells, which is necessary for proper analysis, given the large variations in patient hematocrit. Following dilution, the sample is pipetted into a -tall chamber, which is made in-house by punching a hole in double-sided Scotch tape and sticking one side of the tape to a coverslip. After the sample is introduced to the chamber, it is sealed using another coverslip. This sealed chamber technique reduces the mechanical stress imposed on the cells during sample preparation, offers precise control over the sample volume, prevents drying, and reduces cell translation. The samples are measured after being sealed to allow them to settle to the bottom of the chamber and to reach a steady state in the solution. The DPC setup utilized in this experiment uses a diffraction phase microscope7, 8 as its core platform. In short, the DPC setup is a common path interferometer, in which a diffraction grating located at the image plane of a microscope is used to generate diffraction orders, each containing full spatial and phase information of the sample. The zero-order or undeviated beam is then spatially low pass filtered using a pinhole in the Fourier plane so that it can be used as a reference beam. The diffraction order is used as the sample beam, and all the other orders are blocked. A second lens is then introduced to project the interferogram onto the charge-coupled device (CCD) plane for recording. The phase map of the sample is retrieved from a single CCD exposure by applying a spatial Hilbert transform.9 For each sample, 1600, interferograms are recorded, which cover a total area of . A total of is required to scan this area at a rate of . The analysis of the phase images is carried out in MATLAB (The Mathworks 2008, Natick, Massachusetts) using a cell detection and analysis software developed in-house. To find the cells in each image, a standard particle detection algorithm is used.10 Once the pixels occupied by individual cells are identified, we can proceed to quantify the 2-D and 3-D morphological parameters of each cell. The 2-D parameters such as diameter, projected area, and circularity are easily obtained using region property descriptors available in MATLAB. To obtain physiologically relevant and accurate 3-D parameters from the retrieved phase map, we translate it to a height map using an index of refraction calculated based on the mean cell hemoglobin concentration of each sample, as measured by the impedance analyzer. Due to the linear dependence on the protein concentration,11 the refractive index can be calculated as: , where is the refractive increment of hemoglobin and MCHC is the concentration of dry protein expressed in g/dL. The phase map is then translated to a height map using the contrast in refractive index (Δn) between the cells and surrounding media, where is the wavelength of the illumination and . Once the height information is retrieved, the volume of each cell is calculated by integrating the height map over the projected area as . The surface area of individual cells is determined using Monge parameterization,12 where the area of each pixel element is calculated aswhere and are the width and height of each pixel, and and are the gradients along the and directions, respectively. The surface area of each cell is then the sum of all the area elements and the projected area, assuming the cell is sitting flat on the coverslip. Knowing the surface area and volume, we can calculate parameters such as sphericity and minimum cylindrical diameter (MCD). The sphericity of RBCs was first determined as an important parameter by Canham and Burton.5 It is defined as the ratio between the surface area (SA) of a sphere with the same volume as the cell, to the actual surface area of the cell, with values ranging from 0 (for a laminar disk) to 1 for a perfect sphere, and is calculated as . The MCD, also introduced by Canham and Burton, is a theoretical parameter that predicts the smallest capillary diameter that a given RBC can squeeze through. The MCD is obtained by solving the following polynomial equation that defines the cell volume: .Overall, for each cell imaged we obtain the following 16 parameters: perimeter, projected area, circular diameter, surface area, volume, sphericity, eccentricity, minimum, maximum, and mean height, minimum, cylindrical diameter, circularity, integrated density, kurtosis, skewness, and variance. Thus, it is possible to identify and characterize abnormal cells that would otherwise be difficult or impossible to detect manually in a smear. This type of analysis could be utilized for early detection of diseases, infections, and abnormalities such as poikliocytosis2 and malarial infection,13 or for detection of reactions to treatments such as chemotherapy and bone marrow transplants.14 If manual analysis of the abnormality is still necessary to confirm the diagnosis, a physician may simply examine the cell images that have been labeled as abnormal by the DPC system, rather than manually scanning a smear in search of abnormalities. Given the wealth of information available about each cell, it is possible to study the distributions of and correlations between parameters to establish the parameters expected from a normal sample and to characterize various abnormalities. 3.ResultsIn this study, samples from 32 patients were analyzed using both a clinical Coulter impedance counter and the DPC system; with the DPC system we analyzed an average of 828 cells per sample. We show that there is high correlation between the CBC and DPC data, and provide examples of the advantages associated with our interferometric, image-based cytometry technique. To evaluate the consistency of the DPC analysis with that of the Coulter counter, we compared the mean corpuscular volumes (MCV) obtained by both methods (Fig. 1 ). Initially the data was analyzed assuming a constant refractive index contrast for all samples, which resulted in a weak correlation (Pearson correlation coefficient, ) between the DPC and CBC volume data (“×” symbols in Fig. 1). However, once the MCHC values are taken into account and the refractive index contrast is corrected according to Eq. (1), the correlation improves to (triangular symbols in Fig. 1). Fig. 1MCV values measured by DPC versus impedance counter (CBC). The DPC data is shown before the correction for the refractive index (raw) and after refractive index correction (corrected). Pearson correlation coefficients for both datasets are shown in the legend. The straight line, included for comparison, represents the CBC MCV values. 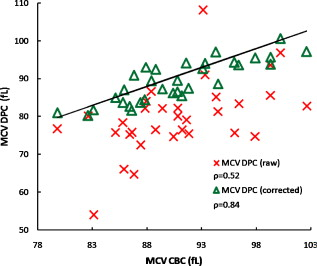 The MCHC is currently used by pathologists to help diagnose abnormalities such as anisochromasia (large variation in MCHC) and spherocytosis (high MCHC).3 However, with current automated counters a pathologist has to manually examine a smear to confirm diagnosis of spherocytosis or any other morphological abnormalities that would result in an abnormal MCHC distribution. With the current DPC system, it is possible to provide this diagnosis directly using the spherecity index. Figure 2 is an example of a sphericity distribution obtained from a -old female patient exhibiting anisocytosis (diagnosed by a large variation in MCV). By examining cell images along the sphericity distribution, the capabilities of the DPC to differentiate between flat and spherical cells are made clear. If a larger spherocytic subpopulation were to exist in this patient, it would appear as a secondary maximum in the distribution, or could be identified by a positive shift in the sample’s mean sphericity value. Fig. 2Comparison of cells across the sphericity distribution for a -old female patient exhibiting anisocytosis. i through iv show examples of cells at the different sphericity values as follows: i. 0.50, ii. 0.54, iii. 0.57, iv. 0.61, v. 0.65 and vi. 0.72. 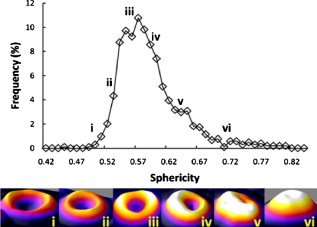 An important advantage of DPC as an emerging technology is that it recovers all metrics that are familiar and intuitive to pathologists, such as the MCV. One disorder that is fairly common and easy to diagnose using the MCV is anisocytosis, which is characterized by large variations in the cell volumes and quantified by the red cell distribution width (RDW). Figure 3 shows volume distributions from two patients, one normal and one exhibiting anisocytosis. Again we show images of cells across the distribution to illustrate the information available about each cell. Fig. 3Comparison of volume distributions of a patient exhibiting anisocytosis versus a normal patient. The DPC measures red cell distribution width (RDW) values of 12.65 and 16.28 for the normal and abnormal patient, respectively. More subpopulations are apparent in the patient with anisocytosis. i through iv show examples of cells at the different volume peaks as follows: i. , ii. , iii. , iv. , v. , and vi. . 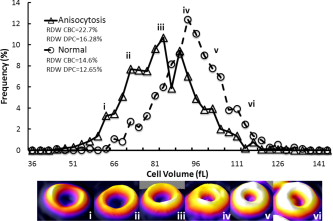 This type of analysis enables the DPC system to accurately identify the morphological abnormalities that are responsible for the anisocytosis. Since anisocytosis could be a result of a variety of disorders such as thalassemia (decreased globin synthesis) and myelodisplastic syndrome (preleukimia),3 more detailed information on the cause will aid in a quick and early automatic diagnosis of these conditions. 4.Discussion and ConclusionsWe have demonstrated the ability of the DPC system to operate as an automatic blood analyzer, which recovers the parameters provided by current clinical instruments. We showed that the additional set of parameters measured by DPC offers insight into the nature of the numerical abnormalities used to identify morphological disorders. Using this type of analysis can aid in an automatic diagnosis of conditions that currently require manual smear analysis. Even though the current DPC system has lower throughput and speed than state of the art impedance counters, these are practical issues that can be overcome due to the rapid advances in automated image acquisition and processing technologies. The strong dependence of our results on the cell hemoglobin content indicates that an accurate measurement of individual cell protein content needs to be made. A previous method entails measuring the cells in two solutions with different refractive indices.15 Though this decoupling method is an effective way to calculate the refractive index, it may be impractical in a clinical setting due to throughput considerations and because exposing the cells to different solutions may affect their properties. It has recently been shown that DPC can directly measure single cell hemoglobin concentration by either utilizing a broadband source16 or by performing DPM at different wavelengths.17 Both of this techniques rely on the dispersion properties of hemoglobin to infer the protein concentration. These new methods free the DPC from relying on any external measurements and thus greatly add to both its practical application in a clinic and its power in aiding differential diagnosis. In conclusion, DPC offers a powerful new blood screening utility that can be used to aid in making differential diagnosis by an experienced pathologist. DPC can be simply added on as a modality to any existing microscope, and no special sample preparation is necessary to integrate it into the clinical workflow. Furthermore, the outputs of DPC are intuitive morphological characteristics, such as sphericity and skenewss, meaning that no new specialized knowledge is necessary to take advantage of DPC. Advancements in spectroscopic phase measurements, image processing, and computing power will continue to augment the abilities of DPC, while maintaining its position as a low cost, high throughput, and highly sensitive instrument. AcknowledgmentsThis research was supported in part by the National Science Foundation (CAREER 08-46660) and the Grainger Foundation. ReferencesM. Piagnerelli,
K. Z. Boudjeltia,
D. Brohee,
A. Vereerstraeten,
P. Piro,
J. L. Vincent, and
M. Vanhaeverbeek,
“Assessment of erythrocyte shape by flow cytometry techniques,”
J. Clin. Pathol., 60 549
–554
(2007). https://doi.org/10.1136/jcp.2006.037523 0021-9746 Google Scholar
B. J. Bain, Blood Cells A Practical Guide, Blackwell Science, London
(2002). Google Scholar
B. J. Bain,
“Diagnosis from the blood smear,”
New England J. Med., 353 489
–507
(2005). https://doi.org/10.1056/NEJMra043442 Google Scholar
M. Mir,
Z. Wang,
K. Tangella, and
G. Popescu,
“Diffraction phase cytometry: blood on a CD-ROM,”
Opt. Express, 17 2579
–2585
(2009). https://doi.org/10.1364/OE.17.002579 1094-4087 Google Scholar
P. B. Canham and
A. C. Burton,
“Distribution of size and shape in populations of normal human red cells,”
Circ. Res., 22 405
–422
(1968). 0009-7330 Google Scholar
P. B. Canham,
“Difference in geometry of young and old human erythrocytes explained by a filtering mechanism,”
Circ. Res., 25 39
–45
(1696). 0009-7330 Google Scholar
G. Popescu,
T. Ikeda,
R. R. Dasari, and
M. S. Feld,
“Diffraction phase microscopy forquantifying cell structure and dynamics,”
Opt. Lett., 31 775
–777
(2006). https://doi.org/10.1364/OL.31.000775 0146-9592 Google Scholar
H. Ding,
Z. Wang,
F. Nguyen,
S. A. Boppart, and
G. Popescu,
“Fourier transform light scattering of inhomogeneous and dynamic structures,”
PRL, 101 238102
–238104
(2008). https://doi.org/10.1103/PhysRevLett.101.238102 Google Scholar
T. Ikeda,
G. Popescu,
R. R. Dasari, and
M. S. Feld,
“Hilbert phase microscopy for investigatingfast dynamics in transparent systems,”
Opt. Lett., 30 1165
–1167
(2005). https://doi.org/10.1364/OL.30.001165 0146-9592 Google Scholar
R. C. Gonzalez,
R. E. Woods, and
S. L. Eddins, Digital Image Processing Using MATLAB, Pearson Prentice Hall, Englewood Cliffs, NJ
(2004). Google Scholar
G. Popescu,
Y. Park,
N. Lue,
C. Best-Popescu,
L. Deflores,
R. R. Dasari,
M. S. Feld, and
K. Badizadegan,
“Optical imaging of cell mass and growth dynamics,”
Am. J. Physiol.: Cell Physiol., 295 C538
–C544
(2008). https://doi.org/10.1152/ajpcell.00121.2008 0363-6143 Google Scholar
S. A. Safran, Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, Addison-Wesley, New York
(1994). Google Scholar
Y. K. Park,
M. Diez-Silva,
G. Popescu,
G. Lykorafitis,
W. Choi,
M. S. Feld, and
S. Suresh,
“Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum,”
Proc. Natl. Acad. Sci., 105 13730
–13735
(2008). Google Scholar
G. d’Onofrio,
R. Chirillo,
G. Zini,
G. Caenaro,
M. Tommasi, and
G. Micciulli,
“Simultaneous measurement of reticulocyte and red blood cell indices in healthy subjects and patients with microcytic and macrocytic anemia,”
Blood, 85 818
–823
(1995). 0006-4971 Google Scholar
B. Rappaz,
A. Barbul,
Y. Emery,
R. Korenstein,
C. Depeursinge,
J. M. Pierre, and
P. Marquet,
“Comparative study of human erythrocytes by digital holographic microscopy, confocal microscopy, and impedance volume/Analyzer,”
Cytometry, Part A, 73A 895
–903
(2008). https://doi.org/10.1002/cyto.a.20605 1552-4922 Google Scholar
H. Ding and
G. Popescu,
“Instantaneous spatial light interference microscopy,”
Opt. Express, 18 1569
–1575
(2010). https://doi.org/10.1364/OE.18.001569 1094-4087 Google Scholar
Y. K. Park,
T. Yamauchi,
W. Choi,
R. Dasari, and
M. S. Feld,
“Spectroscopy phase microscopy for quantifying hemoglobin concentrations in intact red blood cells,”
Opt. Lett., 34 3668
–3670
(2009). https://doi.org/10.1364/OL.34.003668 0146-9592 Google Scholar
|

