|
|
1.IntroductionIn previous research, we investigated the pharmacokinetic relationship of forearm tissue alcohol concentration relative to breath, venous, and capillary blood. 1, 2 That work showed a first order kinetic model used by other researchers to explain alcohol pharmacokinetics between arterial and venous blood 3, 4, 5, 6 also reasonably explained the pharmacokinetic differences between forearm tissue and blood alcohol concentrations. However, the kinetic constants associated with the forearm tissue measurement were smaller in magnitude (a larger pharmacokinetic difference) than those observed when comparing blood types to each other. Clearly, a noninvasive tissue measurement that exhibits improved pharmacokinetic agreement with venous blood alcohol would be advantageous as it is the gold standard in the majority of alcohol testing applications. Glucose monitoring is an active area of research where site-dependent pharmacokinetic differences have been observed. This “alternate site” phenomenon has been investigated by many researchers 7, 8, 9, 10, 11 and refers to sites other than the finger tip (the current standard of care) where capillary blood or interstitial fluid can be obtained for the glucose assay. Several clinical studies have shown that finger and forearm glucose concentrations can exhibit significant concentration differences over time. Coincidentally, first order pharmacokinetic models similar to those in alcohol research have been used to quantify these concentration differences. 12, 13 These works generally indicate that finger capillary blood glucose concentration “leads” the concentrations measured at other sites, such as the forearm, in a pharmacokinetic sense. The alternate-site phenomenon observed for glucose suggests that a finger measurement site could also exhibit improved agreement with blood concentration relative to a forearm measurement for other analytes such as alcohol. Consequently, the objective of the present work is to investigate a noninvasive finger tissue alcohol measurement and compare it to contemporaneously measured forearm tissue, breath, and venous alcohol concentrations in a controlled drinking study. This work, to our knowledge, provides the first investigation of the relationships between breath alcohol, venous blood alcohol, and interstitial tissue alcohol concentration measured at multiple skin sites. 2.Methods2.1.Clinical Study DescriptionAlcohol excursions were induced in 26 subjects (demographics shown in Table 1) at Lovelace Scientific Resources (Albuquerque, New Mexico) following overnight fasts in order to compare finger and forearm tissue alcohol concentrations to venous blood and breath alcohol concentrations. Written consent was obtained from each participant following explanation of the Institutional Review Board-approved protocols (Quorum Review). Baseline venous blood, breath, and noninvasive tissue alcohol measurements were taken upon arrival in order to verify zero initial alcohol concentration in all subjects. Table 1Study participant demographics.
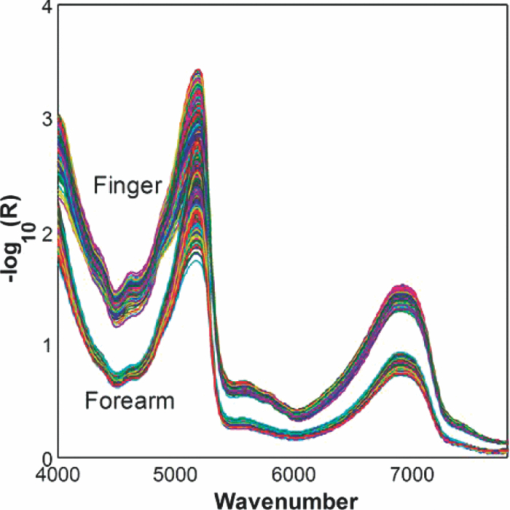
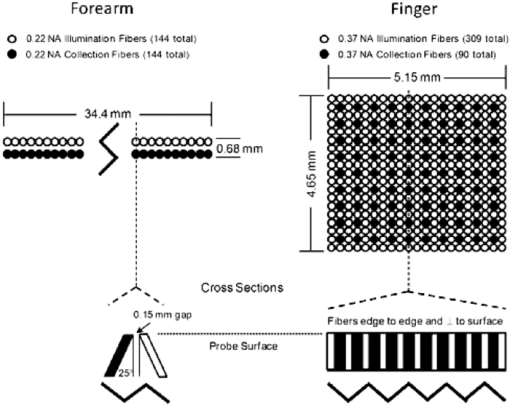
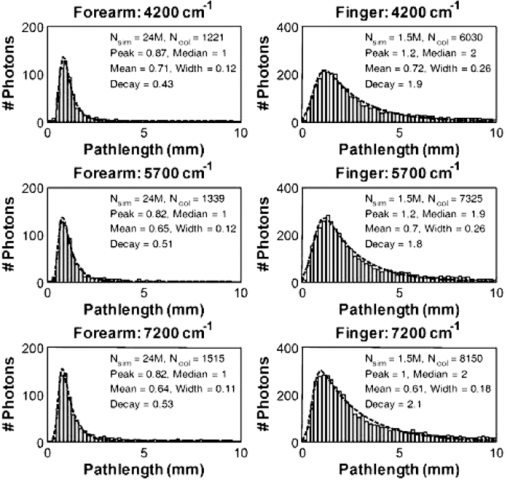
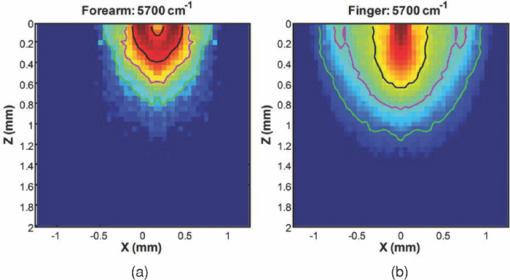
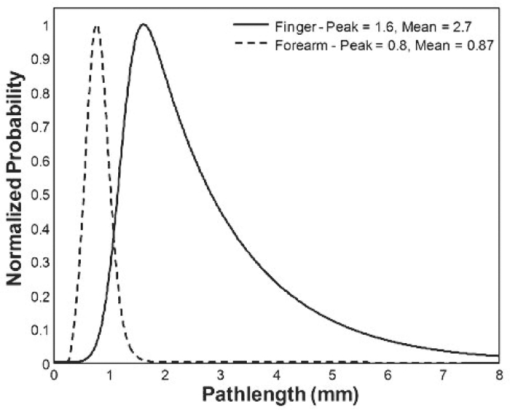
The alcohol dose for all subjects was ingested orally with a target peak blood alcohol concentration of 120 mg/dL (0.12%). The mass of the alcohol dose was calculated for each subject using an estimate of total body water based upon gender and body mass.14 An alcohol dose limit of 110 g was imposed to prevent overdosing obese subjects whose weight tended to overestimate their total body water. The alcohol doses were mixed 50% by volume with orange juice to ease consumption. Upon ingestion of the alcohol dose, repeated cycles of breath, venous blood, and tissue alcohol measurements were acquired (∼20 min/cycle) from each subject until his or her blood alcohol concentration reached its peak and then declined to <20 mg/dL (0.02%). Under these conditions, the average excursion lasted ∼7 h and yielded ∼14 sets (minimum of 9 and maximum of 20) of tissue, blood, and breath alcohol measurements per subject. A total of 360 sets of measurements were acquired from the 26 subjects. 2.2.Blood Sample Acquisition and Alcohol AssaysA catheter was inserted into the right median cubital vein of each subject and was used to collect venous blood samples into gray top vacuettes containing sodium fluoride and potassium oxalate. Alcohol assays were performed on the blood samples using headspace gas chromatography (GC) analysis performed at the S.E.D. Toxicology Laboratory (Albuquerque, New Maxico). The blood assay used an Agilent 5890 II gas chromatograph with a flame ionization detector, an Agilent 3396 integrator, and a Tekmar 7000 headspace autosampler. The GC employed a Supelco 1% SP-1000 active phase on a 60/80 carbopack substrate for the separation of the analytes. The instrument was calibrated using a 50-mg/dL ethanol calibration standard (Cerilliant, Round Rock, Texas part E-029) and verified using negative, low, and high controls (Cliniqa Diagnostics, Kuala Lampur, Malaysia). 100.0 μL of n-propanol was added as an internal standard and ethanol selectivity was verified using a mixed standard of methanol, ethanol, acetone, and isopropanol. The sample volume was 100 μL for all samples. 2.3.Breath Sample Acquisition and Alcohol AssayBreath alcohol concentrations were used in this work as an alternative means for investigating the arterial blood space (acquisition of arterial blood carries greater risk to the subject due to the greater arterial blood pressure). Several studies have shown that breath alcohol closely tracks the arterial blood space. 15, 16, 17 A factory-calibrated Drager Alcotest 6510 was used to acquire all breath alcohol measurements. A new mouthpiece was used for each subject (part no. A6510). As breath testers measure the alcohol concentration present in the breath, a multiplicative conversion factor referred to as the blood-breath ratio (BBR) must be applied that relates the much lower breath alcohol concentration to blood alcohol concentration. Although the blood-breath ratio is known to vary between people (1981–2833),18 in the United States it is mandated to be 2100 for evidentiary breath alcohol measurements. However, studies have shown that a value of 2400 better represents the average BBR across a broad subject population. 18, 19 Because the objective of this work is to compare tissue alcohol concentration to the concentrations in blood, the recorded breath alcohol values (with implicit 2100 BBR) were converted to concentrations corresponding to a BBR of 2400 in order to better represent the arterial blood space. 2.4.Spectroscopic Tissue MeasurementsAnatomically, human skin is comprised of epidermal, dermal, and subcutaneous layers, each of which has different properties that influence their relative utility for noninvasive alcohol measurements. The epidermis has very little extracellular fluid, and therefore contains minimal information about hydrophilic analytes such as alcohol. The subcutaneous layer is largely comprised of lipids that have low water (and consequently alcohol) solubility which make it poorly suited to alcohol measurements. However, the dermal layer has high water content and an extensive capillary bed conducive to the transport of alcohol, which makes it the important layer of skin tissue for alcohol measurements. The tissue alcohol measurement employs near-infrared (NIR) spectroscopy (4000–8000 cm−1), which is of interest for noninvasive alcohol measurements because it offers specificity for a number of analytes, including alcohol and other organic molecules, while allowing optical path-lengths of several millimeters through tissue and thus allowing penetration into the dermal tissue layer, where alcohol is present in the interstitial fluid. 20, 21, 22 The skin at the finger (posterior surface of the index finger at the medial phalange) and volar forearm measurement sites exhibit the same layered structure and general analyte composition. However, the layer thicknesses and specific analyte concentrations are likely different. This, combined with the smaller physical size of the finger measurement location, necessitated distinct optical probe designs. Consequently, two tissue alcohol devices were included in the clinical study: one for the forearm site and one for the finger site. The forearm device was identical in design to the device reported in previous works. 1, 2 The only fundamental difference between the finger and forearm devices was the optical probe design (discussed in Sec. 2.5). The source and interferometer designs, spectral resolution (32 cm−1), scan speed (0.8 cm/s), spectral processing, and measurement time (2 min) were all identical. The only requirement of the tissue measurements was passive contact between the skin of the subject and the tissue optical probe during the 2-min period. The stability of the spectroscopic devices was verified at 10 min intervals throughout the study using spectroscopically and environmentally inert reflectance samples placed in contact with the optical probes between subject measurements. The forearm and finger tissue spectra acquired from the study are shown in Fig. 1. Examination of Fig. 1 indicates that the measurements from finger site exhibit more spectral variation than those from the forearm site. The larger spectral variation of the finger is likely a combination of physiological (increased variability of finger tissue structure and analyte concentrations) and spectroscopic (the finger measurement exhibits a longer mean path) effects. However, given that the wavelength-dependent coefficients of variation of each data-set are comparable (not shown), it is likely that the majority of the increased variance is due to the finger measurement's intrinsically larger path-length. The origins of the difference in path-length as well as a quantitative assessment are examined in subsequent sections. 2.5.Tissue Optical Probe DesignsThe designs of the fiber optic based tissue optical probes were the only difference between the forearm and finger devices. Although there are substantial differences in the geometric arrangement of the optical fibers at the tissue surface (discussed later), the optical probe designs do have several common design features. First, both optical probes used optical fibers comprised of fused silica core and cladding in order to avoid the signal loss and absorption features associated with plastic clad fibers in the NIR. Second, each design was based on distinct illumination and collection fibers. One set of optical fibers delivered near-infrared radiation from the source to the skin/probe surface and a separate set of optical fibers collected diffusely reflected radiation and delivered it to the interferometer. Both optical probe designs terminated the illumination and collection fiber bundles with circular hex-pack configurations. 2.5.1.Forearm optical probe designThe forearm optical probe design is identical to the design used in prior tissue alcohol measurement characterizations 1, 2 and was comprised of two linear rows (1 illumination row and 1 collection row) of 144, 0.22NA fibers (±12 deg in air). Because of the limited angular acceptance of the 0.22 NA fibers, the two rows were angled towards each other at 25 deg from normal to the probe surface in order to increase throughput. A consequence of the inclination angle is the expectation of reduced photon penetration depth and overall path lengths through the tissue when compared to fibers normal to the tissue-probe surface. The illumination and collection rows were separated by 150 microns in order to prevent collection of a significant number of specular photons (photons that reflect off the skin surface without penetrating into it). See Fig. 2 for a schematic of the skin/probe surface of the forearm optical probe. 2.5.2.Finger optical probe designThe forearm optical probe was not suitable for measuring the finger site due to the 34.4-mm linear arrangement of optical fibers. Consequently, an optical probe was developed that was consistent with the smaller physical size of the finger site. The finger optical probe design was a 21×19 array of 0.37 NA optical fibers (399 total, 309 illumination, and 90 collection). The wider angular acceptance of the 0.37 NA fibers (±21.7 deg in air) enabled the fibers to be perpendicular to the probe surface and packed edge to edge within the array. The illumination and collection fibers were arranged such that each collection fiber was surrounded by eight illumination fibers (see Fig. 2). The experimental data were imported into Matlab 7.5, which was used to perform all analyses and generate the results presented in subsequent sections. 3.Results and DiscussionAlthough the ultimate objective of the present work is to investigate the finger and forearm tissue alcohol concentrations and compare them to contemporaneous breath and blood alcohol measurements, the influence of different optical probe designs on the measured spectra is an important consideration that warrants investigation. Because optical probe design in part determines spectral figures of merit such as effective path-length and signal-to-noise ratio (SNR), it is expected that the optical probe will directly contribute to the quality of any subsequent analyte measurements. Consequently, the results and discussion is divided into two parts: investigation of the influence of the optical probe designs on the tissue spectra, and the determination of finger and forearm tissue alcohol concentration and quantitative comparison to breath and blood alcohol. 3.1.Influence of Optical Probe Design on Tissue SpectraThe influence of the optical probe design on the effective path-length and SNR will be examined using a two-pronged strategy. First, optical modeling using Monte-Carlo simulations will be used to investigate the differences in photon propagation associated with the finger and forearm optical probe designs. Second, effective path-length and SNR estimates will be obtained directly from the experimentally acquired tissue measurements. 3.2.Monte Carlo simulationsIn past works, we used Monte-Carlo simulations to estimate the wavenumber-dependent effective path-length [l eff, Eq. 1] through tissue of a given optical probe design. 1, 23, 24 Similarly, Monte Carlo simulations were used in this work to provide insights into the differences in effective path-length between the two optical probe designs under investigation. The effective path-length is defined as: Eq. 1[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} l_{\rm eff} ({{\rm {\nu}}}) = \frac{{\sum_{i = 1}^N {l_i e^{ - \mu _{\rm a} ({\rm \nu})l_i} } }}{{\sum_{i = 1}^N {e^{ - \mu _{\rm a} ({\rm \nu})l_i } } }} \end{equation}\end{document}The Monte-Carlo simulation traced photon propagation at three wavelengths (4200, 5700, and 7200 cm−1) through a model of human skin to determine l i for a large number of photons (1.5–24 million per wavelength per probe) introduced to the skin surface with a spatial and angular distribution consistent with the location, angle, and numerical aperture of the illumination optical fibers. The skin tissue model was a semi-infinite, homogeneous bulk-scattering medium. The scattering coefficient varied with wavenumber (9.2, 10.8, and 11.8 mm−1 at 4200, 5700, and 7200 cm−1, respectively). A Henyey-Greenstein scattering phase function with an anisotropy (g) of 0.9 was assumed at all wavelengths. 25, 26, 27 The cumulative trajectory of each photon (e.g., the location of scattering events within the tissue model and the associated incoming and outgoing vectors of photon travel) was stored in a database. On the basis of the optical probe design, the database of photon trajectories was filtered to include only the photons that exhibited trajectories leaving the skin tissue model at a location and angle consistent with the acceptance of the probe's collection fibers. Each of the remaining N photons had an associated l i corresponding to the cumulative distance travelled through the tissue model. The path-length distribution (PLD) is the distribution of l i at a given wavelength. Figure 3 shows histograms of l i for the collected photons (forearm probe in the left column and the finger probe in the right column) and exponentially weighted Gauss-ian fits of the histograms (dashed lines) with their associated statistics. As anticipated, for a fixed set of tissue optical properties, the PLDs of the finger optical probe are shifted toward substantially longer paths than those of the forearm. This behavior is in part due to the perpendicular orientation of the finger probe's illumination and collection optical fibers, in part to the fact that a single illumination fiber contributes signal to multiple collection fibers, and in part to the larger numerical aperture of the finger sampler's fibers. Furthermore, although the scattering coefficient varied as a function of wavenumber in a manner consistent with literature values, 25, 26, 27 the exponentially weighted Gaussian distribution parameters (mean, width, decay, etc.) do not appear to vary strongly with wavenumber. The most apparent wavelength-dependent effect observed in the simulation results was an increase in the number of photons collected as a function of wavelength wavenumber (N col), which is consistent with expectations (more photons are scattered back to the tissue surface as the scattering coefficient increases). As can be seen from Eq. 1, the contribution of each photon to the effective path-length is exponentially weighted by μ a at the wavelength of interest. Thus, photons that travel short path-lengths through tissue have an exponentially larger influence on the effective path-length due to their larger contrbution to the integrated signal. Figure 4 provides a pictorial representation of this effect using the PLDs obtained from the 5700 cm−1 forearm and finger simulations and a μ a of 0.45 mm−1 (the absorptivity of 8 × 104 mg/dL of water). The color scale indicates the relative contribution of photons passing through a given voxel to the total detected signal, and the black, magenta, and green contours bound the volumes cotributing to the first 50, 75, and 90% of the signal. As expected, the finger sampler interrogates tissue regions that are approximately 200–300 μm deeper than the forearm sampler. The greater width of the region probed by the finger sampler arises from the larger range of source-receiver separations inherent in the sampler's design. These two factors combine to yield the longer and more variable pathlenths for the finger sampler reflected in Fig. 3. 3.3.Experimental estimates of effective pathlengthUsing the information obtained from the Monte Carlo simulations, a means for estimating the effective pathlength directly from the experimentally acquired NIR spectra was examined. Nonlinear regression was used to estimate the effective path-length versus wavenumber of each measured tissue spectrum by minimizing the function in the following: Eq. 2[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm rms}_{{\rm Fit}} = \sqrt {\frac{{\sum {[ - \log (R) - (\mu _{\rm a} l_{{\rm eff}} + B_\nu)]} ^2 }}{{n_\nu }}} \end{equation}\end{document}For the purposes of this work, it was assumed that μ a could be reasonably described by Eq. 3[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \mu _{\rm a} = c_{{\rm water}} \mu _{{\rm water}} + c_{{\rm collagen}} \mu _{{\rm collagen}} \end{equation}\end{document}Examination of Eq. 1 shows that knowledge of the distribution of pathlengths for the collected photons is required to determine l eff. On the basis of the results of the Monte Carlo simulations, this work assumed that an exponentially weighted Gaussian distribution reasonably approximated the underlying distribution of path-lengths at each wavelength. In aggregate, six parameters were varied in order to determine the estimated tissue spectrum that minimized the root-mean square (rms) error in Eq. 2. The six parameters were c water (and therefore c collagen due to the concentration restriction), the slope and offset of the linear baseline, and the exponentially weighted Gaussian distribution mean, width, and decay. As the Monte Carlo simulations suggested the absence of strong wavelength dependence on the distribution parameters, they were constant for all wavelengths for a given spectrum in order to minimize the number of regression parameters. The nonlinear regression was performed for each measured tissue spectrum (360 from the finger device and 360 from the forearm). The resulting rmsFit across the 360 finger and 360 forearm measurements were 0.019 ± 0.002 AU (2 SD) and 0.030±0.003 AU (2 SD), respectively. Table 2 shows a summary of the regression parameters that were obtained from the finger and forearm path-length estimations. Figure 5 shows the average exponentially weighted Gaussian PLD's obtained from the finger and forearm measurements. Comparison of Figs. 3 and 5 shows that both the Monte Carlo simulations and the experimental PLD estimates exhibit a similar forearm and finger relationship. (forearm peak: MC – 0.85 mm, Exp – 0.8; finger peak: MC – 1.2 mm, Exp – 1.6 mm). Table 2Summary of effective path regression parameters (Mean ± 2SD).
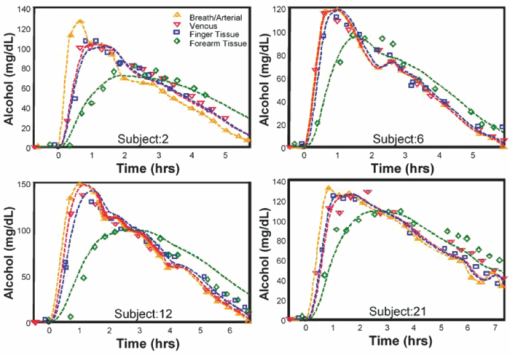
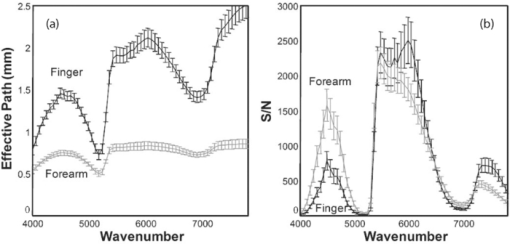
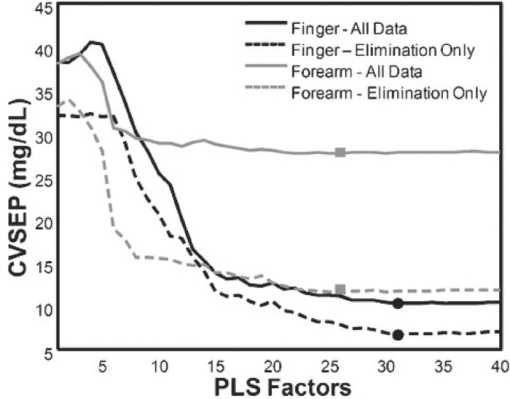
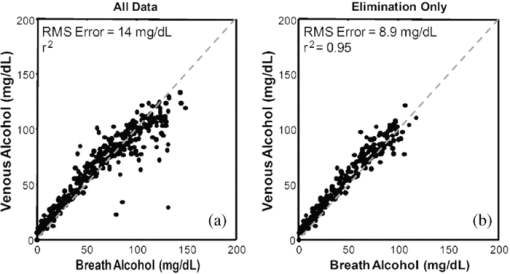
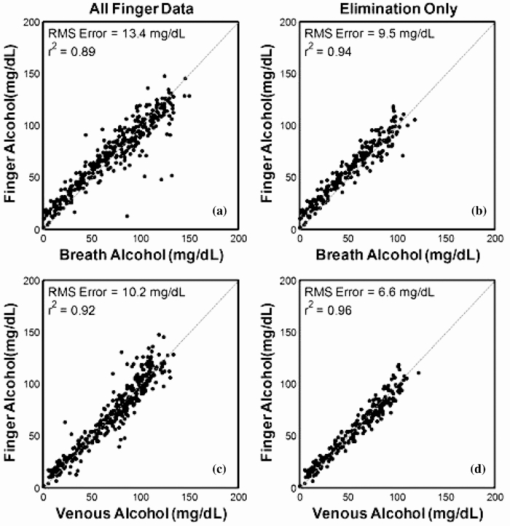
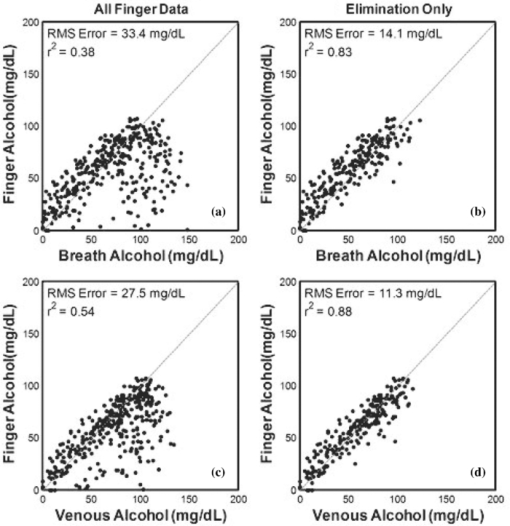
It is worthy to note that although the mean estimated forearm collagen concentration of this work (16,844±3,726 mg/dL) is somewhat higher than the mean of those obtained from 53 patients using a forearm punch biopsy (11,541±11,238 mg/dL),28 all of the estimated collagen concentrations fall within the range exhibited by the biopsied patients. Furthermore, although research quantitatively comparing collagen concentration at different skin sites is limited, there is some qualitative evidence that the larger average collagen concentration at the finger relative to the forearm was anticipated by prior research.29 The solid lines in Fig. 6A show the average effective path-length (l eff) versus wavenumber for the finger and forearm optical probes and the bars represent the associated standard deviation of the effective path-length across the corresponding 360 measurements. The simulation results suggested that the perpendicular illumination and collection of the finger probe results in a longer overall effective pathlength relative to the inclined fiber arrangement of the forearm probe. The experimental PLD's and effective pathlength estimates support this conclusion as the finger PLD's are shifted towards longer pathlengths and the overall effective pathlengths as a function of wavenumber are approximately twice as long relative to their forearm counter-parts. 3.4.Experimental estimates of signal-to-noise ratioThe interferometers of both devices acquired scans at a rate of ∼8/s. As a result, ∼1000 scans were collected for each tissue measurement which allows estimation of the SNR of the two devices. Although detector efficiency and source intensity differences are likely present between the systems despite their common design, for the purposes of this work the differences in SNR were assumed to be dominated by the probe designs and skin sites. The single scan signal to rms noise ratio of each measurement was determined using equation 4. Eq. 4[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \frac{S}{N} = \frac{{\bar X}}{{\sqrt {[\sum ({X_d - \bar X_d)]^2 } /2(n - 1)} }} \end{equation}\end{document}Because tissue is not a static sample, physical contact with the optical probe initiates physiological changes that result in spectral time trends. These time trends would inflate the rms noise estimate if left unaccounted. Consequently, Eq. 4 is slightly different from standard formulas for computing the signal to rms noise. The row-wise difference of X has the effect of suppressing (but not eliminating) the contribution of the time trends to the rms noise estimate. However, it also inflates the variance of all sources of white noise by a factor of 2 which necessitates its correction in the rms calculation. Equation 4 was applied to each set of scans obtained from the clinical study (360 sets for each of the finger and forearm devices). Figure 6B shows the average (solid lines) and standard deviations (bars) of the rms SNR for the finger and forearm measurements. The difference in the finger and forearm SNR in Fig. 6B is the result of two competing influences of the probe designs. As the finger probe exhibits longer effective pathlengths relative to the forearm probe, it must therefore collect a smaller fraction of the photons incident to the tissue. However, in terms of the SNR, this reduction is partially offset by the finger probe's larger ratio of illumination to collection fibers (8:1 in the finger probe). Consequently, the finger probe's larger number of higher NA illumination fibers results in an increase in the amount of NIR radiation delivered to the tissue relative to the forearm probe. The net result, despite some wavenumber-dependent differences between the two systems, is that the finger probe exhibits a similar SNR as the forearm probe. The critical distinction is that the finger probe achieves that SNR with a significantly longer pathlength through the skin which can be a significant advantage in absorbance measurements. 3.5.Analysis of Breath, Blood, and Tissue Alcohol MeasurementsBoth the Monte Carlo simulations and experimental effective path-length estimates indicate that significant differences exist between the spectra measured at the two sites. These differences are largely attributed to the optical probe designs and site-dependent skin optical properties. However, in addition to the observed spectroscopic differences, the two measurement locations could also exhibit site-dependent pharmacokinetics. The purpose of the remainder of this work is to examine the spectroscopic and pharmacokinetic effects of the optical probes and measurement sites on in vivo ethanol concentration. 3.6.Tissue Alcohol MeasurementsFor the purposes of the clinical study in this work, the baseline NIR measurements acquired prior to the alcohol excursions were used to “enroll” their associated subjects on each of the two tissue measurement devices. Enrollment was achieved by subtracting each subject's baseline spectrum (with known zero alcohol concentration) from the remaining tissue spectra acquired during his/her alcohol excursion experiment. The subtraction of the enrollment spectrum removes major spectral attributes that are unique to each subject while retaining any analyte variation within the subjects that occurs over the course of the experiment (e.g., changes in ethanol concentration). Similar methods for in vivo spectroscopy have been previously described. 1, 2, 24, 30 Prior works have indicated that the pharmacokinetic differences between blood and tissue alcohol concentrations can be pronounced during the initial period following the ingestion of the alcohol dose (termed the absorption phase) relative to the descending portion of the alcohol experiment (termed the elimination phase). 1, 2, 23, 24 As a result, inclusion of tissue spectra and associated blood references from the absorption phase in the calibration regression is perilous as they are likely to contain significant reference error. In order to mitigate this risk, the data from each device were divided into two sets: “elimination only” for inclusion in the regression and a validation set containing all data (absorption and elimination). An initial cross-validation was performed for each of the finger and forearm elimination data to screen for calibration outliers. This was done in “subject-out” fashion, meaning that all spectra from 1 of the 26 subjects were held out during each of the 26 resulting cross-validation iterations. Akaike's Information Criterion31 was used to select the optimum number of calibration factors. Egregious concentration outliers (studentized residuals > 4) were removed from the elimination data sets. The remaining elimination data (246 finger and 250 forearm measurements) formed the final “calibration” set for subsequent cross-validations. A second subject-out cross-validation was then performed for each of the finger and forearm data sets. Within each subject-out iteration, the remaining data in the elimination set were used to form the regression (with the held-out subject removed) and predictions were obtained for all data from the held-out subject (absorption and elimination, no outliers removed) in the validation set. In this fashion, predictions were obtained for all spectroscopic measurements while preventing the reference error corrupted absorption phase measurements from deleteriously influencing the regressions. Figure 7 shows the cross validated standard error of prediction (CVSEP) curves for the full finger and forearm validation sets (solid lines) as well as the elimination phase only sets (dashed lines). As anticipated from prior studies, the significant improvement in cross-validated error observed for both the finger and forearm is indicative that concentration differences are significantly larger during the absorption phase of each subject (the difference in the solid and dashed lines of the same gray level in Fig. 7). A similar phenomenon is also observed when comparing breath and venous alcohol concentrations (Fig. 8). Figures 8A, 8B show comparisons of the breath alcohol and venous blood alcohol concentrations acquired during the study. Examination of Figure 8A indicates that there are several measurements where the difference between breath and venous blood alcohol concentration is large with the majority of disparate pairs generally having a breath concentration that is larger than the venous blood concentration. Because breath alcohol is related to arterial alcohol, these differences are indicative that concentration gradients also exist between the arterial and venous blood spaces during periods of rapid change in alcohol concentration. However, once the alcohol has been absorbed into the blood stream, the compartments tend to equilibrate and concentration differences become smaller (but not zero). This is evidenced by Fig. 8B which shows the subset of data from Fig. 8A, which corresponds to the elimination portion of each subjects excursion experiment. All the points that exhibited large concentration differences in Fig. 8A are absent from Fig. 8B, which reinforces that the large concentration differences primarily manifest during the absorption phase of the alcohol excursions. Figures 9 and 10 similar “all” and “elimination-only” comparisons for the finger and forearm, respectively. In all cases, the elimination-only rms errors are significantly lower than their all data counterparts. However, the forearm results (Fig. 10) exhibit a much more dramatic change in rms error, similar to that shown in Fig. 7. Relative to the comparisons of the other compartments in Figs. 8 and 9, a larger number of forearm tissue alcohol concentrations are significantly lower than their contemporaneous blood and breath measurements. This suggests the forearm rises more slowly over time and significantly “lags” the blood, breath, and finger compartments. This phenomenon has been observed in past alcohol efforts as well as in the measurement of other analytes such as glucose at different skin locations. 7, 8, 9, 10, 11 An alternative view of the observed concentration differences is depicted in Figs. 11A, 11B which shows the rms error by hour from consumption relative to breath Fig. 11A and venous blood Fig. 11B. Both windows show that the measurements immediately following consumption exhibit the largest error, which is indicative of a larger pharmacokinetic difference between compartments that is induced by the rapid consumption of the alcohol dose. The forearm tissue alcohol measurement is clearly different from the other three compartments because it exhibits significantly larger rms concentration differences at all times in both windows. Fig. 11rms error relative to (a) breath alcohol and (b) venous alcohol by hour from the alcohol dose. 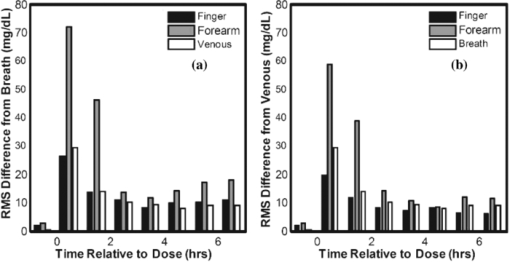 Interestingly, during the absorption phase (the first hour or two post dose), the finger tissue measurement exhibits a lower rms difference from both breath [black bars in Fig. 11A] and venous alcohol [black bars in Fig. 11B] when compared to the rms difference between venous and breath alcohol [white bars in Figs. 11A, 11B]. As pharmacokinetic differences between compartments are more pronounced during the absorption phase, this suggests that the finger tissue measurement lies somewhere between the arterial and venous compartments in a pharmacokinetic sense. 3.7.Quantification of Pharmacokinetic DifferencesThe comparisons of the blood, breath, and tissue alcohol measurements indicate that concentration gradients exist between compartments over time. As such, a means for quantifying pharmacokinetic differences is desirable in order to estimate the relative contributions of the assay methods and pharmacokinetics to the observed concentration differences. The concentration differences between blood types have been previously examined using compartmental analysis and a first order kinetic model [Eq. 5] to explain the equilibration of alcohol between compartments. 1, 2, 3, 4, 5, 6 Eq. 5[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \frac{{dC_2 }}{{dt}} = k_{12} (C_1 - C_2) \end{equation}\end{document}Pharmacokinetic rate constants were estimated for the venous and tissue compartments relative to the arterial (breath) compartment for each subject using the experimentally measured alcohol concentrations and Eq. 5. The rate constant estimation was performed using the same procedure as in previous work. 1, 2 For each pair of compartments the subscript 12 was replaced by a subscript denoting the corresponding compartments with Art, Ven, Fin, and For, for arterial (breath), venous, finger tissue, and forearm tissue, respectively. For example, k Art-Ven is the rate constant where C 1 is the arterial compartment and C 2 is the venous compartment. Figure 12 shows exemplary k Art-Ven, k Art-Fin, and k Art-For estimates from four subjects. The symbols in Fig. 12 represent the experimentally measured alcohol concentrations. With the exception of the orange dashed lines which are cubic interpolations of the breath experimental data, the colored dashed lines are the estimated concentrations of the venous, finger tissue, and forearm tissue determined by integration of Eq. 5 at the final solution of the nonlinear regression. Table 3 summarizes the rate constant estimates obtained in this work. Each entry in Table 3 was generated from 26 rate constant estimates (one from each of the 26 study participants). Furthermore, in prior work the underlying distribution of each set of estimates was determined to be lognormal at 95% confidence.2 Consequently, the parameterization in Table 3 reflects the lognormal distribution of the rate constant estimates. Table 3Summary of pharmacokinetic parameters.
Table 3 also shows the rms concentration difference between compartments from the experimental data (rmsexp), the rms concentration difference between the experimental breath (arterial) concentrations and the estimated concentrations determined by integration of Eq. 5 at the final solutions of the nonlinear regressions (rmsFit), the residual rms concentration difference (rmsRes = √(rmsexp 2 – rmsFit 2)), and the percent of the concentration variance explained by the first-order kinetic model. The percent variance explained was calculated using Eq. 6 and indicates the percentage of the concentration variance between the experimentally measured alcohol concentrations that is attributable to the pharmacokinetic differences between the compartments: Eq. 6[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \% \sigma _{\exp }^2 = 100\left(\frac{\sum(\hat{C}_2 - C_1)^2 /n}{{\sum {({C_2 - C_1 })^2 /n} }}\right) \end{equation}\end{document}Examination of Table 3 shows that a significant fraction of the concentration variance of all compartment combinations is attributable to alcohol pharmacokinetics. The residual rms concentrations shown in Table 3 are comprised of the accuracy and precision associated with the assay methods of the two compartments and residual pharmacokinetic error (the first order model is unlikely to be perfect). Although the residual rms concentrations cannot be easily decomposed into individual terms, the fact they are comparable for the tested pairs of compartments could suggest that the accuracy and precision of the assay methods are similar in magnitude. It is important to note that as no gold standard assay technique exists for tissue alcohol concentration, experimental efforts to estimate the accuracy and precision of the noninvasive tissue measurement will always be clouded by pharmacokinetics when either breath or blood alcohol is used as the reference method. 4.Conclusions and Future DirectionsThrough both simulation and experimental measurements, tissue optical probe design was shown to be a significant contributor to the effective path length and signal-to-noise ratios of the NIR spectra obtained from forearm and finger skin tissue during a 26-patient clinical study. The finger optical probe's perpendicular orientation of the illumination and collection fibers at the probe-skin interface resulted in a longer pathlength through tissue at all wavelengths relative to the lower numerical aperture, inclined illumination and collection fibers of the forearm optical probe. Although the longer finger probe pathlengths came at the expense of increased attenuation due to absorption, the larger numerical aperture and greater number of illumination fibers of the finger optical probe largely offset the attenuation which resulted in approximately equivalent SNRs for the two probe designs despite the differences in pathlength. The comparison of the tissue alcohol measurements to blood and breath measurements indicated that both the optical probe designs and alcohol pharmacokinetics contributed significantly to the observed alcohol concentrations. The rms concentration differences of the finger measurement site relative to both breath and blood were smaller than their forearm counterparts in both the absorption and elimination phases of the 26 patient's alcohol excursions. Furthermore, the first-order pharmacokinetic model reasonably explained the differences between the arterial (breath), venous, finger, and forearm compartments and demonstrated that the finger measurement exhibited rate constants in excellent agreement with those observed between the arterial and venous blood. As with prior studies, the forearm tissue measurement exhibited significantly lower rate constants indicative of a larger pharmacokinetic difference from the other compartments. The faster kinetics of the finger site relative to the forearm is consistent with the site-dependent concentration differences observed in recent glucose monitoring research and is indicative that a tissue-based alcohol measurement can closely track the venous blood compartment. One of the complicating factors of the present study was that the difference in optical probe designs was coincident with the difference in measurement sites. As such, spectroscopic differences caused by the optical probe designs cannot be severed from those caused by site-dependent optical properties and analyte concentrations. Future work will investigate forearm spectroscopic measurements using both the finger and forearm optical probes, which would allow better isolation of the influences of the optical probe designs. Another avenue for future investigation is the application of effective path-length estimates as a spectroscopic correction for variation in path-lengths between samples. The effective path-length model used in this work is semi-physical in nature and attempts to accommodate variability in both absorption (through analyte concentrations) and scattering (through variations in the PLD parameters) properties. A recognized limitation of the effective path-length approach is that some a priori knowledge of the samples, such as pure component spectra of dominant absorbers, is required. Regardless, the effective path-length approach would seem to be amenable to a variety of samples measured in reflectance. AcknowledgmentsThe authors thank Lovelace Scientific Resources for the execution of the alcohol dosing study. We also acknowledge the S.E.D. Toxicology Laboratory for its analysis of venous blood samples throughout the study. This study was funded in part by a contract awarded from the Automotive Coalition for Traffic Safety (ACTS) and the National Highway Traffic Safety Administration. ReferencesT. Ridder, B. Ver Steeg, and
B. Laaksonen,
“Comparison of spectroscopically measured tissue alcohol concentration to blood and breath alcohol measurements,”
J. Biomed. Opt., 14
(5), 054039
(2009). https://doi.org/10.1117/1.3253353 Google Scholar
T. Ridder, B. Ver Steeg, S. Vanslyke, and
J. Way,
“Noninvasive NIR monitoring of interstitial ethanol concentration,”
Proc. SPIE, 7186 71860E
(2009). https://doi.org/10.1117/12.809944 Google Scholar
M. D. Levitt and
D. G. Levitt,
“Use of a two-compartment model to predict ethanol metabolism,”
Alcohol Clin. Exp. Res., 24 409
–410
(2000). https://doi.org/10.1111/acer.2000.24.issue-4 Google Scholar
A. Norberg,
“Clinical pharmacokinetics of intravenous ethanol: relationship between the ethanol space and total body water,”
Kongl Carolinska Medico Chirurgiska Institutet,
(2001). Google Scholar
A. Norberg, A. W. Jones, R. G. Hahn, and
J. L. Gabrielsson,
“Role of variability in explaining ethanol pharmacokinetics,”
Clin. Pharmacokinet., 42
(1), 1
–31
(2003). https://doi.org/10.2165/00003088-200342010-00001 Google Scholar
A. Norberg, J. L. Gabrielsson, A. W. Jones, and
R. G. Hahn,
“Within and between-subject variations in pharmacokinetic parameters of ethanol by analysis of breath, venous blood and urine,”
Br. J. Clin. Pharmacol., 49 399
–408
(2000). https://doi.org/10.1046/j.1365-2125.2000.00194.x Google Scholar
J. M. Ellison, J. M Stegmann, S. L. Colner, R. H. Michael, M. K. Sharma, K. R. Ervin, and
D. L. Horowitz,
“Rapid changes in postprandial blood glucose produce concentration differences at finger, forearm, and thigh sampling sites,”
Diabetes Care, 25
(6), 961
–964
(2002). https://doi.org/10.2337/diacare.25.6.961 Google Scholar
N. Peled, D. Wong, and
S. L. Gwalani,
“Comparison of glucose levels in capillary blood samples obtained from a variety of body sites,”
Diabetes Technol. Ther., 4
(1), 35
–44
(2002). https://doi.org/10.1089/15209150252924067 Google Scholar
P. J. Stout, J. R. Racchini, and
M. E. Hilgers,
“A novel approach to mitigating the physiological lag between blood and interstitial fluid glucose measurements,”
Diabetes Technol. Ther., 6
(5), 635
–644
(2004). https://doi.org/10.1089/dia.2004.6.issue-5 Google Scholar
T. Koschinsky, K. Jungheim, and
L. Heinemann,
“Glucose sensors and the alternate site testing-like phenomenon: relationship between rapid blood glucose changes and glucose sensor signals,”
Diabetes Technol. Ther., 5
(5), 829
–842
(2003). https://doi.org/10.1089/DIA.2003.5.issue-5 Google Scholar
D. M. Lee, S. E. Weinert, and
E. E. Miller,
“A study of forearm versus finger stick glucose monitoring,”
Diabetes Technol. Ther., 4
(1), 13
–23
(2002). https://doi.org/10.1089/15209150252924049 Google Scholar
M. E. Wilinska, M. Bodenlenz, L. J. Chassin, H. C. Schaller, L. A. Schaupp, T. R. Pieber, and
R. Hovorka,
“Interstitial glucose kinetics in subjects with type 1 diabetes under physiologic conditions,”
Metabolism, 53
(11), 1484
–1492
(2004). https://doi.org/10.1016/j.metabol.2004.05.014 Google Scholar
D. W. Schmidke, A. C. Freeland, A. Heller, and
R. T. Bonnecaze,
“Measurement and modeling of the transient difference between blood and subcutaneous glucose concentrations in the rat after injection of insulin,”
Proc. Natl. Acad. Sci. U.S.A., 95 294
–299
(1998). https://doi.org/10.1073/pnas.95.1.294 Google Scholar
B. T. Davies and
C. K. Bowen,
“Peak blood alcohol prediction: an empirical test of two computer models,”
J. Stud. Alcohol Drugs, 61 187
–191
(2000). Google Scholar
A. W. Jones, A. Norberg, and
R. G. Hahn,
“Concentration-time profiles of ethanol in arterial and venous blood and end-expired breath during and after intravenous infusion,”
J. Forensic Sci., 42
(6), 1088
–1094
(1997). Google Scholar
L. Lindberg, S. Brauer, P. Wollmer, L. Goldberg, A. W. Jones, and
S. Olsson,
“Breath alcohol concentration determined with a new analyzer using free exhalation predicts almost precisely the arterial blood alcohol concentration,”
Forensic Sci. Int., 168
(2–3), 200
–207
(2007). https://doi.org/10.1016/j.forsciint.2006.07.018 Google Scholar
E. Martin, M. Moll, P. Schmid, and
L. Dettli,
“The pharmacokinetics of alcohol in human breath, venous and arterial blood after oral ingestion,”
Eur. J. Clin. Pharmacol., 26 619
–626
(1984). https://doi.org/10.1007/BF00543496 Google Scholar
M. P. Hlastala,
“The alcohol breath test—a review,”
Appl. Physiol., 84 401
–408
(1998). https://doi.org/10.1063/1.368080 Google Scholar
A. W. Jones and
L. Andersson,
“Comparison of ethanol concentrations in venous blood and end-expired breath during a controlled drinking study,”
Forensic Sci. Int., 132 18
–25
(2003). https://doi.org/10.1016/S0379-0738(02)00417-6 Google Scholar
G. L. Cote,
“Noninvasive and Minimally-invasive Optical Monitoring Techniques,”
Nutrition, 131 1596S
–1604S
(2001). Google Scholar
H. M. Heise, A. Bittner, and
R. Marbach,
“Near-infrared reflectance spectroscopy for non-invasive monitoring of metabolites,”
Clin. Chem. Lab. Med., 38 137
–145
(2000). https://doi.org/10.1515/cclm.2000.38.issue-2 Google Scholar
V. V. Tuchin, Handbook of Optical Sensing of Glucose in Biological Fluids and Tissues, CRC Press, Boca Raton
(2008). Google Scholar
T. D. Ridder, S. P. Hendee, and
C. D. Brown,
“Noninvasive alcohol testing using diffuse reflectance near-infrared spectroscopy,”
Appl. Spectrosc., 59
(2), 181
–189
(2005). https://doi.org/10.1366/0003702053085098 Google Scholar
T. D Ridder, C. D. Brown, and
B. J. VerSteeg,
“Framework for multivariate selectivity analysis, part II: experimental applications,”
Appl. Spectrosc., 59
(6), 804
–815
(2005). https://doi.org/10.1366/0003702054280739 Google Scholar
A. Bashkatov, E. Genina, V. Kochubey, V. Tuchin,
“Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000 nm,”
J. Phys. D, 38 2543
–2555
(2005). https://doi.org/10.1088/0022-3727/38/15/004 Google Scholar
E. Chan, B. Sorg, D. Protsenko, M. O’Neil, M. Motamedi, and
A. Welch,
“Effects of compression on soft tissue optical properties,”
IEEE J. Quantum Electron., 2 943
–950
(1996). https://doi.org/10.1109/2944.577320 Google Scholar
T. Troy and
S. Thennadil,
“Optical properties of human skin in the near infrared wavelength range of 1000 to 2200 nm,”
J. Biomed. Opt., 6 167
–176
(2001). https://doi.org/10.1117/1.1344191 Google Scholar
S. Shuster, M. Black, and
E. McVitie,
“The influence of age and sex on skin thickness, skin collagen and density,”
Br. J. Dermatol., 93 639
–643
(1975). https://doi.org/10.1111/bjd.1975.93.issue-6 Google Scholar
D. Aghassi, T. Monoson, and
I. Braverman,
“Reproducible measurements to quantify cutaneous involvement in scleroderma,”
Arch. Dermatol., 131 1160
–1166
(1995). https://doi.org/10.1001/archderm.131.10.1160 Google Scholar
E. V. Thomas,
“Adaptable multivariate calibration models for spectral applications,”
Anal. J. Chem., 72
(13), 2821
–2827
(2000). https://doi.org/10.1021/ac000009j Google Scholar
H. Akaike,
“A new look at the statistical identification model,”
IEEE Trans. Automat. Control, 19 716
(1974). https://doi.org/10.1109/TAC.1974.1100705 Google Scholar
|