Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy

Nienke Bosschaart; Dirk J. Faber; Ton G. van Leeuwen; Maurice C. G. Aalders

doi:10.1117/1.3553005

Journal of Biomedical Optics | Volume 16 | Issue 3 | JBO Letters >

< Previous Article Next Article >

JBO Letters

Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy

Nienke Bosschaart ; Dirk J. Faber ; Ton G. van Leeuwen ; Maurice C. G. Aalders

[+] Author Affiliations

Nienke Bosschaart, Dirk J. Faber, Maurice C. G. Aalders

University of Amsterdam, Biomedical Engineering and Physics, Academic Medical Center, P.O. Box 22700, NL-1100 DE Amsterdam, The Netherlands

Ton G. van Leeuwen

University of Amsterdam, Biomedical Engineering and Physics, Academic Medical Center, P.O. Box 22700, NL-1100 DE Amsterdam, The Netherlands

University of Twente, Biomedical Photonic Imaging Group, MIRA Institute for Biomedical Technology and Technical Medicine, P.O. Box 217, NL-7500 AE Enschede, The Netherlands

J. Biomed. Opt. 16(3), 030503 (December 03, 2010January 08, 2011January 17, 2011March 01, 2011March 01, 2011). doi:10.1117/1.3553005

Text Size: A A A

Open Access

Article

Figures

References

Abstract

Abstract | Acknowledgments | References

Quantitative measurements of scattering properties are invaluable for optical techniques in medicine. However, noninvasive, quantitative measurements of scattering properties over a large wavelength range remain challenging. We introduce low-coherence spectroscopy as a noninvasive method to locally and simultaneously measure scattering μ_s and backscattering μ_b coefficients from 480 to 700 nm with 8 nm spectral resolution. The method is tested on media with varying scattering properties (μ_s = 1 to 34 mm⁻¹ and μ_b = 2.10⁻⁶ to 2.10⁻³ mm⁻¹), containing different sized polystyrene spheres. The results are in excellent agreement with Mie theory.

Figures in this Article

Quantitative determination of the optical properties of tissue is invaluable in biomedical optics. The majority of optical diagnostic techniques rely on the spectral absorption and scattering properties of tissue, which provide information on its composition and structure. The same optical properties are of essential importance for the development and optimization of optical therapeutic techniques. However, despite the existence of many spectroscopic methods, it is still a challenge to do noninvasive, quantitative measurements of the absorption and scattering properties in vivo over a large wavelength range.

Recently, we introduced low-coherence spectroscopy (LCS) to do quantitative and localized measurements of absorption coefficients

${{\bf{\umu}}_{\bf{a}}}$

μ_{a}

over a wavelength range of 480 to 700 nm with a spectral resolution of 8 nm¹ (all wavelength dependent parameters in this paper will be denoted by a boldfaced character). In this study, we use LCS to quantitatively and simultaneously measure scattering

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and backscattering

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

coefficients on a wide range of scattering media (

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

= 1 to 34 mm⁻¹ and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

= 2.10⁻⁶ to 2.10⁻³ mm⁻¹). Thereby, we demonstrate new opportunities for noninvasive scattering property measurements. In vivo measurements of the quantitative value of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

can assist in differentiating between tissue types² and modeling of light-tissue interactions. The spectrally resolved information of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

gives additional valuable information such as the power dependency of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

on wavelength and wavelength dependent oscillations in

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

, which have shown to be related to tissue morphology.^3- 4

Whereas extensive study on tissue (back)scattering has been performed in the areas of light scattering spectroscopy³ and angle-resolved low-coherence interferometry,⁴ these studies lack quantification of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

, since their primary aim has been to retrieve the size of the scattering particles. Quantification of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

has been shown in optical coherence tomography studies,^2,5 but these studies were limited to the measurement of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

averaged over the bandwidth of the spectrum, i.e., no spectral information was obtained. Moreover, in these studies, quantitative agreement with theory is rarely obtained for highly scattering media, due to multiple scattering contributions to the signal.⁵ Other (diffuse) reflectance spectroscopy techniques are able to measure

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

and the reduced scattering coefficient

$\rm{{\bm{\umu}^{\prime}}_{\bf{s}}}$

{μ^{'}}_{s}

,⁶ but this requires additional information on the scattering anisotropy g to obtain

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

. Thus, compared to the existing methods for scattering property measurements, LCS offers the unique possibility for a combination of simultaneous, quantitative, and spectrally resolved measurement of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

. Therefore, these measurements will assist in a more complete, and likely more accurate, characterization of the tissue of interest. In addition, like other low coherence interferometry techniques,^2,5,7 LCS measures a controlled and confined volume, which is important when measuring local optical properties in an often inhomogeneous tissue.

Using LCS, we measured

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

and

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

of aqueous nonabsorbing suspensions of different sized polystyrene spheres and validated our results with Mie theory. Therefore, we measured backscattered power spectra S(ℓ) at controlled geometrical path lengths ℓ of the light in a sample. Our LCS system, which is described in detail in Ref. ¹, consists of a Michelson interferometer and is optimized for 480 to 700 nm. The geometrical round trip path length ℓ (ℓ = 0 to 2 mm, with ℓ = 0 the sample surface) is controlled by translating the reference mirror, in steps of 27 μm. By translating the sample, focus tracking of the 64 μm² spot size in the sample is achieved. Around ℓ, the signal is modulated by scanning the piezo-driven reference mirror (23 Hz) resulting in a scanning window of Δℓ ≈ 44 μm. The optical power at the sample is 6 mW.

A multimode fiber (ø = 62.5 μm) guides the reflected light from both arms to a photodiode. Signal processing after acquisition, which is described in detail in Ref. ¹, results in averaged spectra S(ℓ) with 8-nm resolution [∼500 averages per ℓ, to avoid any spectral modulations on S(ℓ) caused by interference between scattering particles]. We describe S(ℓ) with a single exponential decay model (Ref. ²) S(ℓ) = S₀·T·Δℓ·

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

·exp(−

$\rm{{\bf{\umu}}_{\bf{t}}}$

μ_{t}

·ℓ),² where S₀ is the source power spectrum and T is the system coupling efficiency. When S(ℓ) is dominated by a single backscattered light,

$\rm{{\bf{\umu}}_{\bf{t}}}$

μ_{t}

is the attenuation coefficient of the sample and

$\rm{{\bf{\umu}}_{\bf{t}}}$

μ_{t}

equals

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

for nonabsorbing samples (this study). The system dependent parameters will be denoted by ζ = S₀·T·Δℓ. The spectra S(ℓ) are collected over the detection numerical aperture (NA) of the system, therefore, we define the measured backscattering coefficient

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

as the product of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and the phase function p(

$\bm\theta$

θ

), integrated over the solid angle of the NA in the medium: Display Formula

\documentclass[12pt]{minimal}\begin{document}\begin{eqnarray} {\bf {\rm{\umu _{\bf b,NA} = \umu _{\bf s}} \cdot 2\pi \int\nolimits_{{{{\bm\theta} = {\bm \pi} - {\bf{NA}}}}}^\pi {{{\bf p}\left( {\bm{\theta}} \right) \cdot {\rm{sin}}\left( {\bm{\theta}} \right) \cdot d{\bm{\theta}} }}}}. \end{eqnarray}\end{document}

\begin{matrix} μ_{b, NA} = μ_{s} \cdot 2 π \int_{θ = π - NA}^{π} p (θ) \cdot \sin (θ) \cdot d θ . \end{matrix}

We measured the wavelength dependent point spread function in the medium⁷ and derived the NA (ranging from 0.035 to 0.045 between 480 to 700 nm) from the resulting Rayleigh length of the system. The terms

$\rm{{{\bm \uzeta\cdot\umu}}_{\bf{b,NA}}}$

{ζ \cdot μ}_{b, NA}

and

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

are obtained by fitting a two-parameter (amplitude and decay, respectively) exponential function to S(ℓ) versus ℓ. Uncertainties are estimated by the 95% confidence intervals (c.i.) of the fitted parameters.¹ The model is fitted to the measured S(ℓ) up to a path length in the sample of five times the mean free path (5/

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

from Mie theory at 480 nm, varying from 100 to 1950 μm). Spectra acquired from ℓ < 50 μm suffer from boundary artifacts and are therefore excluded from the fits. Prior to fitting the model to S(ℓ), a noise level is subtracted from S(ℓ), which is the sum of the dc spectra of the sample and reference arm. Now,

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

can be calculated from the fitted amplitude

$\rm{{\bm{\uzeta\cdot\umu}}_{\bf{b,NA}}}$

{ζ \cdot μ}_{b, NA}

, if ζ is determined in a separate calibration measurement in which

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

is exactly known from Mie theory and Eq. 1. To this end, we used National Institute of Standards and Technology (NIST)-certified polystyrene spheres of ø = 409±9 nm (diameter±SD, Thermo Scientific, USA). The obtained ζ was used to determine

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

in subsequent measurements.

In our Mie calculations, we used wavelength dependent refractive indices of water and polystyrene⁸ and integrated over the size distribution of the spheres (2*SD), given by the manufacturer. Brownian motion of the polystyrene spheres causes Doppler broadening of the measured LCS spectra. For adequate comparison, we convolved the Mie spectra with a Lorentzian, with a linewidth of 5 to 13 nm, depending on the sphere size-dependent Doppler frequency distribution of the Brownian motion of the spheres, similar to our analysis in Ref. ¹.

Figure 1 shows LCS measurements (dots) of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

for four aqueous suspensions of different sized NIST-certified polystyrene spheres: 0.071% with ø = 409±9 nm, 0.048% with ø = 602±6 nm, 0.038% with ø = 799±9 nm, and 0.033% with ø = 1004±10 nm, which lie within the range of scatterer sizes in biological cells.³ The sphere concentrations, indicated in volume percentages, were chosen such that

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

was approximately equal for all samples (∼1.5 mm⁻¹ at 600 nm). The LCS measurements agree within 0.2 mm⁻¹ with

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

from Mie theory (thick solid lines) over the entire wavelength range of 480 to 700 nm. The scattering coefficient has a power dependence on wavelength, with different scatter power for different particle sizes. We also measured the attenuation coefficient of water, which, as expected, is ∼0 mm⁻¹ for all wavelengths.

LCS (dots) and Mie (thick solid lines) results for (a) scattering coefficients $\rm{{\bf{\umu}}_{\bf{s}}}$μs, and (b) backscattering coefficients $\rm{{\bf{\umu}}_{\bf{b,NA}}}$μb,NA for four aqueous suspensions of different sized polystyrene spheres and water. Error bars, representing the 95% c.i. of the fitted values, may fall behind data points. The $\rm{{\bf{\umu}}_{\bf{b,NA}}}$μb,NA were calibrated using the 409-nm sample.

View Large | Save Figure | Download Slide (.ppt) | View in Article Context

Figure 1 shows the LCS measurements (dots) of

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

on a logarithmic scale for the polystyrene suspensions, after measuring

${\bm{\uzeta}}$

ζ

on the 409-nm sample. The error bars in this graph are on the same order of magnitude as the marker size. The

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

differ over an order of magnitude between samples, since the phase function changes considerably with sphere size. The measured

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

are in agreement with Mie theory (thick solid lines), showing the characteristic sphere size dependent oscillations. The

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

of water shows no pronounced spectral features, which implies that our calibration method was applied correctly. We attribute the small differences between measurements and Mie calculations to uncertainties in particle size distribution and refractive index that were used as Mie-input (depending on wavelength, a 1% change in the polystyrene refractive index results in a 11 to 14% change in

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and a 11 to 25% change in

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

To test the range of validity of the single exponential decay model to obtain

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

, it is important to also test the model for media with higher scattering densities. Therefore, we increased the particle concentration for the 409 nm sample several times (from 0.071% to 0.950%) and measured

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

. Figure 2 shows that the measured

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

agrees with Mie calculations of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

within 14%, up to values as high as 34 mm⁻¹, which lies well within the range of tissue scattering. In addition, the measured

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

is in agreement with Mie theory [(Fig. 2], except for the two highest volume concentrations, where the measurement overestimates

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

at the shorter wavelengths.

LCS (dots) and Mie (thick solid lines) results for (a) scattering coefficients $\rm{{\bf{\umu}}_{\bf{s}}}$μs, and (b) backscattering coefficients $\rm{{\bf{\umu}}_{\bf{b,NA}}}$μb,NA for six concentrations of 409-nm polystyrene sphere suspensions. Error bars, representing the 95% c.i. of the fitted values, may fall behind data points. The $\rm{{\bf{\umu}}_{\bf{b,NA}}}$μb,NA were calibrated using the 0.071% sample.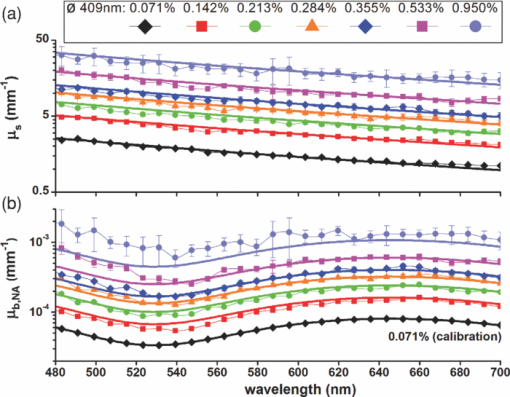

View Large | Save Figure | Download Slide (.ppt) | View in Article Context

The measurements of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

in Figs. 1- 2 demonstrate that disagreement with the Mie calculated values for the highest volume concentrations (Fig. 2) is only manifested in

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

and not in

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

(i.e.,

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

agrees with the Mie calculated

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

within the 95% c.i.). For these samples (0.533% and 0.950%), the average surface-to-surface distance between the spheres is comparable to the wavelength: 760 and 556 nm, respectively. Since the effect of multiple scattering would be visible in the measured value of both coefficients, we speculate that another effect may cause this disagreement, i.e., the total scattered field cannot be treated as the superposition of the scattered field by the individual particles (dependent scattering).⁹ Our results indicate that for these sphere concentrations,

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

is altered to favor more backward than forward directed scattering. Further study is needed to assess the influence of the particle phase function and interparticle distance on the measured

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

The presented results show that LCS enables sample characterization based on absolute values of

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

and

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

, the scatter power in

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and oscillations in

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

. This very combination of optical properties is characteristic for particle or tissue type^2- 7 and therefore offers new opportunities for tissue characterization. Clinical studies have been reported where the measurement of only one parameter was not sufficient to differentiate between tissue types, such as the value of μ_t for measuring (morphological) changes between grades of urothelial carcinoma of the bladder.¹⁰ For these studies, the measurement of both

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

by LCS may assist in better differentiation because low contrast in

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

can be accompanied by high contrast in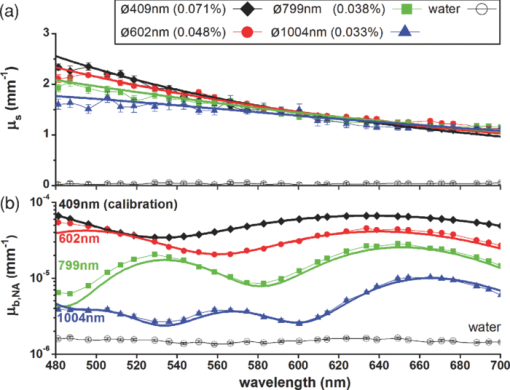

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

(Fig. 1).

In nonabsorbing samples,

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

is extracted directly from the measurement and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

requires calibration on a sample with known

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

. To obtain

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

from tissue, the measured

$\rm{{\bf{\umu}}_{\bf{t}}}$

μ_{t}

needs to be corrected for tissue absorption. Several methods to separate

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\umu_{\rm \bf a}$

μ_{a}

from a single attenuation profile have been proposed.^11- 12 In addition, the simultaneous measurement of both

$\rm{{\bf{\umu}}_{\bf{t}}}$

μ_{t}

and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

by LCS may eventually assist in separating scattering and absorption contributions to the LCS signal, since the

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

is proportional to

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

but independent of

$\umu_{\rm \bf a}$

μ_{a}

Whereas in this study, the scattering properties are measured in nonlayered, homogeneous samples, LCS has the potential to measure

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

in individual layers of layered media such as human skin. The controlled path length and the confined measurement volume due to the confocality of the system, in principle, allow to measure within a layer of choice, which will be a subject of further study. Even for a confined tissue volume, the

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

is likely to consist of the contribution of a range of scatterer sizes and therefore, it will not exhibit oscillations as clearly presented in Figs. 1- 2. Nevertheless, tissue specific spectral features in backscattering have been observed^3- 4 and also the absolute value of

$\rm{{\bf{\umu}}_{\bf{b,NA}}}$

μ_{b, NA}

contains information on tissue type.²

In conclusion, we present quantitative and wavelength dependent measurements of scattering and backscattering coefficients from polystyrene sphere suspensions. Our method applies for a broad range of sphere sizes and particle densities, and is in excellent agreement with Mie theory up to scattering coefficients as high as 34 mm⁻¹. LCS measures

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

simultaneously, over a large wavelength range and with good spectral resolution. The combined wavelength dependent information of

$\rm{{\bf{\umu}}_{\bf{s}}}$

μ_{s}

and

$\rm{{\bf{\umu}}_{\bf{b}}}$

μ_{b}

is likely to assist in more accurate tissue characterization in tissue optics.

Acknowledgments

Abstract | Acknowledgments | References

This research was funded by personal grants in the Vernieuwingsimpuls program (DJF: UNSPECIFIED AGT07544 ; MCGA: UNSPECIFIED AGT07547 ) by the Netherlands Organization of Scientific Research (NWO) and the Technology Foundation STW.

References

Abstract | Acknowledgments | References

Bosschaart N., , Aalders M. C. G., , Faber D. J., , Weda J. J. A., , Gemert M. J. C. van, , and Leeuwen T. G. van, “ Quantitative measurements of absorption spectra in scattering media by low-coherence spectroscopy. ,” Opt. Lett.. 34, , 3746–3748 ((2009)).

Schmitt J. M., , Knuttel A., , and Bonner R. F., “ Measurement of optical properties of biological tissues by low-coherence reflectometry. ,” Appl. Opt.. 32, , 6032–6042 ((1993)).

Hielscher A. H., , Mourant J. R., , and Bigio I. J., “ Influence of particle size and concentration on the diffuse backscattering of polarized light from tissue phantoms and biological cell suspensions. ,” Appl. Opt.. 36, , 125–135 ((1997)).

Wax A., , Yang C., , Backman V., , Badizadegan K., , Boone C. W., , Dasari R. R., , and Feld M. S., “ Cellular organization and substructure measured using angle-resolved low-coherence interfometry. ,” Biophys. J.. 82, , 2256–2264 ((2002)).

Oldenburg A. L., , Hansen M. N., , Zweifel D. A., , Wei A., , and Boppart S. A., “ Plasmon resonant gold nanorods as low backscattering albedo contrast agents in optical coherence tomography. ,” Opt. Express. 14, , 6724–6738 ((2006)).

Ungureanu C., , Amelink A., , Rayavarapu R. G., , Sterenborg H. J. C. M., , Manohar S., , and Leeuwen T. G. van, “ Differential pathlength spectroscopy for the quantitation of optical properties of gold nanoparticles. ,” ACS Nano. 4, , 4081–4089 ((2010)).

Faber D. J., , Meer F. J. Van Der, , and Aalders M. C., , Leeuwen T. G. van, “ Quantitative measurement of attenuation coefficients of weakly scattering media using optical coherence tomography. ,” Opt. Expr.. 12, , 4353–4365 ((2004)).

Kasarova S. N., , Sultanova N. G., , Ivanov C. D., , and Nikolov I. D., “ Analysis of the dispersion of optical plastic materials. ,” Opt. Mater.. 29, , 1481–1490 ((2004)).

Göbel G., , Kuhn J., , and Fricke J., “ Dependent scattering effects in latex-sphere suspensions and scattering powders. ,” Waves Random Complex Media. 5, , 413–426 ((1995)).

Cauberg E. C. C., , Bruin D. M. de, , Faber D. J., , Reijke T. M. de, , Visser M., , Rosette J. J. M. C. H. de la, , and Leeuwen T. G. van, “ Quantitative measurement of attenuation coefficients of bladder biopsies using optical coherence tomography for grading urothelial carcinoma of the bladder. ,” J. Biomed. Opt.. 15, , 066013 ((2010)).

Robles F. E., and Wax A., “ Separating the scattering and absorption coefficients using the real and imaginary parts of the refractive index with low-coherence interferometry. ,”Opt. Lett.. 35, , 2843–2845 ((2010)).

Xu C., , Marks D. L., , Do M. N., , and Boppart S. A., “ Separation of absorption and scattering profiles in spectroscopic optical coherence tomography using a least-squares algorithm. ,” Opt. Express. 12, , 4790–4803 ((2004)).

Citation

Nienke Bosschaart ; Dirk J. Faber ; Ton G. van Leeuwen and Maurice C. G. Aalders
"Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy", J. Biomed. Opt. 16(3), 030503 (December 03, 2010January 08, 2011January 17, 2011March 01, 2011March 01, 2011). ; http://dx.doi.org/10.1117/1.3553005

Figures

View Large | Save Figure | Download Slide (.ppt) | View in Article Context

LCS (dots) and Mie (thick solid lines) results for (a) scattering coefficients $\rm{{\bf{\umu}}_{\bf{s}}}$μs, and (b) backscattering coefficients $\rm{{\bf{\umu}}_{\bf{b,NA}}}$μb,NA for six concentrations of 409-nm polystyrene sphere suspensions. Error bars, representing the 95% c.i. of the fitted values, may fall behind data points. The $\rm{{\bf{\umu}}_{\bf{b,NA}}}$μb,NA were calibrated using the 0.071% sample.

View Large | Save Figure | Download Slide (.ppt) | View in Article Context

Tables

MultiMedia

References

Schmitt J. M., , Knuttel A., , and Bonner R. F., “ Measurement of optical properties of biological tissues by low-coherence reflectometry. ,” Appl. Opt.. 32, , 6032–6042 ((1993)).

Kasarova S. N., , Sultanova N. G., , Ivanov C. D., , and Nikolov I. D., “ Analysis of the dispersion of optical plastic materials. ,” Opt. Mater.. 29, , 1481–1490 ((2004)).

Göbel G., , Kuhn J., , and Fricke J., “ Dependent scattering effects in latex-sphere suspensions and scattering powders. ,” Waves Random Complex Media. 5, , 413–426 ((1995)).

Some tools below are only available to our subscribers or users with an online account.

PDF
Print
Email

SPIE

You must be logged in as an individual user to share content.

Return to: Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy

Copyright in the material you requested is held by SPIE (unless otherwise noted). This email ability is provided as a courtesy, and by using it you agree that you are requesting the material solely for personal, non-commercial use, and that it is subject to SPIE's Terms of Use. The information provided in order to email this topic will not be used to send unsolicited email, nor will it be furnished to third parties. Please refer to SPIE's Privacy Policy for further information.

SPIE © 1962-2012. All rights reserved.
Share
Get Citation

Bosschaart N, Faber DJ, Leeuwen T, Aalders MG; Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy. J. Biomed. Opt. 0001;16(3):030503-030503-3. doi:10.1117/1.3553005.

Download citation file:

RIS (Zotero)

EndNote

BibTex

Medlars

ProCite

RefWorks

Reference Manager

Copyright © SPIE Digital Library
Get Permissions
Article Alerts

Processing your request... Please Wait.

Create a Personal Profile
Slideset (.ppt)

Measurements of wavelength dependent scattering and backscattering coefficients by low-coherence spectroscopy

Open Access

Conference Presentation Video

Abstract

Figures in this Article

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Conference Presentation Video

Acknowledgments

Conference Presentation Video

Conference Presentation Video

References

Conference Presentation Video

Figures

Tables

MultiMedia

References

Related Content

Related Journal Articles

Related Proceedings Articles

Related Book Chapters

Topic Collections

PubMed Articles

Site Map

Services

Other Resources

Information for Authors