|
|
1.IntroductionDespite the recognized superiority of Fourier domain optical coherence tomography (FD-OCT) over conventional time domain OCT (TD-OCT) in terms of sensitivity1 and acquisition speed, FD-OCT presents two major disadvantages: (i) mirror terms and (ii) decay of sensitivity with optical path difference (OPD). In terms of mirror terms, the same image (upside down) results for the same modulus value of the OPD. If the OPD = 0 value is placed inside the tissue, then the image corresponding to a positive OPD is overlapped over the image for the negative OPD. The elimination of one of the image is equivalent to the modification of the sensitivity profile versus depth. In a standard FD-OCT system, the sensitivity profile is symmetric around OPD = 0, where it achieves a maximum. Making the sensitivity zero for one of the images is equivalent with producing an instrument, which in sensing applications2, 3, 4 would be sensitive for only one sign of the OPD range. In FD-OCT, in order to avoid mirror terms corrupting the image, the OPD = 0 value is placed well in front of the tissue. If the object exhibits involuntary movements, then the OPD = 0 value is crossed again and ghost images are produced. As another disadvantage, by moving away from OPD = 0, less sensitivity of the standard FD-OCT setup is used. Different methods have been devised to attenuate the symmetric terms in order to obtain a correct image. These methods rely on the generation of the complex signal, where its imaginary component is inferred by producing a second interferogram shifted in phase by π/2. Various techniques have been employed to generate such phase-shifted interferograms. At least two acquisition steps are required to synthesize the complex signal and then use it to cancel the term corresponding to the sign of OPD, which is to be eliminated. Such methods allow correct reconstruction of layers in depth as well as double the axial OPD range. 1.1.Sequential Phase-Shifting InterferometryBy introducing exact phase shifts between the two optical interferometer paths in successive signal collection steps and combining the signals such collected, it is possible to reduce the noise as well as eliminate the autocorrelation terms in the electrical Fourier transform spectrum of the OCT signal. However, phase-shifting spectral interferometry has some disadvantages. The phase-shift values must be accurate to within a few degrees, which requires precise control of the device used to introduce the phase shifts. Also, because the final spectrum is delivered only after at least a P number of spectra are collected,5 the process is P times slower than conventional methods. However, the most important disadvantage associated with phase-shifting spectral interferometry is sensitivity to movement of the tissue being examined.6 Movement of tissue alters the phase and, hence, the phase shift steps applied in the process of constructing the complex conjugate signal. Errors in the values of the phase shifts applied lead to less attenuation of the mirror terms. 1.2.Phase Shifting Using a 3 × 3 SplitterA 3 × 3 coupler could be used for both FD-OCT and swept source optical coherence tomography (SS-OCT) to produce the instantaneous complex conjugate Fourier transformation.7 The principle of operation is based on the non-complementary phase relationship, which exist between the waves at the output fibers of a 3 × 3 coupler. For a truly fused 3 × 3 coupler having an even power splitting ratio between its ports, a phase delay between detector ports of 120 deg should be obtained. Noneven splitting ratios or couplers with higher port counts can be employed for such applications to generate different phase shifts between their output ports. However, this method requires a more complex optical and electronic processing setup and the coupling ratios vary with the optical frequency, limiting the bandwidth wherein the mirror terms can be efficiently attenuated. 1.3.Modulation TechniquesDifferent modulation techniques have been researched, using a phase modulator, a frequency modulator, or a path modulator using either a vibrator in the reference arm or the galvoscanner itself in the object arm. Using a phase modulator, the mirror terms spectra are separated in frequency8 or the imaginary and real components can be detected simultaneously as the first and second harmonics of the phase-modulated interferogram.9 A frequency carrier was also created by moving the reference mirror at constant speed.10 By shifting the incident beam in the object path away from the pivot of the transverse scanner, the spectrum shifts in frequency due to lateral scanning, where the shift is proportional to the angular scanning speed and the offset of the beam from the pivot.11, 12, 13 Two disadvantages of this method are: (i) it requires readjustments when changing the image size and (ii) the chromatic phase error increases when large bandwidth sources are used, as required for good depth resolution. This causes the mirror terms to no longer be suppressed. Therefore, an achromatic solution is better suited, such as that of beating signals generated by two acousto-optic modulators used as frequency shifters.14 By subtracting two complex signals with a relative time delay of half of the beating period, the parasitic directional coupler (DC) and autocorrelation terms can be removed. 1.4.Dispersion-Encoded Mirror Term EliminationIf the interferometer and sample have dispersion left uncompensated, then as the OPD is scanned, it can be noted that the height and width of the peak from a mirror in the A-scan is different for different sign OPD values equal in modulus. This suggests a different method to reduce the mirror terms, where the OPD sign is encoded by dispersion.15 An iterative algorithm was proposed to cancel complex conjugate mirror terms in individual A-scans and generate full-range tomograms, algorithm termed as dispersion-encoded full-range (DEFR) OCT. DEFR-OCT has higher postprocessing complexity than conventional FD-OCT; however, it does not require acquisition of additional A-scans. The algorithm uses numerical dispersion compensation. Further reduction of mirror terms is achieved by employing a priori knowledge of the power spectrum of the light source. Using a 256-step iteration process on B-scan fovea images, a suppression ratio of mirror terms of >50 dB was obtained, comparable to values achieved by complex spectral domain techniques based on multiple A-scans presented above. All the methods mentioned above are cancellation techniques that need several images or steps to acquire accurate values to be compounded and finally combined to cancel the mirror terms. Cancellation techniques require good stability of parameters because any mechanical instability or sample movement will affect the equilibrium of quantities involved. Talbot bands16, 17 present a solution to mirror terms in FD-OCT that does not require calculations or cancellation algorithms, and therefore, such a solution is not affected by sample movements or parameter instabilities. Simply put, in Talbot bands configurations, mirror terms do not exist. In a Talbot bands configuration, the two interferometer beams are spatially separated in their way toward the disperser (prism or grating),18, 19 separation that introduces a delay between the diffracted wave trains equal or larger than their wave-train length. Our previous reports mainly focused on the elimination of mirror terms in FD-OCT.18, 19, 20, 21 Also, the generation of the Talbot bands in FD-OCT has not been fully explored when imaging tissue. We present here further research on using Talbot bands, where the emphasis is shifted toward improving the sensitivity of FD-OCT from depths inside the tissue. 2.Experimental SetupA schematic diagram of an FD-OCT system capable of generating Talbot bands is shown in Fig. 1. Light from a superluminescent diode [(SLD), central wavelength 840 nm, spectral bandwidth 45 nm], is divided by a DC into an object and a reference beam collimated by the microscope objectives MO1 and MO2, respectively, 10% of the power being directed toward the sample (∼800 μW) and 90% toward the reference. In the reference arm, light propagates through a dispersion compensation slab toward a microscope objective MO3, which focuses light into a single-mode fiber that launches light via an achromatic lens, Lr toward a beam splitter [(BS), splitting ratio 10/90]. In the object arm, light is scanned laterally over the sample under test using a galvanometer scanner, SX and a microscope objective MO. Light returned from the sample is launched towards the BS using an achromatic lens, Ls. The two achromatic lenses, Ls and Lr of 7.5 cm focal length, determine diameters of 1.8 cm for the beams directed toward the spectrometer via the BS. The spectrometer consists of a transmission diffraction grating [(TG), 1200 l/mm, Wasatch Photonics, Logan, Utah], a spherical mirror (SM) of focal length 20 cm, a flat mirror (FM), a cylindrical lens (Lc) of focal length 10 cm, and a 12-bit, 2048-pixel (each 14 × 14 μm in size) linear CCD1 camera (Aviiva M2 CL). The system usually operated at an exposure time of 50 μs (acquisition speed 18 × 103 A-scans/s), which determined an acquisition rate of 18 Hz of B-scan OCT images when 1000 lines were used per frame. In order to implement a Talbot bands configuration, the two-interferometer beams are laterally shifted with respect to each other before being incident on the diffraction grating by actuating on the translation stage (TS), which translates the fiber launcher in the reference arm in a direction orthogonal to the direction of the reference beam launched toward BS. A 2-D CCD camera (CCD2) was used to monitor the gap (G) between the two interferometer beams. The OPD is adjusted by altering the distance between the microscope objectives MO2 and MO3. Fig. 1Schematic diagram of the Talbot bands FD-OCT system. SLD: superluminescent diode, MO, MO1–MO3: microscope objectives, Lr, Ls: achromatic lenses; Lc: cylindrical lens; TG: transmission grating; SM: spherical mirror; FM: flat mirror BS: bulk beam-splitter; DC: directional coupler; TS: translation stage; SX: galvoscanner; G is the gap between the centers of the two beams originating from the reference and object arm respectively; CCD1: 1-D CCD camera in the spectrometer; CCD2: 2-D CCD camera to monitor the lateral displacement, G, of the two beams, using the zero order of diffraction. 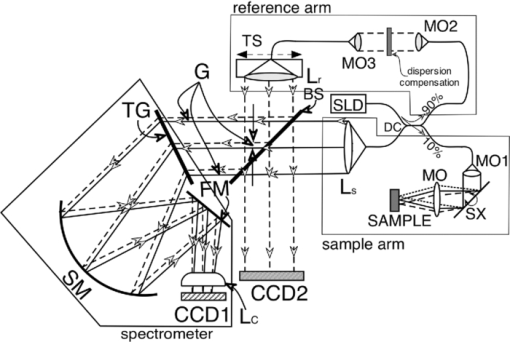 3.TheoryA simple explanation of the Talbot band visibility profile versus OPD is based on a pulse description of the light diffracted by the diffraction grating.18 According to the Bragg equation and considering the first diffraction order, there is a differential delay ±λ between rays originating from adjacent grating lines. Consequently, if the two beams—sample and reference—illuminate each an equal number of grating lines N, and then for the first order of diffraction, the two diffracted beams can be considered each as wave trains of approximate length Nλ, where λ is the central wavelength of the source light spectrum. As shown in Refs. 18 and 19, the visibility profile of the Talbot bands is proportional to the amount of overlap of the two wave trains, CTB. Thus, a complete description of the visibility decay, V(OPD), can be found by multiplying C TB with a sinc function due to the limited number of pixels in the CCD array of the spectrometer,21 Eq. 1[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm V(OPD)} = C_{{\rm TB}} \left({\frac{{\sin \zeta }}{\zeta }} \right)^2, \end{equation}\end{document}Eq. 2[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \zeta = \frac{\pi }{2}\frac{{{\rm OPD}}}{{Z_{\rm max} }}, \end{equation}\end{document}Eq. 3[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} Z_{\max } = \frac{{M\lambda ^2 }}{{4\Delta \lambda }}, \end{equation}\end{document}Fig. 2Sensitivity profile of FD-OCT due to the limited number of pixels in the spectrometer array (the sinc function). Zero sensitivity is achieved at OPD values equal to ±2Z max = 7.5 mm. 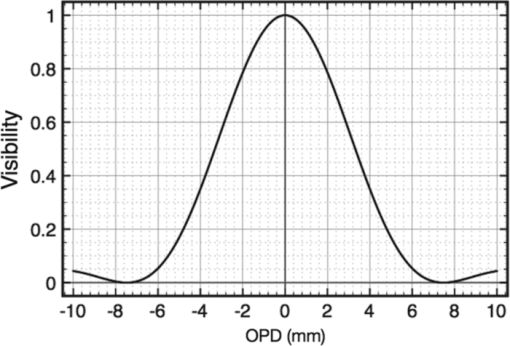 Assuming that the two beams cover each N grating lines and excite the grating lines equally, then if the two beams are superposed in their way toward the TG, the factor C TB is a triangle with a base between –Nλ and Nλ. In reality, the power distribution within the beams is not uniform and this effect was evaluated in Ref. 19. Irrespective of the exact profile of the power distribution within the beam cross section, the extension of the C TB can be well approximated as 2Nλ. To make use of the full sinc profile in Fig. 2, the width of the C TB profile should be larger than the width of the sinc factor. This leads to the condition that the length Nλ of the wave train should exceed 2Z max = 7.5 mm Eq. 4[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm N}\lambda > 2Z_{\max }. \end{equation}\end{document}Eq. 5[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} N = \frac{D}{{a\cos \beta }}, \end{equation}\end{document}There is another reason why the beam diameter should be large; this is due to the fact that the ratios of focal lengths of SM and of Lr (L s) magnifies the fiber core size, ∼5.6 μm of the launching fiber into the spot size on the CCD. For maximum efficiency, the spot size should not be larger than the camera pixel size, 14 μm. On the other hand, the focal length of SM is determined by the need to spread the spectrum, for a given diffraction power, over as many pixels as possible on the CCD camera. A choice of 20 mm for the focal length of SM, determines a focal length of 7.5 cm for Ls and Lr to achieve a vertical size of the pixel of 14 μm. Elimination of mirror terms requires a large lateral displacement, G, of the two beams equal to or larger than their beam diameter.18, 19, 20, 21 Unfortunately, this would shift the profile of CTB laterally within the OPD range as determined by the graph in Fig. 2, to regions where the amplitude of the sinc factor is less and much less than the maximum value achieved at OPD = 0. This suggests that, instead of aiming to achieve total elimination of mirror terms, a trade-off should be adopted between the sensitivity and mirror terms attenuation, by using a smaller lateral displacement, G, of the two beams than their beam diameter. This is what makes this study different from our previous experimental reports20, 21 on Talbot bands, where the extension of the wave-train length was less or comparable to the width of the sinc factor in Eq. 1. In our previous reports, for any given sinc profile, the C TB profile was easier to be inferred if its width, 2Nλ, was much smaller or smaller than the sinc width, 4Z max {i.e., inequality [Eq. 4] not satisfied}. Because in this paper, the emphasis is not on elimination of mirror terms but more on the sensitivity from inside the sample, we aimed for parameters values adopted in the practice of FD-OCT, where a large number of grating lines, N, is illuminated and the sensitivity decay, is practically given by the sinc factor {inequality [Eq. 4] satisfied}. A useful range of gap values, G up to G max, can be inferred from the simple observation that the maximum of the factor C TB, moves in OPD by Pλ, where the number of grating lines covered by the gap G is P. A useful range would be to shift the maximum OPD value where C TB exhibits a maximum to the middle of the interval between the maximum of the sinc factor and its zero. This means Pλ = Z max, which gives a maximum Eq. 6[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} G_{\max } = Z_{\max } \frac{{a\cos (\beta)}}{\lambda }, \end{equation}\end{document}We experimentally show the effect of increasing the gap G on images collected from a tilted paper sheet, a thick phantom and a finger, where the quality of images can be interpreted from the amplitude of the C TB sensitivity profile shifted underneath the curve in Fig. 2. 4.ResultsIt should be noted that in a standard FD-OCT system, the two beams interfere first and their results is spectrally analyzed (i.e., the order of operation is interference first, diffraction second). In a Talbot bands configuration, with no lateral superposition of the two beams, the order of operation is diffraction for each beam first, followed by interference on the photodetectors of the CCD linear array second. Therefore, in a Talbot bands configuration employing a lens in front of the camera, different thicknesses of glass lens are traversed by the two beams and, therefore, some dispersion is cumulated in this process. In all our previous experimental studies on Talbot bands, a lens was used in front of the camera19, 20, 21 and we believe that some of the decay of sensitivity reported was also partly due to the dispersion created between the two beams. Therefore, we investigated here a reflective spectrometer, where an SM was used. Choice of a reflective spectrometer would be also justified in the future by the trend toward higher depth resolution, which requires handling large bandwidths, even if a standard FD-OCT configuration was used. To reduce the astigmatism introduced by the SM, a cylindrical lens, Lc, was placed in front of the CCD.24 This does not introduce dispersion when laterally displacing the two beams, because both beams will traverse equal lengths of glass through the cylindrical mirror. Therefore, first we evaluated the effect of replacing the lens with the group formed from an SM plus a cylindrical lens, Lc, in the spectrometer. For simplicity, when referring to the mirror configuration spectrometer we will mean the group of SM plus Lc replacing the converging lens (lens configuration spectrometer used in Refs. 20 and 21). Figure 3 comparatively presents the sensitivity decay with depth for two configurations, where a converging lens or the group of SM plus Lc were employed as a focusing element between the grating and the CCD camera. In the two different spectrometer configurations, the spherical mirror and the converging lens had the same focal length (20 cm) and the two beams were superposed, as in any traditional FD-OCT setup. In this case, the two beams traversed through the same part of the focusing element and, therefore, no dispersion was incurred in the spectrometer lens. The flat mirror (F), required for compactness of the setup when using the spherical mirror, was removed when a lens was used. Fig. 3Sensitivity of the FD-OCT setup measured as a function of depth. Squares: spectrometer using a lens between the grating and the CCD in a standard FD-OCT configuration (G = 0). Circles: spectrometer using a spherical mirror plus cylindrical lens in a standard FD-OCT configuration (G = 0). Triangles: spectrometer using a spherical mirror plus cylindrical lens in a Talbot bands configuration (gap value G adjusted for each OPD value to maximize signal). 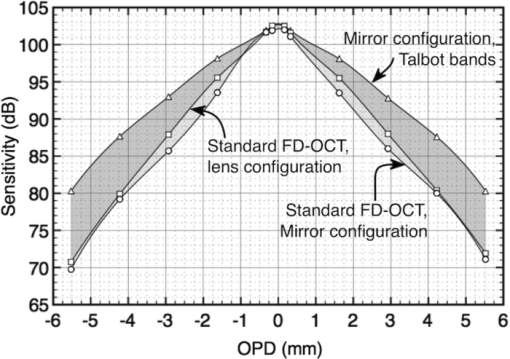 For the standard FD-OCT configuration (beams superposed), in Fig. 3 a sensitivity decay of 6 dB is noted for OPD ∼ 1.5 mm when using the lens configuration and the sensitivity curve when using the SM and Lc configuration is slightly less (by 1–2 dB) than the sensitivity curve when using the lens configuration. However, the sensitivity decay is much better than the case of a spectrometer using SM alone. If SM only was used, then the decay with depth was more pronounced, with a sensitivity profile 15–20 dB less than that of the lens configuration for OPD values of >5 mm. The curves corresponding to the standard FD-OCT scheme (lens and SM+Lc configuration) were obtained by fully overlapping the two reference and sample beams (gap between the centers of the reference and sample beams G = 0 mm). To evaluate the Talbot band configuration, the reference beam is displaced laterally. In the lens-based configuration, we could not note any improvement in sensitivity for any gap between the two beams. We explain this by the effect of dispersion introduced between the two beams traversing different glass parts. Figure 3 presents the sensitivity decay curve when using SM and Lc, which is obviously above the curve obtained using the standard scheme, especially for large OPD values. This curve was obtained by adjusting the gap G for each OPD value to achieve a maximum signal. Figure 3 clearly demonstrates that a Talbot bands scheme could bring >9 dB gain in sensitivity for OPD values of>5.5 mm. The results presented in this paper from now on are all obtained using a mirror-based spectrometer (SM + Lc). The procedure of measuring the sensitivity was similar to that presented in Ref. 1, as follows:
Then, we devised a simple procedure to evaluate the sensitivity of the FD-OCT system over both positive and negative OPD values in one process by using a tilted scattering surface. We used a sheet of plane paper placed over a flat metal plate. To reduce the effect of confocal gating affecting the depth sensitivity, a long focal-length objective (MO) of 5 cm was used. Even with such a long focal length, the confocal profile measured by moving a mirror through focus and registering the strength of signal collected in the fiber exhibited a narrow FWHM axial range of only 1 mm. The paper was placed in the focal point of the microscope objective MO tilted at 30 deg from the optical axis. When the reference and sample beams are perfectly superposed (standard FD-OCT), the B-scan shows an image similar to a letter “V” rotated by 90 deg (Fig. 4), with the bottom part of “V” (extreme left) corresponding to the lower frequencies delivered by the CCD readout. The two “arms” of the letter “V” correspond each to the positive and negative OPD values. In this way, a display of sensitivity versus OPD for both signs of OPD in a single B-scan is produced in real time. Figure 4a demonstrates this procedure for the standard configuration, with beams overlapped. The paper sample was sufficiently tilted to extend the whole depth range of the system within the lateral scan. For the standard FD-OCT, as expected, due to mirror terms, similar intensity is obtained for the two arms of the “V” letter. The horizontal axis in the B-scans extends up to 3.5 mm, value obtained experimentally by keeping a sample mirror in focus and varying the reference path length. This value is in good agreement with Z max = 3.75 mm evaluated using Eq. 3. The maximum intensity is obtained at OPD = 0 and the reduction in brightness along the branches of the letter “V” is the result of the combined effect of V(OPD) in 1 with the profile of the confocal gate, centered at OPD = 0. Fig. 4B-scans images from flat paper sufficiently tilted (by 30 deg from the optical axis of the system) to display both positive and negative OPD values. The nine B-scan images correspond to values of the gap, G, between the centers of the two beams of (a) 0, (b) 0.25, (c) 0.5, (d) 0.75, (e) 1, (f) 1.25, (g) 1.5, (h) 1.75, and (i) 2 mm, respectively. The dashed vertical lines correspond to two axial positions, A at Z = 0.4 mm and B at to Z = 1.6 mm. Superior branches in the letter “V” correspond to the signal, of intensity S, inferior branches to the mirror term, intensity MT.  As soon as the reference and sample beams are shifted laterally, the maximum of sensitivity moves from OPD = 0, as explained in Refs. 18 and 19. This effect is shown in Figs. 4b, 4c, 4d, 4e, 4f, 4g, 4h, 4i, where a gap G of 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, and 2 mm, respectively, between the centers of the reference and sample beams was created by laterally shifting the TS. It can be easily noted that the maximum sensitivity continuously shifts away from OPD = 0, as a unique feature of a Talbot bands configuration. Considering the number of grating lines corresponding to a gap G and using similar reasoning as in the derivation of Eq. 6, the position of the C TB maximum moves to Eq. 7[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm Z}_{{\rm TB}} = \frac{{\lambda G}}{{2a\cos (\beta)}}. \end{equation}\end{document}Unfortunately, as the gap G between the centers of the two beams is increased, less sensitivity is achieved because the C TB profile, with maximum away from zero OPD, is multiplied by the sinc curve in Fig. 2, which has its maximum at OPD = 0. If the gap between the two beams equals their beam diameter, then the mirror terms are totally removed; however, the sensitivity is relatively low, which renders the method inefficient. In all the measurements in Fig. 4, the focus position of the object beam interface, determined by the two microscope objectives MO and MO1, was kept constant, at OPD = 0. To evaluate the attenuation of mirror terms when a Talbot bands configuration is used, we collected the strength values from the “V”-like curves in Fig. 4 intersected by the dashed vertical lines, A and B, placed at respective Z values of 0.4 and 1.6 mm. Given the orientation of the grating and the relative position of the two beams, the top point on these lines gives the signal strength (S) and the bottom point gives the strength of the mirror term (MT). These values were then used to construct the graphs in Fig. 5. They represent in logarithmic scale the ratio S/MT between the strength of the signal and the strength of its mirror term for the two particular Z values. The attenuation of the mirror term (qualitatively observed in Fig. 4) is more obvious at large OPD values (position B), where the it can be attenuated in respect to the signal by as much as 17 dB, as shown in Fig. 5a, by simply creating a gap as small as G = 2 mm. For a superficial depth position (A), the ratio S/MT barely exceeds 6 dB for G ∼ 1 mm [Fig. 5a]. Fig. 5Ratios of the intensity values at the intersections between the letter “V” and the vertical lines in Fig. 4. S/MT are evaluated as 20 log[(strength of the signal)/(strength of its mirror term)] versus gap G, measured for Z = 0.4 mm (curves A) and Z = 1.6 mm (curves B) using: (a) focus at Z = 0; (b) focus shifted to Z = 0.75 mm, found experimentally as the focus adjustment value where the strength of the image in Fig. 4e was enhanced. To obtain these graphs, data were collected from similar “V” letters obtained as in Fig. 4, but with the focus at Z = 0.75 mm. 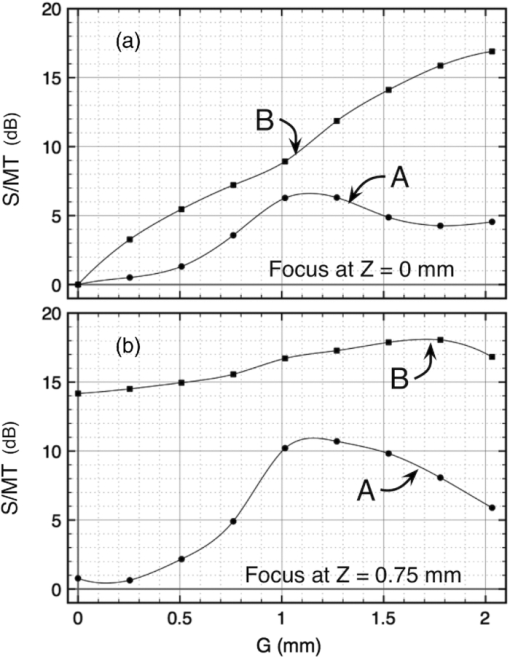 In the practice of OCT imaging using spectral OCT methods, it is common to shift the focus to enhance the sensitivity at larger depth and compensate for the disadvantage of sensitivity decay with depth as well as for the limited extension of the confocal profile. Therefore, the focus position was adjusted so that for the case when G = 1 mm [Fig. 4c], more brightness was achieved on the superior branch of the “V”. This approximately corresponds to placing the focus position at Z = 0.75 mm. Keeping this focus position, we have acquired new B-scan images similar to those presented in Fig. 4 (not shown), exhibiting different variation of sensitivity along the branches of the letter “V”. Using the new “V”-like images, we produced Fig. 5b, where the ratio S/MT versus G, for the two particular OPD values is plotted. At position B, the S/M ratio is as high as 14 dB for G = 0. By increasing G (Talbot bands configuration), up to 4 dB more attenuation is achieved (i.e., in this particular case, the confocal profile contributed more than C TB to the reduction of the mirror terms). On the other hand, at a superficial depth (A), the focus shift and Talbot bands scheme bring together a 10-dB enhancement for G = 1 mm. In order to quantitatively demonstrate that better sensitivity at large OPD values can be obtained using a Talbot bands configuration instead of a standard FD-OCT configuration, in Fig. 6, we show for the same two positions A and B, how the ratio between the signal strength in a Talbot bands configuration, S TB and the signal strength in a standard FD-OCT configuration, S st varies with G. Figures 6a, 6b were obtained when the beam was focused by the optical interface at Z = 0 mm, while Figs. 6c, 6d were obtained for the focus shifted to Z = 0.75 mm. Ratios between mirror term strength M TB in the Talbot bands configuration and mirror term strength M st in a standard FD-OCT configuration are also shown. Figures 6a, 6c show that for a superficial depth (such as for a point A at Z = 0.4 mm), a Talbot bands configuration either does not affect the signal for G < 1 or reduce it for G > 1. There is however more effect on the M TB/M st ratio. Fig. 6STB/Sst evaluated as 20 log[(signal strength in a Talbot bands configuration)/(signal strength in a standard FD-OCT configuration)] versus gap, G, and MTTB/MTst evaluated as 20 log[(mirror term strength in a Talbot bands configuration)/mirror term strength in a standard FD-OCT configuration)] versus gap, G, measured for (A) Z = 0.4 mm and (B) Z = 1.6 mm using focus at Z = 0 in (a) and (b) and focus shifted towards Z = 0.75 mm in (c) and (d). 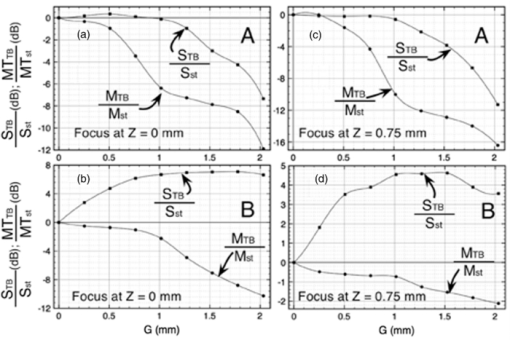 Figures 6b, 6d show that for deeper positions (such as for a point B at Z = 1.6 mm), a Talbot bands configuration can improve the sensitivity even for small G values. Figure 6d demonstrates some improvement even when the focus was shifted in depth (which advantages both the standard configuration and the Talbot bands configuration), although the improvements in terms of signal enhancement and mirror term reduction are less than in Fig. 6b. To have a clearer picture on how a Talbot bands configuration affects the sensitivity profile within B-scans, we imaged a thick rectangular slab of resin with a high concentration of scattering titanium dioxide. Figure 7 shows such B-scans images in the first and the third rows, with a lateral size of 2 mm, obtained for a standard FD-OCT configuration (G = 0 mm, first column), and Talbot bands configurations (G = 0.75 mm, second column, and G = 1.5 mm, third column). Because FD-OCT works under a fixed focus, we acquired two sets of B-scans. In the first row, the images (a1), (b1), and (c1) were collected with the focus fixed at OPD = 0. In the third row, the focus was shifted so that the brightness of the B-scan image in (c1) was enhanced. Fig. 7B-scan images of a TiO2 resin-based sample (first and third row) and averaged A-scans over each B-scan image above, obtained for G = 0 mm (first column), 0.75 mm (second column), and 1.5 mm (third column). (a1), (b1), and (c1): B-scan images with focus at OPD = 0; (d1), (e1), and (f1): B-scan images with focus adjusted to enhance the brightness in the image (c1). 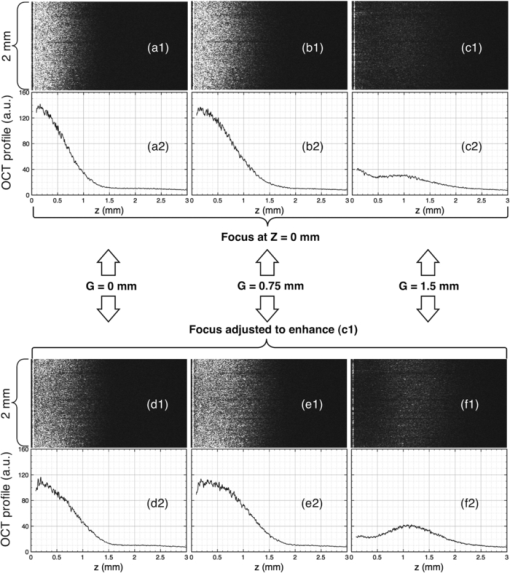 For each B-scan image, we averaged over all the A-scans and constructed the profiles shown in the second and fourth rows. These profiles show that as the gap G increases, the maximum sensitivity of the V(OPD) shifts toward deeper depths in the sample (larger OPD value). Initial tests with a spectrometer made using a lens between the grating and the CCD, did not show such an effect, possibly due to the dispersion exacerbated by the large-beam diameters employed. This difference in behavior in comparison to our previous experimental reports20, 21 prompted us to construct a reflective spectrometer to cope with the case of large-beam diameters used in this study. To have a clearer quantitative picture of the enhancement due to a Talbot bands configuration, Fig. 8a shows the ratios of the OCT profiles in Fig. 7 in logarithmic scale: the ratio of the profile (b2) over the profile (a2) and the ratio of the profile (c2) over the profile (a2). This demonstrates the improvement brought by implementing a Talbot bands configuration in comparison to a standard FD-OCT configuration, with the focus at Z = 0. Figure 8b shows the ratio of profile (e2) over the profile (d2) and the ratio of profile (f2) over the profile (d2), to illustrate improvement even when compared to a standard FD-OCT case enhanced by shifting the focus deeper. The graphs (c2)/(a2) in Fig. 8a and (f2)/(d2) in Fig. 8b show that a standard FD-OCT configuration can exhibit a higher sensitivity than a Talbot bands configuration in a range of depths from zero to 1.0 mm for G = 1.5 mm. However, as commented above, this does not represent a usable range for imaging moving targets, whereas the Talbot bands configuration can achieve more sensitivity from larger depths. For instance, larger sensitivity is obtained in a Talbot bands configuration for G = 1.5 mm, from 1.0 to 2.3 mm in Fig. 8a for focus at zero and up to 2.75 mm in Fig. 8b for deep focus. The graphs in Fig. 8 demonstrate the potential for a novel application of a Talbot bands configuration, that of improving the sensitivity at depths by synchronizing the focus change with the change in the gap, G. This procedure can advantageously be employed to alleviate another drawback of FD-OCT that of working under fixed focus. Recently a solution was proposed, based on Gabor fusion technique,25 where several B-scans are collected for successive focus changes and a compound image is formed from the regions of the B-scans, which are within the confocal gate. Similarly, a compound image can be formed from several B-scans collected in a Talbot bands configuration for several G values, where the focus position was optimized for each G value. In this way, successive contributions from deeper depths are collected. The smaller sensitivity shown by the graphs (c2)/(a2) and (f2)/(d2) for shallower depths does not represent a disadvantage, as these parts are eliminated when using the fusion technique of those parts of the images selected from within the B-scans which coincide with the maximum sensitivity imprinted by a given G (and matched by focus shift). Fig. 8(a) Ratio of the profiles in the second row in Fig. 7 versus axial distance, 20 log[(b2)/(a2)] and 20 log[(c2)/(a2)]; (b) ratio of the profiles in the fourth row in Fig. 7 versus axial distance, 20 log[(e2)/(d2)] and 20 log[(f2)/(d2)]. 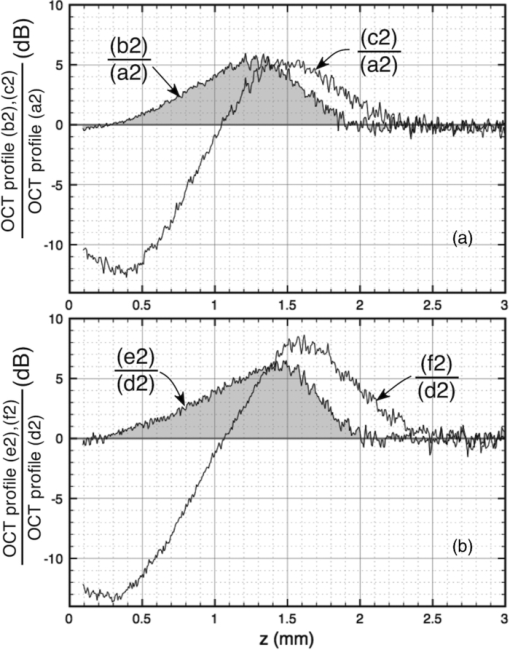 In order to demonstrate the improvement in the quality of in vivo images obtained using a Talbot bands configuration, B-scan OCT images of a fingertip are generated for different values of the gap, G (Fig. 9). The camera was operated at 18 kHz producing B-scan OCT images of 1024 A-scans. The focus was fixed at Z = 0. As the gap G is increased, the OPD was also adjusted to track the shift of the C TB profile in depth, while the finger was kept at the same distance from the MO. This is shown by the fingertip appearing at successive larger distances from OPD = 0 as G is increased. By increasing the lateral gap between the two beams, similar effects to those noted in Figs. 4, 5, 6, 7 are seen. Fig. 9Cross-sectional OCT images from the thumb of a volunteer, for different gap values, G, between the centers of the reference and sample beams: 0, 0.25, 0.50, 0.75, 1, and 1.25 mm. Lateral size of images: 6 mm, vertical size: 3.5 mm, measured in air. 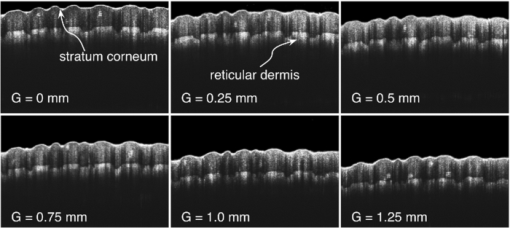 To evaluate the strength of signal in the OCT images in Fig. 9, we averaged 50 A-scans collected in the middle of each image and produced the overall reflectivity profiles in Fig. 10. It can be noted that even when the tip of the finger is placed at large OPD values, sufficient strength of signal at both stratum corneum (superficial) and reticular dermis (deep) is obtained. As G is increased, the peak of the C TB profile is shifted in depth to deeper positions Z TB and this improves the strength of the signal despite decay imprinted by the confocal profile and the sinc factor. Fig. 10Reflectivity profiles obtained by averaging 50 A-scans in the middle of each B-scan OCT image presented in Fig. 9. 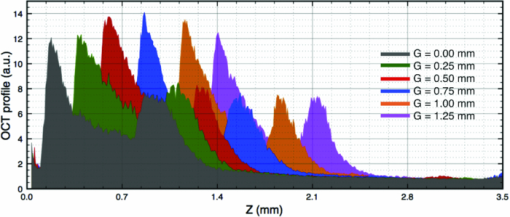 5.ConclusionsAn improved Talbot bands low coherence interferometer configuration is demonstrated. The configuration presented is different in two respects to the configurations that we reported before, because it employs: (i) large-diameter beams to excite a large number of grating lines, as used in the practice of conventional FD-OCT in order to maximize the axial range, and (ii) a reflective spectrometer. This second change was motivated by two reasons. The first reason was to avoid the dispersion introduced by the two beams traversing different thicknesses of glass if a lens was used between the grating and the CCD, as in a Talbot bands configuration, the spectrometer becomes part of the interferometer. A second reason was to widen the bandwidth of the OCT configuration as a preliminary step before testing a Talbot bands configuration with an ultrawide bandwidth optical source. The replacement of the lens in the spectrometer with a spherical mirror has however introduced astigmatism, and therefore, another configuration improvement is marked by the addition of a tilted cylindrical lens. The variation of sensitivity with depth was evaluated for different values of the gap G created between the centers of the two interfering beams in their way towards the CCD. In order to avoid the reduction in signal efficiency due to the attenuation introduced by the sinc factor in Eq. 1, the lateral shift, G, was limited, of up to 2 mm while the beam diameter of the two interfering beams was much larger, 18 mm. In the configuration presented, the two beams were partially superposed, in which case the interference takes place partially before diffraction for the proportion of overlapped beams and partially after diffraction, on the CCD array, for the proportion of nonoverlapping parts of the beams. This regime was found more suitable in terms of sensitivity than a genuine Talbot configuration, with beams separated by their beam diameter as a trade-off between sensitivity decay and attenuation of mirror terms. In a classical Talbot band configuration, there is no overlap between the two beams and interference takes place on the CCD after diffraction only. A tilted scattering flat surface was used to display the sensitivity profile in a B-scan over both positive and negative OPD values. This method has allowed a suggestive illustration of the sensitivity modulation due to the gap between the centers of the two beams and due to the confocal profile of the interface optics. Then images of a finger were acquired, and in-depth features were employed to assess the contrast values with respect to the strength of signal acquired from superficial layers. Because the skin is thin as an object for OCT, returning single scattering photons from depths of <1 mm, while the axial range of the setup was over 3 mm, we also used a phantom thicker than the axial range, of less attenuation than skin to display the whole sensitivity profile predicted by Eq. 1. The Talbot bands configuration presented has the added advantage of reducing the sensitivity for small values of OPD, where normally the scattering centers with the largest reflection are placed. There is a trade-off between the shift of peak sensitivity toward larger depths in the tissue and the overall sensitivity. Larger shifts of maximum sensitivity of the C TB toward higher depths with less reduction in the overall sensitivity are achievable by using linear cameras with larger number of pixels. This will allow better attenuation of mirror terms as well. AcknowledgmentsThe authors acknowledge support from the United Kingdom Biotechnology and Biological Sciences Research Council, Grant No. BB/E002870/1, the Engineering and Physical Sciences Research Council, Grant No. EP/H004963/1, and the European Research Council, Grant No. 249889. ReferencesR. Leitgeb, C. K. Hitzenberger, and
A. F. Fercher,
“Performance of Fourier domain vs. time domain optical coherence tomography,”
Opt. Express, 11 889
–894
(2003). https://doi.org/10.1364/OE.11.000889 Google Scholar
S. Taplin, A. Gh. Podoleanu, D. J. Webb, and
D. A. Jackson,
“Displacement sensor using channeled spectrum dispersed on a linear CCD array,”
Electron. Lett., 29
(10), 896
–897
(1993). https://doi.org/10.1049/el:19930598 Google Scholar
A. Gh. Podoleanu, S. Taplin, D. J. Webb, and
D. A. Jackson,
“Channeled spectrum liquid refractometer,”
Rev. Sci. Instrum., 64
(10), 3028
–3029
(1993). https://doi.org/10.1063/1.1144355 Google Scholar
A. Gh. Podoleanu, S. Taplin, D. J. Webb, and
D. A. Jackson,
“Channeled spectrum display using a CCD array for student laboratory demonstrations,”
Eur. J. Phys., 15 266
–271
(1994). https://doi.org/10.1088/0143-0807/15/5/008 Google Scholar
M. Wojtkowski, A. Kowalczyk, P. Targowski, and
I. Gorczynska,
“Fourier-domain optical coherence tomography: next step in optical imaging,”
Opt. Appl., 32
(4), 569
–580
(2002). Google Scholar
E. Götzinger, M. Pircher, R. Leitgeb, and
C. Hitzenberger,
“High speed full range complex spectral domain optical coherence tomography,”
Opt. Express, 13
(2), 583
–594
(2005). https://doi.org/10.1364/OPEX.13.000583 Google Scholar
M. V. Sarunic, M. A. Choma, C. H. Yang, and
J. A. Izatt,
“Instantaneous complex conjugate resolved spectral domain and swept-source OCT using 3 × 3 fiber couplers,”
Opt. Express, 13
(3), 957
–967
(2005). https://doi.org/10.1364/OPEX.13.000957 Google Scholar
J. Zhang, J. S. Nelson, and
Z. Chen,
“Removal of a mirror image and enhancement of the signal-to-noise ratio in Fourier-domain optical coherence tomography using an electro-optic phase modulator,”
Opt. Lett., 30 147
–149
(2005). https://doi.org/10.1364/OL.30.000147 Google Scholar
A. B. Vakhtin, K. A. Peterson, and
D. J. Kane,
“Fourier-domain OCT by harmonic lock-in detection of the spectral interferogram,”
Opt. Lett., 31
(9), 1271
–1273
(2006). https://doi.org/10.1364/OL.31.001271 Google Scholar
R. K. Wang,
“In vivo full range complex Fourier domain optical coherence tomography,”
Appl. Phys. Lett., 90 054103
(2007). https://doi.org/10.1063/1.2437682 Google Scholar
L. An and
R. K. Wang,
“Use of a scanner to modulate spatial interferograms for in vivo full-range Fourier-domain optical coherence tomography,”
Opt. Lett., 32
(23), 3423
–3425
(2007). https://doi.org/10.1364/OL.32.003423 Google Scholar
R. A. Leitgeb, R. Michaely, T. Lasser, and
S. C. Sekhar,
“Complex ambiguity free Fourier domain optical coherence tomography through transverse scanning,”
Opt. Lett., 32
(23), 3453
–3455
(2007). https://doi.org/10.1364/OL.32.003453 Google Scholar
B. Baumann, M. Pircher, E. Götzinger, and
C. K. Hitzenberger,
“Full range complex spectral domain optical coherence tomography without additional phase shifters,”
Opt. Express, 15
(20), 13375
–13387
(2007). https://doi.org/10.1364/OE.15.013375 Google Scholar
A. H. Bachmann, R. A. Leitgeb, and
T. Lasser,
“Heterodyne Fourier domain optical coherence tomography for full range probing with high axial resolution,”
Opt. Express, 14
(4), 1487
–1496
(2006). https://doi.org/10.1364/OE.14.001487 Google Scholar
H. Bernd, B. Považay, A. Unterhuber, L. Wang, B. Hermann, S. Rey, G. Matz, and
W. Drexler,
“Fast dispersion encoded full range optical coherence tomography for retinal imaging at 800 nm and 1050 nm,”
Opt. Express, 18
(5), 4898
–4919
(2010). https://doi.org/10.1364/OE.18.004898 Google Scholar
F. Talbot,
“An experiment on the interference of light,”
Philos. Mag., 10 364
(1837). Google Scholar
A. L. King and
R. Davis,
“The curious bands of Talbot,”
Am. J. Phys., 39 1195
–1198
(1971). https://doi.org/10.1119/1.1976602 Google Scholar
A. Gh. Podoleanu,
“Unique interpretation of Talbot bands and Fourier domain white light interferometry,”
Opt. Express, 15 9867
–9876
(2007). https://doi.org/10.1364/OE.15.009867 Google Scholar
D. Woods and
A. Gh. Podoleanu,
“Controlling the shape of Talbot bands’ visibility,”
Opt. Express, 16 9654
–9670
(2008). https://doi.org/10.1364/OE.16.009654 Google Scholar
A. Gh. Podoleanu and
D. J. Woods,
“Power efficient FDOCT set-up for selection in the optical path difference sign using Talbot bands,”
Opt. Lett., 32 2300
–2302
(2007). https://doi.org/10.1364/OL.32.002300 Google Scholar
M. Hughes, D. Woods, and
A. Gh. Podoleanu,
“Control of visibility profile in spectral low-coherence interferometry,”
Electron. Lett., 4 182
–183
(2009). https://doi.org/10.1049/el:20092512 Google Scholar
Z. Hu, Y. Pan, and
A. M. Rollins,
“Analytical model of spectrometer-based two-beam spectral interferometer,”
Appl. Opt., 46
(35), 8499
–8505
(2007). https://doi.org/10.1364/AO.46.008499 Google Scholar
S. H. Yun, G. Tearney, B. Bouma, B. Park, and
Johannes de Boer,
“High-speed spectral-domain optical coherence tomography at 1.3 mm wavelength,”
Opt. Express, 11
(26), 3598
–3604
(2003). https://doi.org/10.1364/OE.11.003598 Google Scholar
K. S. Lee, K. P. Thompson, and
J. P. Rolland,
“Broadband astigmatism-corrected Czerney–Turner spectrometer,”
Opt. Express, 4 23378
–23384
(2010). https://doi.org/10.1364/OE.18.023378 Google Scholar
J. P. Rolland, P. Meemon, S. Murali, K. P. Thompson, and
K.-s. Lee,
“Gabor-based fusion technique for optical coherence microscopy,”
Opt. Express, 18 3632
–3642
(2010). https://doi.org/10.1364/OE.18.003632 Google Scholar
|


