|
|
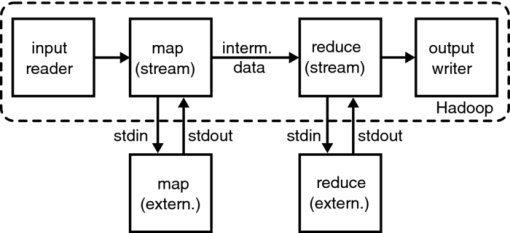
1.IntroductionResearchers have long relied on single-threaded programming for solving computational problems. However, in many applications, the growth of scientific data has outpaced the performance of single-core processors. Furthermore, multicore processors and many-core graphics processing units (GPUs) are now the industry standard for high-performance computing. As a result, scientific computing is inexorably shifting to parallel architectures. In biomedical applications, the need for high-performance computing is growing as technology evolves toward more accurate imaging and treatment delivery methods. Monte Carlo simulation is the gold standard for modeling complex physical systems, such as photon migration in biological tissue.1, 2, 3 Yet the use of Monte Carlo methods is still hampered by the high computational cost. For instance, it is still not practical to conduct Monte Carlo simulations for planning of photodynamic therapy,4 especially when using inhomogeneous tissue models.5, 6 Several distributed approaches have been proposed and implemented to accelerate Monte Carlo simulation of photon transport. Monte Carlo simulation belongs to a class of problems referred to as “embarrassingly parallel”, because little effort is required to split the problem into parallel tasks. Several high-energy Monte Carlo packages have been ported onto computer clusters using tools such as MPI (Refs. 7, 8, 9) and shell scripting.10 Light transport in turbid medium has also been accelerated using computer clusters,11 multiprocessor systems,12 and field-programmable gate arrays.13 In recent years, the graphics processing unit has become a popular platform for running distributed biomedical computations.14 For simple homogeneous media, GPU computing can dramatically accelerate Monte Carlo simulation of photon migration.15 Very high acceleration can also be achieved for voxelized and multilayer geometries.16, 17 Acceleration is more modest for complex mesh-based geometries18 because the distributed calculation of the intersection of a set of rays with a triangular mesh is challenging on the GPU. Monte Carlo simulation for high-energy physics has also been investigated on the GPU.19, 20 Because high-energy particles can undergo a wide range of physical interactions with matter, these implementations use complex optimization strategies for efficient processing.21 While parallel processing techniques can accelerate Monte Carlo simulations, practical considerations can be an obstacle to porting existing single-threaded codes onto parallel architectures. To utilize parallel resources efficiently, programmers must be skilled in parallel programming and spend substantial effort optimizing the parallel portion of their code. Parallel code is also harder to debug and maintain. Last, large computer clusters are not always available at a medical institution for running massively parallel applications. All these practical issues are important drawbacks to the development and use of distributed algorithms. Recently, Internet-scale computation has emerged as a major driver for new parallel processing technologies. Internet companies routinely process very large datasets such as log files, user information, pictures, or videos. Most of these processing tasks are quite simple; however, the size of the input data is large and the computation has to be distributed to hundreds of nodes for practical processing times. Usually, porting these simple tasks onto parallel architectures requires far more effort than required for a single-thread implementation. To address this issue, MapReduce was developed at Google as a new framework to facilitate the development of parallel algorithms.22 MapReduce can hide the complexity of parallelization, data distribution, fault-tolerance, and load balancing to the developer, which can focus on developing the actual algorithm. In this programming model, the developer specifies simple tasks which are applied in a distributed fashion to large datasets. MapReduce is also well integrated with existing commercial cloud computing infrastructure. Cloud computing refers to the outsourcing of one's compute resources to third-party companies. Cloud computing providers offer services such as web-based software, data warehousing, and scalable clusters of virtual nodes. In a cloud computing environment, hardware resources are often virtual: computer nodes can be allocated on demand with custom specifications, and can migrate from one physical host to another. In a cluster, the number of nodes can also be scaled in real-time, according to demand for computation. MapReduce and cloud computing technologies are already widely used in applications such as web crawling and analytics,23, 24 data mining,25 machine learning,26 and bioinformatics.27, 28, 29, 30 In this paper, we investigate the use of MapReduce for biomedical Monte Carlo simulation. As a proof-of-concept, we ported an existing photon migration Monte Carlo code to Hadoop, an open-source MapReduce framework, and characterized the performance of this new implementation in a cloud computing environment. 2.MapReduceMapReduce is a programming model for processing large data sets.22 In this framework, the user specifies two functions called Map and Reduce, respectively. Although neither function is explicitly parallel, many instances of these functions are executed concurrently by the framework. Input data, stored on a distributed storage system, are split by MapReduce into chunks and distributed to parallel Map tasks for processing (Fig. 1). No communication is possible between Map tasks; however, the outputs of Map tasks can be combined by Reduce tasks. Fig. 1An overview of the MapReduce framework. A master node assigns Map and Reduce tasks to worker nodes. Input files are split into chunks, that are processed by independent Map tasks, producing a stream of intermediary key/value records. These records are selectively read by Reduce tasks according to their key, and combined finally into multiple outputs. 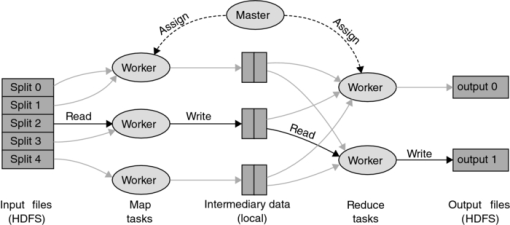 Data communication between Map and Reduce tasks is handled using key/value pairs (KVPs). In MapReduce, keys and values can be stored in any format, provided that keys can be compared to one another and sorted. While processing input data, Map tasks emit a sequence of intermediary records formatted as KVPs (Fig. 1). Intermediary records that share a common key are assigned to the same Reduce task. A partition function determines how keys are assigned to Reduce tasks. The role of the Reduce step is to combine intermediary records into the final output. Each Reduce task sequentially reads records associated with a given key. The user specifies how these records are combined. For example, the user can sum the values associated with a common key. The output of the Reduce function is automatically written in KVP format to a distributed storage system, from which it can be retrieved. Conceptually, Map and Reduce functions can be described as Eq. 1[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \text{map:} & v_{1} & \rightarrow \text{list}\,(k_{2},v_{2})\nonumber\\ \text{reduce:} & (k_{2},\text{list}\,(v_{2})) & \rightarrow \text{list}\,(v_{3}). \end{eqnarray} \end{document}A feature of MapReduce is its tolerance for hardware failures. In a large cluster, the probability that one or more nodes fail is non-negligible. When a node fails, MapReduce reschedules the compromised tasks onto other nodes in the cluster. A related issue is the heterogeneous performance of worker nodes. For instance, a node in the cluster might be crippled by a defective hardware component and run slowly. Such straggling nodes can substantially reduce the performance of the entire cluster. MapReduce uses a technique called speculative execution to overcome this type of situation. Worker nodes that finish their workload early can attempt to execute clones of tasks in progress elsewhere in the cluster. A task is considered completed when either its original or clone completes. The original MapReduce software framework developed by Google is not publicly available but several open-source alternatives exist. Hadoop,31 maintained by the Apache Software Foundation, is used by Internet companies for large-scale data processing, financial simulations and bioinformatics calculations. Hadoop set a record in 2009 by sorting 1 Petabyte of data in 16.3 h on 3658 nodes.32 The Hadoop project includes the Hadoop distributed file system (HDFS), designed for storing extremely large data files (Petabytes and up) on a distributed network of computers, and Hadoop MapReduce, the parallel computation engine. Although Hadoop is written in Java, developers can write jobs in any other programming language using a utility called Hadoop Streaming. Hadoop Streaming implements Map and Reduce functions as interfaces to external user-specified applications (Fig. 2). External Map and Reduce applications communicate with Hadoop Streaming through standard Unix streams. They read input KVPs via standard input (stdin) and write back their output via standard output (stdout). KVPs can be formatted as Text or TypedBytes, which are sequences of bytes in which the first byte is a type code. 3.Methods3.1.Monte CarloMC321, a steady-state optical Monte Carlo package for simulating photon migration in homogeneous turbid media,2 was implemented using Hadoop. In this package, photons are launched in packets with a virtual weight initially set to 1. As the photon packet propagates in the medium, it can scatter or be absorbed. The step size is sampled randomly based on the probability density function of free path. Once the photon packet has reached an absorption site, a fraction of its weight is absorbed and scored into a 256×256 detection grid. Next, the photon packet direction is updated by sampling the deflection angle in a manner consistent with anisotropic light scattering. Once the weight of a photon packet drops below 0.01, a Russian roulette test with a 10% survival probability is performed. If the packet survives, its weight is renormalized and the simulation continues. If the roulette test fails, the packet is terminated and a new photon packet may be initiated. No index mismatch or boundary conditions are considered in this simple simulation. Photons that reach the phantom's boundary escape the medium and are automatically terminated. The MC321 package is a simplified Monte Carlo method that has been utilized to study treatment planning for photodynamic therapy2 and x-ray luminescence imaging.33 MC321 cannot model heterogeneous media with spatially-varying optical properties, or photon propagation through material boundaries. However, MC321 shares common features with more accurate packages, such as MCML (Ref. 3) or tMCimg.5 3.2.MapReduce ImplementationWe propose two novel distributed implementations of MC321 using MapReduce. The first method, termed Monte Carlo event-based processing (MC-EP), splits the production and aggregation of photon histories into Map and Reduce steps, respectively. In this scheme, Map tasks run parallel Monte Carlo simulations, emitting intermediary KVPs every time a photon packet deposits a fraction of its weight into the medium (Fig. 3, top panel). In these intermediary records, the key is an integer index to the nearest two dimensional (2D) detection bin, and the value a floating-point number representing the photon weight absorbed in that bin. These intermediary records are then aggregated by parallel Reduce tasks in the following way: records that share the same key are sequentially read while the corresponding values are accumulated in a local variable. Once all the records for a given key have been processed, the Reduce tasks outputs the cumulated photon weight absorbed in the corresponding detection bin (Fig. 3, bottom panel). Fig. 3An overview of the MC-EP implementation. (Map) For each random seed loaded from stdin, N photon packets are simulated. Individual photon events are written to stdout. (Reduce) The stream of photon events, now sorted by key, are aggregated such that the total photon weight absorbed at every location is computed and written out to stdout. 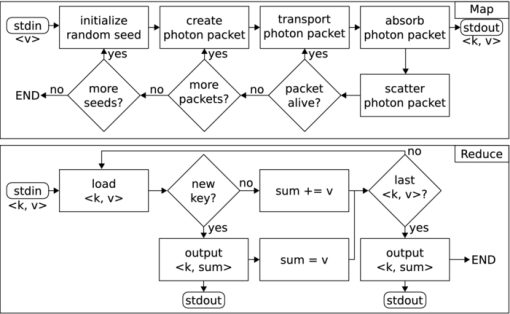 The MC-EP approach is highly flexible because it separates the production and the aggregation of photon histories. In general, little modification is required to implement the MC-EP scheme using an existing single-threaded Monte Carlo code. Streaming photon events to stdout using the KVP format requires minimal code change. (Typically, only a few fwrite statements need to be added to the code.) However, a drawback of the MC-EP approach is that large amounts of intermediary data are produced. To decrease the amount of data exchanged between Map and Reduce steps, intermediary KVPs can be partially aggregated within the Map stage prior to being transferred to the Reduce stage. In this scheme, termed Monte Carlo histogram-based processing (MC-HP), each Map task outputs a partial scoring array corresponding to the photon histories it has computed. In turn, Reduce tasks accumulate these partial outputs into a complete scoring array. In the MC-HP scheme, intermediary KVPs consist of a unique key (arbitrarily set to 1) and an array of floating-point values representing partial 2D scoring arrays. Most Monte Carlo packages (including MC321) score photon events using a local array, which they write to a disk once the simulation completes. To implement the MC-HP scheme, the developer only needs to write the scoring array to stdout instead of a local file. For both implementations, Mapper and Reducer are written as standalone C applications. To ensure that Monte Carlo simulations performed in parallel are uncorrelated, a text file containing 10,000 distinct seeds is used as the input of the MapReduce job. The large number of seeds allows Hadoop to execute up to 10,000 parallel Map tasks for fine processing granularity. We also ensure that the Map function, given the same input, always produces the same output. Random number generators (RNGs) that use a system-wide state are problematic with MapReduce because re-execution and speculative execution assume deterministic functions. All communications through UNIX streams use the TypedBytes data format. The MapReduce implementation of the MC321 Monte Carlo package described in this paper is available for research purpose. The codes can be downloaded from http://xinglab.stanford.edu/research/downloads.html. 3.3.Computing EnvironmentTwo different Hadoop clusters were used. To develop and debug MapReduce jobs, we set up a pseudo-distributed cluster by installing Hadoop 0.21 on a quad-core computer. Input and output data were stored on a local installation of HDFS. To run and profile large jobs, we allocated a remote Hadoop cluster on Amazon's Elastic Compute Cloud (EC2), using the Elastic MapReduce (EMR) service. EMR is an implementation of Hadoop 0.20 tightly integrated with other Amazon web services, such as the Simple Storage Service (S3). Map and Reduce applications were compiled remotely on an EC2 node using GCC version 4.3.2, and uploaded onto S3 together with the input random seeds. EMR jobs were submitted from a local computer using a freely-available command-line tool. 3.4.System EvaluationFor benchmarking purposes, we simulated the diffusion of a 633 nm laser beam within a turbid 5-cm radius cylinder filled with a 5% milk/95% water mixture.34 The phantom properties were set as follows: the absorption and scatter coefficients were [TeX:] \documentclass[12pt]{minimal}\begin{document}$\mu _{\text{a}}=0.0025\,\text{cm}^{-1}$\end{document} and [TeX:] \documentclass[12pt]{minimal}\begin{document}$\mu _{\text{s}}=7.8\,\text{cm}^{-1}$\end{document} , respectively; the index of refraction was n = 1.3; and the anisotropy coefficient was g = 0.9. The photons were initialized at a single point on the surface of the phantom and directed toward its center. For simplicity, only the x and y coordinates of each absorbed photon were scored. In a first experiment, we compared the original MC321 code against the MC-EP and MC-HP implementations. The benchmark consisted in simulating 100 million photon packets. The original Monte Carlo code was run single-threaded on an Intel Core2 Q9650 CPU with 4 GB of memory. The MapReduce implementations were run on EC2 using 20 high-memory nodes (code-named m2.xlarge). The m2.xlarge node configuration is specially adapted for tasks with large memory requirements, which we found was necessary for the MC-EP implementation. A single m2.xlarge node comes with 17.1 GB of memory, two 64-bit virtual cores with 3.25 EC2 compute units each, and 420 GB of local storage. The output data were downloaded back to a local computer and analyzed with MATLAB. In a second experiment, the total simulation time was recorded for a variable number of photon packets, ranging from 10 million to 100 billion. At this point, we focused our investigation on the more efficient MC-HP implementation. Twenty high-CPU nodes (codename c1.medium) were used in these tests. These nodes have 1.7 GB of memory, two 32-bit virtual cores with 2.5 EC2 compute units each, and 350 GB of local storage. Each c1.medium node is configured for running four MapReduce tasks simultaneously. In a third experiment, 100 billion photon packets were simulated using MC-HP on a variable number of nodes, ranging from 1 to 240. The c1.medium node configuration was used. Five thousand Map tasks and one Reduce task were run, providing very fine task granularity and good load balancing. The total run time was recorded and the output of the simulations compared. Because we were not authorized to allocate more than 240 EC2 nodes, we additionally ran the same simulation on the high-CPU extra-large node configuration (c1.xlarge). These nodes have 8 virtual cores with 2.5 EC2 compute unit each, 7 Gb of memory, and 1.7 Tb of local storage. A cluster of 240 c1.xlarge nodes is roughly equivalent to 960 c1.medium nodes. In a fourth experiment, a 4-node Hadoop cluster was allocated on EC2 and profiled using built-in tools while simulating 300 million photons. The number of Map and Reduce tasks was set to 100 and 1, respectively. Disk I/O, network I/O, and CPU utilization were recorded every minute. In a last experiment, 100 million photon packets were simulated with MC-HP on 20 nodes of type c1.medium. After 3 min, a set number of worker nodes were terminated to mimic node failure and test Hadoop's fault tolerance. 4.ResultsThe simulation time for 100 million photon packets is reported for the original and distributed implementations (Table 1). For MapReduce, processing time is defined as the duration of the Hadoop job, not including cluster initialization. For both MapReduce jobs, a timeline was generated from Hadoop log files using Karmasphere Studio (Fig. 4). Overall, MC-EP is slower than MC-HP because MC-EP transfers many intermediary records between Map and Reduce tasks. In MC-EP, shuffle, merge, and reduce tasks represent a significant portion of all tasks (Fig. 4, top). In contrast, MC-HP runs a single reduce task (Fig. 4, bottom). Fig. 4MapReduce execution timeline for the MC-EP and MC-HP implementations, showing the number of active tasks at each time point. The MC-EP timeline spans 18 min 09 s, versus 1 min 54 s for the MC-HP timeline. Waste denotes speculative execution.  Table 1Simulation time comparison.
The output of the MC-HP simulation is compared for a variable number of simulated photon packets, ranging from 10 million to 100 billion [Figs. 5a, 5b, 5c, 5d, 5e]. The output of the MC-HP simulation is virtually identical to that of the original MC321 package. For 10 million photon packets, the relative root-mean-square error between the two photon absorption distributions is lower than 4.1 × 10−7 [Fig. 5f]. The discrepancy between the two outputs is due to round-off errors during the conversion of the Reduce output to 10 digit ASCII in the final file. The simulation time also increases linearly with the number of photons packets [Fig. 6a]. Note that the curvature of the linear fit is due to the logarithmic scale on both axes. Fig. 5(a)–(e) Output of the MC-HP simulation for a variable number of photon histories ranging from 10 million to 100 billion, shown on a base-10 logarithmic scale. (f) Error between the original Monte Carlo package and the MapReduce implementation, shown for 10 million photon histories on a base-10 logarithmic scale. 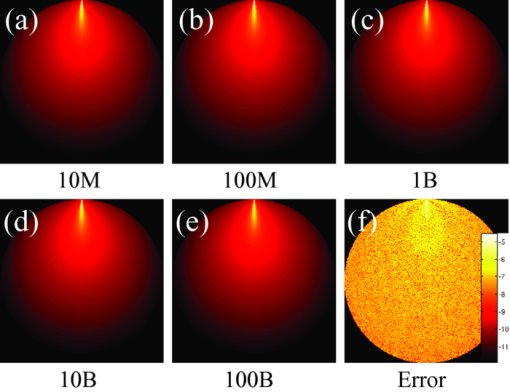 Fig. 6(a) MC-HP simulation time for a varying number of photon histories. Dashed line: least-square linear regression (r 2 = 0.9998). The curvature of the linear fit is due to the logarithmic scale. (b) MC-HP simulation time for a varying number of CPU cores. Dashed line: ideal inverse scaling of the single-node simulation time (r 2 = 0.98). 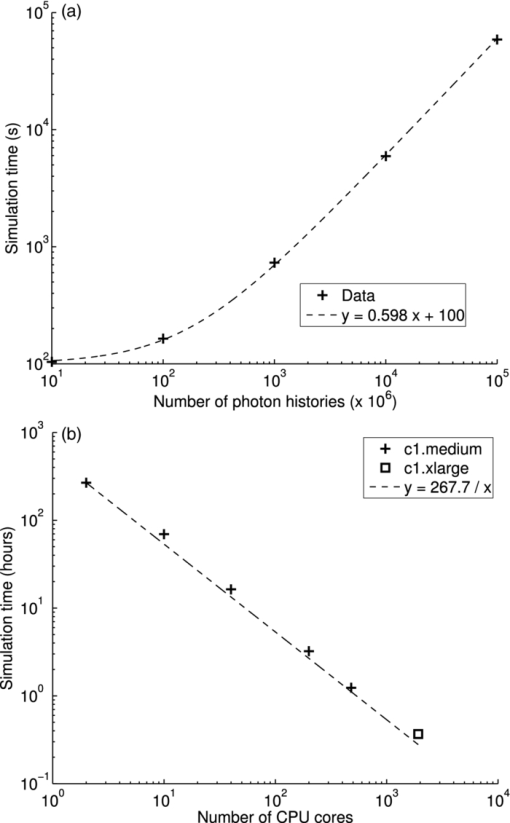 For 100 billion photon packets, the simulation time scaled inversely with the number of nodes [Fig. 6b]. On a single dual-core EC2 node, simulating 100 billion photons took 11.2 days, a 1.8 × speed-up compared with the single-threaded MC321 implementation. The same simulation took only 22 min on 240 c1.xlarge nodes, a 1258 × speed-up. Nodes based on the c1.xlarge (8 cores) configuration ran the MC-HP simulation 3.3 times faster than c1.medium nodes (2 cores). To better understand the use of resources, a 4-node Hadoop cluster was profiled while simulating 300 million photons (Fig. 7). The total runtime for this experiment was 20 min. It can be observed that the execution of the simulation was clearly compute-bound because the CPU utilization was maximized on all three slave nodes. Only the CPU capacity of the master node was not fully utilized. The pattern of network I/O was different for nodes running Map tasks only and nodes running both Map and Reduce tasks. In MC-HP, Map tasks are data producers; they input little data (the random seeds) but output large amounts of data (the scoring arrays). In contrast, Reduce tasks are data consumers: they continuously receive data from Map tasks, which they only write to HDFS at the end of the simulation. Fig. 7Resource profile showing I/O and computing during simulation of 300 million photons on a 4-node Hadoop cluster. 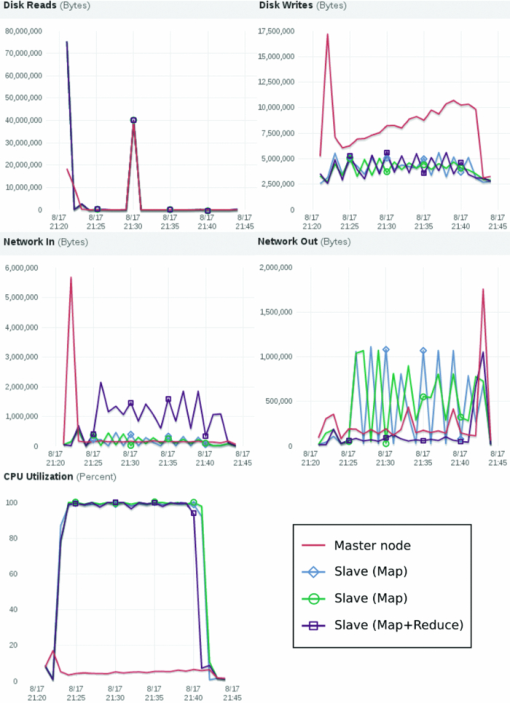 Hadoop's fault tolerance was also evaluated by shutting down 1 and 10 worker nodes, respectively, during the simulation of 100 million photons on 20 nodes. The termination of these nodes did not prevent Hadoop from successfully completing its job, provided that the master node was kept alive. Upon node failure, EMR allocated new nodes dynamically and relaunched failed Map and Reduce tasks. The output of the Hadoop simulation with some nodes terminated was identical to that obtained by running the simulation with no failure. The failure of 1 and 10 nodes lengthened the total simulation by 15 and 18 min, respectively. 5.DiscussionWhile MapReduce is often used to crunch large datasets such as website logs, we demonstrated that it is also well suited for computationally-demanding Monte Carlo simulations. MapReduce's architecture is largely decentralized for efficient data processing on large clusters. Even with 240 nodes, the performance of the MC-HP implementation scales linearly with the number of CPU cores [Fig. 6b], showing few signs of diminishing returns. On average, the simulation times were within 12% of the ideal inverse scaling [Fig. 6b, dashed line]. This result suggests that, if needed, the MC-HP implementation could run on many more nodes without suffering from interconnect latencies and limited network throughput. The MC-HP simulation also scaled linearly with the number of photon packets simulated. When the number of photons was incremented from 10 million to 100 billion, the simulation time followed a linear trend [Fig. 6a, r 2 = 0.9998]. Each incremental one million photons can be simulated on 20 nodes in 0.6 s. Furthermore, the computation overhead, which consists of cluster initialization, task distribution, and data reduction, is on the order of 100 s, which is negligible when billions of photon packets are simulated [Fig. 6a]. By combining the information from the first and second experiment, the performance of the MC-HP implementation can be better characterized. The throughput and latency were found to be 85,178 photons per node per second, and 100 s, respectively. In a separate experiment (data not shown), latency was found to be independent of the number of nodes. Hadoop also proved to be a highly reliable framework that could withstand the accidental failure of 50% of the worker nodes. Upon node failure, EMR allocates new nodes to replace failed ones. Currently, the process of resizing a running Hadoop cluster on EC2 is rather slow, requiring around 15 min, but a substantial effort is under way to improve the efficiency of the process. There also exist simpler implementations of MapReduce that do not resize the cluster, but rather redistribute failed tasks to nodes not affected by the failure. A drawback of cloud computing is that a virtual cluster must be allocated on the cloud before running a job, a process that involves deploying a large number of operating system images on physical computers. Such initialization contributes to the overall execution time by increasing the latency, especially for very large cluster configurations. The solution we adopted consisted in keeping our virtual Hadoop cluster alive after the completion of its first job, such that it would remain available for other jobs. A word should also be said about the cost of performing Monte Carlo simulation in a commercial cloud computing environment. As of August 2011, the price of Amazon's EC2 nodes ranges from $0.025/h for micronodes to $2.28/h for quadruple extra-large nodes. Most of the simulations presented in our study were performed on high-CPU medium nodes, which are priced at $0.19/h. Hence, large-scale simulations, such as those with 1011 photon packet histories [Fig. 6b], can cost a few hundred dollars to run. Cloud computing is ideal for research institutions that do not have a sufficient demand to maintain a full-size cluster on site. Furthermore, cloud resources have very low downtime. The main alternatives to cloud computing is the operation of a dedicated cluster, a solution currently used by many research groups. This approach has a few advantages, namely the absence of a virtualization layer and better control over the hardware. However, energy, maintenance, and storage costs can be significantly higher. Furthermore, the lack of elastic scaling results in under- or overutilization of compute resources. MapReduce is highly optimized for data-intensive processing tasks, such as indexing web pages or mining large datasets. It uses a loosely-coupled distributed memory system, which does not allow parallel tasks to communicate with one another directly. By its design, MapReduce is suboptimal for compute-bound tasks or for tasks that require frequent internode data exchange, such as, for instance, iterative image reconstruction. In MapReduce, internode communication can be achieved by reducing the Map outputs with Reduce tasks, and splitting these data again using a new set of Map tasks. For tasks with a large amount of internode communication, this mechanism may be less efficient than a shared memory approach. For instance, GPUs provide on-chip memory shared by threads in a same block, and global memory shared by all threads. As a result, GPU threads can exchange data efficiently. Many scientific computation strategies have used the GPU’s fast shared memory to achieve impressive performance.33 Furthermore, GPU can access global memory with nearly 5-fold higher bandwith than state-of-the-art CPUs: For instance, the memory bandwidth of a Tesla C2050 GPU is 144 GB/s, versus 32 GB/s for an Intel Xeon X5650 CPU. However, the peak performance of the two architectures should be compared with caution because the GPU’s peak memory bandwidth is only achieved when memory transfers are fully coalesced (i.e., they occur in continous 128-bit chunks). For random memory accesses (such as scoring during a Monte Carlo simulation), this is seldom the case and the achieved bandwith can be lower than the peak theoretical value. At this time, the use of a distributed memory system such as MapReduce for scientific applications other than Monte Carlo is still being investigated.35 The performance of the MC-HP implementation can be put into perspective by comparing it against other published simulations of photon migration in homogeneous media (Table 2). These performance figures should be compared with caution because of the diverse set of parameters used in these studies. The speed of the simulation can be affected by a number of parameters, including the RNG, the optical properties, the size of the scoring grid, and the roulette parameters. With this caveat in mind, the cloud-based approach provides speed-up of the same order of magnitude as its GPU-based counterparts (Table 2). A GPU platform has several advantages for Monte Carlo simulation, such as built-in hardware-accelerated arithmetic functions, no thread-switching overhead, a compact form factor, and the relatively low price of the hardware.14 Table 2Comparison of various photon migration Monte Carlo codes, according to the following parameters: RNG; the absorption and scatter coefficients \documentclass[12pt]{minimal}\begin{document}$\mu _{\text{a}}$\end{document} μa and \documentclass[12pt]{minimal}\begin{document}$\mu _{\text{s}}$\end{document} μs , respectively; the size of the scoring grid; the acceleration platform; the photon throughput \documentclass[12pt]{minimal}\begin{document}${\it T}_{\text{acc}}$\end{document} Tacc and \documentclass[12pt]{minimal}\begin{document}${\it T}_{\text{ref}}$\end{document} Tref , expressed in photons/ms, for the accelerated and reference (CPU) platform, respectively; and the speed up achieved.
However, one issue with GPU computing is that many threads share access to the same memory. Hence, race conditions may arise when two or more threads attempt to write to the same grid element, since only one thread can write to a given memory location on a clock cycle. This situation occurs most frequently in high fluence regions, such as near the light source, and is less problematic in low-fluence regions.16 GPU atomic operations can be used to serialize the memory writes when needed, at the cost of slower memory access. For instance, the MCX package is four times slower when such atomic operations are used (Table 2). A variant of MCX (mcx_cached) and the GPU-MCML package use a different approach to mitigate race condition issues: The high-fluence region of the scoring array is cached in fast shared memory and accessed atomically, while the low-fluence region is stored in global memory. Use of fast shared memory reduces the penalty associated with atomic operations since fewer threads access the grid at any time, and shared memory has much lower latency than global memory. In our MapReduce implementation, each task allocates its own detection grid locally, which avoids data write hazards. Local detection grids are combined using parallel Reduce tasks. Additionally, MapReduce offers better scalability than GPUs. To achieve higher photon throughput, multiple GPUs must be employed and integrated into a cluster.17 The software must be adapted to provide inter-GPU and intercomputer communications, which adds another layer of complexity. In contrast, the number of nodes in a MapReduce cluster can be scaled by modifying a single parameter. However, if used intensively, a GPU cluster can be more economical over time than computing capacity purchased on demand from a cloud computing operator. In the context of a Monte Carlo simulation, a loosely-coupled parallel architecture such as a Hadoop cluster has some advantages over a GPU. The GPU architecture is based on a single-program multiple-data programming model which penalizes diverging threads. Briefly, a GPU is composed of several multiprocessors, each of which processes parallel threads in batches called warps. Even though threads within a warp can follow diverging paths, a GPU multiprocessor can only issue one instruction per clock cycle. Hence, the execution of diverging threads is serialized: only those threads programmed to execute the current instruction can advance to the next instruction; others must wait for the multiprocessor to execute their instruction. In a Monte Carlo simulation, particle paths can diverge. For instance, high-energy photons can undergo a wide range of physical interactions with matter. Furthermore, a comprehensive model of dose deposition in matter requires simulation of the electrons induced by Compton scatter and photoelectric absorption. Because of these effects, naive GPU implementations result in high thread divergence and modest efficiency.10, 20 Simulation of photon migration in turbid media can also lead to thread divergence: within one iteration, some photons may traverse a boundary or be reflected; others may be scattered or absorbed. Unlike GPU cores, CPU cores have dedicated instruction units. Therefore, each parallel thread can issue its own instruction on a clock cycle, independently of the other threads. In a MapReduce job, parallel tasks are executed as independent processes by CPU cores, and are not penalized if they diverge and follow different code branches. It should be noted that the cores in a modern CPU can also issue special streaming SIMD extension (SSE) instructions, which are applied simultaneously to up to four single-precision floating-point registers. This lower level of parallelism cannot be automatically utilized by MapReduce and requires the developer to specifically use SSE instructions when developping the Map and Reduce tasks. The Monte Carlo code used in this paper was intended as a case study of MapReduce for a biomedical application. The simplicity of the Monte Carlo code helped focus our presentation on the mechanisms of task distribution. The principles described in this paper can be applied to more complex photon migration simulations, such as those that include a three dimensional (3D) map of the optical coefficients5 or a multilayered geometry.3 Hadoop has a distributed cache that can make a set of files available to all the nodes in the cluster. This mechanism can be used to broadcast the optical coefficient map to all the nodes prior to starting the simulation. In our implementation, the distributed cache was used to transfer the MC321 binaries (100 kB) to all the nodes. Once the optical coefficients are available on all the nodes, complex Monte Carlo simulations using heterogeneous geometries may be performed by parallel map tasks, with no internode communications. The outputs of these parallel simulations may be combined by simple reduced tasks, as demonstrated in this work. Apart from the initial broadcast of the optical coefficient map, the use of a more accurate Monte Carlo package would require no additional data transfer between nodes. The present work suggests that these more complex Monte Carlo simulations would be accelerated by a factor approximately equal to the number of nodes in the cluster. In the MC-HP implementation, a singe Reduce task is used to aggregate the outputs from all Map tasks. This approach may not be fast enough to reduce large outputs (such as for instance a 3D photon fluence matrix) from many Map tasks. Network throughput may also be problematic since data are transferred from many nodes to a single node, creating a bottleneck. To alleviate this issue, parallel Reduce tasks can be generated by setting Map tasks to output their data block by block, using the key to encode the block index. The blocks may be composed of slices for a 3D matrix, or rows in a 2D matrix. This data transfer strategy has the advantage that it is decentralized: many data transfer can occur in parallel, increasing the total bandwidth of the cluster. For optimal efficiency, the number of Reduce tasks can be set to the number of such blocks. After the Reduce step, the blocks—which combine the computations of many Map tasks—are written to distributed storage, from which they can be downloaded. Although it has its roots in text processing, Hadoop is an evolving technology, continuously adding new features to address the specific needs of a wider spectrum of users. As the framework evolves, we expect that it will become more general-purpose, and even better suited for scientific computation. For example, Hadoop currently requires worker nodes to sort intermediary records by key before applying the Reduce function. This sorting step is unnecessary in scientific applications that use keys as array indices. The open-source status of the Hadoop project allows any developer to modify the framework as needed, and possibly contribute back to the project. 6.ConclusionThe inexorable shift of computing to parallel architectures forces us to rethink how algorithms are implemented. Porting an application to a distributed environment is problematic because of the complexity of the software development and the cost of a large-scale computer cluster. For photon migration Monte Carlo simulation, MapReduce helps overcome these two challenges by providing a simple way to deploy massively-parallel applications in a cloud computing environment. The port of the MC321 package to MapReduce was rapid, taking only a week; yet, the code execution scaled to 1920 cores with few signs of diminishing returns. The new distributed code includes features such as fault tolerance and automated load balancing. AcknowledgmentsFunding for this work was provided by the Stanford Dean's fellowship, the AAPM research seed grant, a DoD BCRP postdoctoral award (W81XWH-11-1-0070), and a NIH research grant (1R01 CA 133474). The authors would like to acknowledge the Oregon Medical Laser Center for making the MC321 package available online. ReferencesB. C. Wilson and
G. Adam,
“A Monte Carlo model for the absorption and flux distributions of light in tissue,”
Med. Phys., 10
(6), 824
–830
(1983). https://doi.org/10.1118/1.595361 Google Scholar
S. Jacques,
“Light distributions from point, line and plane sources for photochemical reactions and fluorescence in turbid biological tissues,”
Photochem. Photobiol., 67
(1), 23
–32
(1998). https://doi.org/10.1111/j.1751-1097.1998.tb05161.x Google Scholar
L. Wang,
S. L. Jacques, and
L. Zheng,
“MCML–Monte Carlo modeling of light transport in multi-layered tissues,”
Comput. Meth. Prog. Bio., 47
(2), 131
–146
(1995). https://doi.org/10.1016/0169-2607(95)01640-F Google Scholar
T. J. Dougherty,
“Photodynamic therapy,”
Photochem. Photobiol., 58
(6), 895
–900
(1993). https://doi.org/10.1111/j.1751-1097.1993.tb04990.x Google Scholar
D. Boas,
J. Culver,
J. Stott, and
A. Dunn,
“Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head,”
Opt. Express, 10 159
–170
(2002). Google Scholar
Q. Fang,
“Mesh-based Monte Carlo method using fast ray-tracing in Plücker coordinates,”
Biomed. Opt. Express, 1 165
–175
(2010). https://doi.org/10.1364/BOE.1.000165 Google Scholar
N. Tyagi,
A. Bose, and
I. J. Chetty,
“Implementation of the DPM Monte Carlo code on a parallel architecture for treatment planning applications,”
Med. Phys., 31
(9), 2721
–2725
(2004). https://doi.org/10.1118/1.1786691 Google Scholar
J. Sempau,
A. Sanchez-Reyes,
F. Salvat,
H. O. ben Tahar,
S. B. Jiang, and
J. M. Fernandez-Varea,
“Monte Carlo simulation of electron beams from an accelerator head using PENELOPE,”
Phys. Medi. Biol., 46
(4), 1163
–1186
(2001). https://doi.org/10.1088/0031-9155/46/4/318 Google Scholar
H. Wang,
Y. Ma,
G. Pratx, and
L. Xing,
“Toward real-time Monte Carlo simulation using a commercial cloud computing infrastructure,”
Phys. Med. Bio., 56
(17), N175
–N181
(2011). https://doi.org/10.1088/0031-9155/56/17/N02 Google Scholar
A. Badal and
J. Sempau,
“A package of Linux scripts for the parallelization of Monte Carlo simulations,”
Comput. Phys. Commun., 175
(6), 440
–450
(2006). https://doi.org/10.1016/j.cpc.2006.05.009 Google Scholar
A. Page,
S. Coyle,
T. Keane,
T. Naughton,
C. Markham, and
T. Ward,
“Distributed Monte Carlo simulation of light transportation in tissue,”
254
(2006). Google Scholar
A. Colasanti,
G. Guida,
A. Kisslinger,
R. Liuzzi,
M. Quarto,
P. Riccio,
“Multiple processor version of a Monte Carlo code for photon transport in turbid media,”
Comput. Phys. Communi., 132
(1–2), 84
–93
(2000). https://doi.org/10.1016/S0010-4655(00)00138-7 Google Scholar
W. C. Y. Lo,
K. Redmond,
J. Luu,
P. Chow,
J. Rose, and
L. Lilge,
“Hardware acceleration of a Monte Carlo simulation for photodynamic therapy treatment planning,”
J. Biomed. Opt., 14
(1), 014019
(2009). https://doi.org/10.1117/1.3080134 Google Scholar
G. Pratx and
L. Xing,
“GPU computing in medical physics: A review,”
Med. Phys., 38
(5), 2685
–2697
(2011). https://doi.org/10.1118/1.3578605 Google Scholar
E. Alerstam,
T. Svensson, and
S. Andersson-Engels,
“Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration,”
J. Biomed. Opt., 13
(6), 060504
(2008). https://doi.org/10.1117/1.3041496 Google Scholar
Q. Fang and
D. A. Boas,
“Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units,”
Opt. Express, 17 20178
–20190
(2009). https://doi.org/10.1364/OE.17.020178 Google Scholar
E. Alerstam,
W. C. Y. Lo,
T. D. Han,
J. Rose,
S. Andersson-Engels, and
L. Lilge,
“Next-generation acceleration and code optimization for light transport in turbid media using GPUs,”
Biomed. Opt. Express, 1 658
–675
(2010). https://doi.org/10.1364/BOE.1.000658 Google Scholar
N. Ren,
J. Liang,
X. Qu,
J. Li,
B. Lu, and
J. Tian,
“GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues,”
Opt. Express, 18
(7), 6811
–6823
(2010). https://doi.org/10.1364/OE.18.006811 Google Scholar
A. Badal and
A. Badano,
“Accelerating Monte Carlo simulations of photon transport in a voxelized geometry using a massively parallel graphics processing unit,”
Med. Phys., 36
(11), 4878
–4880
(2009). https://doi.org/10.1118/1.3231824 Google Scholar
X. Jia,
X. Gu,
J. Sempau,
D. Choi,
A. Majumdar, and
S. B. Jiang,
“Development of a GPU-based Monte Carlo dose calculation code for coupled electron-photon transport,”
Phys. Med. Bio., 55
(11), 3077
–3086
(2010). https://doi.org/10.1088/0031-9155/55/11/006 Google Scholar
S. Hissoiny,
B. Ozell,
H. Bouchard, and
P. Despres,
“GPUMCD: A new GPU-oriented Monte Carlo dose calculation platform,”
Med. Phys., 38
(2), 754
–764
(2011). https://doi.org/10.1118/1.3539725 Google Scholar
J. Dean and
S. Ghemawat,
“MapReduce: Simplified data processing on large clusters,”
Commun. ACM, 51
(1), 107
–113
(2008). https://doi.org/10.1145/1327452.1327492 Google Scholar
P. Mika and
G. Tummarello,
“Web semantics in the clouds,”
IEEE Intell. Syst., 23 82
–87
(2008). https://doi.org/10.1109/MIS.2008.94 Google Scholar
R. Baeza-Yates,
C. Castillo,
F. Junqueira,
V. Plachouras, and
F. Silvestri,
“Challenges on distributed web retrieval,”
6
–20
(2007). Google Scholar
C. Moretti,
K. Steinhaeuser,
D. Thain, and
N. Chawla,
“Scaling up classifiers to cloud computers,”
472
–481
(2008). Google Scholar
J. Wolfe,
A. Haghighi, and
D. Klein,
“Fully distributed EM for very large datasets,”
1184
–1191
(2008). Google Scholar
E. Schadt,
M. Linderman,
J. Sorenson,
L. Lee, and
G. Nolan,
“Computational solutions to large-scale data management and analysis,”
Nat. Rev. Genet., 11
(9), 647
–657
(2010). https://doi.org/10.1038/nrg2857 Google Scholar
A. McKenna,
M. Hanna,
E. Banks,
A. Sivachenko,
K. Cibulskis,
A. Kernytsky,
K. Garimella,
D. Altshuler,
S. Gabriel,
M. Daly, and
M. A. DePristo,
“The Genome analysis toolkit: A MapReduce framework for analyzing next-generation DNA sequencing data,”
Genome Res., 20
(9), 1297
–1303
(2010). https://doi.org/10.1101/gr.107524.110 Google Scholar
M. Schatz,
“Cloudburst: highly sensitive read mapping with MapReduce,”
Bioinformatics, 25
(11), 1363
–1369
(2009). https://doi.org/10.1093/bioinformatics/btp236 Google Scholar
F. Wang,
V. Ercegovac,
T. Syeda-Mahmood,
A. Holder,
E. Shekita,
D. Beymer, and
L. H. Xu,
“Large-scale multimodal mining for healthcare with MapReduce,”
479
–483
(2010). Google Scholar
T. White, Hadoop: The Definitive Guide, O’Reilly Media(2009). Google Scholar
O. O’Malley and
A. Murthy,
“Winning a 60 second dash with a yellow elephant,”
(2009) http://sortbenchmark.org Google Scholar
G. Pratx,
C. Carpenter,
C. Sun, and
L. Xing,
“X-ray luminescence computed tomography via selective excitation: A feasibility study,”
IEEE Trans. Med. Imag., 29 1992
–1999
(2010). https://doi.org/10.1109/TMI.2010.2055883 Google Scholar
Z. Zhao and
R. Myllyla,
“The effects of optical scattering on pulsed photoacoustic measurement in weakly absorbing liquids,”
Meas. Sci. Technol., 12
(12), 2172
–2177
(2001). https://doi.org/10.1088/0957-0233/12/12/319 Google Scholar
B. Meng,
G. Pratx, and
L. Xing,
“Ultra-fast and scalable cone-beam CT reconstruction using MapReduce in a cloud computing environment,”
Med. Phys., Google Scholar
|