Validation of diffuse correlation spectroscopic measurement of cerebral blood flow using phase-encoded velocity mapping magnetic resonance imaging

Erin M. Buckley; Dalton Hance; Jennifer M. Lynch; Rickson C. Mesquita; Arjun G. Yodh; Daniel J. Licht; Thomas Pawlowski; Felice B. Wilson; Mark A. Fogel; Turgut Durduran; Laura K. Diaz; Mary E. Putt

doi:10.1117/1.JBO.17.3.037007

27 March 2012 Validation of diffuse correlation spectroscopic measurement of cerebral blood flow using phase-encoded velocity mapping magnetic resonance imaging

Erin M. Buckley, Dalton Hance, Jennifer M. Lynch, Rickson C. Mesquita, Arjun G. Yodh, Daniel J. Licht, Thomas Pawlowski, Felice B. Wilson, Mark A. Fogel, Turgut Durduran, Laura K. Diaz, Mary E. Putt

Author Affiliations +

Journal of Biomedical Optics, Vol. 17, Issue 3, 037007 (March 2012). https://doi.org/10.1117/1.JBO.17.3.037007

Abstract

Diffuse correlation spectroscopy (DCS) is a novel optical technique that appears to be an excellent tool for assessing cerebral blood flow in a continuous and non-invasive manner at the bedside. We present new clinical validation of the DCS methodology by demonstrating strong agreement between DCS indices of relative cerebral blood flow and indices based on phase-encoded velocity mapping magnetic resonance imaging (VENC MRI) of relative blood flow in the jugular veins and superior vena cava. Data were acquired from 46 children with single ventricle cardiac lesions during a hypercapnia intervention. Significant increases in cerebral blood flow, measured both by DCS and by VENC MRI, as well as significant increases in oxyhemoglobin concentration, and total hemoglobin concentration, were observed during hypercapnia. Comparison of blood flow changes measured by VENC MRI in the jugular veins and by DCS revealed a strong linear relationship, R = 0.88, p<0.001, slope = 0.91±0.07. Similar correlations were observed between DCS and VENC MRI in the superior vena cava, R = 0.77, slope = 0.99±0.12, p<0.001. The relationship between VENC MRI in the aorta and DCS, a negative control, was weakly correlated, R = 0.46, slope = 1.77±0.45, p<0.001.

1. Introduction

Assuring adequate tissue perfusion is central for support of patients in the critical care arena. In particular, information about cerebral blood flow is valuable for assessment of brain perfusion and prevention of secondary injury. Very few technologies, however, provide clinicians with bedside access to this information. Current cerebral perfusion diagnostics, such as transcranial Doppler ultrasound, arterial spin-labeled magnetic resonance imaging (MRI), Xenon-133 clearance, and positron emission tomography, are either low-throughput, indirect, expensive, invasive, or require patient transport.¹^,² Diffuse correlation spectroscopy (DCS), is a novel optical technique that appears to be an excellent tool for assessing cerebral blood flow in a continuous and non-invasive manner at the bedside. The technique, however, must be validated in a variety of clinical settings and against numerous well-established blood flow modalities in order for this new optical tool to gain wide acceptance.

Patients with congenital heart defects represent one population that could benefit from a non-invasive bedside monitor of cerebral blood flow. Recent work has shown that whencompared to healthy full-term children, patients with complex congenital heart defects have a high incidence of peri-operative brain injury and a significantly higher incidence of neurocognitive impairments.³^–⁵ During periods of hemodynamic instability, such as peri-operative care, a monitor of cerebral blood flow could provide insight into the timing, development, and evolution of these brain injuries.

DCS⁶^–⁹ has shown promise as a monitor of relative changes in cerebral blood flow.¹⁰^–¹⁶ The DCS technique uses near-infrared, NIR, light in the tissue absorption windowto probe the dynamics of deep tissues. Within this window scattering, rather than absorption, dominates photon transport, so that near-infrared light experiences thousands of scattering events and propagates centimeters into the tissue before it is either detected at the tissue surface or lost due to absorption. DCS monitors changes in blood flow by capturing temporal fluctuations of scattered light detected at the tissue surface.¹⁰ These temporal light intensity fluctuations are sensitive to blood flow in the tissue microvasculature and such measurements can be made in a continuous fashion with data acquisition rates of 0.3 Hz and even faster.¹⁵

The present contribution validates DCS measurement of relative changes in cerebral blood flow (CBF) against a well-established magnetic resonance technique known as phase encoded velocity mapping (VENC MRI). VENC MRI does not measure cerebral blood flow in the brain; rather, it measures blood flow in the main vessel supplying blood to the brain, the aortic arch, and blood flow in the main vessels draining blood from the brain, the right and left common jugular veins, and the superior vena cava. These measures of flow in the jugular veins have been shown to agree with other measures of cerebral blood flow. These measures of flow in the jugular veins have been shown to agree strongly with other measures of cerebral blood flow.¹⁷^,¹⁸ However, while VENC MRI provides high-quality, reliable blood flow data, these measurements must be carried out in an MRI scanner making them unsuitable for continuous monitoring. We find that relative changes of blood flow in the jugular veins and superior vena cava correlate strongly with relative changes in CBF measured with DCS. Additionally, we find that blood flow changes in the aorta, a negative control, were only weakly correlated with relative changes in CBF measured with DCS. These results indicate DCS may be employed as a continuous bedside monitor of CBF in patients with congenital heart defects as well as in a wide variety of other patients.

2. Materials and Methods

Children with single ventricle complex congenital heart defects at The Children’s Hospital of Philadelphia were recruited for this study and approved by the Institutional Review Board. All measurements were performed on the morning of the child’s staged cardiac surgery. Immediately prior to surgery, general anesthesia was induced via mask inhalation of sevoflurane. After intravenous access was obtained, pancuronium $0.2 mg / kg$ was administered for neuromuscular blockade and a nasal endotracheal tube was then placed. The patient was subsequently mechanically ventilated, utilizing 1% to 2% sevoflurane for maintenance of general anesthesia while an arterial catheter was placed in an upper extremity. Patients were brought to the MRI scanner and a non-invasive optical probe was placed on the forehead for continuous optical monitoring. Figure 1 shows the experimental timeline. Briefly, after a 30-min baseline period of ventilation with $Fi O_{2}$ , fraction inspired oxygen, of 0.21, inspired ${CO}_{2}$ was added to the room air mixture to achieve a $Fi {CO}_{2}$ of approximately 0.039. The ${CO}_{2}$ mixture remained on for a 30-min hypercapnic period to allow for gas equilibration and stabilization of the higher hypercapnic blood flow. During this period of equilibration, anatomical brain MRI was obtained. Non-invasive, cuff blood pressures, electrocardiogram, peripheral oxygen saturation, and $Fi {CO}_{2}$ were monitored and recorded throughout the duration of the study. Arterial blood gases were obtained at the start of the baseline period and at the end of the hypercapnia period to assess changes in partial pressure of carbon dioxide, $p {CO}_{2}$ , in the blood.

Fig. 1

Timeline of hypercapnia protocol. The patient inhaled room air for 30 min at which point ${CO}_{2}$ was added to the gas mixture for a fraction of inspired ${CO}_{2}$ of approximately 3%.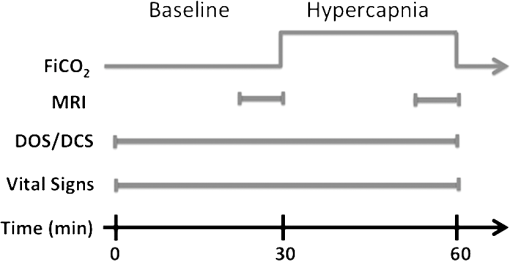

2.1.

Phase Encoded Velocity Mapping MRI

To measure blood flow in the main vessels supplying and draining from the brain, a magnetic resonance technique known as phase-encoded velocity mapping, VENC MRI, was employed.¹⁹^–²¹ In brief, the technique relies on the fact that magnetic spins of intravascular protons flowing along a magnetic field acquire a phase-shift that is linearly proportional to their velocity:

Eq. (1)

Δ φ = γ v δ A_{g} .

In Eq. (1),

Δ φ

is the phase-shift,

γ

is the gyromagnetic ratio,

v

is the velocity,

δ

is the time between the centers of two magnetic pulses, and

A_{g}

is the area of one of the gradient pulses. A magnetic field gradient is aligned along the axis of the vessels of interest, namely the aorta, jugular veins, and superior vena cava, thereby inducing a phase shift in spins that move or flow along this gradient. The phase shift accumulated by the MRI signal obtained from a specific voxel is proportional to the velocity within that voxel. The direction of flow is aligned with the use of oblique magnetic field gradients. Combined with phase error correction techniques, velocity is accurately measured.

Our investigation used a Siemens 1.5-Tesla Avanto MRI system, manufactured by Siemens Medical Systems, Malvern, New Jersey. After localizers in multiple planes, a stack of static, steady-state free precession axial images were acquired spanning the entire thorax and neck. These images evaluated cardiovascular anatomy and were used for localized through-plane velocity mapping. The effective repetition time was the R-R interval (range 450 to 650 ms). The echo time was 1.5 to 3 ms, the number of segments per heartbeat was 29, the number of excitations was 3, the image matrix size was $128 \times 128$ pixels, interpolated to $256 \times 256$ , with a field of view ranging from 180 to 200 mm and slice thickness of 3 mm. Multiplanar reconstruction, a software package resident on the Siemens MRI system, used the transverse images to calculate the exact slice position and double-oblique angles to obtain a ventricular outflow tract view and long-axis images of the jugular veins and superior vena cava. If two ventricular outflow tracts were present, each one was obtained separately. An imaging plane perpendicular to flow was then determined for the ventricular outflow tract at the sinotubular junction, right and left common jugular veins above the superior vena cava and the superior vena cava proximal to the pulmonary artery anastomosis and distal to the innominate and subclavian veins. The retrospective phase encoded velocity mapping sequence was then performed with a repetition time of 35 ms, echo time of 3 ms, number of segments per heartbeat of 3, field of view of 180 mm, a slice thickness of 5 mm, obtaining 20 to 23 phases depending upon the heart rate utilizing parallel imaging and 5 averages. VENC MRI encoding was 60 to $90 cm / \sec$ .

Quantitative velocities were obtained in a region of interest (ROI) that was semi-automatically traced along the margins of the blood vessels of interest. Blood flow was computed by the sum of the product of the velocities measured in each pixel and the area of each pixel in the ROI. By integrating this flow over the cardiac cycle and multiplying by the heart rate, we obtained an average blood flow in units of liters per minute. The protocol not only included VENC MRI, but also a contiguous stack of static, steady state free precession images in the axial plane. This stack was used to locate the exact slice positions for VENC MRI so that this plane was perpendicular to flow.

For each patient, velocity maps were obtained at the sinotubular junction in the aortic root, in the left and right common jugular veins, and in the superior vena cava during room air inhalation and during hypercapnia as seen in Figs. 1 and 2. From these maps, we calculated a net flow, as described above, per cardiac cycle. The signal was averaged over multiple cardiac cycles to minimize effects of respiratory motion. Averaging also had the advantage of improving the signal-to-noise ratio, yielding an average blood flow value for each vessel acquired over approximately 1 min. Thus, we obtained a mean blood flow with units of liters/minute in the aorta ( ${BF}_{Aorta}$ ), superior vena cava ( ${BF}_{SVC}$ ), and by summing the blood flow in the right and left common jugulars, the jugular veins ( ${BF}_{Jug}$ ). Relative changes in blood flow ( $r BF$ ) through these vessels due to hypercapnia were computed using the following formula: $r BF = ({BF}_{{CO}_{2}} / {BF}_{Room Air}) \times 100 %$ . Cerebrovascular reactivity (CVR), defined as the change in blood flow divided by the change in partial pressure of ${CO}_{2}$ ( $Δ p {CO}_{2}$ ), was computed as $CVR = (r BF - 100 %) / Δ p {CO}_{2}$ .

Fig. 2

(Top) Phase encoded velocity mapping magnitude (a, b) and phase (c, d) images of the jugular veins taken during baseline (left) and hypercapnia (right). (Bottom) Sample time series of optical data. DOS measures of $Δ Hb$ and $Δ Hb O_{2}$ are shown on the top by dotted line and open circle, respectively, while DCS measures of rCBF are shown on the bottom. The grey shading indicates the time of the velocity mapping scans. Mean DCS data were acquired in these regions for comparison to VENC MRI results.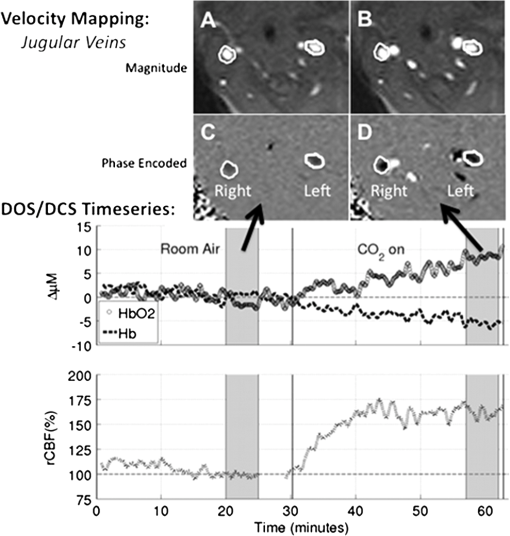

2.2.

Diffuse Optical and Correlation Spectroscopies

Optical measurements of changes in oxy- and deoxy-hemoglobin concentration ( $Δ H b$ and $Δ {H b O}_{2}$ , respectively) and relative changes in cerebral blood flow (rCBF) were obtained continuously with a custom-made optical probe, manufactured by Fiberoptic Systems, Inc., Simi Valley, California. The probe contained two separate source-detector pairs, one for diffuse optical spectroscopy (DOS) and one for DCS, both separated by 2.5 cm; thus, the mean penetration depth of diffusing photons reached into the cortical tissues. The DCS detector was a bundle of eight single-mode fibers used to improve the signal-to-noise ratio. The probe was secured gently to the forehead with a soft head wrap. Additionally, a fiducial marker was placed over the probe to locate fiber positions on anatomical MRI images.

Optical data were acquired using a hybrid diffuse optical spectrometer consisting of a commercially available DOS system (Imagent, ISS, Champaign, Illinois) and a diffuse correlation spectrometer custom-made in our laboratory. The DOS instrument operates in the frequency domain at 110 MHz with three wavelengths, 686, 786, and 826 nm. It uses a heterodyne detection at 5 kHz to quantify diffusive wave AC amplitude attenuation, phase shift, and average DC value of the detected light. For DOS data analysis, the modified Beer-Lambert law,²²^,²³ was employed to compute changes in the absorption coefficient, $Δ μ_{a} (λ)$ :

Eq. (2)

\log [I (λ) / I_{0} (λ)] = r \times DPF (λ) \times Δ μ_{a} (λ),

μ_{a} (λ)

is linearly dependent on the changes in concentrations of oxy- and deoxy-hemoglobin (

Δ {H b O}_{2}

and

Δ H b

, respectively).²⁴ In Eq. (2),

I (λ)

is the AC light intensity measured at wavelength

λ

and time

t

,

I_{0} (λ)

is the mean AC light intensity measured at wavelength

λ

during the 5 min of room air inhalation when VENC MRI scans were obtained,

DPF (λ)

is the wavelength dependent diffuse pathlength factor accounting for the increase in photon pathlength due to multiple scattering, equal to 5.4, 5.0, and 4.7 for 686, 786, and 826 nm, respectively,²⁵ and

r

is the DOS source detector separation distance (2.5 cm for this experiment). If the detected AC light intensity was outside the linear range of our instrument, the DOS data were excluded from our analysis. Note, the measured DC amplitude attenuation and phase-shift were not employed in this analysis.

The DCS instrument uses a long-coherence-length laser, CrystaLaser, RCL-080-785S, operating at 785 nm to deliver coherent light to the tissue. Light is detected at the tissue surface with a bundle of eight single-mode detection fibers and is transmitted to a fast photon counting avalanche photodiode that outputs a TTL signal for every photon detected. A custom built 8-channel correlator board (FLEX03OEM-8CH, correlator.com, Bridgewater, New Jersey) uses this TTL signal to derive the intensity autocorrelation function based on the photon arrival times.²⁶

For DCS analysis, we employed the semi-infinite homogeneous medium solution to the correlation diffusion equation to fit our measured intensity autocorrelation curves, $g_{2} (τ)$ , for a blood flow index (BFI). BFI is related to the motion of red blood cells and their concentration.¹⁰ DCS data were discarded if the intensity (i.e., photon count rate) of all detectors was less than 5 kHz (i.e., if the intensity signal-to-noise ratio was less than 10). Intensity autocorrelation curves were fit for BFI using fminsearchbnd.m, (Matlab 2010a, MathWorks) to find the optimal solution to the objective function, $f$ , where $f$ is defined as

Eq. (3)

f = \sqrt{Σ_{i} {[g_{2} {(τ_{i})}_{Fit} - g_{2} {(τ_{i})}_{Measured}]}^{2}} .

The fitting procedure assumes an initial value of

μ_{a}

and

μ_{s}^{'}

, (

0.1 {cm}^{- 1}

and

9 {cm}^{- 1}

, respectively, at 785 nm) for all patients.²⁷ The reduced scattering coefficient,

μ_{s}^{'}

, was assumed to remain constant, but the measured changes in

μ_{a}

at 786 nm computed with the DOS setup were incorporated into each fit of

g_{2} (τ)

. Additionally, we fit the data assuming the mean squared displacement of the moving scatterers obeys a Brownian motion model. In this case, the leading exponential decay rate of

g_{2} (τ)

should be proportional to the sq uare root of the correlation time,

τ

.⁷^,¹⁰^,²⁴

For comparison with velocity mapping MRI data, a mean relative change in CBF obtained by DCS was calculated for each patient. A mean and standard deviation of the blood flow index, $〈 BFI 〉$ and $σ_{BFI}$ respectively, were computed during the approximately 5-min long room air and hypercapnia velocity mapping scans. We defined the relative change in CBF due to hypercapnia as $r {CBF}_{DCS} = ({〈 BFI 〉}_{{CO}_{2}} / {〈 BFI 〉}_{Room Air}) \times 100 %$ , where the subscript indicates data acquired during the hypercapnic or room air velocity mapping MRI scan. Additionally, erebrovascular reactivity, CVR, was defined as $CVR = (r {CBF}_{DCS} - 100 %) / Δ p {CO}_{2}$ .

2.3.

Statistical Analysis

To test the hypothesis that each of the relative variables differed from room air during hypercapnia, we carried out a Wilcoxon signed rank test.²⁸ Analyses used R 2.11,²⁹ hypotheses tests and associated $p$ -values ( $p$ ) were two-sided. Statistical significance was declared for $p$ -values $< 0.05$ .

To quantify the relationship between relative changes in blood flow in the jugular veins, superior vena cava, and aorta measured by velocity mapping MRI against relative changes in cerebral blood flow measured by DCS, we fit a simple linear regression model and estimated Pearson’s correlation coefficient. Pearson’s correlation, $R$ , varies from 0 to 1.0 and measures the extent to which a linear model explains variability in the data. Note that $R$ can approach 1.0, even for a case where the slope of the line between the two measures varied substantially from unity. We used Lin’s concordance correlation coefficient, CCC, to measure agreement between the two measures. The CCC is the product of Pearson’s $R$ , a measure of precision, and a bias correction factor which reflects the degree that the linear association between two variables differs from 45 deg through the origin. For example, $R = CCC / Bias$ Correction. Bland-Altman plots of the difference versus the mean of the two measures of relative flow changes were constructed as a graphical approach to assessing agreement.³⁰

3. Results

Fifty-three children with single ventricle congenital heart defects were recruited. All patients were scheduled for cardiac surgical repair on the day of the study. Fifty-two patients completed the entire study, one was eliminated due to time constraints. Forty-six out of 52 remaining patients satisfied the inclusion criteria of having high-quality DOS, DCS, and VENC MRI data. Table 1 lists the median and interquartile range values of patient age, weight, height, skull/scalp/CSF thickness, sex, and surgical procedure for the study cohort. Patients had a median age of 2.8 years and were largely male, 70%.

Table 1

Patient demographics. Average skull, scalp, and CSF thickness was computed underneath the optical probe using anatomical MRI images.

	Median (IQR)
Age (yrs)	2.8 (3.0)
Weight (kg)	12.7 (8.0)
Height (cm)	91.3 (30.5)
Sex (Male:Female)	32:14
Skull/scalp/CSF thickness (cm)	0.81 (0.28)

Figure 2 shows velocity mapping MRI and DOS/DCS data from a typical subject. The top images show the phase maps of the region in and around the right and left common jugular veins during the room air, left, and hypercapnia, right. The veins are circled in white for ease of viewing. It is evident that during hypercapnia, the phase contrast in both vessels increases, indicating an increase in velocity in these vessels. The middle and bottom portions of Fig. 2 show the continuous time trace of DOS measures of $Δ Hb$ and $Δ {HbO}_{2}$ , middle, and DCS measures of rCBF, bottom. The shaded grey regions indicate the time periods in which VENC MRI scans were taken. For comparison between DCS and VENC MRI, the DCS data were averaged over the grey shaded regions to extract an average rCBF due to hypercapnia for each patient.

Table 2 summarizes the median and interquartile range of both the baseline, room air, and changes due to hypercapnia in all physiological parameters of interest. Since the DOS and DCS measures were all relative to the room air baseline, we report only changes for all variables. Hypercapnia induced significant, $p < 0.01$ , increases in CBF as measured by DCS and by phase-encoded velocity mapping MRI. Additionally, hypercapnia led to significant increases in heart rate, mean arterial blood pressure, oxy- and total hemoglobin concentration, and $p {CO}_{2}$ . Arterial pH decreased significantly with ${CO}_{2}$ administration, and no population-averaged changes were observed in de-oxyhemoglobin concentration changes.

Table 2

Median (interquartile range) baseline values followed by median (interquartile range) changes due to hypercapnia, and p-values obtained by Wilcoxon signed rank test.

Source	Variable	Baseline	Change due to ${CO}_{2}$	$p$ -value
Arterial blood gas	pH	7.39 (0.04)	$- 0.18$ (0.08)	$< 0.001$
Arterial blood gas	${pCO}_{2}$	39 (6) mmHg	$+ 31$ (14) mmHg	$< 0.001$
EKG	Heart rate	109 (21) bpm	$+ 14$ (13) bpm	$< 0.001$
Cuff	Mean arterial pressure	60 (10) mmHg	$+ 4$ (20) mmHg	0.002
Transcutaneous	${Sp O}_{2}$	82 (10)%	$+ 1$ (6)%	0.40
Velocity mapping MRI	${BF}_{Aorta}$	3.05 $(0.93) L / \min$	$+ 126.2$ (26.6)%	$< 0.001$
	${BF}_{Jugular}$	0.78 $(0.50) L / \min$	$+ 141.0$ (46.4)%	$< 0.001$
	${BF}_{SVC}$	0.99 $(0.42) L / \min$	$+ 135.5$ (49.0)%	$< 0.001$
	CVR-Aorta	—	$+ 1.0$ $(1.0) % / mmHg$	$< 0.001$
	CVR-Jug.	—	$+ 1.4$ $(3.0) % / mmHg$	$< 0.001$
	CVR-SVC	—	$+ 1.3$ $(2.5) % / mmHg$	$< 0.001$
DCS	CBF	—	$+ 148.5$ (42.8)%	$< 0.001$
DCS	CVR	—	$+ 1.8$ $(2.0) % / mmHg$	0.001
DOS	Hb	—	$- 1.3$ (5.4) µM	0.07
	$Hb O_{2}$	—	$+ 12.1$ (5.1) µM	$< 0.001$
	THC	—	$+ 10.1$ (8.0) µM	$< 0.001$

As seen in Fig. 3 and summarized in Table 3, a comparison of phase encoded velocity mapping MRI measures of relative changes in cardiac output in the superior vena cava to DCS measures of changes in cerebral blood flow were linearly related with high Pearson and concordance correlation coefficients, $R = 0.77$ , $CCC = 0.74$ , and a slope (95% CI) of 0.99 (0.74, 1.23). A similar correlation to DCS flow changes was observed with MRI measures of relative changes in cardiac output in the jugular vein, $R = 0.88$ , $CCC = 0.87$ , slope $(95 % CI) = 0.91 (0.75, 1.05)$ . Weaker correlations were also observed between rBF in the aorta and rCBF from DCS with a slope (95% CI) of 1.77 (0.72, 2.51) ( $p < 0.001$ ).

Fig. 3

(Top) Changes in blood flow (rBF) measured with velocity mapping MRI in the jugular veins (left), superior vena cava (middle), and aorta (right) compared to ${r CBF}_{DCS}$ . The solid line represents the best-fit line to the data, while the dashed line indicates the line of perfect concordance. The grey ribbon denotes the 95% confidence interval for the mean ${r CBF}_{DCS}$ . (Bottom) Bland-Altman plots of the difference in rBF, measured with VENC-MRI, and rCBF, measured with DCS, versus the mean of these parameters. Solid horizontal lines indicate the mean difference between each VENC parameter and rCBF measured with DCS, while the dotted lines indicate the 95% limits of agreement.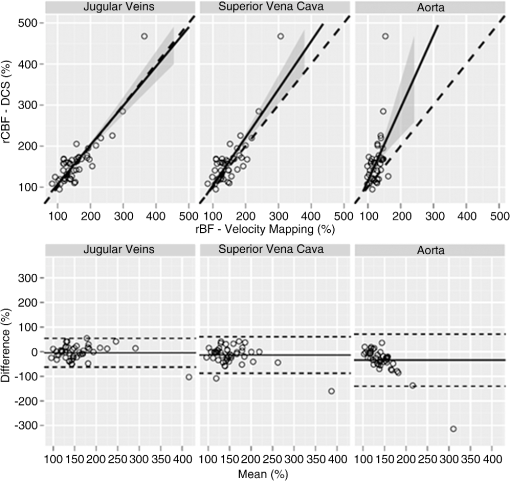

Table 3

Summary of concordance correlation coefficients (CCC) and bias correction factor, along with the estimated slope and intercept for a linear regression between DCS measures of rCBF and phase encoded velocity mapping rBF and the adjusted R2 and p-values.

Site	CCC	Bias correction	Slope estimate (95% CI)	Intercept estimate (95% CI) [%]	R, $p$ -value
Jugular veins	0.87	1.00	0.91 (0.75, 1.05)	15.3 ( $- 9.1$ , 39.7)	0.88, $p < 0.001$
Superior vena cava	0.74	0.95	0.99 (0.74, 1.23)	11.4 ( $- 25.9$ , 48.6)	0.77, $p < 0.001$
Aorta	0.20	0.42	1.77 (0.72, 2.51)	$- 62.2$ ( $- 159.1$ , 66.8)	0.46, $p < 0.001$

4. Discussion

We observed significant agreement between changes in CBF measured with diffuse correlation spectroscopy and changes in blood flow in the common jugular veins and superior vena cava measured with VENC MRI. Although the two techniques measure entirely different vascular structures related to cerebral hemodynamics, this strong agreement is encouraging. DCS measures cerebral blood flow in the microvasculature. The optical probe was secured to the forehead, thus, we were monitoring changes in CBF at the surface of the frontal cortex. VENC MRI measures blood flow in the jugular veins and superior vena cava, both of which are capacitance vessels that accommodate the large volume of blood flowing through them. Hypercapnia induces significant global changes in cerebral blood flow in the grey and white matter.³¹^,³² Therefore, in normal function, the micro vascular CBF changes in the frontal cortex measured by DCS should represent similar changes throughout the brain and these micro vascular changes should also be reflected in the macro vascular changes in blood flow drainage in the jugular veins.¹⁷^,¹⁸ Naturally, this micro/macro agreement presumes the patient has a healthy brain with no regions of watershed or hypoxia that may cause the frontal cortex to be a poor representation of the whole brain. Further, all patients were studied under conditions of general anesthesia with mechanical ventilation and neuromuscular blockade. These conditions preclude regional activation of cerebral cortex due to cognitive processes or movement.

This agreement between VENC MRI and DCS is encouraging, as one of the major advantages of DCS is its portability. Thus, by contrast to the sporadic CBF measures provided by phase encoded velocity mapping MRI, these results suggest DCS may be employed to accurately assess relative changes in CBF in a continuous fashion at the patient’s bedside. DCS may be a particularly attractive option for critically ill patients who are difficult to transport safely to an MRI, patients who are unable to have an MRI due to metallic implants, and patients who would benefit from continuous CBF monitoring.

A priori we would not expect changes in aortic flow due to hypercapnia to accurately represent microvascular CBF changes seen with DCS, thus, the weak correlation observed between DCS and aortic flow is readily explained. Aortic blood flow represents systemic blood flow, flow to both the brain and the body. Since CBF represents only one portion of the total cardiac output, we should expect the fractional change in CBF from the aorta during hypercapnia to be dependent on cerebrovascular reactivity as well as the geometry of the aortic arch and its branches. Total flow changes to both body and brain should match total aortic flow changes, however, the individual components of brain and body flows alone will not necessarily track aortic flow changes as not all tissues respond to ${CO}_{2}$ in a uniform way.

A handful of publications have studied the cerebral hemodynamic effects of hypercapnia on patients with congenital heart defects.¹¹^,³³^–³⁶ Durduran et al.¹¹ measured a mean, cerebrovascular reactivity due to increased ${CO}_{2}$ of $3.1 % / mmHg$ in neonates with congenital heart defects using DCS. The population studied in this work was considerably older than the neonates previously studied, ranging in age from 3 months to 5 years old. In our population, we found a slightly lower mean ${CO}_{2}$ reactivity of $1.8 % / mmHg$ . Fogel et al.³⁶ studied older CHD patients with VENC-MRI during hypercapnia, mean age of 2.2 years. They found a mean increase in jugular flows of 230% with a mean change in $p {CO}_{2}$ of 23 mmHg indicating a cerebrovascular reactivity of approximately $5 % / mmHg$ . Our results fall within the published values for this patient population of infants with congenital heart defects.

4.1.

Optical Approximations

Due to limitations in probe size, we were restricted to a single source-detector separation for DOS measurements. Thus, the modified Beer-Lambert law was used to quantify changes in the absorption coefficient and changes in oxy- and deoxy-hemoglobin. However, assumptions are required to employ the modified Beer-Lambert Law. In particular, it is assumed that $Δ μ_{a}$ is small relative to its baseline value and we assume that $μ_{s}^{'}$ remains constant. These assumptions appear to be valid in the present experiment. On average, $Δ μ_{a}$ at 786 nm was $0.015 {cm}^{- 1}$ , a change of approximately 15% of the presumed baseline value of $Δ μ_{a} = 0.1 {cm}^{- 1}$ at 786 nm. Similar results were found for 688 and 826 nm. Additionally, although $μ_{s}^{'}$ was not explicitly measured in this experiment, we feel justified in assuming $μ_{s}^{'}$ does not change due to hypercapnia.³⁷ Red blood cells contribute very little to the total cell volume of brain tissue, thus the majority of light scattering events are most likely due to mitochondria and other organelles as well as cell nuclei.³⁸^,³⁹ Thus, even if the blood volume increases substantially due to hypercapnia, this increase would have a small effect on the net scattering coefficient.

To fit the DCS data for a blood flow index, we assumed initial values for the absorption and reduced scattering coefficients, $μ_{a}$ and $μ_{s}^{'}$ . Because we are only interested in relative changes in the BFI, our choice of initial $μ_{a}$ and $μ_{s}^{'}$ has little to no effect on the resulting value of rCBF. However, changes from these initial values of $μ_{a}$ and $μ_{s}^{'}$ that occur during the duration of the study may influence the magnitude of rCBF. Thus, we incorporated changes in $μ_{a}$ obtained with DOS into our fitting procedure for BFI. However, as mentioned previously, our DOS analysis assumed that the scattering coefficient remained constant during the duration of the study. This assumption is most likely valid for hypercapnia. If false, a 10% increase in the scattering coefficient could alter the magnitude of rCBF by approximately 20%. Thus, future work would benefit greatly from the use of multiple source detector DOS amplitude and phase measurements used to continuously quantify $μ_{a}$ and $μ_{s}^{'}$ .

We have anatomical brain images of each patient, and we computed the mean skull/scalp/CSF thickness underneath our optical probe to be 0.81 cm. Because of the 2.5 cm source-detector separations used for both DOS and DCS, photons travel on average a depth of 1 cm into the tissue. Thus, we are confident the optical measurements are probing the surface of the cortex. However, in the future, DCS quantification of rCBF can be further improved. A semi-infinite model was used to fit DCS data and the fits were restricted to the early delay times, wherein $g_{2} (τ) > 1.2$ , to isolate contributions from photons penetrating deeply into tissue. As known from the anatomical scans, this model greatly simplifies the head geometry of these patients. In reality, the scalp, skull, cerebral spinal fluid, grey matter, and white matter possess different optical properties that can be accounted for in Monte Carlo simulations of light propagation.⁴⁰^–⁴² Although the semi-infinite model can be improved upon, it provides a sufficient approximation for this pilot study.

4.2.

MRI Assumptions

VENC MRI is a very accurate technique that does not depend on assumptions of flow profiles. Nevertheless, eddy currents and higher order Maxwell terms can introduce errors into the measurements. In addition, if a blood vessel is tortuous, flow may not be perpendicular to the imaging plane and this may introduce errors as well. Finally, partial volume effects will average out velocities in a given voxel, decreasing the accuracy of the measurement. In our study, eddy currents and Maxwell terms were minimized and the authors took great pains to ensure the imaging plane was perpendicular to flow. The dimensions of our VENC MRI images were $1 \times 1 \times 5 mm$ , which was well within accepted norms. Prior to each MRI scan, phantoms were used to calibrate the system.

5. Conclusion

In this paper, we demonstrate a highly significant correlation between measures of relative changes in cerebral blood flow derived with diffuse correlation spectroscopy and relative changes in blood flow in the common jugular veins and superior vena cava in pediatric patients with congenital heart defects. This agreement further strengthens the promise of DCS as an accurate and non-invasive modality for continuous CBF monitoring at the bedside.

Acknowledgments

This work would not have been possible without the help of the following people: Peter Schwab, Ellen Foster, Wesley Baker, Steven Schenkel, Varsha Jain, Justine Wilson, Matthew Harris, Cardiac Anesthesia staff, and, most importantly, the patients and their families. This work was supported by the NIH (NS-052380, NS-060653, RR-002305, HL090615, T32NS007413), by the Dana Foundation, and by the Steve and Judy Wolfson Family Trust.

References

1.

M. Wintermarket al., “Comparative overview of brain perfusion imaging techniques,” Stroke, 36 (9), E83 –E99 (2005). http://dx.doi.org/10.1161/01.STR.0000177884.72657.8b SJCCA7 0039-2499 Google Scholar

2.

K. D. LiemG. Greisen, “Monitoring of cerebral haemodynamics in newborn infants,” Early Hum. Develop., 86 (3), 155 –158 (2010). http://dx.doi.org/10.1016/j.earlhumdev.2010.01.029 EHDEDN 0378-3782 Google Scholar

3.

K. K. Galliet al., “Periventricular leukomalacia is common after neonatal cardiac surgery,” J. Thorac. Cardiovasc. Surg., 127 (3), 692 –704 (2004). http://dx.doi.org/10.1016/j.jtcvs.2003.09.053 JTCSAQ 0022-5223 Google Scholar

4.

D. J. Lichtet al., “Brain maturation is delayed in infants with complex congenital heart defects,” J. Thorac. Cardiovasc. Surg., 137 (3), 529 –537 (2009). http://dx.doi.org/10.1016/j.jtcvs.2008.10.025 JTCSAQ 0022-5223 Google Scholar

5.

D. B. Andropouloset al., “Brain immaturity is associated with brain injury before and after neonatal cardiac surgery with high-flow bypass and cerebral oxygenation monitoring,” J. Thorac. Cardiovasc. Surg., 139 (3), 543 –556 (2010). http://dx.doi.org/10.1016/j.jtcvs.2009.08.022 JTCSAQ 0022-5223 Google Scholar

6.

G. MaretP. Wolf, “Multiple light scattering from disordered media. The effect of Brownian motion of scatterers,” Zeitschrift für Physik B Condensed Matter, 65 (4), 409 –413 (1987). Google Scholar

7.

D. A. Boaset al., “Detection and characterization of optical inhomogeneities with diffuse photon density waves: a signal-to-noise analysis,” Appl. Opt., 36 (1), 75 –92 (1997). http://dx.doi.org/10.1364/AO.36.000075 APOPAI 0003-6935 Google Scholar

8.

D. J. Pineet al., “Diffusing wave spectroscopy,” Phys. Rev. Lett., 60 (12), 1134 –1137 (1988). http://dx.doi.org/10.1103/PhysRevLett.60.1134 PRLTAO 0031-9007 Google Scholar

9.

D. A. BoasL. E. CampbellA. G. Yodh, “Scattering and imaging with diffusing temporal field correlations,” Phys. Rev. Lett., 75 (9), 1855 –1858 (1995). http://dx.doi.org/10.1103/PhysRevLett.75.1855 PRLTAO 0031-9007 Google Scholar

10.

C. Cheunget al., “In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies,” Phys. Med. Biol., 46 (8), 2053 –2065 (2001). http://dx.doi.org/10.1088/0031-9155/46/8/302 PHMBA7 0031-9155 Google Scholar

11.

T. Durduranet al., “Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects,” J. Biomed. Opt., 15 (3), 037004 (2010). http://dx.doi.org/10.1117/1.3425884 JBOPFO 1083-3668 Google Scholar

12.

M. N. Kimet al., “Noninvasive measurement of cerebral blood blow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,” Neurocrit. Care, 12 (), 173 –180 (2010). NCEACB 1541-6933 Google Scholar

13.

C. Zhouet al., “Diffuse optical monitoring of hemodynamics in piglet brain with head trauma injury,” J. Biomed. Opt., 14 (3), 034015 (2009). http://dx.doi.org/10.1117/1.3146814 JBOPFO 1083-3668 Google Scholar

14.

T. Durduranet al., “Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation,” Opt. Lett., 29 (15), 1766 –1768 (2004). http://dx.doi.org/10.1364/OL.29.001766 OPLEDP 0146-9592 Google Scholar

15.

G. Dietscheet al., “Fiber-based multispeckle detection for time-resolved diffusing-wave spectroscopy: characterization and application to blood flow detection in deep tissue,” Appl. Opt., 46 (35), 8506 –8514 (2007). http://dx.doi.org/10.1364/AO.46.008506 APOPAI 0003-6935 Google Scholar

16.

M. Diopet al., “Calibration of diffuse correlation spectroscopy with a time-resolved near-infrared technique to yield absolute cerebral blood flow measurements,” Biomed. Opt. Express, 2 (7), 2068 –2081 (2011). http://dx.doi.org/10.1364/BOE.2.002068 BOEICL 2156-7085 Google Scholar

17.

E. M. WilsonJ. H. Halsey Jr.J. J. Vitek, “Validation of jugular venous flow as an index of total cerebral blood flow,” Stroke, 3 (3), 300 –321 (1972). http://dx.doi.org/10.1161/01.STR.3.3.300 SJCCA7 0039-2499 Google Scholar

18.

J. S. Meyeret al., “Quantitative measurement of cerebral blood flow with electromagnetic flowmeters: recording internal jugular venous flow of monkey and man,” Trans. Am. Neurol. Assoc., 88 78 –83 (1963). TANAA4 0065-9479 Google Scholar

19.

D. J. Bryantet al., “Measurement of flow with NMR imaging using a gradient pulse and phase difference technique,” J. Comput. Assist. Tomogr., 8 (4), 588 –593 (1984). http://dx.doi.org/10.1097/00004728-198408000-00002 JCATD5 0363-8715 Google Scholar

20.

C. L. DumoulinH. R. Hart, “Magnetic resonance angiography,” Radiology, 161 (3), 717 –720 (1986). RADLAX 0033-8419 Google Scholar

21.

N. J. Pelcet al., “Quantitative magnetic-resonance flow imaging,” Magn. Reson. Quart., 10 (3), 125 –147 (1994). MRQUEN 0899-9422 Google Scholar

22.

D. T. Delpyet al., “Estimation of optical pathlength through tissue from direct time of flight measurement,” Phys. Med. Biol., 33 (12), 1433 –1442 (1988). http://dx.doi.org/10.1088/0031-9155/33/12/008 PHMBA7 0031-9155 Google Scholar

23.

S. Fantiniet al., “Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy,” Phys. Med. Biol., 44 (6), 1543 –1563 (1999). http://dx.doi.org/10.1088/0031-9155/44/6/308 PHMBA7 0031-9155 Google Scholar

24.

T. Durduranet al., “Diffuse optics for tissue monitoring and tomography,” Rep. Progr. Phys., 73 (7), 43 (2010). http://dx.doi.org/10.1088/0034-4885/73/7/076701 RPPHAG 0034-4885 Google Scholar

25.

A. Duncanet al., “Measurement of cranial optical path length as a function of age using phase resolved near infrared spectroscopy,” Pediatr. Res., 39 (5), 889 –894 (1996). http://dx.doi.org/10.1203/00006450-199605000-00025 PEREBL 0031-3998 Google Scholar

26.

J. BruceR. P. Berne, Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics, Courier Dover Publications, Mineola, NY (2000). Google Scholar

27.

J. Zhaoet al., “In vivo determination of the optical properties of infant brain using frequency-domain near-infrared spectroscopy,” J. Biomed. Opt., 10 (2), 024028 (2005). http://dx.doi.org/10.1117/1.1891345 JBOPFO 1083-3668 Google Scholar

28.

F. Wilcoxon, “Individual comparisons by ranking methods,” Biometrics Bulletin, 1 (6), 80 –83 (1945). http://dx.doi.org/10.2307/3001968 BIBLA5 0099-4987 Google Scholar

29.

R: A Language and Environment for Statistical Computing, R Development Core Team, (2011). Google Scholar

30.

L. I. Lin, “A concordance correlation-coefficient to evaluate reproducibility,” Biometrics, 45 (1), 255 –268 (1989). http://dx.doi.org/10.2307/2532051 BIOMB6 0006-341X Google Scholar

31.

H. Itoet al., “Changes in human cerebral blood flow and cerebral blood volume during hypercapnia and hypocapnia measured by positron emission tomography,” J. Cerebr. Blood Flow Metab., 23 (6), 665 –670 (2003). http://dx.doi.org/10.1097/01.WCB.0000067721.64998.F5 JCBMDN 0271-678X Google Scholar

32.

E. Rostrupet al., “Regional differences in the CBF and BOLD responses to hypercapnia: a combined PET and fMRI study,” Neuroimage, 11 (2), 87 –97 (2000). http://dx.doi.org/10.1006/nimg.1999.0526 NEIMEF 1053-8119 Google Scholar

33.

S. Tabbuttet al., “Impact of inspired gas mixtures on preoperative infants with hypoplastic left heart syndrome during controlled ventilation,” Circulation, 104 (12), I159 –I164 (2001). CIRCAZ 0009-7322 Google Scholar

34.

C. Ramamoorthyet al., “Effects of inspired hypoxic and hypercapnic gas mixtures on cerebral oxygen saturation in neonates with univentricular heart defects,” Anesthesiology, 96 (2), 283 –288 (2002). http://dx.doi.org/10.1097/00000542-200202000-00010 ANESAV 0003-3022 Google Scholar

35.

K. Toiyamaet al., “Changes in cerebral oxygen saturation and blood flow during hypoxic gas ventilation therapy in HLHS and CoA/IAA complex with markedly increased pulmonary blood flow,” Circul. J., 74 (10), 2125 –2131 (2010). http://dx.doi.org/10.1253/circj.CJ-09-0833 CJIOBY 1346-9843 Google Scholar

36.

M. A. Fogelet al., “Brain versus lung: hierarchy of feedback loops in single-ventricle patients with superior cavopulmonary connection,” Circulation, 110 (11), II147 –II152 (2004). http://dx.doi.org/10.1161/01.CIR.0000138346.34596.99 CIRCAZ 0009-7322 Google Scholar

37.

M. Diop, “Calibration of diffuse correlation spectroscopy with a time-resolved near-infrared technique to yield absolute cerebral blood flow measurements,” Biomed. Opt. Express, 2 2068 –2081 (2011). Google Scholar

38.

J. R. Mourantet al., “Predictions and measurements of scattering and absorption over broad wavelength ranges in tissue phantoms,” Appl. Opt., 36 (4), 949 –957 (1997). http://dx.doi.org/10.1364/AO.36.000949 APOPAI 0003-6935 Google Scholar

39.

J. R. Mourantet al., “Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics,” Appl. Opt., 37 (16), 3586 –3593 (1998). http://dx.doi.org/10.1364/AO.37.003586 APOPAI 0003-6935 Google Scholar

40.

L. H. WangS. L. JacquesL. Q. Zheng, “MCML—Monte Carlo modeling of light transport in multilayered tissues,” Comput. Meth. Program Biomed., 47 (2), 131 –146 (1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar

41.

L. Gagnonet al., “Investigation of diffuse correlation spectroscopy in multi-layered media including the human head,” Opt. Express, 16 (20), 15514 –15530 (2008). http://dx.doi.org/10.1364/OE.16.015514 OPEXFF 1094-4087 Google Scholar

42.

D. Boaset al., “Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head,” Opt. Express, 10 (3), 159 –170 (2002). OPEXFF 1094-4087 Google Scholar

Citation Download Citation

Erin M. Buckley, Dalton Hance, Jennifer M. Lynch, Rickson C. Mesquita, Arjun G. Yodh, Daniel J. Licht, Thomas Pawlowski, Felice B. Wilson, Mark A. Fogel, Turgut Durduran, Laura K. Diaz, and Mary E. Putt "Validation of diffuse correlation spectroscopic measurement of cerebral blood flow using phase-encoded velocity mapping magnetic resonance imaging," Journal of Biomedical Optics 17(3), 037007 (27 March 2012). https://doi.org/10.1117/1.JBO.17.3.037007

Published: 27 March 2012

Access the abstract

JOURNAL ARTICLE
9 PAGES

DOWNLOAD PAPER SAVE TO MY LIBRARY

GET CITATION

CITATIONS

Cited by 84 scholarly publications.

Explore citations on Lens.org

RIGHTS & PERMISSIONS

Get copyright permission Get copyright permission on Copyright Marketplace

KEYWORDS

Magnetic resonance imaging

Blood circulation

Cerebral blood flow

Veins

Spectroscopy

Phase velocity

Brain

1.

Introduction

2.

Materials and Methods