Double peacock eye optical element for extended focal depth imaging with ophthalmic applications

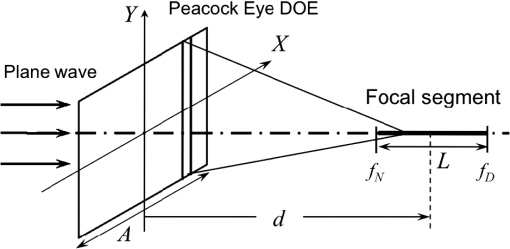
Defocus is one of the most common and important sources of image degradation that affect the maximum lateral resolution achievable in optical imaging systems. The depth of field defines the axial range in the object space that can form images with high lateral resolution at a given image distance. Conversely, the depth of focus defines the axial range of high lateral resolution in the image space for a fixed object position. Out of this range, defocus causes a spatial low-pass filter effect that can be described mathematically in terms of the pupil function and the optical transfer function of the system.^1,2 The simple ability to control the depth of field with the lens aperture has been widely exploited in photography. But it has two clear drawbacks: a dramatic reduction in the energy that reaches the image plane, and a loss of resolution. A large number of refractive as well as diffractive optical elements (DOEs) have been designed to overcome this situation and obtain an extended depth of focus (EDOF). Some solutions, for instance a cubic phase element combined with the imaging lens,^3,4 involve the introduction of certain amount of aberration, even stronger than defocus, that keeps nearly constant along the EDOF axial segment. A digital deconvolution in a postprocessing stage is required to obtain a sharp output image.

When the human eye ages and is affected by presbyopia, it gradually loses accommodation, i.e., the capability to form images of objects placed at different distances; beyond the age of about 50, the human eye becomes a system with a fixed focal length.⁵ Traditional solutions to the problem consist of multifocal lenses in a variety of compound refractive and diffractive designs and categories (spectacles, contact, and intraocular lenses). They are not fully satisfactory but a discrete solution that ensures, at least, a couple of focused images (named near and far powers) for two (near and far) positions of an object. Bifocal and progressive spectacle lenses are widely used still today as well as bifocal and multifocal contact lenses, the latter with less success though. The application of multifocal designs to the intraocular lenses conventionally used in cataract surgery has opened a new possibility for the simultaneous compensation of defocus and presbyopia (for a short review see, for instance, ⁶). Since a monofocal intraocular lens only provides clear vision for a very limited depth of field, surgeons prescribe an additional corrective lens for either distance or near vision. Multifocal intraocular lenses are designed to reduce the dependence on spectacles. They are mostly bifocal, although trifocal designs have been reported too.⁷ Multifocal intraocular lenses address the lack of accommodation using the principle of simultaneous vision and brain adaptation, which implies to choose between the near and distance images, both superimposed on the retina, depending on the object at which the observer is looking. The superposition of images may lead to rivalry or confusion, often associated with other unpleasant visual phenomena, such as glare and halos, in mesopic and scotopic conditions. These multifocal lenses can be classified according two basic designs, named refractive and diffractive.⁸ Refractive multifocal intraocular lenses are multizone lenses with either concentric arrangement or circular asymmetry.⁹ A diffractive multifocal intraocular lens uses the base lens curvature and the zeroth and first diffraction orders to simultaneously produce the two focal points.¹⁰ While the power corresponding to the zeroth diffraction order is used to image distance objects, the first order is used for near vision. Some designs of multifocal intraocular lenses aim to distribute the energy between the near and far images as a function of the pupil diameter, which in turn varies with the focusing distance. However, the aperture aberrations affect the result and thus such lenses provide little improvement in comparison with less sophisticated designs.¹¹ The accommodative intraocular lens is an alternative solution that relies on the physiological function of the ciliary muscle of the eye after a cataract surgery to produce a forward shift of the intraocular lens. The effectiveness of this technique, however, is still a matter of controversy.¹² Clearly, the aged human eye has a need for EDOF and different approaches have already been reported to meet this demand. Unlike the hybrid optodigital EDOF imaging systems, the human eye cannot apply digital deconvolution to the retinal image before the brain processes it. Several diffractive elements with EDOF imaging properties, of radial (e.g., axicons¹³ and axilens¹⁴) and angular (e.g., light sword¹⁵) modulation, have been recently considered for presbyopia compensation in aged human vision.^16–18

In ¹⁹, the authors describe a family of computer-generated DOEs that perform as generalized zone plates capable to focus light into an arbitrary line segment with any orientation with respect to the optical axis. In this paper, we are particularly interested in the so-called “peacock eye,”¹⁹ which focuses the incident plane wave into a segment of the optical axis. To the best of our knowledge, this is the first time the peacock eye is used as an EDOF imaging component whose performance can be applied for presbyopia compensation. We adapt its original design to tailor the following focal segments:

These DOEs will be displayed on a parallel-aligned liquid crystal on silicon spatial light modulator (LCoS SLM), which works in phase only modulation regime.²⁰ For the double multiplexed peacock eye, two codifications of the phase will be considered:

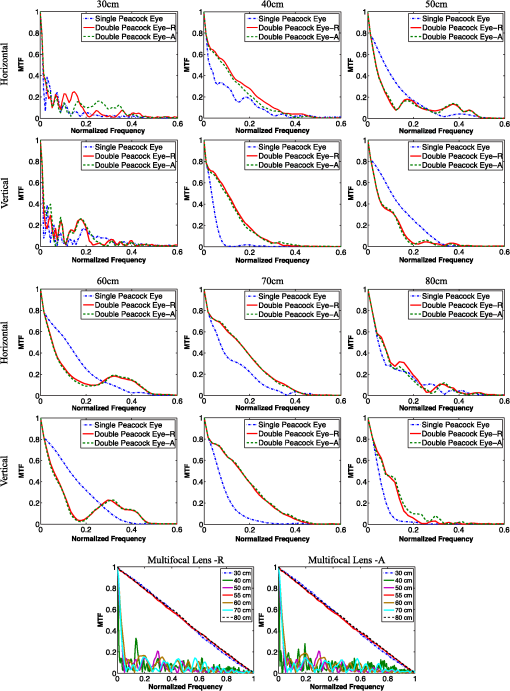
The results obtained with all the peacock eye optical elements will be compared with a multifocal lens. The latter consists of three phase diffractive lenses with the same axis that are spatially multiplexed. It has three focal points coinciding with the extremes and the center of the required depth of focus segment.²¹ For the sake of comparison, the phase codifications of the resulting multifocal lens will be the same as those used for the peacock eye (random distribution and addition of transmittances). To test the optical performance of all the elements, we obtain the point-spread function (PSF), the modulation transfer function (MTF), and their evolution along the optical axis. Additional results concerning incoherent imaging of extended objects placed at different distances are included. All the results have been obtained by both numerical simulation and experimentally.

The peacock eye optical element is a particular type of a family of computer-generated DOEs capable of focusing light onto segments of arbitrary length, inclination, orientation, and longitudinal intensity distribution.¹⁹ In the case of the peacock eye element, the focal segment is aligned with the optical axis. Its design derives from a spherical zone plate whose focal length varies continuously along with one of the aperture Cartesian coordinates. Let us consider a square aperture of $A×A$ size, uniformly illuminated by a plane wave of wavelength $λ$ (Fig. 1) and transmittance $T(x,y)=exp[ikϕ(x,y)]$, where $k=2π/λ$ and $ϕ(x,y)$ is its phase function. Jaroszewicz et al.¹⁹ derived the phase function $ϕ(x,y)$ by focusing the incident plane wave onto a focal segment of the optical axis with uniform intensity distribution along the segment. This phase function takes the expression Display Formula

The resulting element was named “peacock eye” because of the shape of the zones of equal phase (see, for instance, the top left element of Fig. 2). In ¹⁹, the peacock eye element was demonstrated to be, in first approximation, a spherical zone plate with an added aberration term resembling coma that appears in the central field. However, the angle between the lines limiting the aberration pattern is 70.53 deg, whereas for the third-order coma it is 60 deg.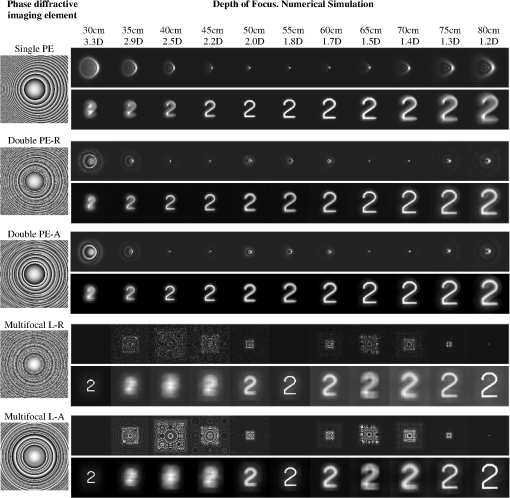

A multifocal lens can be obtained by multiplexing a number of spherical zone plates (or phase Fresnel lenses) $l1,…,ln$ of different focal lenses $f1,…,fn$. They can be spatially multiplexed in a single aperture. They are multiplexed with coaxial configuration when the lenses are combined to share a common optical axis.²¹ We consider trifocal lenses in the experiments of this work.

The sublenses can be combined by a simple random distribution of the respective phases, as it has been detailed in Sec. 1.

Alternatively, the sublenses can be combined by adding their respective transmittances. According to this procedure and from the phase function of a single sublens $ϕi(x,y)=−(x2+y2)/2fi$, the complex valued multifocal lens function turns into Display Formula

We have designed a set of peacock eye optical elements with EDOF. For the sake of comparison, the requested total focal segment ($fN$, $fD$) was the same in all cases, with fixed extremes at the axial distances of $fN=30cm$ (power in diopters of 3.33 D) and $fD=80cm$ (1.25 D). The Holoeye-HEO LCoS SLM used to display the phase diffractive elements in the experiment has been characterized for an optimized performance as reported in ²⁰. Taking into account the Nyquist criterion for the representation of phase, the pixel pitch ($p=8microns$) of the SLM, the resolution of the device ($1920[H]×1080[V]pixels$, of which a square window of size $N=1080pixels$ was used to display the computer generated phase DOEs), and the wavelength of the light from a He–Ne laser ($λ=633nm$), the shortest focal length was determined²¹ by the expression $fmin=Np2/λ$. In our experimental conditions $fmin≈11cm$, thus we have chosen a higher value for $fN=30cm$ (3.33 D).

The single peacock eye had a focal segment ($f1$, $f2$) that coincided with the requested focal segment, that is $f1=fN$ and $f2=fD$. The double peacock eye had two focal segments ($f1$, $f2$) and ($f3$, $f4$) that covered the requested total focal segment, with some overlap (of about 5 cm) in the center, that is, $f1=fN$, $f2=58cm$ (1.72 D), $f3=53cm$ (1.89 D), and $f4=fD$. The multifocal lens focused the light beam on three focal points placed at $f1=fN$, $f2=55cm$ (1.82 D), $f3=fD$. The phase function was codified in the LCoS SLM, which operated in phase-only modulation regime, with 8-bit dynamic range. The codification was different for each element: in the case of a single peacock eye, each pixel of the device aperture displayed the phase of the single peacock eye function at its position. In the case of the double peacock eye with random distribution of phases, the pixels of the SLM aperture were grouped in small windows of $3×3pixel$ size. Each window was randomly assigned to display the phase function of only one of the two peacock eyes at its precise position of the aperture. Regarding the double peacock based on the addition of the individual peacock eye transmittances, each pixel of the aperture displayed the phase value of the resulting transmittance function. In the case of the multifocal lens, the codification of the phase was analogous to that used for the double peacock eye (i.e., random distribution and addition of transmittances).

The PSF, MTF, and the image of an extended object (number 2 from the USAF test) have been obtained in each case. In the numerical simulation of the imaging process, we have considered the scale effects, and we have convolved scaled versions of both the PSF and the extended object (number 2 from the test USAF) at different image distances. In the optical experiment, each phase diffractive element was displayed on a LCoS SLM controlled by computer. A He–Ne laser beam was spatially filtered by means of a microscope objective and a small pinhole. To obtain the PSF of each DOE displayed on the SLM, we used on-axis collimated illumination. Alternatively, a rotating diffuser was used to obtain spatially incoherent light to illuminate the extended object whose image was formed on the CCD sensor. The extended object is the character #2 (from USAF test, 1.5 mm lateral size), which was placed at the front focal distance of an auxiliary lens of $faux=20cm$. The extended object covered an angular field equal to 0.07’ $≈4.3$”. We fixed the capturing parameters of the CCD camera (PCO 1600 with large dynamic range of 16 bits) so as to avoid the saturation of the camera. This is important in order to establish a correct basis for PSF and MTF comparison between the different optical elements.

Figure 2 shows the numerical results for the PSFs and the images of an extended object along different positions in the focal segment obtained with the designed elements. In each case, the phase function of the phase diffractive element is represented in gray levels on the left column. With the same distribution of content, Fig. 3 shows the experimental results. Figure 4 shows the MTFs computed from the experimental results presented in Fig. 3 versus the normalized spatial frequency. As for the constant of normalization, we have considered the diffraction-limited cutoff spatial frequency in the object space ($fcutoff=238cycles/deg$ in our experiment).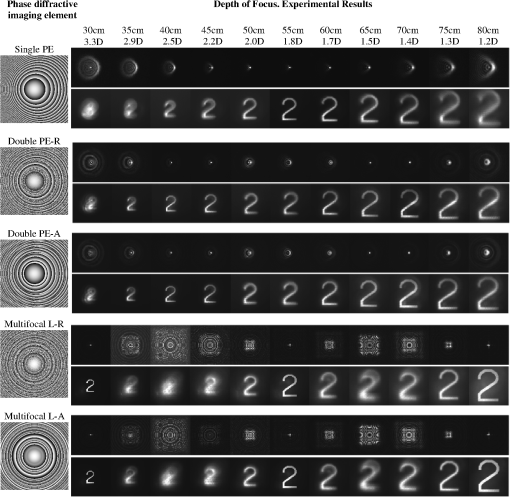

Figures 2 and 3 present a very good agreement between simulated and experimental results. The performances of the peacock-based elements show a real focal segment, somewhat shorter than expected, where defocus is remarkably reduced. In case of the single peacock eye, the best image quality appears in the central part of the focal segment, let us say, from 50 cm up to 60 cm. Images degrade rather quickly outside this central part toward the extremes of the designed focal segment (from 30 to 80 cm). In case of the double peacock eyes, however, the image quality benefits from two separate segments of good performance (the first, from 35 cm up to 45 cm and the second, from 65 to 75 cm), yet maintaining an acceptable performance in the central part (from 50 cm up to 60 cm) of the total focal segment, where both focal components overlap. Even in the extremes of the total focal segment (30 cm, 80 cm) the images obtained with the double peacock eyes are sharper than with the single peacock eye. All the above results lead us to conclude that the double peacock eye performance is better than the single one. As for the multifocal lens, the image quality obtained at the three designed focal lengths (30, 55, and 80 cm) is very good, much better than that obtained with the peacock-based elements at the same distances. However, out of these three positions, the images appear severely affected by defocus and poor quality. A much poorer result would have been obtained if a bifocal lens, with two focal lengths of design at 30 and 80 cm, had been considered instead of the trifocal lens.

Regarding the methods used to codify the multiplexed elements, that is, random distribution and addition of transmittances, no clear differences have been obtained in this experiment to claim one of them superior to the other.

The MTFs functions plotted in Fig. 4 are consistent with the former analysis.

In this section, we illustrate the potential applicability of the phase peacock-based diffractive elements as EDOF imaging components for presbyopia compensation. From the results obtained in the image space (Sec. 3) and in order to have a long depth of field in the object space, we fixed the output image plane (the CCD camera sensor that acts as virtual retina) at a distance of 65 cm from the LCoS SLM (Fig. 5). Otherwise, if we had fixed the output image plane at, for instance, 40 cm from the SLM, the depth of field would have been much shorter. The object was axially shifted from the infinite (object vergence in diopters equal to 0 D) toward the LCoS SLM. To cover long object distances [from infinite (0 D) to 1 m (1 D), approximately], we shifted the real object within the front focal distance of the auxiliary lens ($faux=20cm$). For shorter object distances, we removed the auxiliary lens and directly shifted the own object along the bench toward the LCoS SLM. Figure 6 shows the experimental images captured by the camera for two elements: the single peacock eye and the double peacock eye. The latter was multiplexed based on the addition of transmittances. At short and intermediate object distances (up to 165 cm or object vergence 0.61 D), Fig. 6 demonstrates that the double peacock eye forms sharper images than the single peacock eye. For far object distances (from 165 cm to infinite), however, the single peacock eye achieves sharper images.

In case of the double peacock eye, we should say that the image obtained for the object placed at 90 cm (object vergence 1.1 D) is still acceptable in comparison with the others; consequently, this position constitutes the “near object point” for the EDOF imaging element. Since the image plane of the near object point is located at 65 cm (image vergence 1.5 D) behind the LCoS SLM, it implies that the double peacock eye is operating with a focal length of 38 cm (power of 2.6 D) approximately according to a simple calculation in the paraxial optics approach. This result is consistent with the values considered in the design of this DOE (a total focal segment from $fN=30cm$ to $fD=80cm$). The “near object point” for the single peacock eye would be at 142 cm (object vergence 0.70 D) approximately.

The “remote object point” would be infinite for the single peacock eye, whereas for the double peacock eye it would be at about 2 m (0.5 D). For the double peacock eye working with objects located at this distance or further, there is an effect that reminds the simultaneous double image, with one of them better focused than the other.

The simulated and experimental results presented in this paper prove that the peacock eye optical element, designed to focus an incident plane wave into a segment of the optical axis, satisfactorily performs as an EDOF imaging component. We have considered a single peacock eye element, which produces one focal segment along the axis with length covering the required depth of focus, and a double peacock eye element, which is a spatial multiplexed element that produces two successive focal segments along the axis with partial overlapping between them. The depth of focus obtained by the peacock eye-based elements is by far smoother than that obtained with a multifocal spherical Fresnel lens. Except for the precise positions that correspond to the focal lengths of design in the multifocal lens, the achieved image quality is much better with the peacock eye-based elements, particularly for the images at intermediate positions along the focal segment.

In the case of the single peacock eye, the image quality is high in the central part of the focal segment but quickly degrades toward the extremes. In the case of the double peacock eye, however, the image quality shows two separate segments of good performance yet maintaining an acceptable sharpness in the central part of the total focal segment. The images obtained with the double peacock eye at the extremes of the focal segment are better quality than with the single peacock eye. Overall, it can be said that the double peacock eye performs better than the single one in terms of sharpness, optical resolution, and MTF values along the focal segment (depth of focus).

In the multiplexed elements, no clear advantages have been noticed between the two procedures used to codify the phase function, i.e., the random distribution and the addition of transmittances.

We have illustrated the potential applicability of the phase peacock-based diffractive elements as EDOF imaging components for presbyopia compensation. In such a case, the extreme points of the depth of field would represent the remote and the near object points. They have been experimentally obtained for both the single and the double peacock eye optical elements. For short and intermediate object distances, the double peacock eye element achieves definitely better resolution and sharpness than the single peacock eye. For far object distances, however, the single peacock eye brings better results.

The peacock eye and its variants studied in this work show promising properties in ophthalmic optics for presbyopia compensation. We have demonstrated the validity and the experimental feasibility of the proposal although it has not been fit to the human eye scale. The peacock eye-based element and multifocal lens performances have been compared at the same scale and, therefore, the results can be extrapolated to the human eye scale. For the multifocal lens, we have considered a trifocal design, which is less favorable than a standard bifocal lens for comparison with the peacock element at intermediate image positions. The results obtained prove that the peacock eye elements show extended depth of focus and therefore, form sharper images and have superior performance for intermediate distances. Although some aberration resembling coma appears in the central visual field of peacock eye elements, it has less degrading effect than defocus for intermediate distances and, therefore, they are still advantageous in comparison with a trifocal lens. For all these reasons, the peacock eye elements represent an interesting alternative to replace the diffractive lens component already existing in some designs of currently available diffractive multifocal intraocular lenses. To this end, other relevant aspects concerning scale, aperture, aberrations, and materials need to be considered in a future study.

L. A. Romero and M. S. Millán acknowledge the financial support of Spanish Ministerio de Educación y Ciencia and FEDER under project DPI2009-08879 and L. A. Romero acknowledges a PhD scholarship from the aforementioned ministry. Z. Jaroszewicz and A. Kolodziejczyk acknowledge the financial support of the Polish Ministry of Science and Higher Education under grant NN-514-149038.