|
|
1.IntroductionNear infrared spectroscopy (NIRS) is a noninvasive optical technique to study hemodynamic changes and oxygenation in tissue. It utilizes differences in the absorption spectra of oxygenated and deoxygenated hemoglobin and the relatively good transparency of tissues for light in the near-infrared region.1,2 NIRS is based on illumination of the tissue and detection of diffusely remitted light in a spot located a few centimeters apart from the source position. The NIRS technology has been mostly used in muscle3–5 and brain studies.6–9 Regarding the assessment of brain hemodynamic changes and oxygenation in the brain, there is a growing field of clinical applications.4,6,7,10–17 In the early stage of development, NIRS was used for evaluation of changes of oxy- and deoxyhemoglobin in the brain of neonates.18–23 With advances of light detection efficiency the technique was applied in adult humans, as well. Many authors reported evidence that NIRS signals do contain information originating from the cerebral cortex.9,10,24 A major obstacle in routine application of NIRS instruments in clinical practice is the contamination of the measured signals of changes of oxy- and deoxyhemoglobin in the brain by changes in extracerebral tissue.25–27 Several methods allowing for compensation or removal of the influence of the extracerebral tissue contamination were proposed. They are based on multi-distance continuous wave measurements,28,29 frequency-domain experiments30 or the analysis of the broadening of short laser pulses during their propagation in the tissue under investigation.25,27,31–35 The present paper is related to time-resolved near-infrared spectroscopy which is currently extensively studied as a tool that allows separation of extra- and intracerebral changes of oxy- and deoxyhemoglobin.35–37 The depth-selective determination of absorption changes in the adult human head can be achieved by analysis of ratios of time windows of the distributions of times of flight (DTOF) of photons27,38,39 or by evaluation of their statistical moments.31 Previously we showed the significant advantages of using moments for assessing depth-resolved changes of absorption.31,35,40 A particular feature of the analysis based on moments is that the elimination of the influence of the instrumental response function is straightforward.41 We found that depth-resolved profiles of absorption changes can be derived from multi-distance time-resolved measurements and evaluation of the moments: integral, mean time of flight and variance.31,42 The changes in the absorption coefficient of the tissue can be connected to functional activation of the cortex and corresponding changes in the concentrations of oxy- and deoxyhemoglobin. Absorption changes also occur during a bolus of an optical contrast agent. For our previously published study on depth-resolved assessment of absorption changes the moments at several source-detector separations were required.31,42 However, multi-distance time-resolved measurements may not always be feasible. In particular, multi-site and multi-distance continuous wave measurements allow rather high lateral spatial resolution in optical brain imaging to be achieved.29 However, in the case of time-resolved light detection a multi-distance approach with recording at various distances by the same detector is rather difficult because of the limited dynamic range of the fast detectors. Furthermore, time-resolved measurements that are necessary to record DTOFs and their moments, in particular variance, most commonly rely on time-correlated single photon counting43 and are instrumentally demanding. This technology remains expensive and is not widely used in NIRS brain studies. The less sophisticated and commercially available frequency domain technique in principle provides access to mean time of flight via phase measurements.44 The present paper addresses experimental design considerations, in particular the selection of source-detector separations used, as well as the available types of measurements corresponding to continuous wave, frequency or time domain methods, represented by the various subsets of moments. We compare the various approaches with respect to the standard deviation of the obtained absorption changes in a two-layered tissue model due to photon noise. We assume the thickness of the upper layer to be known. The upper layer corresponds to extracerebral tissue (skin, skull) whereas the lower layer mimics the brain tissue. For this model, the number of measured quantities, i.e., the three moments recorded at one or more distances, exceeds the number of unknown quantities to be determined, i.e., the changes of the absorption coefficients in the two layers. The goal is to investigate whether the number of different measurements can be significantly reduced without substantially increasing the standard deviation of the estimated absorption changes in the two layers. To this aim we study the standard deviations of estimates of varying the number of measured quantities and the source-detector separations. 2.TheoryThe equations that will be derived in this section are related to the general case of a medium with compartments. The specific results shown in Sec. 4 refer to a two-layered medium, i.e., a superficial layer with thickness on top of a semi-infinite compartment (see Fig. 1). This model mimics the layered structure of the human head consisting of extracerebral tissue (skin, skull, cerebro-spinal fluid) and brain tissue. We assume that changes in DTOFs are mainly due to changes in the absorption coefficients of the tissues whereas the scattering properties remain constant (). Fig. 1Geometry of a two-layered model and configuration of the multi-distance measurement with positions of source and detectors, –thickness of upper layer, –source-detector separation for th detector, –absorption change in upper (lower) layer. 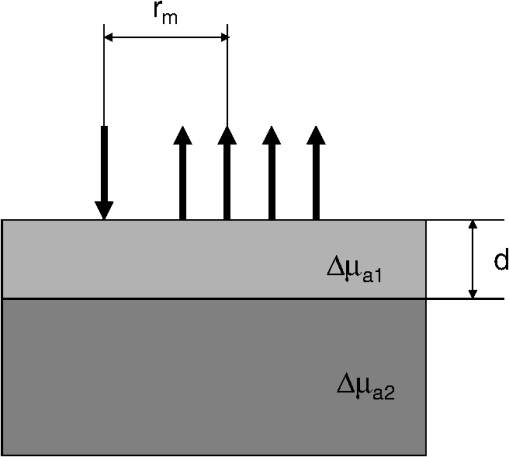 The time-of-flight distributions are obtained as histograms of photon counts in time channels . We start from the following statistical moments of measured DTOFs, the 0th moment or total photon count the first moment or mean time of flight and the second centralized moment or variance where is the second moment of the DTOF. Here and in the following the sum is extended over a finite number of time channels of the DTOF from to .The following depth-resolved analysis is based on the changes in attenuation , mean time of flight and variance where the symbols with star denote the quantity after an absorption change. Assuming that the changes of the absorption coefficient are small, the relationship between in the individual compartments of the model and changes of moments of DTOFs is linear, See Ref. 31. The vectors , and contain changes of attenuation, mean time of flight and variance of the DTOFs at source-detector separations , i.e., , , . The vector contains changes of in different compartments of the model, i.e., .The sensitivity matrices MPP (mean partial pathlength), MTSF (mean time of flight) and VSF (variance of the DTOF) are matrices that represent the sensitivity of the measured quantities to small changes of the absorption coefficients for the various source-detector separations and compartments of the medium. These sensitivities can be obtained by Monte Carlo simulations31 or by applying a perturbation method based on the diffusion equation.37,45,46 For a measurement carried out at source-detector separations the system of equations given by Eqs. (5)–(7) consists of equations with unknowns, i.e., the changes of the absorption coefficient in the compartments of the model. Let , and denote the estimates for , and , i.e., the measured data. An estimate may then be determined by the weighted least-squares approach according to47 where represents the combined matrix of sensitivity matrices and is the covariance matrix of the measurements under consideration (attenuation, mean time of flight and variance of the DTOFs), given by Each of the nine entries in Eq. (10) is an covariance matrix of the corresponding measurements.The covariance matrix of is then obtained as The diagonal elements of Eq. (11) are the variances. The expression represents the standard deviation of the estimated absorption changes for the j-th compartment. Note that care needs to be taken in the calculations when is nearly rank-deficient.47In the following we give expressions for the covariance matrix (for details see Appendix), assuming that the (dominant) photon noise follows a Poisson distribution. where and denote the indices of the matrix elements running from 1 to . The quantities on the right side represent data derived from measured DTOFs, and are the third and fourth centralized moments, respectively. The expressions for those submatrices of given in Eqs. (12)–(14) and (17) indicate that the respective moments are statistically dependent in case they are derived from the same DTOF, i.e., from the same distance . The covariances between and as well as between and turn out to be zero even for [Eqs. (15) and (16)]. However, they do not vanish in general as a property of the moments, but rather because of the specific property of the Poisson distribution (see Appendix).3.ImplementationFor the following application we focused on the particular case of layers, i.e., we assumed that the tissue consists of an upper and a lower layer which represent extra- and intracerebral tissue compartments. The sensitivity matrix as well as the covariance matrix depend on the background optical properties. We presumed a semi-infinite homogeneous turbid medium with absorption coefficient , reduced scattering coefficient and refractive index which are values typically taken for simple head models.25,31,48 The sensitivity matrix [see Eq. (9)] was determined by Monte-Carlo simulations. Details of the Monte Carlo code for a layered turbid medium used for these calculations were described elsewhere.25,31 For the calculation of sensitivity factors the medium was divided into nine layers each 2 mm thick on top of a semi-infinite bottom layer. The sensitivity matrices MPP, MTSF, and VSF were calculated for all layers of the model according to algorithms given in.31 In these calculations the DTOFs were sampled in time channels, each 25 ps wide. For the two-layered model we summed up the values of MPP, MTSF, and VSF obtained for an upper and a lower group of layers of the 10-layered structure. This approach allows us to perform the analysis for various values of the thickness of the upper layer. Monte Carlo calculations were carried out for a total of photon packages detected at source–detector separations between 5 and 62 mm. The DTOFs, as well as the sensitivities, were calculated simultaneously for a set of 19 concentric, consecutive, ring-shaped detectors, each 3 mm wide. The source-detector separations mentioned below in the description of results refer to the inner diameter of the detector rings. The calculation of the matrix [see Eq. (10)] requires the knowledge of the moments , and as well as the total photon count [see Eqs. (12)–(17)]. For each source-detector separation the higher moments were derived from the DTOFs as obtained from the Monte-Carlo simulations described above. Regarding , we introduced experimentally realistic conditions. We assumed the total number of detected photons to be , independently of the inter-optode distance, corresponding to a measurement at a count rate of 1 MHz with an acquisition time of 1 s. These conditions are typical for measurements based on state-of-the-art time-correlated single photon counting technology that is capable of recording at count rates as high as a few MHz.43 The covariance matrix in Eq. (11) for the least-squares estimate depends only on the covariance matrix of the data Eq. (10) and on the design of the experiment. It does not, however, depend on the data, as the problem is linear. We can therefore calculate the covariance matrix of the least-squares estimate without carrying out the experiment, provided that the covariance matrix of the data is available (or can be calculated) as well as the sensitivity matrix in Eq. (9). Both can be (approximately) calculated using the Monte Carlo simulations as described above. In doing so, we were able to investigate the effect of the selection of source-detector separations and of the number of measured quantities on the accuracy of the obtained estimate of the absorption change. Subsequently we present the obtained standard deviations of these estimates in dependence on the selected source-detector separations and the chosen number of measured quantities. 4.ResultsThis section presents the results for the standard deviations of the absorption changes in the two layers of the turbid medium. We start from a dataset , or related to , or , each obtained at four source-detector separations (8, 17, 26, and 35 mm). In such case the system of equations [Eqs. (5)–(7)] contains 12 equations to evaluate the two unknowns and and is highly over-determined. Hence the number of input quantities can be reduced. In particular, several scenarios were studied in which a subset of measurements was selected from the full data set. All calculations of were repeated with sensitivity matrices corresponding to various values of the thickness of the upper layer. Figure 2 displays the results obtained for various combinations of moments when all four inter-optode distances were included. The calculated standard deviations and of the changes of the absorption coefficient of the lower and upper layer, respectively, are shown as a function of thickness of the upper layer. The results for the lower layer (index 2) are always shown first since this case is of major importance in brain imaging. Note that all standard deviations are given in absolute units. Here and within each subsequent figure, the scales of all panels are the same. Fig. 2Standard deviations due to photon noise of the estimated absorption changes in the lower (a,b) and in the upper (c,d) layer as a function of thickness of the upper layer. Various combinations of moments at all four inter-optode distances (8, 17, 26, and 35 mm) were considered. Panels (a) and (c) refer to the use of a single quantity (, or ). Panels (b) and (d) illustrate the effect of starting with and stepwise including higher moments. The plots corresponding to are the same in both upper panels and in both lower panels. 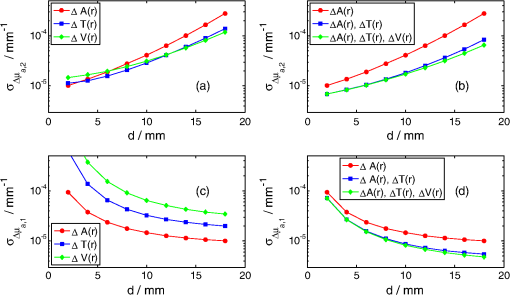 In general, increases and decreases for increasing thickness . This observation is connected to a “partial volume” effect, i.e., the relative magnitude of the contribution of the absorption change in the respective layer to the measured signal change. Comparing the results for single moments [, or , see Fig. 2(a) and 2(c)], is definitely most suitable when analyzing the upper layer [Fig. 2(c)], whereas and become similarly advantageous when determining , in particular for larger . This finding is in line with the different depth dependence of the sensitivity factors of the various moments31 that also changes with the inter-optode distance . As can be seen in Fig. 2(b) and 2(d), in all cases is reduced when including higher moments. In particular, we compared the standard deviations obtained for the following three cases, (i) only, measured at four source-detector separations, (ii) combined with , (iii) the full set , and at four source-detector separations is taken into account. As an example, for , a realistic thickness of the extracerebral layer in an adult, the inclusion of improves the precision of by a factor of 2.5. Additional inclusion of yields in another improvement by about 4%. Next, we analyzed the influence of the number of source-detector separations at which the moments were measured, on . As a start, a single detector at a large distance () was chosen, and shorter source-detector separations were incorporated step by step. The data set containing changes in two moments of DTOFs, i.e., and was considered for this analysis. The results presented in Fig. 3 confirm that the increase of the number of source-detector separations always leads to a reduction of . The influence of the inclusion in the analysis of data acquired at shorter is particularly small for the deeper layer in case of large [see Fig. 3(a)]. This finding is obvious, since detection of moments at small distances is rather insensitive to deep absorption changes. Analysis of the analogous data set containing all three moments of DTOFs, i.e., , and , showed a similar pattern of changes in as a function of for the various combinations of source-detector separations. Fig. 3Standard deviations due to photon noise of the estimated absorption changes in the lower layer (a) and in the upper layer (b) as a function of thickness of the upper layer. The curves in each panel were obtained by analysis of two moments of DTOFs, i.e., and . 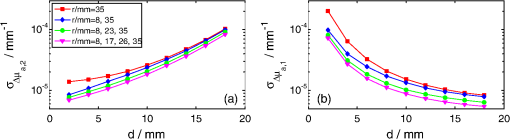 In order to study the potential of a single-distance time-resolved measurement, the analysis of was performed for a single source-detector separation and various combinations of moments (see Fig. 4). In general, the best option is always to take all three moments into account. But any combination of two of them is sufficient to retrieve the two unknown absorption changes. The exclusive use of changes of mean time of flight and variance ( and ) results in high , in particular for the upper layer [see Fig. 4(b)]. This effect can be explained by the insensitivity of these two moments to superficial absorption changes31 which is a consequence of their normalization to by definition [see Eqs. (2) and (3)]. Comparison of the results for the combination , with the results for all moments , , shows that both options lead to almost identical at large thickness [see Fig. 4(a) and 4(b)]. In contrast, at small the values of converge for the combinations , and , , . Fig. 4Comparison of the effect of various combinations of moments of DTOFs for a single-source-detector separation of 35 mm. Standard deviations due to photon noise of the estimated absorption changes in the lower layer (a) and in the upper layer (b) as a function of . 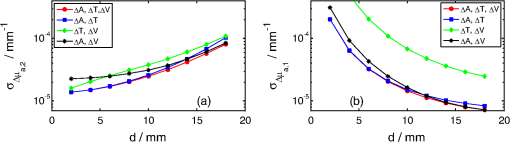 Since the investigation of cortical activation is the major goal of time-domain brain imaging, the retrieval of the absorption changes in the lower layer from measurements at a single distance is of particular interest. Therefore, the analysis illustrated in Fig. 4(a) was extended to other source-detector separations (see Fig. 5). As expected, the absorption change in the lower layer is advantageously determined at large source-detector separations. Comparing Fig. 5(a)–5(d), it can be seen that increases by 1 to 2 orders of magnitude with decreasing source-detector separation. Moreover, the range of between small (2 mm) and large (18 mm) thickness is much smaller (one order of magnitude) for larger inter-optode distance (35 mm) than for short source-detector separation (up to two orders of magnitude for 8 mm). That means the thicker the upper layer, the more important it is to increase . Nevertheless, the relative order of curves obtained for different combinations of moments, as well as the improvement when including more input quantities, are generally preserved for different source-detector separations. Fig. 5Standard deviations due to photon noise of the estimated absorption changes in the lower layer for a source-detector separation of 8 mm (a), 17 mm (b), 26 mm (c), and 35 mm (d) as a function of thickness of the upper layer. The curves in each panel refer to different selections of moments of DTOFs taken at fixed source-detector separation. Note that panel (d) contains the same data as Fig. 4(a). 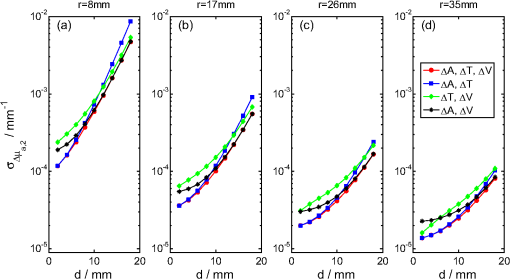 5.Discussion and ConclusionsThe paper is devoted to the determination of absorption changes in several tissue compartments that are derived from various moments of DTOFs measured at a single or multiple distances. The reconstruction of the absorption changes that are assumed to be small is performed by solving the corresponding system of linear equations. The calculation of the standard deviations of the results is done by propagating the standard deviations of the measurements that are not necessarily statistically independent. In particular, various moments derived from the same measured DTOF may be correlated, and their nonvanishing covariances have to be included. The calculation of the covariance matrix of the absorption changes according to Eq. (11) accounts for such correlations. Our analysis may serve as an example for the application of this approach to similar problems, e.g., the reconstruction of absorption changes based on photon counts in time windows of measured DTOFs. Necessary pieces of information for the analysis performed in this paper are the sensitivities that relate the measured changes in moments to the underlying absorption changes, and covariance matrices of the measurements. It is important to note that due to the linearity of the problem the knowledge of the magnitude of the absorption changes in the tissue compartments is not required for the calculation of their standard deviations. Thus the standard deviations calculated should apply to any absorption changes, as long as the assumption of linearity is not violated. The sensitivities depend on the geometry, in particular on the thickness of the upper layer and the source-detector separation, as well as on the background optical properties of the medium. The sensitivity factors used in the analysis were obtained from Monte Carlo simulations (see Ref. 31). Expressions to calculate the covariance matrix of the measurements, i.e., attenuation, mean time of flight and variance of the DTOF, were derived based on the assumption of Poisson-distributed photon noise of the DTOF. They contain moments of the DTOF up to the 4th order. All standard deviations of shown above were calculated assuming the same number () of photons acquired at all source-detector separations. Since all elements of the covariance matrix scale with , the results can be simply rescaled to other common values of . Individual integral photon counts for different source-detector separations can also be taken into account easily. As to the absolute magnitude of the standard deviations obtained in the analysis presented above, the optimal values range between and in most cases. With an assumed background absorption coefficient of , a signal-to-noise ratio of 1 would be attained with a relative absorption change between 0.1% and 1%. Most of the results were presented as a function of the thickness of the upper layer that was assumed to be known. This is realistic if anatomical images are available. In principle, could also be estimated from the measurements. However, the dependence of the measurands on is nonlinear. In such a case the linear approach outlined above would not apply. In particular, the standard deviations of the estimates would depend on the estimates themselves. Our analysis has been restricted to the consideration of standard deviations due to photon noise. The major factor that limits the accuracy of the quantification of absorption changes is the insufficient knowledge of the optical properties of the various tissues of the head that are required to calculate the sensitivities. In addition, systematic deviations can originate from the necessary limitation of the integration range in the calculation of moments, especially of higher order, from measured DTOFs. For the practical application of the approach presented here it is important to discuss the influence of an instrument response function (IRF) of finite width, which has so far been neglected. The results of the measurement, i.e., the absorption changes themselves, do not depend on the IRF since the changes in mean time of flight as well as in variance are virtually independent of the IRF.41 On the contrary, the elements of the covariance matrix of the input measurands contain (absolute) moments of the DTOFs [see Eqs. (12)–(14) and (17)] that definitely depend on the IRF. Consequently, width and shape of the IRF will influence the evaluated standard deviations of absorption changes. In this sense, the values for and shown in this paper represent lower bounds. However, an in-depth quantitative study on the effect of realistic IRFs would go beyond the scope of this paper. When analyzing real measurements, the moments needed to calculate the covariance matrix can be easily obtained from the measured DTOFs. The analysis of standard deviations of absorption changes as presented above may facilitate the design of experiments in functional brain imaging. The consideration of various subsets of moments may lead to conclusions regarding the choice of continuous-wave (cw), frequency-domain or time-domain methods. However, different sources of noise present in these techniques should be carefully considered. Moreover, the choice of source-detector separations can be optimized, and the effect of photon count rates can be studied. On the other hand, the quality of a given set of measured data can be assessed and combinations of moments can be identified for which the standard deviation of the absorption changes is lowest. In general, inclusion of additional moments and source-detector separations leads to better estimates of the absorption changes in the two layers. Mean time of flight and variance of the DTOFs are important to estimate which is the major measurand in brain imaging. However, a reconstruction based on and alone is not the optimum choice (see Fig. 4). This combination would have the advantage to be independent of amplitude and movement artifacts. But the depth sensitivity profiles of both measurands are similar, and they are statistically correlated. Another observation is that the inclusion of in addition to and did not improve the analysis considerably [see Figs. 2(b), 2(d), 4 and 5]. Thus inclusion of variance seems to be of minor relevance. It should be noted, however, that the variance of the DTOF has several advantages that are of practical relevance for brain imaging but were not subject of the present analysis.37,40,49 These are primarily its depth selectivity, i.e., high sensitivity to deep and low sensitivity to superficial absorption changes, and its robustness against amplitude and timing drifts. AppendicesAppendixHere the derivation of the elements of the covariance matrix is described in more detail. We consider the sub-matrices of where and stand for the vectors , and which contain the estimates of changes in attenuation, mean time of flight and variance measured at source-detector separations. Since these measurements are statistically independent it follows that each sub-matrix is diagonal, i.e., Due to the independence of the two measurements with and without absorption change the diagonal elements of any sub-matrix further simplify to Since small absorption changes are assumed, the measured values with and without absorption do not differ remarkably, are statistically independent and exhibit comparable noise which leads to We show the evaluation for one diagonal element (variance) and one off-diagonal element of . We consider the moments as a function of photon counts in the individual time channels of the DTOF and apply propagation of covariances based on the Poisson distribution of noise of , i.e., . The measured in different time channels are uncorrelated. Only one distance is considered, the corresponding index is omitted for simplicity of notation. The following derivations make repeated use of the definition of the moments [Eqs. (1)–(4)]. The total attenuation is where the number of input photons is assumed to be constant. It should be noted that the covariance does not vanish in general for this combination of moments, but only because of the specific property of the Poisson-distributed photon noise , i.e., the variance of observed counts equals their expectation. Following the procedure shown above for two examples, all relevant elements of [Eqs. (12)–(17)] can be derived.AcknowledgmentsThe research leading to these results has received funding from the European Community’s Seventh Framework Programme (No. FP7/2007-2013) under Grant Agreement FP7-HEALTH-F5-2008-201076. The study is also partly financed by the Polish–German project: “Hypo- and Hyperperfusion during Subacute Stroke. Tracking Perfusion Dynamics in Stroke Patients with Optical Imaging.” ReferencesS. Wrayet al.,
“Characterization of the near infrared absorption spectra of cytochrome aa3 and haemoglobin for the noninvasive monitoring of cerebral oxygenation,”
Biochim. Biophys. Acta, 933
(1), 184
–192
(1988). http://dx.doi.org/10.1016/0005-2728(88)90069-2 BBACAQ 0006-3002 Google Scholar
F. F. Jobsis,
“Noninvasive, infrared monitoring of cerebral and myocardial oxygen sufficiency and circulatory parameters,”
Science, 198
(4323), 1264
–1267
(1977). http://dx.doi.org/10.1126/science.929199 SCIEAS 0036-8075 Google Scholar
B. Chanceet al.,
“Time-resolved spectroscopy of hemoglobin and myoglobin in resting and ischemic muscle,”
Anal. Biochem., 174
(2), 698
–707
(1988). http://dx.doi.org/10.1016/0003-2697(88)90076-0 ANBCA2 0003-2697 Google Scholar
T. Hamaokaet al.,
“Near-infrared spectroscopy/imaging for monitoring muscle oxygenation and oxidative metabolism in healthy and diseased humans,”
J. Biomed. Opt., 12
(6), 062105
(2007). http://dx.doi.org/10.1117/1.2805437 JBOPFO 1083-3668 Google Scholar
A. KienleT. Glanzmann,
“In vivo determination of the optical properties of muscle with time-resolved reflectance using a layered model,”
Phys. Med. Biol., 44
(11), 2689
–2702
(1999). http://dx.doi.org/10.1088/0031-9155/44/11/301 PHMBA7 0031-9155 Google Scholar
M. WolfM. FerrariV. Quaresima,
“Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications,”
J. Biomed. Opt., 12
(6), 062104
(2007). http://dx.doi.org/10.1117/1.2804899 JBOPFO 1083-3668 Google Scholar
E. M. Hillman,
“Optical brain imaging in vivo: techniques and applications from animal to man,”
J. Biomed. Opt., 12
(5), 051402
(2007). http://dx.doi.org/10.1117/1.2789693 JBOPFO 1083-3668 Google Scholar
H. ObrigA. Villringer,
“Beyond the visible—imaging the human brain with light,”
J. Cereb. Blood Flow Metab., 23
(1), 1
–18
(2003). http://dx.doi.org/10.1097/00004647-200301000-00001 JCBMDN 0271-678X Google Scholar
A. VillringerB. Chance,
“Non-invasive optical spectroscopy and imaging of human brain function,”
Trends Neurosci., 20
(10), 435
–442
(1997). http://dx.doi.org/10.1016/S0166-2236(97)01132-6 TNSCDR 0166-2236 Google Scholar
A. VillringerJ. SteinbrinkH. Obrig,
“Editorial comment—cerebral near-infrared spectroscopy: how far away from a routine diagnostic tool?,”
Stroke, 35
(1), 70
–72
(2004). http://dx.doi.org/10.1161/01.STR.0000110122.57772.C3 SJCCA7 0039-2499 Google Scholar
C. Zweifelet al.,
“Continuous assessment of cerebral autoregulation with near-infrared spectroscopy in adults after subarachnoid hemorrhage,”
Stroke,
(2010). SJCCA7 0039-2499 Google Scholar
M. J. Herrmannet al.,
“Reduced prefrontal oxygenation in Alzheimer disease during verbal fluency tasks,”
Am. J. Geriatr. Psych., 16
(2), 125
–135
(2008). http://dx.doi.org/10.1097/JGP.0b013e3180cc1fbc Google Scholar
C. Hocket al.,
“Decrease in parietal cerebral hemoglobin oxygenation during performance of a verbal fluency task in patients with Alzheimer’s disease monitored by means of near-infrared spectroscopy (NIRS)—correlation with simultaneous rCBF-PET measurements,”
Brain Res., 755
(2), 293
–303
(1997). http://dx.doi.org/10.1016/S0006-8993(97)00122-4 BRREAP 1385-299X Google Scholar
H. E. A. van Beek Arendaet al.,
“Cortical oxygen supply during postural hypotension is further decreased in Alzheimer’s disease, but unrelated to cholinesterase-inhibitor use,”
J. Alzheimers Dis., 21
(2), 519
–526
(2010). http://dx.doi.org/10.3233/JAD-2010-100288 JADIF9 1387-2877 Google Scholar
R. CarandangD. W. Krieger,
“Near infrared spectroscopy: finding utility in malignant hemispheric stroke,”
Neurocrit. Care, 6
(3), 161
–164
(2007). http://dx.doi.org/10.1007/s12028-007-0023-y NCEACB 1541-6933 Google Scholar
D. R. Hargroveset al.,
“Near-infrared spectroscopy in stroke: from research to clinical practice,”
Stroke, 35
(11), 2430
–2431
(2004). http://dx.doi.org/10.1161/01.STR.0000144656.77330.18 SJCCA7 0039-2499 Google Scholar
C. W. Pennekampet al.,
“The value of near-infrared spectroscopy measured cerebral oximetry during carotid endarterectomy in perioperative stroke prevention: a review,”
Eur. J. Vasc. Endovasc. Surg., 38
(5), 539
–545
(2009). http://dx.doi.org/10.1016/j.ejvs.2009.07.008 1078-5884 Google Scholar
P. RolfeY. A. WickramasingheM. Thorniley,
“The potential of near infra-red spectroscopy for detection of fetal cerebral hypoxia,”
Eur. J. Obstet. Gyn. Reprod. Biol., 42
(Suppl. S), S24
–S28
(1991). EOGRAL 0301-2115 Google Scholar
P. M. O’BrienP. M. DoyleP. Rolfe,
“Near infrared spectroscopy in fetal monitoring,”
Br. J. Hosp. Med., 49
(7), 483
–487
(1993). BJHMAB 0007-1064 Google Scholar
D. T. Delpyet al.,
“Cerebral monitoring in newborn infants by magnetic resonance and near infrared spectroscopy,”
Scand. J. Clin. Lab. Invest., 47
((Suppl. 188)), 9
–17
(1987). Google Scholar
M. Ferrariet al.,
“Cerebral blood volume and hemoglobin oxygen saturation monitoring in neonatal brain by near IR spectroscopy,”
Adv. Exp. Med. Biol., 200 203
–211
(1986). http://dx.doi.org/10.1007/978-1-4684-5188-7 AEMBAP 0065-2598 Google Scholar
M. CopeD. T. Delpy,
“System for long-term measurement of cerebral blood and tissue oxygenation on newborn infants by near infra-red transillumination,”
Med. Biol. Eng. Comput., 26
(3), 289
–294
(1988). http://dx.doi.org/10.1007/BF02447083 MBECDY 0140-0118 Google Scholar
J. S. Wyattet al.,
“Quantification of cerebral oxygenation and haemodynamics in sick newborn infants by near infrared spectrophotometry,”
Lancet, 328
(8515), 1063
–1066
(1986). http://dx.doi.org/10.1016/S0140-6736(86)90467-8 LANCAO 0140-6736 Google Scholar
G. LitscherG. Schwarz, Transcranial Cerebral Oximetry, Pabst-Science Publisher, Lengerich
(1997). Google Scholar
J. Steinbrinket al.,
“Determining changes in NIR absorption using a layered model of the human head,”
Phys. Med. Biol., 46
(3), 879
–896
(2001). http://dx.doi.org/10.1088/0031-9155/46/3/320 PHMBA7 0031-9155 Google Scholar
Y. Hoshiet al.,
“Reevaluation of near-infrared light propagation in the adult human head: implications for functional near-infrared spectroscopy,”
J. Biomed. Opt., 10
(6), 064032
(2005). http://dx.doi.org/10.1117/1.2142325 JBOPFO 1083-3668 Google Scholar
J. Selbet al.,
“Improved sensitivity to cerebral hemodynamics during brain activation with a time-gated optical system: analytical model and experimental validation,”
J. Biomed. Opt., 10
(1), 11013
(2005). http://dx.doi.org/10.1117/1.1852553 JBOPFO 1083-3668 Google Scholar
V. Quaresimaet al.,
“Noninvasive measurement of cerebral hemoglobin oxygen saturation using two near infrared spectroscopy approaches,”
J. Biomed. Opt., 5
(2), 201
–205
(2000). http://dx.doi.org/10.1117/1.429987 JBOPFO 1083-3668 Google Scholar
B. W. Zeffet al.,
“Retinotopic mapping of adult human visual cortex with high-density diffuse optical tomography,”
Proc. Natl. Acad. Sci., 104
(29), 12169
–12174
(2007). http://dx.doi.org/10.1073/pnas.0611266104 0370-0046 Google Scholar
J. Steinbrinket al.,
“Relevance of depth resolution for cerebral blood flow monitoring by near-infrared spectroscopic bolus tracking during cardiopulmonary bypass,”
J. Thorac. Cardiovasc. Surg., 132
(5), 1172
–1178
(2006). http://dx.doi.org/10.1016/j.jtcvs.2006.05.065 0022-5223 Google Scholar
A. Liebertet al.,
“Time-resolved multidistance near-infrared spectroscopy of the adult head: intracerebral and extracerebral absorption changes from moments of distribution of times of flight of photons,”
Appl. Opt., 43
(15), 3037
–3047
(2004). http://dx.doi.org/10.1364/AO.43.003037 APOPAI 0003-6935 Google Scholar
D. Continiet al.,
“Multi-channel time-resolved system for functional near infrared spectroscopy,”
Opt. Express, 14
(12), 5418
–5432
(2006). http://dx.doi.org/10.1364/OE.14.005418 OPEXFF 1094-4087 Google Scholar
J. C. HebdenT. Austin,
“Optical tomography of the neonatal brain,”
Eur. Radiol., 17
(11), 2926
–2933
(2007). http://dx.doi.org/10.1007/s00330-007-0659-1 EURAE3 1432-1084 Google Scholar
J. SelbD. K. JosephD. A. Boas,
“Time-gated optical system for depth-resolved functional brain imaging,”
J. Biomed. Opt., 11
(4), 044008
(2006). http://dx.doi.org/10.1117/1.2337320 JBOPFO 1083-3668 Google Scholar
H. Wabnitzet al.,
“Time-resolved near-infrared spectroscopy and imaging of the adult human brain,”
Adv. Exp. Med. Biol., 662 143
–148
(2010). http://dx.doi.org/10.1007/978-1-4419-1241-1 AEMBAP 0065-2598 Google Scholar
D. Continiet al.,
“Design and characterization of a two-wavelength multichannel time-resolved system for optical topography,”
in Biomedical Optics 2006, Technical Digest,
(2006). Google Scholar
M. Kacprzaket al.,
“Time-resolved optical imager for assessment of cerebral oxygenation,”
J. Biomed. Opt., 12
(3), 034019
(2007). http://dx.doi.org/10.1117/1.2743964 JBOPFO 1083-3668 Google Scholar
J. Selbet al.,
“Discrimination between superficial and cerebral signals during functional brain imaging with a time-gated system,”
in European Conferences on Biomedical Optics (ECBO),
(2005). Google Scholar
D. Continiet al.,
“Novel method for depth-resolved brain functional imaging by time-domain NIRS,”
Proc. SPIE, 6629 662908
(2007). http://dx.doi.org/10.1117/12.728104 Google Scholar
A. Liebertet al.,
“Bed-side assessment of cerebral perfusion in stroke patients based on optical monitoring of a dye bolus by time-resolved diffuse reflectance,”
Neuroimage, 24
(2), 426
–435
(2005). http://dx.doi.org/10.1016/j.neuroimage.2004.08.046 NEIMEF 1053-8119 Google Scholar
A. Liebertet al.,
“Evaluation of optical properties of highly scattering media by moments of distributions of times of flight of photons,”
Appl. Opt., 42
(28), 5785
–5792
(2003). http://dx.doi.org/10.1364/AO.42.005785 APOPAI 0003-6935 Google Scholar
A. Liebertet al.,
“Intra- and extracerebral changes of hemoglobin concentrations by analysis of moments of distributions of times of flight of photons,”
Proc. SPIE, 5138 126
–130
(2003). http://dx.doi.org/10.1117/12.500578 Google Scholar
W. Becker, Advanced Time-Correlated Single Photon Counting Techniques, SpringerBerlin, Heidelberg,2005). Google Scholar
B. Chanceet al.,
“Phase measurement of light absorption and scatter in human tissue,”
Rev. Sci. Instrum., 69
(10), 3457
–3481
(1998). http://dx.doi.org/10.1063/1.1149123 RSINAK 0034-6748 Google Scholar
S. Carraresiet al.,
“Accuracy of a perturbation model to predict the effect of scattering and absorbing inhomogeneities on photon migration,”
Appl. Opt., 40
(25), 4622
–4632
(2001). http://dx.doi.org/10.1364/AO.40.004622 APOPAI 0003-6935 Google Scholar
H. Wabnitzet al.,
“A time-domain NIR brain imager applied in functional stimulation experiments,”
Proc. SPIE, 5859 58590H
(2005). http://dx.doi.org/10.1117/12.632837 PSISDG 0277-786X Google Scholar
C. GolubC. van Loan, Matrix Computations, The Johns Hopkins University Press, Baltimore and London
(1996). Google Scholar
A. Liebertet al.,
“Monte Carlo algorithm for efficient simulation of time-resolved fluorescence in layered turbid media,”
Opt. Express, 16
(17), 13188
–13202
(2008). http://dx.doi.org/10.1364/OE.16.013188 OPEXFF 1094-4087 Google Scholar
O. Steinkellneret al.,
“Optical bedside monitoring of cerebral perfusion: technological and methodological advances applied in a study on acute ischemic stroke,”
J. Biomed. Opt., 15
(6), 061708
(2010). http://dx.doi.org/10.1117/1.3505009 JBOPFO 1083-3668 Google Scholar
|


