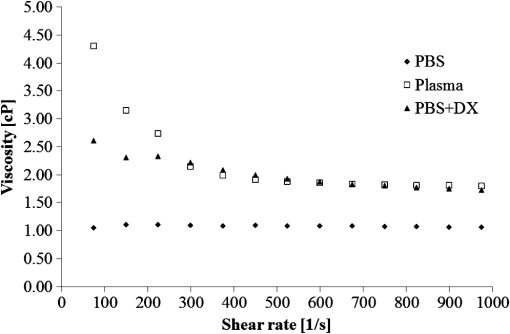
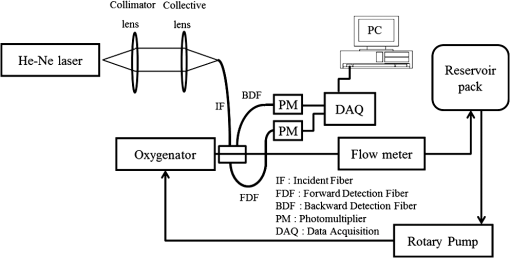
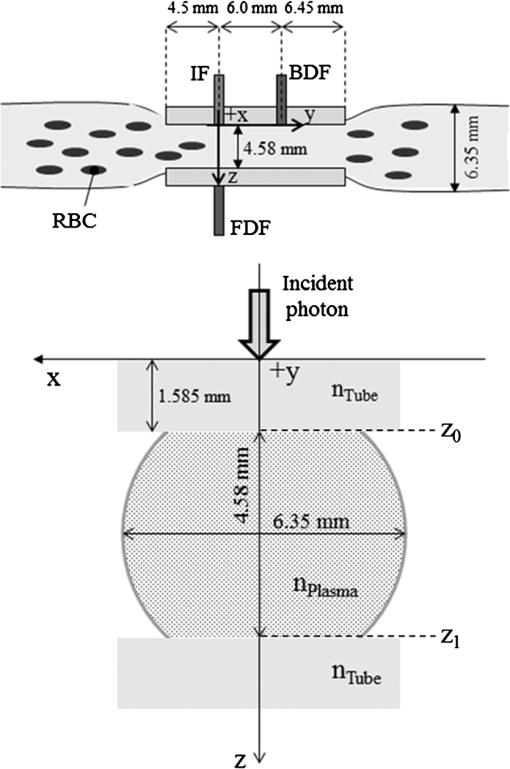
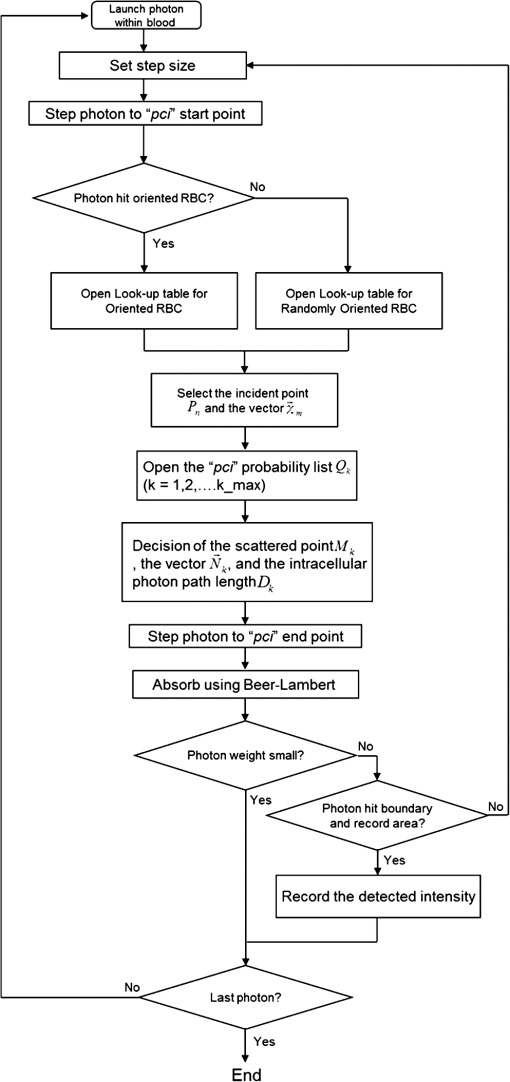
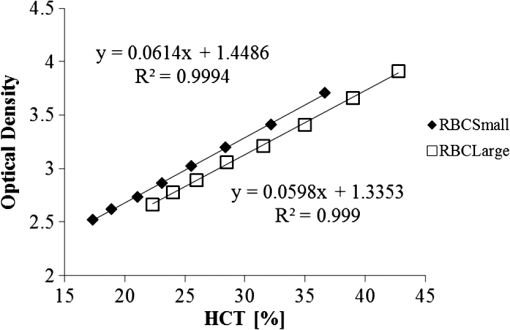
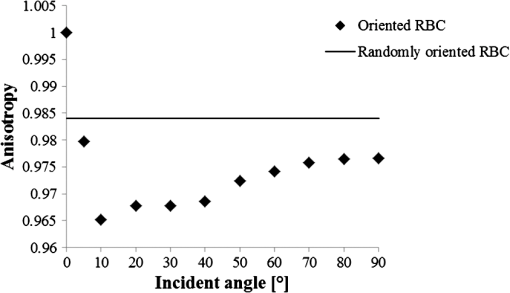
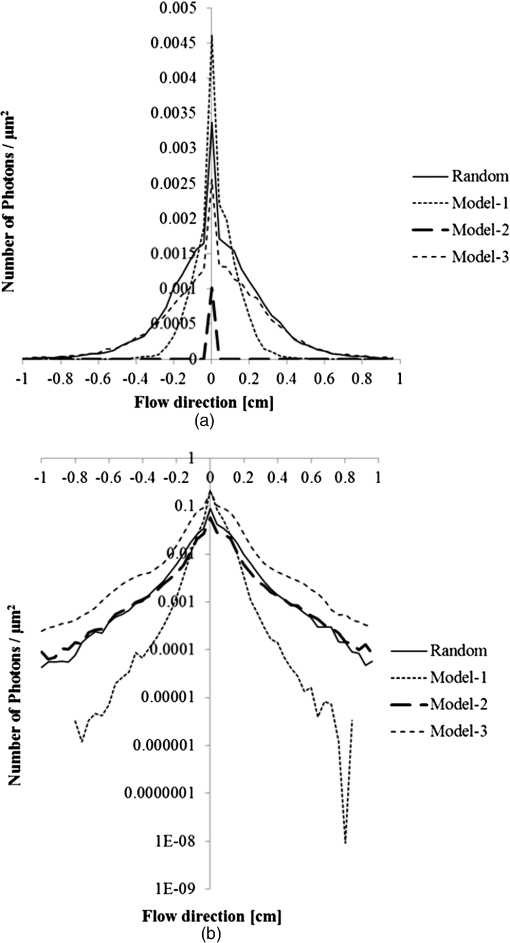
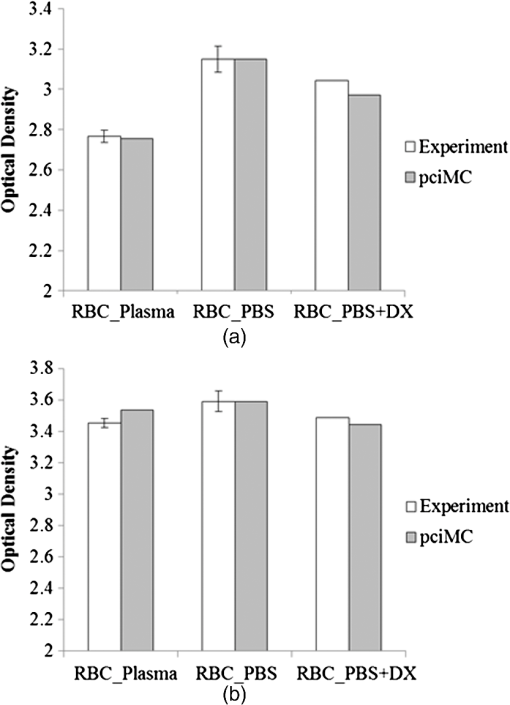
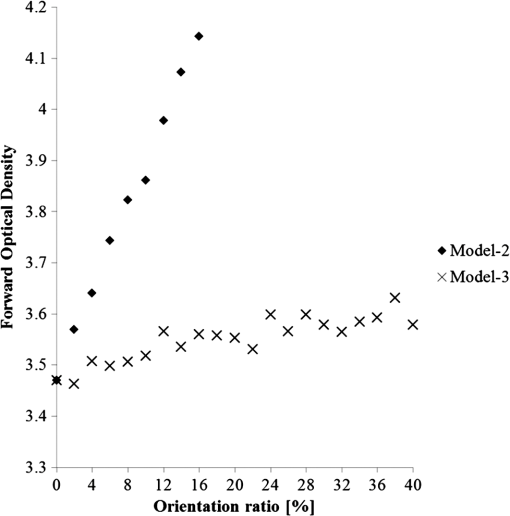
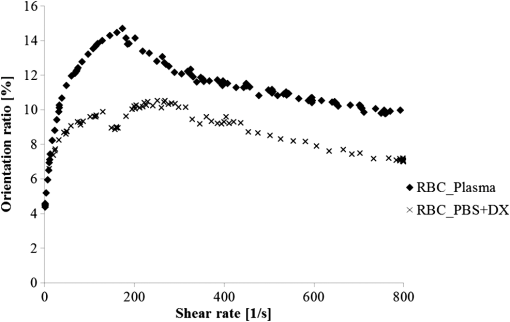
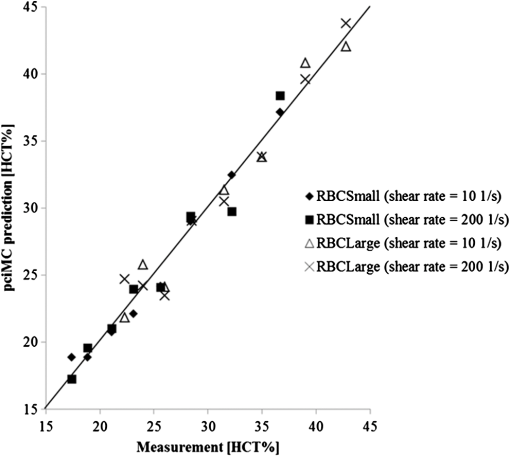
2.1.

Blood Sample Preparation

Fresh porcine blood samples anti-coagulated with 4% sodium citrate ($100\mathrm{cc}\text{sodium citrate}/1000\mathrm{cc}$ blood) were obtained from a local slaughterhouse. Prior to the experiments, no significant hemolysis was seen. The blood was centrifuged and then plasma and buffy coat was excluded. To investigate aggregation and viscosity effects on RBCs’ orientation during blood flow study, three types samples, “RBC_Plasma,” “RBC_PBS,” and “$\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$” were prepared, where RBC_Plasma was made by suspending the centrifuged RBCs in plasma, RBC_PBS by washing and suspending the centrifuged RBCs with isotonic phosphate buffer solution (PBS) ($300\mathrm{mosmo}\mathrm{l}/\mathrm{l}$, pH 7.4), and finally, $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$ by adding 60,000 molecular weight dextran (Dextran 60,000, Wako Pure Chemical industries. Ltd., Osaka, Japan) at a ratio 5 g Dextran to 335 cc PBS. It is well known that approximately 150,000 high-molecular wt. Dextran promotes RBCs aggregation whereas the lower-molecular Dextran has no influence as such.²⁷ The RBCs’ aggregation effect in each sample was confirmed visually using a microscope. As a result, the apparent aggregation was confirmed in RBC_Plasma within 1 min. In $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$, the aggregation was hardly seen after 3 min observation. Finally, in the RBC_PBS sample, the RBCs almost uniformly dispersed in the solution. The viscosities of the extracellular solution of each sample with respect to shear rate were shown in Fig. 1. These were measured by a cone-plate viscometer ($\mathrm{DV}\text{-}\Vert +\mathrm{Pro}$ VISCOMETER, BROOK-FIELD Inc., MA, USA). The viscosity of PBS is almost equal to that of water at $1.07\pm 0.02\mathrm{cP}$. For shear rate from 0 to $200\mathrm{l}/s$, viscosity differences were noticed between Plasma and $\mathrm{PBS}+\mathrm{DX}$. However, above $300\mathrm{l}/s$, the Plasma and $\mathrm{PBS}+\mathrm{DX}$ viscosity showed very similar value at $1.83\pm 0.10\mathrm{cP}$ and $1.80\pm 0.17\mathrm{cP}$, respectively. In addition, the refractive index of each extra cellular media was also measured by an Abbe refractometer (DR-M2, ATAGO Inc., Tokyo, Japan). The wavelength of source light was 656 nm. The refractive indices of Plasma, PBS, $\mathrm{PBS}+\mathrm{DX}$ were 1.3461, 1.3323, and 1.3348, respectively. In all of the measurements and experiments, the temperature was kept constant at 20°C.

Fig. 1

Viscosity of extracellular solution with respect to shear rate.

In order to investigate the effects of MCV and MCHC on the optical characteristics, the RBCs were separated into large and small cells, ${\mathrm{RBC}}_{\text{Large}}$, ${\mathrm{RBC}}_{\text{Small}}$ by centrifugation and ${\mathrm{RBC}}_{\text{Large}}\_\mathrm{PBS}+\mathrm{DX}$ and ${\mathrm{RBC}}_{\text{Small}}\_\mathrm{PBS}+\mathrm{DX}$ samples were prepared according to the following procedure. The whole blood was first centrifuged to exclude the buffy coat and plasma. The resultant packed RBCs with the hematocrit of around 80% to 90% were further centrifuged for 60 min with 40,000 G and 10°C. After the second centrifugation, approximately 20% of the top layers with lower specific gravity were extracted as relatively larger RBCs (${\mathrm{RBC}}_{\text{Large}}$) and the bottom 20% with higher specific gravity as smaller RBCs (${\mathrm{RBC}}_{\text{Small}}$). These cells were washed in $\mathrm{PBS}+\mathrm{DX}$ to remove free plasma hemoglobin and to adjust the hematocrit level.

2.2.

Optical Measurements in the Extracorporeal Circuit

The closed loop circuit shown in Fig. 2 was primed with 500 cc of blood. The circuit comprises a rotary blood pump (HPM-15, Nikkiso Co., Japan), an oxygenator (Baby-RX, Terumo Co., Japan), a reservoir pack, and $1/4$ inch (6.35 mm) transparent Tygon tubing (Saint-Gabain, Tokyo, Japan). The blood was continuously pumped through the circuit by the rotary blood pump, and the flow rate was monitored by an electromagnetic flow meter. The oxygen saturation was maintained at 100% by the oxygenator. The blood parameters, the HCT, the total hemoglobin (tHb), and the oxygen saturation levels were determined by a blood gas analyzer (ABL520, Radiometer Co., Copenhagen, Denmark), and the MCV and MCHC were measured by an automated blood cell analyzer (Celltac $\alpha$ MEK-6358, Nihon Kohden Co., Tokyo, Japan).

Fig. 2

Schematic of an experimental set-up.

As for the optical measurement system, a He-Ne laser (output of 30 mW, wavelength of 632.8 nm) was used as the light source. The emitted light was guided into an optical glass fiber (core diameter of 200 μm, outer diameter of 2.4 mm, beam spread angle of 20 deg) using collimator and collector lenses. The incident fiber, the forward, and the backward scattering detection fibers were fixed in the designed probe as shown in Fig. 3. The probe slightly squeezes the circuit tube to flatten the incident and detection surfaces resulting in the thickness of the tube to be 4.58 mm at this point. The distance between the incident and detection fibers is 6.0 mm. Both the forward and backward scatterings were detected by optical glass fibers with core diameters of 50 μm and guided to photomultipliers (H9305-03, Hamamatsu photonics Co., Hamamatsu, Japan). The signal was acquired by a data acquisition system (Labview DAQ system (NI USB-6008), National Instruments Co., Tokyo, Japan), and the acquired data was processed and analyzed using a PC.

Fig. 3

Geometry of an optical probe attached to a circular tube.

Optical measurements were conducted at various flow rates and HCTs. The HCT was varied by diluting the given sample with each extra cellular media. The blood flow rate was varied from approximately 0 to $2\mathrm{l}/\min$. Then the average shear rate $\gamma$ was calculated by the following formula:³²

To control the effect of RBCs aggregation, the optical measurement at no flow condition was immediately conducted when the flow suddenly came to stop from $2\mathrm{l}/\min$. After that, the flow rate was gradually increased to increase the shear rate to $800\mathrm{l}/\text{s}$, while the optical measurement was conducted at each shear rate.

2.3.

Analysis of Optical Properties of Flowing Blood Using pciMC

2.3.1.

Photon-cell interactive Monte Carlo model

The detailed description of pciMC can be found else where.³¹ The pciMC models optical interaction at the plasma-cell boundary based on the geometric optics theory. In the first step in the analysis using pciMC, the program calculates the photon step size $S$ from the following equation:

Eq. (2)

$$S=\text{Rund}(0,1)\frac{1}{{\mu }_c}$$

Eq. (3)

$${\mu }_c=\frac{\mathrm{HCT}}{\mathrm{MCV}}{\sigma }_c,$$

where $\text{Rund}(0,1)$ is a uniform random number between 0 and 1, ${\mu }_c$ is a geometric interaction constant in ${\mathrm{cm}}^{-1}$, and HCT is the volume fraction of the RBCs, i.e., the hematocrit ($0<\mathrm{HCT}<1$). The MCV is the RBC volume in ${\mathrm{cm}}^3$, and ${\sigma }_c$ is the mean geometrical cross section of the RBCs in ${\mathrm{cm}}^2$. The geometric structure of the RBCs was defined by an axially symmetric biconcave model, with surface coordinates $S(x,y,z)$ defined as follows:

Eq. (4)

$$S(x,y,z)=(r(\theta )\sin \theta \cos \varphi ,r(\theta )\sin \theta \sin \varphi ,r(\theta )\cos \theta ),(0\leqq \theta \leqq \mathrm{\pi }),(0\leqq \varphi \leqq 2\mathrm{\pi })r(\theta )=3{\sin }^4\theta +0.75.$$

Equation (4) expresses the perfect axial symmetry of the 3-D biconcave surface coordinates; ($x,y,z$) are the coordinates used in the photon-RBC interaction; $r(\theta )$ is the biconcave RBC surface function,¹⁴ where $\theta$ is the angle between the position vector and the $z$ axis; and $\varphi$ is the angle formed by projection of the position vector and the $x$ axis onto the $x\text{-}y$ plane. Incremental angles of $\mathrm{\Delta }\theta =1.8\mathrm{deg}$ and $\mathrm{\Delta }\varphi =3.6\mathrm{deg}$ were used to discretize the surface data, with the total number of nodes being $100\times 100$. After the photon has advanced one step, a scattering event takes place as shown in Fig. 4. Upon interaction of the photon with a RBC, the pciMC program selects the incident point $P_n$ and the vector ${\overrightarrow{\chi }}_m$ as follows:

Eq. (5)

$$P_n=[P_x(\theta ,0),0,P_z(\theta ,0)]$$

Eq. (6)

$${\overrightarrow{\chi }}_m=[{\chi }_x(\alpha ,\beta ),{\chi }_y(\alpha ,\beta ),{\chi }_z(\alpha ,\beta )],$$

where $\alpha$ $(0\leqq \alpha \leqq \mathrm{\pi }/2)$ is the angle formed between the incident vector and the normalized vector at the incident point, and $\beta$ $(0\leqq \beta \leqq \mathrm{\pi }/2)$ is the rotational angle about the normalized vector. In this study, incremental angles of $\mathrm{\Delta }\theta =1.8\mathrm{deg}$, $\mathrm{\Delta }\alpha =9\mathrm{deg}$, and $\mathrm{\Delta }\beta =36\text{deg}$ are used. Therefore, the total number of incident photon patterns is $50\times 100$ ($\text{point pattern}\times \text{vector pattern}$). After selecting $P_n$ and ${\overrightarrow{\chi }}_m$, the program opens look-up tables to extract the value of $Q_k(P_n,{\overrightarrow{\chi }}_m)$ specific to the interaction point. This contains the pre-calculated probability distribution of the photon escaping from the intracellular space of the RBC and returns output parameters $(M_k,\overrightarrow{N_k},D_k)$, where, $M_k$ are the coordinates of the scattering point, ${\overrightarrow{N}}_k$ is the propagation vector at the scattering point, and $D_k$ is the intracellular photon path length for the $k$-th interaction. The scattering points and vectors are calculated from the geometric optics, and the photon’s escape probability is calculated using the Fresnel formula assuming the reflectance to be the average of the two orthogonal polarization directions. For each photon, the pre-calculation is pursued until the quantity $Q_k$ becomes less than 0.001% or until the number of interactions reaches 100. If the probability of escape is not satisfied at any point, the photon is indefinitely trapped within the intracellular hemoglobin solution and is completely absorbed.

Fig. 4

Schematic of photon-cell interaction events.

As for the absorption event, using the propagation distance $D_k$ inside the RBC, the photon’s weight loss is estimated by the Beer-Lambert law:

Eq. (7)

$$\frac{P_s}{P_i}=\exp [-2.303\times e(\lambda )\times (10\times \mathrm{MCHC})/\mathrm{mHb}\times D_k],$$

where $P_i$ and $P_s$ are the incident and scattered photon weights, respectively, $e(\lambda )$ is the molecular extinction coefficient for the wavelength $\lambda$ in ${\mathrm{cm}}^{-1}/\mathrm{mol}/\mathrm{l}$, and $\mathrm{mHb}$ is the molecular weight of hemoglobin is equal to $64,500\mathrm{g}/\mathrm{mol}$. For the wavelength of 632.8 nm used in the experiment, e(632.8 nm) is equal to $536.8{\mathrm{cm}}^{-1}/\mathrm{mol}/\mathrm{l}$.³³

After the photon is scattered, it moves from point $P_n$ to point $M_k$ by traveling an intracellular distance of $D_k$, and the propagation vector is changed from ${\overrightarrow{\chi }}_m$ to ${\overrightarrow{N}}_k$. To minimize the calculation cost, the pciMC simulation separates the simulation coordinates and the photon-RBC interaction coordinates. Since the scattering data are in photon-RBC interaction coordinates, the data must be converted to pciMC simulation coordinates. The translation process for randomly oriented RBCs was shown in a previous paper.³¹

2.3.2.

RBC orientation patterns in extracorporeal circuit

In this study, the step size given by Eq. (2) was kept constant throughout the simulation. In addition, since the maximum shear stress in the circuit tube was estimated to be less than $800\mathrm{1}/s$, we assumed that the shape of the RBCs moving in the circuit tube remained unchanged.²⁹ Taking these things into consideration, we hypothesized that the changes in scattering with respect to the flow conditions were mainly caused by the changes in RBCs’ orientation. Figure 5 shows a schematic diagram of the coordinates used to describe the orientation of the RBCs. The long axis of the RBCs is in the $r$-direction and the RBC rotates randomly about the long axis. We assumed that all of the RBCs within the circuit were randomly oriented when there was no flow; when the blood starts to flow, the orientation of the RBCs begins to change. In this study, three types of RBC orientation patterns, as shown in Fig. 6, were considered. Figure 6 shows the $xz$-plane as cross section of optical measurement area. The $y$-axis means the tube and flow direction. We assumed the light scattering distributions to be symmetrical about the $z$-axis. In addition, the orientation of the RBCs should be symmetrical about the center of the circulation tube.

Fig. 5

Schematic of RBC orientation.

Fig. 6

RBC orientation models in the circular tube (the vector ‘$r$’ is the orientation direction shown in Fig. 5). Model 1: the orientation is in the direction of flow; model 2: the orientation is perpendicular to the flow and pointing toward the center of the tube; and model 3: the orientation is perpendicular to that in model 2.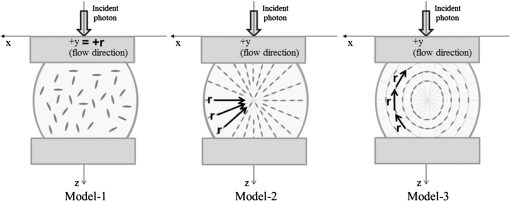

On the left hand side of Fig. 6, in model 1, the RBCs orient with their long axes pointing in the direction of flow. In the center of Fig. 6, in model 2, the RBCs have their long axes pointing toward the center of the tube. Finally, on the right hand side of Fig. 6, in model 3 the long axes are perpendicular to those in model 2.

2.3.3.

Algorithm of analysis based on the pciMC code

Figure 7 shows a flow chart of the pciMC program to simulate photon propagation through the extra corporeal circuit. Within the model, there are both randomly oriented RBCs and RBCs as defined by orientation models 1, 2, and 3 of Fig. 6. After the photon has advanced by one step, calculated by Eq. (1), the program chooses between a randomly oriented or an oriented RBCs’ scattering event based on the orientation ratio (OR). The OR was defined by the following equation:

Eq. (8)

$$\mathrm{OR}[\%]=(\text{The number of oriented RBCs}/\text{The total number of RBCs})\times 100.$$

When the photon hits a randomly oriented RBC, the pciMC program randomly selects the incident point and propagation vectors based on the calculations using geometric optics theory. After the scattering event, the photon steps to the next scattering point. In addition, the photon weight is reduced by the Beer-Lambert law using the intracellular optical path length. Finally, the vector of the next scattering point is translated from the photon-RBC interaction coordinate to the pciMC simulation coordinate. A series of processes for randomly oriented RBCs were reported in Ref. 31. As for oriented RBCs, the process is very similar. The possible incident points, however, were restricted because some points might be inaccessible to the photon. For example, in the case of model 1, if the incident photon vector were in the flow direction, it would not be possible for the photon to reach the biconcave region. Thus in an oriented RBC scattering event, the probability of selecting an incident point and vector from the look-up table depends on the photon vector in the simulation coordinates. To account for this, the look-up table for oriented RBCs was organized by the relationship between the incident photon vector and the direction of the RBCs’ long axis. Selection of the appropriate look-up table was performed using the following calculation:

Eq. (9)

$$U_{\mathrm{pciMC}}(x,y,z)=(U_x,U_y,U_z)\to U_{\mathrm{pciMC}}(r,s,t)=(U_r,U_s,U_t)$$

Eq. (10)

$$T=\sqrt{U_s^2+U_t^2}\times {\text{Rund}}_{\mathrm{int}}(0,T_{\text{size}}),$$

where $U_{\mathrm{pciMC}}(x,y,z)$ is the incident photon vector described by the pciMC simulation coordinates, $(x,y,z)$. The vector was translated to the coordinate system of the RBC, $(r,s,t)$, as shown in Fig. 5. The $s$-and $t$-directions are perpendicular to the $r$-direction, which is along the long axis of the RBC. For example, in the case of model 1, is translated to $U_{\mathrm{pciMC}}(r=y,s=z,t=x)$. Equation (10) gives the look-up table parameter. The pciMC program opens the appropriate look-up table, Table [T], identified by $\sin A=\sqrt{U_s^2+U_t^2}$ where the $A$ is the angle between $U_{\mathrm{pciMC}}(r,s,t)$ and the $r$-axis. ${\text{Rund}}_{\mathrm{int}}(0,T_{\text{size}})$ is a random counting number between 0 to $T_{\text{size}}$ (in this study, $T_{\text{size}}=99$). $T_{\text{size}}$ is the total number of patterns in the data set of $Q_k(P_n,{\overrightarrow{\chi }}_m)$. The inner products of each of the incident vectors in Table [T] and the direction $r$ are greater than $T/T_{\text{size}}$ but less than $(T+1)/T_{\text{size}}$. Table [T] stores the vectors and the possible incident point data, the photon escape probabilities $Q_k(P_n,{\overrightarrow{\chi }}_m)$, and the output parameters $(M_k,\overrightarrow{N_k},D_k)$. The means by which the possible incident point data are identified is shown in Appendix A. For example, if $\sin A=\sqrt{U_s^2+U_t^2}=1$, all of the points on the surface of the RBC are accessible. In contrast, $\sin A=0$ means the possible incident points are restricted because the incident photon meets the cell edge-on. A description of the translation from the interaction coordinates to the simulation coordinates is shown in Appendix B.

Fig. 7

Flow chart for the pciMC simulation for flowing blood.

3.1.

Experimental Results: Changes in Light Scattering with Respect to Shear Rate

Figure 8(a) and 8(b) shows the experimental forward and backward relative optical densities (OD_rel), respectively. In Fig. 8, $\mathrm{MCV}=58.4\mathrm{fL}$, $\mathrm{MCHC}=31.7g/\mathrm{dL}$, and $\mathrm{HCT}=27\%$. The OD_rel($\text{shear rate}\mathrm{l}/s$) was calculated by $\mathrm{OD}(\text{shear rate}\mathrm{l}/s)/\mathrm{OD}(0\mathrm{l}/s)$. As for forward OD(0) value, the OD(0) was $2.766\pm 0.030$ in RBC_Plasma, $3.150\pm 0.008$ in RBC_PBS, and $3.041\pm 0.065$ in $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$, respectively.

Fig. 8

Experimentally obtained forward and backward scattered relative optical density versus shear rate. (a) Forward direction, and (b) backward direction.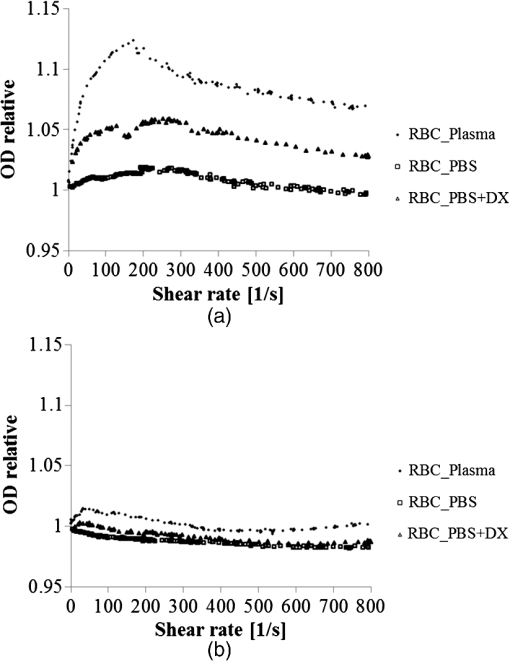

The forward OD_rel of RBC_Plasma was rapidly increased in the shear rate range from 0 to $200\mathrm{l}/s$. The forward OD_rel of $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$ showed similar trend with RBC_Plasma but the change was milder. In RBC_PBS, the OD was hardly changed. The peak value of OD_rel was shown to be around $200\mathrm{l}/s$ shear rate. The peak OD_rel(200) of RBC_Plasma, RBC_PBS, and $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$ were 1.12, 1.05, and 1.01, respectively. As for the backward OD_rel, the values remained almost constant in all the samples. The OD(0) was $2.766\pm 0.030$ in RBC_ Plasma, $3.150\pm 0.008$ in RBC_PBS, and $3.041\pm 0.065$ in $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$, respectively.

3.2.

Changes in Light Scattering with Respect to MCV, MCHC, HCT

For ${\mathrm{RBC}}_{\text{Large}}\_\mathrm{PBS}+\mathrm{DX}$, MCV and MCHC were $54.08\pm 0.19\mathrm{fL}$ and $30.1\pm 0.67\mathrm{g}/\mathrm{dL}$, respectively. On the other hand, for ${\mathrm{RBC}}_{\text{Small}}\_\mathrm{PBS}+\mathrm{DX}$, MCV and MCHC were $49.44\pm 0.10\mathrm{fL}$ and $31.7\pm 0.26\mathrm{g}/\mathrm{dL}$, respectively. About both MCV and MCHC, there were statistically significant differences between ${\mathrm{RBC}}_{\text{Large}}$ and ${\mathrm{RBC}}_{\text{Small}}$ for $n=5$. The $P$ values was $5.6\times {10}^{-7}$ and $2.6\times {10}^{-6}$ for MCV and MCHC, respectively.

The optical density with respect to hematocrit for both samples was shown in Fig. 9. Obviously, ${\mathrm{RBC}}_{\text{Large}}\_\mathrm{PBS}+\mathrm{DX}$ showed smaller OD than ${\mathrm{RBC}}_{\text{Small}}\_\mathrm{PBS}+\mathrm{DX}$ for the same hematocrit value.

Fig. 9

Experimentally obtained forward optical density versus Hematocrit for ${\mathrm{RBC}}_{\text{Small}}$ and ${\mathrm{RBC}}_{\text{Large}}$.

3.3.

Simulation Results: Photon Scattering Distribution

In these results, the input parameters were $\mathrm{MCV}=60.0\mathrm{fL}$, $\mathrm{MCHC}=30.7\mathrm{g}/\mathrm{dL}$, and $\mathrm{HCT}=23.7\%$. Figure 10 shows the influence of the angle between the incident direction of photon and the RBC orientation axis or long axis on the forward scattering probability. The forward scattering probability is reduced as the angle of incidence decreases. For a 90 deg incident angle, since the RBCs rotate around the orientation axis, overall forward scattering becomes less than those of the randomly oriented RBCs. Figure 11 shows the relationship between the angle of incidence and the anisotropy factor $g$. The scattering probability in the pciMC method was expressed by the histogram of the photon escape probability distribution about the scattering angle, $Q(\theta )$. The anisotropy was calculated as the mean cosine from Eq. (11):

Fig. 10

Scattering probability for incident angles of 10, 50, and 90 deg with respect to the axis of orientation.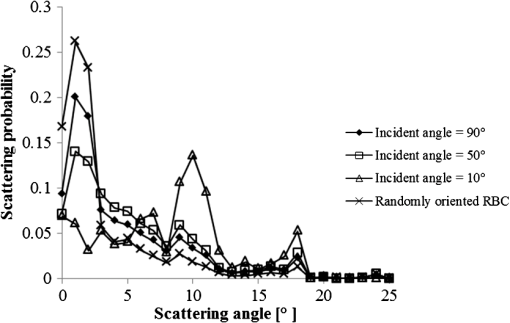

Fig. 11

Anisotropy of oriented and randomly oriented RBCs versus incident angles.

As expected, the anisotropy for randomly oriented RBCs remained constant to be 0.983989 regardless of the incident angle. For an incidence angle of 0 deg, indicating perfect edge-on incidence, $g(0\mathrm{deg})=1.0$. The reason for this is that the photon strikes the RBC perpendicular to its surface so that the photon is transmitted without refraction. However, as the angle of incidence increases, the anisotropy rapidly decreases with the photons scattering toward sides and backward directions. The minimum value of the anisotropy is $g(10\mathrm{deg})=0.965215$. Above 20 deg, the anisotropy recovers and approaches $g_{\text{random}}$ as the angle of incidence increases.

Figure 12(a) and 12(b) shows the forward and backward scattering distributions of photons along the flow axis, respectively, for the random orientation model with no flow, and for models 1, 2, and 3. In calculating numbers of scattered photons for the models 1, 2 and 3, the OR was set at 100%. At the point where the forward scattering was detected,$(x,y,z)=(0,0,9.52)[\mathrm{mm}]$, the random orientation model gave $3.37\times {10}^{-3}\text{photons}/{\mathrm{\mu m}}^2$, while models 1, 2 and 3 gave $4.61\times {10}^{-3}$, $1.02\times {10}^{-3}$ and $2.56\times {10}^{-3}\text{photons}/{\mathrm{\mu m}}^2$, respectively. As for the backward scattering, at the point (0, 6.0, 0) [mm], the random orientation model gave $4.66\times {10}^{-4}\text{photons}/{\mathrm{\mu m}}^2$, while models 1, 2 and 3 yielded $0.164\times {10}^{-4}$, $5.22\times {10}^{-4}$ and $17.9\times {10}^{-4}\text{photons}/{\mathrm{\mu m}}^2$, respectively. Clearly, the photons in model 1, in which the cell orientation is in the direction of the flow, were inhibited from scattering in the flow direction so that the photon distribution in the direction perpendicular to flow exceeded that of random orientation model and became narrower.

Fig. 12

Distribution of forward and backward scattered photons along the flow axis. (a) Forward direction and (b) backward direction.

4.1.

Validation of pciMC for Analysis of Optical Characteristics of Flowing Blood

Conventionally, the optical properties of blood have been determined macroscopically using a scattering constant, an absorption constant, and an anisotropy value. In particular, the anisotropy was treated to be constant and independent of the photon vector within the scattering media. The macroscopic approaches like conventional MC, thus, do not yield an accurate description of microscopic interaction between photons and blood cells. In contrast, the pciMC method, which is based on the geometric optics theory, utilizes blood cell parameters, such as MCV, MCHC, HCT, and the shape and orientation of the RBCs to provide a quantitative analysis of optical interaction between photons and cells without relying on the macroscopic parameters.

As shown by Figs. 10 and 11, both forward scattering probability and anisotropy were affected by the angle between the incident direction of photons and orientation axis of flowing RBCs. The pciMC, which is based on the geometric optics theory and which utilizes blood physiological characteristics, such as MCV, MCHC, HCT as input parameters for analysis is better suited for analysis of optical characteristics of flowing blood.

4.2.

Model Validation at Flow Stop

In this study, the OD(0) was measured immediately as the flow came to stop. Under this condition, RBCs in PBS seem to have been randomly oriented and uniformly distributed. In the previous study, we confirmed that the pciMC model of photon propagation within random orientated RBCs showed good agreement with experimental values of RBC_PBS at no flow condition.³¹ To investigate the orientation and distribution of RBCs in other blood media including RBC_Plasma and $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$, the OD(0) was simulated by pciMC at $\mathrm{OR}=0\%$. The comparisons between the experiments and pciMC simulation results were shown in Fig. 13. Figure 13(a) shows forward optical densities while Fig. 13(b) shows backward optical densities. The OD values of pciMC showed very good agreement with the experiments. The changes in the optical density among the sample at flow stop were speculated to be caused mainly by the differences in the refractive index of the extra cellular medium. Therefore, in this study, an extra care was rendered to avoid occurrence of aggregation. Although a few minor RBCs clusters might have occurred in RBC_Plasma, the influence could be ignored. In conclusion, RBCs within each extracellular solution would be almost randomly oriented and uniformly distributed at flow stop.

Fig. 13

Comparison of optical density at flow stop between the experiment and pciMC simulation. (a) Forward direction, and (b) backward direction.

4.3.

Effects of RBC Orientation on Light Scattering

Our study showed significant changes in the optical density for shear rates from 0 to $200\mathrm{l}/s$. The results indicate that the deformation of RBCs does not have an impact on the optical properties of the blood as Friebel reported previously.²⁹ In this study, we speculated that the changes in the optical properties were caused by the changes in orientation of the RBCs due to flow conditions. The interaction angle between photons and RBCs thus vary depending on the orientation of RBCs affected by the blood flow. As shown in Fig. 12, the distribution of the scattered photons changed significantly with the orientation of the RBCs. As the angle between the incidence direction and the orientation axis or the long axis of the RBCs decreased, the forward scattering decreased due to the decrease in the anisotropy factor (Fig. 11). When the photons’ incident direction approached the orientation axis or the long axis of RBCs, the forward scattering was reduced, but scattering in the sides or backward increased. When we reviewed the experimental results of Fig. 8(a) and 8(b), with the increase in the shear rate from 0 to $200\mathrm{l}/s$, the optical density in the forward direction increased, while the backward optical density was almost constant, respectively. The light would be scattered more in the flow direction or sides or to back, reducing forward scattered intensity. As the flow increased, the blood cells seem to have been lined up in a particular direction and to have rotated around the orientation axis so as to affect interaction angle between photons and cells.

When we compared the experimental results against those of the simulation using pciMC for three different orientation models as shown in Fig. 12(a) and 12(b), it is apparent that the model 1 which is the RBCs oriented in the flow direction showed an opposite indication to the experimental results. Based on the model 1, numbers of forward scattered photons increased while the backward scattered photons decreased, respectively, with larger forward scattering than the randomly oriented model. In contrast, the simulations using model 2 and model 3, which have RBCs with their long axes oriented perpendicular to the flow direction, did replicate the experimental trends.

4.4.

Effects of RBCs’ Orientation Ratio on Forward Scattering

Since the model 2 and model 3 seemed to have better described experimental results, effects of orientation ratio and distribution patterns in the circuit on the forward scattering probabilities were investigated, where, OR distribution was defined as uniform distribution in the circuit.

The results are shown in Fig. 14. For model 2, the forward optical density increases linearly and monotonically with orientation ratio and has a correlation coefficient of $R^2=0.9684$. However, for model 3 the correlation fluctuates and the gradients are less than those for model 2. Since less scattering change was produced with the model 3 than the model 2, it was considered that the orientation of the RBCs used in model 3 do not make a large contribution to the changes in photon propagation with respect to blood flow. In conclusion, the pciMC model that best predicts the experimental results has the RBCs in the extracorporeal circulation migrating with their long axes perpendicular to the direction of flow and pointing towards the center of the circulation tube.

Fig. 14

Optical density in the forward direction vs. orientation ratio for model 2 and model 3 orientation models.

4.5.

Comparison with the Published Rheological Studies

In the past rheological studies, it has become well known that RBCs in a shear field exhibit two types of motion, ‘tumbling’ motion for lower shear stress and ‘tank treading’ motion for higher shear stress.^35–37 The tumbling RBCs roll over periodically just like our orientation model. The rolling direction is parallel to the flow direction like model 2 and model 3. For the micro-vascular research, Mamisashvili et al. observed the orientation of RBCs in frogs’ mesenteric microvessels for the diameter of 25 to 35 μm and the result showed the orientation of RBCs was essentially perpendicular to the vascular walls.³⁷ Also in the macroscopical flow channel, Bitbol observed the light forward scattering patterns across a plane Poiseuille flow whose cross-section is rectangular ($15\times 0.3\mathrm{mm}$) and the result showed the same tendency as we observed.³² Bitbol reported at zero shear rate the RBCs were randomly oriented and the scattering pattern was merely circular. However, when the flow rate was increased, the scattering pattern became elongated in the flow direction and as a result the forward light flux was decreased as shown in our study. Bitbol and Okagawa³⁸ additionally investigated the light scattering changes in the moment phase of the flow onset. As a result, the forward light flux was conversely increased. It was documented that the initial behavior of the RBCs as they became aligned parallel to the plane of equal velocity vectors like model 1. Okagawa explained the phenomenon using the Rayleigh-Debye light scattering theory.³⁸ In other words, the decrease of forward light flux as the scattering pattern elongated indicates that the RBCs’ oriented direction was perpendicular to the flow direction. Therefore these past rheological studies support the RBCs behavior like model 2. In a future study, a combination of these optical results with hydrodynamic theory will be investigated. The pciMC method would then become a powerful tool for rheological studies.

4.6.

Density of Oriented RBCs in Extracorporeal Circuit

The accuracy with which models 1, 2, and 3 replicate the experimental data with respect to flow rate was investigated. Obviously model 1 did not replicate the experimental results. Model 3 did hardly contribute to the changes in the light scattering. Therefore, by using model 2, the inverse problem to obtain the orientation ratio, expressed in Eq. (8), was conducted. The inverse problem pursued the orientation ratio for which the simulation results of both the forward and backward optical densities were closest to those of the experimental results.

The result is shown in Fig. 15. The orientation with respect to flow rate rapidly increased and saturated around $200\mathrm{l}/s$. The maximum value was 14.7% for RBC_Plasma, and 10.3% for $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$, while the orientation of RBC_PBS was hardly confirmed. The reproducibility error of the inverse problem was calculated using the following equation:

Fig. 15

Orientation ratio versus shear rate predicted by pciMC simulation.

For the shear rate from 0 to $300\mathrm{l}/s$, significant differences in the orientation ratio were noticed. The tendency was also similar with the viscosity characteristics with respect to shear rate shown in Fig. 1. In $\mathrm{RBC}\_\mathrm{PBS}+\mathrm{DX}$, the aggregation hardly occurred. Therefore, the orientation would be mainly caused by the viscosity of the extracellular solution. On the other hand, the orientation in RBC_PBS hardly occurred due to lower viscosity. Hence, it might be speculated that the orientation ratio depends on the viscosity of extracellular solution. Or the difference might be caused by the effect of RBCs aggregation. Although the severe aggregation was avoided in the experiments, RBCs might begin to flow by colliding with neighboring RBCs when flow start. Then the RBCs are influenced by the plasma protein and they align with the neighboring oriented RBC. As a result, the plasma protein might assist the orientation like rouleaux effect. Friebel et al. reported the effect of the plasma protein below $200\mathrm{l}/s$.²⁹ Our result also showed the high orientation occurred in the shear range. On the other hand, in the shear range above $300\mathrm{l}/s$, the viscosities of extracellular medium of both samples were almost the same. Therefore, the difference of orientation ratio in the shear range might be caused by the plasma protein effect. In conclusion, it is speculated that the orientation of RBCs in plasma is influenced by both the viscosity of plasma and the effect of the plasma protein.

4.7.

Validation of pciMC About MCV, MCHC, HCT

To validate the model and confirm its utility, the non-invasive measurement of the hematocrit using the optimized model was conducted in the experiment of ${\mathrm{RBC}}_{\text{Large}}\_\mathrm{PBS}+\mathrm{DX}$ and ${\mathrm{RBC}}_{\text{Small}}\_\mathrm{PBS}+\mathrm{DX}$. The orientation ratio for a given shear rate, based on its relationship with the shear rate given in Fig. 15, was also used. An estimate of HCT was entered to calculate the optical density that best matched the measured optical density. When the simulation and measured results matched, the program output the HCT. The result of the non-invasive prediction of the hematocrit was shown in Fig. 16. The predictions were conducted in the shear range from 10 to $200\mathrm{l}/s$. The error was calculated using the following equation:

Fig. 16

Prediction of hematocrit by pciMC simulation.

The optical characteristics of the blood changed significantly with shear rate from 0 to $200\mathrm{l}/\text{s}$. The pciMC simulation accurately predicted the hematocrit in spite of the limited flow range. Furthermore, the influence of light scattering by changes in MCV and MCHC could be replicated. Fortunately, the prediction could be achieved using the single relationship between the orientation ratio and the shear rate as shown in Fig. 15 only. The results indicate that the orientation of the RBCs hardly depend on the value of the hematocrit from approximately 20 to 40%. As a result, the simpler prediction system could be applied. The low flow range, in which the optical properties are affected, is clinically applied in cases such as pediatric ECMO and hemodialysis. Conventional optical monitors have the limitation of a low flow range with poor accuracy. The technique using pciMC simulation would help the development of a device applicable to various extracorporeal circulation therapies.

4.8.

Future Prospects

The optical properties of blood are strongly related to the physiological and rheological conditions. In this study, the pciMC simulations brought up various rheological issues. Thus pciMC will contribute to the development of both hemo-rheology and optical non-invasive diagnosis. Although the effects of RBCs orientation in continuous flow on light scattering were based on the experiment, the elucidation of correct oriented RBCs distribution would require more detailed analysis and versatile detection conditions. Shvartsman speculates the aggregation is main factor of changes in the light scattering in pulsatile blood flow.^27,28 In the pulsatile blood flow, the intensive aggregation would occur in the diastolic phase which is low shear rate. In this condition, the intensive aggregation, the RBCs cluster should be defined in pciMC, and the step size would reduce. The detailed analysis of these encouraging results is scope of future publications.