|
|
1.IntroductionIn the last two decades, the development of nonlinear optical microscopy1–5 has opened a field of biomedical optics with ever-expanding perspectives both in basic research and in the development of very powerful noninvasive diagnostic tools.6–10 Nonlinear optical transitions, in fact, ensure confinement of excitation to the focal volume, leading to intrinsic three-dimensional (3-D) sample optical sectioning. Further, the near-infrared (NIR) wavelengths employed reduce scattering and maximize tissue penetration. These characteristics have boosted nonlinear microscopy as an elective method for imaging cells with micrometer-resolution deep into living tissues. In two-photon fluorescence (TPF) microscopy, nonlinear excitation is coupled with detection of fluorescence, the contrast method most used in biological microscopy. Fluorescence contrast can arise from exogenous labels,11 genetically encoded fluorescent proteins,12 or specific autofluorescent cellular substrates.7,13–16 Imaging methods based on this source of contrast are most sensitive to the density of the fluorescence emitters but typically do not provide information on their subdiffraction spatial distribution. In this review, we focus on second-harmonic-generation (SHG), a nonlinear source of contrast which in some tissues arises directly from unlabeled proteins arranged in ordered arrays.17,18 This property of SHG offers the unique opportunity of combining the advantage of nonlinear microscopy with probing of structural order within a living tissue at different hierarchical levels, ranging from protein molecular conformation to supramolecular arrangement. SHG is a nonlinear second-order optical process occurring in systems without a center of symmetry and with a large molecular hyperpolarizability. For example, these conditions are easily fulfilled at the molecular level by the presence of electron-donor and electron-acceptor moieties connected by a -conjugated system. Such a conjugated system can be engineered in organic membrane dyes, which permit exogenous labeling of biological samples for SHG imaging. The membrane contrast achievable with these dyes and their sensitivity to membrane potential lead to important applications in functional imaging of cell electrical activity.19–25 In addition, SHG signal can be endogenously produced by polypeptide chains.18,26–37 Previous studies aiming at characterizing the molecular source of this signal concluded that peptide SHG mainly arises from chiral and achiral susceptibility components that are resonantly enhanced in the region of the amide transition of the single amino acid residue.38 The tilt of the amide group planes in an -helix relative to the helical axis leads to detectable SHG signal in tissues characterized by a high degree of structural anisotropy, offering the opportunity to probe structural order and molecular conformation in vivo. Below, we review the physical principles leading from a single-molecule second-harmonic response to a bulk SHG signal; we then describe how these principles determine which biological tissues do indeed generate SHG contrast. Understanding the basis of the phenomenon allows exploiting it for structural probing of living tissues. 2.From SHR to SHG Through Coherent SummationIn the description of the light–matter interaction, the optical properties of a molecule are determined by its dipole moment , described as where is the driving electro-magnetic field, is the permanent molecular dipole, is the molecular polarizability describing linear absorption and scattering of light, and is a tensor describing the first hyperpolarizability term, responsible for the second-order nonlinear process known as second-harmonic response (SHR). The condition for a nonzero value of in a molecule is the presence of a resonance axis with an asymmetry of charge distribution. A general description of the principles of SHR can be found in excellent textbooks.39,40SHR is characterized by phase and energy conservation, leading to the possibility of coherent summation of the waves radiated from all the molecules. The dependence of SHR coherent summation on the orientation of emitters is described in Fig. 1. The top panel of Fig. 1(a) shows two parallel emitters located within a distance smaller than the optical wavelength. Due to the alignment of their resonance axis, the two emitters scatter in-phase SHR photons that will constructively interfere. The bottom panel of Fig. 1(a) shows the case of two molecules with antiparallel orientation: the opposition of their resonance axis produces out-of-phase SHR photons that will destructively interfere. Figure 1(b) shows an experimental demonstration of the principles illustrated in Fig. 1(a): when the membrane of giant unilamellar vesicles (GUVs) is labeled with Di-6-ASPBS membrane dye (uniform membrane labeling is demonstrated by the TPF image), strong SHG signal arises from the GUVs’ surface, except for areas in which the membranes of two GUVs juxtapose (shown by the yellow arrowhead). In these areas, in fact, SHR emitters (SHREs) from the two membranes are oriented antiparallel, leading to destructive interference of the scattered photons. The dependence of SHG signal on the ordered arrangement of emitters in the focal volume has relevant applications for membrane imaging, as shown in Fig. 1(c). When labeling a cell membrane, diffusion of the dye from the plasma membrane to inner cell compartments occurs (shown by the presence of fluorescence inside the cell, as detected by TPF). However, the internalized dye molecules are randomly oriented and, therefore, do not produce coherent summation, resulting in a high-contrast SHG image, in which only the cell membranes are visible. The dependence of signal on isotropic versus anisotropic SHRE distributions is the basis for high-contrast imaging of ordered structures. Fig. 1Coherent summation. (a) The figure shows examples of the second-harmonic response (SHR) waves produced by two pairs of irradiated emitters. If the molecules are parallel (upper panel), their SHR waves are in phase with the driving field and can interfere constructively. If the molecules are antiparallel (bottom panel), their SHR waves have opposite phases and interfere destructively. The figure is inspired by Ref. 41. (b) Simultaneous two-photon fluorescence (TPF) and second-harmonic-generation (SHG) images of three vesicles labeled with Di-6-ASPBS dye. The radiating dye molecules are symmetrically distributed in the adherence regions between the vesicles. In the left region, a symmetric distribution results in a nearly perfect cancellation of SHG (yellow arrowhead). In the right region, the cancellation is imperfect because of a disparity in labeling density. . The figure is modified from Ref. 42. (c) Simultaneous TPF and SHG images of a SY5Y cell labeled with RH237 membrane dye. The randomly oriented dye that is internalized into the cell cytoplasm (as apparent from the TPF image) does not produce coherent second-harmonic response. . The figure is modified from Ref. 43. 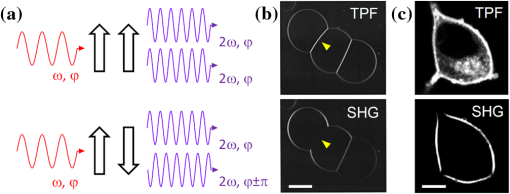 In this regard, it is particularly interesting to notice that some tissues exhibit the intrinsic capability of producing SHG. The first SHG biological imaging was reported by Freund et al.26 on connective tissue. In this tissue, in fact, the structural organization of collagen in fibrils and fibers disposes the SHREs in a lattice leading to SHG. Indeed, endogenous SHG signal is displayed by biological samples characterized by a high degree of order: Fig. 2 shows the three most prominent examples of intrinsic SHG in biology, namely collagen [Fig. 2(a)], microtubules [Fig. 2(b)], and myosin in muscle [Fig. 2(c)]. In all these samples the cylindrical symmetry of protein arrangement within the biopolymer and the supramolecular arrangement of polymers within the tissue warrants a high degree of alignment of the endogenous SHREs (as described in more detail below), leading to the strong SHG signal detected. The anisotropic distribution of SHREs underlying coherent summation in biological samples also determines the polarization of SHG signal. Quantitative measurements of SHG polarization anisotropy can, therefore, provide information on the SHRE distribution itself. Fig. 2Endogenous second-harmonic-generation (SHG) imaging. (a) SHG image from a mature rat tail tendon collagen. . Figure modified from Ref. 28. (b) SHG imaging in living cells. SHG arises from mitotic spindles and from interphase microtubule ensembles in RBL cells. . Figure modified from Ref. 36. (c) SHG image of a gastrocnemius muscle. The bright bands in the image correspond to sarcomeric A-bands. . Figure modified from Ref. 34.  3.Polarization AnisotropyTo derive the dependence of SHG anisotropy on SHRE distribution within the focal volume, we start from the general description of the polarization in a medium: This equation is nothing but the bulk equivalent of Eq. (1). The tensor describes the second-order susceptibility. In the general case, the susceptibility tensor is a third-rank tensor with () elements. In the specific case of SHG, in which two fields with the same frequency () generate a third field with frequency , each component of the second-order polarization can be expressed as Therefore, the susceptibility tensor has the following symmetry: With these symmetries, the number of independent elements of the tensor decreases to 18. Hence, the second-order induced polarization can be written as a function of the components of the tensor and of the electric field as follows: In a bulk sample made of a distribution of individual SHREs, the susceptibility tensor can be calculated, summing each individual hyperpolarizability term (expressed in the molecule’s system of coordinates ): Considering SHRE with a single dominant axis of hyperpolarizability and defining the molecular system of coordinates with the axis coinciding with the hyperpolarizability axis, the only nonzero component of is (which, with abuse of notation, will be hereafter denoted simply as ). Then, Eq. (6) can be re-written as:where is the number of the emitters. As noted above, biologically relevant SHG-emitting samples are characterized by a distribution of SHREs with cylindrical symmetry. We define the laboratory system of coordinates (, , ) with the -axis along the axis of sample cylindrical symmetry [see Fig. 3(a)]. Under the assumption that, within the cylindrical symmetry, the emitters are oriented at a fixed polar angle with respect to the symmetry axis [see Fig. 3(b)], computation of the tensor elements using Eq. (7) produces the following nonzero components: The second-order susceptibility tensor, therefore, can be written as Considering an electric field propagating along the -axis and linearly polarized at an angle with respect to the -axis [Fig. 3(a)], and substituting Eqs. (9) and (10) into Eq. (5), the second-order polarization can be written as The intensity of SHG () is proportional to the square of the second-order polarization: The simple case illustrated in Fig. 1(a) (extended to molecules) can be described by setting the polar angle to zero so that This equation provides a quantitative description of the coherent summation at the basis of SHG described in the previous section.Fig. 3Second-harmonic response emitter (SHRE) spatial distributions. (a) Diagram of coordinate system for calculating the second-harmonic-generation (SHG) intensity from a distribution of SHREs with cylindrical symmetry. The system of coordinate is defined with the -axis along the axis of cylindrical symmetry. The excitation light propagates along the -axis and is linearly polarized at an angle with respect to the -axis. (b) Schematic representation of SHREs distributed on the surface of a cone with an aperture angle . Three different aperture angles are shown: 25 deg (black), 40 deg (dark grey), 70 deg (light grey). (c) Dependence of SHG polarization anisotropy (SPA) on polar angle in cylindrically symmetric sample. SPA curves are calculated for the three SHRE distributions shown in (b). The intensity of SHG is represented as a function of the angle between the laser polarization and the cone axis [see panel (a)]. 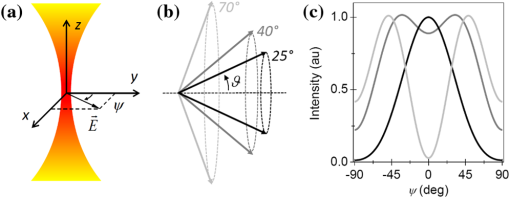 In general, Eq. (12) provides the foundation for using SHG measurements to assess the structural distribution of emitters in a sample. In fact, if is measured as a function of the laser polarization angle , the resulting SHG polarization anisotropy (SPA) data can be fitted with Eq. (12) in the following form: withAs an example, Fig. 3(b) and 3(c) shows three different profiles for samples characterized by different values of the angle . This example provides a clear demonstration that SPA data can be used to access information on the structural distribution of SHREs in the sample. All the above treatment rests on the assumption of a uniformly distributed medium illuminated by a simple plane wave. However, experimental measurements are typically performed with high numerical aperture objectives and on samples characterized by inhomogeneously distributed SHREs. A full mathematical calculation of SHG in these conditions was provided by Mertz and Moreaux.44 In that work, the authors demonstrated that, under the assumption that there is no correlation between SHRE orientation and position within the illumination focal volume, the considered inhomogeneities affect only the SHG spatial radiation pattern and total power without affecting SPA. These results, therefore, justify the simplified SPA calculation employed in all experimental and theoretical works based on SPA in which explicit 3-D spatial distribution of SHREs is neglected and only their angular distribution is considered. Another factor to be considered in a full description of SPA is the sample thickness. In fact, a thick anisotropic tissue could affect, in a polarization-dependent manner, both the illumination and SHG emitted beam propagation. This effect has been recently investigated45–48 and, with the development of theoretical models, the birefringence and attenuation of the excitation propagation can be taken into account, correcting SPA measurements. 4.Assessment of Molecular Order in TissuesThe exquisite dependence of both SHG intensity and polarization anisotropy on SHRE distribution (in combination with the advantages conferred in microscopy by its nonlinear nature) leads to interesting biomedical applications. SHG imaging, for example, is a valuable tool for assessing the degree of order of collagen fibrils within different types of tissue, from morphological characterization of healthy and pathological connective tissue in vivo16,27,49–51 to quantitative measurement of fibril orientation within the pixel size.28,29 Collagen type I features a hierarchical organization ranging from the atomic and molecular scale (tropo-collagen molecules: 280 nm length and 1.5 nm diameter), to the microscopic scale (fibrils: 1 µm length and 30 nm diameter) and the macroscopic scale (fiber bundles). The sensitivity of SHG to these different hierarchical organizations allows probing the thermally induced structural changes of collagen52–55 as shown in Fig. 4. In Fig. 4(a) the loss of order caused in porcine cornea upon laser-induced heating is demonstrated by SHG images collected at different distances from the irradiation spot. As the distance decreases, image contrast gets poorer due to decreased overall alignment of SHREs within the focal volume; moreover, at a higher dimensional scale, the imaged collagen fibrils themselves display higher angular dispersions, as demonstrated by the image fast Fourier transform (FFT) (shown in the inset of each image). Fig. 4Supramolecular order quantification. (a) Heat-induced disorder in porcine corneal stroma. Second-harmonic-generation (SHG) images acquired from the periphery to the center of a laser-irradiated spot area. The radial distance of the images from the center of the irradiation spot area are indicated above each panels. The fast Fourier transform (FFT) of each image is also shown in inset. . Figure modified from Ref. 54. (b) Heat-induced disorder in rat tail tendon fascicle. Progressive changes in SHG data in rat tail tendon fascicles exposed to 58°C heat. SHG intensity (left panels) decreased across the entire tip. SHG maps of a disorder index (central panel) underline that disorder is detectable across the tip, consistent with loss of SHG signal. The orientation maps (right panel) indicate that the loss of parallel alignment occurs in some fibril bundles faster than in others and is associated with increased levels of disorder. Figure modified from Ref. 56. 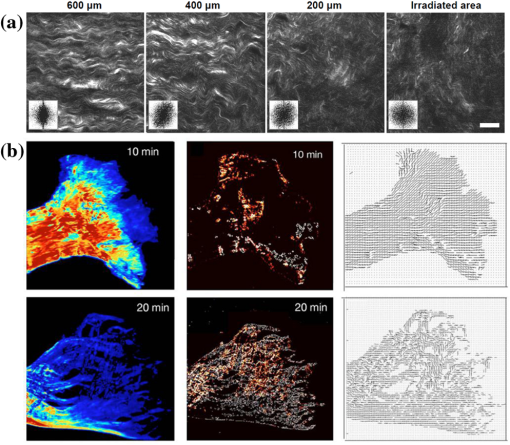 Quantitative analysis56 can be employed to extract a disorder index from SHG images and measure, for example, topology and dynamics of collagen heat denaturation, as shown in Fig. 4(b). The possibility to monitor collagen thermal modifications is an important issue in biomedical optics. In fact, several laser-based treatments (such as corneal thickening, vascular treatment, and skin rejuvenation) can cause collateral thermal damage. The examples shown in Fig. 4 provide a clear demonstration of how SHG microscopy extends the range of imaging to polymer orientation analysis. Next we will further extend this powerful capability of SHG microscopy into the realm of probing molecular conformations in unstained living samples. This application has found thus far its most extensive development in the study of muscle tissue. 5.SHRE Organization in ProteinsStrong SHG signal has been detected in skeletal muscle.33,35 As shown in the example of Fig. 2(c), the signal arising from muscle tissue displays a striking alternation of bright and dark bands, typical of the sarcomeric striations. The possibility of imaging sarcomeres by SHG allows measuring sarcomere length with nanometric resolution.57 More generally, the possibility of imaging unstained muscle in vivo18,58 with 3-D capabilities holds great promise for the development of biomedical diagnostic tools for muscular pathologies involving alterations and/or loss of sarcomeric structure.34,59 The organization of most muscle proteins in helical filaments and the distribution of such filaments in cylindrically symmetric and repetitive structures along the fiber clearly represent an ideal structural configuration to give rise to SHG. Measurements on peptides suggest that the main SHR source lies within the amide groups (HN-CO) of polypeptide chains.38 In the case of proteins characterized by sequence repeats with amino acids containing methylene groups (for example, proline) this additional element of resonance should be considered.60 For example, in collagen (rich of the -ProHypGly- repeat) the second-order susceptibility arises mainly from peptide groups in the backbone,61,62 but also from the symmetric stretch of the methylene groups in the side chain. Analysis of collagen SPA data showed that the helical pitch angle estimated including methylene groups resonance agrees more closely63 with the known pitch angle of 45.3 deg. The analysis of large conformational changes in a protein (see next section), on the other hand, can be satisfactorily conducted with the simplified assumption of all SHREs residing within the amide group. Because of the predominant role of the polypeptide amide groups in SHG, secondary structures are particularly relevant in considering the effects of coherent summation within a protein. The arrangement of amide groups in the -helix is shown in Fig. 5(a). An individual -helix is characterized by cylindrical symmetry with all SHREs tilted at a fixed polar angle with respect to the helical axis [the same geometry described in Fig. 3(b)]. The generation of SHG signal through coherent summation requires an anisotropic distribution of the SHREs. Proteins characterized by randomly oriented -helices do not fulfill such anisotropy and are not expected to be good SHG sources. On the other hand, proteins with a high degree of alignment of their -helices should produce coherent summation. In other words, a first level of order (required for constructive interference) is achieved by organization of peptide bonds in a helical pattern; however, a second level of order is also necessary, consisting in substantial alignment of the helices themselves in the protein. Considering, for example, the two main constituents of muscle (myosin and actin), the -helices of actin display an orientational dispersion limiting SHG, whereas myosin is endowed with some extraordinarily long -helices which are highly aligned, especially in the tail portion. Clearly, a single protein would produce too low an intensity of SHG to be detected. Thus, a third level of structural organization is required in which SHG-emitting proteins are arranged with a symmetry leading to further summation of the signal up to a detectable level. These considerations provide an interpretation for SHG being observable only in specific samples such as collagen, microtubules, and muscle. Fig. 5Probing protein structural conformation. (a) Example of location of two HN-CO second-harmonic response emitters (SHREs) (black arrows) in -helix. (b) Atomic structure of myosin molecule with light meromyosin (LMM) and S2 portion shown in cyan and the S1 globular head shown in blue. (c) Atomic structure of an actin monomer in ribbon representation. (d) Sarcomeric acto-myosin array. (e) Computed second-harmonic-generation (SHG) intensities. The relative contributions of actin and myosin were calculated modeling the acto-myosin array inside the excitation volume. (f) Scheme of the myosin molecule (in blue) detached from actin (red line). The two S1 heads are indicated by S1 and . (g) Calculation of (surface color plot) as a function of and for different values of . The value of on the surface plot is pointed by the arrow. (h) Scheme of the myosin molecule attached to actin. The catalytic domains are rigidly fixed to actin. (i) Calculation of as a function of and for different values of . The black iso- curves (; ) report the measured value of . The asterisks show the geometry of rigor heads according to cryo-EM. Figure modified from Ref. 64. 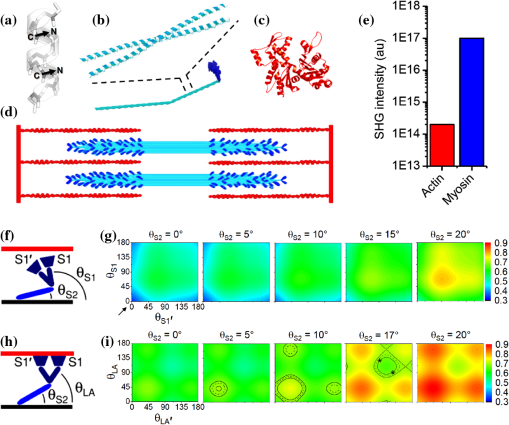 6.Probing Molecular StructureKnowledge of the atomic structure of a protein allows placing all its HN-CO SHREs in space so that the bulk second-order susceptibly tensor [] can be calculated, assuming that all HN-CO SHREs have the same nonlinear hyperpolarizability tensor (characterized by as the only nonzero component in the molecular reference system) and using Eq. (7). Because all biological samples capable of SHG emission are characterized by a cylindrically symmetric distribution of their protein constituents, structural information can be experimentally obtained in terms of the factor from SPA data [see Eq. (14)]. On the other hand, can also be calculated from computed from the atomic model of the protein. Comparing the experimentally measured with the theoretically computed ones allows determining which modeled protein structure is most representative of the conformation inside the tissue under investigation. This approach has been applied to probing the structural conformation of myosin in skeletal muscle.64 The atomic structures of myosin [Fig. 5(b)] and actin [Fig. 5(c)], their polymeric organization in filaments, and the overall sarcomeric ultrastructure are known. In detail, the atomic-resolution structure of full-length myosin can be reconstructed using the atomic coordinates from the Proteins Data Bank: -helix coiled coil light meromyosin (LMM) and S2 (Ref. 65) and double-headed rigor S1 (Ref. 66). Further, based on the thick filament structure, full-length myosin molecules, repeated with the proper axial periodicity and helical symmetry, generate the quasihelical 42.9 nm-long elementary unit containing nine myosin molecules. The structure of the actin filament, on the other hand, is published.66 With this information, the full spatial distribution of HN-CO SHREs in a muscle sarcomere can be reconstructed [Fig. 5(d)]. Equation (12) can be used to estimate the from knowledge of hyperpolarizability tensor, defining an intensity indicator that considers the contributions from both parallel and perpendicular incident polarizations. Using this approach, the contribution of myosin is three orders of magnitude larger than that of actin [Fig. 5(e)], in agreement with the experimental evidence of SHG as myosin-based35 and with structural distributions of SHRE within proteins (as described above). Construction of the full 3-D distribution of SHREs also allows calculation of [see Eq. (15)]. Experimental SPA measurements in different physiological states of muscle (resting and rigor, characterized by different myosin conformations) yield and , highlighting SHG sensitivity to the myosin structural changes.64 For calculation of different values corresponding to different myosin structures, the conformation of myosin can be varied with rigid body rotations about selected hinges. The myosin molecule can be divided into globular heads (S1), a first coiled-coil portion (S2), and a longer coiled-coil portion (LMM). For detached heads, the whole S1 was considered as a rigid body and free rotations at the S1-S2 and S2-LMM junctions allowed variations of the and angles, respectively [see Fig. 5(f)]. Figure 5(g) shows computed as a function of the orientation of each head ( and ) of the same myosin molecule for different orientations of S2 () ranging from 0 to 20 deg, limited by geometrical constraints determined by molecular dimensions and the sarcomere lattice spacing. The general features of the landscape are determined by and , whereas increasing tilt of S2 away from the fiber axis offsets the whole landscape toward higher values. Comparing the experimentally measured [indicated by the black arrow in Fig. 5(g)] with the computed , it can be seen that only a myosin configuration with both S1 heads and S2 parallel to the fiber axis is compatible with the SPA result. This finding is in agreement with the cry-EM experiments. In the simulation of rigor state, due to the attachment of myosin to actin, the catalytic domain of S1 is fixed and only the lever-arm angles ( and ) can vary [Fig. 5(h)]. Comparison of the results shown in Fig. 5(g) with those in Fig. 5(i) demonstrates that fixing the catalytic domain in the rigor configuration produces an overall increase of Similarly to what was observed in Fig. 5(g), tilting of S2 away from the fiber axis shifts the landscape upward. Indeed, for or , no orientation of lever arm can produce a value compatible with the rigor measurement. On the other hand, for ranging from 5 to 17 deg, several lever-arm orientations produce values compatible with the measured [black iso- curves in Fig. 5(i)]. In particular, for , the lever-arm angles measured in rigor by cryo-EM66 produce a value of consistent with the SPA measurement [see asterisks in Fig. 5(i)]. 7.ConclusionsThe properties of SHR coherent summation leading to SHG render this type of microscopy unique for its capability to conjugate the advantages of nonlinear processes with the possibility of probing molecular and supramolecular organization in living tissues. In this work, we have reviewed the physical bases of SHG in relation with its source in biological specimens, describing the mathematical modeling through which SHG polarization anisotropy data can be used to obtain information on protein conformation and degree of order within the tissue. This technique finds applications in biomedical optics both at the molecular level (for example, study of myosin conformations in muscle) and at the supramolecular level (for example, the characterization of fibril order and arrangement in collagen tissue). Important advances in biophysical and biomedical research, as well as in diagnostics, can be gained from a new generation of imaging tools capable of probing molecular structures and their dynamics in vivo. AcknowledgmentsWe thank Dr. Anna Letizia Allegra Mascaro for useful discussion about the manuscript. The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement N. 228334 and Human Frontier Science Program research grant RGP0027/2009. This research project has been also supported by the Ente Cassa di Risparmio di Firenze (private foundation). ReferencesW. R. ZipfelR. M. WilliamsW. W. Webb,
“Nonlinear magic: multiphoton microscopy in the biosciences,”
Nat. Biotechnol., 21
(11), 1369
–1377
(2003). http://dx.doi.org/10.1038/nbt899 NABIF9 1087-0156 Google Scholar
F. HelmchenW. Denk,
“Deep tissue two-photon microscopy,”
Nat. Methods, 2
(12), 932
–940
(2005). http://dx.doi.org/10.1038/nmeth818 1548-7091 Google Scholar
W. DenkJ. H. StricklerW. W. Webb,
“Two-photon laser scanning fluorescence microscopy,”
Science, 248
(4951), 73
–76
(1990). http://dx.doi.org/10.1126/science.2321027 SCIEAS 0036-8075 Google Scholar
W. Minet al.,
“Coherent nonlinear optical imaging: beyond fluorescence microscopy,”
Annu. Rev. Phys. Chem., 62 507
–530
(2011). http://dx.doi.org/10.1146/annurev.physchem.012809.103512 ARPLAP 0066-426X Google Scholar
J. Mertz,
“Nonlinear microscopy: new techniques and applications,”
Curr. Opin. Neurobiol., 14
(5), 610
–616
(2004). http://dx.doi.org/10.1016/j.conb.2004.08.013 COPUEN 0959-4388 Google Scholar
L. Sacconiet al.,
“Action potential propagation in transverse-axial tubular system is impaired in heart failure,”
Proc. Natl. Acad. Sci. USA, 109
(15), 5815
–5819
(2012). http://dx.doi.org/10.1073/pnas.1120188109 NERNET 0896-6273 Google Scholar
W. R. Zipfelet al.,
“Live tissue intrinsic emission microscopy using multiphoton-excited native fluorescence and second harmonic generation,”
Proc. Natl. Acad. Sci. USA, 100
(12), 7075
–7080
(2003). http://dx.doi.org/10.1073/pnas.0832308100 1091-6490 Google Scholar
D. A. DombeckM. Blanchard-DesceW. W. Webb,
“Optical recording of action potentials with second-harmonic generation microscopy,”
J. Neurosci., 24
(4), 999
–1003
(2004). http://dx.doi.org/10.1523/JNEUROSCI.4840-03.2004 JNRSDS 0270-6474 Google Scholar
M. J. Milleret al.,
“Two-photon imaging of lymphocyte motility and antigen response in intact lymph node,”
Science, 296
(5574), 1869
–1873
(2002). http://dx.doi.org/10.1126/science.1070051 SCIEAS 0036-8075 Google Scholar
K. SvobodaD. W. TankW. Denk,
“Direct measurement of coupling between dendritic spines and shafts,”
Science, 272
(5262), 716
–719
(1996). http://dx.doi.org/10.1126/science.272.5262.716 SCIEAS 0036-8075 Google Scholar
J. W. LichtmanJ. A. Conchello,
“Fluorescence microscopy,”
Nat. Methods, 2
(12), 910
–919
(2005). http://dx.doi.org/10.1038/nmeth817 1548-7091 Google Scholar
B. N. Giepmanset al.,
“The fluorescent toolbox for assessing protein location and function,”
Science, 312
(5771), 217
–224
(2006). http://dx.doi.org/10.1126/science.1124618 SCIEAS 0036-8075 Google Scholar
M. C. Skalaet al.,
“In vivo multiphoton microscopy of NADH and FAD redox states, fluorescence lifetimes, and cellular morphology in precancerous epithelia,”
Proc. Natl. Acad. Sci. USA, 104
(49), 19494
–19499
(2007). http://dx.doi.org/10.1073/pnas.0708425104 1091-6490 Google Scholar
R. Cicchiet al.,
“Time- and spectral-resolved two-photon imaging of healthy bladder mucosa and carcinoma in situ,”
Opt. Express, 18
(4), 3840
–3849
(2010). http://dx.doi.org/10.1364/OE.18.003840 OPEXFF 1094-4087 Google Scholar
R. Cicchiet al.,
“Nonlinear laser imaging of skin lesions,”
J. Biophoton., 1
(1), 62
–73
(2008). http://dx.doi.org/10.1002/jbio.200710003 Google Scholar
R. Cicchiet al.,
“Multidimensional non-linear laser imaging of basal cell carcinoma,”
Opt. Express, 15
(16), 10135
–10148
(2007). http://dx.doi.org/10.1364/OE.15.010135 OPEXFF 1094-4087 Google Scholar
P. J. CampagnolaL. M. Loew,
“Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms,”
Nat. Biotechnol., 21
(11), 1356
–1360
(2003). http://dx.doi.org/10.1038/nbt894 NABIF9 1087-0156 Google Scholar
P. J. Campagnolaet al.,
“Three-dimensional high-resolution second-harmonic generation imaging of endogenous structural proteins in biological tissues,”
Biophys. J., 82
(1), 493
–508
(2002). http://dx.doi.org/10.1016/S0006-3495(02)75414-3 BIOJAU 0006-3495 Google Scholar
L. Sacconiet al.,
“Optical recording of electrical activity in intact neuronal networks with random access second-harmonic generation microscopy,”
Opt. Express, 16
(19), 14910
–14921
(2008). http://dx.doi.org/10.1364/OE.16.019410 OPEXFF 1094-4087 Google Scholar
L. SacconiD. A. DombeckW. W. Webb,
“Overcoming photodamage in second-harmonic generation microscopy: real-time optical recording of neuronal action potentials,”
Proc. Natl. Acad. Sci. USA, 103
(9), 3124
–3129
(2006). http://dx.doi.org/10.1073/pnas.0511338103 1091-6490 Google Scholar
D. A. Dombecket al.,
“Optical recording of fast neuronal membrane potential transients in acute mammalian brain slices by second-harmonic generation microscopy,”
J. Neurophysiol., 94
(5), 3628
–3636
(2005). http://dx.doi.org/10.1152/jn.00416.2005 JONEA4 0022-3077 Google Scholar
A. C. Millardet al.,
“Direct measurement of the voltage sensitivity of second-harmonic generation from a membrane dye in patch-clamped cells,”
Opt. Lett., 28
(14), 1221
–1223
(2003). http://dx.doi.org/10.1364/OL.28.001221 OPLEDP 0146-9592 Google Scholar
J. JiangK. B. EisenthalR. Yuste,
“Second harmonic generation in neurons: electro-optic mechanism of membrane potential sensitivity,”
Biophys. J., 93
(5), L26
–L28
(2007). http://dx.doi.org/10.1529/biophysj.107.111021 BIOJAU 0006-3495 Google Scholar
M. Nuriyaet al.,
“Imaging membrane potential in dendritic spines,”
Proc. Natl. Acad. Sci. USA, 103
(3), 786
–790
(2006). http://dx.doi.org/10.1073/pnas.0510092103 1091-6490 Google Scholar
L. Moreauxet al.,
“Electro-optic response of second-harmonic generation membrane potential sensors,”
Opt. Lett., 28
(8), 625
–627
(2003). http://dx.doi.org/10.1364/OL.28.000625 OPLEDP 0146-9592 Google Scholar
I. FreundM. Deutsch,
“Second-harmonic microscopy of biological tissue,”
Opt. Lett., 11
(2), 94
–96
(1986). http://dx.doi.org/10.1364/OL.11.000094 OPLEDP 0146-9592 Google Scholar
T. M. Brownet al.,
“Dynamic imaging of collagen and its modulation in tumors in vivo using second harmonic generation,”
Nat. Med., 9
(6), 796
–800
(2003). http://dx.doi.org/10.1038/nm879 JBOIBX 1078-8956 Google Scholar
R. M. WilliamsW. R. ZipfelW. W. Webb,
“Interpreting second-harmonic generation images of collagen I fibrils,”
Biophys. J., 88
(2), 1377
–1386
(2005). http://dx.doi.org/10.1529/biophysj.104.047308 BIOJAU 0006-3495 Google Scholar
P. Stolleret al.,
“Polarization-modulated second harmonic generation in collagen,”
Biophys. J., 82
(6), 3330
–3342
(2002). http://dx.doi.org/10.1016/S0006-3495(02)75673-7 BIOJAU 0006-3495 Google Scholar
R. K. Jainet al.,
“Dynamic imaging of collagen and its modulation in tumors in vivo using second-harmonic generation,”
Nat. Med., 9
(6), 796
–800
(2003). http://dx.doi.org/10.1038/nm0603-685 JBOIBX 1078-8956 Google Scholar
G. Coxet al.,
“3-dimensional imaging of collagen using second harmonic generation,”
J. Struct. Biol., 141
(1), 53
–62
(2003). http://dx.doi.org/10.1016/S1047-8477(02)00576-2 JSBIEM 1047-8477 Google Scholar
F. Vanziet al.,
“New techniques in linear and non-linear laser optics in muscle research,”
J. Muscle Res. Cell Motil., 27
(5–7), 469
–479
(2006). http://dx.doi.org/10.1007/s10974-006-9084-3 JMRMD3 0142-4319 Google Scholar
M. Bothet al.,
“Second harmonic imaging of intrinsic signals in muscle fibers in situ,”
J. Biomed. Opt., 9
(5), 882
–892
(2004). http://dx.doi.org/10.1117/1.1783354 JBOPFO 1083-3668 Google Scholar
S. V. Plotnikovet al.,
“Measurement of muscle disease by quantitative second-harmonic generation imaging,”
J. Biomed Opt., 13
(4), 044018
(2008). http://dx.doi.org/10.1117/1.2967536 JBOPFO 1083-3668 Google Scholar
S. V. PlotnikovP. J. CampagnolaW. A. Mohler,
“Characterization of the myosin-based source for second-harmonic generation from muscle sarcomeres,”
Biophys. J., 90
(2), 693
–703
(2006). http://dx.doi.org/10.1529/biophysj.105.071555 BIOJAU 0006-3495 Google Scholar
D. A. Dombecket al.,
“Uniform polarity microtubule assemblies imaged in native brain tissue by second-harmonic generation microscopy,”
Proc. Natl. Acad. Sci. USA, 100
(12), 7081
–7086
(2003). http://dx.doi.org/10.1073/pnas.0731953100 1091-6490 Google Scholar
A. C. KwanD. A. DombeckW. W. Webb,
“Polarized microtubule arrays in apical dendrites and axons,”
Proc. Natl. Acad. Sci. USA, 105
(32), 11370
–11375
(2008). http://dx.doi.org/10.1073/pnas.0805199105 1091-6490 Google Scholar
S. A. Mitchellet al.,
“Second-harmonic generation optical activity of a polypeptide alpha-helix at the air/water interface,”
J. Chem. Phys., 122
(11), 114707
(2005). http://dx.doi.org/10.1063/1.1862613 JCPSA6 0021-9606 Google Scholar
Y. R. Shen, The principles of nonlinear optics, John Wiley and Sons, Hoboken, NJ
(2002). Google Scholar
R. W. Boyd, Nonlinear optics, Academic Press, Burlington, MA
(2008). Google Scholar
J. Mertz,
“Applications of second-harmonic generation microscopy,”
Handbook of biomedical nonlinear optical microscopy, Oxford University press, Oxford, UK
(2008). Google Scholar
L. MoreauxO. SandreJ. Mertz,
“Membrane imaging by second-harmonic generation microscopy,”
J. Opt. Soc. Am. B, 17
(10), 1685
–1694
(2000). http://dx.doi.org/10.1364/JOSAB.17.001685 JOBPDE 0740-3224 Google Scholar
L. Sacconiet al.,
“Cell imaging and manipulation by nonlinear optical microscopy,”
Cell Biochem. Biophys., 45
(3), 289
–302
(2006). http://dx.doi.org/10.1385/CBB:45:3 CBBIFV 1085-9195 Google Scholar
J. MertzL. Moreaux,
“Second-harmonic generation by focused excitation of inhomogeneously distributed scatterers,”
Opt. Commun., 196
(1–6), 325
–330
(2001). http://dx.doi.org/10.1016/S0030-4018(01)01403-1 OPCOB8 0030-4018 Google Scholar
I. GusachenkoG. LatourM. C. Schanne-Klein,
“Polarization-resolved second harmonic microscopy in anisotropic thick tissues,”
Opt. Express, 18
(18), 19339
–19352
(2010). http://dx.doi.org/10.1364/OE.18.019339 OPEXFF 1094-4087 Google Scholar
J. C. Mansfieldet al.,
“Collagen fiber arrangement in normal and diseased cartilage studied by polarization sensitive nonlinear microscopy,”
J. Biomed. Opt., 13
(4), 044020
(2008). http://dx.doi.org/10.1117/1.2950318 JBOPFO 1083-3668 Google Scholar
O. NadiarnykhP. J. Campagnola,
“Retention of polarization signatures in SHG microscopy of scattering tissues through optical clearing,”
Opt. Express, 17
(7), 5794
–5806
(2009). http://dx.doi.org/10.1364/OE.17.005794 OPEXFF 1094-4087 Google Scholar
P. Stolleret al.,
“Polarization-modulated second harmonic generation in collagen,”
Biophys. J., 82
(6), 3330
–3342
(2002). http://dx.doi.org/10.1016/S0006-3495(02)75673-7 BIOJAU 0006-3495 Google Scholar
X. Hanet al.,
“Second harmonic properties of tumor collagen: determining the structural relationship between reactive stroma and healthy stroma,”
Opt. Express, 16
(3), 1846
–1859
(2008). http://dx.doi.org/10.1364/OE.16.001846 OPEXFF 1094-4087 Google Scholar
R. Cicchiet al.,
“Scoring of collagen organization in healthy and diseased human dermis by multiphoton microscopy,”
J. Biophoton., 3
(1–2), 34
–43
(2010). http://dx.doi.org/10.1002/jbio.200910062 Google Scholar
M. WangK. M. ReiserA. Knoesen,
“Spectral moment invariant analysis of disorder in polarization-modulated second-harmonic-generation images obtained from collagen assemblies,”
J. Opt. Soc. Am. A Opt. Image Sci. Vis., 24
(11), 3573
–3586
(2007). http://dx.doi.org/10.1364/JOSAA.24.003573 Google Scholar
S. J. Linet al.,
“Monitoring the thermally induced structural transitions of collagen by use of second-harmonic generation microscopy,”
Opt. Lett., 30
(6), 622
–624
(2005). http://dx.doi.org/10.1364/OL.30.000622 OPLEDP 0146-9592 Google Scholar
T. Theodossiouet al.,
“Thermally induced irreversible conformational changes in collagen probed by optical second harmonic generation and laser-induced fluorescence,”
Laser. Med. Sci., 17
(1), 34
–41
(2002). http://dx.doi.org/10.1007/s10103-002-8264-7 LMSCEZ 1435-604X Google Scholar
P. Matteiniet al.,
“Photothermally-induced disordered patterns of corneal collagen revealed by SHG imaging,”
Opt. Express, 17
(6), 4868
–4878
(2009). http://dx.doi.org/10.1364/OE.17.004868 OPEXFF 1094-4087 Google Scholar
Y. Sunet al.,
“Investigating mechanisms of collagen thermal denaturation by high resolution second-harmonic generation imaging,”
Biophys. J., 91
(7), 2620
–2625
(2006). http://dx.doi.org/10.1529/biophysj.106.085902 BIOJAU 0006-3495 Google Scholar
K. M. Reiseret al.,
“Quantitative analysis of structural disorder in intervertebral disks using second harmonic generation imaging: comparison with morphometric analysis,”
J. Biomed. Opt., 12
(6), 064019
(2007). http://dx.doi.org/10.1117/1.2812631 JBOPFO 1083-3668 Google Scholar
T. Boulesteixet al.,
“Secondharmonic microscopy of unstained living cardiac myocytes: measurements of sarcomere length with 20-nm accuracy,”
Opt. Lett., 29
(17), 2031
–2033
(2004). http://dx.doi.org/10.1364/OL.29.002031 OPLEDP 0146-9592 Google Scholar
M. E. Llewellynet al.,
“Minimally invasive high-speed imaging of sarcomere contractile dynamics in mice and humans,”
Nature, 454 784
–788
(2008). http://dx.doi.org/10.1038/nature07104 NATUAS 0028-0836 Google Scholar
E. Ralstonet al.,
“Detection and imaging of non-contractile inclusions and sarcomeric anomalies in skeletal muscle by second harmonic generation combined with two-photon excited fluorescence,”
J. Struct. Biol., 162
(3), 500
–508
(2008). http://dx.doi.org/10.1016/j.jsb.2008.03.010 JSBIEM 1047-8477 Google Scholar
I. Rocha-Mendozaet al.,
“Sum frequency vibrational spectroscopy: the molecular origins of the optical second-order nonlinearity of collagen,”
Biophys. J., 93
(12), 4433
–4444
(2007). http://dx.doi.org/10.1529/biophysj.107.111047 BIOJAU 0006-3495 Google Scholar
A. Deniset-Besseauet al.,
“Measurement of the second-order hyperpolarizability of the collagen triple helix and determination of its physical origin,”
J. Phys. Chem. B, 113
(40), 13437
–13445
(2009). http://dx.doi.org/10.1021/jp9046837 JPCBFK 1520-6106 Google Scholar
A. E. Tueret al.,
“Nonlinear optical properties of type I collagen fibers studied by polarization dependent second harmonic generation microscopy,”
J. Phys. Chem. B, 115
(44), 12759
–12769
(2011). http://dx.doi.org/10.1021/jp206308k JPCBFK 1520-6106 Google Scholar
P. J. Suet al.,
“Determination of collagen nanostructure from second-order susceptibility tensor analysis,”
Biophys. J., 100
(8), 2053
–2062
(2011). http://dx.doi.org/10.1016/j.bpj.2011.02.015 BIOJAU 0006-3495 Google Scholar
V. Nucciottiet al.,
“Probing myosin structural conformation in vivo by second-harmonic generation microscopy,”
Proc. Natl. Acad. Sci. USA, 107
(17), 7763
–7768
(2010). http://dx.doi.org/10.1073/pnas.0914782107 1091-6490 Google Scholar
W. Blankenfeldtet al.,
“Crystal structures of human cardiac beta-myosin II S2-Delta provide insight into the functional role of the S2 subfragment,”
Proc. Natl. Acad. Sci. USA, 103
(47), 17713
–17717
(2006). http://dx.doi.org/10.1073/pnas.0606741103 1091-6490 Google Scholar
L. F. Chenet al.,
“Molecular modeling of averaged rigor crossbridges from tomograms of insect flight muscle,”
J. Struct. Biol., 138
(1–2), 92
–104
(2002). http://dx.doi.org/10.1016/S1047-8477(02)00013-8 JSBIEM 1047-8477 Google Scholar
|

