|
|
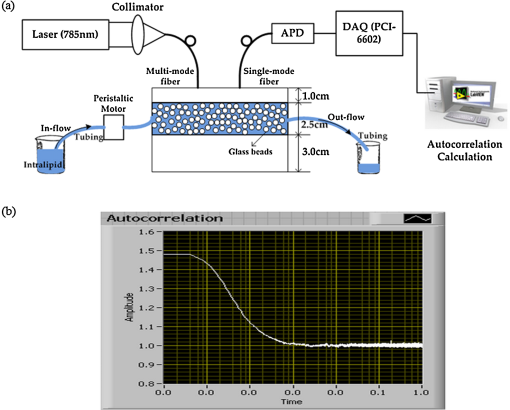
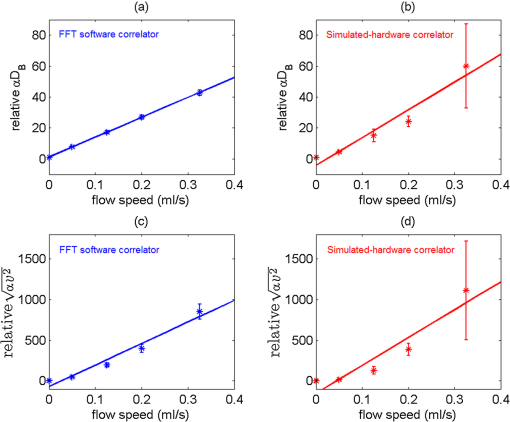
1.IntroductionNear-infrared diffuse correlation spectroscopy (DCS), also known as diffusing-wave spectroscopy (DWS), is established on the well-known spectral window in the near-infrared (NIR, 650 to 900 nm) range, wherein the relatively low biological tissue absorption enables deep penetration of light. It is an emerging technique for continuous noninvasive measurement of blood flow in biological tissues. In the last decade or so, DCS technology has been developed,1–3 extensively validated, and vigorously employed to noninvasive probe the blood flow information in deep tissue vasculature, such as brain,4–19 muscle,20–25 and breast.26,27 Compared to other blood flow measurement techniques, such as positron emission tomography (PET), single photon emission computed tomography (SPECT), and xenon-enhanced computed tomography (XeCT), DCS uses nonionizing radiation and needs no contrast agents. In contrast to dynamic susceptibility contrast magnetic resonance imaging (DSC-MRI) and arterial spin labeling MRI (ASL-MRI), it has no interference with commonly used medical devices, such as pacemaker and metal implants.28 Therefore, it has also been applied to cancer therapy monitoring29–32 and bedside monitoring in clinical settings.33 The typical setup of the DCS technique consists of a laser with along coherence length as the light source, a photon-counting avalanche photodiode (APD) or photomultiplier tube (PMT) as the detector, and a hardware autocorrelator. As one of the critical components, the autocorrelator computes the autocorrelation function of the temporal fluctuation of the light intensity, which was subject to multiple scattering events before emerging from the investigated position on the sample surface. There are many commercial correlators available, such as the ones manufactured by ALV (Langen, F. R. Germany) and by Correlators.com (Bridge-water, New Jersey). To date, most published works have used these hardware autocorrelators for autocorrelation calculations,4,5,7,13,20,25,27,32,34 although a few of them had designed a multitau software correlator for dynamic light scattering and validated it by particle size measurement.35,36 The hardware correlators utilized multitau scheme, so they could be operated at a fast sampling speed thus offered real-time computing across a wide range of lag times from several nanoseconds to hours. However, they are relatively costly and not flexible since the fixed number of bits per channel results in a fixed lag time scale. Meanwhile, the software autocorrelator mentioned earlier was capable of measuring correlation functions over a time scale of in real time,35,36 but it was not capable of recording the raw photon-count signal and therefore had limitations in terms of preprocessing of the raw photon count and post-measurement sanity checking. In this paper, we demonstrate an alternative approach of DCS analysis using a software correlator based on fast Fourier transform (FFT). It is cost-effective, flexible, and can be easily implemented with other technologies. Furthermore, the ability of recording raw photon-count signal holds the potential of signal preprocessing before autocorrelation calculation, such as filtering out the noise caused by fluctuation of the laser source. It also provides room for investigating the methods other than autocorrelation to extract flow information from raw signals. To achieve data acquisition, recording, and autocorrelation calculation, we used the graphical programming language LabVIEW (National Instruments), which is one of the most popular and powerful tools for signal acquisition and processing. The FFT, which is one of the most efficient algorithms known in the history of signal processing, was applied for autocorrelation calculation. The sampling rate of the system can reach up to and thus enables the minimum lag time of , which is significantly shorter than the decay constant (between tens to hundreds of microseconds) in DCS applications. Through comparison with a simulated hardware autocorrelator that works the same way as a hardware correlator (correlator.com) does, we evaluated the performance of the FFT-based software autocorrelator. For the purpose of validation, in-house flow phantom experiment, a human arm cuff occlusion experiment as well as a photodynamic therapy (PDT) response monitoring experiment were conducted. This paper is organized as follows. In Sec. 2, we recall the theoretical background of DCS. In Sec. 3, a detailed description of our FFT-based software autocorrelator, as well as comparison with a simulated hardware autocorrelator are presented. The experimental setup for both phantom and in vivo experiments are described in Sec. 4, followed by an interpretation of the experimental results in Sec. 5. The concluding remarks are presented in Sec. 6. 2.Theoretical Background of DCSThe biological tissue can be characterized by its optical properties, such as the absorption coefficient and the reduced scattering coefficient ’. When diffusing photons scatter from moving scatterers, they experience phase shifts and cause the speckle fluctuation at the detector side. The motion information below the tissue surface is carried in the electric field of diffuse light and can be extracted from the electric field autocorrelation function, which is defined as . It has been shown that satisfies a correlation diffusion equation, i.e.,1,3,4,37 where is the wavenumber of the light in a medium, is the fraction of photon scattering events from moving scatterers out of total scatterers, and represents the mean square displacement of the moving scatterers, and is commonly described using two different models, namely the Brownian motion and random flow model in biological tissues. The Brownian motion model considers the motion of scatterers as diffusive motion and ,38,39 where is the effective diffusion coefficient of the scatterers. Meanwhile, the random flow model assumes the random ballistic motion of scatterers and (Refs. 40 and 41), where represents the mean square velocity of the scatterers. Experimentally, the diffuse light electric field autocorrelation function is usually derived from the measured normalized intensity autocorrelation by using the Siegert relation:4,13,42 where is the detected diffusing light intensity at position and time , the angle bracket denotes an ensemble average, and here is a numerical factor related to the detector geometry, number of detected speckles, and other experimental parameters. The assumption for applying the Siegert relation to obtain the electric field autocorrelation function is that the system is ergodic, which means the time average is equal to the ensemble average. The analytic solution of the correlation diffusion equation for a point light source upon a semi-infinite medium is4,43 where , () are the distance between source (image source) and detector, respectively, in which is the source detector separation, , and represents the effective reflectance. Although physically the motion of blood cells may be considered as random flow, the Brownian motion model showed better fitting in the majority of cases, ranging from brain4,7–9,11–14,17 to muscle20,23 and tumor models.27,29,30,32 Therefore, the measurements of can be fitted to yield a blood flow index () to parameterize the relative blood flow.The BFI and were obtained by minimizing the difference between the analytical model of the autocorrelation in the reflectance geometry and the measured autocorrelation function . The optimization of the objective function was done by using Matlab (Mathwork, Inc.). The relative blood flow (rBF), which is the deviation of BFI with respect to the baseline, is reported in the unit of percent. 3.Data Acquisition and ProcessingThe DCS system consisted of a continuous-wave laser with a long coherence length () operating at 785 nm (DL785-100-S, , CrystaLaser, Reno, Nevada, USA) as the source and a photon-counting APD (SPCM-AQRH-13-FC, Perkin-Elmer, Vudreuil-Dorion, Quebec, Canada), whose output was a stream of transistor-transistor logic (TTL) pulses, as the detector. The light from the source was coupled to a multi-mode optical fiber (200-μm diameter) and contacted with a sample surface. The detecting fiber was single-mode operated at 785 nm (9-μm diameter), which was located several centimeters away from the source fiber and fed to the APD. The TTL output generated by the APD was connected to the 32-bit, eight-input channel counter/timer board with the maximum input rate of 80 MHz (PCI-6602, National Instruments). The counter/timer board was connected to a PC (CPU: Intel Core 2 Duo, RAM: 3-Gbyte) through a shielded I/O connector block for DAQ devices (SCB-68, National Instruments). 3.1.Data Acquisition PrincipleThe performance was controlled by LabVIEW (National Instruments), which is one of the most popular and powerful program tools and suitable for interactive data acquisition and signal processing. The TTL output of the detector was counted over sampling time by the counter/timer board. The PCI-6602 has a timebase of 80 MHz, which means the fastest input pulses that can be counted are 12.5 ns () apart. The PCI-6602 is the 32-bit counter and can count up to 4,294,967,295 () before it rolls over. The counter can count the events continuously and store the data in the buffer. Due to the limitation of buffer size, time resolution of anything less than 2 μs would fill up the buffer in less than 1 s. For the purpose of stable data acquisition, we conducted experiments using 2.5 μs. In the data acquisition program, we applied “queue” structure to link the “producer” loop and the “consumer” loop, which were in charge of reading photon counts and writing results to a file, respectively. By using this kind of structure, the two loops were able to work in parallel so that a faster speed can be achieved. Simultaneously, another LabVIEW program detected the latest written photon-counting file and calculated the autocorrelation function by FFT algorithm. The result was then displayed and saved to a specified folder. Running on our current system, one core of CPU was fully occupied to acquire the data, while the other core was used for the autocorrelation calculation. 3.2.Data ProcessingIn this section, the working principle of the hardware correlator board will be briefly described, based on the instruction manual of a most commonly used commercial product (Flex99R-12) from Correlator.com. The algorithm behind the hardware correlator will be simulated by the software approach, and its performance will be compared against our new FFT-based approach in a later section. 3.2.1.Simulating hardware autocorrelator boardInside the hardware autocorrelator boardThe typical hardware correlators such as the ones manufactured by ALV and Correlator.com are based on a multitau scheme, and have a multiple tier structure which contains a certain amount of registers as shown in Fig. 1. If we take the one from Correlator.com for instance, the first tier has 32 registers, and higher tiers have 16 registers each. The incoming photon count starts filling up the registers in the first tier from the left with a given delay time (typically 160 ns). When it reaches the right end, the second tier fills up from the left at a twice as slow rate, since the sum of two register values in the right end of the first tier constructs the first register value of the second tier. Likewise, the first register value of nth tier is constructed by sum of the last two register values in ()th tier, which means the registers of ’th tier is updated every . The hardware correlator can have upto 31 tiers, which means there are registers with 512 different delay times. However, registers at the 31st tier updates every , which is too long with a practical value of , so later tiers are hardly used in practice. Fig. 1The diagram of hardware autocorrelator inner structure, with several tiers of registers where the delay times are the power of two times of initial delay time . 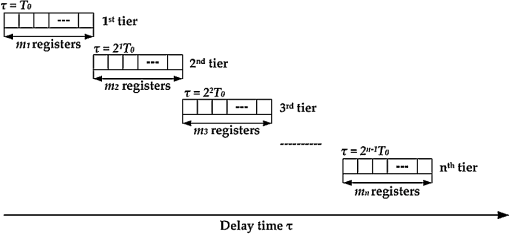 For each shift that occurs in the register, the unnormalized intensity autocorrelation coefficient for the ith register, , is calculated as the average value of , where indicates the photon count in the ith register, is the photon count at zero delay time with the same bin width as the ith register, and is the delay time between and .28 The delay time is calculated as the summation of all the bin widths on the left of the ith register. With a few hundred register channels (512 channels for a 31 tier system, for example), a delay time that ranges from hundred of nanoseconds to minutes can be achieved, greatly reducing the computational load compared to the linear autocorrelator. Software implementationThe above mentioned hardware correlator algorithm is implemented in Matlab, in order to examine its behavior with a known input signal, generated either by simulation or experiment. The number of tiers, , was given as a variable (normally set at around 10), and a cell array variable with a size of [32 for 1st tier, and afterwards] was allocated for register channels. The Matlab script initiates a loop, where the register channels in the first tier shifts to the right by one register per iteration and a new datum is read in the left-most register. When the iteration number reaches , registers in ’th tier become shifted to the right by one register, after which a new value [the sum of two register values at the end of ()’th tier] is assigned to the left-most register in ’th tier. Figure 2 shows a snapshot of the register profile in different tiers, where the register values are represented in a logarithmic scale to better visualize the wide-range of the values. Fig. 2A snapshot of the registers of simulated hardware correlator. Color represents the logarithm of the photon count in each register. Ignore the blue portion on the left where there are no registers. 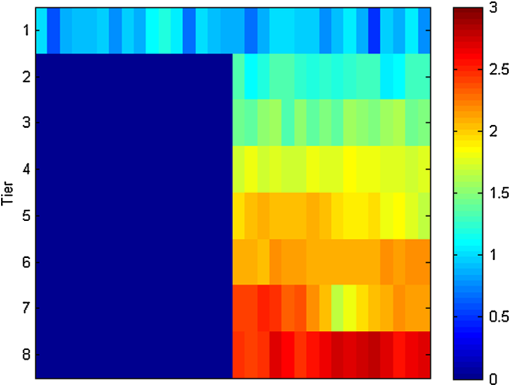 When the register fully fills up, the autocorrelation coefficient between ith register and the 0th register (with the same bin width, as described previously in the hardware correlator section) is calculated. The autocorrelation curve for whole register is calculated for each shift event in the last tier, and they are averaged over hundreds of trials before being plotted. 3.2.2.FFT-based software autocorrelatorThe unnormalized intensity autocorrelation, represented as , resembles the convolution operation, except that in the convolution calculation, the second term being multiplied has to be the time-reversal of the original function , namely . Therefore, the same autocorrelation can be obtained by convolution between two functions and . Then, by the convolution theorem, one can obtain the autocorrelation function based on the Fourier transform as follows: where and refer to forward and inverse Fourier transform, respectively, and is the Fourier transform of . Note that the last equality of Eq. (4) is also called Wiener-Khinchin theorem and real valued always results in real values of .Since the Fourier transform can be very efficiently implemented by the fast Fourier transform (FFT), one can obtain the linear autocorrelation function in a very fast and stable manner using above equation. Figure 3 shows the comparison between the two normalized intensity autocorrelation calculations, one from the multi-tau approach simulating the hardware correlator board, and the other from the FFT-based linear approach. The data used in Fig. 3(a) was from a flow phantom experiment, acquired by the NI counter board (PCI-6602) at the sampling rate of 400 kHz. For the FFT-based approach, the data size used was about , covering about 1 s. For the hardware simulating approach, the delay time was only calculated upto about 30 ms due to the small number of tiers (10 tiers were used), but it was averaged over 500 autocorrelation calculations, and the total length of data used is about the same. The FFT-based calculation always ends up showing a spike near the highest delay time, but that is due to the cyclic nature of the FFT-based result, and our visualization in Fig. 3 only shows the first half, thereby removing the unwanted peak. Both of them show a nice convergence to the value of 1 for long delay times, and they nicely overlap with each other. For the experimental data in general, we were able to observe a trend that the hardware (multitau) algorithm tends to show higher fluctuation for small delay times, whereas the FFT-based algorithm always show the smoothest behavior for small delay times due to its single-tau calculation. Fig. 3Comparison between hardware and software autocorrelation calculations. (a) Autocorrelation calculated from a typical flow phantom data. (b) Autocorrelation calculated from a simulated data. Hardware-simulating algorithm (red squares) was implemented under the assumption of a 10-tier register, averaged over 500 different autocorrelations. The sampling rate was 400 kHz. 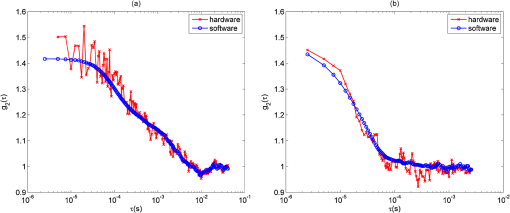 The comparison was also performed using simulated data based on a Markov chain with a Gaussian noise, and the result was always overlapping unless the average count value of the data was too low. When the average was low, we were able to regain the equivalence between the two methods by binning the data, thereby increasing the average photon count value. Typical autocorrelation curves for simulated data are shown in Fig. 3(b). 4.Experiment4.1.In-House Flow Phantom ExperimentPhantom, which is the tissue-simulating object to mimic the properties of human or animal tissues, has played an important role in the evolvement of diagnostic systems, and most physical therapeutic interventions. It can be used for the purposes of initial testing of system design, optimizing signal to noise ratio (SNR) in existing system, and so on.44 In order to validate and assess the ability of our system, a flow phantom was built as shown in Fig. 4. Fig. 4The in-house silicon flow phantom, in which an acrylic cylindrical tube was embedded to mimic the blood vessel. The tube was filled up with glass beads with a diameter of 3 mm in order to make random flow directions.  The phantom making procedure can be found elsewhere.45 Briefly, RTV 12A was the base compound, RTV 12C (Momentive Performance Materials) was the curing agent, while carbon black and were mixed to adjust the absorption coefficient and scattering coefficient, respectively. The optical properties of the solid flow phantom were and (measured by OxiplexTS, ISSInc, at 830 nm), which satisfied the criterion, and the photon diffusion equation remains valid. The schematic of the DCS experimental setup is shown in Fig. 5. The Lipofundin N 20% (B.BraunMelsungen AG, Germany) with a concentration of 0.6% was pumped through the cylindrical tube, with flow speeds of , , , , and . The source-detector pair was centered over the solid phantom surface at a distance of 1 cm from the flow tube surface. Reflection geometry was adopted in which incident light was injected into the phantom by the source fiber and detected 3.0 cm away along with the cylindrical tube direction. 4.2.In Vivo Cuff Occlusion Experiment on a Human ArmAfter the flow phantom experiment, we conducted the validation study on a human subject. The in vivo cuff occlusion experiment was done on the arm of a 28 year-old healthy male subject. In order to vary the blood flow speed, a cuff on the subject’s upper arm was constricted for 15 s for temporary arterial occlusion. The source-detector separation was 1.5 cm and the probes were located on the forearm. The cuff inflation pressure was 200 mmHg. 4.3.Photodynamic Therapy Response MonitoringBesides the flow phantom and in vivo human arm cuff occlusion experiments, we also applied our instrument to a lab-based PDT experiment for evaluation. Since the antivascular effects of PDT is a key indicator of tissue response to treatment,29 we aim to provide instantaneous hemodynamic feedback on treatment response. The in vivo PDT experiment was approved by the Institutional Animal Care and Use Committee of Singapore Health Services Pte Ltd and carried out at the National Cancer Centre Singapore. A Balb/c mouse bearing xenograft tumors on the flanks was used as an animal model. The mouse received chlorin e6 (Ce6) as the photosensitizer at a dose of . Approximately 4 h after injection, the tumors were irradiated with laser light. The irradiation lasted 2450 s, consisting of alternating 250-s light exposures and 300-s dark intervals. The treatment light for PDT was delivered by a 665-nm medical-grade laser (Biolitec, Germany). The light dose used was , delivered at a rate of via an optical fiber. The treatment light was expanded to a 2.5-cm diameter on the tumor surface. Our DCS measurement was carried out before and immediately after each exposure, as well as at 25 and 50 min after the last treatment. Source-detector separation was 1 cm, which fitted the size of the tumors. 5.Results and Discussion5.1.In-House Flow Phantom ExperimentFigure 6 shows the normalized intensity autocorrelation functions in a semilogarithm plot with varying flow speed. It can be observed that the normalized intensity autocorrelation function showed an initial constant plateau, but decayed exponentially with increasing delay time. As speed increased, the decay rate of the autocorrelation curve increased. If we recall the definition of autocorrelation, the finite data length will always cause the copy of the data shift out of the data window, thus eventually the autocorrelation function will go down to zero naturally. However, by employing an FFT, one can actually get the cyclic autocorrelation, thus it avoids the edge effect caused by data finiteness and offers a faster calculating speed. Ideally, the zero flow () was not supposed to show any decay, but we observed a decay that is mainly attributed to the intrinsic fluctuation of the laser source and the room temperature Brownian motion of the Lipofund in remaining in the tubing. The autocorrelation function calculating speed was less than 20 milliseconds for 800,000 data points with the type of double-precision integer, which is faster than the data writing speed (new file generating speed) and enables the display of the autocorrelation curve in almost real-time. We note from the autocorrelation curves, that increasing the flow causes the plateau region of the curves to be shorter and makes it difficult to determine the value. Therefore, it might cause inaccuracy in measuring high flow, but one can obtain stable plateaus for most of the relevant flow ranges in vivo. Fig. 6Autocorrelation curves of the phantom with varied speed of flow (, , , , and ) as a function of delay time, . 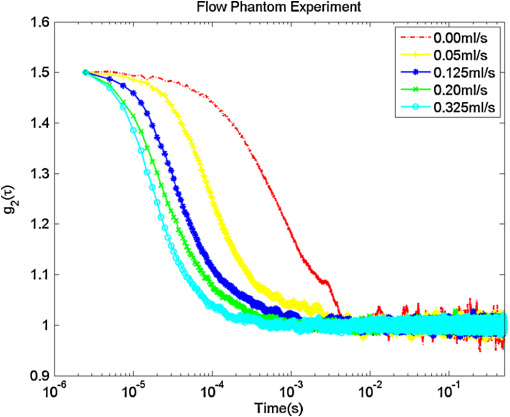 Since FFT-based autocorrelation calculation provided smoother starting and ending plateaus, it was obviously able to improve curve fitting. For better comparison between the Brownian motion and random flow model, we performed curve fitting by using both models. The Levenberg-Marquardt algorithm was applied in Matlab (Mathwork, Inc., nlinfit function). As indicated by Fig. 7, which was the autocorrelation function of the flow with speed of , the Brownian motion model fit the experimental data better than the random flow model did. This result also suggested that our self-designed phantom is able to mimic the capillary flow of the human body. Therefore, we conducted curve fitting by using the Brownian motion model, and the blood flow index () was obtained. The fitting result in general depends highly on the methods of data sampling. In order to obtain better fitting with a uniform weightage in the logarithmic time scale, we sampled the entire autocorrelation function equally on 2-base logarithm scale as shown in Fig. 7. This subsampling helps with faster fitting speed without compromising its accuracy. Fig. 7Comparison between Brownian motion and the random flow model. The autocorrelation function was calculated from the flow phantom data with a speed of . The entire autocorrelation data was sampled and shown as dots. 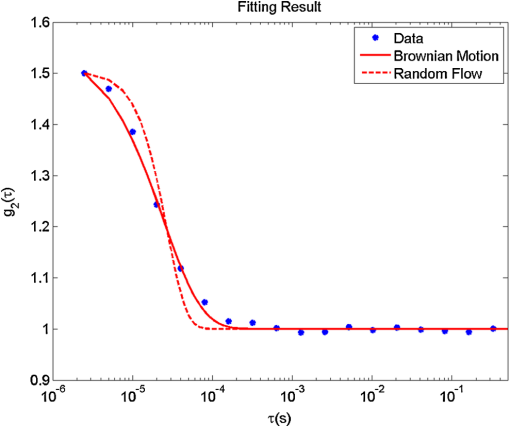 In order to compare the goodness of fitting of the FFT-based software autocorrelator with that of the simulated hardware autocorrelator, we calculated a 95% confidence interval of fitted parameters by using an nlparci function in Matlab (Mathwork, Inc.,). As shown in Fig. 8, by using a speed of as a base, relative and with their standard deviations at different flow speeds were calculated in both software and hardware cases. It can be found that in either the Brownian motion or random flow model, the standard deviations of the fitted parameter in FFT-based software autocorrelator were always smaller than in the hardware one. Concurrently, in the same autocorrelator, the parameter fitted for the Brownian motion had a smaller standard deviation than that for the random flow model and it also can be observed from individual fitting as shown in Fig. 7. Moreover, we performed a linear regression of the relative and . It showed higher linearity to flow speed in the software autocorrelator case than in the hardware one. In addition, as mentioned previously, the autocorrelation calculating speed is faster than the data writing speed, our instrument holds the potential to make full use of this time to accomplish data fitting and provide the rBF values in real-time. 5.2.In Vivo Human Arm Cuff Occlusion ExperimentFigure 9(a) shows the normalized intensity autocorrelation function of three stages of the in vivo cuff occlusion experiment, namely baseline, cuff inflation, and cuff deflation. The baseline curve was averaged over the first 15 s, the inflation curve was averaged over the 15th to 35th seconds, while the deflation curve was the average of only the 35th to 45th seconds. The decay rate of shows significant change. Figure 9(b) reveals rBF, which was obtained by fitting to the solution of the photon diffusion correlation equation. For the first 15 s, the blood flow was constant as no constriction was applied. Once the constriction was applied to the cuff, the blood flow dropped down sharply and when constriction was released, the blood flow immediately showed an overshoot followed by a slow decrease to the baseline due to homeostasis. Fig. 9(a) Autocorrelation functions of cuff occlusion stages, namely baseline (blue solid line), cuff inflation (red dash-dot line), and cuff deflation (green dashed line). (b) Representative time response of relative blood flow (rBF) during cuff occlusion experiment, including baseline recording, cuff inflation (cuff occlusion period on the figure), and cuff deflation stages. 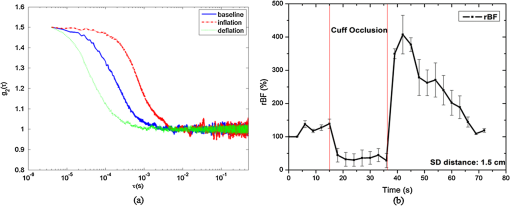 5.3.PDT Monitoring ExperimentWe plotted the DCS monitoring result during the PDT treatment in Fig. 10. The color bars in the figure represent PDT light intervals. Fig. 10The time behavior of relative blood flow (rBF) before, during, and after PDT treatment. The color bars represent the light exposures during treatment; there was no data recorded during light exposure intervals. 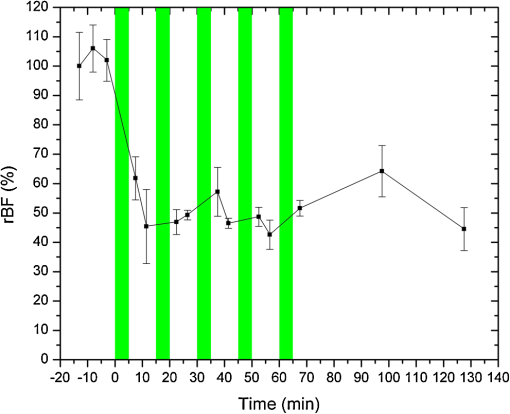 The mean tumor rBF decreased by immediately after the whole PDT, and decreased to of the baseline 60 min after treatment. During each PDT dark interval, blood flow changes showed minor fluctuations. They indicate impermanent vessel occlusion during PDT light intervals. These temporary vessel occlusions can be reversible, and it allows flow recovery during the dark intervals. A similar trend was observed using laser Doppler measurements, although different animal models were used in each case.46 However, the results after 60 min suggest that permanent vessel occlusion had occurred due to PDT. 6.ConclusionIn this paper, we have demonstrated an implementation of DCS system with an FFT-based software autocorrelator. The operation of the system was controlled by LabVIEW. The software autocorrelator has undergone the validation and assessment by an in-house flow phantom experiment, in vivo cuff occlusion experiment on a human arm, as well as a PDT response monitoring experiment. It is easy to operate and relatively cost-effective. Besides, though the data sampling speed is moderate, the minimum lag time is much shorter than the decay constant, thus the extraction of the desired parameter is still valid. Furthermore, smoother starting and ending plateaus improve the accuracy in data fitting, and hence in the blood flow index. In addition, the system still holds the potential of being a real-time flow indicator and can be used for future DCS systems in research and clinical settings. AcknowledgmentsThis work is supported by the Singapore Ministry of Education under the Academic Research Fund Tier1 Grant RG37/07 and partially supported by a SingHealth Foundation Grant (SHF/FG385P/2008). The PDT experiment was performed in collaboration with the National Cancer Centre Singapore. We thank Dr. Hamid Dehghani for useful discussions, and Mr. Bobby Chow and Mr. Peng Zu for helpful technical assistance. We also thank Ms. Hui Jin Toh and Mr. Chuan-Sia Tee of the National Cancer Centre Singapore for assistance with the PDT experiments. Support from Ms. Melda and Dr. Yongjin are also gratefully acknowledged. ReferencesD. A. BoasL. E. CampbellA. G. Yodh,
“Scattering and imaging with diffusing temporal field correlations,”
Phys. Rev. Lett., 75
(9), 1855
–1858
(1995). http://dx.doi.org/10.1103/PhysRevLett.75.1855 PRLTAO 0031-9007 Google Scholar
D. A. Boaset al.,
“Diffusion of temporal field correlation with selected applications,”
Biophys. J., 70
(2), WP306
–WP306
(1996). BIOJAU 0006-3495 Google Scholar
D. A. BoasA. G. Yodh,
“Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,”
J. Opt. Soc. Am. A, 14
(1), 192
–215
(1997). http://dx.doi.org/10.1364/JOSAA.14.000192 JOAOD6 0740-3232 Google Scholar
C. Cheunget al.,
“In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies,”
Phys. Med. Biol., 46
(8), 2053
–2065
(2001). http://dx.doi.org/10.1088/0031-9155/46/8/302 PHMBA7 0031-9155 Google Scholar
J. P. Culveret al.,
“Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia,”
J. Cereb. Blood Flow Metab., 23
(8), 911
–924
(2003). JCBMDN 0271-678X Google Scholar
J. P. Culveret al.,
“Diffuse optical measurement of hemoglobin and cerebral blood flow in rat brain during hypercapnia, hypoxia and cardiac arrest,”
Adv. Exp. Med. Biol., 510 293
–297
(2003). http://dx.doi.org/10.1007/978-1-4615-0205-0 AEMBAP 0065-2598 Google Scholar
T. Durduranet al.,
“Diffuse optical measurement of blood flow, bloodoxygenation, and metabolism in a human brain during sensorimotorcortex activation,”
Opt. Lett., 29
(15), 1766
–1768
(2004). http://dx.doi.org/10.1364/OL.29.001766 OPLEDP 0146-9592 Google Scholar
J. Liet al.,
“Noninvasive detection of functional brain activity with near-infrared diffusing-wave spectroscopy,”
J. Biomed. Opt., 10
(4), 044002
(2005). http://dx.doi.org/10.1117/1.2007987 JBOPFO 1083-3668 Google Scholar
C. Zhouet al.,
“Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,”
Opt. Express, 14
(3), 1125
–1144
(2006). http://dx.doi.org/10.1364/OE.14.001125 OPEXFF 1094-4087 Google Scholar
M. N. Kimet al.,
“Validation of diffuse correlation spectroscopy against xenon CTCBF in humans after traumatic brain injury or subarachnoid hemorrhage,”
in Neurocritical Care Society Annual Meeting,
(2008). Google Scholar
J. Liet al.,
“Transient functional blood flow change in the human brain measured noninvasively by diffusing-wave spectroscopy,”
Opt. Lett., 33
(19), 2233
–2235
(2008). http://dx.doi.org/10.1364/OL.33.002233 OPLEDP 0146-9592 Google Scholar
E. M. Buckleyet al.,
“Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound,”
Opt. Express, 17
(15), 12571
–12581
(2009). http://dx.doi.org/10.1364/OE.17.012571 OPEXFF 1094-4087 Google Scholar
T. Durduranet al.,
“Transcranial optical monitoring of cerebrovascular hemodynamics in acute stroke patients,”
Opt. Express, 17
(5), 3884
–3902
(2009). http://dx.doi.org/10.1364/OE.17.003884 OPEXFF 1094-4087 Google Scholar
C. Zhouet al.,
“Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury,”
J. Biomed. Opt., 14
(3), 034015
(2009). http://dx.doi.org/10.1117/1.3146814 JBOPFO 1083-3668 Google Scholar
S. A. CarpG. P. DaiD. A. Boas,
“Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling MRI; towards MRI-optical continuous cerebral metabolic monitoring,”
Biomed. Opt. Express, 1
(2), 553
–565
(2010). http://dx.doi.org/10.1364/BOE.1.000553 BOEICL 2156-7085 Google Scholar
M. Kimet al.,
“Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,”
Neurocrit. Care, 12
(2), 173
–180
(2010). http://dx.doi.org/10.1007/s12028-009-9305-x NCEACB 1541-6933 Google Scholar
N. Roche-Labarbeet al.,
“Noninvasive optical measures of CBV, StO(2), CBF index, and rCMRO(2) in human premature neonates’ brains in the first six weeks of life,”
Human Brain Mapp., 31
(3), 341
–352
(2010). http://dx.doi.org/10.1002/hbm.v31:3 HBRME7 1065-9471 Google Scholar
P. Ziraket al.,
“Effects of acetazolamide on the micro- and macro-vascular cerebral hemodynamics: a diffuse optical and transcranial doppler ultrasound study,”
Biomed. Opt. Express, 1
(5), 1443
–1459
(2010). http://dx.doi.org/10.1364/BOE.1.001443 BOEICL 2156-7085 Google Scholar
Y. Shanget al.,
“Diffuse optical monitoring of repeated cerebral ischemia in mice,”
Opt. Express, 19
(21), 20301
–20315
(2011). http://dx.doi.org/10.1364/OE.19.020301 OPEXFF 1094-4087 Google Scholar
G. Yuet al.,
“Time-dependent blood flow and oxygenation in human skeletal muscles measured with noninvasive near-infrared diffuse optical spectroscopies,”
J. Biomed. Opt., 10
(2), 024027
(2005). http://dx.doi.org/10.1117/1.1884603 JBOPFO 1083-3668 Google Scholar
G. Yuet al.,
“Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI,”
Opt. Express, 15
(3), 1064
–1075
(2007). http://dx.doi.org/10.1364/OE.15.001064 OPEXFF 1094-4087 Google Scholar
M. Belauet al.,
“Noninvasive observation of skeletal muscle contraction using near-infrared time-resolved reflectance and diffusing-wave spectroscopy,”
J. Biomed. Opt., 15
(5), 057007
(2010). http://dx.doi.org/10.1117/1.3503398 JBOPFO 1083-3668 Google Scholar
Y. ShangT. B. SymonsT. Durduran,
“Effects of muscle fiber motion on diffuse correlation spectroscopy blood flow measurements during exercise,”
Biomed. Opt. Express, 1
(2), 500
–511
(2010). http://dx.doi.org/10.1364/BOE.1.000500 BOEICL 2156-7085 Google Scholar
G. Yuet al.,
“Intraoperative evaluation of revascularization effect on ischemic muscle hemodynamics using near-infrared diffuse optical spectroscopies,”
J. Biomed. Opt., 16
(2), 027004
(2011). http://dx.doi.org/10.1117/1.3533320 JBOPFO 1083-3668 Google Scholar
N. Munket al.,
“Noninvasively measuring the hemodynamic effects of massage on skeletal muscle: a novel hybrid near-infrared diffuse optical instrument,”
J. Bodywork Movement Therap., 16
(1), 22
–28
(2012). http://dx.doi.org/10.1016/j.jbmt.2011.01.018 Google Scholar
T. Durduranet al.,
“Diffuse optical measurement of blood flow in breast tumors,”
Opt. Lett., 30
(21), 2915
–2917
(2005). http://dx.doi.org/10.1364/OL.30.002915 OPLEDP 0146-9592 Google Scholar
C. Zhouet al.,
“Diffuse optical monitoring of blood flow and oxygenation in human breast cancer during early stages of neoadjuvant chemotherapy,”
J. Biomed. Opt., 12
(5), 051903
(2007). http://dx.doi.org/10.1117/1.2798595 JBOPFO 1083-3668 Google Scholar
D. A. BoasC. PitrisN. Ramanujam, Handbook of Biomedical Optics, CRC Press, Boca Raton
(2011). Google Scholar
G. Yuet al.,
“Noninvasive monitoring of murine tumor blood flow during and after photodynamic therapy provides early assessment of therapeutic efficacy,”
Clin. Cancer Res., 11
(9), 3543
–3552
(2005). http://dx.doi.org/10.1158/1078-0432.CCR-04-2582 CCREF4 1078-0432 Google Scholar
U. Sunaret al.,
“Noninvasive diffuse optical measurement of blood flow and blood oxygenation for monitoring radiation therapy in patients with head and neck tumors: a pilot study,”
J. Biomed. Opt., 11
(6), 064021
(2006). http://dx.doi.org/10.1117/1.2397548 JBOPFO 1083-3668 Google Scholar
G. Yuet al.,
“Real-time in situ monitoring of human prostate photodynamic therapy with diffuse light,”
Photochem. Photobiol., 82
(5), 1279
–1284
(2006). http://dx.doi.org/10.1562/2005-10-19-RA-721 PHCBAP 0031-8655 Google Scholar
U. Sunaret al.,
“Hemodynamic responses to antivascular therapy and ionizing radiation assessed by diffuse optical spectroscopies,”
Opt. Express, 15
(23), 15507
–15516
(2007). http://dx.doi.org/10.1364/OE.15.015507 OPEXFF 1094-4087 Google Scholar
T. Durduran,
“Diffuse optical monitors for bed-side monitoring of cerebral hemodynamics at the neuro-intensive care unit,”
in IEEE Leos Annual Meeting Conf. Proc.,
270
–271
(2009). Google Scholar
Y. Shanget al.,
“Portable optical tissue flow oximeter based on diffuse correlation spectroscopy,”
Opt. Lett., 34
(22), 3556
–3558
(2009). http://dx.doi.org/10.1364/OL.34.003556 OPLEDP 0146-9592 Google Scholar
D. MagattiF. Ferri,
“Fast multi-tau real-time software correlator for dynamic light scattering,”
Appl. Opt., 40
(24), 4011
–4021
(2001). http://dx.doi.org/10.1364/AO.40.004011 APOPAI 0003-6935 Google Scholar
D. MagattiF. Ferri,
“25 ns software correlator for photon and fluorescence correlation spectroscopy,”
Rev. Sci. Instrum., 74
(2), 1135
–1144
(2003). http://dx.doi.org/10.1063/1.1525876 RSINAK 0034-6748 Google Scholar
M. Heckmeieret al.,
“Imaging of dynamic heterogeneities in multiple-scattering media,”
J. Opt. Soc. Am. A, 14
(1), 185
–191
(1997). http://dx.doi.org/10.1364/JOSAA.14.000185 JOAOD6 0740-3232 Google Scholar
G. MaretP. E. Wolf,
“Multiple light scattering from disordered media. The effect of brownian motion of scatterers,”
Zeitschrift für Physik B Condens. Matter, 65
(4), 409
–413
(1987). Google Scholar
D. J. Pineet al.,
“Diffusing wave spectroscopy,”
Phys. Rev. Lett., 60
(12), 1134
(1988). http://dx.doi.org/10.1103/PhysRevLett.60.1134 PRLTAO 0031-9007 Google Scholar
R. NossalS. H. ChenC. C. Lai,
“Use of laser scattering for quantitative determinations of bacterial motility,”
Opt. Commun., 4
(1), 35
–39
(1971). http://dx.doi.org/10.1016/0030-4018(71)90122-2 OPCOB8 0030-4018 Google Scholar
R. BonnerR. Nossal,
“Model for laser Doppler measurements of blood flow in tissue,”
Appl. Opt., 20
(12), 2097
–2107
(1981). http://dx.doi.org/10.1364/AO.20.002097 APOPAI 0003-6935 Google Scholar
T. DorfmüllerB. J. BerneR. Pecora, Dynamic Light Scattering, John Wiley and Sons Ltd., Baffins Lane
(1976). Google Scholar
D. A. Boas,
“Diffuse photon probes of structural and dynamical properties of turbid media theory and biomedical applications,”
(1996). Google Scholar
B. W. PogueM. S. Patterson,
“Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry,”
J. Biomed. Opt., 11
(4), 041102
(2006). http://dx.doi.org/10.1117/1.2335429 JBOPFO 1083-3668 Google Scholar
R. Choe,
“Diffuse optical tomography and spectroscopy of breast cancer and fetal brain,”
(2005). Google Scholar
B. W. Pogueet al.,
“Analysis of the heterogeneity of pO2 dynamics during photodynamic therapy with verteporfin,”
Photochem. Photobiol., 74
(5), 700
–706
(2001). http://dx.doi.org/10.1562/0031-8655(2001)074<0700:AOTHOP>2.0.CO;2 PHCBAP 0031-8655 Google Scholar
|