|
|
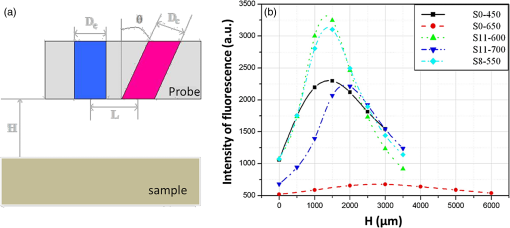
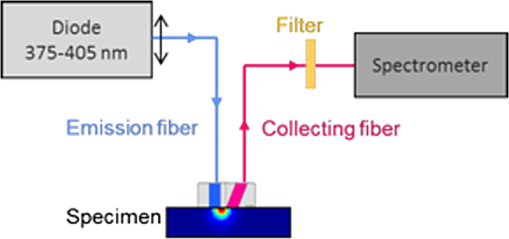
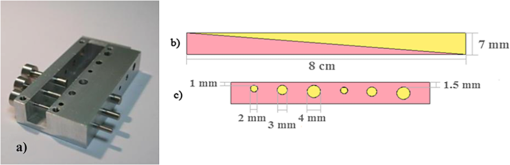
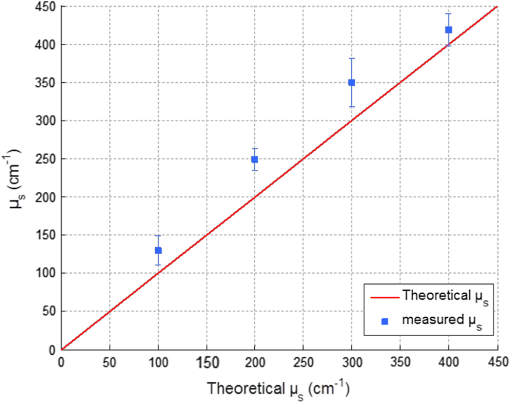
1.IntroductionIn biomedical applications, the interest in novel optical approaches has grown and consequently so has the use of optically calibrated phantoms. A phantom is a tool that provides known or determined parameters that can be used to characterize and/or calibrate experimental devices and to understand the biological data. Optical phantoms are widely used for developing, testing and optimizing optical instrumentation for fluorescence, diffuse reflectance and Raman spectroscopy.1,2 Optical phantoms are important to link experimental results to theoretical models. Depending on their use, various optical phantoms exist in varying consistencies, shapes, employed components, optical ranges, etc. When defining a new phantom, the first step is to clearly identify its desired functionalities. Among these functionalities is the stability over time to get optical references that allow calibration of optical systems or comparison of different setups. Most of the time, these stable phantoms are solid and made out of polymers3,4 and do not typically model the anatomic shapes and chemical composition of tissues. Liquid or gelatine phantoms can be an alternative when long-term stability is not required. To imitate biological tissues, different layers are often required, such as mimicking tumors in healthy tissues. In the case of multi-layer phantoms, several options are possible, such as successive gel layers5 or one solid layer with a liquid layer above.6 Other characteristics of phantoms are their geometry and optical properties, the latter being mainly defined through the refractive index and scattering and absorption coefficients. The most common tissue-like phantom scatterers are intralipids,7,8 used generally in liquid phantoms. In the case of gelatine or solid phantoms, microspheres like polystyrene beads can be used instead.5,6 Several types of microsphere compositions covering the anisotropy scattering range of tissues and different diameters are available as SiO2-304 nm (anisotropy coefficient and scattering cross-section ), SiO2-585 nm ( and ) and Melamine MF 410 ( and ). A commonly used absorber is ink.7,8 Sometimes fluorescence characteristics are also required.3,7–9 A phantom can include several types of fluorophores that might be either organic fluorophores, such as Rhodamine 6G6,8 or Protoporphyrin IX,7 or fluorescent particles, such as coloured resins,3 quantum dots9 or endogenous fluorophores.10 Due to their hydrophobic property, solid phantoms cannot contain organic or biological fluorophores. In this paper, new gelatin phantoms are presented that mimic brain tissue properties. These phantoms should help to define and optimize a new prototype fiber optic instrument. This instrument is dedicated for surgical treatment of brain tumors by discriminating healthy from tumorous tissues through endogenous fluorescent measurements. Two geometries are used-bilayer phantoms and phantoms with inclusions. The first models tumorous and healthy tissue layers, whereas the latter mimics cylindrical tumors in a healthy environment. It is our intention to use the phantoms to simulate the following situation: a cancerous layer of various thicknesses is placed in front of a noncancerous layer or vice versa. In the first case, it will allow for identification of the minimum thickness of cancerous tissue necessary to be detectable with the probe. In the latter case the maximum layer thickness of noncancerous tissue would be estimated to still allow for detecting the cancerous layer behind. In this first study, different fluorophores are used for the two types of tissues. This is the easiest way to know where the detected photon originates and to get a first-order estimate of detectable configurations. In a future extension of the study, different fluorophores will be used with different concentrations in each layer to analyze the impact on the detectability of cancerous tissue. The optical parameters of brain tissue were taken from literature.11,12 Gelatine phantoms are well suited to reach these different geometries. In addition, organic chromophores that emit in the range of endogenous fluorophores were chosen.13 We also took into account the wavelength dependence of these phantoms for fluorescence study. Our phantoms have the specificity to be excited at 405 nm, an interesting excitation wavelength for endogenous fluorophores, much like nicotinamide adenine dinucleotide (NADH), flavins, lipopigments, porphyrins and chlorins.14 Most of the time optical commercial phantoms are calibrated to be excited at wavelengths longer than 450 nm. For an endogenous fluorescence study of cerebral tissues, 405 nm is an interesting choice of excitation wavelength. Our phantoms are also used to validate physical models and a Monte Carlo simulation. 2.Materials and Methods2.1.Experimental SetupThe light source is a 405-nm-pulsed-laser (PicoQuant, Berlin, Germany); its frequency is up to 40 MHz with a pulse width of less than 100 ps and a maximum power of 1 mW. A home-made 2-fiber-probe has been used [Fig 1(a)]. The fibers used are step index multimode Si-fibers. More details of this probe are described in Ref. 15. The excitation and the fluorescence collection fibers have a 200 and a 365 µm core-diameter, respectively. Several probe configurations were previously tested by our group15 for varied fiber distance and inclination of the collection fiber relative to the excitation fiber (the distance of the probe relative to the phantom/tissue was also taken into account) to estimate the best fluorescence collection efficiency. This was done through various ways: Geometrical excitation/collection cone recovery of both fibers, measurements and simulations. The denomination of the fiber is , where is in degree and in micrometer. As shown in Fig 1(b), the S11-600 probe was identified as collecting the highest fluorescence intensity and so was chosen for the present work. The best fluorescence collection is obtained with an around 11 deg tilted fiber, the fiber distance being around 600 µm. The optimal distance between the tissue and the probe, allowing for detection of the maximal intensity, is 1.5 mm and the spatial resolution of this probe is about 500 µm measured by using a test target (R3LS1P, Thorlabs, France). The collected light is filtered by a high-pass filter (M54-650, Edmund Optics, Barrington NJ, USA) before being analyzed by a spectrometer (QE6500, Ocean Optics, Dunedin FL). Figure 2 shows a diagram of the experimental device. The setup was similar to the one used in our previous work.15 2.2.Phantoms—Optical PropertiesIn the present work, the purpose of the phantoms is to characterize a probe for auto-fluorescence brain tissue measurements. Thus, the different components of the phantoms should offer brain tissue optical parameters. 2.2.1.Refractive indexGelatine from porcine skin (A-type, G1890, Sigma-Aldrich, Saint Quentin Fallavier, France) was used. It is well suited to our phantoms because it produces very little fluorescence when excited at 405 nm. For all gels, a mixture of water and 10% gelatine powder was employed. Measurements of solid gelatine made by our team,16 basing on Snell’s law, yielded a refractive index of . This index corresponds to the refraction parameter of biological tissues.17 2.2.2.AbsorptionIndia ink diluted in water (no. 17, Pelikan, Hannover, Germany) was used. Light transmission measurements have been made for several ink concentrations to determine the absorption coefficient . The samples were placed in quartz cuvettes and measured with an UVICON 923 spectrometer (Bio-Tek Kontron Instrument, Milan, Italy). Transmission through a reference (water placed in the same cuvette) was also measured. The absorption coefficient is linear with the ink concentration (vol./vol.) . A linear fit provided the calibration equation that was used to obtain the defined . The absorption coefficient of gel and spheres was measured and it is equal to . This absorption coefficient was taken into account when we calculate the concentration of ink for a wanted absorption coefficient of our phantom. By this . In order to correspond to optical absorption coefficients for brain tissues in literature,11,12 the absorption coefficient was varied from 3 to . Note that after measurements the absorption due to the fluorophores was not taken into account: from the fluorophores was always less than and thus negligible compared to the used ink absorption coefficients. Compared measurements between two sets of diluted ink in water were made. One set (A) was diluted less than 24 h ago and the other one (B) was aged for about three months. The absorption coefficient differed by around 15%, with the recent dilution seemingly more absorbent. Therefore to be completely sure that ink dilutions are correct, we choose to always prepare the ink dilutions less than 48 h before casting the phantoms. 2.2.3.ScatteringMicrospheres (micro-particles GmbH, Berlin, Germany) have been used for finding the scattering properties of phantoms. For our manipulation we used microspheres of Melamine MF delivered in 10% solution with these manufactured data (410 nm of diameter, with a density of for each sphere, the refractive index is 1.68) dispersed homogeneously in water. By varying the concentration of spheres, we made suspensions with the desired scattering properties. The dependence of the scattering cross-section and the anisotropy on the wavelength according to the parameters of spheres is established thanks to the Mie theory. They were computed using Mie theory (FdMie program, based on Refs. 1819.20.21. to 22). For a low concentration of scatterers (independent scattering approximation), the power scattered by the unit volume is obtained simply by adding the power scattered by each particle. For independent scatterers, we can assume that the phantom-scattering coefficient is a linear function of the microsphere concentration, calculated using Eq. (1), where is the density.21,23–26 We can use this approximation because the density of our samples is lower than 0.01 (i.e., the volume occupied by scattering particles is less than 1% of the total volume).27 It is defined that the scattering cross-section and thus the anisotropy are related to the size of the particles.28–30 It is possible to calculate the coefficient , following the Mie theory (FdMie program)15,19 for scattering spheres, knowing their diameter as well as their refractive index. From the literature in Refs. 11 and 12, we know that brain tissue is in the range from 100 to and the anisotropy varies from 0.75 to 0.95. MF-410 allows for obtaining the scattering coefficient in the interval of cerebral tissues. For a concentration of and a density of and using a computed Mie theories (Fd Mie program) was calculated to be and using a 405-nm excitation wavelength. 2.2.4.Optical properties measurementsA single integrating sphere (IS200 Thorlabs) was used to measure reflection and transmission of 1-mm-thick phantom samples. Another device with diaphragms allows the measurement of the collimated transmission of the same sample. The samples do not contain any fluorophore. The measured quantities are analyzed with the program inverse adding-doubling (IAD) (available at Ref. 19) to retrieve the optical coefficients , and . The anisotropy of scattering is found to be , close to the expected value of 0.87. The measured absorption coefficients also correspond to the expected ones if an offset of is applied; this might be due to the gelatine and micro-particles absorption. The scattering coefficient is also overestimated by less than 10% compared to the expected value, which is considered acceptable. In conclusion, the phantoms we built were validated. 2.2.5.FluorescenceEither Rhodamine B (RhB) (Sigma Aldrich Fluka, Saint-Quentin Fallavier, France) or Fluorescein (FITC) acide libre, (Sigma Aldrich Fluka, Saint-Quentin Fallavier, France), each diluted in water, are also added to provide fluorescence in the phantom. Even if it is far off their absorption maximum, both absorb light at 405 nm. Moreover, RhB emits light at around 580 nm, similar to Lipopigments, and FITC emission is around 515 nm, right in the Flavin range. A typical fluorophore concentration used for our phantoms is . The absorption spectra of these molecules were measured by an absorption spectrometer (UVICON 932, Bio-Tek, Kontron Instrument, Milan, Italy). The values of absorption coefficients of FITC and RhB at a 405-nm excitation wavelength, for a concentration of are 0.13 and , respectively. These are very weak compared with absorption coefficients of cerebral tissues. Thus it is not necessary to make an additional correction to the definition of the ink concentration of the phantoms. 2.2.6.Phantom fabrication protocolCorresponding to the desired optical parameters, the concentrations of each phantom component are calculated according to the above-mentioned methods. Water and ink are mixed before the gelatine powder is added. This mixture is then heated in a 90°C hot water bath. While the powder dissolves, the solution is gently agitated to avoid air bubbles. Finally, fluorophores and scatterers are added and the mixture is placed in an ultrasound bath for a few minutes to obtain a homogeneous solution. While still liquid, the gel is poured into a mold, which is subsequently placed in a refrigerator for 1.5 h, where the jellification is faster and evaporation is reduced. In order to minimize drying effects that could influence optical and geometrical properties, the phantom is not used for more than 1 h in a temperature-controlled room at about 17°C. 2.3.Phantoms—Geometrical Possibilities2.3.1.Mono-and bilayer phantomsA triangular-shaped mold (, see Fig. 3) can provide monolayer phantoms with a continued variation of thicknesses. In addition, similar to those from Pfefer,31 bilayer phantoms can be produced using two triangular phantoms by putting one onto the other to obtain a rectangular shaped 2-layer phantom [Fig. 4(b)]. Each of the layers—labelled with either Fluorescein or Rhodamine B—has its own specific set of optical parameters. A very thin (13 µm thickness) nonfluorescent film is placed in between the two layers to prevent fluorophores from migrating into the other layer. Due to the flexible texture of the gelatine phantoms, an almost perfect interface is obtained, in most cases without any air bubbles. In contrast to Pfefer’s phantoms having only two determined thicknesses (0.3 and 0.6 mm), in our case any thickness of the upper layer can be addressed as it depends only on the probe position. 2.3.2.Phantom with cylindrical inclusionsA specific mold [Fig. 4(a)] was designed for phantoms with gel inclusions, allowing a total of six cylindrical inclusions split into two groups of three inclusions with 2, 3, and 4 mm diameters each. For the first group, the inclusions can be placed at a depth from 0 to 3 mm, whereas the second group is situated at a depth of [Fig. 4(c)], with being defined as the distance between the phantom surface and the closest point of the cylinders to the surface. The phantom production procedure is done as follows: the gel inclusions are produced in the horizontal cylindrical holes in the right part of the mold. The body of the phantom is molded in the rectangular shaped space on the left while aluminum cylinders are in place as illustrated for the first group of inclusions on Fig. 4(a). After gel polymerization, the aluminum cylinders are taken out, leaving open spaces facing the gel inclusions in mold. By using aluminum cylinders again, the gel inclusions can be pushed into the holes. The whole procedure is done underwater to avoid creating air bubbles. The resulting phantom can be seen in Fig. 4(c). Contrary to the bilayer phantoms, no film is used between the inclusions and the surrounding gel. In order to minimize the effect resulting from the migration of the inclusions’ fluorophores towards the surrounding gel and vice versa, measurements on inclusion phantoms have been made within 10 min after inserting the inclusions. 3.Data AnalysisAll obtained fluorescence spectra are analyzed by home-written Matlab programs. A typical spectrum measured from a bilayer phantom is shown in Fig. 5. corresponds to the weighted sum of two components: the emission spectrum of Rhodamine B, , and that of Fluorescein, . Background contributions were already subtracted from the raw data. Fig. 5Measured spectrum from a bilayer phantom; fitted by its two components RhB and FITC after subtraction of the contributions of noise. 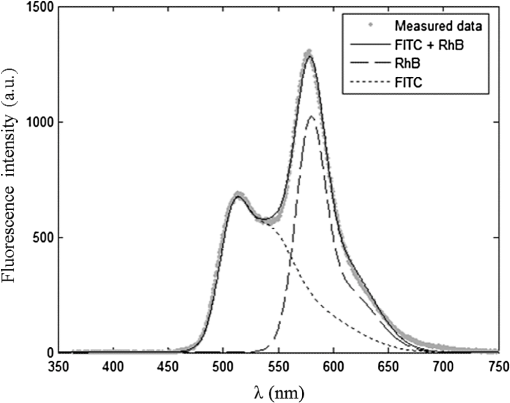 If more than one fluorophore was used, e.g., in case of bilayer phantoms or inclusion phantoms, the contribution of each fluorophore has to be determined. In a first step, a characteristic emission spectrum and of each utilized fluorophore ( for each fluorophore) has been measured using monolayer phantoms with equivalent optical parameters and concentrations. These spectrum are averaged then modelled by weighted sums of Gaussians, two for Rhodamine and three for Fluorescein, the Gaussian number chosen to obtain the best correspondence measure/sum of Gaussian (coefficient of adjusted ). Every spectra of fluorophore is normalized by the area under the curve of the corresponding fluorophore. In this way, the yield of fluorescence is corrected. Indeed, and correspond respectively to the area under the curve of the specter of Rhodamine and the area under the curve of FITC corrected by the yield of the fluorescence. To simplify, these factors ( and ) will be likened to fluorescence intensity. These spectra were then used to fit the experimental data from bilayer or inclusion phantoms, as presented in Eq. (2). The result of this procedure is also shown in Fig. 5. The fitted RhB (dashed line) and FITC (dotted line) contributions are shown with their sum (black line). This sum fits well the measured data (grey dots). The specific labelling of the layers with different fluorophores allows for identification of the fluorescence origin and, at the same time, the relative contribution from each layer or inclusion. Consequently, the layer thickness that can be detected as a function of the different geometrical and optical parameters of probe and phantom was estimated. For a given probe-phantom distance, the fluorescence intensity is measured at each position corresponding to different thicknesses () of the upper layer. The result is then divided by the maximal fluorescence intensity collected from the superior layer of the bilayer phantom (equivalent to a monolayer phantom). This estimates the percentage of emitted fluorescence of the upper layer from a specific thickness. To compare the different configurations, we defined a value that indicates the thickness of the upper layer that gives 80% of the detected light. In other words, in a monolayer phantom, about 80% of the detected light would come from this layer thickness. Such obtained fluorescence intensities for each part or layer of the phantom can be used to define the detectability of the layer. In consequence, all emissions of the different chromophores contributing to the total signal have to be taken into account. The percentages of the upper and lower layers are calculated with Eqs. (3) and (4), respectively and a typical example is given in Fig. 6. Fig. 6The fluorescence contributions (P) of FITC (upper layer, black line) and RhB (lower layer, grey line) of a bilayer phantom. Data have been smoothed. The optical properties of both layers are the same, except for the fluorophore ; ; ; ; . 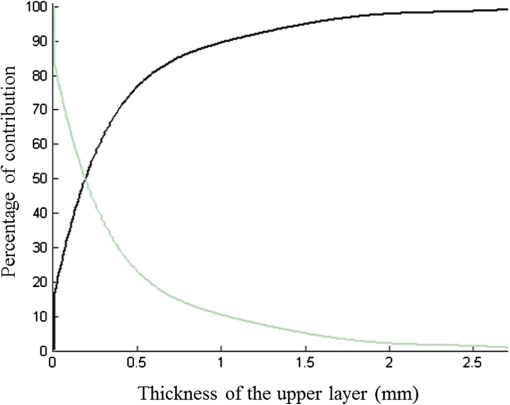 We consider a layer detectable if it contributes to at least 10% of the total signal. As varies with the thickness of the layer, we can therefore define two indicators, , which is the minimal thickness of the upper layer needed to be detected and , which corresponds to the maximal thickness of the upper layer allowing the detection of the lower layer. The 10% value used to define detectability was arbitrarily chosen and real tissue tests will have to be performed to adjust this value. But the 10% contribution value can provide a good estimation to evaluate probes. corresponds to a contribution of 10% of the upper layer from the total recorded signal. It illustrates the capacity to detect a tumoral on-surface layer. If a layer has a superior thickness to it will be considered detectable. The coefficient is equal to a thickness of the upper layer corresponding to a contribution of 10% of the lower layer of the total collected signal. In that case, the tumoral layer is considered as being covered by a healthy layer of tissue. If the healthy layer of tissue has a lower thickness of , the tumoral layer is detectable. 4.ResultsBefore use, the absorption and scattering coefficients of the phantom have been experimentally verified with an integrating sphere and the obtained results matched the expected coefficients. These measurements were accomplished for different couples of (,). Figure 7 exposes the values of measured according to the expected values (in agreement with Mie theory). Theoretical values are realized by the red line. The error bars shown in the following graphs had been always estimated using eight identical phantoms. These errors are estimated by the standard deviation between the measurements made for every scattering coefficient. An overestimation of the scattering coefficient is observed with respect to what we expected, with an average relative error of 15% and a maximal relative error of 23%. In the phantom study, only one optical parameter of a layer was varied, either the scattering or the absorption coefficient. While, the other parameters were always , and . When varying , was . On the other hand, was , when the absorption coefficient was changed. 4.1.Probe Positioning and GeometryAs shown in previous research, the position of the probe relative to the phantom plays an important role in terms of fluorescence light collection.16,31,32 In our case, we evaluated the optimal position by means of monolayer phantoms. Several phantoms with different scattering coefficients were fabricated and the intensity of fluorescence light was measured as a function of the distance between the probe and the sample. As illustrated in Fig. 8, for all the collected fluorescence intensities change considerably with the probe-sample distance. The shape of the curves is similar for all scattering coefficients. Qualitatively, this shape can be understood by the changing acceptance overlap of the excited and collected fibers and the collection efficiency, both varying with distance. The highest fluorescence collection yield is found at a probe-sample distance between 1.2 and 1.5 mm. This is important for future clinical applications, where a spacer will be necessary to position the probe correctly. Fig. 8Fluorescence intensity measured for several probe-sample separation distances and scattering coefficients. The other optical properties of the phantoms used for these measurements are: ; ; ; . 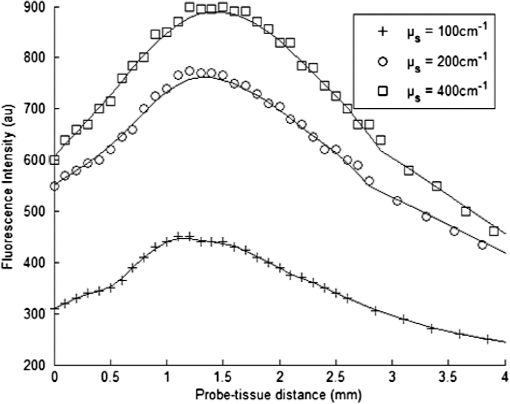 The error of the estimated probe-tissue distance is about , mainly due to limited precision in measuring this distance (flatness of probe and phantom support). Accordingly, the distance used between the probe and the phantom was always 1.5 mm within this study. It should be noted that this distance is specific for our probe characteristics. Consequently, the 1.5 mm distance has to be changed when the probe geometry is modified, especially when the distance between emitting and collecting fiber is varied as this which affects the collection acceptance.31 4.2.Sample and Layer ThicknessesThe collected fluorescence intensity changes with the thickness of the sample. This can easily be measured with a triangular-shaped layer [Figs. 3 or 4(b)], where the sample thickness only depends on the position of the probe. This can be seen in Fig. 6, where a saturation effect is observed. What is more interesting; these kind of well-calibrated phantoms can be used to evaluate precisely the spatial origin of the fluorescence emission. For monolayer phantoms (), Table 1 shows the estimated thickness where 80% of the signal comes from, corresponding to four different scattering coefficients. We observe that even for a high-scattering medium, this penetration depth only marginally changes. In conclusion, we estimated the thickness of the explored bulk by our system to be typically around 0.5 mm. This parameter does not seem to vary significantly according to and is about , corresponding to the average and the standard deviation of the values presented in Table 1. A statistical error was evaluated by calculating the standard deviation between the determined on several phantoms () with identical optical properties and was estimated to be 0.06 mm. This error is of the same order as the standard deviation of the values of Table 1, what strengthens the conclusion of independency between and . Table 1T80% values for various scattering coefficients of monolayer phantoms.
For bilayer phantoms: In this case, the optical parameters of both layers are identical, except for the fluorophore. We view two cases, the variation of the scattering coefficient and that of absorption coefficient. A variation of , is fixed to and when is different, . Every point of the curve represents the average between two values of defined on two lines of measurements acquired on the same phantom; the average distance between these measurements for the different phantom is lower than 2%. The error bars () result from a standard deviation between eight values of effective penetration, calculated on eight phantoms of identical optical properties. Figure 9(a) shows the variation of as a function of scattering coefficient and Fig. 9(b) as a function of absorption coefficient. Fig. 9Variation of the depth of detection of 80% of the signal of the superior layer according to (a) and of (b). 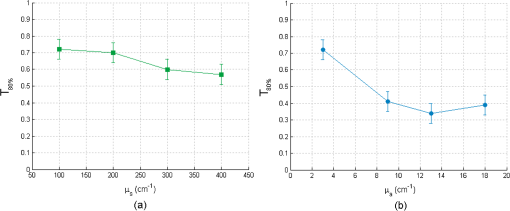 To determine if the effective depth of detection varies with or , we compared the standard deviation of the points of the curve, with the square of the statistical error, , corresponding to 95% of confidence interval (a Shapiro test was used). If the criterion presented in Eq. (5) is validated, then depends on the varied coefficient in the considered curve. By applying this method, we find that, for Fig. 9(a), is lower than 2. , we cannot thus consider that the depth of detection varies with the scattering coefficient. This conclusion is added to that made on the monolayer phantom. Concerning Fig. 9(a), the corresponding point in is statistically different from others, making them not differentiated. We can conclude that the effective depth of detection does not vary with but depends on . For an absorption coefficient () of , is about , and decreases to a value of 0.38 mm for higher . 4.3.DetectabilityIn this case, the optical coefficients of the upper and lower layers are not always identical. These new analyses aim at bringing information about the capacity of the probe to detect the one or the other layer of both superimposed different layers. These results will be approached by the detection of a tumoral surface layer or in-depth. The maximum thickness of the upper layer allowing the detection of the lower layer has been measured for different and . As can be seen in Fig. 10, a study of the maximal thickness of the upper layer according to of the upper layer was made when the absorption coefficient is fixed to Every curve corresponds to a fixed of the lower layer. Fig. 10Variation of the maximal thickness of upper layer allowing the detection of the lower layer according to different scattering coefficient of both layers. is . 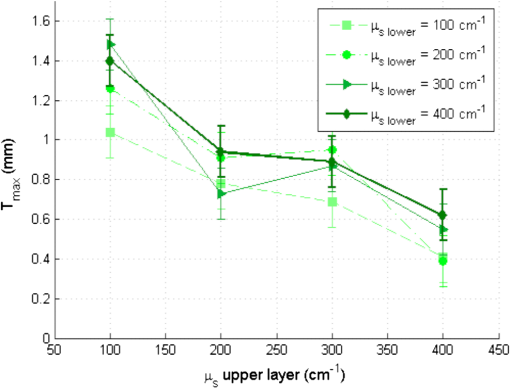 A criterion identical to that presented in Eq. (5) was used to define if the observed variation was significant or not. In that case, the critical value is 2. and the standard deviation is calculated for values according to fixed , either for the lower or upper layer. Table 2 present the values of . Table 2(a) contains the values of calculated for a fixed scattering coefficient of the upper layer and variable scattering coefficient of the lower layer. In Table 2(b), it is the of the upper layer which is changed while the of the lower layer is fixed. Table 2Standard deviation Smax for fixed μs of the upper (a) and lower (b) layer.
By comparing the values of Table 2 to the critical value , we can deduce that the maximal thickness of detection does not depend on the scattering coefficient of the lower layer, but it is influenced by the scattering properties of the upper layer. The more scattering the upper layer has, the less the thickness will be, with average values included between 1.3 and 0.49 mm. A high scattering corresponds to a low mean free path in tissues. If we consider an average number of steps of scattering identical, whatever , a photon will penetrate less deeply in tissue with higher scattering coefficient. This can explain qualitatively the decrease of for higher . For various scattering and absorption coefficients, the value is always found less than 60 µm. An error was also estimated by using identical bilayer phantoms. The estimated error is . taking into account this error, the upper layer will always be detected, if its thickness is at least 80 µm. Optical problems in tissues are especially difficult regarding scattering and absorption. For this reason, a study similar to that of the variation of was made by varying the absorption coefficient . Figure 11 present results of according to of the upper layer, where each curve corresponds to a fixed of the lower layer. The standard deviation is also calculated in these cases and the results are recapitulated in Table 3. Fig. 11Variation of the maximal thickness of upper layer allowing the detection of the lower layer according to different absorption coefficient of both layers. 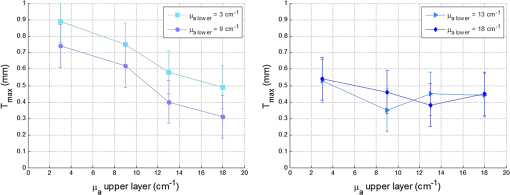 Table 3Standard deviation Smax for fixed μa of the upper (a) and lower (b) layer.
We cannot conclude the existence of any dependence of the thickness on the absorption coefficient in the range included between 3 and from Table 3. Qualitatively, we can observe a decrease of with of the upper layer for small values of of the lower layer, as seen in Fig. 11. The deducted values of are always lower than 70 µm for different , for an average value of 30 µm. Note that in the case of cancer tissue that has necessarily a higher underneath healthy tissue, the explored thickness is between 1.3 and 0.5 mm (Table 2). We conclude that depends on the of the upper layer and is not affected by the variation of and of the lower layer. Further study and measurements will be accomplished to evaluate this thickness for tissues combining high scattering and high absorption coefficients. 4.4.Phantoms With InclusionThe use of inclusion phantoms [Fig. 4(c)] allows the analysis of very local “tissue” modifications and to evaluate its fluorescence contribution to the whole detected signal, which depends on its size and depth within the phantom. Evidently, optical parameters can be varied as well. The probe is moved across these phantoms similarly to the bilayer phantoms and the measured data are fitted in the same way. A typical result can be seen in Fig. 12. Fluorescence intensities of FITC inclusions are shown as a function of the -axis position of the scan when the probe is displaced laterally across the phantom. Each peak has already been fitted with a Gaussian curve to get position and full width at half maximum (FWMH) of the inclusion. Fig. 12FITC intensity as a function of probe position. The optical properties of the FITC inclusions are: ; ; ; ; . The surrounding gel has the same parameters except for the scattering coefficient and the fluorophore, which is RhB. The inclusion depths are 1 and 1.5 mm. 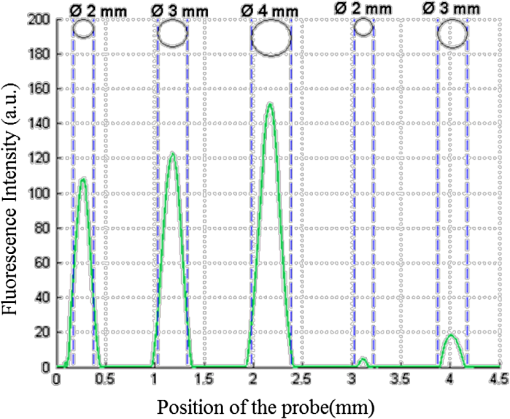 Several phantoms were built to cover a range of inclusion depths between 0 and 3.5 mm. Figure 12 presents the variation of the detected intensity maximum as a function of this depth. Squares, circles and triangle represent 2-, 3- and 4-mm diameter inclusions, respectively. The parameters of interests are the maximum and the FWHM. The error on the maximal intensity measured on an inclusion was calculated by means of six phantoms each one contain six inclusions, half in 1 mm depth and the others 1.5 mm deep. The average variation of the maximal intensity was estimated with a relative standard deviation of the order of 1%, with a maximal standard deviation of 3%. Figure 13 recapitulates the maxima of the inclusions’ contributions for different depths and diameters. The contributions in 0 mm depth are lower than 100%. This is understandable by the spatial resolution of the probe which is 500 µm and thus it measures a superior surface of the outcrop of the inclusion. The red line represents the limit of 10% detectability. The detection is quasi-independent from the diameter of the inclusions, when it is included between 2 and 4 mm. The maximal depth of the inclusion allowing its detection is about 0. 9 mm. Fig. 13Normalized maximum peak intensities measured for inclusions of 2, 3, and 4 mm diameters, corresponding to squares, circles and triangles, respectively, as a function of the inclusion depth.  The FWHM does not vary with the depth of the inclusion. Table 4 contains the average values of FWHM for different diameters. The relationship between FWHM and the diameter is constant with a ratio of about 0.6. Table 4Average values of FWHM for different diameters.
5.DiscussionUsing our homemade probe, several scattering, absorbing and fluorescent phantoms with different geometries have been developed to evaluate the detection properties. To achieve this study, we took into account various thicknesses or depths, inclusions of several sizes and optical parameters. In case of a monolayer phantom, the thickness from where 80% of the total signal is collected, is independent of the scattering coefficient and is around . When considering bilayer phantoms, two different indicators, and , were investigated corresponding to the minimal and maximal thicknesses of the upper layer that still permits detection of the upper or lower layer, respectively. For both indicators, absorption and scattering coefficients have been varied. Being independent of absorption and scattering coefficients, the minimum thickness of the upper layer to be detected is never larger than 80 µm and in most cases even smaller. On the other hand, the maximum thickness of the upper layer allowing detection of the lower layer is strongly –dependent. For increasing scattering coefficient of the upper layer, decreases. In consequence, even a rather thin layer of tumorous tissue at the surface having a high-scattering coefficient will inhibit a signal contribution from underlying healthy tissue, property that should help in tumorous tissue identification. More generally it can be stated that high differences of the scattering coefficients of two tissue layers favor the detection of the high diffusive tumorous one. Detectability of inclusions has also been examined. At least for inclusion diameters larger than 2 mm, the inclusions are detectable to depths of 1.5 mm. While the detectability does not vary with diameter, the inclusion widths (FWHM) are underestimated by about 40%. Both properties can be explained by geometrical considerations: the inclusions have a circular, not a rectangular shape, and the determined depth is the distance between the phantom surface and the inclusion’s top edge. We determined the limit of detection, defined as a minimal contribution of 10% of the measured total signal, in a depth slightly lower than 1 mm. Nevertheless, the signal resulting from inclusions is very well defined because of the adjustment method of the emission spectrum and the same for superior depths. The value of the threshold of detection defined arbitrarily in 10% of the total signal seems too radical. In fact, it is possible, due to the method of spectrum processing, to detect inclusions more profoundly than the defined threshold. 6.ConclusionIn the present work, the making of original mono-and bilayer phantoms, as well as phantoms with inclusions, was presented. These phantoms with calibrated and verified optical parameters are suited to fluorescence spectroscopy. They provide an accurate tool to characterize and compare fiber probe detection characteristics. The phantom optical parameters have been fitted to mimic healthy and tumorous brain tissues. These phantoms are also well fabricated to be excited with 405 nm, a wavelength frequently used for autofluorescence measurements of tissues. In the end, the benefits of a phantom with variable optical parameters and adaptable geometries were shown for detection-probe characterization. However, phantom studies are quite time-consuming. Complementary ways to validate probes include Monte Carlo simulations that can be easily used to make a systematic characterization of different probe geometries. We have developed such a simulation program and its validation via phantom measurements is under study.33 Detailed results will be published soon. AcknowledgmentsThe authors gratefully acknowledge the AnBioPhy laboratory for letting them use their spectrophotometer, especially Imène Chebbi for her welcome and help. This work is supported by Paris Diderot University (BQR). ReferencesF. W. Esmonde-Whiteet al.,
“Biomedical tissue phantoms with controlled geometric and optical properties for Raman spectroscopy and tomography,”
The Analyst, 136
(21), 4437
–4446
(2011). http://dx.doi.org/10.1039/C1AN15429J Google Scholar
B. W. PogueM. S. Patterson,
“Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry,”
J. Biomed. Opt., 11
(4), 041102
(2006). http://dx.doi.org/10.1117/1.2335429 JBOPFO 1083-3668 Google Scholar
G. C. Becket al.,
“Design and characterisation of a tissue phantom system for optical diagnostics,”
Laser Med. Sci., 13
(3), 160
–177
(1998). http://dx.doi.org/10.1007/s101030050070 LMSAET 0736-9417 Google Scholar
K. P. RaoS. RadhakrishnanM. R. Reddy,
“Brain tissue phantoms for optical near infrared imaging,”
Exp. Brain Res., 170
(4), 433
–437
(2006). http://dx.doi.org/10.1007/s00221-005-0242-4 EXBRAP 0014-4819 Google Scholar
L. T. NiemanM. JakovljevicK. Sokolov,
“Compact beveled fiber optic probe design for enhanced depth discrimination in epithelial tissues,”
Opt. Express, 17
(4), 2780
–2796
(2009). http://dx.doi.org/10.1364/OE.17.002780 OPEXFF 1094-4087 Google Scholar
K. VishwanathM. A. Mycek,
“Time-resolved photon migration in bi-layered tissue models,”
Opt. Express, 13
(19), 7466
–7482
(2005). http://dx.doi.org/10.1364/OPEX.13.007466 OPEXFF 1094-4087 Google Scholar
D. Kepshireet al.,
“Fluorescence tomography characterization for sub-surface imaging with protoporphyrin IX,”
Opt. Express, 16
(12), 8581
–8592
(2008). http://dx.doi.org/10.1364/OE.16.008581 OPEXFF 1094-4087 Google Scholar
M. A. AnsariR. MassudiM. Hejazi,
“Experimental and numerical study on simultaneous effects of scattering and absorption on fluorescence spectroscopy of a breast phantom,”
Opt. Las. Technol., 41
(6), 746
–750
(2009). http://dx.doi.org/10.1016/j.optlastec.2008.12.019 OLTCAS 0030-3992 Google Scholar
I. Noiseuxet al.,
“Development of optical phantoms for use in fluorescence-based imaging,”
Proc. SPIE, 7567 75670B
(2010). http://dx.doi.org/10.1117/12.841887 PSISDG 0277-786X Google Scholar
Q. LiuG. GrantT. Vo-Dinh,
“Investigation of synchronous fluorescence method in multicomponent analysis in tissue,”
IEEE J. Sel. Top. Quantum Electron, 16
(4), 927
–940
(2010). IJSQEN 1077-260X Google Scholar
S. C. GebhartW. C. LinA. Mahadevan-Jansen,
“In vitro determination of normal and neoplastic human brain tissue optical properties using inverse adding-doubling,”
Phys. Med. Biol., 51
(8), 2011
–2027
(2006). http://dx.doi.org/10.1088/0031-9155/51/8/004 PHMBA7 0031-9155 Google Scholar
A. N. Yaroslavskyet al.,
“Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range,”
Phys. Med. Biol., 47
(12), 2059
–2073
(2002). http://dx.doi.org/10.1088/0031-9155/47/12/305 PHMBA7 0031-9155 Google Scholar
G. WagnièresW. StarB. C. Wilson,
“In vivo fluorescence spectroscopy and imaging for oncological applications,”
Photochem. Photobiol., 68
(5), 603
–632
(1998). http://dx.doi.org/10.1111/j.1751-1097.1998.tb02521.x PHCBAP 0031-8655 Google Scholar
D. Abi-Haidaret al.,
“Spectral and lifetime domain measurements of rat brain tumors,”
Proc. SPIE, 8207 82074P
(2012). http://dx.doi.org/10.1117/12.907411 PSISDG 0277-786X Google Scholar
M. H. Vu Thiet al.,
“Intra-operative probe for brain cancer: feasibility study,”
Proc. SPIE, 6628 66281Q
(2008). http://dx.doi.org/10.1117/12.729454 PSISDG 0277-786X Google Scholar
M. H. Vu Thi,
“Développement d’une sonde per-operatoire basée sur la détection d’autofluorescence pour l’assistance au traitement chirurgical des tumeurs cérébrales,”
Université Paris XI,
(2008). Google Scholar
T. K. BiswasT. M. Luu,
“In vivo MR measurement of refractive index, relative water content and T2 relaxation time of various brain lesions with clinical application to discriminate brain lesion,”
Int. J. Radiol., 13
(1),
(2011). http://dx.doi.org/10.5580/1483 Google Scholar
C. F. BohrenD. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York
(1983). Google Scholar
M. BornE. Worlf, Principals of Optics, 6th ed.Pergamon Press, Oxford
(1980). Google Scholar
H. C. Van de Hulst, Light Scattering by Small Particles, Wiley, New York
(1964). Google Scholar
W. J. Lentz,
“Generating Bessel functions in Mie scattering calculations using continued fraction,”
Appl. Opt., 15
(3), 668
–671
(1976). http://dx.doi.org/10.1364/AO.15.000668 APOPAI 0003-6935 Google Scholar
A. IshimaruY. Kuga,
“Attenuation constant of a coherent field in a dense distribution of particles,”
J. Opt. Soc. Am., 72
(10), 1317
–1320
(1982). http://dx.doi.org/10.1364/JOSA.72.001317 JOSAAH 0030-3941 Google Scholar
A. LagendijkB. A. van Tiggelen,
“Resonant multiple scattering of light,”
Phys. Rep., 270 143
–215
(1996). http://dx.doi.org/10.1016/0370-1573(95)00065-8 PRPLCM 0370-1573 Google Scholar
B. Gélébartet al.,
“Phase function simulation in tissue phantoms: a fractal approach,”
Pure Appl. Opt., 5
(4), 377
–388
(1996). http://dx.doi.org/10.1088/0963-9659/5/4/005 PAOAE3 0963-9659 Google Scholar
S. L. Jacques,
“Short course note: tissue optics,”
SPIE Education Courses,
(2012). Google Scholar
F. Martelliet al., Light Propagation Through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Software, 193 SPIE Press Monograph, San Jose
(1970). Google Scholar
L. HenyeyJ. Greenstein,
“Diffuse radiation in the galaxy,”
Astrophys. J., 93 70
–83
(1941). http://dx.doi.org/10.1086/144246 ASJOAB 0004-637X Google Scholar
S. Jacqueset al.,
“Specifying tissue optical properties using axial dependence of confocal reflectance images: confocal scanning laser microscopy and optical coherence tomography,”
Proc. SPIE, 6446 64460N
(2007). http://dx.doi.org/10.1117/12.716535 PSISDG 0277-786X Google Scholar
D. Abi-HaidarT. Oliver,
“Confocal reflectance and two-photon microscopy studies of a songbird skull for preparation of transcranial imaging,”
J. Biomed. Opt., 14
(3), 034038
(2009). http://dx.doi.org/10.1117/1.3155522 JBOPFO 1083-3668 Google Scholar
T. J. Pfeferet al.,
“Selective detection of fluorophore layers in turbid media: the role of fiber optic probe design,”
Opt. Lett., 28
(2), 120
–122
(2003). http://dx.doi.org/10.1364/OL.28.000120 OPLEDP 0146-9592 Google Scholar
T. Papaioannouet al.,
“Effects of fiber-optic probe design and probe-to-target distance on diffuse reflectance measurements of turbid media: an experimental and computational study at 337 nm,”
Appl. Opt., 43
(14), 2846
–2860
(2004). http://dx.doi.org/10.1364/AO.43.002846 APOPAI 0003-6935 Google Scholar
B. Lehet al.,
“Development of an autofluorescence probe far brain cancer: probe characterization thanks to phantom studies,”
Proc. SPIE, 7567 756707
(2010). http://dx.doi.org/10.1117/12.841371 PSISDG 0277-786X Google Scholar
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||