Hybrid Green’s function of the time-dependent radiative transfer equation for anisotropically scattering semi-infinite media

Emanuel Simon; Florian Foschum; Alwin Kienle

doi:10.1117/1.JBO.18.1.015001

4 January 2013 Hybrid Green’s function of the time-dependent radiative transfer equation for anisotropically scattering semi-infinite media

Emanuel Simon, Florian Foschum, Alwin Kienle

Author Affiliations +

Journal of Biomedical Optics, Vol. 18, Issue 1, 015001 (January 2013). https://doi.org/10.1117/1.JBO.18.1.015001

Abstract

A semi-infinite space Green’s function of the time-dependent radiative transfer equation is derived based upon an exact solution for anisotropic scattering in infinite space and the approximated extrapolated boundary condition. The obtained solution is compared to Monte Carlo simulations and used for retrieving the optical parameters of simulated data in a nonlinear fit. It is shown that the solution performs well for boundaries with mismatched refractive indices. The relative errors in the fitted optical parameters are considerably smaller than by using the diffusion theory.

1. Introduction

The radiative transfer equation (RTE) describes the propagation of light in diffusive media like biological tissue, but despite its use in many fields of physics for the modeling of waves in scattering media, analytical solutions are available only for simple cases. This integro-partial differential equation is solved by numerical methods like Monte Carlo simulations,¹ the discrete ordinate method,²^,³ or finite element methods⁴ or is approximated by simpler models like diffusion theory.⁵^,⁶

The most widely used approximation for the modeling of light propagation in typical geometries for experiments in biomedical optics is the diffusion equation (DE), for which solutions are available, e.g., for semi-infinite geometries, slabs, and cylinders, both homogeneous and layered.⁷^–¹⁰ However, investigations based on the DE are limited by the approximations of the theory. In the time domain especially, early photons have to be disregarded as the validity of the DT is limited to photons that are scattered many times. Results can be improved by models based on the more exact RTE solutions. A possible approach to solve the RTE for the semi-infinite geometry is the use of scaled Monte Carlo simulations,¹¹^–¹³ leading to good results but depending on high computational effort in calculation time and memory use.

Martelli et al. used a solution for an infinite medium presented by Paasschens¹⁴ to derive a heuristic analytical solution for the time-dependent RTE for the case of isotropic scattering and a isotropic point source in a semi-infinite medium.⁶^,¹⁵

Recently, approaches for solving the RTE were presented in steady-state for the infinite¹⁶^,¹⁷ and the semi-infinite geometry.¹⁸ These solutions can be transformed to the frequency-domain and by using the Fourier transform one obtains solutions for the time-dependent RTE. But the Green’s function of the steady-state RTE is not square integrable. Therefore, the resulting signal can be strongly oscillating, causing difficulties for the use of this approach in the inverse problem based on fitting procedures.

However, a Green’s function with an analytical dependence on the time variable was recently presented for the infinite space and anisotropic scattering,¹⁹ leading to more stable results as it is not necessary anymore to transform the results from the frequency-domain. This new approach starts from the RTE dependent on distance, time, and angle. The expansion in Legendre polynomials leads to a linear and time invariant system that gives a time-dependent Green’s function by applying a one-sided Laplace transform. The resulting set of only linear equations can be solved by a matrix exponential giving the time-dependent solution as long as an inverse Laplace transform can be carried out. The matrix exponential can be computed advantageously by an eigenvalue decomposition to obtain the results for all time values in one step.

This study follows the approach of Martelli et al. but uses the accurate solution for the time-dependent RTE recently presented in Ref. 19 in order to obtain a Green’s function that is based on a solution for anisotropical scattering and can be used for mismatched refractive indices, as exist in most measurement situations²⁰^–²³ and especially for noncontact approaches.²⁴ The model is compared to Monte Carlo simulations to test its accuracy and to show the improvements compared to the diffusion model. It is used for the inverse problem of deriving the optical parameters of Monte Carlo simulations by a nonlinear fitting routine. The resulting errors are compared with the ones produced by the well-known diffusion theory.

2. Theory

The derivation starts from the $P_{N}$ -solution of the RTE for the time-dependent fluence rate caused by a isotropic point source in an infinite medium. The solution is given by the coefficient of zeroth order of a Legendre series for the radiance¹⁹

Eq. (1)

Φ_{\inf} = \frac{1}{2 π^{2}} \int_{0}^{\infty} I_{0} (k, t) j_{0} (k r) k^{2} d k,

where the coefficient of the Legendre series

I_{0} (k, t)

is given by Eq. (21) with

l = 0

in Ref. 19 and

j_{0} (x) = \sin (x) / x

is the spherical Bessel function of the first kind. The expansion coefficients can be calculated by an eigenvalue decomposition of the matrix

A

defined in Eq. (14) in Ref. 19, which can be done easily in Matlab for example.

The solution for the fluence in the infinite case is shown to agree with results of Monte Carlo simulations,¹⁹ with the relative differences being only dependent on the number of photons used in the latter ones. Furthermore, the solution conforms the expectations to perform well also for situations with high absorption where the DT breaks down. Additionally, it has the advantage to be applicable for anisotropic scattering. The anisotropy factor $g$ of the often used Henyey-Greenstein model,²⁵ for instance, is contained in the matrix $A$ .¹⁹

The component $J_{r}$ of the flux $J = J_{r} \cdot \hat{r}$ in the infinite medium is given by the first order moment of the Legendre series

Eq. (2)

J_{r, \inf} (r, t) = \frac{j}{2 π^{2}} \int_{0}^{\infty} I_{1} (k, t) j_{1} (k r) k^{2} d k,

with

I_{1} (k, t)

also given by Eq. (21) in Ref. 19 but for

l = 1

, the spherical Bessel function of the first kind

j_{1} (x) = \sin (x) / x^{2} - \cos (x) / x

and where

j

is the imaginary unit.

This study does not use the numerical implementation suggested by Liemert and Kienle¹⁹ that employs a finite Hankel transformation. Instead, the integrations in Eqs. (1) and (2) are solved by a Gauss quadrature leading to a greater numerical stability of the solution.

The main problem in the description of a semi-infinite geometry is the representation of the boundary. In the time domain there is no solution available for exact boundaries. Thus, approximated boundary conditions have to be used. Following the choice of Martelli et al.¹⁵ for the heuristic boundary condition, the extrapolated boundary condition (EBC), using the method of images can be applied to derive the semi-infinite boundary as it is done with the diffusion equation. ⁵^,²⁶ For an assumed isotropic source at a depth $z = z_{0}$ , a negative image source is introduced outside the medium so that at a distance $z = - z_{e}$ the fluence rate composed by the fluence rates for an infinite medium from each source, vanishes at that extrapolated boundary. This leads to the following expressions for the fluence rate in the semi-infinite medium with $ρ = {(x^{2} + y^{2})}^{1 / 2}$ as the source-detector separation:

Eq. (3)

Φ_{si} (ρ, z, t) = Φ_{\inf} (| r - r^{+} |, t) - Φ_{\inf} (| r - r^{-} |, t), | r - r^{+} | = \sqrt{ρ^{2} + {(z - z_{0})}^{2}}, | r - r^{-} | = \sqrt{ρ^{2} + {(z + z_{0} + 2 z_{e})}^{2}} .

In transport theory, the dependence on the absorption coefficient is given by the factor $\exp (- μ_{a} ct / n)$ . To obtain the same dependence in DT and transport theory, the isotropic source is assumed to be at a depth of $z_{0} = 1 / (μ_{s}^{'})$ .⁶ In the case of a difference in refractive indices at the boundary, the Fresnel reflections can be accounted for by defining the extrapolated distance as $z_{e} = 2 D A$ . The diffusion coefficient $D$ is assumed to be $D = 1 / ({3 μ}_{s}^{'})$ .

The time-resolved reflectance at the boundary is often calculated by using Fick’s law to obtain a representation of the flux through the boundary. This approximation is not necessary here, since the exact flux is given by Eq. (2). The $z$ -component in the negative $z$ -direction is

Eq. (4)

J_{z, \inf} (ρ, z, t) = - J_{r, \inf} (r, t) \cdot (z - z^{'}) / r,

where

r = {(ρ^{2} + z^{2})}^{1 / 2}

and

z^{'}

is the position of the source that is either

z_{0}

or

z_{img} = - z_{0} - 2 z_{e}

for the positive source and the negative image source, respectively. The flux at the boundary

z = 0

leaving the medium can then be calculated by

Eq. (5)

J_{z, si} (ρ, z = 0, t) = J_{z, \inf} (| r - r^{+} |,0, t) - J_{z, \inf} (| r - r^{-} |,0, t) .

Following the argumentation of Haskell et al.²⁶ and Kienle and Patterson,²⁷ the reflectance can then be given as a combination of fluence and flux as

Eq. (6)

R (ρ, t) = \frac{1 - r_{ϕ}}{4} Φ_{si} (ρ, z = 0, t) + \frac{1 - r_{j}}{2} J_{z, si} (ρ, z = 0, t),

where the coefficients

r_{ϕ}

and

r_{j}

are defined as in Ref. 26. For the comparison shown in the results section, the Green’s function based on the Paasschens solution presented by Martelli et al.¹⁵ was modified in the same way. That means the choice of

z_{e} = 2 D A

and the same combination of fluence and flux in the calculation of the reflectance as given in Eq. (6) was used, for which the flux was calculated by Fick’s law as presented in Ref. 15.

3. Results

Results of the Green’s function for the semi-infinite medium derived here are compared with Monte Carlo simulations for validation, since the latter converge against an exact solution of the RTE for an infinitely large number of photons.

The source in the simulations is represented by a pencil beam of light and the Henyey-Greenstein phase function is used. The simulations were done for an absorption free medium, taking the dependence on attenuation into account by multiplication with $\exp (- μ_{a} ct / n)$ as shown by Kienle and Patterson.¹¹ This leads to better statistics, especially for the cases of high absorption. Photon packages with a time of flight longer than $3 ns$ were discarded for performance reasons as they were out of the interesting detection interval. In the following, the reduced scattering coefficient is assumed to be $μ_{s}^{'} = 1 {mm}^{- 1}$ . The refractive index of the surrounding medium and the semi-infinite scattering medium are $n = 1.0$ and $n = 1.4$ , respectively, as this is close to the value of biological tissues. Every photon package exiting the scattering medium was binned with a radial resolution of $0.1 mm$ and temporal bin size of $2 ps$ . The simulations were carried out with $2 \cdot 10^{9} photons$ .

Figure 1(a) and 1(b) shows the obtained results for the reflectance from a semi-infinite medium for the order of $N = 7$ , Eq. (6), compared with Monte Carlo simulations (MC) for an anisotropically scattering medium. The derived reflectance agrees much better with the MC results than the DT (also shown), especially for early times where DT is inaccurate since its validity is limited to photons that are scattered many times. Since the Monte Carlo simulations and both analytical solutions use the same dependence on absorption, the ratios shown in Fig. 1(c) and 1(d) are the same for all values of the absorption coefficient. The differences between the hybrid solution and MC are below 5% for all times shortly after the peak. Due to the ballistic peak, there are numerical instabilities in the solution of the infinite case at early times. Therefore, the Green’s function is multiplied with Heaviside functions $Θ (t - | r - r^{\pm} | / c)$ for both sources, respectively, suppressing the signal at small times and limiting the rising edge when the source-detector separation becomes comparable to the distance to the image source. It has to be noted that the ratios in Fig. 1(c) and 1(d) are zero for all times where the Monte Carlo simulations are zero and, therefore, do not show the violation of causality as DT predicts non-null values for short times as can clearly be seen in Fig. 1(a) and 1(b).

Fig. 1

Comparison between DT, the Green’s function derived here (Hy) and MC for an anisotropically scattering medium with $μ_{s}^{'} = 1 {mm}^{- 1}$ , $g = 0.9$ , and $μ_{a} = 0.1 {mm}^{- 1}$ (a) and (c) or $μ_{a} = 1 {mm}^{- 1}$ (b) and (d). The figures (a) and (b) show the time-resolved reflectance at three source-detector separations $ρ = 3.95 / 5.95 / 8.95 mm$ , (c) and (d) show the ratio between the MC results and each analytical solution for a source-detector separation of $ρ = 3.95 mm$ and $ρ = 5.95 mm$ , respectively.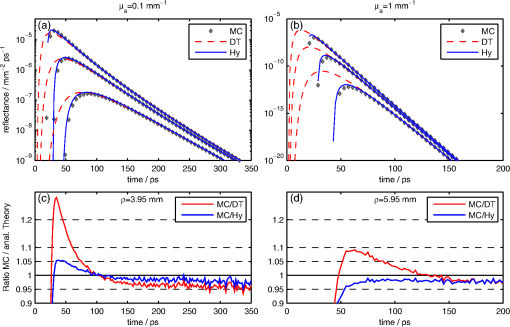

The situation for media with different anisotropy factors is shown in Fig. 2, where Fig. 2(a) and 2(b) shows the time-resolved reflectance for $g = 0.5$ and $g = 0.8$ , respectively. The Green’s function presented by Martelli et al. based on the Paaschens solution and modified as described above is also included for comparison. As expected for a solution of only the isotropic case, it performs better for $g = 0.5$ than for $g = 0.8$ . In both cases it performs better than DT for short times but gets worse for later times because of the mismatched refractive indices as already stated in Ref. 15. The hybrid solution presented in this study again models early time values best. As can be seen in Fig. 2(c) and 2(d), the difference in the Monte Carlo results is again below 5% at all times shortly after the maximum even for the small source-detector separation of 3.95 mm.

Fig. 2

Comparison between DT, the Green’s function derived here (Hy), and the one based on the Paaschens solution (Paa) and MC. Compared for $μ_{s}^{'} = 1 {mm}^{- 1}$ , $μ_{a} = 0.1 {mm}^{- 1}$ . On the left side for $g = 0.5$ , on the right for $g = 0.8$ . The figures (a) and (b) show the time-resolved reflectance at three source-detector separations $ρ = 3.95 / 5.95 / 8.95 mm$ , (c) and (d) show the ratio between the MC results and the analytical solutions, at the source-detector separation of 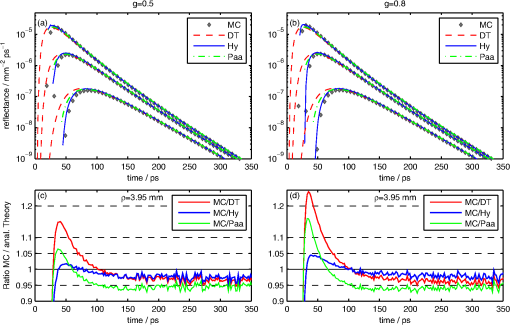$ρ = 3.95 mm$ .

In the following, the derived solution is used to retrieve the optical parameters of time-resolved reflectance curves from Monte Carlo simulations. A Levenberg-Marquardt routine is used to fit the analytical solution to the simulation data. The weights $σ_{i}$ used in the fitting are defined by the standard deviation of the Monte Carlo simulation data that is⁶

Eq. (7)

σ (ρ_{k}, t_{i}, μ_{a}) = \frac{R (ρ_{k}, t_{i}, μ_{a})}{\sqrt{N_{k, i}}} .

Table 1 shows the results of the nonlinear fitting of Monte Carlo data in order to retrieve $μ_{a}$ and $μ_{s}^{'}$ of the medium. The routine used the Levenberg-Marquardt algorithm provided in the Matlab Optimization toolbox and fitted both optical parameters $μ_{s}^{'}$ and $μ_{a}$ , as well as an amplitude factor $K$ . So the residual to be minimized is

Eq. (8)

χ^{2} = \sum_{i = 1}^{N} {[\frac{K \cdot R (ρ, t_{i}, μ_{a}, {μ^{'}}_{s}) - MC (ρ, t_{i})}{σ (ρ, t_{i})}]}^{2} .

Table 1

Relative error in the absorption coefficient εa and the reduced scattering coefficient εs for different source-detector separations (SDS) after fitting to MC simulations with μs′=1 mm−1, g=0.9, n=1.4, and varying absorption.

	$μ_{a} = 0.001 {mm}^{- 1}$				$μ_{a} = 0.01 {mm}^{- 1}$
$SDS / mm$	DT		Hy		DT		Hy
$SDS / mm$	$ε_{s} / %$	$ε_{a} / %$	$ε_{s} / %$	$ε_{a} / %$	$ε_{s} / %$	$ε_{a} / %$	$ε_{s} / %$	$ε_{a} / %$
3.95	42.8	109.3	13.8	14.6	47.4	18.1	12.8	2.5
4.95	32.2	14.8	4.5	2.5	32.1	1.8	4.2	0.1
5.95	13.5	17.8	0.8	4.0	15.3	3.1	1.0	0.6
6.55	9.0	13.7	0.3	2.9	10.7	2.6	0.1	0.5
7.95	4.5	8.7	1.1	2.3	5.8	1.7	0.9	0.4
8.95	2.7	4.8	1.6	0.2	3.2	0.9	1.9	0.1
11.95	0.7	1.8	1.8	1.1	1.2	0.5	1.6	0.0

	$μ_{a} = 0.1 {mm}^{- 1}$				$μ_{a} = 1 {mm}^{- 1}$
$SDS / mm$	DT		Hy		DT		Hy
$SDS / mm$	$ε_{s} / %$	$ε_{a} / %$	$ε_{s} / %$	$ε_{a} / %$	$ε_{s} / %$	$ε_{a} / %$	$ε_{s} / %$	$ε_{a} / %$
3.95	38.0	3.8	5.3	1.3	79.0	10.7	34.2	4.6
4.95	22.8	0.6	0.2	0.7	107.7	14.3	28.8	4.0
5.95	12.9	0.0	1.1	0.3	104.4	13.1	24.5	3.4
6.55	7.5	0.3	2.4	0.4	102.0	12.5	23.1	3.3
7.95	1.6	0.7	3.2	0.4	82.9	8.6	17.5	2.3
8.95	0.4	0.7	2.7	0.1	77.6	6.9	15.8	2.0
11.95	4.4	1.1	2.4	0.1	64.8	2.8	14.1	2.4

The region on the curve used for the fitting was chosen to be from 90% of the maximum behind the peak to 0.1% of the maximum. The fitting region is chosen only on the falling slope of the curve since the DT does not calculate the rising part correctly and is invalid for too early photons. The second limit is chosen on the grounds that experiments based on time correlated single photon counting typically can detect count values over three orders of magnitude. Even if the hybrid model based on the RTE performs better for early times as seen in the comparisons of the forward calculations with MC, the results for fitting just the falling part are better also for this model. Furthermore, the values of the reduced $χ_{r}^{2}$ as a measure of the quality of the fit²⁸ are better for the fitting range after the peak for both solutions.

The relative errors for the optical coefficients determined by the fit are calculated by

Eq. (9)

ε (μ_{a}) = | \frac{μ_{a,fit} - μ_{a}}{μ_{a}} | and ε (μ_{s}^{'}) = | \frac{μ_{s, fit}^{'} - {μ^{'}}_{s}}{{μ^{'}}_{s}} |,

and are given for different source-detector separations

ρ

in Table 1 as percentages.

The relative errors in the optical parameters retrieved by fitting with the hybrid RTE solution (Hy) given in Table 1 are consistently smaller than the ones obtained with DT. Especially for small distances, and when both the scattering and absorption coefficient are considered together the hybrid model yields better results. The errors in the determined absorption are smaller than 5% even for the case of a high absorption of $μ_{a} = 1 {mm}^{- 1}$ and decrease for larger source-detector separations. For all cases also the values of the reduced $χ^{2}$ are better for the hybrid solution, indicating a better modeling of the data. That the DT performs especially well for large distances in the case of $μ_{a} = 0.1 {mm}^{- 1}$ originates in the choice of the fitting range. As stated above the ratios in Fig. 1(c) and 1(d) are the same for all absorption values as the simulations and all analytical solutions have the same dependence on absorption. The different results shown in Table 1 are caused by the different time intervals of the fitting range, since the end of the interval where the intensity value is at $0.1 %$ of the maximum shifts for different values of $μ_{a}$ . In this particular case, the interval on the falling slope of the simulated data seems to cover time values favorable for the DT so that the errors of different approximations cancel each other for that set of parameters. The values of the reduced $χ^{2}$ , however, are worse than for the hybrid solution here as well.

Possible reasons for the residual discrepancy in the fit with the hybrid RTE solution are, for instance, that the radial or temporal bin sizes of the simulations were not taken into account. All photons are binned at detection with a radial bin size of $0.1 mm$ and $2 ps$ for the time-axis, while the analytical solutions use the central value of the bins. This effect can be stronger in real measurements where the size of the detection fiber is mostly larger than $0.1 mm$ . But most important the use of the extrapolated boundary condition and the method of image sources are only an approximation of the exact boundary condition considering Fresnel’s formulas.

Similar results as in Table 1 were also obtained for the simulated data with different anisotropy factors $g = 0.8$ and $g = 0.5$ .

4. Discussion

In this study, a time-dependent Green’s function for the fluence in an infinite geometry has been used to derive an approximate solution for the time-resolved reflectance from a semi-infinite medium using the extrapolated boundary condition. This analytical solution avoids the problem of long computation times linked to numerical RTE solutions, which is especially important for the inverse problem, i.e., retrieving the optical properties of the scattering medium. Even though there now already exist validated RTE solutions for the semi-infinite case in the steady state domain, there is no solution known in the time domain. The presented hybrid Green’s function has the benefit of avoiding Fourier transforms of frequency-domain solutions, since this procedure can produce strong oscillations depending on the parameters chosen and, therefore, introduces problems for solving the inverse problem by a fitting routine.

The comparisons with Monte Carlo simulations show that the derived solution based on an exact RTE solution of the infinite medium performs well also for semi-infinite geometries. The deviations depend on the construction of the boundary condition and how the reflectance is computed. Whereas the solution presented by Martelli et al.¹⁵ is a solution for isotropic scattering and works well for matched refractive indices, the hybrid solution presented here performs well for mismatched boundaries and anisotropical scattering as existent in biological tissues.

In the fitting of Monte Carlo simulations with typical optical and geometrical parameters, the errors in the retrieved optical parameters are smaller for the presented hybrid solution than with DT. The fitting was done only for time values after the peak of the simulated data leading to better results and smaller values of the reduced $χ^{2}$ . When keeping the peak in the fitting region to allow more stable fitting, especially for a low number of points as for high absorption, the presented solution still yields better results than DT. For real measurements the convolution with an instrument response function will inevitably spread parts of the signal before the peak over the time axis making the hybrid solution even more valuable for avoiding the violation of causality in the DT. The parameters of the simulations were varied in the absorption and different source-detector separations are shown, what relates to different values of the reduced scattering coefficient for a fixed distance.¹¹ The results for different values of the anisotropy factor are similar to the ones shown.

Acknowledgments

The authors thank André Liemert for helpful discussion and advice. E. Simon gratefully acknowledges financial support by the Cusanuswerk.

References

1.

F. Martelliet al., “Accuracy of the diffusion equation to describe photon migration through an infinite medium: numerical and experimental investigation,” Phys. Med. Biol., 45 (5), 1359 –1373 (2000). http://dx.doi.org/10.1088/0031-9155/45/5/318 PHMBA7 0031-9155 Google Scholar

2.

A. D. KloseA. H. Hielscher, “Iterative reconstruction scheme for optical tomography based on the equation of radiative transfer,” Med. Phys., 26 (8), 1698 –1707 (1999). http://dx.doi.org/10.1118/1.598661 MPHYA6 0094-2405 Google Scholar

3.

T. FengP. EdströmM. Gulliksson, “Levenberg-Marquardt methods for parameter estimation problems in the radiative transfer equation,” Invest. Probl., 23 (3), 879 –891 (2007). http://dx.doi.org/10.1088/0266-5611/23/3/002 INPEEY 0266-5611 Google Scholar

4.

P. S. Mohanet al., “Variable order spherical harmonic expansion scheme for the radiative transport equation using finite elements,” J. Comput. Phys., 230 (19), 7364 –7383 (2011). http://dx.doi.org/10.1016/j.jcp.2011.06.004 JCTPAH 0021-9991 Google Scholar

5.

M. S. PattersonB. ChanceB. C. Wilson, “Time resolved reflectance and transmittance for the noninvasive measurement of tissue optical properties,” Appl. Opt., 28 (12), 2331 –2336 (1989). http://dx.doi.org/10.1364/AO.28.002331 APOPAI 0003-6935 Google Scholar

6.

F. Martelliet al., Light Propagation Through Biological Tissue and Other Diffusive Media, SPIE, Bellingham (2010). Google Scholar

7.

S. R. ArridgeM. CopeD. T. Delpy, “The theoretical basis for the determination of optical pathlengths in tissue: temporal and frequency analysis,” Phys. Med. Biol., 37 (7), 1531 –1560 (1992). http://dx.doi.org/10.1088/0031-9155/37/7/005 PHMBA7 0031-9155 Google Scholar

8.

F. Martelliet al., “Analytical approximate solutions of the time-domain diffusion equation in layered slabs,” JOSA A, 19 (1), 71 –80 (2002). http://dx.doi.org/10.1364/JOSAA.19.000071 JOAOD6 1084-7529 Google Scholar

9.

A. LiemertA. Kienle, “Light diffusion in a turbid cylinder. II Layered case,” Opt. Express, 18 (9), 9266 –9279 (2010). http://dx.doi.org/10.1364/OE.18.009266 OPEXFF 1094-4087 Google Scholar

10.

A. Zhanget al., “Photon diffusion in a homogeneous medium bounded externally or internally by an infinitely long circular cylindrical applicator. I. Steady-state theory,” JOSA A, 27 (3), 648 –662 (2010). http://dx.doi.org/10.1364/JOSAA.27.000648 JOAOD6 1084-7529 Google Scholar

11.

A. KienleM. S. Patterson, “Determination of the optical properties of turbid media from a single Monte Carlo simulation,” Phys. Med. Biol., 41 (10), 2221 –2227 (1996). http://dx.doi.org/10.1088/0031-9155/41/10/026 PHMBA7 0031-9155 Google Scholar

12.

A. Pifferiet al., “Real-time method for fitting time-resolved reflectance and transmittance measurements with a Monte Carlo model,” Appl. Opt., 37 (13), 2774 –2780 (1998). http://dx.doi.org/10.1364/AO.37.002774 APOPAI 0003-6935 Google Scholar

13.

E. AlerstamS. Andersson-EngelsT. Svensson, “White Monte Carlo for time-resolved photon migration,” J. Biomed. Opt., 13 (4), 041304 (2008). http://dx.doi.org/10.1117/1.2950319 JBOPFO 1083-3668 Google Scholar

14.

J. C. Paasschens, “Solution of the time-dependent Boltzmann equation,” Phys. Rev. E, 56 (1), 1135 –1141 (1997). http://dx.doi.org/10.1103/PhysRevE.56.1135 PLEEE8 1063-651X Google Scholar

15.

F. Martelliet al., “Heuristic Green’s function of the time dependent radiative transfer equation for a semi-infinite medium,” Opt. Express, 15 (26), 18168 –18175 (2007). http://dx.doi.org/10.1364/OE.15.018168 OPEXFF 1094-4087 Google Scholar

16.

V. A. Markel, “Modified spherical harmonics method for solving the radiative transport equation,” Waves Random Media, 14 (1), L13 –L19 (2004). http://dx.doi.org/10.1088/0959-7174/14/1/L02 WRMEEV 0959-7174 Google Scholar

17.

A. LiemertA. Kienle, “Analytical solution of the radiative transfer equation for infinite-space fluence,” Phys. Rev. A, 83 (1), 158041 (2011). http://dx.doi.org/10.1103/PhysRevA.83.015804 PLRAAN 1050-2947 Google Scholar

18.

A. LiemertA. Kienle, “Light transport in three-dimensional semi-infinite scattering media,” JOSA A, 29 (7), 1475 –1481 (2012). http://dx.doi.org/10.1364/JOSAA.29.001475 JOAOD6 1084-7529 Google Scholar

19.

A. LiemertA. Kienle, “Infinite space Green’s function of the time-dependent radiative transfer equation,” Biomed. Opt. Express, 3 (3), 543 –551 (2012). http://dx.doi.org/10.1364/BOE.3.000543 BOEICL 2156-7085 Google Scholar

20.

J. C. Hebdenet al., “Three-dimensional optical tomography of the premature infant brain,” Phys. Med. Biol., 47 (23), 4155 –4166 (2002). http://dx.doi.org/10.1088/0031-9155/47/23/303 PHMBA7 0031-9155 Google Scholar

21.

A. Bassiet al., “Time-resolved spectrophotometer for turbid media based on supercontinuum generation in a photonic crystal fiber,” Opt. Lett., 29 (20), 2405 –2407 (2004). http://dx.doi.org/10.1364/OL.29.002405 OPLEDP 0146-9592 Google Scholar

22.

A. Torricelliet al., “Mapping of calf muscle oxygenation and haemoglobin content during dynamic plantar flexion exercise by multi-channel time-resolved near-infrared spectroscopy,” Phys. Med. Biol., 49 (5), 685 –699 (2004). http://dx.doi.org/10.1088/0031-9155/49/5/003 PHMBA7 0031-9155 Google Scholar

23.

T. Svenssonet al., “Near-infrared photon time-of-flight spectroscopy of turbid materials up to 1400 nm,” Rev. Sci. Instrum., 80 (6), 063105 (2009). http://dx.doi.org/10.1063/1.3156047 RSINAK 0034-6748 Google Scholar

24.

M. Mazurenkaet al., “Non-contact time-resolved diffuse reflectance imaging at null source-detector separation,” Opt. Express, 20 (1), 283 –290 (2012). http://dx.doi.org/10.1364/OE.20.000283 OPEXFF 1094-4087 Google Scholar

25.

L.G. HenyeyJ.L. Greenstein, “Diffuse radiation in the galaxy,” Astrophys. J., 93 70 –83 (1941). http://dx.doi.org/10.1086/144246 ASJOAB 0004-637X Google Scholar

26.

R. C. Haskellet al., “Boundary conditions for the diffusion equation in radiative transfer,” JOSA A, 11 (10), 2727 –2741 (1994). http://dx.doi.org/10.1364/JOSAA.11.002727 JOAOD6 1084-7529 Google Scholar

27.

A. KienleM. S. Patterson, “Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium,” JOSA A, 14 (1), 246 –254 (1997). http://dx.doi.org/10.1364/JOSAA.14.000246 JOAOD6 1084-7529 Google Scholar

28.

W. H. Presset al., Numerical Recipes in C: the Art of Scientific Computing, Cambridge University Press, New York, NY (1992). Google Scholar

Citation Download Citation

Emanuel Simon, Florian Foschum, and Alwin Kienle "Hybrid Green’s function of the time-dependent radiative transfer equation for anisotropically scattering semi-infinite media," Journal of Biomedical Optics 18(1), 015001 (4 January 2013). https://doi.org/10.1117/1.JBO.18.1.015001

Published: 4 January 2013

Access the abstract

JOURNAL ARTICLE
7 PAGES

DOWNLOAD PAPER SAVE TO MY LIBRARY

GET CITATION

CITATIONS

Cited by 11 scholarly publications.

Explore citations on Lens.org

RIGHTS & PERMISSIONS

Get copyright permission Get copyright permission on Copyright Marketplace

KEYWORDS

Monte Carlo methods

Scattering

Absorption

Reflectivity

Radiative transfer

Picosecond phenomena

Diffusion

1.

Introduction

2.

Theory