|
|
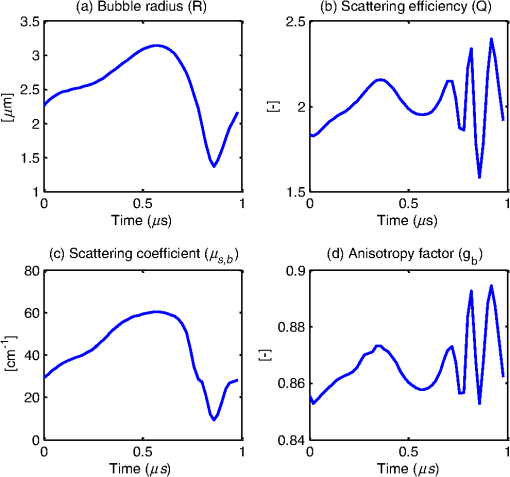
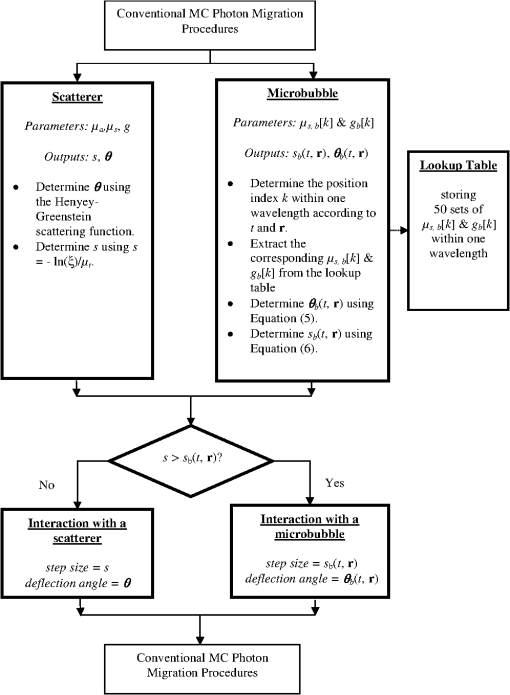
1.IntroductionSurfactant stabilized microbubbles, with diameters of a few micrometers, are used as clinical contrast agents for ultrasound imaging. While their acoustic properties have been studied extensively,1 their optical properties are less well known. When excited by ultrasound, microbubbles undergo volumetric oscillations and thus within a population their sizes vary both in time and space, as the ultrasound wavefronts pass through them. The optical scattering from an object depends on its size.2 Therefore a microbubble’s optical scattering is expected to change during insonification. Indeed, this property has enabled the application of optical measurement techniques to investigate the sizes of insonified microbubbles and their dynamics.3 It has also been suggested that the size change of insonified microbubbles can be exploited for fluorescence imaging with fluorophore labeled microbubbles.4,5 A pulse oximeter is a medical optical device that exploits the light intensity change caused by the arterial pulsation to measure arterial oxygen saturation. Recently, we proposed that a change in light intensity can also be produced in a vein, which unlike an artery has no distinctive pulsations, by exciting microbubbles inside the vein with ultrasound. In this way, venous oxygen saturation could potentially be measured noninvasively based on the microbubble-induced intensity change.6,7 This feasibility study was based on a Monte Carlo (MC) light transport model which is fully described and validated in the present paper. Venous oxygen saturation, which is currently measured by an invasive catheter, is an important diagnostic parameter reflecting the amount of oxygen extracted by an organ, e.g., the venous oxygen saturation in the internal jugular vein, a big vein in the neck draining blood from the brain, provides a measure of oxygen extraction in the brain.8 Light transport modeling in a turbid medium is often performed using either the diffusion equation (DE) or MC simulations. In the presence of microbubbles, the DE approach has been adopted to model a fluorescence imaging system with fluorophore labeled microbubbles as mentioned earlier.5 In this work, we describe an MC model of light transport in a turbid medium with insonified microbubbles. The MC model was first validated with an N-layered DE based model in a semi-infinite half-space geometry.9 To further validate the MC results, they were then compared with results from a series of experiments performed using clinical contrast agent microbubbles (SonoVue®). 2.MethodsPhoton migration in a turbid medium has been widely studied using MC simulations and the MC model described here is based on a popular one known as MCML.10 The main feature of our current MC model is the incorporation of radially oscillating microbubbles with temporally and spatially varying optical properties. This in turn leads to varying fluence within the medium. To improve the speed of computation, a graphics processing unit (Nvidia) has been used as a platform to implement the MC model, which is a modification of the MC models of ultrasound modulated light that we published recently.11,12 All the numerical values of the parameters in this work are based on those used in Ref. 1. 2.1.Monte Carlo Simulations2.1.1.Microbubble dynamicsThe dynamic response of a single microbubble can be described by the Rayleigh-Plesset equation:13–15 where is the applied US pressure, is the additional elastic resistance due to the surface coating, is the additional dissipative resistance due to the surface coating, is the instantaneous radius of the microbubble (m), m is the initial radius of the microbubble, is the density of the surrounding fluid, is the ambient pressure of the surrounding, is the pressure due to the applied US field (Pa), is the pressure of the gas inside the microbubble (Pa), , is the peak negative pressure (Pa), is the location of the US (m), is the equilibrium surface tension for a coated microbubble, , is the acoustic wavenumber (), is the coating’s effective shear modulus, is the coating’s effective shear viscosity and m is the coating’s effective thickness. Given the applied pressure , Eq. (1) can be solved numerically to obtain .2.1.2.Time- and space-dependent scattering coefficientsConsider a population of microbubbles as shown in Fig. 1(a). Without ultrasound, all microbubbles have the same size and are uniformly distributed throughout the medium. The corresponding scattering coefficient is therefore a constant. With ultrasound turned on, microbubbles have different sizes depending on their locations with respect to the propagating ultrasound waves. During rarefactions, microbubbles become larger, while under compression they become smaller. Figure 1(b) depicts the effect of an ultrasound plane wave (half a cycle) on the size of microbubbles. Since microbubbles now have a nonuniform size distribution, its corresponding is no longer a constant. Fig. 1(a) Ultrasound off: microbubbles have the same size, is constant, and the step size has a negative exponential distribution; (b) ultrasound on: microbubble sizes,, and the distribution of the step size all vary temporally and spatially. 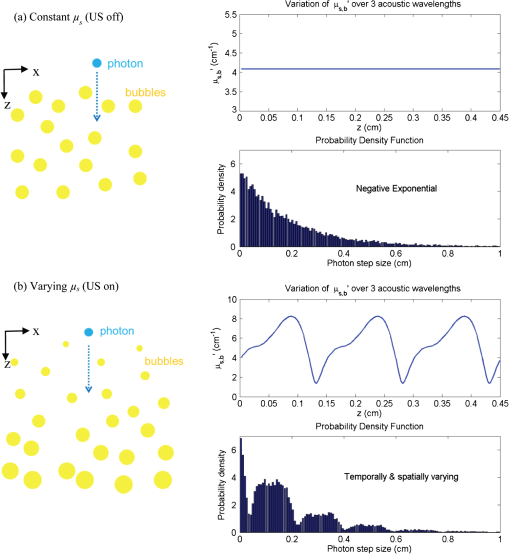 Consider the definition of of a population of microbubbles based on the general definition:16 where is the scattering coefficient of microbubble (), is the scattering efficiency of the microbubble (dimensionless), is the location of the microbubble (m), and is the microbubble concentration (). Equation (2) is a classical definition of except that two parameters, namely the scattering efficiency of the microbubble and the radius , are now defined as time- and space-dependent to reflect the change in optical properties and the size of the oscillating microbubbles. While can be obtained using the Rayleigh-Plesset equation as mentioned in the previous section, the calculation of is less direct. The scattering efficiency is defined as the ratio of the cross-sectional area of scattering to the geometrical cross-sectional area of the particle (microbubble), and is related to the magnitude of refractive index mismatch between the particle and its surrounding medium.16 The refractive index of a microbubble is, in turn, governed by its internal pressure , which itself is a function of :1 where is the polytropic index. With now known, the refractive index inside the microbubble, can be calculated using the Lorentz-Lorenz equation:17 where is the refractive index inside the microbubble, is the molar refractivity, () is absolute temperature and is the molar gas constant. Mie theory can be used to describe the interaction between light and a spherical scatterer (microbubble). Using Mie theory, can now be derived from , and the predefined refractive index external to the microbubble . Note that the external refractive index here is a constant, implicitly assuming that the external refractive index is not influenced by the applied ultrasound pressure or the radiated pressure from an oscillating microbubble. Also derived from Mie theory is the anisotropy factor for the microbubble. We used a published MATLAB toolbox for the implementation of the Mie solution.18 With the knowledge of and , the time- and space- dependent scattering coefficient can now be obtained using Eq. (2). Figure 2 shows examples of the variation of , , and of an oscillating microbubble over one acoustic cycle (1 μs) at a particular location .2.1.3.Anisotropic factorTo determine the deflection angle of a photon after its collision with a microbubble, the Henyey-Greenstein scattering function10 is used. Since the anisotropy factor of a microbubble is both time- and space-dependent, the Henyey-Greenstein scattering function becomes where is a uniformly distributed random number. The Henyey-Greenstein scattering function is a widely accepted scattering phase function in diffuse optics for MC simulations because it only involves a few arithmetic operations and can therefore be efficiently implemented in MC simulations typically involving more than 10 million iterations. Although Mie theory can provide a more theoretically accurate scattering phase function, its calculation is much more complicated and would demand much more processing power, which is the reason why it is rarely used in the MC simulations of common problems in diffuse optics.2.1.4.Photon step sizeThe photon step size in a homogenous medium can be easily generated using a conventional formula:10,16 and , where is the absorption coefficient. In a medium with the varying scattering coefficient , the step size cannot be simply generated by the conventional formula. Instead, we consider a more general case in which the attenuation of light due to spatially varying scattering can be expressed as16 and is derived by solving the equation . The microbubble’s is assumed to be zero here. To implement this in a computer, a piecewise-linear approximation is proposed here which can be used in the current scenario of an ultrasound plane wave propagating from the top to the bottom of a homogenous slab: where is the layer index (starting layer has an index of 1), is the number of layers of media that a photon has encountered and the index of the last layer that a photon arrives at, is the thickness of a layer, is the scattering coefficient of layer , is the step size within layer , and is the angle between the propagation direction of the photon and that of the ultrasound wave. Although the radii of microbubbles are in fact continuously varying along the propagation direction of the ultrasound plane wave, the piecewise-linear scheme quantizes the radii with fixed values as shown in Fig. 3. Subsequently, is also quantized to . The main unknown in Eq. (6) is , from which and can both be derived. Other variables such as , and have been preassigned before the photon propagation. To solve Eq. (6), a random number is first drawn, and , and are then found iteratively by trying a range of values for until both sides of Eq. (6) are equal. The total step size is the summation of all the intermediate steps: for , for , for . In this work, a 1 MHz ultrasound with a wavelength of 1.5 mm was used. Each wavelength was divided into 50 layers, each having a length of 0.03 mm. The 50 layers also correspond to 50 values of and , which were precalculated and stored in a lookup table for the MC simulations.Fig. 3Piecewise-linear scheme to determine the photon step size in a medium with rapidly changing scattering coefficients. 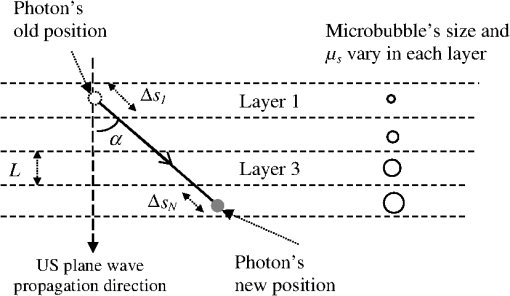 In a turbid medium, the distance (step size) that a photon travels before it hits a scatterer is determined by . Since the scatterers are randomly distributed, it is impossible to predict the exact step size for each photon collision. However, the probability of a given photon step size is deterministic in simple cases and the function that describes such probability over different photon step sizes is known as probability density function (PDF). In the case of a turbid medium with uniformly distributed microbubbles having the same size, the corresponding is also uniformly distributed before the ultrasound is switched on and the PDF has a negative exponential distribution10 as shown in Fig. 1(a). When the ultrasound is switched on, microbubbles vary in size spatially and temporally, causing to vary as well. Figure 1(b) depicts the scenario when an ultrasound plane wave propagates vertically downwards in the -direction. The variation of over three acoustic wavelengths in the -direction is also shown here. In this scenario, the PDF has a more complicated shape. The “humps” in the PDF correspond to the photon traveling a distance of several wavelengths, experiencing varying along the way. The PDF shown in Fig. 1(b) was obtained by launching photons in the -direction, calculating the first step sizes using Eq. (6) and the methodology introduced in the last paragraph, and binning the step sizes to form a histogram. In the subsequent steps, when the photons are within the medium, the direction of travel may not be along the -direction. As a result, the corresponding PDF will look different from the one shown in Fig. 1(b). Also, the microbubble sizes and therefore vary over time, again resulting in different PDFs. Therefore, the PDF of the photon step size in a turbid medium with insonified microbubbles is temporally and spatially varying. 2.1.5.FlowchartThe additional part of the MC model to account for the insonified microbubbles is shown in a flowchart in Fig. 4. The current absolute position and the time instant of the photon is considered so that its relative position, i.e., the position index , in an acoustic wavelength can be determined which also provide appropriate and for that position. The step sizes from the current photon position to the next native scatterer , i.e., one present naturally in the medium, and microbubble are both calculated. If is larger than , the photon packet is treated as colliding with a microbubble. Otherwise, the photon packet collides with a native scatterer. The rest of the MC model is the same as the conventional MCML model.10 2.2.Validation with an N-Layered Diffusion Equation ModelTo validate the MC code, an N-layered DE model9 has been adopted to generate reflectance data to compare with the MC results. This DE model allows the modeling of light propagation through many thousands of layers, each with different optical properties. For the MC model, the geometry was a rectangular block measuring ( or ) and photons were launched from the middle point of the top layer. For a 1 MHz ultrasound plane wave that propagated from top to bottom, the total number of layers was 1634 including the top layer (1 mm thick) and the subsequent 1633 layers, each with a thickness of 0.03 mm because each wavelength, i.e., 1.5 mm, was divided into 50 layers. The optical wavelength was 500 nm. In the first validation, the light model was a simple homogenous medium for both the DE and MC models in reflection mode. This was to ensure that the additional algorithms described in Secs. 2.1.1 to 2.1.4 did not alter the basic operation of the MC code. In the MC model, all the 1634 layers had the same optical properties with , , , and refractive index . The reflectance was calculated using a series of ring detectors at a distance from the source, each with a radial width , so that the reflectance was given by , where is the reflectance at radial distance , is the sum of all photon weights detected in the th ring, and is the total number of photons launched from the source. As for the N-layered DE model, only one layer was used, which had the same optical properties as the MC model, i.e., , and . In the second validation, microbubbles were considered in the medium. Two conditions were simulated: ultrasound on and ultrasound off. The background , , and were chosen. It was assumed that microbubbles had negligible optical absorption. Without ultrasound, microbubbles had the same size in the medium, and the scattering coefficient and anisotropy factor were also constant throughout. The N-layered DE model had the same layer structure as the MC model, i.e., , followed by 1633 layers, each with a thickness of 0.03 mm. The scattering for each layer was calculated as the sum of the background and microbubble at that location. With ultrasound on, the optical scattering due to the insonified microbubbles became variable throughout the medium as described in Sec. 2.1.2. This was handled by the MC model using piece-wise integration along photon paths as described in Sec. 2.1.4. The microbubbles’ scattering coefficients and anisotropy factor at each layer are shown in Fig. 2. As before, the N-layered DE modeling was performed with the same background , the same varying at each layer plus the background and at the same time instant as the MC model. 2.3.ExperimentsThe experimental studies involved transmittance measurement of near infrared light through a transparent silicone gel phantom (Encapso K). This phantom had a dimension of () and contained a cuboidal cavity measuring at the center, filled with Intralipid and a microbubble suspension, providing optical scattering and absorption. A schematic diagram of this setup is given in Fig. 5. The concentration of the Intralipid was 0.1% corresponding to a scattering coefficient of according to a previous study.19 The microbubbles were the clinical grade SonoVue® prepared according to the manufacturer’s instructions and diluted, and the concentration was estimated using a microscopy technique, which involved automated counting of microbubbles from images obtained with an optical microscope.20 An example of a microscopy image of a SonoVue® suspension with an estimated concentration of is shown in Fig. 6. Fig. 5Experimental setup: LA: laser (780 nm), AMP: RF amplifier, SG: signal generator, UT: ultrasound transducer, DAQ: data acquisition module, PC: computer, SPC: single photon counter, W: water in a water tank, MF: multimode optical fiber, P: transparent phantom, I: Intralipid & microbubbles. 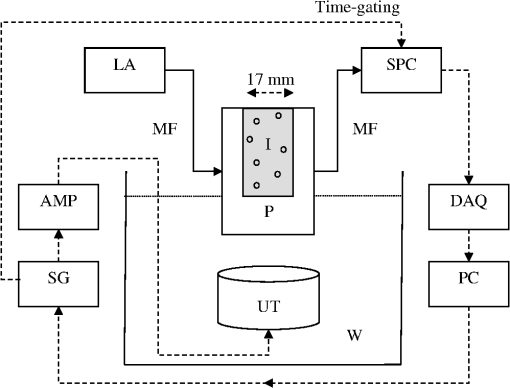 The ultrasound transducer was an A392S-SU Olympus immersion unfocused cylindrical transducer with a central frequency of 1 MHz and a nominal element diameter of 39 mm. It was positioned 60 mm below the phantom to avoid near-field effects. Microbubbles were insonified with ultrasound pulses instead of continuous wave to avoid destroying them. The duty cycle and repetition rate of the ultrasound pulses were 0.5% and 1 kHz, with 5 cycles in each burst. The maximum acoustic pressure inside the mixture was 111 kPa as measured by a hydrophone (1 mm diameter, Precision Acoustics, United Kingdom). The optical source was a 780 nm fiber coupled laser (FCLM780.25-PLR48-H-MM, Ondax, USA), and the light was collected by a multimode fiber and detected by a single photon counter (SPCM-AQRH-14-FC, PerkinElmer, USA), which was chosen because of its superior performance in detecting small light intensity change. It was time-gated so that it only detected light when the mixture was insonified. The output of the single photon counter was connected to the digital input channel of an analogue-to-digital converter (NI USB-6221, National Instruments, USA) which provided a digital count of the number of photons recorded. The average photon count was recorded both with ultrasound and in the absence of ultrasound. These measurements were taken in an interleaved pattern: for 5 s, ultrasound was applied with a 0.5% duty cycle and the photon count was recorded. For the following 5 s, the ultrasound was turned off and the photon count was recorded in a similar way. This process was repeated for a total of 30 s. After this point the mixture was lightly stirred to ensure the microbubbles were still well distributed, and the process repeated 10 times. The photon count was averaged over 0.75 s () in total to provide each measurement. The average photon count per second with ultrasound, proportional to , and the photon count per second without ultrasound, proportional to , are used to calculate a measure of the microbubble enhanced optical attenuation (MOA): where is the optical attenuation and the incident light intensity.Two series of experiments were conducted. In the first, the peak negative ultrasound pressure was increased from 5 to 110 kPa and the microbubble concentration was . In the second, different microbubble concentrations from 0.5 to were used and . The MC modeling was also performed with the same optical wavelength, same geometry, and similar peak negative ultrasound pressure and microbubble concentrations as those of the experiments. The photons were recorded by a circular area detector with a radius of 1 mm, centered on the face of the phantom opposite to the source (transmission mode). For each condition, five sets of independent MC simulations were performed to provide the mean and standard deviation of MOA for assessing the quality of the MC results. For each of the five sets of MC simulations, another five MC simulations corresponding to different scattering changes in the medium induced by the insonified microbubbles over time during five evenly spaced points in an acoustic cycle were also performed. The resulting five MOAs were then averaged to provide an MOA for the set of MC simulations. In total, each condition involves 25 sets of MC simulations, with 50 million photons in each set. 3.Results3.1.Validation with the N-Layered Diffusion Equation Based ModelIn the first validation, a homogenous case without microbubbles was considered. Figure 7 depicts the radially resolved reflectance calculated by the MC and DE models which shows a reasonably good agreement. Fig. 7Validation in a homogenous medium: reflectance calculated by the MC and DE models show a reasonably good agreement (, , , , ). 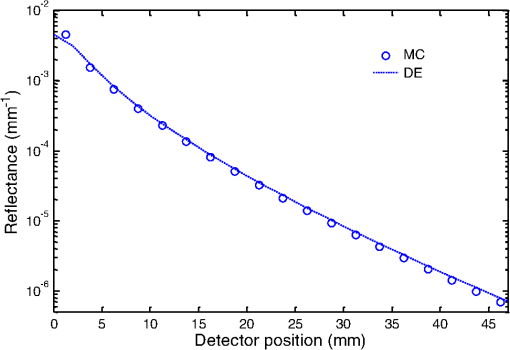 In the second validation, microbubbles were considered both with and without ultrasound exposure. Figure 8 shows the reflectance calculated by both the MC and DE models with ultrasound on and off, respectively. The results indicate a good agreement between the two. At larger source detector spacing, e.g., at 40 mm, the reflectance was smaller when the ultrasound was on. This is expected because insonified microbubbles have a larger mean size, giving rise to a larger optical scattering and therefore a smaller reflectance. In general, the discrepancies between the MC and DE results in Figs. 7 and 8 have similar magnitudes to those described in the original paper that first proposed this DE model.9 Fig. 8Validation in a heterogeneous medium with rapidly changing due to insonified microbubbles: reflectance calculated by the MC and DE models for ultrasound off (blue crosses and blue dashed line, respectively), and (ii) ultrasound on (red dots and red line, respectively) (background , , , , , , ). 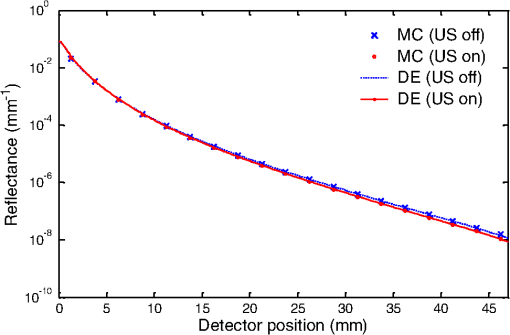 3.2.Experimental ResultsFigure 9 shows that in general MOA increases with the peak negative ultrasound pressure for both experimental and MC results. This is expected because a higher ultrasound pressure will lead to a larger mean size of the insonified microbubbles which also means a higher optical scattering and therefore a larger MOA. The MC model predicted smaller MOAs than the experimental MOAs for similar peak negative ultrasound pressures. After the application of continuous ultrasound for 30 s at 110 kPa, microbubbles were all destroyed and its MOA became zero (marker “star” in Fig. 9). For comparison, the MOA for the medium with only Intralipid is also shown which has a zero MOA as expected because no microbubbles were present. Fig. 9Comparison of experimental and MC results: the MOA generally increases with the peak negative ultrasound pressure for the SonoVue® suspension and the MC model. The MOA is constant and close to zero for samples without microbubbles (background , , , , , ). 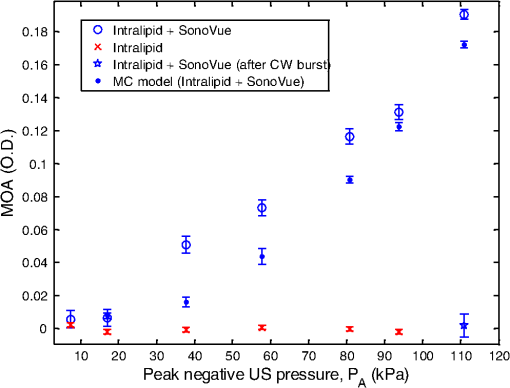 Figure 10 shows that MOA increases with the microbubble concentration for both experimental and MC results. This again is expected because a higher density means a higher optical scattering and therefore a higher MOA. In comparison to the experimental MOA, the MC MOA is larger for lower microbubble density, i.e., lower than , and smaller for a higher microbubble density. Fig. 10Comparison of experimental (crosses) and MC (squared dots) results: the MOA generally increases with the microbubble density. For the experimental results, there are uncertainties related to both the estimation of MOA and the microbubble density. The means and the standard deviations of both the MOA and microbubble density are shown (background , , , , , ). 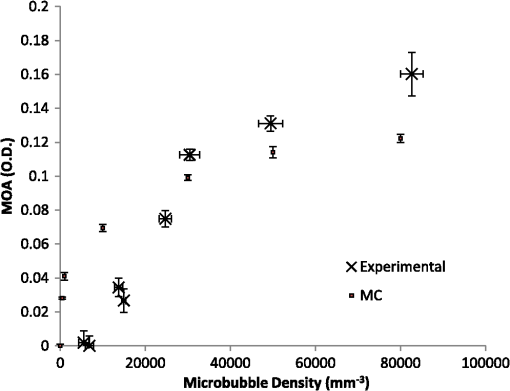 4.Discussion4.1.Assumptions in the MC ModelThe interaction between light, ultrasound and microbubbles is a complex process and several factors have not been considered in the current model. First, while the MC model assumes all microbubbles have the same size in the absence of ultrasound, real microbubbles always have different sizes as shown in the microscopy image of SonoVue® in Fig. 6. Second, it has been pointed out that ultrasound propagation causes the local acoustic pressure to change, leading to a change in refractive index. Therefore, photons may not travel in a straight line21 as assumed in this MC model. Third, it is known that the volumetric oscillation of a microbubble changes the acoustic pressure surrounding the microbubble (radiated pressure)1 which in turn also changes the refractive index and again causes photons to bend. The MC model presented here does not consider this. Another reason for the discrepancy between the MC and experimental results is that the optical and acoustic properties of the medium in the MC model and experiments may not match completely. However, based on the general agreement with the experimental results, the MC model is considered a reasonably accurate model. All the factors mentioned above can be considered with a more sophisticated MC model in future works. 4.2.Microbubble Density and the MOAIncreasing the microbubble density also leads to increase in . For a homogenous medium, when the is increasing, one would expect the optical attenuation to increase, and the transmittance to decrease, accordingly in a nonlinear fashion. In our scenario, however, the medium is highly heterogeneous with many layers of varying . Figure 10 shows that the nonlinearity between the MOA and microbubble density is very prominent, especially for the MC results. In general, the rise in MOA is more rapid for a smaller microbubble density below a certain threshold. Above this threshold, the MOA rise becomes more moderate. For the MC results, this threshold is quite low at but for the experimental results, the threshold is higher at a microbubble density of . In reality, microbubbles have a distribution of sizes and only microbubbles with certain sizes (and therefore resonant frequencies) resonate at a particular ultrasound frequency. In other words, only a portion of the microbubbles contribute to the MOA amplitude. All the microbubbles in the MC simulations, on the other hand, have the same sizes. They all resonate and contribute to the MOA amplitude. It is likely that the discrepancy between microbubble sizes causes this microbubble density threshold being at different values for the MC and experimental MOAs. In future studies, it would be interesting to investigate this microbubble density threshold further with different geometries and parameters. 4.3.Microbubble Size DistributionIn general, larger resonating microbubbles tend to have a larger effect on the amplitude of MOA than smaller resonating microbubbles do. Ultrasound frequency is another factor to consider because it governs the resonation of microbubbles of certain sizes. We have performed a series of analyses to investigate the effect of having a distribution of microbubble sizes on the MOA amplitude (results not shown here). In comparison to the MOA of a microbubble population with the same size, the MOA of the microbubbles with different sizes is larger. For a distribution with microbubble sizes between 0.6 and 7 μm, which is in a similar range as the commercial SonoVue® microbubbles,22 the MOA could be a few times higher. Although smaller microbubbles are also present in the latter case, their contribution to the MOA amplitude is more than compensated by that of the larger microbubbles. The simulations shown in this paper are all based on a single-size microbubble population, when ultrasound is off, for simplicity which could be a reason of the MC MOA being smaller than the experimental MOA as shown in Fig. 9 and part of Fig. 10. This issue will be revisited in more detail in future work. 4.4.Comparison with Ultrasound Modulated Optical TomographyThe use of ultrasound to modulate light, a technique known as ultrasound modulated optical tomography (UOT) or acousto-optic imaging, has been investigated for more than a decade.23,24 It is capable of providing both good optical contrast for tissue and spatial resolution similar to that of ultrasound imaging. This technique relies on the detection of a ultrasound-modulated laser speckle which has a very low signal-to-noise ratio and requires a coherent laser. The MOA approach has the potential to be used in similar areas as UOT, especially in sensing applications, and yet the detection of MOA is much easier and more economical because MOA only involves light intensity, rather than laser speckle, measurement which can be performed with any monochromatic light, coherent or not, using low cost optical detectors. However, the requirement of microbubbles in the medium inevitably increases the complexity of the technique. 5.ConclusionAn MC model has been developed for light propagation in a turbid medium with insonified microbubbles, and has been validated using a DE model and experiments with clinical grade microbubbles (SonoVue®). While near infrared contrast agents such as indocyanine green have been widely used for their absorption properties,25,26 we have shown that insonified microbubbles can be used as a “scattering” contrast agent. Although there are discrepancies between the MC and experimental results as evident in Figs. 9 and 10, it is encouraging to see that their MOAs have the same general trends and orders of magnitude. Since MOA is by nature an optical attenuation and a ratio, it is less influenced by instrumentation factors, such as the power of incident light and detection efficiency. Another advantage of MOA is that optical attenuation is readily related to chromophore concentration through the modified Beer-Lambert law, which is useful for oxygen saturation measurement.7 As we have explored in our previous studies using the MC model developed here,6,7 the MOA technique may potentially be applied to the estimation of venous oxygen saturation. AcknowledgmentsThe authors would like to thank Andre Liemert and Samuel Powell for their help in implementing the N-layered Diffusion and MC models. This research was partly funded by the Engineering and Physical Sciences Research Council (Grant Code EP/G005036/1) and the British Heart Foundation. ReferencesE. StrideM. X. TangR. J. Eckersley,
“Physical phenomena affecting quantitative imaging of ultrasound contrast agents,”
Appl. Acous., 70
(10), 1352
–1362
(2009). http://dx.doi.org/10.1016/j.apacoust.2008.10.003 AACOBL 0003-682X Google Scholar
H. C. van de Hulst, Light Scattering by Small Particles, Dover Publications, New York
(1981). Google Scholar
J. GuanT. J. Matula,
“Using light scattering to measure the response of individual ultrasound contrast microbubbles subjected to pulsed ultrasound in vitro,”
J. Acous. Soc. Am., 116
(5), 2832
–2842
(2004). http://dx.doi.org/10.1121/1.1795334 JASMAN 0001-4966 Google Scholar
B. YuanJ. GamelinQ. Zhu,
“Mechanisms of the ultrasonic modulation of fluorescence in turbid media,”
J. Appl. Phys., 104
(10), 103102
(2008). http://dx.doi.org/10.1063/1.3021088 JAPIAU 0021-8979 Google Scholar
B. Yuan,
“Ultrasound-modulated fluorescence based on a fluorophore-quencher-labeled microbubble system,”
J. Biomed. Opt., 14
(2), 024043
(2009). http://dx.doi.org/10.1117/1.3120493 JBOPFO 1083-3668 Google Scholar
J. HoneysettE. StrideT. S. Leung,
“Ultrasound-modulated optical sensing of oxygenation enhanced by microbubbles,”
Proc. SPIE, 7899 789919
(2011). http://dx.doi.org/10.1117/12.876111 PSISDG 0277-786X Google Scholar
J. Honeysettet al.,
“An algorithm for sensing venous oxygenation using ultrasound-modulated light enhanced by microbubbles,”
Proc. SPIE, 8223 82232Z
(2012). http://dx.doi.org/10.1117/12.907952 PSISDG 0277-786X Google Scholar
M. Smith,
“Neuromonitoring,”
Anaesth. Intensive Care Med., 9
(5), 187
–192
(2008). http://dx.doi.org/10.1016/j.mpaic.2008.03.006 ANIMD2 0171-1814 Google Scholar
A. LiemertA. Kienle,
“Light diffusion in N-layered turbid media: steady-state domain,”
J. Biomed. Opt., 15
(2), 025003
(2010). http://dx.doi.org/10.1117/1.3368685 JBOPFO 1083-3668 Google Scholar
L. WangS. L. JacquesL. Zheng,
“MCML—Monte Carlo modeling of light transport in multi-layered tissues,”
Comput. Methods Programs Biomed., 47
(2), 131
–146
(1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar
T. S. LeungS. Powell,
“Fast Monte Carlo simulations of ultrasound-modulated light using a graphics processing unit,”
J. Biomed. Opt., 15
(5), 055007
(2010). http://dx.doi.org/10.1117/1.3495729 JBOPFO 1083-3668 Google Scholar
S. PowellT. S. Leung,
“Highly parallel Monte-Carlo simulations of the acousto-optic effect in heterogeneous turbid media,”
J. Biomed. Opt., 17
(4), 045002
(2012). http://dx.doi.org/10.1117/1.JBO.17.4.045002 JBOPFO 1083-3668 Google Scholar
T. G. Leighton, The Acoustic Bubble, Academic Press, London
(1997). Google Scholar
M. PlessetA. Prosperetti,
“Bubble dynamics and cavitation,”
Ann. Rev. Fluid Mech., 9 145
–185
(1977). http://dx.doi.org/10.1146/annurev.fl.09.010177.001045 ARVFA3 0066-4189 Google Scholar
L. HoffP. C. SontumJ. Hovem,
“Oscillations of polymeric microbubbles: effect of the encapsulating shell,”
J. Acous. Soc. Am., 107
(4), 2272
–2280
(2000). http://dx.doi.org/10.1121/1.428557 JASMAN 0001-4966 Google Scholar
F. Martelliet al., Light Propagation Through Biological Tissue and other Diffusive Media, SPIE Press, Bellingham, WA
(2010). Google Scholar
M. BornE. Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Cambridge University Press, Cambridge
(1999). Google Scholar
C. Matzler,
“Matlab functions for Mie scattering and absorption,”
(2002). Google Scholar
H. J. Van Staverenet al.,
“Light scattering in Intralipid-10% in the wavelength range of 400–1100 nm,”
Appl. Opt., 30
(31), 4507
–4514
(1991). http://dx.doi.org/10.1364/AO.30.004507 APOPAI 0003-6935 Google Scholar
C. A. Sennogaet al.,
“On sizing and counting of microbubbles using optical microscopy,”
Ultrasound Med. Biol., 36
(12), 2093
–2096
(2010). http://dx.doi.org/10.1016/j.ultrasmedbio.2010.09.004 USMBA3 0301-5629 Google Scholar
Q. LiuS. NortonT. Vo-Dinh,
“Modeling of nonphase mechanisms in ultrasonic modulation of light propagation,”
Appl. Opt., 47
(20), 3619
–3630
(2008). http://dx.doi.org/10.1364/AO.47.003619 APOPAI 0003-6935 Google Scholar
J. M. GorceM. ArditiM. Schneider,
“Influence of bubble size distribution on the echogenicity of ultrasound contrast agents: a study of SonoVue,”
Invest. Radiol., 35
(11), 661
–671
(2000). http://dx.doi.org/10.1097/00004424-200011000-00003 INVRAV 0020-9996 Google Scholar
L. V. Wang,
“Ultrasound-mediated biophotonic imaging: a review of acousto-optical tomography and photo-acoustic tomography,”
Dis. Markers, 19
(2–3), 123
–138
(2004). DMARD3 0278-0240 Google Scholar
S. G. ResinkA. C. BoccaraW. Steenbergen,
“State-of-the art of acousto-optic sensing and imaging of turbid media,”
J. Biomed. Opt., 17
(4), 040901
(2012). http://dx.doi.org/10.1117/1.JBO.17.4.040901 JBOPFO 1083-3668 Google Scholar
T. S. Leunget al.,
“A new method for the measurement of cerebral blood volume and total circulating blood volume using near infrared spatially resolved spectroscopy and indocyanine green: application and validation in neonates,”
Pediatr. Res., 55
(1), 134
–141
(2004). http://dx.doi.org/10.1203/01.PDR.0000099775.87684.FB PEREBL 0031-3998 Google Scholar
T. S. Leunget al.,
“Theoretical investigation of measuring cerebral blood flow in the adult human head using bolus Indocyanine Green injection and near-infrared spectroscopy,”
Appl. Opt., 46
(10), 1604
–1614
(2007). http://dx.doi.org/10.1364/AO.46.001604 APOPAI 0003-6935 Google Scholar
|