Monte Carlo lookup table-based inverse model for extracting optical properties from tissue-simulating phantoms using diffuse reflectance spectroscopy

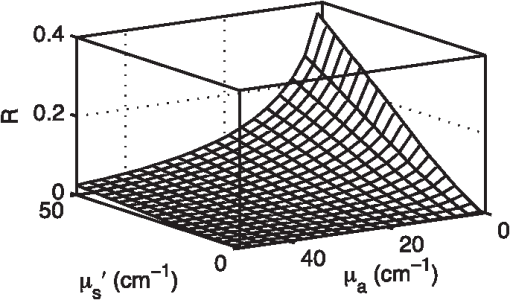
Diffuse reflectance spectroscopy (DRS) has been widely used to characterize tissue optical properties for disease diagnosis.^1–4 Typically, DRS uses a fiber to deliver light to tissue. The delivered light is both scattered and absorbed by the tissue and is then recollected by another fiber a short distance from the source fiber. The collected light, or diffuse reflectance, contains quantitative information about tissue structure and composition. While the instrumentation for a DRS system is very simple, the accurate extraction of optical properties from the collected signal is a significant challenge. An accurate tissue model is needed to relate the collected signal to tissue optical properties. One method for analyzing diffuse reflectance spectra relies on the solution to the diffuse approximation of the radiative transport equation. However, the diffusion approximation is not valid for short source-detector separations or in highly absorbing tissues.⁵

Because most cancers originate in the epithelial layer, it is necessary to use probes with a short source-detector distance in order to sample photons that travel through the epithelial layer.⁶ In addition, angiogenesis, an indicator of early cancer, can cause a significant increase in absorption due to blood. Unfortunately, the diffuse approximation is not valid in these regimes. Recently, reflectance lookup tables have been used to analyze diffuse reflectance spectra.^7,8 These lookup tables are created in two different ways: experimental measurements of phantoms with known optical properties⁷ or Monte Carlo simulations.⁹ Creating a lookup table (LUT) with experimental measurements has the advantage of incorporating unknown system responses into the LUT. However, the creation of an experimental LUT is time-consuming, and the accuracy is dependent on the skill and experience of the investigator. The Monte Carlo method is especially useful for creating an LUT, because it provides the ability to model complex probe geometries and tissue structures. However, intensive computation is required to achieve results with desirable variance, which can make it extremely time-consuming to populate an LUT containing thousands of values.

Much prior work has been undertaken to improve the speed and efficiency of the Monte Carlo method for modeling light transport in turbid media. These methods can be separated into three groups:

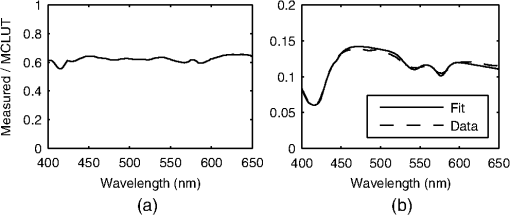
The first set of methods has the advantage of not requiring a large number of simulations to create an LUT. However, errors arise because the photon trajectory information necessary to perform the scaling operation can be recorded only in several depth intervals with finite widths.¹³ Geometry splitting techniques decrease the number of photons needed for a simulation to converge, but their implementation is very difficult for complex probe geometries. The third set of methods uses classical Monte Carlo simulations and therefore does not make any sacrifices in accuracy, flexibility, or implementation difficulty. Speedup is achieved by simulating multiple photons simultaneously on different processors. Because each photon is independent of every other photon, this problem is considered “embarrassingly parallel.” Alerstam et al. have shown that general-purpose graphic processing units (GPGPUs) can increase the speed of Monte Carlo simulations of photon transport by three orders of magnitude on a relatively inexpensive GPU when compared to the sequential implementation.¹² We present, for the first time, a Monte Carlo LUT-based model where all values in the LUT were created by independent Monte Carlo simulations by using a parallel implementation on a GPGPU.

A two-dimensional Monte Carlo code written in ANSI $C$ implemented on an NVIDIA GTX 560 Ti GPU with NVIDIA’s Compute Unified Device Architecture (CUDA) was used to simulate photon reflectance in a single-layer tissue model on 386 parallel threads.¹² The multiply with carry random number generator was used. The refractive index above the tissue was set to 1.452 to match the refractive index of the fiber, and the refractive index of the tissue was set to 1.33 to match the refractive index of the phantoms. To test the effect of errors in the refractive index, we created LUTs with different refractive indices and repeated the extraction of optical properties with the different LUTs. We found a 5% error rate in the refractive index corresponds to error increases of 1.3% for extracted $μs′$ values and 0.8% for extracted $μa$ values. To prevent photons from exiting the tissue volume, the radius and width of the tissue volume were set to 3 cm. A total of $1×106$ photons were launched to obtain the impulse response. To ensure stochastic noise would be sufficiently low in LUT locations with high albedo, 100 separate MC simulations were performed with the optical properties in the LUT that would give the lowest value of reflectance. We found that using $1×106$ photons reduced the standard deviation of the 100 different reflectance values to less than 0.5% of the mean. The diffuse reflectance for our specific probe geometry was then calculated by convolving the impulse response with the beam profile.¹⁴ Our probe was modeled using a Gaussian shaped beam profile of collimated light with a diameter of 200 μm, a detector diameter of 200 μm, and a source-detector separation of 250 μm. The diffuse reflectance values for all physiological realistic combinations of scattering and absorption were calculated using the GPGPU Monte Carlo implementation with the tissue and probe geometry described above. Twenty increments ($N$) were used for both scattering (0 to $50cm−1$) and absorption (1 to $50cm−1$), meaning a total of 400 separate Monte Carlo simulations were needed to create the LUT. The Henyey-Greenstein phase function was used for sampling scattering angles. The scattering anisotropy ($g$) was set to 0.85 for all simulations. For the range of $g$ values present in human tissue ($g>0.8$), it has been shown¹⁰ that the diffuse reflectance will be the same for any values of $μs$and $g$ that generate the same $μs′$. The resulting MCLUT is shown in Fig. 1. It took 2 min to run the 400 separate Monte Carlo simulations.

For the forward model used to generate diffuse reflectance spectra, the reduced scattering coefficient was constrained to the form Display Formula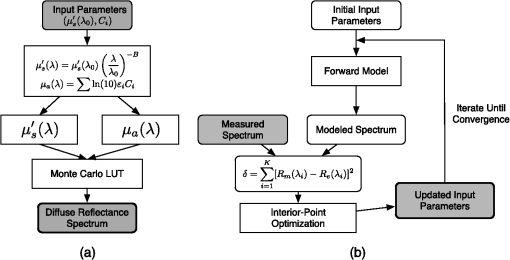

Figure 2(b) shows the inverse model used to fit our diffuse reflectance spectra. First, we made an initial guess for the optical properties, and then the forward model was used to generate a spectrum. Next, the sum of squares error between the predicted reflectance and the measured reflectance was calculated using Display Formula

To test the performance of our MCLUT-based inverse model, we created 21 tissue phantoms with hemoglobin (Hb) (Sigma-Aldrich) as the absorber and polystyrene beads ($diameter=1μm$) as the scatterer. Hb concentration [(Hb)] ranged from 0 to $3mg/ml$, and the reduced scattering coefficient [$μs′(λ0=630nm)$] ranged from 6.4 to $27.5cm−1$. We used Mie theory to calculate the $μs'$ of the tissue phantoms. For our inverse model, we assumed the absorption in the visible range was due to oxy-hemoglobin. We measured the optical density for the $HbO2$ solution using a spectrophotometer and calculated the absorption spectrum using Beer’s law. Because the addition of $HbO2$ dilutes the solution, a small change in $μs′$ was accounted for when calculating the known values for $μs′$. The DRS system consisted of a xenon flash lamp (Model: E6611, Hamamatsu) as the light source, a spectrograph (Model SP2150i, Princeton Intruments) and camera (Cool-SNAP, Photometrics) as the spectrometer; and a fiber optic probe with the geometry described above (FiberTechOptica, Ontario, Canada). The diffuse reflectance spectrum and its associated fit can be seen in Fig. 3(b) and shows that the inverse model can accurately fit the experimental data. Figure 4(a) and 4(b) shows scatter plots of the extracted versus expected for $μs′(λ0)$ and [Hb], respectively. The solid line in each graph is the line of perfect agreement. The results indicate there is excellent agreement between the extracted and expected optical properties. The MCLUT inverse model estimated the optical properties over a wide range with average root-mean-square percent errors of 1.74% for $μs′$, 0.74% for $μa$, and 2.42% for [Hb]. We compared the performance of our MCLUT-based model to an experimental LUT-based model. The MCLUT model was able to estimate $μs′$ and $μa$ with decreases in percent error of 3.16% and 10.86%, respectively, when compared to the experimental LUT model.⁷

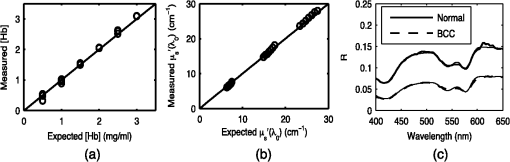Our inverse model was then tested on previously collected data from a clinical feasibility study¹⁵ to illustrate the application of the model for noninvasive detection of skin cancer. Figure 4(c) shows representative spectra from two groups: clinically normal and basal cell carcinoma (BCC). The plot shows good agreement between the MCLUT fit and the measured in vivo spectra. For this analysis, the absorption coefficients calculated in the forward model were determined by melanin, deoxy-hemoglobin, and oxy-hemoglobin.

Although other inverse models have recently been developed for extracting optical properties from diffuse reflectance spectra, this work represents the first Monte Carlo lookup table-based inverse model where the LUT was generated entirely by Monte Carlo simulation. Previously, the amount of time required to generate a LUT entirely by Monte Carlo simulation made this technique infeasible. However, recent advances in GPGPU computing have allowed parallel Monte Carlo implementations capable of running three orders of magnitude faster than traditional, serial implementations of Monte Carlo simulations. By creating an LUT entirely by Monte Carlo simulation, our method is not subject to the errors that arise from using either the diffusion approximation or the Monte Carlo scaling method. When compared to an experimental LUT, our method was more accurate, but, more importantly, it has the advantages of being easier to implement and repeatable. This model can also be adapted to more complex probe and tissue geometries.

The funding for this project was provided by the NIH (NIBIB R21EB0115892 and NCI RO1 CA132032), the NSF (DGE-1110007), and the Texas Higher Education Coordinating Board.