|
|
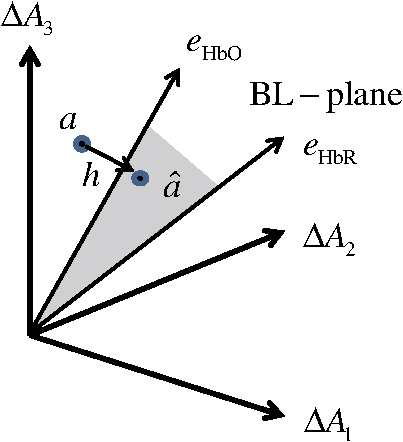
1.IntroductionFunctional near-infrared spectroscopy (fNIRS) is effective for the noninvasive investigation of cerebral oxygenation and hemodynamics.1–3 When executing an fNIRS measurement over a broad area of the cerebral cortex, many probes have to be placed on the surface of the subject’s head. In such a case, it is often observed that, compared to the other channels, some channels are very noisy and/or have a very unstable baseline. This phenomenon is very common in fNIRS studies with infants, whose movements are difficult to restrict. These types of noise and baseline fluctuations are obstacles to effective imaging using fNIRS and to accurate statistical comparison analyses between channels and subjects. Such noise and baseline fluctuations are considered to originate from the interface between the probes and the scalp, which is often covered by hair and is prone to insufficient probe fixation. Measures taken to resolve such problems include the removal of the hair from the space under the probe and the improvement of the fixation of the probes to the scalp. However, because of time constraints, measurements sometimes need to be taken even if the problem has not been completely resolved. In such cases, the obtained data may not be sufficiently accurate for the study and sometimes this data must be discarded. There is currently no systematic and practical method for identifying a problematic probe and improving its contact. Many studies have been carried out to find and remove baseline fluctuations,4 including the Wiener filter and Kalman filter approaches.5,6 For a multichannel fNIRS measurement, a method based on principal component analysis (PCA) was also proposed for study with infants.7 PCA is effective for removing the baseline fluctuation observed in a global area.8 However, the effectiveness of these methods can be evaluated only after applying them to the data, and if the result is not sufficiently acceptable, it must be discarded with the data. Therefore, it is important to identify problematic probe contacts before starting the experiment. In this study, we propose a method for the detection of two types of problematic probe contacts from the preliminary data before the experiment: a probe contact at which light easily fluctuates with body motion, and a probe contact at which light transmission is constantly small. We refer to the former as an unstable contact and the latter as a weak contact. In the fNIRS measurement, if any absorbance changes originate from unstable and/or weak contacts, they are interpreted as hemoglobin concentration change based on the modified Beer–Lambert law (the modified BL law). However, when using measurement lights with more than three wavelengths, some of those absorbance changes cannot be interpreted as hemoglobin concentration changes, because they do not show the same spectroscopic property as hemoglobin absorption. In this study, we calculate such absorbance changes and use them to detect unstable and/or weak contacts. This enables us to ignore the absorbance change induced by the hemoglobin concentration change and to concentrate on the problem related to probe contacts. Because a channel consists of a pair of source and detector probes, either or both probes may cause a large baseline fluctuation and/or noise in the channel. It is not possible to determine which probe is unstable and/or weak by checking a single channel. However, in multichannel fNIRS measurements, source and detector probes are shared by many different channels. The sharing configuration is determined by the probe arrangement. Thus, the baseline fluctuation and noise of the channels are related to the probes’ contact instability and weakness due to improper probe arrangement. Unstable and/or weak probes are determined by solving the inverse problem of this relation. 2.Theory and Method2.1.Orthogonal Component of the Absorbance Change to the BL PlaneIn fNIRS, changes in hemoglobin concentration are calculated from the observed absorbance change by using the modified BL law. Ignoring differences in optical path length among light wavelengths used, the law is given as where is the measurement light wavelength; is the absorbance change of ; and are the molar extinction coefficients of oxy- and deoxy-hemoglobin, respectively; and are changes in oxy- and deoxy-hemoglobin concentration, respectively; and is the optical path length. This equation shows that the absorbance change induced by oxy- and deoxy-hemoglobin concentration changes is on the plane that is expanded by molar extinction coefficient vectors, and , respectively (see Fig. 1). We call this plane the BL plane. Hence, for absorbance changes whose wavelength dependence is different from that of the hemoglobin absorption, a component is present that is orthogonal to the BL plane. Further, if only two wavelengths are used, the absorbance change can be interpreted as a hemoglobin concentration change; therefore, more than three wavelengths are required to detect such a component. In this study, three wavelengths are used.If the molar extinction coefficient matrix is given by , the orthogonal component of the absorbance change to the BL plane is given as where is the pseudo inverse of . When using three wavelengths, this equation is also written as where is the third column vector (having no corresponding singular value) of when the singular value decomposition of is given as . This equation shows that the elements of the component orthogonal to the BL plane have the same time series, but not the same scales. Hence, to evaluate the component orthogonal to the BL plane, a scalar value is used, which is defined asThe following are considered to be the origins of the component orthogonal to the BL plane.
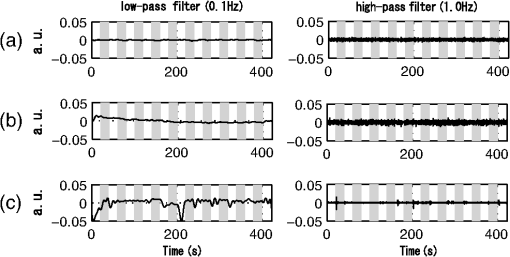
2.2.Light Transmission at the Probe ContactSince the amplitudes of the baseline fluctuation and noise are directly related to the property of the probe contact, several definitions for the contact property are given here. The optical transmittance at the probe contact is denoted by , where . We decompose into two components as where represents the average value of the transmittance, and represents the fluctuation of the transmittance around . This decomposition is defined such that the mean value of is , and the temporal average of is 0.Because each fNIRS channel consists of a pair of source and detector probes, its baseline fluctuation is determined by the product of the fluctuations in the transmittance at the source and detector probes. Thus, for any channel, if of at least one contact fluctuates largely, a large fluctuation in the baseline is observed at that channel. We call this type of contact unstable, and we evaluate its instability using the variance of . Similarly, the average apparent noise power is determined by the product of the average transmittance of the source and detector probes and the amplitude of instrumental noise generated by the photodetector device (see Sec. 2.3.2). Thus, for any channel, if of at least one contact is small, a large noise is observed at that channel. We call this type of contact as weak, and we evaluate its weakness using the value of . 2.3.Evaluation of Contact Instability and WeaknessIn a multichannel fNIRS measurement, the source and detector probes are shared by different channels. Thus, we need to calculate the contact instability and weakness of each probe as an inverse problem. Here we give a theoretical model and an analytical procedure for this problem. 2.3.1.Probe arrangement matrixHere we define a probe arrangement matrix to provide information about which source and detector probes constitute a channel. Let and be the number of source and detector probes, respectively, and let be the total number of channels. If the source probe and the detector probe constitute a channel , the probe arrangement matrix is an matrix, and the element of the matrix is defined as 2.3.2.A component orthogonal to the BL planeWe assume that the source probe and the detector probe constitute a channel , and the light intensity observed at is the sum of the light intensity and the instrumental noise at the detector . Thus, the absorbance change at is given as If the instrumental noise is sufficiently small compared to the light intensity , the approximation formula when can be used. Thus, Eq. (8) is approximated as The second term represents the apparent noise, and this equation shows that the intensity of the apparent noise is inversely proportional to the observed light intensity.Next, we assume that the optical transmittance of contacts and are and , respectively. Let be the incident light intensity of source , and let be the light transmittance caused by tissue hemoglobin absorption at the channel . We have Then, The first term of this equation is the absorbance change induced by the hemoglobin concentration change. The second term is the baseline fluctuation induced by the body motion, and the third is the apparent noise induced by the instrumental noise.The component orthogonal to the BL plane is given by applying Eq. (4) to the absorbance change . Because the first term of Eq. (12) is the absorbance change induced by the hemoglobin concentration change, the orthogonal component of this term is apparently zero. Thus, if the optical transmittance at a contact is independent of wavelength, the orthogonal component is given as where and is a column vector whose elements are all 1. The first term in Eq. (14) corresponds to the body motion and contact instability, and the second term corresponds to the instrumental noise and contact weakness.2.3.3.Evaluation of contact instabilityFrom Eqs. (13) and (14), the following equation for the contact instability is given, where the temporal average of both sides of the equation is set to 0. Let be a column vector whose elements are for all . We write , and let be a column vector whose elements are for all . The term is the logarithm of the fluctuation of the optical transmittance at probe contact . These two vectors are related by the probe arrangement matrix , such that Thus, we have The contact instability of the probe can be evaluated by the variance of . We write as a vector consisting of these variances.2.3.4.Evaluation of contact weaknessThe following equation for the contact weakness is given from Eq. (13). To consider the average of the apparent noise power, we set , and the tissue transmittance is constant for all channels and wavelengths. We also set the incident light power and the variance of the instrumental noise to be constant, and , respectively, for all probes and wavelengths. From these assumptions, the variance of is given as . If we write as a variance of , we get Because is independent of and , and we do not need to know the absolute values of and to compare the contact weakness, we set . Taking the logarithm of both sides of Eq. (22), we get Let be a column vector whose elements are for all (). We write , and let be a column vector whose elements are for all (); is the logarithm of the average value of the optical transmittance at the probe contact . These two vectors are related by , such that Then we have If is small, the contact of is weak.2.3.5.Decomposition of the orthogonal component in terms of motion and noiseTo evaluate contact instability and weakness, we need to decompose into and . To do so, we apply low- and high-pass filters to . Because is white noise, its low-pass filter output is very small. On the other hand, because originates from body motion, and most of its spectrum is in the low-frequency region, this component is not significantly affected by the low-pass filter. As a result, the low-pass filter output of can be used as . On the other hand, the high-pass filter output of mainly consists of , and it includes only a small baseline fluctuation. Although the apparent noise may change according to this fluctuation, it is also filtered out by a high-pass filter. Therefore, we can use the high-pass filter output as . We cannot know the absolute amplitudes of and . However, their relative amplitudes over channels are invariant under such filtering operations. Thus, we can determine the relatively unstable and/or weak probes. 2.3.6.Classification of more unstable and/or weaker contactsThe instability and weakness of all contacts are given by and . However, in practice, we cannot improve the contacts of all probes according to the degree of the problems. Therefore, it is important to distinguish the probes having significantly unstable and/or weak contacts. To classify such contacts, for example, we can use the criteria where and are the means of and , respectively, and and are their respective standard deviations. Using this classification, we need only improve the contacts that satisfy these criteria. The parameters and are used to control the number of classified contacts. If these parameters are small, the number of classified contacts is large, and we have to check many probes. However, if these parameters are large, the number is small, and we may miss the very unstable and/or weak probes. We need to determine these parameters on an empirical basis.3.ExperimentFigure 2(a) shows our high-density probe array for the multichannel fNIRS measurement. The 16 black and white circles in the figure denote the source and detector probes, respectively. Straight lines represent channels, and there are 44 channels in total. When placing the probe array on a subject’s head, the center of the array was placed at the Cz position of the EEG 10–20 system [see Fig. 2(b)]. All probes were set to be as firm as possible. We used the OMM-3000 fNIRS system (Shimadzu Corp., Japan), and the wavelengths of the measurement lights were 780, 805, and 830 nm. The sampling rate of the measurement is 0.13 s. The system automatically checks the signal level of all channels before a measurement and gives a warning when any detectors receive only very weak light. Our probe settings passed this check before each experiment. Fig. 2(a) High-density probe array with 16 sources (black) and 16 detectors (white). Measurement pairs (channels) are represented by straight lines. (b) Schematic showing the placement of the probe array over a head.  Three subjects (A, B, and C) participated in the experiment. They were instructed to open and close their left or right palms as quickly as possible, while the absorbance changes during the task were recorded. The task sequence was as follows: Open and close the left palm as fast as possible (20 s), rest (20 s), open and close the right palm as fast as possible (20 s), rest (20 s). This sequence was repeated five times during the task. Before starting the sequence, an additional rest period (20 s) was set. The study was approved by the Institutional Review Board of the National Institute of Advanced Industrial Science and Technology (Japan). A written informed consent was obtained from the participants. Figure 3 shows the scattering plot of the observed absorbance changes in the experiments. Data from the time period of 130 to 230 s are shown. Figure 3(a)–3(c) were observed in channel 20 [indicated by the asterisk in Fig. 2(a)] of subjects A, B, and C, respectively. These figures show that the absorbance changes are not all on the BL plane, because of body motion and instrumental noise. In particular, a large orthogonal component due to body motion is observed in Fig. 3(c). Fig. 3Scattering plot of absorbance changes. Data from the time period of 130 to 230 s are shown. (a) Subject A, ch. 20. (b) Subject B, ch. 20. (c) Subject C, ch. 20.  The left column in Fig. 4 shows absorbance changes at 780 nm for the entire experimental period, in which Fig. 4(a)–4(c) correspond to those in Fig. 3. These subfigures indicate changes that may originate from the tissue hemoglobin change associated with the task execution. Also, we observed a gradual drift over the entire period in Fig. 4(b), as well as a distinctive fluctuation in Fig. 4(c). Instrumental noise (white noise) was observed in all subfigures, but their amplitudes were apparently different. It was very small in Fig. 4(c) compared with Fig. 4(a) and 4(b). The components of these absorbance changes orthogonal to the BL plane are shown in the right column of Fig. 4. The changes associated with the task execution disappeared completely in all cases, while changes in the baseline or noise in each case were well conserved. Fig. 4Left: Original absorbance change (780 nm). Right: Component orthogonal to the BL plane. (a) Subject A, ch. 20. (b) Subject B, ch. 20. (c) Subject C, ch. 20. Periods of task execution are indicated by shading. 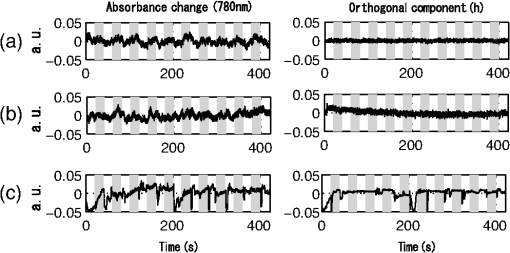 To separate the contact instability and contact weakness, we applied low-pass (0.1 Hz) and high-pass (1.0 Hz) filters to the orthogonal component in Fig. 4. The outputs of these filters are shown in Fig. 5. Figure 5(a)–5(c) in the left column are low-pass filter outputs, which clearly show only the baseline fluctuation of the channel. On the other hand, Fig. 5(a)–5(c) of the right column are high-pass filter outputs, which show only the apparent noise of the channel. These figures show that this filtering approach is an effective method for the decomposion of the orthogonal component in terms of instability and weakness. 4.ResultsThe power (variance) of the component orthogonal to the BL plane was calculated for each channel of the multichannel measurement. Figure 6(a) shows the colormap for subject B. Forty-four channels of the multichannel fNIRS measurement are shown. Low-pass (0.1 Hz) and high-pass (1.0 Hz) filters were applied to the orthogonal component, and the power colormap of these filter outputs are shown in Fig. 6(b) and 6(c), respectively. Based on the results shown in Fig. 5, we consider that the total power of the baseline fluctuation and noise [Fig. 6(a)] could be effectively decomposed into two different components [Fig. 6(b) and 6(c)]. Fig. 6Power colormap of the component orthogonal to the BL plane, Subject B. (a) Orthogonal component. (b) Low-pass filtered orthogonal component (0.1 Hz). Unstable source contact is indicated by a white circle. (c) High-pass filtered orthogonal component (1.0 Hz). Weak probe contacts are indicated by a white circle (source) and white squares (detector). 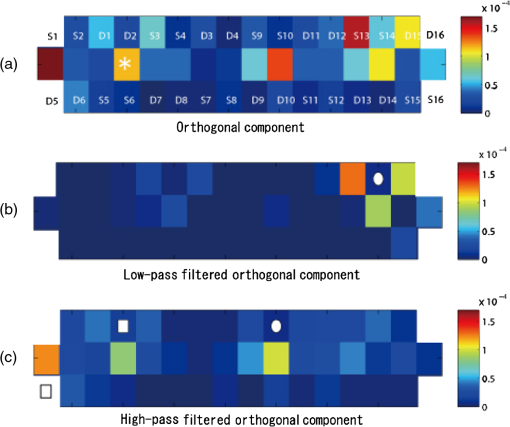 Next, we use the low-pass filter output as in Eq. (18) and obtain . The variance of gives the contact instability of the probe . The obtained values are shown in Fig. 7(a). The source and detector probe instabilities are and , respectively. A larger value indicates higher instability. This figure shows that (S14) has a much higher value than the others. Hence, source probe 14 is unstable. Fig. 7Evaluation of probe contact instability and weakness. (a) Probe contact instability . (b) Probe contact weakness . 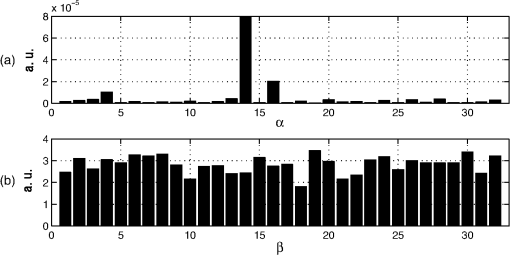 The logarithm of the standard deviation of the high-pass filter output is used as in Eq. (24), and the contact weakness is obtained using Eq. (25). The obtained values are shown in Fig. 7(b). The source and detector probe weaknesses are and , respectively. Smaller values indicate a weaker contact. This figure shows no significantly weak contact, but several contacts, such as (S10), (D2), and (D5), are relatively weak compared to other contacts. Several probes were classified as being very unstable and/or weak according to the criteria in Sec. 2.3.6. These probes are shown as white marks in Fig. 6(b) and 6(c). The white circle marks are the selected source probes, and the white square marks are the selected detector probes. The threshold parameters for classification were set to . This example clearly shows the effectiveness of the proposed method. For example, Fig. 6(a) shows that channel 18 (marked by the asterisk) has a significantly large variance of data. The decomposition by the filters [Fig. 6(b) and 6(c)] reveals that most of the variance is caused by the contact weakness. Figure 6(c) also shows that all three channels using D2 (channels surrounding D2) have a comparatively significant contact weakness. On the other hand, with the exception of channel 18, the channels using S6 (channels surrounding S6) indicate little contact weakness. Therefore, the cause of the contact weakness is not source S6, but detector D2. Figures 8 and 9 show the results for subjects A and C, respectively. In both cases, our method gives a good classification of unstable and weak contacts. Fig. 8Power colormap of the component orthogonal to the BL plane, Subject A. (a) Orthogonal component. (b) Low-pass filtered orthogonal component (0.1 Hz). Unstable source contacts are indicated by white circles. (c) High-pass filtered orthogonal component (1.0 Hz). Weak probe contacts are indicated by a white circle (source) and white squares (detectors). 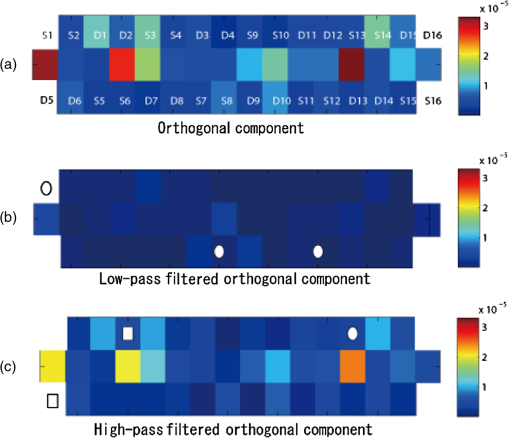 Fig. 9Power colormap of the component orthogonal to the BL plane, Subject C. (a) Orthogonal component. (b) Low-pass filtered orthogonal component (0.1 Hz). Unstable source contacts are indicated by white circles. (c) High-pass filtered orthogonal component (1.0 Hz). Weak source contacts are indicated by white circles. 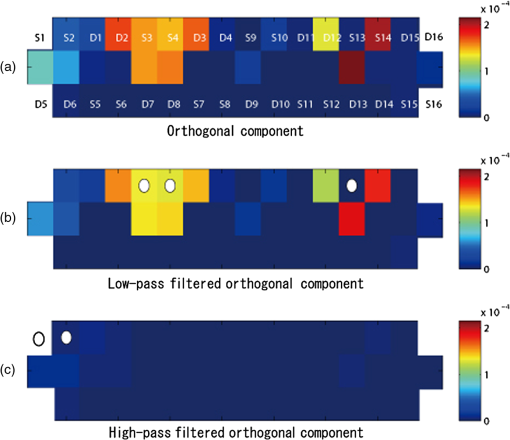 5.DiscussionIn Sec. 2, we introduced many assumptions to simplify the equation. A more accurate evaluation of contact instability and weakness may be possible if these assumptions are disregarded. For example, we assumed that the power of the instrument noise is constant for all detectors. If photomultipliers are used for the photodetectors, their approximate noise levels may be determined on the basis of the applied voltage, and this information may give a more accurate evaluation of contact weakness. However, for the efficient execution of the experiment, extreme accuracy of the evaluation is less important than a fast cycle of evaluation and improvement. In fact, the results of Sec. 4 show that appropriate detection of unstable and/or weak contacts is realized even under such assumptions. Therefore, we believe that the assumptions in Sec. 2 are suitable for the execution of such cycles. When unstable and/or weak contacts are classified by the proposed method, we should improve them by clearing hair off the contact and stabilizing the probes and optical cables. After that, the effect of this treatment is verified by applying the proposed method again. This process is repeated until all contacts satisfy an appropriate condition. In order to implement the fast cycle of evaluation and improvement, four or five contacts at a maximum should be classified with one evaluation. If these contain the unstable and weak contacts evenly, the number of unstable or weak contacts corresponds to about 7% of the 32 probes used in the experiments. In this case, we can expect in Eqs. (26) and (27) if the measures of contact instability and weakness, and , are normally distributed. In practice, however, these are not necessarily the normal distributions. Therefore, we investigated the dependencies of the classified number of unstable and weak contacts against and , respectively. Figure 10 shows the result. In each subfigure, the numbers were different among subjects in smaller range of and . However, they converged on a value about two in the range larger than 1.5. Based on these findings, we set for the present experiments. Fig. 10The number of contacts classified as unstable (a) and weak (b) contacts for various classification parameter values. Solid, dashed, and dotted lines are for Subjects A, B, and C, respectively.  It is easy to display the positions of unstable and/or weak probes on the monitor display of conventional fNIRS equipment. However, in this case, the probe position must be checked on the equipment side, and the contact must be improved on the subject side. This is a tedious process, because we have to pass between both sides. On the other hand, if a display device (for example, an LED lamp) indicating contact instability and weakness is attached to each probe, one can know directly the positions of problematic probes. This helps to realize the prompt stabilization of all contacts. High-density measurement methods, such as diffuse optical tomography, are becoming popular in fNIRS studies.9 The prompt and stable setting of probes on subjects’ heads is extremely important, because many probes are required in such measurement systems. We believe that the proposed method is useful as a basic tool for performing such measurements. ReferencesE. M. C. Hillman,
“Optical brain imaging in vivo: techniques and applications from animal to man,”
J. Biomed. Opt., 12
(5), 051402
(2007). http://dx.doi.org/10.1117/1.2789693 JBOPFO 1083-3668 Google Scholar
Y. Hoshi,
“Functional near-infrared spectroscopy: current status and future prospects,”
J. Biomed. Opt., 12
(6), 062106
(2007). http://dx.doi.org/10.1117/1.2804911 JBOPFO 1083-3668 Google Scholar
H. ObrigA. Villringer,
“Beyond the visible—imaging the human brain with light,”
J. Cereb. Blood Flow Metab., 23
(1), 1
–18
(2003). http://dx.doi.org/10.1097/00004647-200301000-00001 JCBMDN 0271-678X Google Scholar
T. J. HuppertM. A. FranceschiniD. A. Boas,
“Noninvasive imaging of cerebral activation with diffuse optical tomography,”
In Vivo Optical Imaging of Brain Function, 2nd ed.CRC Press, Boca Raton
(2009). Google Scholar
L. Gagnonet al.,
“Improved recovery of the hemodynamic response in diffuse optical imaging using short optode separations and state-space filtering,”
NeuroImage, 56
(3), 1362
–1371
(2011). http://dx.doi.org/10.1016/j.neuroimage.2011.03.001 NEIMEF 1053-8119 Google Scholar
M. Izzetogluet al.,
“Motion artifact cancelation in NIR spectroscopy using Wiener filtering,”
IEEE Trans. Biomed. Eng., 52
(5), 934
–938
(2005). http://dx.doi.org/10.1109/TBME.2005.845243 IEBEAX 0018-9294 Google Scholar
T. Wicoxet al.,
“Using near-infrared spectroscopy to assess neural activation during object processing in infants,”
J. Biomed. Opt., 10
(1), 11010
(2005). http://dx.doi.org/10.1117/1.1852551 JBOPFO 1083-3668 Google Scholar
Y. Zhanget al.,
“Eigenvector-based spatial filtering for reduction of physiological interference in diffuse optical imaging,”
J. Biomed. Opt., 10
(1), 011014
(2005). http://dx.doi.org/10.1117/1.1852552 JBOPFO 1083-3668 Google Scholar
B. W. Zeffet al.,
“Retinotopic mapping of adult human visual cortex with high-density diffuse optical tomography,”
Proc. Natl. Acad. Sci. U.S.A., 104
(29), 12169
–12174
(2007). http://dx.doi.org/10.1073/pnas.0611266104 1091-6490 Google Scholar
|