|
|
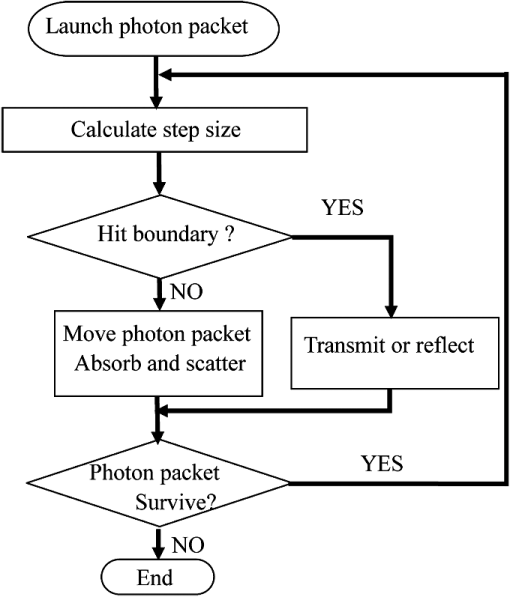
1.IntroductionMonte Carlo (MC) methods are a category of computational methods that involve the random sampling of a physical quantity.1,2 The term “the Monte Carlo method” can be traced back to 1940s,1 in which it was proposed to investigate neutron transport through various materials. Such a problem cannot be solved by conventional and deterministic mathematical methods. Due to its versatility, this method has found applications in many different fields3 including tissue optics. It has become a popular tool for simulating light transport in tissues for more than two decades4 because it provides a flexible and rigorous solution to the problem of light transport in turbid media with complex structure. The MC method is able to solve radiative transport equation (RTE) with any desired accuracy,5 assuming that the required computational load is affordable. For this reason, this method is viewed as the gold standard method to model light transport in tissues, results from which are frequently used as reference to validate other less rigorous methods such as diffuse approximation to the RTE.6,7 Due to its flexibility and recent advances in speed, the MC method has been explored in tissue optics to solve both the forward and inverse problems. In the forward problem, light distribution is simulated for given optical properties, whereas in the inverse problem, optical properties are estimated by fitting the light distribution simulated by the MC method to experimentally measured values. In this review paper, the principles of MC modeling for the simulation of light transport in tissues, including the general procedure of tracking an individual photon packet, common light–tissue interactions that can be simulated such as light absorption and scattering, frequently used tissue models, common contact and noncontact illumination and detection setups, and the treatment of time-resolved and frequency-domain optical measurements, are described in detail to help interested readers achieve a quick start. Following that, a variety of methods for speeding up MC simulations, including scaling methods, perturbation methods, hybrid methods, variation reduction techniques, parallel computation, and special methods for fluorescence simulations, and their respective advantages and disadvantages are discussed. Then the biomedical applications of MC methods, including the simulation of optical spectra, estimation of optical properties, simulation of optical measurements in laser Doppler flowmetry (LDF), simulation of light dosage in photodynamic therapy (PDT), simulation of signal source in optical coherence tomography (OCT) and diffuse optical tomography (DOT), are surveyed. Finally, the potential directions for the future development of MC methods are discussed, which are based on their current status in the literature survey and the authors’ anticipation. It should be pointed out that this review is intended to give a general survey on the capability of MC modeling in tissue optics while paying special attention on methods for speeding up MC simulations since the time-consuming nature of common MC simulations could limit its applications. 2.Principles of MC Modeling of Light Transport in Tissues2.1.General Procedure of Steady State MC Modeling of Light Transport in TissuesIn the general procedure of MC modeling, light transport in tissues is simulated by tracing the random walk steps that each photon packet takes when it travels inside a tissue model. For each launched photon packet, an initial weight is assigned as it enters the tissue model, as illustrated in Fig. 1. The step size will be sampled randomly based on the optical properties of the tissue model. If it is about to hit a boundary, either of the following two methods could be used to handle this situation. In the first method, the photon packet will either transmit through or be reflected from the boundary. In the second method, a fraction of the photon packet’s weight will always be reflected and the remaining fraction of the photon packet’s weight will transmit through. The probabilities of transmission or reflection in the first method, and the fraction of the photon packet’s weight transmitting through or being reflected in the second method, are governed by Snell’s law and Fresnel’s equations. At the end of each step, the photon packet’s weight is reduced according to the absorption probability; meanwhile, the new step size and scattering angle for the next step will be sampled randomly based on their respective probability distributions. The photon packet propagates in the tissue model step by step until it exits the tissue model or is completely absorbed. Once a sufficient number of photon packets are launched, the cumulative distribution of all photon paths would provide an accurate approximation to the true solution of the light transport problem and the contribution averaged from all photons can be used to estimate the physical quantities of interest. 2.2.Common Light–Tissue Interactions in MC ModelingSeveral types of common light–tissue interactions, including light absorption, elastic scattering, fluorescence and Raman scattering, have been simulated by the MC methods previously. The absorption coefficient (unit: ) and the scattering coefficient (unit: ) are used to describe the probability of absorption and scattering, respectively, occurring in a unit path length. The anisotropy factor , which is defined as the average cosine of scattering angles, determines the probability distribution of scattering angles to the first-order approximation. In addition, the refractive index mismatch between any two regions in the tissue model or at the air–tissue interface will determine the angle of refraction. The fraction of photon packet weight that, after traveling in the medium, escapes from the same side of the tissue model as the incident light is scored as diffuse reflectance. In contrast, the fraction of photon packet weight that travels through the medium and escapes from the other side of the tissue model is scored as transmittance.5,8,9 To simulate fluorescence emission, one additional parameter, which is fluorescence quantum yield,10,11 needs to be incorporated to describe the probability that the absorbed photon packet weight can be converted to a fluorescence photon at a different wavelength. If time-resolved fluorescence is simulated, the lifetime of fluorescence needs to be defined. The initial direction of the fluorescence photon is isotropic due to the nature of fluorescence emission. As illustrated in Fig. 2, the MC modeling of fluorescence propagation in tissues involves three steps.11–13 The first step involves a general MC simulation to simulate light propagation with optical properties at the excitation wavelength. In the second step, a fluorescence photon may then be generated upon the absorption of an excitation photon with a probability defined by the quantum yield and time delay defined by the lifetime of fluorescence. The third step again involves a general MC simulation to simulate fluorescence light propagation with optical properties at the emission wavelength. It is clear that simulated fluorescence from a tissue model will be related to the absorption and scattering properties of the tissue model in addition to the fluorescence quantum yield and lifetime. Fluorescence simulation is typically much more time-consuming than the simulation of diffuse reflectance due to extra fluorescence photon propagation. Fig. 2Flow chart for MC modeling of the propagation of a single photon packet, in which one set of wavelength change is involved. indicates the excitation wavelength and indicates the emission wavelength. The new photon packet with a different wavelength corresponds to fluorescence or Raman light at a single emission wavelength. 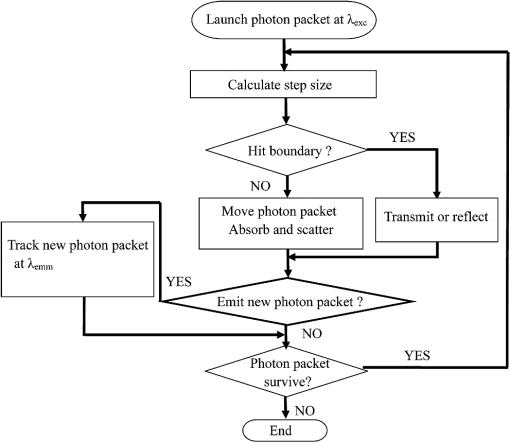 To simulate Raman emission, a parameter similar to fluorescence quantum yield, named as Raman cross-section,14–17 is needed to describe the probability that a Raman photon will be generated at each step. A phase function for Raman photons needs to be determined. The MC simulation procedure for Raman light propagation will be similar to that for fluorescence. Bioluminescence refers to the phenomenon of living creatures producing light, which results from the conversion of chemical energy to bioluminescence photons18 and which has also been investigated using MC modeling. Because bioluminescence does not need an external light source for excitation, the first step in MC simulation of bioluminescence is to generate bioluminescence photons package according to the distribution of bioluminescence sources.19,20 After that, the simulation of bioluminescence photon propagation in a tissue model is exactly the same as the simulation of diffuse reflectance. If the polarization property of light is considered in MC modeling, the polarization of a photon can be represented by Stokes vectors and the polarimetry properties of the tissue model can be described by Jones matrix or Mueller matrices,21,22 which will not be expanded in this review. 2.3.Common Tissue Models in MC ModelingCommon tissue models used in MC simulations include the homogeneous and nonhomogeneous tissue models. The optical properties in a homogeneous tissue model are equal everywhere.4,23 In contrast, the optical properties in a nonhomogeneous tissue model vary with the tissue region. The following survey is focused on nonhomogeneous tissue models because of its high preclinical and clinical relevance. The most commonly used nonhomogeneous tissue model is perhaps the multilayered tissue model,8,9,12,13,24–30 which is frequently employed to mimic epithelial tissues. In a multilayered tissue model, each tissue layer is assumed to be flat with uniform optical properties and it is infinitely large on the lateral dimension. This assumption works fine when the source–detector separation is small so that the spatial variation in the optical properties within the separation is negligible. However, it could cause significant errors if the optical properties change significantly in a small area, such as in dysplasia or early cancer31 and port wine stain (PWS) model.32 To overcome this limitation, tissue models including heterogeneities with well-defined shapes have been used to mimic complex tissue structures from different organs. For example, Smithies et al.32 and Lucassen et al.33 independently proposed MC models in which simple geometric shapes were incorporated into layered structures to model light transport in PWS model. In their PWS models, infinitely long cylinders were buried in the bottom dermal layer to mimic blood vessels. Wang et al.34 reported an MC model in which a sphere was buried inside a slab to model light transport in human tumors. Zhu et al.31,35 proposed an MC model in which cuboid tumors were incorporated into layered tissues to model light transport in early epithelial cancer models including both squamous cell carcinoma and basal cell carcinoma. Voxelated tissue models have been also explored to simulate irregular structures. Pfefer et al.36 reported a three-dimensional (3-D) MC model based on modular adaptable grids to model light propagation in geometrically complex biological tissues and validated the code in a PWS model. Boas et al.37 proposed a voxel-based 3-D MC model to model arbitrary complex tissue structures and tested the code in an adult head model. Patwardhan et al.38 also proposed a voxel-based 3-D MC code for simulating light transport in nonhomogeneous tissue structures and tested the code in a skin lesion model. The three voxel-based MC codes above showed great flexibility in a range of applications. However, to model tissue media with curved boundaries in a voxel-based MC model, the grid density will have to be increased, which requires more memory and computation. A few other approaches have been explored to accommodate this situation. Li et al.19 reported a public MC domain, named mouse optical simulation environment, to model bioluminescent light transport in a living mouse model. The mouse model consists of several segmented regions that are extended from several building blocks such as ellipses, cylinders, and polyhedrons. This platform is particularly suitable for small animal imaging. Margallo-Balbas et al.39 and Ren et al.40 have developed triangular-surface-based MC methods to model light transport in complex tissue structures. The triangular-surface-based approach allows an improved approximation to the interfaces between domains, but it is not able to model complex media with continuously varying optical properties. Moreover, it could be time-consuming to determine ray–surface intersection because a range of triangles will have to be scanned. To overcome the limitations associated with triangular-surface-based MC method, most recently, Shen et al.41 as well as Fang42 have presented mesh-based MC methods, by which one can model much more complex structures and situations. 2.4.Common Illumination and Detection Setups in MC ModelingOne important advantage of MC modeling, as compared to other non-numerical methods such as diffuse approximation, is its capability to faithfully simulate a variety of contact and noncontact illumination and detection setups for optical measurements. Note that the contact setup requires the direct contact between the tip of an optical probe and tissue samples. In contrast, the noncontact setup enables optical measurements from a tissue sample without directly contacting it. 2.4.1.Contact setup for illumination and detectionFiber-optic probes are commonly used in contact illumination and detection configurations as demonstrated in many previous reports.43 In general, these fiber-optic probes could be divided into two groups. In the first group, the same fiber or fiber bundle is used for both illumination and detection,30,44,45 while in the second group, separate fibers are used for illumination and detection.12,46–48 There is no difference in the treatment of these two groups of fiber-optic probes from the point of view of modeling because the first group of probes can be viewed as two separate and identical fibers or fiber bundles for illumination and detection that happen to locate at the same spatial position. The key parameters in simulated fiber-optic probes include the radii, numerical apertures (NA), tilt angles of illumination and detection fibers, and the center-to-center distance between the two sets of fibers (which is called the source–detector separation), as well as the refractive indices of these fibers relative to that of the tissue model. The radius and NA of the illumination fiber in combination with the radial and angular distributions of photons coming out of the fiber define the locations and the incident angles of incident photons. For a commonly used multimode fiber, the spatial locations and incident angles of launched photons are typically assumed to follow uniform distribution and Gaussian distribution. Both spatial locations and incident angles need to undergo spatial coordinate transformation when the tilt angle of the illumination fiber is larger than zero. Here the tilt angle of a fiber refers to the angle of the fiber axis relative to the normal axis of the tissue model. The incident beam could be also assumed to be collimated or focused. Light detection by a fiber usually contains two steps. The first step is to determine whether an exiting photon could enter the area defined by the radius of the detection fiber. If it is true, the second step is to determine whether the exiting direction of the photon falls within the acceptable angle of the detection fiber calculated from the NA and refractive index of the fiber. If the tilt angle of the detection fiber is larger than zero, the exiting location and angle are subject to spatial coordinate transformation. 2.4.2.Noncontact setup for illumination and detectionNoncontact setups usually employ various lenses for illumination and detection. In these setups, an adjunct lens or a combination of lenses is usually placed between a fiber-optic probe and the tissue sample to achieve noncontact measurements while maintaining the well-defined illumination and detection geometry. Jaillon et al.49 proposed a method to simulate a beveled fiber-optic probe coupled with a ball lens to achieve depth-sensitive fluorescence measurements from layered tissue models. Later, the same group incorporated a half-ball lens into the beveled fiber-optic probe to achieve the same purpose with a higher sensitivity.50 Zhu et al.51 proposed a method to simulate a fiber-optic probe coupled with convex lenses to achieve noncontact depth-sensitive diffuse reflectance measurements from early tumors in an epithelial tissue model. By manipulating the lens combination, an ordinary cone configuration and a special cone shell configuration were investigated. It was found that the cone shell configuration provides higher depth sensitivity to the tumor than the cone configuration. 2.5.Time-Resolved and Frequency-Domain MC ModelingTime-resolved optical measurements such as fluorescence lifetime imaging (FLIM)52 and the complementary frequency-domain measurements such as frequency domain photon migration have received increasing attention recently, which have also been investigated in MC modeling. A time-domain technique usually measures the temporal point spread function (PSF) or the spreading of a propagating pulse in time.53,54 A frequency-domain technique measures the temporal modulation transfer function or the attenuation and phase delay of a periodically varying photon density wave.55,56 The two techniques are related by Fourier transform. Several groups have developed time-domain MC models37,57–60 and frequency-domain MC models61–65 to simulate light transport in tissue. In the MC simulation of time-resolved measurements, all the steps are the same as in steady-state measurements, except that one additional parameter, i.e., time, is used to keep track of the time at which each event occurs.37,57–60 The refractive index in each tissue region will influence the time that photons take to travel through. In the simulation of FLIM, it needs to be pointed out that the time delay from photon absorption to fluorescence generation should follow the probability density distribution defined by the fluorescence lifetime.66,67 In the frequency-domain measurements, the modulation and/or phase delay of detected waves were analyzed. The modulation and phase delay can be simulated in either a direct approach64 or an indirect approach, i.e., using Fourier transformation from a time-domain MC simulation.65 3.Methods for the Acceleration of MC SimulationWhile the MC method is the gold standard method to model light transport in turbid media, the major drawback of the MC method is the requirement of intensive computation to achieve results with desirable accuracy due to the stochastic nature of MC simulations, which makes it extremely time-consuming compared to other analytical or empirical methods. Significant efforts have been made to speed up the MC simulation of light transport in tissues during the past decades. These acceleration methods can be roughly divided into several categories as follows. 3.1.Scaling MethodsA typical scaling method requires a single or a few baseline MC simulations, in which the histories of survival photons such as trajectories or step sizes are recorded. Then, diffuse reflectance or transmittance for a tissue model with different optical properties can be estimated by applying scaling relations on the recorded photon histories. These methods take advantage of the fact that the scattering properties determine photon paths and the absorption property only influences the weights of survival photons. Graaff et al.68 proposed a limited scalable MC method for fast calculation of total reflectance and transmittance from slab geometries with different optical properties. It was demonstrated that the trajectory information obtained in a reference MC simulation with a known albedo, i.e., , can be used to find the total reflectance and total transmittance from slabs with other albedos. Kienle et al.69 extended Graaff’s theory to simulate space- and time- resolved diffuse reflectance from a semi-infinite homogeneous tissue model with arbitrary optical properties. Their approach was based on scaling (for different scattering coefficients) and re-weighting (for different absorption coefficients) a discrete representation of the diffuse reflectance from one baseline MC simulation in a nonabsorbing semi-infinite medium. It is powerful, but both the discrete representation and interpolation could introduce errors that are often amplified in scaling. Pifferi et al.70 proposed a similar approach to estimate space- and time-resolved diffuse reflectance and transmittance from a semi-infinite homogeneous tissue model with arbitrary optical properties. Different from Kienle’s method, the evaluation of reflectance and transmittance in Pifferi’s approach is based on interpolation of results from MC simulations for a range of different scattering coefficients, and scaling is performed for absorption coefficients. This approach increases the accuracy of results for different scattering coefficients at the cost of a significantly increased number of baseline MC simulations. The methods reviewed above are fast, but the binning and interpolation involved introduce errors. In order to improve the accuracy of these methods, Alerstam et al.60 improved Kienle’s method by applying scaling to individual photons. In this method, the radial position of the exiting location and the total path length of each detected photon are recorded and the trajectory information of each photon will be individually processed to find the survival photon weight for tissue media with other sets of optical properties. Martinelli et al.71 derived a few scaling relationships from the RTE, and their derivation showed that a rigorous application of the scaling method requires rescaling to be performed for each photon’s biography individually. Two basic relations for scaling a survival photon’s exit radial position and exit weight are listed in Eqs. (1) and (2) below.47 in which , , , and are the exit radial position, exit weight, transport coefficients, and albedo in the baseline simulation, while , , , and are those in the new simulations. is the number of collisions recorded in the baseline simulation before the photon exits. Two relations essentially assume that the same set of random numbers sampled in the baseline simulation are also used in the new simulation and everything remains unchanged in two simulations, except the absorption and scattering coefficients.Illumination and detection geometries have also been incorporated into the scaling procedure. Palmer et al.47 extended Graaff’s scaling method from illumination by a pencil beam to that by an optical fiber, and they also extended the original scaling method from the total reflectance to the reflectance detected by an optical fiber by combing scaling and convolution. Wang et al.72 proposed two convolution formulas for the scaling MC method to calculate diffuse reflectance from a semi-infinite medium for a single illumination–detection fiber. Nearly all the previous papers about scaling dealt only with a homogeneous tissue model. Liu et al.73 developed a method that applies the scaling method to multilayered tissue models. In this method, the homogeneous tissue model in a single baseline MC simulation is divided into multiple thin pseudo layers. The horizontal offset and the number of collisions that each survival photon experienced in each pseudo layer are recorded and used later to scale for the exit distance and exit weight of the photon in a multilayered tissue model with different set of optical properties. The method has been validated on both two-layered and three-layered epithelial tissue models. 3.2.Perturbation MC MethodsSimilar to the scaling method, the perturbation MC (pMC) method requires one baseline simulation in which the optical properties are supposed to be close to the optical properties in the new tissue model so that the approximation made by perturbation is valid.74 The trajectory information including the exit weight, path length, and number of collisions of each detected photon spent in the region of interest will be recorded in the baseline simulation. Then the relation between the survival weight in the baseline simulation and that in the new tissue model based on the perturbation theory,75,76 i.e., is used to estimate diffuse reflectance from the tissue model in which the optical properties of the interesting region are perturbed. In Eq. (3), , , and are the exit weight, scattering coefficient, and transport coefficient in the baseline simulation, while , , and are those in the new simulation. and are the photon path length and the number of collisions that a detected photon experienced in the perturbed region, respectively, recorded in the baseline simulation. It should be pointed out that the pMC is an approximation in nature, so its accuracy depends on the magnitude of difference in the optical properties between the perturbed optical properties in the new tissue model and the original optical properties in the baseline simulation.In contrast, the scaling method is precise in nature regardless of the differences in optical properties because no approximation is made in scaling. One important advantage of the pMC is its simplicity and fast speed when the perturbed region is small, therefore it has been explored in the inverse problem of light transport to estimate optical properties in the perturbed region as surveyed below. Sassaroli et al.75 proposed two perturbation relations to estimate the temporal response in diffuse reflectance from a medium, in which scattering or absorbing inhomogeneities are introduced, from the trajectory information obtained from the baseline simulation of a homogeneous medium. Hayakawa et al.76 demonstrated that the perturbation relation can be directly incorporated into a two-parameter Levenberg-Marquardt algorithm to solve the inverse photon migration problems in a two-layered tissue model rapidly. Recently, the same group77 demonstrated the use of this method for extraction of optical properties in a layered phantom mimicking an epithelial tissue model for given experimental measurements of spatially resolved diffuse reflectance. This method was found effective over a broad range of absorption (50% to 400% relative to the baseline value) and scattering (70% to 130% relative to the baseline value) perturbations. However, this method requires both the thickness of the epithelial layer and the optical properties of one of the two layers. Many other groups also proposed pMC-based methods for the recovery of the optical properties in various tissue models. Kumar et al.78 have presented a pMC-based method for reconstructing the optical properties of a heterogonous tissue model with low scattering coefficients and the method was validated experimentally.29 Their results show that a priori knowledge of the location of inhomogeneities is important to know in the reconstruction of optical properties of a heterogeneous tissue. More recently, Sassaroli et al.79 proposed a fast pMC method for photon migration in a tissue model with an arbitrary distribution of optical properties. This method imposes a minimal requirement on hard disk space; thus it is particularly suitable to solve inverse problems in imaging, such as DOT. Zhu et al.35 proposed a hybrid approach combining the scaling method and the pMC method to accelerate the MC simulation of diffuse reflectance from a multilayered tissue model with finite-size tumor targets. Besides the advantage in speed, a larger range of probe configurations and tumor models can be simulated by this approach compared to the scaling method or the pMC method alone. 3.3.Hybrid MC MethodsHybrid MC methods incorporate fast analytical calculations such as diffuse approximation into a standard MC simulation. Flock et al.80 proposed a hybrid method to model light distribution in tissues. In this model, a series of MC simulations for multiple sets of optical properties and geometrical parameters were performed to create a coupling function. Then, this coupling function was used to correct the results computed by diffusion theory. Wang et al.81 proposed a conceptually different hybrid method to simulate diffuse reflectance from semi-infinite homogeneous media. Wang’s method combined the strength of MC modeling in accuracy at locations near the light source and the strength of diffusion theory in speed at locations distant from the source. Wang et al.82 later extended this method from semi-infinite media to turbid slabs with finite thickness, which is more useful than the previous method in practice. Alexandrakis et al.62 proposed a fast diffusion-MC method for simulating spatially resolved reflectance and phase delay in a two-layered human skin model, which facilitates the study of frequency-domain optical measurements. This method has been proven to be several hundred times faster than a standard MC simulation. Hayashi et al.83 presented a hybrid method to model light propagation in a head model that contains both high-scattering regions and low-scattering regions. Light propagation in high-scattering regions was calculated by diffusion approximation and that in the low-scattering region, i.e., the cerebrospinal fluid layer, was simulated by the MC method. Since the time-consuming MC simulation is employed only in part of the head model, the computation time is significantly shorter than that of the standard MC method. Donner et al.84 presented a diffusion-MC method for fast calculation of steady-state diffuse reflectance and transmittance from layered tissue models. In their method, the steady-state diffuse reflectance and transmittance profiles of each individual layer were calculated and then convolved to generate the overall diffuse reflectance and transmittance to eliminate the need of considering boundary conditions. Luo et al.85 introduced an improved diffusion model derived empirically. Then the modified diffusion model was combined with the MC method to estimate diffuse reflectance from turbid media with a high ratio of the absorption coefficient to the reduced scattering coefficient, which can be as large as 0.07. Di Rocco et al.86 proposed a hybrid method to speed up MC simulations in slab geometries including deep inhomegeneities. In this approach, the tissue model was treated as two sections, i.e., the top layer with a thickness of in which there is no inhomogeneity and the bottom layer with inhomgeneity. Propagation up to the given depth , i.e., the top layer, is replaced by analytical calculations using diffusion approximation. Then photon propagation is continued inside the bottom layer using MC rules until the photon is terminated or detected. Tinet et al.58 adapted the statistical estimator technique used previously in the nuclear engineering field to a fast semi-analytical MC model for simulating time-resolved light scattering problems. There were two steps in this approach. The first step was information generation, in which the contribution to the overall reflectance and transmittance was evaluated for each scattering event. The second step was information processing, in which the results of first step were used to calculate desired results analytically. Chatigny et al.87 proposed a hybrid method to efficiently model the time- and space-resolved transmittance through a breast tissue model that was divided into multiple isotropic regions and anisotropic regions. In this hybrid method, the standard MC method incorporated with the isotropic diffusion similarity rule was applied to the area that contains both isotropic and anisotropic regions, while the analytical MC, which is similar to Tinet’s method, was used for the area that contains isotropic regions only. 3.4.Variance Reduction TechniquesIn addition to hybrid methods reviewed above, multiple variance reduction techniques, which were initially applied in modeling neutron transport,88 have also been investigated in the MC modeling of light transport in tissues. For example, the weighted photon model and Russian roulette scheme have been employed in the public-domain MC code, Monte Carlo modeling of photon transport in Multi-Layered tissues.8 Liu et al.89 have used one of the oldest and the most widely used variance reduction techniques in MC modeling, i.e., geometry splitting, to speed up the creation of an MC database to estimate the optical properties of a two-layered epithelial tissue model from simulated diffuse reflectance. In this strategy, the tissue model is separated into several volumes, and the technique can reduce variances in certain important volumes by increasing the chance of sampling in important volumes and decreasing the chance of sampling in other volumes. Chen et al.90 proposed a controlled MC method in which an attractive point with an adjustable attractive factor was introduced to increase the efficiency of trajectory generation by forcing photons to propagate along directions more likely to intersect with the detector, which is similar to geometry splitting in principle. They first demonstrated this approach in transmission geometry90 and then in reflection geometry.91 Behin-Ain et al.92 extended Chen’s method for the efficient construction of the early temporal PSF created by the visible or near-infrared photons transmitting through an optically thick scattering medium. More recently, Lima et al.93,94 incorporated an improved importance sampling method into a standard MC for fast MC simulation of time-domain OCT, by which several hundred times of acceleration has been achieved. 3.5.Parallel Computation-Based MC MethodsParallel computation has received increasing attention recently in the study of speeding up MC simulations due to advances in computer technology. The acceleration due to parallel computation is independent of all previous techniques and thus could be used in combination with them to gain extra benefit. Kirkby et al.95 reported an approach by which one can run an MC simulation simultaneously on multiple computers, aiming to utilize the unoccupied time slots of networked computers to speed up MC simulations. This method has reduced simulation time appreciably. However, it can be time-consuming to wait for all computers to update the result files in order to get the final result. Moreover, the requirement of saving disk space imposes the use of binary files, and this raised compatibility issues across in various types of computers. Colasanti et al.96 explored a different approach to address the limitations associated with Kirkby’s method. They developed an MC multiple-processor code that can be run on a computer with multiple processors instead of running on many single-processor computers. The results showed that the parallelization reduced computation time significantly. Considerable efforts have also been made to implement MC codes in graphics processing unit (GPU) environment to speed up MC simulations. Erik et al.97 proposed a method that was executed on a low-cost GPU to speed up the MC simulation of time-resolved photon propagation in a semi-infinite medium. The results showed that GPU-based MC simulations were 1000 times faster than those performed on a single standard central processing unit (CPU). The same group98 further proposed an optimization scheme to overcome the performance bottleneck caused by atomic access to harness the full potential of GPU. Martinsen et al.99 implemented the MC algorithm on an NVIDIA graphics card to model photon transport in turbid media. The GPU-based MC method was found to be 70 times faster than a CPU-based MC method on a 2.67 GHz desktop computer. Fang et al.100 reported a parallel MC algorithm accelerated by GPU for the simulation of time-resolved photon propagation in an arbitrary 3-D turbid media. It has been demonstrated that GPU-based approach was 300 times faster than the conventional CPU approach when 1792 parallel threads were used. Ren et al.40 presented an MC algorithm that was implemented into GPU environment to model light transport in a complex heterogeneous tissue model in which the tissue surface was constructed by a number of triangle meshes. The MC algorithm has been tested and validated in a heterogeneous mouse model. Leung et al.101 proposed a GPU-based MC model to simulate ultrasound modulated light in turbid media. It was found that a GPU-based simulation was 70 times faster compared to CPU-based approach on the same tissue model. Most recently, Cai et al.102 implemented a fast perturbation MC method proposed by Angelo79 on GPU. It has been demonstrated that the GPU-based approach was 1000 times faster compared to the conventional CPU-based approach. Besides using GPU to speed up the MC simulations, some researchers have explored using field-programmable gate arrays (FPGA) to accelerate MC simulations. For example, Lo et al.103 implemented an MC simulation on a developmental platform with multiple FPGAs. The FPGA-based MC simulation was found to be 80 times faster and 45 times more energy efficient, on average, than the MC simulation executed on a 3 GHz Intel Xeon processor. Recently, Internet-based parallel computation has gained increasing attention for fast MC modeling of light transport in tissues. Pratx et al.104 reported a method for performing MC simulation in a massively parallel cloud computing environment based on MapReduce developed by Google. For a cluster size of 240 nodes, an improvement in speed of 1258 times was achieved as compared to the single threaded MC program. Doronin et al.105 developed a peer-to-peer (P2P) MC code to provide multiuser access for the fast online MC simulation of photon migration in complex turbid media. Their results showed that this P2P-based MC simulation was three times faster than the GPU-based MC simulations. 3.6.Acceleration of MC Simulation of FluorescenceThe methods reviewed above are all about the acceleration of MC simulation of diffuse reflectance or transmittance. Compared to diffuse reflectance, fluorescence simulation is more complex and much more time-consuming due to the generation of fluorescence photons upon each absorption event of an excitation photon. A number of groups11–13,30,57,106–108 have employed MC modeling to simulate fluorescence in tissues due to the growing interest in fluorescence spectroscopy or imaging for medical applications.109–112 As a consequence, multiple groups have investigated various methods to speed up the MC simulation of fluorescence in biological tissues. Swartling et al.13 proposed a convolution-based MC method to accelerate the simulation of fluorescence spectra from layered tissues. Their method exploited the symmetry property of the problem, which requires the multilayered tissue model to be infinite in the radial dimension. Different from the conventional fluorescence MC code, this method computed the excitation and emission light profiles separately, from which the spatial distribution of absorption and emission probabilities were obtained. Then a convolution scheme will be applied on the absorption probability and emission probability data to get the final fluorescence signals. Swartling’s method has been used by Palmer et al.113,114 to create an MC database for fluorescence spectroscopy to estimate the fluorescence property of a breast tissue model from fluorescence measurement using a fiber-optic probe. Liebert et al.57 developed an MC code for fast simulation of time-resolved fluorescence in layered tissues. In this method, both the spatial distribution of fluorescence generation and the distribution of times arrival (DTA) of fluorescence photons at the detectors were calculated along the excitation photons’ trajectories. Then the distribution of fluorescence generation inside the medium and DTA as well as the fluorescence conversion probability were used to calculate the final fluorescence signal. It should be noted that the reduced scattering coefficients at the excitation and emission wavelengths have to be approximately equal in this method. 3.7.Comparison of Methods for MC AccelerationMost methods surveyed in the previous sections have been compared and summarized in Table 1 with respect to their acceleration performance, relative error in simulated optical measurements, respective advantages, and limitations. It should be noted that those parallel computation-based methods were not listed in this table because its performance highly depends on the computing architecture, and all the methods summarized in this table can be further accelerated by applying parallel computation. Table 1Comparison of various methods in MC acceleration.
Note: The improvement relative to standard MC was defined as the fold of improvement in computation speed compared to a standard MC simulation in order to obtain results with comparable variance. GPU-based methods were not listed in this table because all the methods summarized in this table can be further accelerated by GPU. 4.Applications of MC Methods in Tissue OpticsThe most common application of MC method in tissue optics is the simulation of optical measurements such as diffuse reflectance, transmittance, and fluorescence for a given tissue model and illumination/detection geometry, which is considered as a forward problem. In this situation, MC simulations could provide guidelines for the selection of optimal illumination/detection geometry for selective optical measurements.46,49,115–118 In contrast, MC simulations can also provide data to estimate the optical properties of a tissue model from optical measurements, which is considered as an inverse problem. Solving an inverse problem typically involves the use of a nonlinear least square error algorithm47,89 or a similar algorithm to find a set of optical properties that would yield optical measurements in MC simulations best matching the actual measurements. Due to the slow speed of traditional MC simulations, a database is frequently created a priori in such an inverse problem to speed up the inversion process.119 Most of the acceleration methods discussed above can be employed in the creation of such an MC database. The MC method has been frequently used to find the optimal optical configuration in LDF, one of the oldest techniques in biomedical optics during the past decade. Jentink et al.120,121 used MC simulations to investigate the relationship between the output of laser Doppler perfusion meters and the optical probe configuration as well as the tissue scattering properties. Stern et al.122 used MC modeling to simulate the spatial Doppler sensitivity field of a two-fiber velocimeter, by which an optimal fiber configuration was identified. Similar applications can also be found in Refs. 123124. through 125. Recently, MC method has been incorporated into LDF to estimate blood flow126,127 or the phase function of light scattering.128 The MC method plays an important role in the selection of optimal configuration for PDT because it can generate light distribution in a complex tissue model for PDT dosage determination. Barajas et al.129 simulated the angular radiance in tissue phantoms and human prostate model to characterize light dosimetry using the MC method. Liu et al.130 used the MC method to simulate the temporal and spatial distributions of ground-state oxygen, photosensitizer, and singlet oxygen in a skin model for the treatment of human skin cancer. Valentine et al.131 simulated in vivo protoporphyrin IX (PpIX) fluorescence and singlet oxygen production during PDT for patients with superficial basal cell carcinoma. Later, the same group132 used the MC method to identify optimal light delivery configuration in PDT on nonmelanoma skin cancer. The MC method has also been investigated to simulate the OCT signals133,134 and images135–137 during past years due to its flexibility and high accuracy. Moreover, with the development of efficient MC methods, researchers have started to explore the MC method for image reconstruction in DOT.138,139 5.Discussion on the Potential Future DirectionsDue to advances in computing technology, it is expected that the applications of the MC method will be expanded in the near future. A few potential directions in the development of the MC method are discussed below. 5.1.Phase Function of Raman ScatteringRaman spectroscopy has been explored extensively for tissue characterization15,17,140,141 including cancer diagnosis.14,142–149 Depending on whether the excitation light is coherent or incoherent, Raman scattering can be broken down into two categories, i.e., spontaneous Raman scattering or coherent Raman scattering. The signal generated out of spontaneous Raman scattering is typically very weak, in which the probability of generating a Raman photon for every excitation photon is lower150,151 than . Different from that, coherent Raman techniques utilize laser beams at two different frequencies to produce a coherent output, which result in much stronger coherent Raman signals compared to spontaneous Raman scattering. Because of the high chemical specificity of Raman spectroscopy, it is anticipated that there will be more studies using the MC method for Raman spectroscopy to optimize experimental setup. One important issue in these studies is that, the phase function of Raman scattering from biological components in tissues have not been systematically studied. Recent MC studies on Raman scattering14,15 assumed isotropic Raman emission. This assumption should work fine for spontaneous Raman scattering according to a numerical study.152 However, this assumption is not valid for coherent Raman scattering since the angular distribution of Raman emission is affected by both the wavelength of the pump light source and the propagating beam geometry.152–154 A systematic study on the phase function of Raman scattering on the molecule level for Raman active biological molecules such as protein and DNA and on the subcellular level for organelles such as mitochondria will be very helpful, in which one or a couple of key parameters similar to the anisotropy factor in elastic scattering could accurately describe the angular distribution of Raman scattering in most common cases. The use of such validated phase functions in MC simulations will yield more useful information than the simplistic treatment in the current literature. 5.2.Incorporation of More Realistic Elastic Light Scattering Model into the MC MethodDespite the exploration of various inhomogeneous tissue models discussed above, including the multilayered tissue model, voxel-based and mesh-based tissue models, these tissue models are all based on a few simple optical coefficients including the scattering coefficients and anisotropy factor to characterize optical scatterers. A complete phase function could be used to provide the comprehensive information related to the morphology of optical scatterers, but it is inconvenient for use and its physical meaning is not straightforward. From these scattering properties, the scatterer size and density can be derived47,155 if they are assumed to be uniformly distributed spheres with homogeneous density. In many scenarios, these assumptions are not valid. For example, it is commonly known that the size and shapes of cells vary significantly with the depth from the tissue surface, and they also change with carcinogenesis. From this point of view, the superposition of multiple phase functions156 or the fractal distribution of the scatterer size157 have been proposed to accommodate special situations. An equiphase-sphere approximation for light scattering has also been proposed by Li et al.158 to model inhomogeneous microparticles with complex interior structures. Later, the same group reported two stochastic models,159 i.e., the Gaussian random sphere model and the Gaussian random field model, to simulate irregular shapes and internal structures in tissues. The incorporation of these more realistic elastic light scattering models into the MC method will expand its capability and offer more accurate information about light scatterers in tissues. 5.3.Exploration of the MC Method in Imaging ReconstructionIn most current applications of the MC method, the tissue model is assumed to be a simple layered model or determined a priori, which does not fully exploit the potential of the MC method in preclinical or clinical imaging/spectroscopy. When the MC method becomes adequately fast in the near future, which might be mostly attributed to the combination of the accelerated MC methods and parallel computing discussed above, the MC method could be used to reconstruct the optical properties of a complex tissue in optical tomography, in which the morphological structure could be obtained in real time by fast imaging techniques such as OCT for superficial regions of interest or magnetic resonance imaging for deep regions of interest in a large tissue volume. Those voxelated tissue models,19,36–42 which are more realistic than simplified homogeneous or layered tissue models, can be readily used in such reconstruction. The speed of reconstruction might be comparable to that using diffusion approximation reported in the current literature, but the accuracy would be considerably higher in a tissue model on the millimeter scale. 6.ConclusionIn this review, the principles of MC modeling for the simulation of light transport in tissues were described at the beginning. Then a variety of methods for speeding up MC simulations were discussed to overcome the time-consuming weakness of MC modeling. Then the applications of MC methods in biomedical optics were briefly surveyed. Finally, the potential directions for the future development of the MC method in tissue optics were discussed. We hope this review has achieved its intended purpose to give a general survey on the capability of MC modeling in tissue optics and other relevant key techniques for those readers who are interested in MC modeling of light transport. AcknowledgmentsThe authors would like to acknowledge the financial support from Tier 1 grant and Tier 2 grant funded by the Ministry of Education in Singapore (Grant Nos. RG47/09 and MOE 2010-T2-1-049). ReferencesN. MetropolisS. Ulam,
“The Monte Carlo method,”
J. Am. Stat. Assoc., 44
(247), 335
–341
(1949). http://dx.doi.org/10.1080/01621459.1949.10483310 JSTNAL 0003-1291 Google Scholar
I. LuxL. Koblinger, Monte Carlo Particle Transport Methods: Neutron and Photon Calculations, CRC Press, Boca Raton, Florida
(1991). Google Scholar
M. E. J. NewmanG.T. Barkema, Monte Carlo Methods in Statistical Physics, Clarendon Press, Oxford University Press, Oxford and New York
(1999). Google Scholar
B. C. WilsonG. Adam,
“A Monte Carlo model for the absorption and flux distributions of light in tissue,”
Med. Phys., 10
(6), 824
–830
(1983). http://dx.doi.org/10.1118/1.595361 MPHYA6 0094-2405 Google Scholar
S. T. Flocket al.,
“Monte-Carlo modeling of light-propagation in highly scattering tissues. I. Model predictions and comparison with diffusion-theory,”
IEEE Trans. Biomed. Eng., 36
(12), 1162
–1168
(1989). http://dx.doi.org/10.1109/TBME.1989.1173624 IEBEAX 0018-9294 Google Scholar
S. E. SkipetrovS. S. Chesnokov,
“Analysis, by the Monte Carlo method, of the validity of the diffusion approximation in a study of dynamic multiple scattering of light in randomly inhomogeneous media,”
Quantum Electron., 28
(8), 733
–737
(1998). http://dx.doi.org/10.1070/QE1998v028n08ABEH001313 QUELEZ 1063-7818 Google Scholar
T. J. Farrellet al.,
“A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo,”
Med. Phys., 19
(4), 879
–888
(1992). http://dx.doi.org/10.1118/1.596777 MPHYA6 0094-2405 Google Scholar
L. H. Wanget al.,
“MCML-Monte-Carlo modeling of light transport in multilayered tissues,”
Comput. Meth. Prog. Bio., 47
(2), 131
–146
(1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar
S. T. Flocket al.,
“Monte Carlo modeling of light propagation in highly scattering tissues. II. Comparison with measurements in phantoms,”
IEEE Trans. Biomed. Eng., 36
(12), 1169
–1173
(1989). http://dx.doi.org/10.1109/10.42107 IEBEAX 0018-9294 Google Scholar
A. J. WelchR. Richards-Kortum,
“Monte Carlo simulation of propagation of fluorescent light,”
Laser-Induced Interstitial Thermotherapy, 174
–189 SPIE, Bellingham, Washington
(1995). Google Scholar
A. J. Welchet al.,
“Propagation of fluorescent light,”
Lasers Surg. Med., 21
(2), 166
–178
(1997). http://dx.doi.org/10.1002/(SICI)1096-9101(1997)21:2<166::AID-LSM8>3.3.CO;2-Q LSMEDI 0196-8092 Google Scholar
Q. Liuet al.,
“Experimental validation of Monte Carlo modeling of fluorescence in tissues in the UV-visible spectrum,”
J. Biomed. Opt., 8
(2), 223
–236
(2003). http://dx.doi.org/10.1117/1.1559057 JBOPFO 1083-3668 Google Scholar
J. Swartlinget al.,
“Accelerated Monte Carlo models to simulate fluorescence spectra from layered tissues,”
J. Opt. Soc. Am. A, 20
(4), 714
–727
(2003). http://dx.doi.org/10.1364/JOSAA.20.000714 JOAOD6 0740-3232 Google Scholar
M. D. Kelleret al.,
“Monte Carlo model of spatially offset Raman spectroscopy for breast tumor margin analysis,”
Appl. Spectrosc., 64
(6), 607
–614
(2010). http://dx.doi.org/10.1366/000370210791414407 APSPA4 0003-7028 Google Scholar
C. Rebleet al.,
“Quantitative Raman spectroscopy in turbid media,”
J. Biomed. Opt., 15
(3), 037016
(2010). http://dx.doi.org/10.1117/1.3456370 JBOPFO 1083-3668 Google Scholar
A. M. K. Enejderet al.,
“Blood analysis by Raman spectroscopy,”
Opt. Lett., 27
(22), 2004
–2006
(2002). http://dx.doi.org/10.1364/OL.27.002004 OPLEDP 0146-9592 Google Scholar
W. C. Shihet al.,
“Intrinsic Raman spectroscopy for quantitative biological spectroscopy Part I: theory and simulations,”
Opt. Express, 16
(17), 12726
–12736
(2008). http://dx.doi.org/10.1364/OE.16.012726 OPEXFF 1094-4087 Google Scholar
J. W. Hastings,
“Biological diversity, chemical mechanisms, and the evolutionary origins of bioluminescent systems,”
J. Mol. Evol., 19
(5), 309
–321
(1983). http://dx.doi.org/10.1007/BF02101634 JMEVAU 0022-2844 Google Scholar
H. Liet al.,
“A mouse optical simulation environment (MOSE) to investigate bioluminescent phenomena in the living mouse with the Monte Carlo method,”
Acad. Radiol., 11
(9), 1029
–1038
(2004). http://dx.doi.org/10.1016/j.acra.2004.05.021 1076-6332 Google Scholar
D. Kumaret al.,
“Monte Carlo method for bioluminescence tomography,”
Indian J. Exp. Biol., 45
(1), 58
–63
(2007). IJEBA6 0019-5189 Google Scholar
J. C. Ramella-Romanet al.,
“Three Monte Carlo programs of polarized light transport into scattering media: part I,”
Opt. Express, 13
(12), 4420
–4438
(2005). http://dx.doi.org/10.1364/OPEX.13.004420 OPEXFF 1094-4087 Google Scholar
J. C. Ramella-Romanet al.,
“Three Monte Carlo programs of polarized light transport into scattering media: part II,”
Opt. Express, 13
(25), 10392
–10405
(2005). http://dx.doi.org/10.1364/OPEX.13.010392 OPEXFF 1094-4087 Google Scholar
J. M. Maareket al.,
“A simulation method for the study of laser trans-illumination of biological tissues,”
Ann. Biomed. Eng., 12
(3), 281
–304
(1984). http://dx.doi.org/10.1007/BF02364311 ABMECF 0090-6964 Google Scholar
P. Van der ZeeD. T. Delpy,
“Simulation of the point spread function for light in tissue by a Monte Carlo method,”
Adv. Exp. Med. Biol., 215 179
–191
(1987). Google Scholar
S. Avrillieret al.,
“Monte-Carlo simulation of collimated beam transmission through turbid media,”
J. Phys. France, 51
(22), 2521
–2542
(1990). http://dx.doi.org/10.1051/jphys:0199000510220252100 Google Scholar
Y. Hasegawaet al.,
“Monte-Carlo simulation of light transmission through living tissues,”
Appl. Opt., 30
(31), 4515
–4520
(1991). http://dx.doi.org/10.1364/AO.30.004515 APOPAI 0003-6935 Google Scholar
G. Zaccanti,
“Monte-Carlo study of light-propagation in optically thick media-point-source case,”
Appl. Opt., 30
(15), 2031
–2041
(1991). http://dx.doi.org/10.1364/AO.30.002031 APOPAI 0003-6935 Google Scholar
H. Keyet al.,
“Monte-Carlo modeling of light-propagation in breast-tissue,”
Phys. Med. Biol., 36
(5), 591
–602
(1991). http://dx.doi.org/10.1088/0031-9155/36/5/003 PHMBA7 0031-9155 Google Scholar
P. K. Yalavarthyet al.,
“Experimental investigation of perturbation Monte-Carlo based derivative estimation for imaging low-scattering tissue,”
Opt. Express, 13
(6), 985
–997
(2005). http://dx.doi.org/10.1364/OPEX.13.000985 OPEXFF 1094-4087 Google Scholar
T. J. Pfeferet al.,
“Light propagation in tissue during fluorescence spectroscopy with single-fiber probes,”
IEEE J. Sel. Top. Quant. Electron., 7
(6), 1004
–1012
(2001). http://dx.doi.org/10.1109/2944.983306 IJSQEN 1077-260X Google Scholar
C. G. ZhuQ. Liu,
“Validity of the semi-infinite tumor model in diffuse reflectance spectroscopy for epithelial cancer diagnosis: a Monte Carlo study,”
Opt. Express, 19
(18), 17799
–17812
(2011). http://dx.doi.org/10.1364/OE.19.017799 OPEXFF 1094-4087 Google Scholar
D. J. SmithiesP. H. Butler,
“Modeling the distribution of laser-light in port-wine stains with the Monte-Carlo method,”
Phys. Med. Biol., 40
(5), 701
–731
(1995). http://dx.doi.org/10.1088/0031-9155/40/5/001 PHMBA7 0031-9155 Google Scholar
G. W. Lucassenet al.,
“Light distributions in a port wine stain model containing multiple cylindrical and curved blood vessels,”
Lasers Surg. Med., 18
(4), 345
–357
(1996). http://dx.doi.org/10.1002/(SICI)1096-9101(1996)18:4<345::AID-LSM3>3.0.CO;2-S LSMEDI 0196-8092 Google Scholar
L. H. V. Wanget al.,
“Optimal beam size for light delivery to absorption-enhanced tumors buried in biological tissues and effect of multiple-beam delivery: a Monte Carlo study,”
Appl. Opt., 36
(31), 8286
–8291
(1997). http://dx.doi.org/10.1364/AO.36.008286 APOPAI 0003-6935 Google Scholar
C. ZhuQ. Liu,
“Hybrid method for fast Monte Carlo simulation of diffuse reflectance from a multilayered tissue model with tumor-like heterogeneities,”
J. Biomed. Opt., 17
(1), 010501
(2012). http://dx.doi.org/10.1117/1.JBO.17.1.010501 JBOPFO 1083-3668 Google Scholar
T. J. Pfeferet al.,
“A three-dimensional modular adaptable grid numerical model for light propagation during laser irradiation of skin tissue,”
IEEE J. Sel. Top. Quant. Electron., 2
(4), 934
–942
(1996). http://dx.doi.org/10.1109/2944.577318 IJSQEN 1077-260X Google Scholar
D. A. Boaset al.,
“Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head,”
Opt. Express, 10
(3), 159
–170
(2002). http://dx.doi.org/10.1364/OE.10.000159 OPEXFF 1094-4087 Google Scholar
S. V. Patwardhanet al.,
“Monte Carlo simulation of light-tissue interaction: three-dimensional simulation for trans-illumination-based imaging of skin lesions,”
IEEE Trans. Biomed. Eng., 52
(7), 1227
–1236
(2005). http://dx.doi.org/10.1109/TBME.2005.847546 IEBEAX 0018-9294 Google Scholar
E. Margallo-BalbasP. J. French,
“Shape based Monte Carlo code for light transport in complex heterogeneous tissues,”
Opt. Express, 15
(21), 14086
–14098
(2007). http://dx.doi.org/10.1364/OE.15.014086 OPEXFF 1094-4087 Google Scholar
N. N. Renet al.,
“GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues,”
Opt. Express, 18
(7), 6811
–6823
(2010). http://dx.doi.org/10.1364/OE.18.006811 OPEXFF 1094-4087 Google Scholar
H. ShenG. Wang,
“A tetrahedron-based inhomogeneous Monte Carlo optical simulator,”
Phys. Med. Biol., 55
(4), 947
–962
(2010). http://dx.doi.org/10.1088/0031-9155/55/4/003 PHMBA7 0031-9155 Google Scholar
Q. Q. Fang,
“Mesh-based Monte Carlo method using fast ray-tracing in Plucker coordinates,”
Biomed. Opt. Express, 1
(1), 165
–175
(2010). http://dx.doi.org/10.1364/BOE.1.000165 BOEICL 2156-7085 Google Scholar
U. UtzingerR. R. Richards-Kortum,
“Fiber optic probes for biomedical optical spectroscopy,”
J. Biomed. Opt., 8
(1), 121
–147
(2003). http://dx.doi.org/10.1117/1.1528207 JBOPFO 1083-3668 Google Scholar
S. C. Kanicket al.,
“Monte Carlo analysis of single fiber reflectance spectroscopy: photon path length and sampling depth,”
Phys. Med. Biol., 54
(22), 6991
–7008
(2009). http://dx.doi.org/10.1088/0031-9155/54/22/016 PHMBA7 0031-9155 Google Scholar
Q. Z. Wanget al.,
“Condensed Monte Carlo modeling of reflectance from biological tissue with a single illumination-detection fiber,”
IEEE J. Sel. Top. Quant. Electron., 16
(3), 627
–634
(2010). http://dx.doi.org/10.1109/JSTQE.2009.2029546 IJSQEN 1077-260X Google Scholar
A. M. J. Wanget al.,
“Depth-sensitive reflectance measurements using obliquely oriented fiber probes,”
J. Biomed. Opt., 10
(4), 044017
(2005). http://dx.doi.org/10.1117/1.1989335 JBOPFO 1083-3668 Google Scholar
G. M. PalmerN. Ramanujam,
“Monte Carlo-based inverse model for calculating tissue optical properties. Part I: theory and validation on synthetic phantoms,”
Appl. Opt., 45
(5), 1062
–1071
(2006). http://dx.doi.org/10.1364/AO.45.001062 APOPAI 0003-6935 Google Scholar
C. F. Zhuet al.,
“Effect of fiber optic probe geometry on depth-resolved fluorescence measurements from epithelial tissues: a Monte Carlo simulation,”
J. Biomed. Opt., 8
(2), 237
–247
(2003). http://dx.doi.org/10.1117/1.1559058 JBOPFO 1083-3668 Google Scholar
F. Jaillonet al.,
“Beveled fiber-optic probe couples a ball lens for improving depth-resolved fluorescence measurements of layered tissue: Monte Carlo simulations,”
Phys. Med. Biol., 53
(4), 937
–951
(2008). http://dx.doi.org/10.1088/0031-9155/53/4/008 PHMBA7 0031-9155 Google Scholar
F. Jaillonet al.,
“Half-ball lens couples a beveled fiber probe for depth-resolved spectroscopy: Monte Carlo simulations,”
Appl. Opt., 47
(17), 3152
–3157
(2008). http://dx.doi.org/10.1364/AO.47.003152 APOPAI 0003-6935 Google Scholar
C. ZhuQ. Liu,
“Numerical investigation of lens based setup for depth sensitive diffuse reflectance measurements in an epithelial cancer model,”
Opt. Express, 20 29807
–29822
(2012). http://dx.doi.org/10.1364/OE.20.029807 OPEXFF 1094-4087 Google Scholar
W. Becker,
“Fluorescence lifetime imaging:techniques and applications,”
J. Microsc., 247
(2), 119
–136
(2012). http://dx.doi.org/10.1111/j.1365-2818.2012.03618.x Google Scholar
A. J. Welchet al.,
“Practical models for light-distribution in laser-irradiated tissue,”
Lasers Surg. Med., 6
(6), 488
–493
(1987). http://dx.doi.org/10.1002/lsm.1900060603 LSMEDI 0196-8092 Google Scholar
K. M. YooR. R. Alfano,
“Determination of the scattering and absorption lengths from the temporal profile of a backscattered pulse,”
Opt. Lett., 15
(5), 276
–278
(1990). http://dx.doi.org/10.1364/OL.15.000276 OPLEDP 0146-9592 Google Scholar
J. B. FishkinE. Gratton,
“Propagation of photon-density waves in strongly scattering media containing an absorbing semiinfinite plane bounded by a straight edge,”
J. Opt. Soc. Am. A, 10
(1), 127
–140
(1993). http://dx.doi.org/10.1364/JOSAA.10.000127 JOAOD6 0740-3232 Google Scholar
L. O. Svaasandet al.,
“Reflectance measurements of layered media with diffuse photon-density waves: a potential tool for evaluating deep burns and subcutaneous lesions,”
Phys. Med. Biol., 44
(3), 801
–813
(1999). http://dx.doi.org/10.1088/0031-9155/44/3/020 PHMBA7 0031-9155 Google Scholar
A. Liebertet al.,
“Monte Carlo algorithm for efficient simulation of time-resolved fluorescence in layered turbid media,”
Opt. Express, 16
(17), 13188
–13202
(2008). http://dx.doi.org/10.1364/OE.16.013188 OPEXFF 1094-4087 Google Scholar
E. Tinetet al.,
“Fast semianalytical Monte Carlo simulation for time-resolved light propagation in turbid media,”
J. Opt. Soc. Am. A, 13
(9), 1903
–1915
(1996). http://dx.doi.org/10.1364/JOSAA.13.001903 JOAOD6 0740-3232 Google Scholar
K. VishwanathM. A. Mycek,
“Time-resolved photon migration in bi-layered tissue models,”
Opt. Express, 13
(19), 7466
–7482
(2005). http://dx.doi.org/10.1364/OPEX.13.007466 OPEXFF 1094-4087 Google Scholar
E. Alerstamet al.,
“White Monte Carlo for time-resolved photon migration,”
J. Biomed. Opt., 13
(4), 041304
(2008). http://dx.doi.org/10.1117/1.2950319 JBOPFO 1083-3668 Google Scholar
M. Testorfet al.,
“Sampling of time- and frequency-domain signals in Monte Carlo simulations of photon migration,”
Appl. Opt., 38
(1), 236
–245
(1999). http://dx.doi.org/10.1364/AO.38.000236 APOPAI 0003-6935 Google Scholar
G. Alexandrakiset al.,
“Monte Carlo diffusion hybrid model for photon migration in a two-layer turbid medium in the frequency domain,”
Appl. Opt., 39
(13), 2235
–2244
(2000). http://dx.doi.org/10.1364/AO.39.002235 APOPAI 0003-6935 Google Scholar
A. R. GardnerV. Venugopalan,
“Accurate and efficient Monte Carlo solutions to the radiative transport equation in the spatial frequency domain,”
Opt. Lett., 36
(12), 2269
–2271
(2011). http://dx.doi.org/10.1364/OL.36.002269 OPLEDP 0146-9592 Google Scholar
I. V. Yaroslavskyet al.,
“Effect of the scattering delay on time-dependent photon migration in turbid media,”
Appl. Opt., 36
(25), 6529
–6538
(1997). http://dx.doi.org/10.1364/AO.36.006529 APOPAI 0003-6935 Google Scholar
S. Fantiniet al.,
“Semi-infinite-geometry boundary-problem for light migration in highly scattering media—A frequency-domain study in the diffusion-approximation,”
J. Opt. Soc. Am. B, 11
(10), 2128
–2138
(1994). http://dx.doi.org/10.1364/JOSAB.11.002128 JOBPDE 0740-3224 Google Scholar
J. Chenet al.,
“Monte Carlo based method for fluorescence tomographic imaging with lifetime multiplexing using time gates,”
Biomed. Opt. Express, 2
(4), 871
–886
(2011). http://dx.doi.org/10.1364/BOE.2.000871 BOEICL 2156-7085 Google Scholar
O. Harbateret al.,
“Fluorescence lifetime and depth estimation of a tumor site for functional imaging purposes,”
IEEE J. Sel. Top. Quant. Electron., 16
(4), 981
–988
(2010). http://dx.doi.org/10.1109/JSTQE.2009.2033209 IJSQEN 1077-260X Google Scholar
R. Graaffet al.,
“Condensed Monte-Carlo simulations for the description of light transport,”
Appl. Opt., 32
(4), 426
–434
(1993). http://dx.doi.org/10.1364/AO.32.000426 APOPAI 0003-6935 Google Scholar
A. KienleM. S. Patterson,
“Determination of the optical properties of turbid media from a single Monte Carlo simulation,”
Phys. Med. Biol., 41
(10), 2221
–2227
(1996). http://dx.doi.org/10.1088/0031-9155/41/10/026 PHMBA7 0031-9155 Google Scholar
A. Pifferiet al.,
“Real-time method for fitting time-resolved reflectance and transmittance measurements with a Monte Carlo model,”
Appl. Opt., 37
(13), 2774
–2780
(1998). http://dx.doi.org/10.1364/AO.37.002774 APOPAI 0003-6935 Google Scholar
M. Martinelliet al.,
“Analysis of single Monte Carlo methods for prediction of reflectance from turbid media,”
Opt. Express, 19
(20), 19627
–19642
(2011). http://dx.doi.org/10.1364/OE.19.019627 OPEXFF 1094-4087 Google Scholar
Q. Wanget al.,
“Condensed Monte Carlo modeling of reflectance from biological tissue with a single illumination–detection fiber,”
IEEE J. Sel. Top. Quant. Electron., 16
(3), 627
–634
(2010). http://dx.doi.org/10.1109/JSTQE.2009.2029546 IJSQEN 1077-260X Google Scholar
Q. LiuN. Ramanujam,
“Scaling method for fast Monte Carlo simulation of diffuse reflectance spectra from multilayered turbid media,”
J. Opt. Soc. Am. A, 24
(4), 1011
–1025
(2007). http://dx.doi.org/10.1364/JOSAA.24.001011 JOAOD6 0740-3232 Google Scholar
M. R. OstermeyerS. L. Jacques,
“Perturbation theory for diffuse light transport in complex biological tissues,”
J. Opt. Soc. Am. A, 14
(1), 255
–261
(1997). http://dx.doi.org/10.1364/JOSAA.14.000255 JOAOD6 0740-3232 Google Scholar
A. Sassaroliet al.,
“Monte Carlo procedure for investigating light propagation and imaging of highly scattering media,”
Appl. Opt., 37
(31), 7392
–7400
(1998). http://dx.doi.org/10.1364/AO.37.007392 APOPAI 0003-6935 Google Scholar
C. K. Hayakawaet al.,
“Perturbation Monte Carlo methods to solve inverse photon migration problems in heterogeneous tissues,”
Opt. Lett., 26
(17), 1335
–1337
(2001). http://dx.doi.org/10.1364/OL.26.001335 OPLEDP 0146-9592 Google Scholar
I. Seoet al.,
“Perturbation and differential Monte Carlo methods for measurement of optical properties in a layered epithelial tissue model,”
J. Biomed. Opt., 12
(1), 014030
(2007). http://dx.doi.org/10.1117/1.2697735 JBOPFO 1083-3668 Google Scholar
Y. P. KumarR. M. Vasu,
“Reconstruction of optical properties of low-scattering tissue using derivative estimated through perturbation Monte-Carlo method,”
J. Biomed. Opt., 9
(5), 1002
–1012
(2004). http://dx.doi.org/10.1117/1.1778733 JBOPFO 1083-3668 Google Scholar
A. Sassaroli,
“Fast perturbation Monte Carlo method for photon migration in heterogeneous turbid media,”
Opt. Lett., 36
(11), 2095
–2097
(2011). http://dx.doi.org/10.1364/OL.36.002095 OPLEDP 0146-9592 Google Scholar
S. T. Flocket al.,
“Hybrid Monte Carlo-diffusion theory modeling of light distributions in tissue,”
Proc. SPIE, 908 20
–28
(1988). http://dx.doi.org/10.1117/12.945337 PSISDG 0277-786X Google Scholar
L. H. WangS. L. Jacques,
“Hybrid model of Monte-Carlo simulation and diffusion-theory for light reflectance by turbid media,”
J. Opt. Soc. Am. A, 10
(8), 1746
–1752
(1993). http://dx.doi.org/10.1364/JOSAA.10.001746 JOAOD6 0740-3232 Google Scholar
L. H. V. Wang,
“Rapid modeling of diffuse reflectance of light in turbid slabs,”
J. Opt. Soc. Am. A, 15
(4), 936
–944
(1998). http://dx.doi.org/10.1364/JOSAA.15.000936 JOAOD6 0740-3232 Google Scholar
T. Hayashiet al.,
“Hybrid Monte Carlo-diffusion method for light propagation in tissue with a low-scattering region,”
Appl. Opt., 42
(16), 2888
–2896
(2003). http://dx.doi.org/10.1364/AO.42.002888 APOPAI 0003-6935 Google Scholar
C. DonnerH. W. Jensen,
“Rapid simulation of steady-state spatially resolved reflectance and transmittance profiles of multilayered turbid materials,”
J. Opt. Soc. Am. A, 23
(6), 1382
–1390
(2006). http://dx.doi.org/10.1364/JOSAA.23.001382 JOAOD6 0740-3232 Google Scholar
B. LuoS. L. He,
“An improved Monte Carlo diffusion hybrid model for light reflectance by turbid media,”
Opt. Express, 15
(10), 5905
–5918
(2007). http://dx.doi.org/10.1364/OE.15.005905 OPEXFF 1094-4087 Google Scholar
H. O. Di Roccoet al.,
“Acceleration of Monte Carlo modeling of light transport in turbid media: an approach based on hybrid, theoretical and numerical, calculations,”
J. Quant. Spectrosc. Rad. Trans., 110
(4–6), 307
–314
(2009). http://dx.doi.org/10.1016/j.jqsrt.2008.11.006 JQSRAE 0022-4073 Google Scholar
S. Chatignyet al.,
“Hybrid Monte Carlo for photon transport through optically thick scattering media,”
Appl. Opt., 38
(28), 6075
–6086
(1999). http://dx.doi.org/10.1364/AO.38.006075 APOPAI 0003-6935 Google Scholar
J. S. HendricksT. E. Booth,
“MCNP variance reduction overview,”
in Proc. Monte-Carlo Methods and Applications in Neutronics, Photonics and Statistical Physics,
83
–92
(1985). Google Scholar
Q. LiuN. Ramanujam,
“Sequential estimation of optical properties of a two-layered epithelial tissue model from depth-resolved ultraviolet-visible diffuse reflectance spectra,”
Appl. Opt., 45
(19), 4776
–4790
(2006). http://dx.doi.org/10.1364/AO.45.004776 APOPAI 0003-6935 Google Scholar
N. G. ChenJ. Bai,
“Estimation of quasi-straightforward propagating light in tissues,”
Phys. Med. Biol., 44
(7), 1669
–1676
(1999). http://dx.doi.org/10.1088/0031-9155/44/7/307 PHMBA7 0031-9155 Google Scholar
N. G. Chen,
“Controlled Monte Carlo method for light propagation in tissue of semi-infinite geometry,”
Appl. Opt., 46
(10), 1597
–1603
(2007). http://dx.doi.org/10.1364/AO.46.001597 APOPAI 0003-6935 Google Scholar
S. Behin-Ainet al.,
“An indeterministic Monte Carlo technique for fast time of flight photon transport through optically thick turbid media,”
Med. Phys., 29
(2), 125
–131
(2002). http://dx.doi.org/10.1118/1.1429623 MPHYA6 0094-2405 Google Scholar
I. T. Lima Jr.et al.,
“Improved importance sampling for Monte Carlo simulation of time-domain optical coherence tomography,”
Biomed. Opt. Express, 2
(5), 1069
–1081
(2011). http://dx.doi.org/10.1364/BOE.2.001069 BOEICL 2156-7085 Google Scholar
I. T. Lima Jr.et al.,
“Fast calculation of multipath diffusive reflectance in optical coherence tomography,”
Biomed. Opt. Express, 3
(4), 692
–700
(2012). http://dx.doi.org/10.1364/BOE.3.000692 BOEICL 2156-7085 Google Scholar
D. R. KirkbyD. T. Delpy,
“Parallel operation of Monte Carlo simulations on a diverse network of computers,”
Phys. Med. Biol., 42
(6), 1203
–1208
(1997). http://dx.doi.org/10.1088/0031-9155/42/6/016 PHMBA7 0031-9155 Google Scholar
A. Colasantiet al.,
“Multiple processor version of a Monte Carlo code for photon transport in turbid media,”
Comput. Phys. Commun., 132
(1–2), 84
–93
(2000). http://dx.doi.org/10.1016/S0010-4655(00)00138-7 CPHCBZ 0010-4655 Google Scholar
E. Alerstamet al.,
“Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration,”
J. Biomed. Opt., 13
(6), 060504
(2008). http://dx.doi.org/10.1117/1.3041496 JBOPFO 1083-3668 Google Scholar
E. Alerstamet al.,
“Next-generation acceleration and code optimization for light transport in turbid media using GPUs,”
Biomed. Opt. Express, 1
(2), 658
–675
(2010). http://dx.doi.org/10.1364/BOE.1.000658 BOEICL 2156-7085 Google Scholar
P. Martinsenet al.,
“Accelerating Monte Carlo simulations with an NVIDIA (R) graphics processor,”
Comput. Phys. Commun., 180
(10), 1983
–1989
(2009). http://dx.doi.org/10.1016/j.cpc.2009.05.013 CPHCBZ 0010-4655 Google Scholar
Q. Q. FangD. A. Boas,
“Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units,”
Opt. Express, 17
(22), 20178
–20190
(2009). http://dx.doi.org/10.1364/OE.17.020178 OPEXFF 1094-4087 Google Scholar
T. S. LeungS. Powell,
“Fast Monte Carlo simulations of ultrasound-modulated light using a graphics processing unit,”
J. Biomed. Opt., 15
(5), 055007
(2010). http://dx.doi.org/10.1117/1.3495729 JBOPFO 1083-3668 Google Scholar
F. CaiS. He,
“Using graphics processing units to accelerate perturbation Monte Carlo simulation in a turbid medium,”
J. Biomed. Opt., 17
(4), 040502
(2012). http://dx.doi.org/10.1117/1.JBO.17.4.040502 JBOPFO 1083-3668 Google Scholar
W. C. Y. Loet al.,
“Hardware acceleration of a Monte Carlo simulation for photodynamic therapy treatment planning,”
J. Biomed. Opt., 14
(1), 014019
(2009). http://dx.doi.org/10.1117/1.3080134 JBOPFO 1083-3668 Google Scholar
G. PratxL. Xing,
“Monte Carlo simulation of photon migration in a cloud computing environment with MapReduce,”
J. Biomed. Opt., 16
(12), 125003
(2011). http://dx.doi.org/10.1117/1.3656964 JBOPFO 1083-3668 Google Scholar
A. DoroninI. Meglinski,
“Peer-to-peer Monte Carlo simulation of photon migration in topical applications of biomedical optics,”
J. Biomed. Opt., 17
(9), 90504
(2012). http://dx.doi.org/10.1117/1.JBO.17.9.090504 JBOPFO 1083-3668 Google Scholar
M. Keijzeret al.,
“Fluorescence spectroscopy of turbid media—Autofluorescence of the human aorta,”
Appl. Opt., 28
(20), 4286
–4292
(1989). http://dx.doi.org/10.1364/AO.28.004286 APOPAI 0003-6935 Google Scholar
E. Peryet al.,
“Monte Carlo modeling of multilayer phantoms with multiple fluorophores: simulation algorithm and experimental validation,”
J. Biomed. Opt., 14
(2), 024048
(2009). http://dx.doi.org/10.1117/1.3122368 JBOPFO 1083-3668 Google Scholar
T. J. Pfeferet al.,
“Monte Carlo modeling of time-resolved fluorescence for depth-selective interrogation of layered tissue,”
Comput. Meth. Prog. Bio., 104
(2), 161
–167
(2011). http://dx.doi.org/10.1016/j.cmpb.2010.10.011 CMPBEK 0169-2607 Google Scholar
I. J. BigioJ. R. Mourant,
“Ultraviolet and visible spectroscopies for tissue diagnostics: fluorescence spectroscopy and elastic-scattering spectroscopy,”
Phys. Med. Biol., 42
(5), 803
–814
(1997). http://dx.doi.org/10.1088/0031-9155/42/5/005 PHMBA7 0031-9155 Google Scholar
R. Weisslederet al.,
“In vivo imaging of tumors with protease-activated near-infrared fluorescent probes,”
Nat. Biotechnol., 17
(4), 375
–378
(1999). http://dx.doi.org/10.1038/7933 NABIF9 1087-0156 Google Scholar
Z. Volynskayaet al.,
“Diagnosing breast cancer using diffuse reflectance spectroscopy and intrinsic fluorescence spectroscopy,”
J. Biomed. Opt., 13
(2), 024012
(2008). http://dx.doi.org/10.1117/1.2909672 JBOPFO 1083-3668 Google Scholar
Q. Liuet al.,
“Compact point-detection fluorescence spectroscopy system for quantifying intrinsic fluorescence redox ratio in brain cancer diagnostics,”
J. Biomed. Opt., 16
(3), 037004
(2011). http://dx.doi.org/10.1117/1.3558840 JBOPFO 1083-3668 Google Scholar
G. M. PalmerN. Ramanujam,
“Monte-Carlo-based model for the extraction of intrinsic fluorescence from turbid media,”
J. Biomed. Opt., 13
(2), 024017
(2008). http://dx.doi.org/10.1117/1.2907161 JBOPFO 1083-3668 Google Scholar
G. M. Palmeret al.,
“Quantitative diffuse reflectance and fluorescence spectroscopy: tool to monitor tumor physiology in vivo,”
J. Biomed. Opt., 14
(2), 024010
(2009). http://dx.doi.org/10.1117/1.3103586 JBOPFO 1083-3668 Google Scholar
L. H. V. WangG. Liang,
“Absorption distribution of an optical beam focused into a turbid medium,”
Appl. Opt., 38
(22), 4951
–4958
(1999). http://dx.doi.org/10.1364/AO.38.004951 APOPAI 0003-6935 Google Scholar
L. QuanN. Ramanujam,
“Relationship between depth of a target in a turbid medium and fluorescence measured by a variable-aperture method,”
Opt. Lett., 27
(2), 104
–106
(2002). http://dx.doi.org/10.1364/OL.27.000104 OPLEDP 0146-9592 Google Scholar
T. J. Pfeferet al.,
“Oblique-incidence illumination and collection for depth-selective fluorescence spectroscopy,”
J. Biomed. Opt., 10
(4), 044016
(2005). http://dx.doi.org/10.1117/1.1989308 JBOPFO 1083-3668 Google Scholar
K. B. SungH. H. Chen,
“Enhancing the sensitivity to scattering coefficient of the epithelium in a two-layered tissue model by oblique optical fibers: Monte Carlo study,”
J. Biomed. Opt., 17
(10), 107003
(2012). http://dx.doi.org/10.1117/1.JBO.17.10.107003 JBOPFO 1083-3668 Google Scholar
N. Rajaramet al.,
“Lookup table-based inverse model for determining optical properties of turbid media,”
J. Biomed. Opt., 13
(5), 050501
(2008). http://dx.doi.org/10.1117/1.2981797 JBOPFO 1083-3668 Google Scholar
H. W. Jentinket al.,
“Monte Carlo simulations of laser Doppler blood flow measurements in tissue,”
Appl. Opt., 29
(16), 2371
–2381
(1990). http://dx.doi.org/10.1364/AO.29.002371 APOPAI 0003-6935 Google Scholar
H. W. Jentinket al.,
“Laser Doppler flowmetry: measurements in a layered perfusion model and Monte Carlo simulations of measurements,”
Appl. Opt., 30
(18), 2592
–2597
(1991). http://dx.doi.org/10.1364/AO.30.002592 APOPAI 0003-6935 Google Scholar
M. D. Stern,
“Two-fiber laser Doppler velocimetry in blood: Monte Carlo simulation in three dimensions,”
Appl. Opt., 32
(4), 468
–476
(1993). http://dx.doi.org/10.1364/AO.32.000468 APOPAI 0003-6935 Google Scholar
F. F. de Mulet al.,
“Laser Doppler velocimetry and Monte Carlo simulations on models for blood perfusion in tissue,”
Appl. Opt., 34
(28), 6595
–6611
(1995). http://dx.doi.org/10.1364/AO.34.006595 APOPAI 0003-6935 Google Scholar
G. Soelkneret al.,
“Monte Carlo simulations and laser Doppler flow measurements with high penetration depth in biological tissuelike head phantoms,”
Appl. Opt., 36
(22), 5647
–5654
(1997). http://dx.doi.org/10.1364/AO.36.005647 APOPAI 0003-6935 Google Scholar
Y. WatanabeE. Okada,
“Influence of perfusion depth on laser Doppler flow measurements with large source-detector spacing,”
Appl. Opt., 42
(16), 3198
–3204
(2003). http://dx.doi.org/10.1364/AO.42.003198 APOPAI 0003-6935 Google Scholar
I. Fredrikssonet al.,
“Model-based quantitative laser Doppler flowmetry in skin,”
J. Biomed. Opt., 15
(5), 057002
(2010). http://dx.doi.org/10.1117/1.3484746 JBOPFO 1083-3668 Google Scholar
T. Binzoniet al.,
“A fast time-domain algorithm for the assessment of tissue blood flow in laser-Doppler flowmetry,”
Phys. Med. Biol., 55
(13), N383
–N394
(2010). http://dx.doi.org/10.1088/0031-9155/55/13/N02 PHMBA7 0031-9155 Google Scholar
S. Wojtkiewiczet al.,
“Estimation of scattering phase function utilizing laser Doppler power density spectra,”
Phys. Med. Biol., 58
(4), 937
–955
(2013). http://dx.doi.org/10.1088/0031-9155/58/4/937 PHMBA7 0031-9155 Google Scholar
O. Barajaset al.,
“Monte Carlo modelling of angular radiance in tissue phantoms and human prostate: PDT light dosimetry,”
Phys. Med. Biol., 42
(9), 1675
–1687
(1997). http://dx.doi.org/10.1088/0031-9155/42/9/001 PHMBA7 0031-9155 Google Scholar
B. Liuet al.,
“A dynamic model for ALA-PDT of skin: simulation of temporal and spatial distributions of ground-state oxygen, photosensitizer and singlet oxygen,”
Phys. Med. Biol., 55
(19), 5913
–5932
(2010). http://dx.doi.org/10.1088/0031-9155/55/19/019 PHMBA7 0031-9155 Google Scholar
R. M. Valentineet al.,
“Monte Carlo modeling of in vivo protoporphyrin IX fluorescence and singlet oxygen production during photodynamic therapy for patients presenting with superficial basal cell carcinomas,”
J. Biomed. Opt., 16
(4), 048002
(2011). http://dx.doi.org/10.1117/1.3562540 JBOPFO 1083-3668 Google Scholar
R. M. Valentineet al.,
“Monte Carlo simulations for optimal light delivery in photodynamic therapy of non-melanoma skin cancer,”
Phys. Med. Biol., 57
(20), 6327
–6345
(2012). http://dx.doi.org/10.1088/0031-9155/57/20/6327 PHMBA7 0031-9155 Google Scholar
G. YaoL. V. Wang,
“Monte Carlo simulation of an optical coherence tomography signal in homogeneous turbid media,”
Phys. Med. Biol., 44
(9), 2307
–2320
(1999). http://dx.doi.org/10.1088/0031-9155/44/9/316 PHMBA7 0031-9155 Google Scholar
L. Duanet al.,
“Monte-Carlo-based phase retardation estimator for polarization sensitive optical coherence tomography,”
Opt. Express, 19
(17), 16330
–16345
(2011). http://dx.doi.org/10.1364/OE.19.016330 OPEXFF 1094-4087 Google Scholar
Q. Luet al.,
“Monte Carlo modeling of optical coherence tomography imaging through turbid media,”
Appl. Opt., 43
(8), 1628
–1637
(2004). http://dx.doi.org/10.1364/AO.43.001628 APOPAI 0003-6935 Google Scholar
M. Kirillinet al.,
“Simulation of optical coherence tomography images by Monte Carlo modeling based on polarization vector approach,”
Opt. Express, 18
(21), 21714
–21724
(2010). http://dx.doi.org/10.1364/OE.18.021714 OPEXFF 1094-4087 Google Scholar
I. Meglinskiet al.,
“Simulation of polarization-sensitive optical coherence tomography images by a Monte Carlo method,”
Opt. Lett., 33
(14), 1581
–1583
(2008). http://dx.doi.org/10.1364/OL.33.001581 OPLEDP 0146-9592 Google Scholar
G. T. Quanet al.,
“Monte Carlo-based fluorescence molecular tomography reconstruction method accelerated by a cluster of graphic processing units,”
J. Biomed. Opt., 16
(2), 026018
(2011). http://dx.doi.org/10.1117/1.3544548 JBOPFO 1083-3668 Google Scholar
X. F. Zhanget al.,
“High-resolution reconstruction of fluorescent inclusions in mouse thorax using anatomically guided sampling and parallel Monte Carlo computing,”
Biomed. Opt. Express, 2
(9), 2449
–2460
(2011). http://dx.doi.org/10.1364/BOE.2.002449 BOEICL 2156-7085 Google Scholar
K. E. Shafer-Peltieret al.,
“Model-based biological Raman spectral imaging,”
J. Cell Biochem. Suppl., 87
(39), 125
–137
(2002). http://dx.doi.org/10.1002/jcb.10418 0733-1959 Google Scholar
D. E. Buravtcovet al.,
“Raman spectroscopy and fluorescence analysis in investigation of the protective action of ischemic preconditioning at ischemic insult by estimation of damage of low-density lipoprotein of blood,”
Photomed. Laser Surg., 26
(3), 181
–187
(2008). http://dx.doi.org/10.1089/pho.2007.2147 PLDHA8 1549-5418 Google Scholar
U. Utzingeret al.,
“Near-infrared Raman spectroscopy for in vivo detection of cervical precancers,”
Appl. Spectrosc., 55
(8), 955
–959
(2001). http://dx.doi.org/10.1366/0003702011953018 APSPA4 0003-7028 Google Scholar
A. Nijssenet al.,
“Discriminating basal cell carcinoma from its surrounding tissue by Raman spectroscopy,”
J. Invest. Dermatol., 119
(1), 64
–69
(2002). http://dx.doi.org/10.1046/j.1523-1747.2002.01807.x JIDEAE 0022-202X Google Scholar
N. Stoneet al.,
“Raman spectroscopy for identification of epithelial cancers,”
Faraday Discuss., 126 141169
–157183
(2004). http://dx.doi.org/10.1039/b304992b FDISE6 0301-7249 Google Scholar
J. Choiet al.,
“Direct observation of spectral differences between normal and basal cell carcinoma (BCC) tissues using confocal Raman microscopy,”
Biopolymers, 77
(5), 264
–272
(2005). http://dx.doi.org/10.1002/bip.20236 BIPMAA 0006-3525 Google Scholar
E. Widjajaet al.,
“Classification of colonic tissues using near-infrared Raman spectroscopy and support vector machines,”
Int. J. Oncol., 32
(3), 653
–662
(2008). IJONES 1019-6439 Google Scholar
M. Larraona-Puyet al.,
“Development of Raman microspectroscopy for automated detection and imaging of basal cell carcinoma,”
J. Biomed. Opt., 14
(5), 054031
(2009). http://dx.doi.org/10.1117/1.3251053 JBOPFO 1083-3668 Google Scholar
E. Lyet al.,
“Probing tumor and peritumoral tissues in superficial and nodular basal cell carcinoma using polarized Raman microspectroscopy,”
Exp. Dermatol., 19
(1), 68
–73
(2010). http://dx.doi.org/10.1111/j.1600-0625.2009.00992.x EXDEEY 0906-6705 Google Scholar
D. Linet al.,
“Colorectal cancer detection by gold nanoparticle based surface-enhanced Raman spectroscopy of blood serum and statistical analysis,”
Opt. Express, 19
(14), 13565
–13577
(2011). http://dx.doi.org/10.1364/OE.19.013565 OPEXFF 1094-4087 Google Scholar
The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules, John Wiley & Sons, New York
(2002). Google Scholar
X. N. Heet al.,
“Coherent anti-Stokes Raman scattering and spontaneous Raman spectroscopy and microscopy of microalgae with nitrogen depletion,”
Biomed. Opt. Express, 3
(11), 2896
–2906
(2012). http://dx.doi.org/10.1364/BOE.3.002896 BOEICL 2156-7085 Google Scholar
M. Kerkeret al.,
“Raman and fluorescent scattering by molecules embedded in small particles--numerical results for incoherent optical processes,”
J. Opt. Soc. Am. A, 68
(12), 1676
–1686
(1978). http://dx.doi.org/10.1364/JOSA.68.001676 JOAOD6 0740-3232 Google Scholar
H. Chewet al.,
“Raman and fluorescent scattering by molecules embedded in small particles—results for coherent optical processes,”
J. Opt. Soc. Am. A, 68
(12), 1686
–1689
(1978). http://dx.doi.org/10.1364/JOSA.68.001686 JOAOD6 0740-3232 Google Scholar
J. X. Chenget al.,
“Theoretical and experimental characterization of coherent anti-Stokes Raman scattering microscopy,”
J. Opt. Soc. Am. B, 19
(6), 1363
–1375
(2002). http://dx.doi.org/10.1364/JOSAB.19.001363 JOBPDE 0740-3224 Google Scholar
R. Graaffet al.,
“Reduced light-scattering properties for mixtures of spherical-particles—a simple approximation derived from Mie calculations,”
Appl. Opt., 31
(10), 1370
–1376
(1992). http://dx.doi.org/10.1364/AO.31.001370 APOPAI 0003-6935 Google Scholar
Q. H. LiuF. Z. Weng,
“Combined Henyey-Greenstein and Rayleigh phase function,”
Appl. Opt., 45
(28), 7475
–7479
(2006). http://dx.doi.org/10.1364/AO.45.007475 APOPAI 0003-6935 Google Scholar
B. G’el’ebartet al.,
“Phase function simulation in tissue phantoms: a fractal approach,”
J. Eur. Opt. Soc. A Pure Appl. Opt., 5
(4), 377
–388
(1996). http://dx.doi.org/10.1088/0963-9659/5/4/005 JOAOF8 1464-4258 Google Scholar
X. Liet al.,
“Equiphase-sphere approximation for light scattering by stochastically inhomogeneous microparticles,”
Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys., 70
(5 Pt. 2), 056610
(2004). PLEEE8 1063-651X Google Scholar
X. Liet al.,
“Recent progress in exact and reduced-order modeling of light-scattering properties of complex structures,”
IEEE J. Sel. Topics Quantum Electron., 11
(4), 759
–765
(2005). http://dx.doi.org/10.1109/JSTQE.2005.857691 IJSQEN 1077-260X Google Scholar
|