|
|
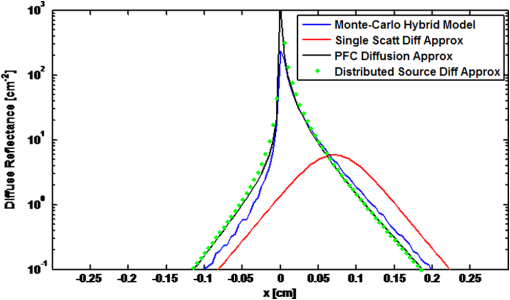
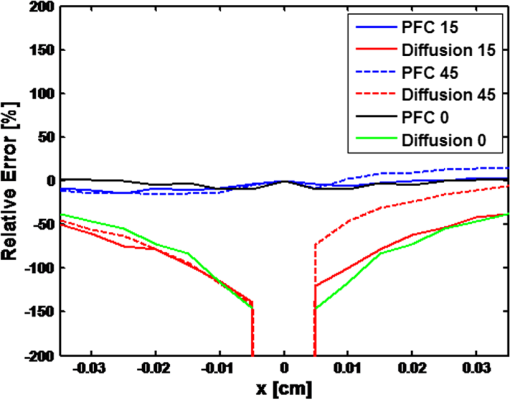
1.IntroductionVarious forms of light-scattering measurements and spectroscopy are showing promise as a biopsy-free means to measure the size distribution of nuclei and associated scattering as an indicator of preinvasive neoplasia and malignancy.1–12 Many of these techniques require or would benefit from accurate models of light transport near the point of entry. Computational models of light transport including Monte Carlo simulations13–16 and numerical implementations of the radiative transport equation17–20 are typically too computationally burdensome to be used for applications where rapid analysis is important. Analytical solutions have primarily been restricted to diffusion-theory approximations21,22 or slightly higher order corrections,23–27 which are inaccurate near the point-of-entry and when absorption is high or comparable with scattering coefficients. Unfortunately, accurate analytical models of light propagation in tissue near the point-of-entry and for cases where absorption is high or comparable with scattering have been difficult to obtain. Recently, Vitkin et al.28 described an elegant phase-function corrected (PFC) diffusion approximation to the radiative transport equation which permitted an analytical description of a pencil beam normally incident on a semi-infinite turbid medium. In this paper, we extend their work to include a pencil beam obliquely incident on a semi-infinite turbid medium, and investigate the accuracy of the models by comparing them with Monte Carlo simulations. The case of oblique incidence is of noteworthy importance as a number of techniques rely on angled illumination, including oblique incidence reflectometry (OIR) and1–6,29–31 angled low-coherence interferometry,32–38 among others.11 In this article, we focus on the applications of OIR, a technique that has seen great success in some clinical studies.6,31 In this technique, diffuse reflectance from an obliquely incident beam is recorded and compared with diffusion models of light transport to estimate the tissue optical properties. However, to obtain accurate estimates, the sensing footprint (defined here as the minimum circular area containing source and detector fibers) generally needs to be larger than a few transport mean-free paths to reliably estimate the centroid of diffuse-reflectance, with some recent exceptions.39,40 Still, the probe sizes in such recent work are too large to be used for micro-endoscopic applications, which would enable a broader range of clinical applications beyond dermatology. Smaller-footprint probes require improved light-propagation models and inversion schemes for diffuse reflectance close to the point of entry. Recent works39,40 leverage the scalable Monte Carlo method,41 which can scale the amplitudes and coordinates of the time-resolved diffuse reflectance of a reference simulation to transform to an effectively different turbid medium. The steady-state diffuse reflectance is then found by integrating over time. This method avoids iterative application of Monte Carlo simulations, and permits small-footprint sensors. Our work provides an alternative approach that avoids stochastic variability associated with Monte Carlo results, and is fast, accurate, and based on analytical models. With future efficient algorithm implementation, the speed of inversion afforded by the analytical models could enable development of microprobes with real-time feedback for tumor margin resection guidance, and clinical classification of suspected tumors and assessment of precancers. 2.BackgroundVitkin et al.28 found that the time-independent radiative transport equation where is radiance, is the source radiance distribution, is a field point, is a unit vector, is the total interaction coefficient, the sum of the absorption and scattering coefficients, respectively, with normally incident collimated pencil-beam entering a semi-infinite turbid medium could be written as two equations, This one follows the diffusion approximation and the other serves as a phase-function-correction termHere is the anisotropy factor, and is the reduced total interaction coefficient, which is the sum of the reduced scattering coefficient and . Boundary conditions are given as and for . Approximations were needed to break up equations in this way, but Vitkin et al. showed excellent agreement with Monte Carlo simulations and experiments, even in the region near the point-of-entry, a regime handled poorly by other approximations. They restricted their attention to normally incident pencil beams and semi-infinite media. The purpose of this paper is to extend this PFC-diffusion theory to the case of obliquely incident pencil beams with a long-term goal of improved OIR for sensing tissue absorption and scattering coefficients. 3.Methods3.1.TheoryFirst, we consider an extension of the work of Farrell et al.42 to model diffuse reflectance from a pencil beam obliquely incident on a surface. Then, we consider the phase-function correction to this diffusion approximation. 3.1.1.Diffusion-theory modelsFirst consider diffuse reflectance due to a number of distributed point sources along the obliquely incident transmitted ray, similar to Farrell et al.42 Assume, without loss of generality, that the incident beam is in the plane as shown in Fig. 1. Effective point sources are located along the obliquely incident trajectory at locations . The Green’s function describing fluence-rate at a point due to an isotropic point source at position in an infinite turbid medium is21 where . The solution for an equivalent point source, at a distance , along the incident trajectory in a semi-infinite medium is given by summing the solutions for the point source and the image source where and is the coordinate of the extrapolated boundary condition with , a factor equal to 1 for index-matched boundary conditions and different than 1 for index-mismatched boundary conditions, as defined by Wang and Wu21 in Eq. (5).Fig. 1A detailed view of the geometry needed to develop analytical approximations for the case of light propagation in a semi-infinite turbid medium due to an obliquely incident pencil beam. 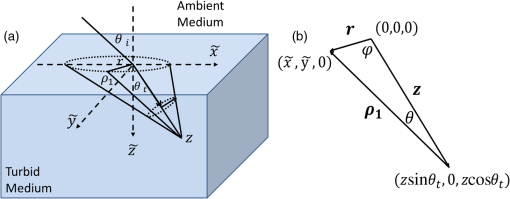 We want the diffuse reflectance (photon current leaving the tissue at ): with and we find andHence, for a single scattering event at location along the incident trajectory, the diffuse reflectance due to the diffusion approximation is When we model all initial scattering as occurring from the depth of the transport mean-free path, , we label the approximation as the single scattering diffusion approximation. It has poor accuracy near the point-of-entry, but has reasonable accuracy in several transport mean-free path-lengths away from the point-of-entry, as discussed by Wang and Wu21 in detail.Next, we consider a superposition of point-sources along the incident trajectory with source-strength or as a function of ballistic depth , given as . Then the diffuse reflectance is given by integrating the diffuse reflectance due to each weighted point source along the trajectory We call this the distributed source diffusion approximation. It is similar to the expression previously published by Farrell et al.,42 and reduces to that expression when (i.e., normal incidence) in which case and . 3.1.2.Phase-function correctionOne way of solving the phase-function correction to the diffusion approximation is to simply integrate over photons that propagate quasi-ballistically, scatter once with large angle, and propagate to the field point or medium surface in an equivalently isotropic scattering medium with the new effective scattering coefficient equal to the reduced scattering coefficient. The anisotropy is embodied via approximations in the source term a critical simplification.Given by the law of cosines or and , so the cosine of the scattering angle is given as . (Note that the scattering angle .) Then the phase-function correction to the diffuse reflectance is given by integrating the component of the radiance exiting the surface from the turbid back into the ambient media over all scattering anglesThis represents the energy scattered at position along the trajectory projected quasi-ballistically to the surface, then taking the component of the radiance in the direction normal to the interface and integrating over all possible exit angles. Because, the exit angles are determined by the depth of scattering, the integration is performed over as an analytic simplification. The factor is needed in the integrand because in a lossless medium, energy scattered from point should be conserved in a sphere with radius so energy density should decay proportionally with the surface area of such sphere. Here, given and , . Note that when (i.e., normal incidence), reduces to the previously derived expression given by Vitkin et al.28 The total PFC diffuse reflectance is the sum of the distributed-source diffusion-approximation estimate and the PFC term 3.2.Monte Carlo SimulationsWe performed custom Monte Carlo simulations to model pencil beams obliquely incident on a semi-infinite turbid medium. We used the hybrid Monte Carlo methods described by Wang and Wu,21 however, instead of using a cylindrical recording geometry we used a Cartesian mesh. Simulations were written in C++ and validated against the normally incident case as modeled by the widely used Monte Carlo for multi-layer media program described by Wang et al.13 Models for oblique incidence were also validated against results in Wang and Wu.21 Our Monte Carlo simulations were used as a gold standard to validate the PFC-diffusion theory. For simplicity, we chose refractive index-matched boundary conditions and modeled an effectively semi-infinite turbid medium. In all cases, five runs were performed for each simulation condition using nine billion photons on a 1.2 cm grid with 50 μm voxels. While it is possible to use Mie21 and other more complicated phase-function distributions, we chose the more common Henyey–Greenstein phase function43 for both Monte Carlo simulations and PFC-diffusion theory. 3.3.Analytical Model Fitting to Monte Carlo Simulations to Estimate Optical PropertiesTo test the utility of the model in estimating optical properties from diffuse reflectance near the point of entry, we generate simulated experimental measurements of diffuse reflectance using Monte Carlo simulations, , then minimize the mean relative absolute error between and the analytic PFC-diffusion theory estimate Here, is a vector of the optical properties and represents the best estimate. Here, for the L1-norm. For one-dimensional (1-D) optical property estimates using 14 data points along the -axis (symmetric about and omitting the point-of-entry), this minimization procedure takes only seconds using the optimization algorithm fminsearch in MATLAB on a laptop with an Intel i5 processor and 4 GB RAM. Minimization of the mean squared error and other p-norms give similar results (data not shown). 4.Results4.1.Simulation ResultsWe first validated that our PFC-diffusion model agreed with Fig. 2 of Vitkin et al.28 for the case of a pencil beam normally incident on a semi-infinite turbid medium with , and (data not shown). We then compared the diffuse reflectance model using the diffusion approximation and PFC-diffusion approximation with Monte Carlo simulations for obliquely incident pencil beams. Results for the normally incident case and the 45-deg incident case are shown in Figs. 2 and 3, respectively. In Fig. 4, we repeat the 45-deg incidence simulation, but with a much higher absorption coefficient of , all other parameters being the same. In this case, the reduced scattering coefficient of is compared with the absorption coefficient, a regime where traditional diffusion approximations are inaccurate, yet where PFC-diffusion models previously showed high accuracy for normally incident pencil beams. Fig. 2Comparison of the diffuse reflectance computed using the phase-function-corrected (PFC)-diffusion approximation, distributed source diffusion approximation [Eq. (14)], and the single-scattering diffusion approximation [Eq. (10)] against a Monte Carlo simulation in the case of a pencil beam normally incident on a semi-infinite turbid medium with ,, and . 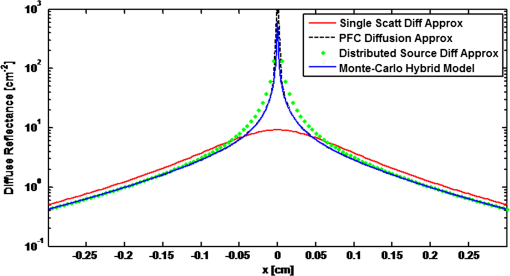 Fig. 3Comparison of the diffuse reflectance computed using the PFC-diffusion approximation, distributed source diffusion approximation [Eq. (14)], and the single-scattering diffusion approximation [Eq. (10)] against a Monte Carlo simulation in the case of a pencil beam obliquely incident on a semi-infinite turbid medium with incident angle of 45-deg and turbid media parameters of ,, and . 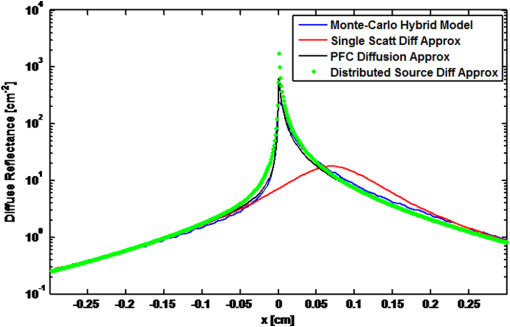 We simulated incident angles of 0, 15, and 45 deg using , and with Monte Carlo, PFC-diffusion, and noncorrected diffusion models and computed the relative error. Results are shown in Fig. 5. 4.2.Results of Analytical Model Fitting to Monte Carlo SimulationsWe used Monte Carlo simulations to compute the diffuse reflectance for a range of scattering coefficients: , 150, 200, 250, and , with a fixed absorption coefficient, , and anisotropy factor . Using only measurements 350 μm on either side of the point-of-entry and omitting the point-of-entry as a data point, Monte Carlo simulations, mimicking optical measurements, were fit to the PFC-diffusion models using 45-deg incident pencil beams in each case. Scattering coefficient estimates (using a starting guess of and in each case) were recovered and closely followed true scattering coefficients used in the forward models. Error bars associated with five replicate runs are smaller than the marker sizes shown in Fig. 6, and are associated with standard deviations of or less. Scattering coefficient estimates were within error of the true value for a wide range of initial guesses of optical parameters, using starting guesses of absorption coefficients ranging from 0.05 to and starting guesses of scattering coefficients ranging from 50 to . Absorption coefficients were recovered with less accuracy and larger variances than scattering coefficients, as is the case with previously published OIR articles. Estimates of absorption coefficients, , ranged from 0.1 to using starting guesses of absorption ranging from 0.05 to and starting guesses of scattering coefficients ranging from 50 to . The standard deviation of these estimates was as high as 330% of the true value. Complementary methods for sensing absorption such as photoacoustic imaging could be considered to improve absorption sensitivity and reduce variance. In all previously mentioned fitting procedures, the phase-function was assumed to be the Henyey–Greenstein phase function, and anisotropy was fixed at 0.9. Model fitting was additionally performed to test the robustness of scattering coefficient estimation when inaccurate values of scattering anisotropy were assumed. For model fitting using inaccurate values of , 0.8, 0.9, and 0.95, estimates were recovered within error in each case. Fig. 6Estimated versus true scattering coefficients in a simulation experiment testing the ability of the analytic PFC-diffusion model to fit to Monte Carlo simulation data mimicking optical measurements of diffuse reflectance. Fitting was performed using only a 700 μm measurement footprint, and is infeasible using previous oblique incidence reflectometry (OIR)-methods relying on more traditional diffusion approximation models. 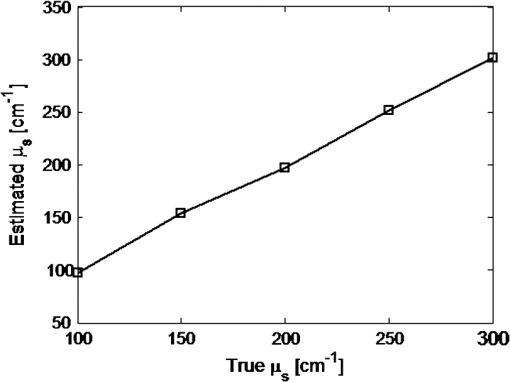 5.DiscussionPFC-diffusion models showed good agreement with Monte Carlo simulations, including improvements over single-scattering and distributed source diffusion models. Agreement was worse in the high-absorption case, shown in Fig. 4, but improvements over the diffusion models were still evident. Robustness to starting guesses of optical parameters shows promise for future experimental work. Scattering coefficient estimation robustness was even seen when incorrect anisotropies were used in model fitting. As was seen in previous OIR reports, accuracy and variance of absorption estimates were significantly worse than scattering coefficient estimation. Complementary techniques such as photoacoustic imaging2,44 could provide improved sensitivity to absorption with reduced variance. Some previous OIR approaches required a sensing footprint of a few transport-mean-free paths (several millimeters) to accurately estimate the centroid of diffuse reflectance and fit to diffusion-regime models which are inaccurate near the point of entry. In the present approach with the new PFC-diffusion analytical models, diffuse reflectance can be fit using a much smaller footprint as there is no longer a prerequisite that the data be collected far enough away from the point-of-entry to permit fitting to the standard single-scattering diffusion approximation. Figure 7 shows the footprint of our present PFC-OIR simulations compared with the footprint of previous diffusion-regime-dependent OIR approaches overlaid over a log-scale image of Monte Carlo simulated diffuse-reflectance for the case with ,, and . Even with the small 700-μm footprint, and using only data along the -axis, optical properties are accurately recovered using various starting guesses of and optical parameters. This encouraging result is the first application of the PFC-diffusion theory to an inverse problem to our knowledge. It may have practical implications in development of a small-footprint probe for measuring optical properties, which in turn may have applications in tumor margin assessment for realtime surgery guidance, detection of dysplasia and precancers for early detection of cancer, improved classification of pigmented lesions as benign nevi or malignant melanoma, among other applications. Our analytical approach is an alternative to using Monte Carlo or scalable Monte Carlo methods, and a future efficient implementation could enable realtime applications which could be of considerable importance in the clinic. The present work represents only simulations, however, this simulation work is an important first step toward designing experiments and miniature-footprint systems for optical property measurements. Fig. 7Diffuse reflectance (colormap in decibel) due to a pencil beam obliquely incident on a semi-infinite turbid media with ,. The white-dashed circle represents the typical minimum footprint of previous OIR systems (which rely on fitting to diffusion-theory models), while the black-dashed circle represents the footprint used in our PFC-diffusion model-fitting.  The simulations use Henyey–Greenstein phase-function distributions, and it should be noted that comparison with results from other phase-function distributions may be warranted for certain scatterer size distributions and may give different fitting performance. Bevilacqua and Depeursinge45 point out that the Henyey–Greenstein phase function is a rather limited phase function, since its higher order moments are coupled to the first moment. Additionally, the phase functions of tissues may very well be better modeled by phase functions other than the Henyey–Greenstein, and in fact such phase functions are unknown. Our framework provides a means to study other phase functions, but this is left for future work. With additional work, it might be interesting to see how the minimization routine performs if the phase function is treated as unknown, and for example, additional degrees of freedom are introduced through higher order phase function moments introduced by Bevilacqua and Depeursinge,45 used in the P3 approximation, and recently employed to semi-empirically model reflectance with “small footprints” by Kanick et al.46 Future work should furthermore investigate refractive-index mismatched boundaries and test the validity of the theory against experimental measurements. It should also be noted that there have been several improvements to the diffusion model described by Farrell et al. (e.g., Ref. 23), and adaptation of these improved models for diffuse reflectance may offer additional improvements to the PFC results. It should also be noted that there has been recent groundbreaking work regarding analytic solutions to the radiative transport equation, in the form of series expansions for cases such as buried point sources and normally incident pencil beam sources in semi-infinite turbid media.47 It is expected that extensions of this work to the oblique-incidence pencil beam problem could provide a computationally efficient analytic solution as an alternative to the present PFC theory. 6.ConclusionsThe PFC-diffusion theory introduced by Vitkin et al.28 has been adapted, with new derivations, to the case of pencil beams obliquely incident on a semi-infinite turbid medium. The new models show improved accuracy compared with more traditional single scattering and distributed source diffusion approximations when validated against Monte Carlo simulations. Monte Carlo simulations mimicking optical measurements of diffuse reflectance are successfully fit to PFC-diffusion models to extract optical property estimates which closely follow true values. Fitting is done using a mere 700-μm footprint which is impractically small for other OIR approaches which rely on traditional diffusion theory. This study represents the first attempt at applying the PFC-diffusion theory to an inverse problem to our knowledge and could have important implications in miniature-footprint systems for rapid measurement of the optical properties of tissues. AcknowledgmentsThis work was supported in part by the National Sciences and Engineering Research Council of Canada (NSERC 355544-2008, 375340-2009, STPGP 396444), as well as the Terry-Fox Foundation and the Canadian Cancer Society (TFF 019237, TFF 019240, CCS 2011-700718). ReferencesL. V. WangG. MarquezS. L. Thomsen,
“Anisotropic absorption and reduced scattering spectra of chicken breast tissue measured using oblique incidence reflectometry,”
Proc. SPIE, 3250 33
–43
(1998). http://dx.doi.org/10.1117/12.305386 PSISDG 0277-786X Google Scholar
J. RanasinghesagaraR. J. Zemp,
“Combined oblique incidence reflectometry, and photoacoustic microscopy for quantitative photoacoustic imaging,”
J. Biomed. Opt., 15
(4), 046016
(2010). http://dx.doi.org/10.1117/1.3470336 JBOPFO 1083-3668 Google Scholar
G. Marquezet al.,
“Measurement of absorption and scattering spectra of chicken breast with oblique incidence reflectometry,”
Proc. SPIE, 2976 306
–317
(1997). http://dx.doi.org/10.1117/12.275539 PSISDG 0277-786X Google Scholar
A. Garcia-Uribeet al.,
“Micromachined oblique incidence reflectometry (OIR) probe for skin cancer detection,”
in International Solid-State Sensors, Actuators and Microsystems Conference, 2007, Transducers 2007,
1099
–1102
(2007). Google Scholar
L. H. Wanget al.,
“Oblique incidence reflectometry: optical-fiber implementation,”
Proc. SPIE, 2681 266
–276
(1996). http://dx.doi.org/10.1117/12.239583 PSISDG 0277-786X Google Scholar
A. Garcia-Uribeet al.,
“Skin cancer detection by spectroscopic oblique-incidence reflectometry: classification and physiological origins,”
Appl. Opt., 43
(13), 2643
–2650
(2004). http://dx.doi.org/10.1364/AO.43.002643 APOPAI 0003-6935 Google Scholar
L. Qiuet al.,
“Multispectral scanning during endoscopy guides biopsy of dysplasia in Barrett’s esophagus,”
Nat. Med., 16
(5), 603
–U140
(2010). http://dx.doi.org/10.1038/nm.2138 1078-8956 Google Scholar
V. Backmanet al.,
“Detection of preinvasive cancer cells,”
Nature, 406
(6791), 35
–36
(2000). http://dx.doi.org/10.1038/35017638 NATUAS 0028-0836 Google Scholar
L. T. Perelmanet al.,
“Observation of periodic fine structure in reflectance from biological tissue: a new technique for measuring nuclear size distribution,”
Phys. Rev. Lett., 80
(3), 627
–630
(1998). http://dx.doi.org/10.1103/PhysRevLett.80.627 PRLTAO 0031-9007 Google Scholar
G. Zonioset al.,
“Diffuse reflectance spectroscopy of human adenomatous colon polyps in vivo,”
Appl. Opt., 38
(31), 6628
–6637
(1999). http://dx.doi.org/10.1364/AO.38.006628 APOPAI 0003-6935 Google Scholar
R. ReifO. A'AmarI. J. Bigio,
“Analytical model of light reflectance for extraction of the optical properties in small volumes of turbid media,”
Appl. Opt., 46
(29), 7317
–7328
(2007). http://dx.doi.org/10.1364/AO.46.007317 APOPAI 0003-6935 Google Scholar
A. Amelinket al.,
“In vivo measurement of the local optical properties of tissue by use of differential path-length spectroscopy,”
Opt. Lett., 29
(10), 1087
–1089
(2004). http://dx.doi.org/10.1364/OL.29.001087 OPLEDP 0146-9592 Google Scholar
L. H. WangS. L. JacquesL. Q. Zheng,
“MCML—Monte-Carlo modeling of light transport in multilayered tissues,”
Comput. Meth. Prog. Biomed., 47
(2), 131
–146
(1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar
L. V. WangS. L. Jacques,
“Source of error in calculation of optical diffuse reflectance from turbid media using diffusion theory,”
Comput. Meth. Prog. Biomed., 61
(3), 163
–170
(2000). http://dx.doi.org/10.1016/S0169-2607(99)00041-3 CMPBEK 0169-2607 Google Scholar
Y. R. Wanget al.,
“GPU accelerated electric field Monte Carlo simulation of light propagation in turbid media using a finite-size beam model,”
Opt. Express, 20
(15), 16618
–16630
(2012). http://dx.doi.org/10.1364/OE.20.016618 OPEXFF 1094-4087 Google Scholar
X. Yiet al.,
“GPU-accelerated Monte-Carlo modeling for fluorescence propagation in turbid medium,”
Proc. SPIE, 8216 82160U
(2012). http://dx.doi.org/10.1117/12.902988 PSISDG 0277-786X Google Scholar
H. GaoL. PhanY. T. Lin,
“Parallel multigrid solver of radiative transfer equation for photon transport via graphics processing unit,”
J. Biomed. Opt., 17
(9), 096004
(2012). http://dx.doi.org/10.1117/1.JBO.17.9.096004 JBOPFO 1083-3668 Google Scholar
A. R. GardnerV. Venugopalan,
“Accurate and efficient Monte Carlo solutions to the radiative transport equation in the spatial frequency domain,”
Opt. Lett., 36
(12), 2269
–2271
(2011). http://dx.doi.org/10.1364/OL.36.002269 OPLEDP 0146-9592 Google Scholar
M. Machidaet al.,
“The Green’s function for the radiative transport equation in the slab geometry,”
J. Phys. A Math. Theor., 43
(6), 065402
(2010). http://dx.doi.org/10.1088/1751-8113/43/6/065402 Google Scholar
L. D. MontejoH. K. KimA. H. Hielscher,
“A finite-volume algorithm for modeling light transport with the time-independent simplified spherical harmonics approximation to the equation of radiative transfer,”
Proc. SPIE, 7896 78960J
(2011). http://dx.doi.org/10.1117/12.875967 PSISDG 0277-786X Google Scholar
L. V. WangH.-I. Wu, Biomedical Optics: Principles and Imaging, John Wiley & Sons, Hoboken, NJ
(2007). Google Scholar
K. M. YooF. LiuR. R. Alfano,
“When does the diffusion-approximation fail to describe photon transport in random-media,”
Phys. Rev. Lett., 64
(22), 2647
–2650
(1990). http://dx.doi.org/10.1103/PhysRevLett.64.2647 PRLTAO 0031-9007 Google Scholar
A. KienleM. S. Patterson,
“Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium,”
J. Opt. Soc. Am. A Opt. Image Sci. Vis., 14
(1), 246
–254
(1997). http://dx.doi.org/10.1364/JOSAA.14.000246 JOAOD6 0740-3232 Google Scholar
Y. Liuet al.,
“Delta-P-1 approximation model of biological tissues,”
Acta Phys. Sin., 60
(7),
(2011). WLHPAR 1000-3290 Google Scholar
D. A. Boaset al.,
“Photon migration within the P-3 approximation,”
Proc. SPIE, 2359 240
–247
(1995). http://dx.doi.org/10.1117/12.209973 PSISDG 0277-786X Google Scholar
P. S. BrantleyE. W. Larsen,
“The simplified approximation,”
Nucl. Sci. Eng., 134
(1), 1
–21
(2000). NSENAO 0029-5639 Google Scholar
E. L. HullT. H. Foster,
“Steady-state reflectance spectroscopy in the P-3 approximation,”
J. Opt. Soc. Am. A Opt. Image Sci. Vis., 18
(3), 584
–599
(2001). http://dx.doi.org/10.1364/JOSAA.18.000584 JOAOD6 0740-3232 Google Scholar
E. Vitkinet al.,
“Photon diffusion near the point-of-entry in anisotropically scattering turbid media,”
Nat. Commun., 2 587
(2011). http://dx.doi.org/10.1038/ncomms1599 NCAOBW 2041-1723 Google Scholar
S. P. Linet al.,
“Measurement of tissue optical properties by the use of oblique-incidence optical fiber reflectometry,”
Appl. Opt., 36
(1), 136
–143
(1997). http://dx.doi.org/10.1364/AO.36.000136 APOPAI 0003-6935 Google Scholar
L. H. Wanget al.,
“Oblique-incidence reflectometry: one relative profile measurement of diffuse reflectance yields two optical parameters,”
Proc. SPIE, 2627 165
–175
(1995). http://dx.doi.org/10.1117/12.228887 PSISDG 0277-786X Google Scholar
A. Garcia-Uribeet al.,
“Skin cancer detection using spectroscopic oblique-incidence reflectometry,”
in Second Joint EMBS-BMES Conf. 2002,
2249
–2250
(2002). Google Scholar
A. Waxet al.,
“Angle-resolved low coherence interferometry for detection of dysplasia in Barrett’s esophagus,”
Gastroenterology, 141
(2), 443
–U502
(2011). http://dx.doi.org/10.1053/j.gastro.2011.06.020 GASTAB 0016-5085 Google Scholar
A. Waxet al.,
“Angular light scattering studies using low-coherence interferometry,”
Proc. SPIE, 2
(8), 32
–42
(2001). http://dx.doi.org/10.1117/12.427903 PSISDG 0277-786X Google Scholar
A. Waxet al.,
“Detection of dysplasia in Barrett’s esophagus with angle-resolved low coherence interferometry,”
Gastroenterology, 136
(5), A592
–A592
(2009). GASTAB 0016-5085 Google Scholar
A. WaxC. H. YangJ. A. Izatt,
“Fourier-domain low-coherence interferometry for light-scattering spectroscopy,”
Opt. Lett., 28
(14), 1230
–1232
(2003). http://dx.doi.org/10.1364/OL.28.001230 OPLEDP 0146-9592 Google Scholar
A. Waxet al.,
“Label-free nuclear morphology measurements of dysplasia in the EGDA rat model using angle-resolved low coherence interferometry,”
Gastroenterology, 136
(5), A122
–A122
(2009). GASTAB 0016-5085 Google Scholar
A. Waxet al.,
“Measurement of angular distributions by use of low-coherence interferometry for light-scattering spectroscopy,”
Opt. Lett., 26
(6), 322
–324
(2001). http://dx.doi.org/10.1364/OL.26.000322 OPLEDP 0146-9592 Google Scholar
A. WaxK. J. Chalut,
“Nuclear morphology measurements with angle-resolved low coherence interferometry for application to cell biology and early cancer detection,”
Anal. Cell. Pathol., 34
(5), 207
–222
(2011). ACPAER 0921-8912 Google Scholar
A. Garcia-Uribeet al.,
“In vivo diagnosis of melanoma and nonmelanoma skin cancer using oblique incidence diffuse reflectance spectrometry,”
Cancer Res., 72
(11), 2738
–2745
(2012). http://dx.doi.org/10.1158/0008-5472.CAN-11-4027 CNREA8 0008-5472 Google Scholar
A. Garcia-Uribeet al.,
“In-vivo characterization of optical properties of pigmented skin lesions including melanoma using oblique incidence diffuse reflectance spectrometry,”
J. Biomed. Opt., 16
(2), 020501
(2011). http://dx.doi.org/10.1117/1.3536509 JBOPFO 1083-3668 Google Scholar
A. KienleM. S. Patterson,
“Determination of the optical properties of turbid media from a single Monte Carlo simulation,”
Phys. Med. Biol., 41
(10), 2221
–2227
(1996). http://dx.doi.org/10.1088/0031-9155/41/10/026 PHMBA7 0031-9155 Google Scholar
T. J. FarrellM. S. PattersonB. Wilson,
“A diffusion-theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical-properties invivo,”
Med. Phys., 19
(4), 879
–888
(1992). http://dx.doi.org/10.1118/1.596777 MPHYA6 0094-2405 Google Scholar
L. G. HenyeyJ. L. Greenstein,
“Diffuse radiation in the galaxy,”
Astrophys. J., 93
(1), 70
–83
(1941). http://dx.doi.org/10.1086/144246 ASJOAB 0004-637X Google Scholar
L. V. WangS. Hu,
“Photoacoustic tomography: in vivo imaging from organelles to organs,”
Science, 335
(6075), 1458
–1462
(2012). http://dx.doi.org/10.1126/science.1216210 SCIEAS 0036-8075 Google Scholar
F. BevilacquaC. Depeursinge,
“Monte Carlo study of diffuse reflectance at source-detector separations close to one transport mean free path,”
J. Opt. Soc. Am. A Opt. Image Sci. Vis., 16
(12), 2935
–2945
(1999). http://dx.doi.org/10.1364/JOSAA.16.002935 JOAOD6 0740-3232 Google Scholar
S. C. Kanicket al.,
“Measurement of the reduced scattering coefficient of turbid media using single fiber reflectance spectroscopy: fiber diameter and phase function dependence,”
Biomed. Opt. Express, 2
(6), 1687
–1702
(2011). http://dx.doi.org/10.1364/BOE.2.001687 BOEICL 2156-7085 Google Scholar
A. LiemertA. Kienle,
“Light transport in three-dimensional semi-infinite scattering media,”
J. Opt. Soc. Am. A Opt. Image Sci. Vis., 29
(7), 1475
–1481
(2012). http://dx.doi.org/10.1364/JOSAA.29.001475 JOAOD6 0740-3232 Google Scholar
|