|
|
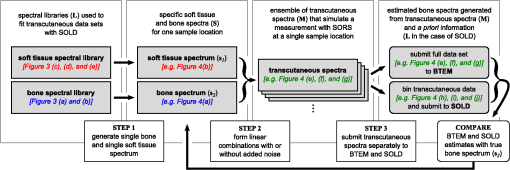
1.IntroductionAlthough the strength of a bone is dependent on its chemical composition,1 technologies that are used to monitor fracture risk primarily measure bone density or structure. For example, bone mineral density (BMD), which is typically measured with dual-energy x-ray absorptiometry, is used clinically as an indirect indicator of bone fragility. Despite its ubiquity, BMD provides limited information about chemical composition, and its discriminatory capacity to identify peri- and early postmenopausal women at high risk of fracture is low.2 Vibrational spectroscopy has been used extensively in ex vivo studies to measure the chemical composition of both the mineral and organic matrix components of bone.3,4 Specifically, Raman spectroscopy has revealed chemical perturbations to cortical bone in animal studies of aging,5 lead exposure,6 osteogenesis imperfecta,7 early-onset osteoarthritis,8 rheumatoid arthritis,9 and glucocorticoid-induced osteoporosis10,11 and in a study of women with postmenopausal osteoporosis.12 Many studies have also revealed correlations between Raman spectroscopy-based measures of chemical composition and the biomechanical properties of bone.5,13,14 In fact, preliminary studies from our group indicate that Raman spectra can generate predictions of biomechanical strength and toughness that are more accurate than those produced by the clinically used parameter of BMD.6,9,10 These results on exposed-bone samples have inspired attempts to perform bone spectroscopy transcutaneously.15–24 Tissue phantoms with controlled optical and chemical properties have also been developed to model transcutaneous measurements.25–27 The majority of these studies have used spatially offset Raman spectroscopy (SORS)28–37 in conjunction with scaled subtractions18 or self-modeling curve resolution algorithms, such as band target entropy minimization (BTEM),38,39 to separate the interfering spectrum of soft tissue from the spectrum of the underlying bone. In essence, these approaches consist of using multiple source–detector combinations to interrogate volumes with different ratios of bone and soft tissue and then exploiting the diversity in the spectral data to elucidate the bone signature. A number of transcutaneous studies employing these methods have reported plausible estimates of underlying bone spectra, with high correlations to reference measurements on exposed bones.20–23 It has not yet been shown, however, that such methods are accurate enough to resolve the subtle spectral differences associated with disease and increased fracture risk. In this publication, a new spectral extraction method is presented and compared to BTEM. The new method is overconstrained to fit a set of transcutaneous measurements of bone with varying amounts of only two spectra (one of bone and one of soft tissue), each of which is built from a unique and separately acquired spectral library. Via two-layer simulations, we demonstrate that the new method is robust when similar chemical components (e.g., type I collagen) are present in both layers, while the assumptions underlying BTEM make it fundamentally unstable. We also show experimentally that applying the overconstrained, library-based fitting method to data acquired transcutaneously from murine tibiae produces accurate estimates of spectra acquired directly from the underlying bone. Analysis shows that these estimates are sensitive to age- and disease-related chemical differences. 2.Background2.1.Biochemistry of Bone and Overlying Soft TissuesBone is a composite of inorganic mineral and organic matrix components. The inorganic component is made up of calcium and phosphate and is often characterized as a carbonated, poorly crystalline hydroxyapatite. The organic matrix of bone is composed of approximately 90% type I collagen by dry weight.40 The biomechanical properties of bone and its susceptibility to fracture in both health and diseases is affected by changes to these components and is not limited to BMD. Bone can be classified into two types, cortical bone and trabecular bone, on the basis of porosity and microstructure. The long bones, such as the tibia, have an outer shell of dense cortical bone with the proximal and distal ends, in the regions known as the epiphyses and metaphyses, reinforced internally by a more porous, mesh-like trabecular bone. The primary soft tissues that contribute interfering signals to transcutaneous Raman measurements include dermal tissue, adipose tissue, and muscle. Transcutaneous Raman spectroscopy is particularly challenging since type I collagen is abundant both in the organic matrix of bone and in soft tissue (e.g., dermal tissue is composed of approximately 80% type I collagen by dry weight40). Although it exhibits a unique pattern of covalent cross-linking in bone,41 type I collagen is genetically identical in all tissues,42 so determining the amount to assign to each tissue region is difficult. Representative Raman spectra of murine bone and soft tissue are displayed in Fig. 1. Fig. 1(a) Representative Raman spectrum of bone. Major Raman bands are labeled along with their peak positions (in parentheses) in Raman shift. Bands associated with mineral content are labeled in dark blue and bands associated with the organic matrix are labeled in light blue. Note that is present both in the organic matrix of bone as well as in adipose tissue found in the medullary cavity. (b) Representative Raman spectrum of soft tissue. Notice the large degree of spectral overlap with the bands associated with organic bone matrix. 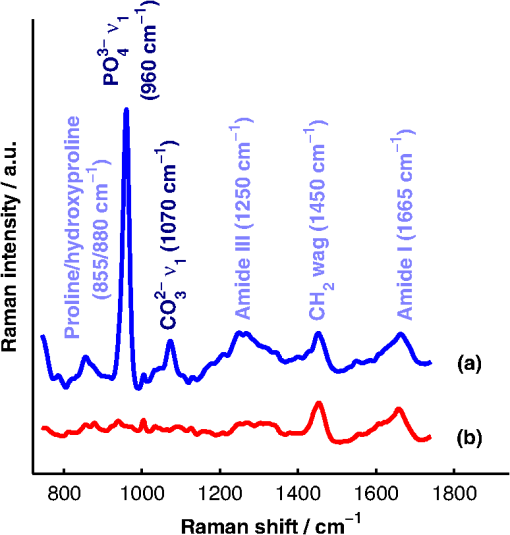 2.2.Spatially Offset Raman Spectroscopy and Band Target Entropy MinimizationIn SORS, Raman scattered light is collected from surface locations that are spatially offset from the illumination location. The spectral contribution from the subsurface layers relative to the contribution from the superficial layer increases with the magnitude of the offset. In the case of transcutaneous Raman spectroscopy of bone, spectra have typically been acquired at multiple spatial offsets. The variation between spectra is then analyzed, often with BTEM, to estimate the spectrum of the underlying bone. BTEM is an example of a self-modeling curve resolution algorithm; i.e., it uses a set of mixture spectra (in the present case, from SORS data sets) to estimate the spectrum of a single pure component. The spectral estimate is constructed from the principal components of the mixture spectra based on the minimization of an objective function. In the case of transcutaneous measurements of bone, the dominant peak (the largest peak in Fig. 1) is targeted, and the BTEM process dictates how the principal components are coadded to render a spectrum exhibiting that peak and others. Despite the success of BTEM in other applications, we show in this publication that the assumptions made by the algorithm are insufficient to produce accurate estimates of bone spectra due to the fact that spectrally similar chemical components (e.g., type I collagen) are present in both bone and soft tissue. 3.Simultaneous, Overconstrained, Library-Based DecompositionIn order to provide improved estimates of bone spectra extracted from transcutaneous measurements, we developed an overconstrained method that fits transcutaneously acquired data with spectral libraries. In this study, the method was used to model transcutaneous Raman data with two spectra, one built from a bone library and the other built from a soft-tissue library. In general notation, the simultaneous, overconstrained, library-based decomposition of spectra that span the same space as spectral components measured over pixels is where is an matrix of measured spectra (e.g., SORS data), is an matrix of the underlying spectral components (e.g., bone and soft tissue), is an matrix of the relative weights of each spectral component, and is an error matrix of spectral features not fit by the model (in this section, boldface uppercase characters represent matrices, boldface lowercase characters represent column vectors, and lowercase italic characters represent scalars). For ease of reference, we refer to this fitting method (simultaneous, overconstrained, library-based decomposition) as SOLD for the remainder of this article.As noted earlier, utilizing transcutaneously acquired Raman data, BTEM has been used to estimate the underlying spectrum of bone (a single column of ) by asserting that the spectrum has a peak near (the peak). In the SOLD model, the a priori information is more extensive: the assertions are that the number of spectral components, , is known and that the regions of spectral space from which the columns of can be built are each bounded by a separately acquired library of spectra. The ’th spectral column of is related to its parent library via where is the library used to model the ’th spectral component and is a vector of fit coefficients that, along with the coefficients of , are tuned to minimize the sum of squared errors, . In order to prevent overfitting, and are required to be non-negative and the model is overconstrained by requiring that the number of measured spectra, , be greater than the number of underlying spectral components, .In this publication, each transcutaneous measurement of bone submitted to SOLD consisted of spectra acquired at different source–detector separations. The SOLD model was overconstrained by fitting this data with spectral components, one for bone and the other for the overlying soft tissue, which allowed for accurate spectral unmixing despite the fact that similar chemical components (e.g., type I collagen) are present in both bone and soft tissue. We elected to set the bounds on the estimated bone and soft-tissue spectra empirically, by acquiring a library of measurements of each tissue type and building our spectral estimates out of non-negative amounts of those spectra only. Other approaches, such as models with tunable spectral peak heights and shifts, could be substituted for the experimentally acquired libraries of spectra. Finally, it should be noted that the SOLD approach is robust against sample-to-sample variability in tissue thickness and optical properties (e.g., scattering and absorption) since the weighting coefficients, , were not fixed a priori, but rather only required to be non-negative. The MATLAB® (version 7.8, The MathWorks™, Natick, MA) code used to fit transcutaneous data sets with SOLD can be obtained by contacting the corresponding author (A.J.B.). 4.Materials and Methods4.1.Instrumentation and Spectral ProcessingAll soft-tissue, exposed-bone, and transcutaneous-bone spectra were acquired on a locally constructed Raman spectroscopy system that utilized an 830-nm semiconductor laser (Model PI-ECL-830-500-FS, Process Instruments Inc., Salt Lake City, UT) to deliver approximately 150 mW of power to the sample as shown in Fig. 2(a). The laser light was filtered with a bandpass filter (Chroma Technology Corp., Bellows Falls, Vermont) and the illumination numerical aperture was 0.34. Fig. 2(a) Raman spectroscopy system for transcutaneous and exposed-bone measurements. Light gray corresponds to the laser illumination path and dark gray corresponds to the Raman scattering collection path. Abbreviations: ST, shutter; L, lens; MMF, multimode fiber; BP, bandpass filter; BS, dichroic beam-splitter; MTS, motorized translation stage; NF, notch filter; FB, fiber bundle; SPEC, spectrograph; HG, holographic grating; CCD, charge-coupled device. (b) Image of the fiber bundle geometry. For the transcutaneous measurements submitted to SOLD, the data were binned together yielding three total spectra per acquisition (one from the center fiber and first annulus, one from the next annulus, and one from the last two annuli) as indicated by the semi-transparent green circle and rings. The circular array of collection fibers is rearranged into a line for delivery to the imaging spectrograph so that the Raman scattered light collected by each fiber can be separately recorded. 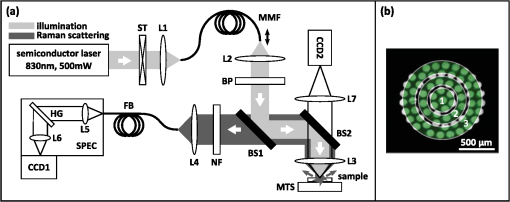 In order to collect the Raman scattered light, lenses L3 and L4 imaged the sample plane onto the face of an optical fiber bundle. The fiber bundle contained 61 multimode optical fibers with core/cladding diameters arranged in a circular array at the collection end as shown in Fig. 2(b). The circular array consisted of a center fiber surrounded by four annuli of fibers. For the transcutaneous measurements, the set of spectra acquired by all of the fibers was submitted to BTEM in accordance with the methods used in previous publications. For the transcutaneous measurements submitted to SOLD, the data were binned together yielding three total spectra per acquisition (one from the center fiber and first annulus, one from the next annulus, and one from the last two annuli). For the exposed-bone and soft-tissue measurements, the spectra from all of the fibers were averaged yielding a single spectrum per acquisition. Each fiber in the fiber bundle viewed a spot of diameter 100 μm at the sample surface. For the transcutaneous measurements, the illumination spot ( ) overlapped with the image of the center fiber of the collection fiber bundle, introducing a range of spatial offsets between the illumination spot and the images of the collection fibers. Although the power delivered by our instrument is greater than the maximum permissible exposure set by the American National Standards Institute,43 no thermal damage was observed. In addition, no adverse consequences were reported in other near-infrared Raman spectroscopy studies of a variety of tissues (including skin) that used power levels greater than ours.44 For the exposed-bone and soft-tissue measurements, the illumination spot was defocused ( ), by adjusting the position of the delivery end of the multimode fiber (MMF in Fig. 2), to overlap with the image of the entire collection fiber bundle. The Appendix contains additional information about the instrument and data processing routines. After processing, the transcutaneously acquired spectra (and simulated spectra described below) were submitted separately to the SOLD and BTEM algorithms to estimate the spectrum of the underlying bone. The smallest subset of principal components that explained at least 70% of the total variance in each transcutaneous data set was submitted to BTEM, the peak near was targeted, and the spectral estimate was formed by minimizing the objective function suggested by Ong et al.39 The Nelder-Mead downhill simplex method45 was used to minimize the BTEM objective function. 4.2.Simulated DataPrior to analyzing experimental, transcutaneously acquired data, a simulated data set was constructed to compare the performances of SOLD and BTEM. The parameters described in this section were chosen to generate data sets that resemble transcutaneous spectra acquired from murine tibiae. 4.2.1.Generation of spectral libraries (L) used to fit simulated dataSpectra of some of the tissue types and chemicals present in bone and soft tissue were acquired as a part of this study. The average spectra of dermal tissue, adipose tissue, and muscle tissue acquired from multiple sites on four different mice are displayed in Fig. 3. Pure ceramic hydroxyapatite (Clarkson Chromatography Products Inc., South Williamsport, PA) was used to represent bone mineral, and dermal tissue was used as a surrogate for the organic matrix of bone since the chemical compositions of these components are similar (approximately 80 and 90% type I collagen, by dry weight, for dermal tissue and organic bone matrix, respectively40). The spectral libraries used to generate and fit the simulated data sets were chosen to create an idealized comparison between SOLD and BTEM. More comprehensive libraries were constructed to fit experimental data as described in Sec. 4.3. Fig. 3Raman spectra of some of the tissue types and chemical components of bone (blue) and soft tissue (red). Two of the primary components of bone are (a) hydroxyapatite and (b) organic bone matrix. The soft tissues overlying bone include (c) dermal tissue, (d) adipose tissue, and (e) muscle tissue. 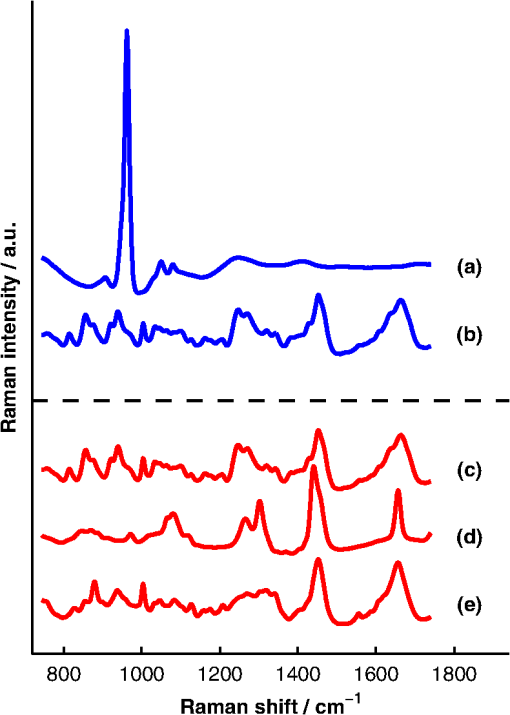 4.2.2.Generation of simulated spectral components (S)To generate a simulated spectrum of bone, a linear combination of the hydroxyapatite spectrum [Fig. 3(a)] and the organic bone matrix spectrum [Fig. 3(b)] was formed, where the ratio of the coefficient multiplied by the hydroxyapatite spectrum to the coefficient multiplied by the organic bone matrix spectrum was varied over a factor of 3. Similarly, a linear combination of the spectra of dermal tissue, adipose tissue, and muscle tissue [Fig. 3(c), 3(d), and 3(e), respectively] formed each simulated spectrum of soft tissue, where the coefficients multiplied by each spectrum were varied over a factor of 10. Finally, the simulated bone and soft-tissue spectra were normalized to their mean absolute deviations (similar to a calculation of the root mean squared spectral intensity). 4.2.3.Generation of simulated transcutaneous spectra (M) measured at a single locationThe process of simulating the transcutaneous spectra from a single-site measurement is summarized in Fig. 4. The ensemble of SORS spectra was constructed by forming linear combinations of a single pair of bone and soft-tissue spectra [components of a single matrix; Fig. 4(a) and 4(b), respectively]. For each source–detector pairing, the bone spectrum was multiplied by a coefficient between 0 and and added to the soft-tissue spectrum. This linear combination was normalized to its mean absolute deviation and added to a spectrum of zero-mean, Gaussian noise [Fig. 4(c)] to form a single transcutaneous spectrum [Fig. 4(d)]. This process was repeated to generate 30 transcutaneous spectra [Fig. 4(e), 4(f), and 4(g)] with varying contributions of the same single pair of bone and soft-tissue spectra. Transcutaneous spectra without added noise were also generated. Fig. 4Example of simulated data set used to compare the performances of SOLD and BTEM. The (a) bone and (b) soft-tissue spectra were generated from the spectra in Fig. 3. A spectrum of zero-mean, Gaussian noise (c) was added to a linear combination of the bone and soft-tissue spectra to form a single transcutaneous spectrum (d). This process was repeated to generate 30 transcutaneous spectra [(e), (f), and (g)] with varying contributions of the bone and soft-tissue spectra. These 30 spectra represent a transcutaneous data set acquired from a single measurement site. The set of 30 spectra was submitted to BTEM to estimate the underlying spectrum of bone. In addition, each set of 10 spectra grouped together in (e), in (f), and in (g) was summed, yielding three spectra [(h), (i), and (j)] that were submitted to SOLD. The entire process summarized in this figure was repeated 100 times (with different pairs of underlying bone and soft-tissue spectra) to simulate transcutaneous data acquired from different samples. The gray bars highlight the peak, which is present in the spectrum of bone. The amplitude of this peak qualitatively represents the contribution of bone to each transcutaneous spectrum. 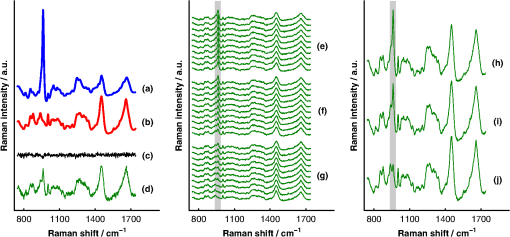 4.2.4.BTEM- and SOLD-produced estimates of simulated bone spectrum (one column of S)The set of 30 transcutaneous spectra was submitted to BTEM to estimate the underlying spectrum of bone. To simulate SORS measurements acquired at three different spatial offsets (corresponding to the three regions depicted in Fig. 2), the 30 transcutaneous spectra were sorted according to the contribution of the underlying bone lineshape. The spectra were then grouped based on their rank order [Fig. 4(e), 4(f), and 4(g)] and each set of spectra was summed yielding three composite spectra [Fig. 4(h), 4(i), and 4(j)] that were submitted to SOLD. The entire procedure described in Sec. 4.2 to generate and process simulated data is depicted as a flow chart in Fig. 5. This procedure was repeated 100 times (with different pairs of underlying bone and soft-tissue spectra and with or without added noise) to simulate transcutaneous data acquired from different samples. 4.3.Experimental Data4.3.1.Acquisition of transcutaneous spectra (M)A variety of mice were used in this study, including two-month-old B6C3Fe and their wild-type (WT) littermates (four per group). The mouse is a model of type III osteogenesis imperfecta, which is a genetic, musculoskeletal disorder characterized by mutations in type I collagen. Mice that are homozygous for the oim mutation are deficient in collagen, which also affects the level of mineralization and ultimately results in a weaker bone.46 In addition to the mice and WT controls, seven C57BL/6J WT mice (between 1 and 7 months of age) and six transgenic mice that constitutively overexpress a human tumor necrosis factor- transgene11,47–49 (between 5 and 14 months of age; C57BL/6J background) were studied; the variations due to age and disease caused a greater spread in the biochemical properties of the bones. The mice that overexpress human tumor necrosis factor- develop chronic inflammation and arthritis with secondary osteoporosis, while C57BL/6J mice are a commonly used inbred mouse strain. The mice were euthanized by inhalation of carbon dioxide, fur was removed from the right hindlimb with a depilatory agent (hair remover cream, Nair®, Church & Dwight Co., Inc., Princeton, NJ), and transcutaneous Raman spectra were acquired from all 21 intact mice. The samples were hydrated for the duration of each measurement in order to prevent laser-induced thermal damage of the tissue and spectra were acquired from the medial side of the mid-diaphysis region over an area of approximately . For each mouse, five transcutaneous measurements were acquired spaced 1 mm apart along the shaft axis of the tibia with an integration time of 5 min per location. The average thickness of soft tissue overlying the measurement sites was approximately 1 mm. This study protocol was approved by the Committee on Animal Resources at the University of Rochester. 4.3.2.Measurement of underlying bone spectrum (one column of S) and generation of spectral libraries (L) used to fit experimental, transcutaneous dataFollowing acquisition of each set of transcutaneous measurements, the soft tissue was removed and gold-standard, colocalized measurements were acquired from the exposed bone for comparison. Similar to the transcutaneous measurements, spectra were acquired from five locations spaced 1 mm apart along the shaft axis of the tibia with an integration time of 5 min per location. A total of 160 spectra of excised soft tissue, including spectra of specific tissue types (Fig. 3) as well as spectra of bulk tissue, were also acquired from the 21 mice. In analyzing the transcutaneous data from each mouse, only data from the other mice were included in the spectral libraries (i.e., leave-one-sample-out analysis). 5.Results5.1.Simulated DataFigure 6 presents the BTEM and SOLD spectral estimates of bone extracted from the single-site, simulated data set shown in Fig. 4. All spectra have been normalized to the height of the peak near . Each algorithm was run twice, once upon the simulated data set without added noise [Fig. 6(a) and 6(b)] and once upon the simulated data set with added noise [Fig. 6(c) and 6(d)]. In both cases, SOLD provided a superior estimate of the true underlying bone spectrum [Fig. 6(e)] as evidenced by the accurate reconstruction of the organic bone matrix peaks (e.g., the starred wag peak near ). The correlation coefficients between the true and SOLD-estimated bone spectra were both greater than 0.999, while the correlation coefficients between the true and BTEM-estimated bone spectra were 0.985 and 0.968 for the transcutaneous data sets without and with added noise, respectively. All of the spectral correlation coefficients reported in this publication were calculated over the 775 to spectral range, which was chosen to match a previous study.23 Qualitatively similar results were observed for correlations calculated over a larger spectral range that included the amide I peak near . Fig. 6Comparison of BTEM and SOLD bone-spectrum estimation methods operating on simulated data. (a) BTEM and (b) SOLD estimates of exposed-bone spectrum from transcutaneous data set without noise. (c) BTEM and (d) SOLD estimates from data set with added noise. (e) True simulated bone spectrum for comparison. To guide comparison, the asterisk highlights the wag peak, which was more accurately reconstructed with SOLD. 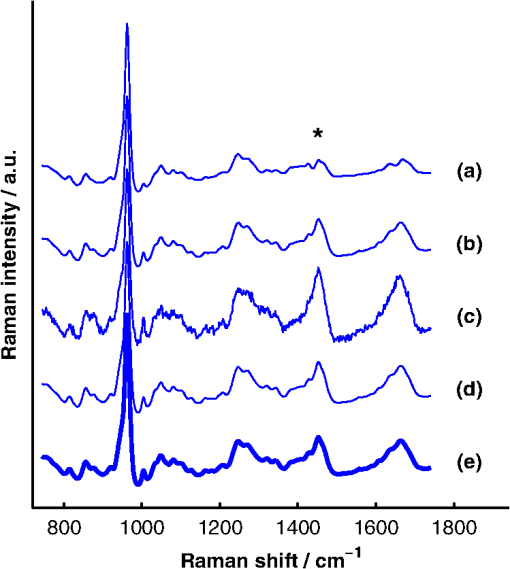 As described previously, the procedure used to generate a simulated, transcutaneous data set was repeated 100 times with a variety of simulated bone and soft-tissue spectra and the transcutaneous data were submitted separately to BTEM and SOLD. The mineral/matrix ratios of all 100 estimated spectra and the corresponding true underlying bone spectra are compared in Fig. 7. The mineral/matrix ratio of each bone spectrum was calculated as the ratio of the fit coefficients produced by least-squares fitting with the pure spectra of hydroxyapatite and organic bone matrix [Fig. 3(a) and 3(b), respectively]. Fig. 7Scatter plots of estimated versus true mineral/matrix ratios. (a) BTEM and (b) SOLD estimates extracted from simulated transcutaneous data sets without noise. (c) BTEM and (d) SOLD estimates extracted from data sets with added noise. The filled-in markers (highlighted by arrow annotations) correspond to the mineral/matrix ratios of the spectra presented in Fig. 6. 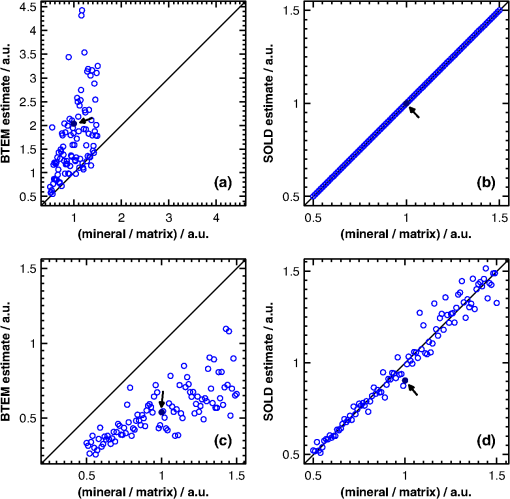 5.2.Experimental DataA representative, transcutaneously acquired data set and the corresponding SOLD fit are presented in Fig. 8. As described previously, the transcutaneously acquired spectra were binned together yielding three total spectra per acquisition [Fig. 8(a), green circles] prior to fitting with SOLD. Variation between these spectra is due to differences in the relative sampling of the bone and soft tissue, which is due to different spatial offsets between the illumination spot and the image of each annulus of collection fibers on the surface of the sample [Fig. 2(b)]. All three transcutaneously acquired spectra are well fit by a single bone and a single soft-tissue spectrum [Fig. 8(c) and 8(d), respectively]; as a reminder, these two spectra are formed by linear combinations of the appropriate spectral library (). Spectrum (c) in Fig. 8 is thus the SOLD estimate of the underlying bone spectrum for this particular sample and location on the tibia. Fig. 8Representative, transcutaneous spectra acquired at three different source–detector separations (offset for clarity). The measured transcutaneous spectra [(a), green circles] are well fit [(a), black lines] by a single bone (c) and a single-soft tissue (d) spectrum as evidenced by the small amplitudes of the three fit residuals (b). 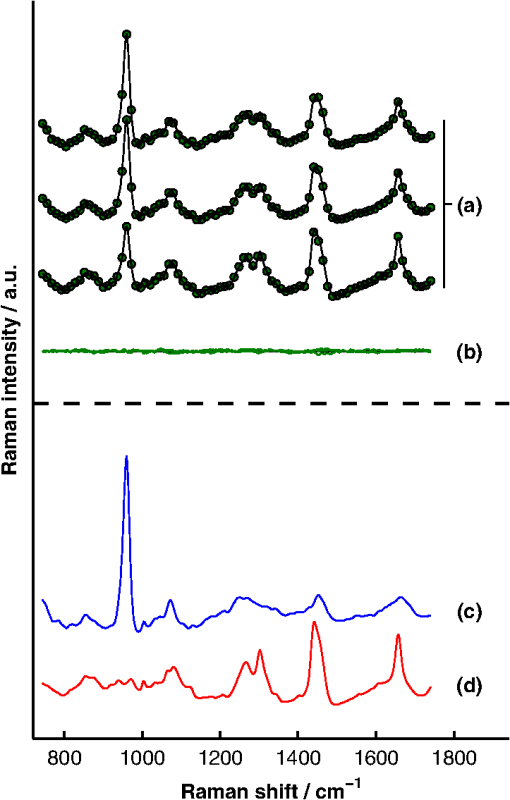 Figure 9 presents the BTEM and SOLD estimates of the underlying bone spectrum extracted from the data set displayed in Fig. 8. All spectra have been normalized to the height of the peak near . Again, SOLD provided a superior estimate of the true underlying bone spectrum [Fig. 9(c)] as evidenced by the accurate reconstruction of the organic bone matrix peaks (e.g., the starred wag peak near ). The correlation coefficient between the exposed-bone measurement and the SOLD-estimated bone spectrum was 0.996, whereas the correlation coefficient between the exposed-bone measurement and the BTEM-estimated bone spectrum was 0.935. Fig. 9Comparison of BTEM and SOLD bone-spectrum estimation methods operating on experimental data. (a) BTEM and (b) SOLD estimates of exposed-bone spectrum from representative transcutaneously acquired data set presented in Fig. 8. (c) True exposed-bone spectrum for comparison. To guide comparison, the asterisk highlights the wag peak, which was more accurately reconstructed with SOLD. 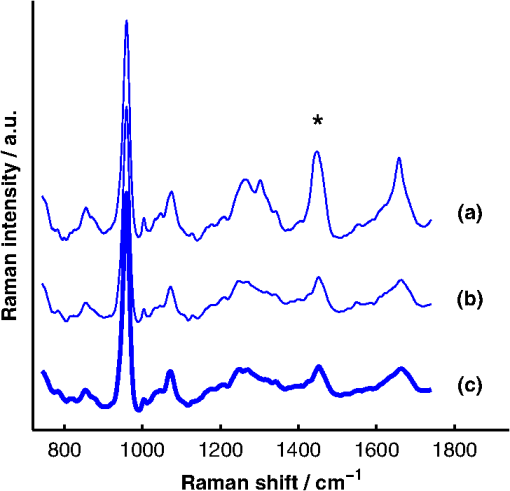 The mean correlation coefficients between all of the SOLD-estimated and BTEM-estimated bone spectra and the corresponding gold-standard reference measurements on exposed bone are compared in Table 1. The mean correlation coefficient between the exposed-bone spectra acquired from all of the mice described in Sec. 4.3.1 and the mean correlation coefficient reported in a study by Schulmerich et al.23 are also tabulated. The Fisher transformation,50 along with a Student’s test, was used to compare the correlations produced by each of the methods. SOLD produced spectra with the greatest correlations to the corresponding reference measurements and the difference between the mean correlation coefficient produced by SOLD and the mean correlation coefficient produced by each other method was statistically significant. Table 1Mean correlation coefficients between estimated and/or directly measured bone spectra. The SOLD and BTEM entries refer to correlations between estimated bone spectra and their corresponding reference measurements. The second BTEM entry lists the result reported by Schulmerich et al.23 in the most recent and comprehensive work that can be directly compared to our study. The mean correlation among the spectra of exposed bones from different mice is also listed. Notice that only SOLD produced a mean correlation coefficient greater than this baseline. Statistically significant differences were tested for with unpaired Student’s t tests operating on the Fisher-transformed correlation coefficients. The correlation coefficients produced by each method were compared with those produced by SOLD and in each case the difference was statistically significant.
The SOLD-estimated spectra were also used to predict the mineral/matrix ratios of the corresponding bones. A leave-one-out cross-validation approach utilizing partial least squares regression (PLSR)51 was used to generate predictions based on the full SOLD-estimated spectra. A scatter plot of these predictions (referred to as PLSR-SOLD) versus the mineral/matrix ratios calculated from the corresponding exposed-bone spectra is displayed in Fig. 10. For the experimental, exposed-bone data sets, the mineral/matrix ratios were calculated as the ratio of the height of the peak near to the heights of the peaks near 855 and , which are due to vibrations of the amino-acids proline and hydroxyproline, respectively.52 All mineral/matrix ratios were normalized to the mean mineral/matrix ratio of the two-month-old WT mice. The relationship between the PLSR-SOLD-derived mineral/matrix ratios and the ratios calculated from the exposed-bone spectra was quantified by a chi-squared test. This test was used to compare the variance of the errors in the PLSR-SOLD estimates (0.030) with the variance of the exposed-bone mineral/matrix ratios (0.176). A one-tailed test revealed that the error variance was significantly less than the variance in the exposed-bone measurements (), suggesting that SOLD, in conjunction with PLSR, is capable of extracting useful estimates of mineral/matrix ratios. Fig. 10Scatter plot of the PLSR-SOLD-estimated mineral/matrix ratios versus the ratios from the corresponding exposed-bone spectra. The filled-in marker (highlighted by the arrow annotation) corresponds to the mineral/matrix ratios of the spectra presented in Fig. 9. 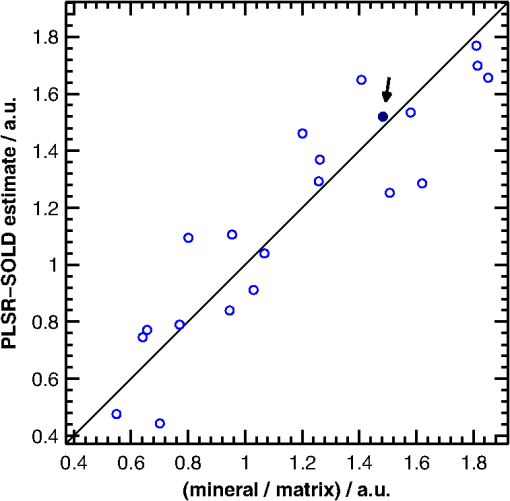 Analysis of the data from the 11 WT mice between 1 and 7 months of age revealed a statistically significant correlation between age and mineral/matrix ratio (, ). This correlation with age was preserved in the PLSR-SOLD-produced mineral/matrix ratios (, ). Regarding disease differences, the mineral/matrix ratios of the two-month-old oim/oim mice and WT littermates are compared in Fig. 11. Both the exposed-bone and PLSR-SOLD-derived ratios completely separate the two groups of mice. Fig. 11Bar plots of the mean mineral/matrix ratios of WT (white) and (gray) mice calculated from exposed-bone spectra and the corresponding PLSR predictions based on the SOLD-estimated spectra. Each circular marker represents the mineral/matrix ratio of a single sample. * as determined by a two-sample, unpaired Student’s test. 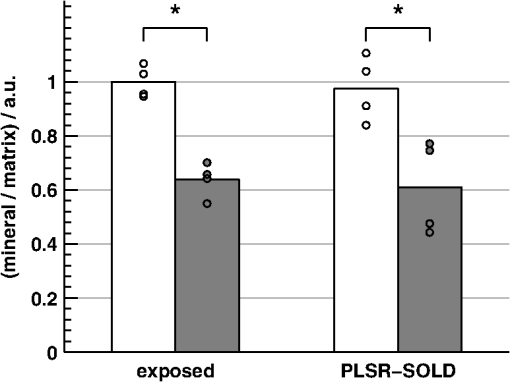 6.DiscussionThe results of this study demonstrate that diagnostically sensitive estimates of the chemical composition of bone can be extracted from transcutaneous measurements using a spectral unmixing method that is overconstrained to fit the data with varying amounts of only two spectra (one of bone and one of soft tissue), each of which is built from a unique and separately acquired spectral library. A number of other studies have utilized BTEM to estimate bone spectra from transcutaneous Raman measurements.17–23 As shown here, however, BTEM is unable to accurately reconstruct spectra of individual layers if spectrally similar chemical components (e.g., type I collagen) are present in more than one layer. This limitation is due to the algorithm not incorporating sufficient a priori information. In particular, BTEM does not assert that the transcutaneously acquired data are made up of a fixed number of spectral components. In the simulated data sets without noise, BTEM consistently overestimated the mineral/matrix ratios of the underlying bone spectra [Fig. 7(a)]. This behavior can be understood by considering the following simplified picture. Since the variation in each simulated transcutaneous data set [e.g., Fig. 4(e), 4(f), and 4(g) without noise] is due to a single bone and a single soft-tissue spectrum [e.g., Fig. 4(a) and 4(b), respectively], the first two principal components span the same space as these spectra. The spectral estimate formed by BTEM (built from these two components) can therefore be thought of as the linear combination of bone and soft-tissue spectra that minimizes the objective function. Since bone and soft tissue have significant levels of spectrally similar protein components (e.g., type I collagen), the bone and soft-tissue spectra can be combined in a weighted subtraction to produce a mineral-dominated spectrum. Since this reduces the intensity of nontargeted bands without making any go negative, BTEM finds this linear combination attractive and, as seen in Fig. 6(a), the nonmineral peaks (e.g., the wag peak near ) in the BTEM-derived spectrum are indeed underestimated. This behavior is a fundamental limitation that cannot be allayed by adjusting the parameters of the algorithm. When noise was added to the simulated data, the mineral/matrix ratios of bone spectra estimated with BTEM were biased in the opposite direction [Fig. 7(c)]. BTEM customarily penalizes negative spectral intensities, including those associated with noise, which can lead to overestimates in spectral intensity of nontargeted peaks [Fig. 6(c)]. Although this particular bias could potentially be mitigated by tuning the objective function, the magnitude of the bias is dependent on the magnitude of the noise in the measured data and its principal components, and applying a correction that is robust over a variety of measurement settings is difficult. Many studies have reported correlations between spectral estimates extracted from transcutaneous measurements with BTEM and reference measurements on exposed bones.20–23 However, these studies did not provide context to the magnitudes of the correlations. For example, the mean spectral correlation coefficient reported in a study by Schulmerich et al.23 was 0.96, a value that in general implies a useful degree of correlation. In our study, however, the spectra acquired from different bones were so similar that the mean spectral correlation coefficient among exposed bones from different mice was 0.988, while the mean spectral correlation with the corresponding BTEM estimates was 0.935. In other words, each spectrum of exposed bone resembled the corresponding BTEM estimate less than it resembled the spectra of other exposed bones. In contrast, the mean correlation coefficient between the SOLD-estimated spectra and the corresponding exposed-bone spectra was 0.996, which was statistically significantly greater than the mean spectral correlation coefficients associated with the other methods. There are many approaches that can be utilized to estimate spectra of subsurface layers in multilayer samples, including, for example, optical depth-sectioning with confocal microscopy. Unfortunately, confocal microscopy is not well suited to measure bone transcutaneously since the penetration depth of this technique is limited to the reduced mean free path of the sample, which is typically a few hundred microns for skin measured at visible and near-infrared wavelengths.53,54 Another broad method is to sample the layers at various source–detector separations (e.g., SORS) and analyze the variation among the spectra. Application of one or more a priori constraints (e.g., targeting a peak as in BTEM or overconstraining a fitting algorithm by using a fixed number of spectral components as in SOLD) can drive the estimation procedure. Blind decomposition methods,55,56 if properly constrained, could also potentially be used to estimate bone spectra based on transcutaneous measurements. The results of this study demonstrate that the mineral/matrix ratio of cortical bone, which has frequently been used as a Raman-based indicator of bone health and strength,4–14 can be measured transcutaneously by processing SORS data sets with SOLD (Figs. 10 and 11). Overconstraining the algorithm to fit multiple transcutaneous measurements with two lineshapes (one for bone and one for soft tissue) produced accurate estimates of the underlying exposed-bone spectra despite the fact that spectrally similar chemical components (e.g., type I collagen) are present in both bone and soft tissue. As the first diagnostically sensitive, transcutaneous measurements of bone using SORS, our results support the feasibility of monitoring bone diseases noninvasively and in vivo in mice. Other studies have reported the transcutaneous acquisition of bone signal beneath up to 5 mm of soft tissue16,17 and from the distal phalanx of a human thumb.18 Although the measurement sites may be limited depending on the thickness of the overlying soft tissue, these studies, along with the results presented here, suggest that our approach could also provide a platform to noninvasively measure bone biochemistry in human patients. AppendicesAppendix:Additional Description of Raman Instrument and Data Processing RoutinesThe optical fiber bundle depicted in Fig. 2 delivered the Raman scattered light to a spectrograph (HolospecTM VPT System, Kaiser Optical Systems Inc., Ann Arbor, MI), where it was dispersed onto a array back-illuminated deep-depletion CCD camera, CCD1 (Model DU 420-BR-DD, Andor Technology, Belfast, Northern Ireland), achieving a spectral resolution of approximately . A dichroic beam splitter (Chroma Technology Corp., Bellows Falls, Vermont) and a holographic notch filter (Kaiser Optical Systems Inc., Ann Arbor, MI) were used to reject the elastically scattered light and pass only the Stokes-shifted light to the spectrograph. Finally, because of the limited height of the CCD array, only spectra from the 40 central fibers of the fiber bundle were imaged onto CCD1. The position of each sample with respect to the laser illumination spot was confirmed by a white-light image of the sample plane acquired with a second CCD camera, CCD2. Raw spectral data were imported into MATLAB® and analyzed through a number of built-in and locally written scripts. Spectral processing included cosmic ray removal, readout and dark-current subtraction, correction for the frequency-dependent response of the system, and correction for the imaging aberrations of the spectrograph system.57 The spectrum of Raman scattered light collected by each fiber was extracted from the full image by fitting with the separately measured spectral response of each fiber.58 Background fluorescence lineshapes were modeled and removed by fitting with a seventh-order polynomial and the spectra were smoothed with a Savitzky-Golay filter59 over a window, chosen to match the resolution of the spectrograph. Portions of the spectra below were discarded due to the presence of a strong uncorrelated fluorescence contribution. Portions of the spectra above were discarded due to the absence of major Raman spectral features in this region and the falloff in CCD sensitivity. Finally, the Raman shift axis was calibrated with N-acetyl-para-aminophenol, better known by the brand name TYLENOL® (McNEIL-PPC Inc., Fort Washington, PA), to correct for spectral instabilities in the excitation source. AcknowledgmentsThis work was supported in part by a University of Rochester Provost’s Multidisciplinary Award and National Institutes of Health Grant No. 1R21AR061285-01. Jason Inzana is supported by National Science Foundation graduate research fellowship 2012116002. ReferencesE. SeemanP. D. Delmas,
“Bone quality—The material and structural basis of bone strength and fragility,”
N. Engl. J. Med., 354
(21), 2250
–2261
(2006). http://dx.doi.org/10.1056/NEJMra053077 NEJMAG 0028-4793 Google Scholar
F. A. Trémolliereset al.,
“Fracture risk prediction using BMD and clinical risk factors in early postmenopausal women: sensitivity of the WHO FRAX tool,”
J. Bone Miner. Res., 25
(5), 1002
–1009
(2010). http://dx.doi.org/10.1002/jbmr.12 JBMREJ 0884-0431 Google Scholar
A. CardenM. D. Morris,
“Application of vibrational spectroscopy to the study of mineralized tissues (review),”
J. Biomed. Opt., 5
(3), 259
–268
(2000). http://dx.doi.org/10.1117/1.429994 JBOPFO 1083-3668 Google Scholar
D. FaibishS. M. OttA. L. Boskey,
“Mineral changes in osteoporosis: a review,”
Clin. Orthop. Relat. Res., 443 28
–38
(2006). http://dx.doi.org/10.1097/01.blo.0000200241.14684.4e CORTBR 0009-921X Google Scholar
O. AkkusF. AdarM. B. Schaffler,
“Age-related changes in physicochemical properties of mineral crystals are related to impaired mechanical function of cortical bone,”
Bone, 34
(3), 443
–453
(2004). http://dx.doi.org/10.1016/j.bone.2003.11.003 8756-3282 Google Scholar
E. E. Beieret al.,
“Heavy metal lead exposure, osteoporotic-like phenotype in an animal model, and depression of Wnt signaling,”
Environ. Health Perspect., 121
(1), 97
–104
(2013). http://dx.doi.org/10.1289/ehp.1205374 EVHPAZ 0091-6765 Google Scholar
K. M. Kozloffet al.,
“Brittle IV mouse model for osteogenesis imperfecta IV demonstrates postpubertal adaptations to improve whole bone strength,”
J. Bone Miner. Res., 19
(4), 614
–622
(2004). http://dx.doi.org/10.1359/JBMR.040111 JBMREJ 0884-0431 Google Scholar
K. A. Dehringet al.,
“Identifying chemical changes in subchondral bone taken from murine knee joints using Raman spectroscopy,”
Appl. Spectrosc., 60
(10), 1134
–1141
(2006). http://dx.doi.org/10.1366/000370206778664743 APSPA4 0003-7028 Google Scholar
J. A. Inzanaet al.,
“Bone fragility beyond strength and mineral density: Raman spectroscopy predicts femoral fracture toughness in a murine model of rheumatoid arthritis,”
J. Biomech., 46
(4), 723
–730
(2013). http://dx.doi.org/10.1016/j.jbiomech.2012.11.039 JBMCB5 0021-9290 Google Scholar
J. R. Maheret al.,
“Raman spectroscopy detects deterioration in biomechanical properties of bone in a glucocorticoid-treated mouse model of rheumatoid arthritis,”
J. Biomed. Opt., 16
(8), 087012
(2011). http://dx.doi.org/10.1117/1.3613933 JBOPFO 1083-3668 Google Scholar
M. Takahataet al.,
“Mechanisms of bone fragility in a mouse model of glucocorticoid-treated rheumatoid arthritis: implications for insufficiency fracture risk,”
Arthritis Rheum., 64
(11), 3649
–3659
(2012). http://dx.doi.org/10.1002/art.34639 ARHEAW 0004-3591 Google Scholar
B. R. McCreadieet al.,
“Bone tissue compositional differences in women with and without osteoporotic fracture,”
Bone, 39
(6), 1190
–1195
(2006). http://dx.doi.org/10.1016/j.bone.2006.06.008 8756-3282 Google Scholar
X. Biet al.,
“Raman and mechanical properties correlate at whole bone- and tissue-levels in a genetic mouse model,”
J. Biomech., 44
(2), 297
–303
(2011). http://dx.doi.org/10.1016/j.jbiomech.2010.10.009 JBMCB5 0021-9290 Google Scholar
M. Raghavanet al.,
“Age-specific profiles of tissue-level composition and mechanical properties in murine cortical bone,”
Bone, 50
(4), 942
–953
(2012). http://dx.doi.org/10.1016/j.bone.2011.12.026 8756-3282 Google Scholar
E. R. Draperet al.,
“Novel assessment of bone using time-resolved transcutaneous Raman spectroscopy,”
J. Bone Miner. Res., 20
(11), 1968
–1972
(2005). http://dx.doi.org/10.1359/JBMR.050710 JBMREJ 0884-0431 Google Scholar
M. V. Schulmerichet al.,
“Transcutaneous fiber optic Raman spectroscopy of bone using annular illumination and a circular array of collection fibers,”
J. Biomed. Opt., 11
(6), 060502
(2006). http://dx.doi.org/10.1117/1.2400233 JBOPFO 1083-3668 Google Scholar
M. V. Schulmerichet al.,
“Subsurface and transcutaneous Raman spectroscopy and mapping using concentric illumination rings and collection with a circular fiber-optic array,”
Appl. Spectrosc., 61
(7), 671
–678
(2007). http://dx.doi.org/10.1366/000370207781393307 APSPA4 0003-7028 Google Scholar
P. Matouseket al.,
“Noninvasive Raman spectroscopy of human tissue in vivo,”
Appl. Spectrosc., 60
(7), 758
–763
(2006). http://dx.doi.org/10.1366/000370206777886955 APSPA4 0003-7028 Google Scholar
S. Srinivasanet al.,
“Image-guided Raman spectroscopic recovery of canine cortical bone contrast in situ,”
Opt. Express, 16
(16), 12190
–12200
(2008). http://dx.doi.org/10.1364/OE.16.012190 OPEXFF 1094-4087 Google Scholar
M. V. Schulmerichet al.,
“Optical clearing in transcutaneous Raman spectroscopy of murine cortical bone tissue,”
J. Biomed. Opt., 13
(2), 021108
(2008). http://dx.doi.org/10.1117/1.2892687 JBOPFO 1083-3668 Google Scholar
M. V. Schulmerichet al.,
“Noninvasive Raman tomographic imaging of canine bone tissue,”
J. Biomed. Opt., 13
(2), 020506
(2008). http://dx.doi.org/10.1117/1.2904940 JBOPFO 1083-3668 Google Scholar
N. A. Macleodet al.,
“Prediction of sublayer depth in turbid media using spatially offset Raman spectroscopy,”
Anal. Chem., 80
(21), 8146
–8152
(2008). http://dx.doi.org/10.1021/ac801219a ANCHAM 0003-2700 Google Scholar
M. V. Schulmerichet al.,
“Transcutaneous Raman spectroscopy of murine bone in vivo,”
Appl. Spectrosc., 63
(3), 286
–295
(2009). http://dx.doi.org/10.1366/000370209787599013 APSPA4 0003-7028 Google Scholar
P. I. Okagbareet al.,
“Development of non-invasive Raman spectroscopy for in-vivo evaluation of bone graft osseointegration in a rat model,”
Analyst, 135
(12), 3142
–3146
(2010). http://dx.doi.org/10.1039/c0an00566e ANLYAG 0365-4885 Google Scholar
F. W. Esmonde-Whiteet al.,
“Biomedical tissue phantoms with controlled geometric and optical properties for Raman spectroscopy and tomography,”
Analyst, 136
(21), 4437
–4446
(2011). http://dx.doi.org/10.1039/c1an15429j ANLYAG 0365-4885 Google Scholar
P. I. Okagbareet al.,
“Noninvasive Raman spectroscopy of rat tibiae: approach to in vivo assessment of bone quality,”
J. Biomed. Opt., 17
(9), 090502
(2012). http://dx.doi.org/10.1117/1.JBO.17.9.090502 JBOPFO 1083-3668 Google Scholar
J.-L. H. Demerset al.,
“Multichannel diffuse optical Raman tomography for bone characterization in vivo: a phantom study,”
Biomed. Opt. Express, 3
(9), 2299
–2305
(2012). http://dx.doi.org/10.1364/BOE.3.002299 BOEICL 2156-7085 Google Scholar
P. Matouseket al.,
“Subsurface probing in diffusely scattering media using spatially offset Raman spectroscopy,”
Appl. Spectrosc., 59
(4), 393
–400
(2005). http://dx.doi.org/10.1366/0003702053641450 APSPA4 0003-7028 Google Scholar
P. Matouseket al.,
“Numerical simulations of subsurface probing in diffusely scattering media using spatially offset Raman spectroscopy,”
Appl. Spectrosc., 59
(12), 1485
–1492
(2005). http://dx.doi.org/10.1366/000370205775142548 APSPA4 0003-7028 Google Scholar
M. V. Schulmerichet al.,
“Subsurface Raman spectroscopy and mapping using a globally illuminated non-confocal fiber-optic array probe in the presence of Raman photon migration,”
Appl. Spectrosc., 60
(2), 109
–114
(2006). http://dx.doi.org/10.1366/000370206776023340 APSPA4 0003-7028 Google Scholar
P. Matousek,
“Inverse spatially offset Raman spectroscopy for deep noninvasive probing of turbid media,”
Appl. Spectrosc., 60
(11), 1341
–1347
(2006). http://dx.doi.org/10.1366/000370206778999102 APSPA4 0003-7028 Google Scholar
P. Matousek,
“Deep non-invasive Raman spectroscopy of living tissue and powders,”
Chem. Soc. Rev., 36
(8), 1292
–1304
(2007). http://dx.doi.org/10.1039/b614777c CSRVBR 0306-0012 Google Scholar
C. EliassonP. Matousek,
“Passive signal enhancement in spatially offset Raman spectroscopy,”
J. Raman Spectrosc., 39
(5), 633
–637
(2008). http://dx.doi.org/10.1002/jrs.1898 JRSPAF 0377-0486 Google Scholar
N. A. MacleodP. Matousek,
“Deep noninvasive Raman spectroscopy of turbid media,”
Appl. Spectrosc., 62
(11), 291A
–304A
(2008). http://dx.doi.org/10.1366/000370208786401527 APSPA4 0003-7028 Google Scholar
P. MatousekN. Stone,
“Emerging concepts in deep Raman spectroscopy of biological tissue,”
Analyst, 134
(6), 1058
–1066
(2009). http://dx.doi.org/10.1039/b821100k ANLYAG 0365-4885 Google Scholar
J. R. MaherA. J. Berger,
“Determination of ideal offset for spatially offset Raman spectroscopy,”
Appl. Spectrosc., 64
(1), 61
–65
(2010). http://dx.doi.org/10.1366/000370210790571936 APSPA4 0003-7028 Google Scholar
K. BuckleyP. Matousek,
“Non-invasive analysis of turbid samples using deep Raman spectroscopy,”
Analyst, 136
(15), 3039
–3050
(2011). http://dx.doi.org/10.1039/c0an00723d ANLYAG 0365-4885 Google Scholar
W. ChewE. WidjajaM. Garland,
“Band-target entropy minimization (BTEM): an advanced method for recovering unknown pure component spectra. Application to the FTIR spectra of unstable organometallic mixtures,”
Organometallics, 21
(9), 1982
–1990
(2002). http://dx.doi.org/10.1021/om0108752 ORGND7 0276-7333 Google Scholar
L. R. Onget al.,
“Fourier transform Raman spectral reconstruction of inorganic lead mixtures using a novel band-target entropy minimization (BTEM) method,”
J. Raman Spectrosc., 34
(4), 282
–289
(2003). http://dx.doi.org/10.1002/jrs.986 JRSPAF 0377-0486 Google Scholar
D. L. Kasperet al., Harrison’s Principles of Internal Medicine, 16th ed.McGraw-Hill, Medical Pub. Division, New York
(2005). Google Scholar
D. A. HansonD. R. Eyre,
“Molecular site specificity of pyridinoline and pyrrole cross-links in type I collagen of human bone,”
J. Biol. Chem., 271
(43), 26508
–26516
(1996). http://dx.doi.org/10.1074/jbc.271.43.26508 JBCHA3 0021-9258 Google Scholar
M. SaitoK. Marumo,
“Collagen cross-links as a determinant of bone quality: a possible explanation for bone fragility in aging, osteoporosis, and diabetes mellitus,”
Osteoporosis Int., 21
(2), 195
–214
(2010). http://dx.doi.org/10.1007/s00198-009-1066-z OSINEP 1433-2965 Google Scholar
Orlando, FL
(2007). Google Scholar
J. T. Motz,
“Development of in vivo Raman spectroscopy of atherosclerosis,”
100
–113 Massachusetts Institute of Technology,
(2003). Google Scholar
J. A. NelderR. Mead,
“A simplex method for function minimization,”
Comput. J., 7
(4), 308
–313
(1965). http://dx.doi.org/10.1093/comjnl/7.4.308 CMPJA6 0010-4620 Google Scholar
C. A. Mileset al.,
“The role of the chain in the stabilization of the collagen type I heterotrimer: a study of the type I homotrimer in oim mouse tissues,”
J. Mol. Biol., 321
(5), 797
–805
(2002). http://dx.doi.org/10.1016/S0022-2836(02)00703-9 JMOBAK 0022-2836 Google Scholar
J. Kefferet al.,
“Transgenic mice expressing human tumour necrosis factor: a predictive genetic model of arthritis,”
EMBO J., 10
(13), 4025
–4031
(1991). EMJODG 0261-4189 Google Scholar
P. LiE. M. Schwarz,
“The TNF- transgenic mouse model of inflammatory arthritis,”
Springer Semin. Immunopathol., 25
(1), 19
–33
(2003). http://dx.doi.org/10.1007/s00281-003-0125-3 SSIMDV 0344-4325 Google Scholar
S. T. Proulxet al.,
“Longitudinal assessment of synovial, lymph node, and bone volumes in inflammatory arthritis in mice by in vivo magnetic resonance imaging and microfocal computed tomography,”
Arthritis Rheum., 56
(12), 4024
–4037
(2007). http://dx.doi.org/10.1002/art.23128 ARHEAW 0004-3591 Google Scholar
R. Fisher,
“Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population,”
Biometrika, 10
(4), 507
–521
(1915). http://dx.doi.org/10.2307/2331838 BIOKAX 0006-3444 Google Scholar
D. M. HaalandE. V. Thomas,
“Partial least-squares methods for spectral analyses. 1 Relation to other quantitative calibration methods and the extraction of qualitative information,”
Anal. Chem., 60
(11), 1193
–1202
(1988). http://dx.doi.org/10.1021/ac00162a020 ANCHAM 0003-2700 Google Scholar
I. A. KarampasM. G. OrkoulaC. G. Kontoyannis,
“A quantitative bioapatite/collagen calibration method using Raman spectroscopy of bone,”
J. Biophotonics,
(2012). http://dx.doi.org/10.1002/jbio.201200053 JBOIBX 1864-063X Google Scholar
W. CheongS. PrahlA. Welch,
“A review of the optical properties of biological tissues,”
IEEE J. Quantum Electron., 26
(12), 2166
–2185
(1990). http://dx.doi.org/10.1109/3.64354 IEJQA7 0018-9197 Google Scholar
C. R. Simpsonet al.,
“Near-infrared optical properties of ex vivo human skin and subcutaneous tissues measured using the Monte Carlo inversion technique,”
Phys. Med. Biol., 43
(9), 2465
(1998). http://dx.doi.org/10.1088/0031-9155/43/9/003 PHMBA7 0031-9155 Google Scholar
V. Vrabieet al.,
“Independent component analysis of Raman spectra: application on paraffin-embedded skin biopsies,”
Biomed. Signal Process. Control, 2
(1), 40
–50
(2007). http://dx.doi.org/10.1016/j.bspc.2007.03.001 1746-8094 Google Scholar
I. KoprivaI. JerićA. Cichocki,
“Blind decomposition of infrared spectra using flexible component analysis,”
Chemom. Intell. Lab. Syst., 97
(2), 170
–178
(2009). http://dx.doi.org/10.1016/j.chemolab.2009.04.002 CILSEN 0169-7439 Google Scholar
F. W. Esmonde-WhiteK. A. Esmonde-WhiteM. D. Morris,
“Minor distortions with major consequences: correcting distortions in imaging spectrographs,”
Appl. Spectrosc., 65
(1), 85
–98
(2011). http://dx.doi.org/10.1366/10-06040 APSPA4 0003-7028 Google Scholar
K. A. DooleyF. W. L. Esmonde-WhiteM. D. Morris,
“Optical fiber bundle coupling errors in Raman spectra: correction via data processing,”
Proc. SPIE, 7560 75600O
(2010). http://dx.doi.org/10.1117/12.842418 PSISDG 0277-786X Google Scholar
A. SavitzkyM. J. E. Golay,
“Smoothing and differentiation of data by simplified least squares procedures,”
Anal. Chem., 36
(8), 1627
–1639
(1964). http://dx.doi.org/10.1021/ac60214a047 ANCHAM 0003-2700 Google Scholar
|