Use of Split Bregman denoising for iterative reconstruction in fluorescence diffuse optical tomography

Judit Chamorro-Servent; Juan F. Abascal; Juan Aguirre; Simon R. Arridge; Teresa M. Correia; Jorge Ripoll; Manuel Desco; Juan Jose Vaquero

doi:10.1117/1.JBO.18.7.076016

17 July 2013 Use of Split Bregman denoising for iterative reconstruction in fluorescence diffuse optical tomography

Judit Chamorro-Servent, Juan F. Abascal, Juan Aguirre, Simon R. Arridge, Teresa M. Correia, Jorge Ripoll, Manuel Desco, Juan Jose Vaquero

Author Affiliations +

Journal of Biomedical Optics, Vol. 18, Issue 7, 076016 (July 2013). https://doi.org/10.1117/1.JBO.18.7.076016

Abstract

Fluorescence diffuse optical tomography (fDOT) is a noninvasive imaging technique that makes it possible to quantify the spatial distribution of fluorescent tracers in small animals. fDOT image reconstruction is commonly performed by means of iterative methods such as the algebraic reconstruction technique (ART). The useful results yielded by more advanced l ₁ -regularized techniques for signal recovery and image reconstruction, together with the recent publication of Split Bregman (SB) procedure, led us to propose a new approach to the fDOT inverse problem, namely, ART-SB. This method alternates a cost-efficient reconstruction step (ART iteration) with a denoising filtering step based on minimization of total variation of the image using the SB method, which can be solved efficiently and quickly. We applied this method to simulated and experimental fDOT data and found that ART-SB provides substantial benefits over conventional ART.

1. Introduction

Fluorescence diffuse optical tomography (fDOT) is a noninvasive imaging technique that enables quantification of tomographic [three-dimensional (3-D)] biodistributions of fluorescent tracers in small animals. It is also called fluorescence molecular tomography in some studies.¹^–³

The fDOT image reconstruction problem of finding the 3-D biodistribution of a fluorescence marker $f$ from acquired data $d$ can be mathematically formulated as a linear system of equations

Eq. (1)

W f = d,

where

W

is an

M \times N

weight matrix that relates the measurements and the unknown fluorescence concentration. fDOT reconstruction is an ill-posed large scale problem⁴^,⁵ that has been solved using a wide variety of reconstruction methods (see a review in Ref. 6).

The algebraic reconstruction technique (ART) is an extensively applied and cost-efficient reconstruction method that yields fast and stable reconstruction in experimental diffuse optical tomography (DOT) and fDOT studies.⁶^–⁹ It solves the linear system of Eq. (1) by projecting a solution estimate onto the hyperplane defined by each row of the linear system. This computationally efficient approach does not require the whole matrix $W$ to be held in memory, thus making it practical for managing large datasets.¹⁰

Convergence of ART is always fast during the first few iterations, after which it can slow down until it stagnates; in addition, the performance of ART deteriorates with the increase in data noise level and modeling error frequency.¹¹

$l_{1}$ -regularized approaches are well suited for signal recovery and image reconstruction and have been widely applied in image denoising and magnetic resonance imaging reconstruction. They have also been used in DOT and fDOT.¹²^–¹⁴ Douri et al.¹² reconstructed the simulated DOT data by combining a strategy based on a priori edge information with a diffusion flux analysis of the local structures at each iteration. Freiberger et al.¹³ introduced an alternating direction minimization method to solve $l_{1}$ regularization. This method splits the reconstruction problem for simulated fDOT data into two subproblems: an $l_{2}$ stage, solved using a Gauss-Newton step,⁶ and an $l_{1}$ regularization stage, solved by thresholding (or shrinkage). Correia et al.¹⁴ introduced an operator splitting method for solving the inverse problem of image reconstruction in fDOT for simulated, phantom, and ex vivo data with nonlinear anisotropic diffusion and edge priors. Of the studies presented above, only one actually validated the method proposed using experimental data.¹⁴

The $l_{1}$ total variation (TV) functional was first introduced by Rudin, Osher and Fatemi (ROF)¹⁵ to address image denoising problems. It is formulated as

Eq. (2)

\min_{\hat{f}} ‖ \nabla \hat{f} ‖_{1} such that ‖ \hat{f} - f ‖_{2}^{2} < σ,

where

\hat{f}

is the reconstructed denoised image,

f

is the noisy image,

‖ \cdot ‖_{1}

is the

l_{1}

-norm,

‖ \cdot ‖_{2}

is the

l_{2}

-norm, and

σ

is an error tolerance included to account for noisy data. TV filters out noise while preserving edges. It has received considerable attention in image processing because it presents advantages over simpler techniques such as linear smoothing, which reduces noise but smooths edges.

Iterative procedures have been proposed based on the success of $l_{1}$ regularization techniques for denoising and image reconstruction. These alternate an iterative method (such as simultaneous ART or the expectation–maximization algorithm) with a denoising step in order to minimize the TV and thus obtain enhanced results in computed tomography and positron emission tomography.¹⁶^–¹⁸ Johnston et al. and Pan et al.¹⁶^,¹⁷ used a standard gradient descent method, whereas Sawatzky¹⁸ applied a dual approach to minimize the TV functional. Consequently, the choice of technique for solving $l_{1}$ regularization-based problems may become crucial, as $l_{1}$ is nonlinear; therefore, the computational burden can increase significantly using classic gradient-based methods.

The recently published Split Bregman (SB) method¹⁹ is a simple and efficient algorithm for solving $l_{1}$ regularization-based problems that makes it possible to split the minimization of $l_{1}$ and $l_{2}$ functionals. By applying the SB method to image denoising and compressed sensing in Ref. 19, the authors showed that SB was computationally efficient, given that the SB formulation leads to a problem that can be solved using Gauss–Seidel and Fourier transform methods.

SB was recently applied for fluorescence tomography reconstruction.²⁰^,²¹ Abascal et al.²⁰ used SB to solve the optimization problem by imposing a non-negativity constraint. The image was updated using a nonlinear Gauss-Newton step⁶ based on the computation of first and second derivatives of the nonlinear TV functional. Behrooz et al.²¹ compared $l_{2}$ regularization methods and ART with TV reconstruction methods based on ROF and SB. The authors implemented a preconditioned conjugate gradient method⁶ in each iteration of SB that led to slow convergence in some cases. To validate the method and compare reconstructions, they used a noncontact constant-wave transillumination fluorescence tomography system and concluded that TV regularization has the potential to offer higher resolution and robustness than conventional $l_{2}$ regularization algorithms and ART.

The objective of our work was to present a new approach to solve the fDOT inverse problem, ART-SB. Based on a two-step iterative procedure, we combined the computationally efficient reconstruction method ART with a denoising step. The denoising step is based on the SB formulation and is efficiently implemented using Gauss-Seidel and shrinkage operations without computing first and second derivatives of the TV functional.

The ART-SB method has been optimized and studied in depth. Unlike other studies based on shrinkage algorithms, it has been tested with both simulated and experimental fDOT data.¹²^–¹⁴

The organization of this article is as follows. Section 2 introduces the fDOT forward problem, briefly presents the well-known ART and SB denoising and describes the proposed ART-SB method. This section also describes data acquisition, experimental setup, and data simulation and finishes by presenting the tools used to compare ART with ART-SB. Section 3 presents the reconstruction and comparative results of simulated and experimental data. Finally, Sec. 4 presents the discussion and conclusions.

2. Methods

2.1.

fDOT Forward Problem

In order to model the forward problem, we take into account that, in highly scattering media where light scattering dominates over absorption, light propagation complies with the diffusion equation²²

Eq. (3)

(- \nabla D \nabla + μ_{a}) ϕ (r) = S (r^{'}),

where

D (r, λ) = {3 [μ_{a} (r, λ) + μ_{s}^{'} (r, λ)]}^{- 1}

is the diffusion coefficient for a wavelength

λ

at position

r

in a domain

Ω

,

μ_{s}^{'} (r, λ)

the reduced scattering term,

μ_{a} (r, λ)

the absorption term,

ϕ (r)

the average intensity, and

S (r^{'})

the source term at position

r^{'}

.

In fDOT, the excitation intensity $ϕ_{ex} (r, λ_{ex})$ at excitation wavelength $λ_{ex}$ and emission intensity $ϕ_{em} (r, λ_{em})$ at emission wavelength $λ_{em}$ are given by a pair of diffusion equations.²³^–²⁵

The excitation intensity is emitted by an external source $q_{0} (r_{s})$ at a location $r_{s} \in Ω$ , and the emission comes from a fluorescent region characterized by a fluorescence yield $f (r_{fl})$ , which accounts for its quantum efficiency, its absorption parameter, and its concentration of fluorescence.

Assuming that the presence of the fluorophore does not affect the absorption coefficient and that we are working on the steady-state regime, excitation and emission intensities are given by

Eq. (4)

- \nabla D (r, λ_{ex}) \nabla ϕ_{ex} (r, λ_{ex}) + μ_{a} (r, λ_{ex}) ϕ_{ex} (r, λ_{ex}) = q_{0} (r_{s}) - \nabla D (r, λ_{em}) \nabla ϕ_{em} (r, λ_{em}) + μ_{a} (r, λ_{em}) ϕ_{em} (r, λ_{em}) = f (r_{fl}) ϕ_{ex} (r, λ_{ex}) .

The diffusion equations can be solved using Green’s function for a homogeneous medium and canonical geometries²³^–²⁵ or using a finite element method for a heterogeneous medium and general geometries.⁶

Generalizing, we define a Green function that solves the heterogeneous problem

Eq. (5)

[- \nabla D (r) \nabla + μ_{a} (r)] G (r, r^{'}) = δ (r - r^{'}) .

Using this function, the photon density solving Eq. (4) is given by

Eq. (6)

ϕ_{ex} (r) = \int d r^{'} G (r, r^{'}) q_{0} (r^{'}) ϕ_{em} (r) = \int d r^{'} G (r, r^{'}) f (r^{'}) ϕ_{ex} (r^{'}) .

In our work, the solutions to Eq. (4) are found with a Garlekin finite element approach using TOAST, the finite elements toolbox for DOT,²⁶^,²⁷ which was adapted for fDOT.

The normalized data component,²⁸ defined as the quotient between the fluorescence measurement and the excitation measurement for each source-detector pair, is applied to the data, as follows:

Eq. (7)

d_{b} (r_{d}) = \frac{ϕ_{em}^{meas} (r_{d})}{ϕ_{ex}^{meas} (r_{d})} = \frac{\int d r^{'} G (r_{d}, r^{'}) f (r^{'}) ϕ_{ex} (r^{'})}{\int d r^{'} G (r_{d}, r^{'}) q (r^{'})} = \frac{\int d r^{'} G (r_{d}, r^{'}) f (r^{'}) \int d r^{''} G (r^{'}, r^{''}) q (r^{''})}{\int d r^{'} G (r_{d}, r^{'}) q (r^{'})} .

To compute the matrix of the linear system, $W$ , we first differentiate the emission photon density with respect to $f$ and discretize the integral as a sum of all finite elements $Ω_{j}$ . The variation of emission photon density is given by

Eq. (8)

δ ϕ_{em} (r_{d}) = \sum_{j} \int_{Ω_{j}} d r_{j} G (r_{d}, r_{j}) δ_{ex} (r_{d}, r_{s}) δ f_{j} = \sum_{j} \int_{Ω_{j}} d r_{j} \tilde{ϕ} (r_{j}, r_{d}) δ_{ex} (r_{j}, r_{s}) δ f_{j},

where

δ_{ex} (r_{j}, r_{s})

is excitation photon density at

r_{j}

induced by a source at

r_{s}

, and

\tilde{ϕ} (r_{j}, r_{d})

is the adjoint field at

r_{j}

given by a source

{\tilde{q}}_{0}

located at the detector position

r_{d}

, taking into account the reciprocity of the Green function. The adjoint field solves the equation

Eq. (9)

[- \nabla D (r) \nabla + μ_{a} (r)] \tilde{ϕ} (r) = {\tilde{q}}_{0} (r_{d}) .

The element $i j$ of the Jacobian matrix $W_{i j}$ relates each measurement ${(d_{b})}_{i}$ (where $i$ denotes each source-detector pair) to the concentration of fluorophore at element $Ω_{j}$ and can be written as

Eq. (10)

W_{i j} = \frac{\partial {(d_{b})}_{i}}{\partial f_{j}} = \frac{1}{ϕ_{ex}^{meas} (r_{d}, r_{s})} \int_{Ω_{j}} d r_{j} \tilde{ϕ} (r_{j,} r_{s}) ϕ_{ex} (r_{j,} r_{s}) .

Combining the elements of the matrix $W$ , the fDOT linear system can be expressed as Eq. (1).

2.2.

Inverse Problem

We applied two inversion methods: ART and ART-SB.

2.2.1.

Reconstruction method: ART

Equation (1) is solved using ART,⁶^–⁹^,¹¹ which modifies the reconstructed image by projecting from one hyperplane to another, defined by each row of Eq. (1), as

Eq. (11)

f_{i}^{it + 1} = f_{i}^{it} + λ \frac{d_{i} - \sum_{n = 1}^{N} w_{in} f_{n}^{it}}{\sum_{n = 1}^{N} w_{in}^{2}} w_{i},

where

f_{i}^{it}

is the it’th estimate of the

i

’th row contribution to the image

f

,

d_{i}

the

i

’th measurement,

w_{i}

the

i

’th row vector of the weight matrix, and

λ

the relaxation parameter that adjusts the projection step at each iteration.

As for data ordering, the selection of an appropriate access order (such as randomized access order) has been shown to speed up the iterative reconstruction algorithm and generate a better image.⁸ Thus, we chose randomized ART in our work.

2.2.2.

Two-step reconstruction method: ART-SB

ART-SB is implemented using a two-step iteration:

• The first step corresponds to the minimization problem
Eq. (12)
$f^{it} = \min_{\tilde{f}} ‖ W \tilde{f} - d ‖_{2}^{2},$
which is solved by ART (Sec. 2.2.1).
• The second step corresponds to the denoising problem for each $z$ -projection
Eq. (13)
$\tilde{f} = \min_{\hat{f}} TV (\hat{f}) + \frac{μ}{2} ‖ \hat{f} - f^{it} ‖_{2}^{2},$
where $μ$ is the weighting parameter for the fidelity term ${‖ \hat{f} - f^{it} ‖}_{2}^{2}$ and TV is an anisotropic TV,
Eq. (14)
$TV (\hat{f}) = ‖ \nabla_{x} \hat{f} ‖_{1} + ‖ \nabla_{y} \hat{f} ‖_{1} = ‖ \frac{\partial}{\partial_{x}} \hat{f} ‖_{1} + ‖ \frac{\partial}{\partial_{y}} \hat{f} ‖_{1},$
that is solved by SB. Thus, the solution $\tilde{f}$ constitutes the estimate for the next ART iteration. Note that ${\tilde{f}}^{0} = [0, \dots, 0] \in R^{n}$ is used as the initial guess in the first ART call.

The SB method¹⁹ that solves Eq. (13) is based on splitting the problem into two subproblems that are easier to solve. To this end, our original unconstrained problem of Eq. (13) is transformed into an equivalent constrained problem

Eq. (15)

\min_{\hat{f}, D_{x}, D_{y}} ‖ D_{x} ‖_{1} + ‖ D_{y} ‖_{1} + \frac{μ}{2} ‖ \hat{f} - f^{it} ‖_{2}^{2} such that D_{i} = \nabla_{i} \hat{f} .

The constraint condition of Eq. (15) is enforced by applying the Bregman iteration¹⁹^,²⁹

Eq. (16)

\min_{\hat{f}, D_{x}, D_{y}} ‖ D_{x} ‖_{1} + ‖ D_{y} ‖_{1} + \frac{μ}{2} ‖ \hat{f} - f^{it} ‖_{2}^{2} + \frac{β}{2} ‖ D_{x} - \nabla_{x} \hat{f} - b_{x}^{k} ‖_{2}^{2} + \frac{β}{2} ‖ D_{y} - \nabla_{y} \hat{f} - b_{y}^{k} ‖_{2}^{2},

where the values of

b_{i}^{k}

given above correspond to the Bregman iteration [

b_{i}^{k} = b_{i}^{k - 1} + (\nabla_{i} {\hat{f}}^{k} - D_{i}^{k})

] and

β

is the denoising parameter.

The $l_{1}$ and $l_{2}$ components of this functional can now be split and efficiently solved by SB,¹⁹ which iteratively minimizes with respect to $\hat{f}$ and $D_{i}$ separately, as follows:

Eq. (17)

{\hat{f}}^{k + 1} = \min_{\hat{f}} \frac{μ}{2} {‖ \hat{f} - f^{it} ‖}_{2}^{2} + \frac{β}{2} {‖ D_{x}^{k} - \nabla_{x} \hat{f} - b_{x}^{k} ‖}_{2}^{2} + \frac{β}{2} {‖ D_{y}^{k} - \nabla_{y} \hat{f} - b_{y}^{k} ‖}_{2}^{2} D_{i}^{k + 1} = \min_{D_{i}} ‖ D_{i} ‖_{1} + \frac{β}{2} {‖ D_{i} - \nabla_{i} {\hat{f}}^{k + 1} - b_{i}^{k} ‖}_{2}^{2} .

Note that SB decouples $\hat{f}$ from the $l_{1}$ portion of the problem, thus making $\hat{f}$ differentiable. In order to solve $\hat{f}$ in a cost-efficient manner, we used the Gauss-Seidel method, as proposed in Ref. 19:

Eq. (18)

{\hat{f}}_{i, j}^{k + 1} = \frac{β}{μ + 4 β} ({\hat{f}}_{i + 1, j}^{k} + {\hat{f}}_{i - 1, j}^{k} + {\hat{f}}_{i, j + 1}^{k} + {\hat{f}}_{i, j - 1}^{k} + D_{x, i - 1, j}^{k} - D_{x, i, j}^{k} + D_{y, i, j - 1}^{k} - D_{y, i, j}^{k} - b_{x, i - 1, j}^{k} + b_{x, i, j}^{k} - b_{y, i, j - 1}^{k} + b_{y, i, j}^{k}) + \frac{μ}{μ + 4 β} f_{i, j}^{it} .

Furthermore, since there is no coupling between elements of $D$ , we can use shrinkage operators to compute the optimal values of $D_{x}$ and $D_{y}$ separately,

Eq. (19)

D_{i}^{k + 1} = shrink (\nabla_{i} {\hat{f}}^{k + 1} + b_{i}^{k}, \frac{1}{β}) = \frac{\nabla_{i} {\hat{f}}^{k + 1} + b_{i}^{k}}{| \nabla_{i} {\hat{f}}^{k + 1} + b_{i}^{k} |} * \max (| \nabla_{i} {\hat{f}}^{k + 1} + b_{i}^{k} | - \frac{1}{β}, 0) .

Further details of shrinkage operators can be found in Refs. 19 and 30. A summary of the ART-SB algorithm can be found in Table 1.

Table 1

ART-SB algorithm.

ART-SB algorithm

{\tilde{f}}^{0} = [0, 0, \cdot \cdot \cdot, 0] \in R^{N}

while

{‖ {\tilde{f}}^{it} - {\tilde{f}}^{it - 1} ‖}_{2}^{2} > tol_1

(where

tol_1

is a given tolerance)

Step 1: ART iteration loop

f^{it} = \min_{{\tilde{f}}^{it}} {‖ W {\tilde{f}}^{it} - d ‖}_{2}^{2}

by ART (11)

Step 2: SB for each $z$ -projection:

for

ξ = 1 \dots n z

(

z

-projection loop,

n z

is the number of

z

-slices)

f_{ξ}^{0} = f^{it} (x, y, ξ)

,

D_{x}^{0} = D_{y}^{0} = b_{x}^{0} = b_{y}^{0} = 0

while

{‖ {\hat{f}}_{ξ}^{k} - {\hat{f}}_{ξ}^{k - 1} ‖}_{2} > tol_2

(SB loop)

{\hat{f}}_{ξ}^{k + 1} = \min_{{\hat{f}}_{ξ}} \frac{μ}{2} {‖ {\hat{f}}_{ξ} - f_{ξ}^{it} ‖}_{2}^{2} + \frac{β}{2} {‖ D_{x}^{k} - \nabla_{x} {\hat{f}}_{ξ} - b_{x}^{k} ‖}_{2}^{2} + \frac{β}{2} {‖ D_{y}^{k} - \nabla_{y} {\hat{f}}_{ξ} - b_{y}^{k} ‖}_{2}^{2}

by (18)

D_{x}^{k + 1} = \min_{D_{x}} {‖ D_{x} ‖}_{1} + \frac{β}{2} {‖ D_{x} - \nabla_{x} {\hat{f}}_{ξ}^{k + 1} - b_{x}^{k} ‖}_{2}^{2}

by (19)

D_{y}^{k + 1} = \min_{D_{y}} {‖ D_{y} ‖}_{1} + \frac{β}{2} {‖ D_{y} - \nabla_{y} {\hat{f}}_{ξ}^{k + 1} - b_{y}^{k} ‖}_{2}^{2}

by (19)

b_{x}^{k + 1} = b_{x}^{k} + (\nabla_{x} {\hat{f}}_{ξ}^{k + 1} - D_{x}^{k + 1})

b_{y}^{k + 1} = b_{y}^{k} + (\nabla_{y} {\hat{f}}_{ξ}^{k + 1} - D_{y}^{k + 1})

end (end of SB loop)

end (end of

z

-projection loop)

{\tilde{f}}^{it + 1} = ({\hat{f}}_{1}^{k + 1}, \dots, {\hat{f}}_{n z}^{k + 1})

end (end of while)

2.3.

Experimental and Simulated Data

2.3.1.

Experimental data

A 10-mm thick slab-shaped phantom was built using a resin base with added titanium dioxide and India ink to provide a reduced scattering coefficient of $μ_{s}^{'} = 0.8 {mm}^{- 1}$ and an absorption coefficient of $μ_{a} = 0.01 {mm}^{- 1}$ .³¹ A 5-mm diameter cylinder hole was drilled and filled with a fluid that matched the optical properties of the resin³² mixed with Alexa fluor 700 1 μM (Invitrogen, Carlsbad, California).

The fDOT fluorescence and excitation data were acquired with a noncontact parallel plate fDOT scanner (Fig. 1)³³^,³⁴ comprising a constant intensity laser diode (675 nm), a beam deflector with two mirrors moved by galvanometers that directs the light emerging from the laser onto the desired points (sources) of the sample, a charge-coupled device camera, a motorized filter wheel, and two matched 10-nm filters to capture the excitation photon wavelength (675 nm) or the fluorescence wavelength (720 nm). All the components are placed inside a light-shielded box as depicted in Fig. 1. The acquisition process was controlled using in-house software.

Fig. 1

fDOT noncontact parallel plate experimental setup.

In this work, $9 \times 9$ source positions and $9 \times 9$ detector positions over a ${12 \times 12 mm}^{2}$ surface were used. The weight matrix was calculated as described in Sec. 2.1.

2.3.2.

Simulated data

In addition, an equivalent phantom was simulated using a fine finite element mesh (145,000 nodes). We used the TOAST toolbox²⁶^,²⁷ adapted for fDOT (introduced in Sec. 2.1) to simulate excitation and fluorescent photon densities and to construct the weight matrix. Sources were modelled as isotropic point sources (located at a depth $1 / μ_{s}^{'}$ below the surface) using Dirichlet boundary conditions. This setting resembles a collimated laser as described in Ref. 27. Measurements were modelled by a Gaussian kernel centered at the detector location and computed as a linear operator $M$ acting on the photon density at the boundary of the domain. Thus measured excitation and emission photon densities at the detector position, $r_{d}$ become $ϕ_{ex}^{meas} (r_{d}) = M ϕ_{ex} (r)$ and $ϕ_{em}^{meas} (r_{d}) = M ϕ_{em} (r)$ . Afterwards, we calculated the normalized data component ${d_{b} (r_{d}) = [ϕ_{em}^{meas} (r_{d})] / [ϕ_{ex}^{meas} (r_{d})]}$ and finally solved the linear system matrix as described in Eqs. (8–10) of Sec. 2.1. The average intensity for the weight matrix was reconstructed on a coarser finite element mesh (55,000 nodes) and mapped into a uniform mesh of $20 \times 20 \times 10 voxels$ . The number of sources, number of detectors, and the surface covered by them were equal to those used with the experimental data.

The simulation was perturbed with different levels of additive Gaussian noise (1, 3, 5 and 10%).

The target, $f_{true}$ , corresponding to the physical slab geometry phantom with a cylindrical region filled with fluorophore was modelled using the same finite element mesh used for the simulated data and subsequently mapped into a uniform mesh of $20 \times 20 \times 10 voxels$ .

2.4.

Comparison of Methods: ART Versus ART-SB

A preliminary study was made of the effect of choice of ART-SB algorithm parameters. Both the acquired and simulated data were reconstructed for a range of relaxation parameters, as follows: $λ = (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1)$ . Then, for each relaxation parameter value, we reconstructed the dataset using a range of weighting parameters, as follows: $μ = (0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5)$ .

The stop criterion for ART and ART-SB was a change lower than 0.1% from the previous iteration in the relative solution error norm.

Once the effect of these parameters was assessed, reconstructions of ART and ART-SB were compared.

2.4.1.

Simulated data

ART and ART-SB were compared in terms of convergence, signal-to-noise ratio (SNR), and image profiles.

Convergence was assessed by visualizing the relative solution error norm compared with the number of iterations. The relative solution error norm (with respect to the target) was calculated as

Eq. (20)

E_{rel} (f) = \frac{{‖ f - f_{true} ‖}_{2}}{{‖ f_{true} ‖}_{2}},

where

f_{true}

is the target solution modelled as explained in Sec. 2.3.2.

Horizontal profiles were drawn at the center of the image. In order to compare ART with ART-SB profiles in terms of contrast, both profiles were normalized by the average of highest voxel values in the corresponding reconstructions within a region of interest around the fluorescent target.

SNR was calculated as

Eq. (21)

SNR = 20 \log_{10} \frac{{‖ signal ‖}_{2}}{{‖ noise ‖}_{2}} .

2.4.2.

Experimental data

Only an approximate estimate of the solution target could be provided for experimental data. In this case, ART and ART-SB were compared in terms of SNR and image profiles.

3. Results

The $z$ -slices of ART and ART-SB reconstructions of simulated and experimental data are shown in Figs. 2 and 3.

Fig. 2

Left: Finite element model corresponding to the simulated phantom. Right: 1 mm $z$ -slices ( $y - x$ planes) of: (a) Target solution corresponding to the left figure; (b) Algebraic reconstruction technique (ART) reconstruction (1% additive noise); (c) ART-Split Bregman (SB) reconstruction (1% additive noise) with $μ = 0.3$ ; (d) ART-SB reconstruction (3% additive noise) with $μ = 0.1$ ; (e) ART-SB reconstruction (5% additive noise) with $μ = 0.1$ ; (f) ART-SB reconstruction of simulated data (10% additive noise) with $μ = 0.1$ . In all cases, the relaxation and denoising parameters were $λ = 0.9$ and $β = 2 μ$ , respectively.

Fig. 3

Left: Image of the experimental phantom used. Right: 1 mm $z$ -slices ( $y - x$ planes) of reconstructions: (a) using ART; (b) using ART-SB method with denoising parameter $β = 2 μ$ , where $μ = 0.5$ . In both ART and ART-SB, the relaxation parameter was $λ = 0.9$ .

3.1.

ART Reconstruction

ART-based zero-noise reconstructions of simulated data within a range of relaxation parameters [ $λ = (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1)$ ] converged approximately to the same relative solution error norm ( $< 0.05 %$ maximum difference) with a different number of iterations (from 22 to 435 iterations), thus demonstrating that the ART is robust in terms of solution error norm for diverse relaxation parameters.

ART, which has a low relaxation parameter, approximates a weighted least square solution leading to over-smoothed images. On the contrary, high relaxation parameters lead to high-resolution images with noise and artifacts.

3.2.

Two-Step Reconstruction (ART-SB)

Figure 4 shows the minimum solution error norm achieved with ART-SB reconstructions of simulated data for different weighting parameters, $μ$ ( $β = 2 μ$ and $λ = 0.9$ ). The relative solution error norm achieved by ART for $λ = 0.9$ is represented by a horizontal dashed line.

Fig. 4

Relative solution error norm of reconstruction of simulated data by ART-SB taking $β = 2 μ$ and varying the weighting parameters, $μ$ , for a relaxation parameter $λ = 0.9$ . The dashed line indicates the relative solution norm of ART with. $λ = 0.9$ . Results are provided for simulated data with 1% additive Gaussian noise.

Selection of the parameters for the ART-SB method was based on the value of $β = 2 μ$ from Ref. 19, who found that this value resulted in good convergence. This relationship between $β$ and $μ$ also provided good results in our setting.

Once $β = 2 μ$ was fixed, it was found that there was a value of $μ$ above which the relative solution error norm stagnates ( $μ \geq 2$ in Fig. 4).

After splitting the problem in Eq. (17), we can see that the choice of $β$ affects the $D$ and $f$ subproblems, whereas the choice of $μ$ affects how much the image is regularized ( $f$ subproblem). Besides, in the $D$ subproblem from Eq. (17), the solution $D$ is equal to $\nabla f + b$ after shrinking its vector magnitude by $1 / β$ [Eq. (19)]; this effect is more dramatic when $β$ is small. Thus, once $β = 2 μ$ is set, lower values of $μ$ lead to smooth reconstructions.

We performed this study for each acquisition of data and each $λ$ value in order to choose optimum $μ$ values. This increases the robustness of the method with regards to selection of the regularization parameter.

3.3.

Comparison of Methods: ART Versus ART-SB

Given the nature of the relaxation parameters of ART, $λ$ (see Sec. 3.1), we compared ART with ART-SB using two high relaxation parameter values: $λ = 0.9$ ( $E_{rel} = 0.6625 %$ for simulated data) and $λ = 0.5$ ( $E_{rel} = 0.6225 %$ for simulated data). Thus, ART was used to fit the data while SB filtered the noise in the reconstructed image.

The faster convergence of ART-SB compared with ART can be observed in a plot of the relative solution error norm against iteration number for simulated data (Fig. 5).

Fig. 5

Relative solution error norm plotted against iteration number to show the convergence of ART and ART-SB for two different relaxation parameter values (simulated data with 1% additive Gaussian noise).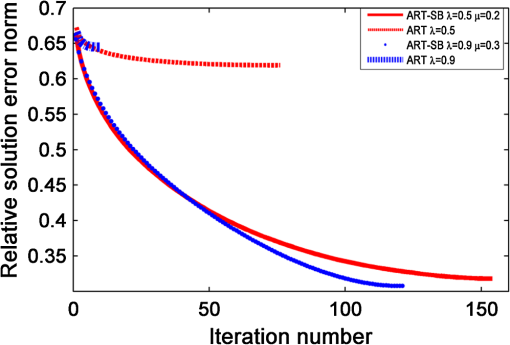

Note that the mean CPU time for performing the SB denoising for each ART iteration (Intel®-Core™ 2 Quad CPU, 2.40 GHz, 4 GB de RAM, Windows Vista) was 0.021 s. Therefore, taking into account that we need around 120 to 160 iterations for the examples in Fig. 5, less than 4 s is necessary for SB denoising.

In terms of SNR, ART-SB led to a higher SNR than ART with both simulated and real data (Fig. 6).

Fig. 6

Signal-to-noise ratio (SNR, dB) plotted against iteration number for ART and ART-SB with relaxation parameter. (a) Simulated data, using relaxation parameter $λ = 0.9$ and denoising parameter $β = 2 μ$ , (different levels of additive normal noise) and (b) experimental data, using relaxation parameter $λ = 0.9$ and denoising parameter 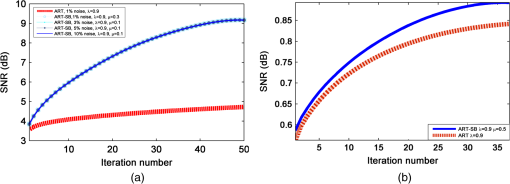$β = 2 μ$ , where $μ = 0.5$ .

The Y-profiles of ART and ART-SB reconstructions for simulated and experimental data are shown in Fig. 7.

Fig. 7

Y-profiles of central $z$ -slice from ART-SB and ART with relaxation parameter $λ = 0.9$ . (a) Analytical target solution (solid black line) and simulated data with different levels of additive normal noise. (b) Experimental data.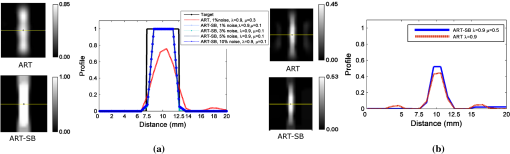

The profiles obtained for a simulated case with ART-SB (left side of Fig. 7) are closer to the real ones than those obtained with ART. Moreover, for the experimental case (right side of Fig. 7), the peak-to-valley relation doubled (ART-SB: 19.326. ART: 9.0427).

4. Discussion and Conclusions

In this article, we propose a novel iterative algorithm, ART-SB, which alternates a cost-efficient reconstruction method (ART) with a denoising step based on the minimization of TV using SB which is also solved in a cost-efficient way. Although ART-SB is a state-of-the-art “shrinkage methodology,”¹²^–¹⁴^,¹⁶^–¹⁸ it provides a solution for $l_{1}$ -regularized problems, minimizing TV by means of the SB method introduced by Ref. 19.

In contrast to Refs. 20 and 21, we used the SB-denoising formulation, which is solved efficiently, without computing first and second derivatives of the TV functional. SB denoising solved using Gauss-Seidel and shrinkage, as was the case in this article, has a relatively small memory footprint compared with second-order methods that require explicit representations of the Hessian matrix.¹⁹ The authors in Ref. 19 also showed that this way of solving SB denoising improves the speed of convergence compared with a gradient descent algorithm based on dual formulation of the ROF functional. Thus, ART-SB is a practical method for solving large dataset problems because ART does not need to hold the system matrix in memory and our implementation of SB denoising does not require explicit representations of the Hessian matrix.

ART-SB and ART were compared in terms of convergence, SNR, and quality of image profiles for simulated data, and in terms of SNR and image profiles for experimental data. The comparison revealed that ART-SB enhanced the quality of reconstructions with lower noise and faster convergence than ART. Convergence of ART (Fig. 5) is fast during the first few iterations, after which it stagnates, in agreement with Ref. 11.

ART-SB significantly improved localization and sharpened edges. ART, on the other hand, led to blurred reconstructions accompanied by a loss of resolution along the $z$ (Figs. 2 and 3). Furthermore, ART deteriorates with increased noise level.¹¹ However, we found that ART-SB was very robust in terms of data noise level in $z$ -slices (Figs. 2 and 3), SNR (Fig. 6) and Y-profiles (Fig. 7). These findings agree with the conclusions of the two-step reconstruction algorithms for computed tomography and positron emission tomography cited above.¹⁶^–¹⁸

Although SB denoising for each $z$ -projection of each 3-D ART reconstruction iteration provided a significant improvement in terms of localization and image quality, we did not test whether implementation of 3-D SB denoising could lead to even better results.

Furthermore, we stress that even if the determination of the optimal denoising parameter ( $β$ ) did not seem critical for the study carried out in Sec. 3.2, only $β$ has an effect on the shrinkage operator. Thus, since the restriction is evaluated in each iteration, the number of required iterations for convergence depends on the $β$ value (further details can be found in Ref. 19). With $β = 2 μ$ , the study of the $μ$ parameter allowed us to understand that there is a value of $μ$ above which the shrinkage operator is more effective. As we point out in Sec. 3.2, low values of $β = 2 μ$ correspond indirectly to the shrinkage operator effect [Eq. (19)], which leads to smooth reconstructions and thus increases the number of necessary iterations before convergence is reached. Consequently, even if the SB iteration converges to the solution for any positive value of $β$ , given the nature of Bregman iteration,¹⁹ the value of $β$ affects the convergence speed of the algorithm.

In conclusion, we showed that the combination of a cost-efficient linear iterative technique (ART) with a denoising method (anisotropic SB) significantly improves the reconstruction of fDOT-simulated data in terms of relative solution error norm and image quality and reconstruction of fDOT experimental data in terms of image quality. In addition, ART-SB appears to be an efficient methodology for handling the large datasets required for fDOT experiments and could be of interest to researchers working with optical tomography.

Acknowledgments

This work was supported by Spanish Ministry of Science and Innovation (FPI program, TEC2008-06715), EU-FP7 project FMTXCT-201792, the Community of Madrid (ARTEMIS S2009/DPI-1802), European Regional Development Funds (FEDER), and CDTI under the CENIT program (AMIT Project, CEN-20101014).

References

1.

A. Martínet al., “Imaging changes in lymphoid organs in vivo after brain ischemia with three-dimensional fluorescence molecular tomography in transgenic mice expressing green fluorescent protein in T lymphocytes,” Mol. Imag., 7 (4), 157 –167 (2008). MIOMBP 1535-3508 Google Scholar

2.

V. Ntziachristoset al., “In vivo tomographic imaging of near-infrared fluorescent probes,” Mol. Imaging, 1 (2), 82 –88 (2002). http://dx.doi.org/10.1162/153535002320162732 MIOMBP 1535-3508 Google Scholar

3.

V. Ntziachristoset al., “Looking and listening to light: the evolution of whole-body photonic imaging,” Nat. Biotech., 23 (3), 313 –320 (2005). http://dx.doi.org/10.1038/nbt1074 NABIF9 1087-0156 Google Scholar

4.

S. Arridge, “Optical tomography in medical imaging,” Inverse Probl., 15 R41 –R93 (1999). http://dx.doi.org/10.1088/0266-5611/15/2/022 INPEEY 0266-5611 Google Scholar

5.

J. Hadamard, “Sur les problèmes aus dérivées partielles et leur signification physique,” Princeton Univ. Bull., 13 49 –52 (1902). Google Scholar

6.

S. ArridgeJ. Scothland, “Optical tomography: forward and inverse problems,” Inverse Probl., 25 (12), 123010 (2009). http://dx.doi.org/10.1088/0266-5611/25/12/123010 INPEEY 0266-5611 Google Scholar

7.

A. D. Zacharopouloset al., “A matrix-free algorithm for multiple wavelength fluorescence tomography,” Opt. Express, 17 (21), 3042 –3051 (2009). http://dx.doi.org/10.1364/OE.17.003042 OPEXFF 1094-4087 Google Scholar

8.

X. Inteset al., “Projection access order in algebraic reconstruction technique for diffuse optical tomography,” Phys. Med. Biol., 47 (1), N1 –N10 (2002). http://dx.doi.org/10.1088/0031-9155/47/1/401 PHMBA7 0031-9155 Google Scholar

9.

V. Ntziachristoset al., “Concurrent MRI and diffuse optical tomography of breast after indocyanine green enhancement,” Proc. Natl. Acad. Sci. U. S. A., 97 (6), 2767 –2772 (2000). Google Scholar

10.

H. JiangY. XuN. Iftimia, “Experimental three-dimensional optical image reconstruction of heterogeneous turbid media from continuous-wave data,” Opt. Express, 7 (4), 204 –209 (2000). http://dx.doi.org/10.1364/OE.7.000204 OPEXFF 1094-4087 Google Scholar

11.

P. C. Hansen, Discrete Inverse Problems: Insights and Algorithms, SIAM, Philadelphia (2010). Google Scholar

12.

A. Douiriet al., “Anisotropic diffusion regularization methods for diffuse optical tomography using edge prior information,” Meas. Sci. Technol., 18 (1), 87 –95 (2007). http://dx.doi.org/10.1088/0957-0233/18/1/011 MSTCEP 0957-0233 Google Scholar

13.

M. FreibergerC. ClasonH. Scharfetter, “Total variation regularization for nonlinear fluorescence tomography with an augmented Lagrangian splitting approach,” Appl. Opt., 49 (19), 3741 –3747 (2010). http://dx.doi.org/10.1364/AO.49.003741 APOPAI 0003-6935 Google Scholar

14.

T. Correiaet al., “Split operator method for fluorescence diffuse optical tomography using anisotropic diffusion regularization with prior anatomical information,” Biomed. Opt. Express, 2 (9), 2632 –2648 (2011). http://dx.doi.org/10.1364/BOE.2.002632 BOEICL 2156-7085 Google Scholar

15.

L. I. RudinS. OsherE. Fatemi, “Nonlinear total variation based noise removal algorithms,” Phys. D, 60 (1), 259 –268 (1992). http://dx.doi.org/10.1016/0167-2789(92)90242-F PDNPDT 0167-2789 Google Scholar

16.

M. JohnstonG. A. JohnsonC. T. Badea, “GPU-based iterative reconstruction with total variation minimization for micro-CT,” Proc. SPIE, 7622 762238 (2010). http://dx.doi.org/10.1117/12.844368 PSISDG 0277-786X Google Scholar

17.

Y. Panet al., “TV-regularized iterative image reconstruction on a mobile C-ARM CT,” Proc. SPIE, 7622 76222L (2010). http://dx.doi.org/10.1117/12.844398 PSISDG 0277-786X Google Scholar

18.

A. Sawatzkyet al., “Accurate EM-TV algorithm in PET with low SNR,” in IEEE Conf. Nuclear Science Symp. Conf. Record, 5133 –5137 (2008). Google Scholar

19.

T. GoldsteinS. Osher, “The split Bregman method for L1 regularized problems,” SIAM J. Imag. Sci., 2 (2), 323 –343 (2009). http://dx.doi.org/10.1137/080725891 1936-4954 Google Scholar

20.

J. F. P.-J. Abascalet al., “Fluorescence diffuse optical tomography using the split Bregman method,” Med. Phys., 38 6275 –6284 (2011). http://dx.doi.org/10.1118/1.3656063 MPHYA6 0094-2405 Google Scholar

21.

A. Behroozet al., “Total variation regularization for 3D reconstruction in fluorescence tomography: experimental phantom studies,” Appl. Opt., 51 (34), 8216 –8227 (2012). http://dx.doi.org/10.1364/AO.51.008216 APOPAI 0003-6935 Google Scholar

22.

A. Ishimaru, Wave Propagation and Scattering in Random Media, Academic Press, New York (1978). Google Scholar

23.

E. E. Graveset al., “A submillimeter resolution fluorescence molecular imaging system for small animal imaging,” Med. Phys., 30 (5), 901 –912 (2003). http://dx.doi.org/10.1118/1.1568977 MPHYA6 0094-2405 Google Scholar

24.

D. Hydeet al., “FMT-CT imaging of amyloid-beta plaques in a murine Alzheimer’s disease model,” Neuroimage, 44 (4), 1304 –1311 (2009). http://dx.doi.org/10.1016/j.neuroimage.2008.10.038 NEIMEF 1053-8119 Google Scholar

25.

V. NtziachristosR. Weissleder, “Experimental three-dimensional fluorescence reconstruction of diffuse media by use of a normalized Born approximation,” Opt. Lett., 26 (12), 893 –895 (2001). http://dx.doi.org/10.1364/OL.26.000893 OPLEDP 0146-9592 Google Scholar

26.

M. Schweiger, Application of the Finite Element Method in Infrared Image Reconstruction of Scattering Media, University College London, United Kingdom (1994). Google Scholar

27.

M. Schweigeret al., “The finite element method for the propagation of light in scattering media: boundary and source conditions,” Med. Phys., 22 (11), 1779 –1792 (1995). http://dx.doi.org/10.1118/1.597634 MPHYA6 0094-2405 Google Scholar

28.

M. BornE. Wolf, Principle of Optics, Cambridge University Press, Cambridge, United Kingdom (1999). Google Scholar

29.

W. Yinet al., “Bregman iterative algorithms for l1-minimization with applications to compressed sensing,” SIAM J. Imag. Sci., 1 (1), 143 –168 (2008). http://dx.doi.org/10.1137/070703983 1936-4954 Google Scholar

30.

S. Setzer, “Split Bregman algorithm, Douglas-Rachford splitting and frame shrinkage,” in Second International Conference on Scale Space and Variational Methods in Computed Vision, 464 –476 (2009). Google Scholar

31.

D. A. Boas, Diffusion Photon Probes of Structural and Dynamical Properties of Turbid Media: Theory and Biomedical Applications, University of Pennsylvania, Pennsylvania (1996). Google Scholar

32.

R. Cubedduet al., “A solid tissue phantom for photon migration studies,” Phys. Med. Biol., 42 (10), 1971 –1979 (1997). http://dx.doi.org/10.1088/0031-9155/42/10/011 PHMBA7 0031-9155 Google Scholar

33.

J. Chamorro-Serventet al., “Feasibility of U-curve method to select the regularization parameter for fluorescence diffuse optical tomography in phantom and small animal studies,” Opt. Express, 19 (12), 11490 –11506 (2011). http://dx.doi.org/10.1364/OE.19.011490 OPEXFF 1094-4087 Google Scholar

34.

J. Chamorro-Serventet al., “FDOT setting optimization and reconstruction using singular value analysis with automatic thresholding,” in IEEE Conf. Nuclear Science Symp. Medical Imaging Conf., 2827 –2829 (2009). Google Scholar

Citation Download Citation

Judit Chamorro-Servent, Juan F. Abascal, Juan Aguirre, Simon R. Arridge, Teresa M. Correia, Jorge Ripoll, Manuel Desco, and Juan Jose Vaquero "Use of Split Bregman denoising for iterative reconstruction in fluorescence diffuse optical tomography," Journal of Biomedical Optics 18(7), 076016 (17 July 2013). https://doi.org/10.1117/1.JBO.18.7.076016

Published: 17 July 2013

Access the abstract

JOURNAL ARTICLE
9 PAGES

DOWNLOAD PAPER SAVE TO MY LIBRARY

GET CITATION

CITATIONS

Cited by 28 scholarly publications and 4 patents.

Explore citations on Lens.org

RIGHTS & PERMISSIONS

Get copyright permission Get copyright permission on Copyright Marketplace

KEYWORDS

Denoising

Reconstruction algorithms

Luminescence

Signal to noise ratio

Diffuse optical tomography

Image restoration

Data acquisition

1.

Introduction

Eq. (1)

Eq. (2)

2.

Methods

2.1.

fDOT Forward Problem

Eq. (3)

Eq. (4)

Eq. (5)

Eq. (6)

Eq. (7)

Eq. (8)

Eq. (9)

Eq. (10)

2.2.

Inverse Problem

2.2.1.

Reconstruction method: ART

Eq. (11)

2.2.2.

Two-step reconstruction method: ART-SB

Eq. (12)

Eq. (13)

Eq. (14)

Eq. (15)

Eq. (16)

Eq. (17)

Eq. (18)

Eq. (19)

Table 1

2.3.

Experimental and Simulated Data

2.3.1.

Experimental data

Fig. 1

2.3.2.

Simulated data

2.4.

Comparison of Methods: ART Versus ART-SB

2.4.1.

Simulated data

Eq. (20)

Eq. (21)

2.4.2.

Experimental data

3.

Results

Fig. 2

Fig. 3

3.1.

ART Reconstruction

3.2.

Two-Step Reconstruction (ART-SB)

Fig. 4

3.3.

Comparison of Methods: ART Versus ART-SB

Fig. 5

Fig. 6

Fig. 7

4.

Discussion and Conclusions

Acknowledgments

References

Show All Keywords

Keywords/Phrases

Search In:

Publication Years