|
|
1.IntroductionEukaryotic cells are supported by three kinds of cytoskeletons: microtubules, actins, and intermediate filaments. The cytoskeletons play an important role in providing structural support with appropriate viscoelasticity to maintain cell morphology, and to facilitate cell movement and cell division.1 During cell division, the cytoskeleton undergoes dynamic changes to help cells divide. Specifically, in the beginning of cell division, microtubules release tubulin, and the free tubulins assemble to form spindles to orient the chromosomes’ arrangement. In telophase, the last stage of cell division, spindles disintegrate, and tubulins resume their role as part of microtubules.2 This dynamic change provides cells with enough strength to divide from one mother cell to form two daughter cells. In more details, the cell cycle can be separated into interphase and mitosis, which make up cell division. During interphase, cells undergo wide arrays of changes to prepare for cell division, such as DNA replication and synthesis of associated proteins. Cell division can be divided into prophase, metaphase, anaphase, and telophase, and at the end of nucleus division, cells undergo cytokinesis.2 In monitoring cell division, we focus on analyzing mitosis and change in elasticity and viscosity during its three phases: metaphase, anaphase, and telophase. Each phase is morphologically distinguishable: metaphase is marked by the condensed chromosomes lining up in the middle of the cell. In anaphase and telophase, the cleavage furrows appear and the chromosomes begin to separate. In telophase, the spindles gradually decompose, and the chromosomes reach their respective poles and decondense.2 It is plausible that the structural changes during the course of cell division outlined above will be concomitant with a change in the intracellular viscoelasticity. In our experiments, we investigated the intracellular viscoelasticity during cell division from metaphase through the end of the telophase. Viscoelasticities of complex materials including polymers,3,4 synovial fluids,5 and cells6–8 can be studied by either active or passive microrheology. Active microrheology refers to the determination of the material’s viscoelasticity by recording motion of the test samples or of particles attached to the test samples in response to an external force.3 In 2001, Jacobson et al.9 used atomic force microscopy (AFM) to measure the cortical stiffness during cell division, and reported that the elasticity of the cortex increased from to and (), respectively, as the cleavage furrow contracted while Potorous tridactylus kidney cells divided from the metaphase through anaphase to telophase. Shimamoto et al.10 also used AFM to examine the dynamic viscoelasticity of microtubules and spindles in metaphase and reported that spindle viscosity could be related to microtubule density and cross-linking, and spindle elasticity to microtubule rigidity. As a complementary technique to active microrheology, passive microrheology measures the viscoelasticity of the sample of interest by tracking and analyzing the thermal motion of one or more probes either embedded inside or attached to the sample.3,6,11–13 In an equilibrium system where only thermal forces act on the probe-particle, motion of the particle is the random walk of the particle caused by thermal fluctuations and collisions with surrounding molecules. It is sensitive not only to the temperature but also to the viscoelasticity of the surrounding material, and particle-tracking microrheology (based on Brownian motion) has been established as a convenient technique to measure the viscoelasticity of complex fluids, especially when the sample is available only in relatively small volumes on the order of a fraction of a microliter3,6,11–13 such that conventional (classical) rheometers are not applicable. From the Brownian motion of the particle [, , and ], standard algorithm11 has been established to calculate the mean square displacement [MSD()] of the particle [where () is the lag time] and the viscoelasticity of the surrounding material in terms of the elastic modulus and viscous modulus as a function of frequency (). It is well known, however, that live cells in general, and live cells during the course of cell division in particular, are by no means in equilibrium state; hence, the validity of the determination of the cellular viscoelasticity by Brownian motion analysis deserves some discussion and justification. As early as 1965, the viscosity of fibroblasts in prophase, metaphase, and anaphase had been measured and reported by Taylor14 to be , , and , respectively, by analyzing the Brownian motion of cytoplasmic granules in dividing fibroblasts to correlate with the movement of anaphase chromosomes. In 1979, the same method was adopted by Schaap and Forer15 to measure the intracellular viscosity of the spermatocytes of two species of crane flies at different temperature to find possible correlation with the speed of the autosome separation in the anaphase; the intracellular viscosity was determined to be in the range of 0.04 to for temperature in the range of 30°C to 5°C. More recently, cytoplasm elasticity and viscosity of many different types of cells, including fibroblasts, mouse embryonic fibroblasts, human umbilical vein endothelial cells, human induced pluripotent stem cells, and human embryonic stem cells, have been studied extensively under different conditions by particle-tracking microrheology by Wirtz and his collaborators,16–24 as well as by others.25,26 The average viscous modulus and elastic modulus (both at the frequency of 1 Hz) were determined to be in the range of 1 to 50 Pa and 1 to 80 Pa, respectively. Theoretically, the determination of cellular viscoelasticity by passive microrheology is valid only if the cell can be regarded as an equilibrium system.27 Gallet et al.,28 however, have shown that (i) even though live cells are far from equilibrium, at frequency higher than 10 Hz (or equivalently, for time scale shorter than 0.1 s), the contribution of nonthermal force to particle fluctuation is much lower than that of the thermal force, and the cells can be regarded as in quasi-equilibrium state; (ii) the contribution of nonthermal energy to particle fluctuation is significantly less for intracellular particles than those tied to cellular cortex. In addition, it has also been reported that the influence of nonthermal energy on the fluctuation of particles injected into the cells by gene gun is in general significantly less than that of the endocytosed particles or the endogenous particles,29–31 and that for injected particles, those with smaller size () are significantly less affected by the nonthermal energy than those with larger size ().27 Hence, in our experiments, we injected 100-nm polystyrene beads into the cells to serve as the probes for subsequent intracellular particle tracking, and demonstrated that the computation of the viscous modulus and elastic modulus based on Brownian motion analysis and the assumption of equilibrium statistics could be a useful and good approximation.17,27,29–31 Since the bead size (100 nm) used in our experiments is much larger than the cytoskeletal mesh size (20–40 nm),32 what we measured should reflect the viscoelasticity of the cytoskeletal networks but not the interstitial fluid of the cytoplasm.29 2.Materials and Methods2.1.Sample PreparationHeLa cells were cultured at 37°C in 5% in Dulbecco’s modified eagle medium with 10% fetal bovine serum on 35-mm-bottom dishes coated with poly-l-lysine (MatTek Corp., Ashland, Massachusetts). Fluorescent carboxylated (negatively charged) beads (Invitrogen, Taipei, Taiwan; ; 100 nm diameter; ) were injected into the HeLa cells by biolistic particle delivery system (PDS-100, pressure 450 psi, 20 μL per injection). Carboxylated polystyrene beads injected into cytoplasm via helium particle injection show less directional motion (i.e., less degree of active transport).29–31 The total number of particles injected into each cell is in the range of 5 to 26; the average number of injected particles per cell is approximately 11. A comparison of the cell growth rate in cultured cells with and without injected particles indicated that the cell viability is not affected by particle injection. Similar result had also been reported by Tseng et al.30 2.2.Experimental Setup and ProcedureMotion of intracellular fluorescent beads was recorded digitally via an inverted epifluorescence microscope (Nikon Eclipse Ti, Tokyo, Japan), equipped with an oil immersion objective (, ) and a charge coupled device (CCD) camera (Hamamatsu, Hamamatsu, Japan, OHCA-Flash 4.0) with a frame rate of 100 frames per second, an image resolution of , and . The experimental setup is shown schematically in Fig. 1. Fluorescence excitation of the bead at 562 nm was provided by light emitted from a Hg lamp (Nikon, Tokyo, Japan) in conjunction with a band-pass filter (pass-band: ), followed by a long-pass dichroic mirror (Semrock, Rochester, New York; with 593 nm cut-off) which reflected 562 nm (excitation light) into the oil immersion microscope objective lens (, ), and transmitted the epi-fluorescence light (605 nm) emitted by the beads for detection by the CCD camera. A second band-pass filter () served to further reduce the stray light from the Hg lamp. Fig. 1A schematic illustration of intracellular microrheology based on video particle tracking (VPT).  Experiments were conducted with cell samples in an incubation chamber (Live cell instrument) at 37°C in 5% . This approach allows us to measure the intracellular viscoelasticity with a high spatial resolution on the order of a micron, high temporal resolution on the order of and , and a relatively short data acquisition time on the order of 10 s. The lower limit () of the frequency range is dictated by the integration time (and the poor signal-to-noise ratio due to the noise), while the upper limit () is dictated by the frame rate of the CCD camera. During the experiment, the broadband light source was switched off and turned on only momentarily every 3 min when bright-field images of the cells were taken to examine and record the cell morphology. 2.3.Experimental Results and DiscussionThe motion of fluorescent beads inside each cell was tracked and recorded for 10 s every 3 min for 15 min, as the cell division took place from metaphase through the end of the telophase. The trajectory of the particle was tracked and analyzed with a standard algorithm;33 from the two-dimensional (2-D) position [, ] of each particle as a function of time, we deduced the statistical distribution of and , the mean square displacement , as a function of the lag time (), and the complex viscoelastic modulus ) as a function of frequency (), where ) represents the elastic modulus and represents the viscous modulus.7,34 The analysis, which is based the generalized form of the Stokes–Einstein relationship, assumes that the motion of the beads is purely Brownian (driven only by thermal fluctuation); according to the theory of Brownian motion, where the exponent characterizes the subdiffusive behavior of the beads inside a complex medium. If either , or if the statistical distributions of and deviate significantly from Gaussian, then the results imply possible involvement of active transport driven by forces other than thermal fluctuations, and the deduction (and the corresponding interpretation) of and are no longer valid.35 Hence, in our data analysis and the determination of and , we keep only those data satisfying the criteria stated above. Of all the particles that we have tracked and analyzed, 13 out of 162 (i.e., 8%) were ignored based on the above criteria. If we treated the cells with 100-nm-diameter particles and left overnight to allow the particles to diffuse and disperse throughout the cytoplasm, we found that a much larger fraction of intracellular particles (35 out of 104; i.e., 33%) exhibited nonthermal motions through out the course of cell division. We speculated that this is due to the fact that these particles could be attached to organelles or cytoskeletons such that their motions were strongly influenced by the motion of the latter. For the sake of simplicity, and also due to the limitation of our spatial resolution along the optical axis (i.e., the -axis), we have chosen to simplify the three-dimensional Brownian motion to a 2-D problem by ignoring the -component. In addition, we also ignored the particles that escaped from the focal plane such that their position data [, ] were truncated during the data acquisition. As a specific example, a fluorescence micrograph of a HeLa cell (in anaphase) with embedded fluorescent beads is shown in Fig. 2(a); the experimental data for the Brownian motion [, ] of a selected particle is shown in Fig. 2(b); the corresponding is shown in Fig. 2(c); and the elastic modulus and viscous modulus as a function of frequency () are shown in Fig. 2(d). From the experimental results obtained from 11 beads inside the cell, at anaphase of the cell division, the mean, the median, and the distribution of elastic modulus and viscous modulus (at ) are displayed graphically in a box–whisker plot in Fig. 2(e). In total, we have analyzed 149 fluorescent beads in four cells to calculate the viscoelasticity of the cells in different phases during the cell division, including metaphase, anaphase, and telophase, and compared the average viscosity and elasticity at different phases as shown in Fig. 3 in box–whisker plots. Our results (at ) indicate that both the elastic modulus and viscous modulus increase during cell division from metaphase to anaphase, and remain approximately the same from anaphase to telophase. Fig. 2A specific example of intracellular particle-tracking microrheology at anaphase. (a) A fluorescence micrograph of a HeLa cell with embedded fluorescent beads; (b) 2-dimensional projection [, ] of the trajectory of the Brownian motion of a selected bead; (c) the mean square displacement (MSD) as a function of the lag time () in a log-log plot with slope “”; (d) the elastic modulus and the viscous modulus as a function of frequency; (e) Box plot of and (at 10 Hz) from 11 beads in a HeLa cell at anaphase. 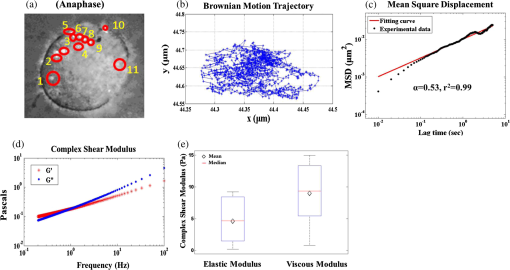 Fig. 3Boxplot of intracellular (a) elastic modulus; (b) viscous modulus, both at 10 Hz, during cell division from metaphase to telophase, measured at 3-min intervals. *Statistical significance with from Student t test. The lower and the upper boundaries of the box represent (25 percentile) and (75 percentile) of the data, respectively; we denote , and indicate IQR by the lowest horizontal line, and IQR by the highest horizontal line; the ⋄ symbol and the horizontal bar inside the box represent the mean and the medium, respectively. 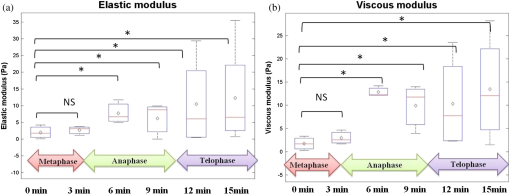 We speculated that the increase in both elasticity and viscosity during cell division, from metaphase to anaphase, may be attributed mainly to the change in structure and the amount of microtubules, a component of the cytoskeleton. During cell division, microtubules polarize to form fiber bundles, which are expected to constrain the movement of fluorescent beads and to increase the intracellular viscoelasticity. This is contradictory to the earlier result obtained by tracking cytoplasmic granules inside a dividing cell15 which might include the contributions from both thermal and nonthermal motions of granules inside a dividing cell, because motor-generated forces could act on granules during anaphase. In this approach, the contribution of nonthermal motion would lead to an underestimation of intracellular viscosity. Our result is consistent with the result reported by Shimamoto et al.,10 where the increase in spindle viscosity was correlated with the microtubule density and cross-linking, whereas the increase in spindle elasticity was correlated with the re-distributions of molecular motors. 3.Summary and ConclusionParticle tracking microrheology, using 100-nm (diameter) carboxylated polystyrene beads injected into the cytoplasm of HeLa cells, has been applied to study the viscoelasticities of living cells during the course of cell division. Although the cytoskeletons and their contribution to intracellular viscoelasticity are expected to play a strong role in cell division, very few studies have applied this technique to study the dynamic intracellular viscoelasticities of the dividing cell and to study its role in cell proliferation. In this research, we measured, by video particle tracking (VPT), the elastic modulus and viscous modulus as a function of frequency () during cell division. Our results indicate that both elastic modulus and viscous modulus increase as a function of time as the cell progresses from metaphase to anaphase, and remain approximately the same from anaphase to telophase. The increase in intracellular viscoelasticity can be attributed to the increase in microtubule density and cross-linking and the re-distributions of molecular motors reported in the literature. Further studies, with fluorescence-labeled microtubules and actin filaments, for example, will be required to correlate these results with the polymerization of fiber bundles to support the force required for the cell division, and to delineate the role of cytoskeletons and the cytoplasmic viscoelasticity in cell division. AcknowledgmentsThis work is jointly supported by the National Science Council, Taiwan, ROC (I-RiCE Program, Project No. NSC100-2911-I-009-101, NSC’s Undergraduate Research Project, NSC101-2815-C-010-008-E) and the Ministry of Education (The Top University Project). ReferencesD. A. FletcherR. D. Mullins,
“Cell mechanics and the cytoskeleton,”
Nature, 463
(7280), 485
–492
(2010). http://dx.doi.org/10.1038/nature08908 NATUAS 0028-0836 Google Scholar
A. J. Bruce Albertset al., Molecular Biology of the Cell, Garland Science, New York
(2007). Google Scholar
C. C. Chiang et al.,
“Optical tweezers based active microrheology of sodium polystyrene sulfonate (NaPSS),”
Optic. Express, 19
(9), 8847
–8854
(2011). http://dx.doi.org/10.1364/OE.19.008847 OPEXFF 1094-4087 Google Scholar
G. Pesceet al.,
“Microrheology of complex fluids using optical tweezers: a comparison with macrorheological measurements,”
J. Opt. Pure Appl. Opt., 11
(3), 034016
(2009). http://dx.doi.org/10.1088/1464-4258/11/3/034016 JOAOF8 1464-4258 Google Scholar
Y. Q. Chenet al.,
“Microrheology of human synovial fluid of arthritis patients studied by diffusing wave spectroscopy,”
J. Biophoton., 5
(10), 777
–784
(2012). http://dx.doi.org/ 10.1002/jbio.201100128. Epub JBOIBX 1864-063X Google Scholar
M.-T. Weiet al.,
“A comparative study of living cell micromechanical properties by oscillatory optical tweezers,”
Optic. Express, 16
(12), 8594
–8603
(2008). http://dx.doi.org/10.1364/OE.16.008594 OPEXFF 1094-4087 Google Scholar
D. Wirtz,
“Particle-tracking microrheology of living cells: principles and applications,”
Annu. Rev. Biophys., 38 301
–326
(2009). http://dx.doi.org/10.1146/annurev.biophys.050708.133724 ARBNCV 1936-122X Google Scholar
J. C. Del Álamoet al.,
“Anisotropic rheology and directional mechanotransduction in vascular endothelial cells,”
Proc. Natl. Acad. Sci., 105
(40), 15411
–15416
(2008). http://dx.doi.org/10.1073/pnas.0804573105 PNASA6 0027-8424 Google Scholar
R. MatzkeK. JacobsonM. Radmacher,
“Direct, high-resolution measurement of furrow stiffening during division of adherent cells,”
Nat. Cell Biol., 3
(6), 607
–610
(2001). http://dx.doi.org/10.1038/35078583 NCBIFN 1465-7392 Google Scholar
Y. Shimamotoet al.,
“Insights into the micromechanical properties of the metaphase spindle,”
Cell, 145
(7), 1062
–1074
(2011). http://dx.doi.org/10.1016/j.cell.2011.05.038 CELLB5 0092-8674 Google Scholar
L. HoughH. Ou-Yang,
“A new probe for mechanical testing of nanostructures in soft materials,”
J. Nanoparticle Res., 1
(4), 495
–499
(1999). http://dx.doi.org/10.1023/A:1010075223642 JNARFA 1388-0764 Google Scholar
D. Mizunoet al.,
“Nonequilibrium mechanics of active cytoskeletal networks,”
Science, 315
(5810), 370
–373
(2007). http://dx.doi.org/10.1126/science.1134404 SCIEAS 0036-8075 Google Scholar
D. J. McGrailet al.,
“Differential mechanical response of mesenchymal stem cells and fibroblasts to tumor-secreted soluble factors,”
PLoS One, 7
(3), e33248
(2012). http://dx.doi.org/10.1371/journal.pone.0033248 1932-6203 Google Scholar
E. W. Taylor,
“Brownian and saltatory movements of cytoplasmic granules and the movement of anaphase chromosomes,”
in Proceedings of the Fourth International Congress on Rheology,
175
–191
(1965). Google Scholar
C. J. SchaapA. Forer,
“Temperature effects on anaphase chromosome movement in the spermatocytes of two species of crane flies (Nephrotoma suturalis Loew and Nephrotoma ferruginea Fabricius),”
J. Cell Sci., 39
(1), 29
–52
(1979). JNCSAI 0021-9533 Google Scholar
T. P. Koleet al.,
“Rho kinase regulates the intracellular micromechanical response of adherent cells to rho activation,”
Mol. Biol. Cell, 15
(7), 3475
–3484
(2004). http://dx.doi.org/10.1091/mbc.E04-03-0218 MBCEEV 1059-1524 Google Scholar
J. S. Leeet al.,
“Ballistic intracellular nanorheology reveals ROCK-hard cytoplasmic stiffening response to fluid flow,”
J. Cell Sci., 119
(9), 1760
–1768
(2006). http://dx.doi.org/10.1242/jcs.02899 JNCSAI 0021-9533 Google Scholar
T. P. Koleet al.,
“Intracellular mechanics of migrating fibroblasts,”
Mol. Biol. Cell, 16
(1), 328
–338
(2005). http://dx.doi.org/10.1091/mbc.E04-06-0485 MBCEEV 1059-1524 Google Scholar
J. S. Leeet al.,
“Nuclear lamin A/C deficiency induces defects in cell mechanics, polarization, and migration,”
Biophys. J., 93
(7), 2542
–2552
(2007). http://dx.doi.org/10.1529/biophysj.106.102426 BIOJAU 0006-3495 Google Scholar
P. Panorchanet al.,
“Microrheology and ROCK signaling of human endothelial cells embedded in a 3D matrix,”
Biophys. J., 91
(9), 3499
(2006). http://dx.doi.org/10.1529/biophysj.106.084988 BIOJAU 0006-3495 Google Scholar
X. Zhouet al.,
“Fibronectin fibrillogenesis regulates three-dimensional neovessel formation,”
Gene. Dev., 22
(9), 1231
–1243
(2008). http://dx.doi.org/10.1101/gad.1643308 GEDEEP 0890-9369 Google Scholar
B. R. DanielsB. C. MasiD. Wirtz,
“Probing single-cell micromechanics in vivo: the microrheology of C. elegans developing embryos,”
Biophys. J., 90
(12), 4712
–4719
(2006). http://dx.doi.org/10.1529/biophysj.105.080606 BIOJAU 0006-3495 Google Scholar
Y. Tsenget al.,
“Micro-organization and visco-elasticity of the interphase nucleus revealed by particle nanotracking,”
J. Cell Sci., 117
(10), 2159
–2167
(2004). http://dx.doi.org/10.1242/jcs.01073 JNCSAI 0021-9533 Google Scholar
E. L. BakerR. T. BonnecazeM. H. Zaman,
“Extracellular matrix stiffness and architecture govern intracellular rheology in cancer,”
Biophys. J., 97
(4), 1013
–1021
(2009). http://dx.doi.org/10.1016/j.bpj.2009.05.054 BIOJAU 0006-3495 Google Scholar
E. L. Bakeret al.,
“Cancer cell stiffness: integrated roles of three-dimensional matrix stiffness and transforming potential,”
Biophys. J., 99
(7), 2048
–2057
(2010). http://dx.doi.org/10.1016/j.bpj.2010.07.051 BIOJAU 0006-3495 Google Scholar
B. R. Danielset al.,
“Differences in the microrheology of human embryonic stem cells and human induced pluripotent stem cells,”
Biophys. J., 99
(11), 3563
–3570
(2010). http://dx.doi.org/10.1016/j.bpj.2010.10.007 BIOJAU 0006-3495 Google Scholar
C. Wilhelm,
“Out-of-equilibrium microrheology inside living cells,”
Phys. Rev. Lett., 101
(2), 028101
(2008). http://dx.doi.org/10.1103/PhysRevLett.101.028101 PRLTAO 0031-9007 Google Scholar
F. Galletet al.,
“Power spectrum of out-of-equilibrium forces in living cells: amplitude and frequency dependence,”
Soft Matter, 5
(15), 2947
–2953
(2009). http://dx.doi.org/10.1039/b901311c 1744-683X Google Scholar
C. M. HaleS. X. SunD. Wirtz,
“Resolving the role of actoymyosin contractility in cell microrheology,”
PloS One, 4
(9), e7054
(2009). http://dx.doi.org/10.1371/journal.pone.0007054 1932-6203 Google Scholar
Y. TsengT. P. KoleD. Wirtz,
“Micromechanical mapping of live cells by multiple-particle-tracking microrheology,”
Biophys. J., 83
(6), 3162
–3176
(2002). http://dx.doi.org/10.1016/S0006-3495(02)75319-8 BIOJAU 0006-3495 Google Scholar
P. H. Wuet al.,
“High-throughput ballistic injection nanorheology to measure cell mechanics,”
Nat. Protocol., 7
(1), 155
–170
(2012). http://dx.doi.org/10.1038/nprot.2011.436 NPARDW 1750-2799 Google Scholar
K. Luby-PhelpsD. L. TaylorF. Lanni,
“Probing the structure of cytoplasm,”
J. Cell Biol., 102
(6), 2015
–2022
(1986). http://dx.doi.org/10.1083/jcb.102.6.2015 JCLBA3 0021-9525 Google Scholar
S. S. Rogerset al.,
“Precise particle tracking against a complicated background: polynomial fitting with Gaussian weight,”
Phys. Biol., 4
(3), 220
–227
(2007). http://dx.doi.org/10.1088/1478-3975/4/3/008 1478-3975 Google Scholar
T. G. Mason,
“Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation,”
Rheol. Acta, 39
(4), 371
–378
(2000). http://dx.doi.org/10.1007/s003970000094 RHEAAK 0035-4511 Google Scholar
M. J. Saxton,
“Single-particle tracking: models of directed transport,”
Biophys. J., 67
(5), 2110
–2119
(1994). http://dx.doi.org/10.1016/S0006-3495(94)80694-0 BIOJAU 0006-3495 Google Scholar
|

