|
|
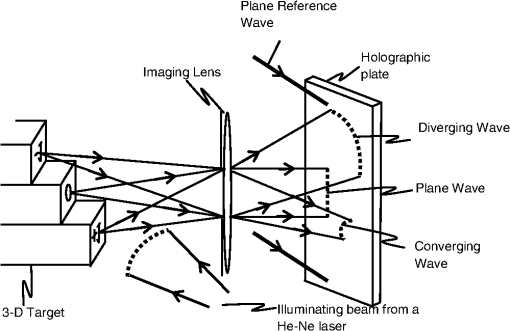
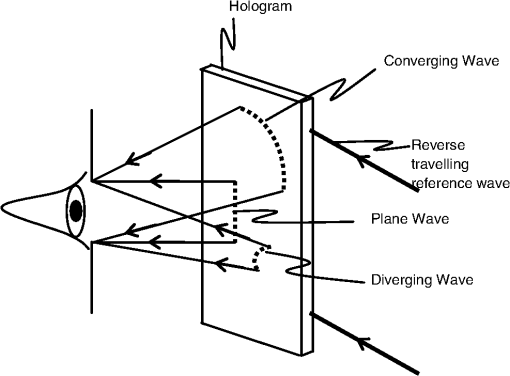
1.IntroductionRecently, we reported an investigation of the vision of spectacle corrected hyperopes and myopes viewing numbers of angular size in a hologram which was recorded using a multivergence target.1 In viewing through this hologram which is illuminated with light from a He-Ne laser, subjects see an array of positive and negative numbers placed at various distances from the eye. The negative numbers are seen in front of the eye as real objects and the positive numbers relate to virtual objects behind the eye. When the focusing error of a subject viewing through the hologram is corrected, he/she will see the number zero (which corresponds to a vergence of zero dioptres) clearly. The negative numbers will be seen clearly if the subject accommodates. However, positive numbers that correspond to positive vergence at the eye will appear blurred as one cannot exercise negative accommodation. When tested for the most positive blurred number recognized by corrected subjects, hyperopes were found to differ from myopes. Hyperopes could recognize numbers with 0.9 D more of positive blur in comparison with myopes. The most positive blur with which a subject can recognize a number is defined as the limiting blur of the subject in this study. There was no difference in the limiting blur when distance corrected subjects viewed characters at 6-m distance under white light illumination with positive lenses to blur at the eye in a phoropter. The observed difference in the limiting blur that was obtained with the multivergence hologram was then attributed to the multivergence nature of the target viewed through the hologram and/or the monochromaticity of the illumination used to view the hologram. To determine the role played by the multivergence target viewed through the hologram in the observed difference between hyperopes and myopes we repeated the experiment with the multivergence hologram, and conducted a second experiment in which subjects were tested with a hologram that contained the record of a logMAR chart at a single distance of infinity. Providing the logMAR chart at infinity in a hologram ensured that the illumination and viewing conditions remained the same as in our experiment with the multivergence hologram. Positive blur was introduced with lenses while subjects viewed through the logMAR hologram. The smallest letters recognized by the subjects were used to measure the vision of the subjects in logMAR units. Results from this experiment showed no difference in the vision of hyperopes and myopes. In this paper, we describe the experiments and the results obtained. 2.Experiment 12.1.The Hologram of a Multivergence TargetA multivergence target is recorded in a hologram. The target and the recording process are illustrated for three vergences in Fig. 1. The target consists of printed upside down mirror images of various numbers that are stuck on to the square ends of wooden rods in cross section as shown in Fig. 1. These rods are placed in front of a high power (20 D) lens such that different numbers are imaged at different predetermined distances from the lens. The numbers are then illuminated by coherent light from a He–Ne laser. The image forming wavefronts from the various numbers are recorded onto a holographic plate ( in size) placed close behind the lens, by interference with an off-axis plane reference wave derived from the same laser. The recorded hologram is then developed and bleached to yield a phase hologram that resembles a thin transparent glass plate. The recorded hologram contains the images of various numbers located at different distances from the lens. These images will be recreated at different distances from the hologram when the hologram is illuminated appropriately. Figure 2 illustrates the illumination and reconstruction of the images from the hologram when it is used in the experiment. It is well known that when the hologram is illuminated by the plane reference wave that was used while recording, the image forming wavefronts are regenerated. However, if the hologram is illuminated from behind by a plane reference wave traveling in the opposite direction, the phase conjugate of the recorded image forming wavefronts is regenerated in which the direction of propagation of each ray of the image forming wavefront is reversed. In testing vision using this hologram, the subject is made to place his or her eye at the same location relative to the hologram as was the imaging lens in the recording geometry. The hologram is illuminated from behind by the reverse travelling reference wave. When the hologram is thus illuminated, A subject viewing through this hologram sees the images of various numbers at different distances from the eye. The angular size of the images seen through the hologram is which corresponds to the angular size of “60-m” letters at 6-m distance. Sixteen wooden rods were used to make the three-dimensional target for Experiment 1 and the vergence range of the images seen through the hologram was designed to be in the range of to in steps of 0.5 D. Refer to our earlier publication for details of the target.1 2.2.Measurements with the Multivergence HologramTen myopes, 9 emmetropes, and 11 hyperopes were included in this study. The mean spherical refractive error for the myopes was in the range of to . Subjects with mean spherical refractive error in the range of to were considered as emmetropes. The mean spherical refractive error for the hyperopes was in the range of to . The subjects included in the study had little (0.25 D) or no astigmatism. Ethics approval was obtained from the Human Research Ethics Committee, UNSW. The spectacle correction for the subject was determined by subjective refraction using a phoropter. The maximum plus lens for best visual acuity was the criterion for the subjective end point. The best corrected visual acuity was or greater and the subjects had no significant pathology. For all the subjects, the right eye was occluded and the left eye was tested in the mesopic illumination of the clinic room. Distance (spectacle) corrected subjects are asked to view through the hologram as shown in Fig. 2. In looking through the hologram with the distance correction in place converging wavefronts reach the eye for the positive numbers. These numbers are therefore seen with positive blur. The subject is asked to call out all the numbers that he or she can recognize. The number with the most positive blur that is recognized by the subject is recorded for various subjects. The vergence corresponding to this number is used to obtain the limiting blur of the subject for the recognition of the numbers viewed through the hologram. 2.3.Results with the Multivergence HologramThe data obtained with the multivergence hologram for all the subjects in Experiment 1 are shown in Tables 1Table 2–3. Table 1The data obtained for the myopic subjects measured with the multivergence hologram.
Table 2The data obtained for the emmetropic subjects measured with the multivergence hologram.
Table 3The data obtained for the hyperopic subjects measured with the multivergence hologram.
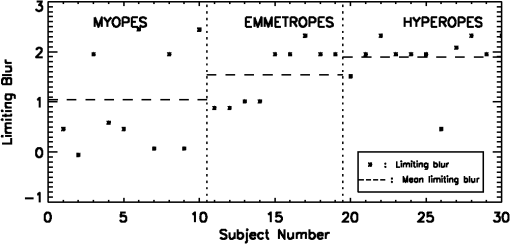
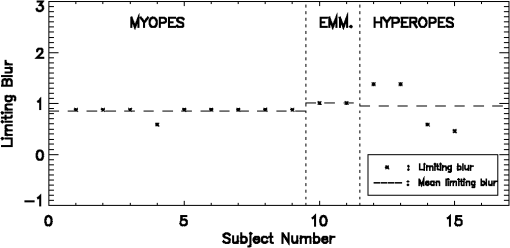
Figure 3 shows the limiting blur for all the subjects versus the subject number. The subject number was ordered according to the refractive error. Subject number 1 corresponds to the most myopic subject (on the left extreme of the -axis) and subject number 30 corresponds to the most hyperopic subject (on the right extreme of the -axis). Dashed vertical lines demarcate the refractive error groups. The horizontal dashed lines correspond to the mean values of the limiting blur that was obtained for each group. The mean limiting blur for myopes was 1.04 D with a standard deviation of 1.03 D while for hyperopes it was 1.89 D with a standard deviation of 0.53 D. Thus, the mean limiting blur for hyperopes was 0.85 D greater than that of myopes and this was statistically significant with a value of 0.02 obtained for unequal variances. The differences in the limit of positive blur with which distance corrected hyperopes and distance corrected myopes recognize the large high contrast letters viewed through the hologram is consistent with the results that were obtained on a larger group with a wider range in age and refractive error in our earlier investigation.1 As reported in our earlier investigation, some emmetropes responded like myopes while some others responded like hyperopes. The mean limiting blur for emmetropes was 1.54 D with a standard deviation of 0.34 D. The difference between the mean limiting blur of emmetropes and hyperopes and the difference between the mean limiting blur of emmetropes and myopes were not statistically significant. The value for the difference in the mean limiting blur of emmetropes and myopes was 0.2 and that for emmetropes and hyperopes was 0.19. As before1 there was poor correlation between the age and the limiting blur or the pupil size and the limiting blur for all subjects. The Pearson correlation coefficient in this study was 0.21 () for the age and the limiting blur and () for the pupil size and the limiting blur. 2.4.Effect of CycloplegiaTo investigate the role of accommodation on the results obtained with the multivergence hologram, nine myopic, two emmetropic, and four hyperopic eyes were tested under cycloplegia. One drop of cyclopentolate hydrochloride 1% was administered in the eye to be tested, with temporally punctual occlusion to minimize systemic absorption. One drop has been found to be effective for cycloplegic refraction whilst minimizing possible adverse effects.2,3 The pupil was checked after 40 min and all subjects showed reasonably dilated pupils. The refractive error of the eye under cycloplegia was then measured by subjective refraction using the criterion of maximum plus lens for the best visual acuity. The cyclopleged eye was provided with the mean sphere of the distance correction and the limiting blur for the eye was measured using the multivergence hologram, with the fellow eye occluded. The data obtained on the limiting blur under cycloplegia for the tested eyes are shown in Tables 4Table 5–6. Figure 4 shows the limiting blur for all the eyes tested under cycloplegia. The mean limiting blur obtained for myopes was 0.85 D with a standard deviation of 0.09 D and for hyperopes it was 0.95 D with a standard deviation of 0.50 D. The difference of 0.1 D in the mean limiting blur was not statistically significant ( for unequal variances). Variations in the limiting blur under cycloplegia for the hyperopic eyes tested appear to be an effect of pupil size. Table 4The data obtained with the multivergence hologram for the myopic eyes under cycloplegia.
Table 5The data obtained with the multivergence hologram for the emmetropic eyes under cycloplegia.
Table 6The data obtained with the multivergence hologram for the hyperopic eyes under cycloplegia.
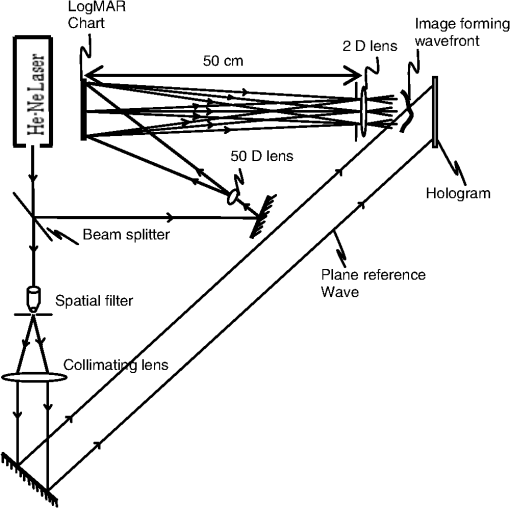
While there was hardly any difference in the limiting blur for all subjects under cycloplegia, the value of the limiting blur for all subjects was close to 1 D under cycloplegia as against the 2 D of limiting blur that was obtained in white light for all the subjects in our earlier investigation.1 This can be attributed to the reduced depth of focus and the effects of aberrations arising from the larger pupil size under cycloplegia. In Experiment 1, the average pupil size of all the subjects was 5.1 mm without cycloplegia and it was 7.1 mm in the investigation under cycloplegia. 3.Experiment 23.1.The Hologram of a logMAR Chart at InfinityFigure 5 shows the arrangement to record the logMAR hologram. A logMAR chart for a testing distance of 50 cm was used as the target in recording the hologram. The chart was illuminated with light from a He-Ne laser and imaged at infinity using a 2 D lens which has a focal length of 50 cm. A hologram of the image forming wavefront emerging from the lens was recorded by interference with a path matched plane reference wave derived from the same laser as shown in Fig. 5. The recorded hologram was developed and bleached to obtain the phase hologram of the logMAR chart at infinity. 3.2.Measurements with the LogMAR HologramTo measure various subjects using the logMAR hologram, the subject places his/her eye close to the hologram, and the hologram is illuminated as described in Experiment 1. The subject will then see the image of the logMAR chart at infinity. As plane waves reach the eye of the subject from the logMAR hologram, the position of the subject’s eye behind the hologram is not critical in this experiment. Subjects were asked to view through the logMAR hologram with a lens placed over the mean sphere of their spectacle correction. The smallest letters recognized in the logMAR chart seen through the hologram was used to measure their vision in the presence of of blur. The measurements were then repeated with a lens to blur. The visual acuity of the subjects without any lens to blur their vision was also measured using the logMAR hologram. Fourteen myopes, 17 emmetropes, and 11 hyperopes participated in this study. The subjects included in the study had little (0.25 D) or no astigmatism. The mean spherical refractive error for the myopes was in the range of to . The mean spherical refractive error for the hyperopes was in the range of to . Subjects with mean spherical refractive error in the range of to were considered as emmetropes. As before, the spectacle correction for the subject was determined by subjective refraction using a phoropter. The best corrected visual acuity was or greater and the subjects had no significant pathology. For all the subjects, the left eye was tested in the mesopic illumination of the clinic room. 3.3.Results Obtained with the LogMAR HologramThe data obtained using the logMAR holograms are shown in Tables 7Table 8–9. The average age and the pupil size of the various refractive groups are fairly close across Experiment 1 and Experiment 2 (see Table 10). Table 7The data obtained for the myopic subjects measured with the logMAR hologram.
Table 8The data obtained for the emmetropic subjects measured with the logMAR hologram.
Table 9The data obtained for the hyperopic subjects measured with the logMAR hologram.
Table 10Average age and pupil size of subjects in Experiment 1 and Experiment 2.
The visual acuity for all the subjects using the logMAR hologram with no lens to blur their vision is plotted against the subject number in Fig. 6. Fig. 6The logMAR values for all the subjects seeing through the hologram of the logMAR chart with no lens to blur. 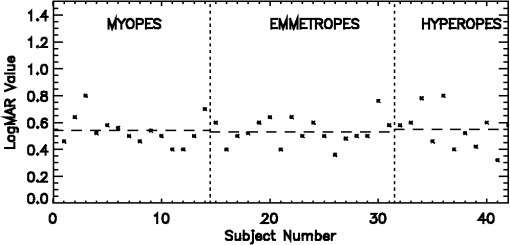 As before, the subject number is ordered according to the refractive error. The horizontal dashed lines correspond to mean values of the limiting blur for each group. The logMAR value of the mean vision of the subjects with no additional lens to blur their vision is around 0.55. There is no difference in the mean vision between the refractive groups. The difference in the mean vision of hyperopes and myopes is 0.01 in logMAR units with a value of 0.84. With a lens to blur, the logMAR value of the mean vision for all the subjects is close to 0.86 logMAR and there is no difference in the vision between the refractive error groups (Fig. 7). With a lens to blur, the vision falls by about 0.3 logMAR for all refractive groups as compared to the vision with no lens to blur. The difference in the mean vision of hyperopes and myopes is 0.01 logMAR with a value of 0.95. The results with the logMAR hologram are summarized in Table 11. Fig. 7The logMAR values for all the subjects seeing through the hologram of the logMAR chart with blur. 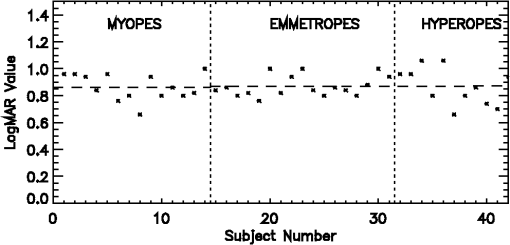 Table 11Summary of the results with the hologram of a logMAR chart at infinity.
The topmost line of the logMAR chart in the hologram corresponds to a logMAR value of 1.0 and the angular size of the letters in this line is . With a lens to blur, some of the subjects in each refractive group could read a few letters from this line while some others could not read any letter from this line. The logMAR value for the vision of the subjects who could not read any letter from this line is . From Tables 7 and 9, one can see that the response of myopes and hyperopes is similar with a lens to blur. 4.DiscussionAs in our earlier study,1 results obtained from Experiment 1 indicate that when a multivergence target is presented through a hologram, distance corrected hyperopes recognize large characters with more positive blur (0.85 D) than distance corrected myopes. The maximum positive blur under which a fixed size character is recognized through the multivergence hologram is used to compare the vision of hyperopes and myopes in this experiment. In Experiment 2, when the blur is provided with a positive lens to distance corrected subjects viewing a logMAR chart at a single distance of infinity in a hologram there is no difference in the vision between hyperopes and myopes. In this experiment, vision is compared using the logMAR values corresponding to the smallest size character that can be recognized in the logMAR hologram. A blur relates to a readability of three lines in the logMAR hologram (0.3 in logMAR units). In both experiments subjects view through a hologram which is illuminated by a plane reference wave from a He–Ne laser. However, a difference in the vision of hyperopes and myopes was obtained in Experiment 1, whereas in Experiment 2 no difference was seen in the vision of hyperopes and myopes. In Experiment 2, as many myopes as hyperopes could recognize large characters with blur, while this was not the case in Experiment 1. As the logMAR hologram provides a target at a single distance of infinity while the multivergence hologram provides targets at various distances from the eye, the observed difference in the vision between hyperopes and myopes in Experiment 1 may be seen as due to an effect that is similar to the Mandelbaum effect.4 In the Mandelbaum effect subjects viewing a distant target through an intervening screen fail in trying to focus on the distant target if the screen is at a certain distance from the subject and in fact find themselves focusing involuntarily on the screen. The distance at which this occurs is different for different subjects. When presented with a pair of stimuli separated dioptrically by 2 D at various distances from the eye, Owens5 found that the subjects had a tendency to involuntarily focus on the target that is closer to the location of the dark focus of the subject indicating that the Mandelbaum effect is due to a response bias of the accommodative system. The dark focus of accommodation is also addressed in the literature as the resting state of accommodation or tonic accommodation.6–9 In our current study with the multivergence hologram, the vergence range of the images seen through the hologram was between and in steps of 0.5 D. Distance corrected myopes were able to recognize large numbers, with only up to of blur in the hologram of this multivergence target. This was not the case, however, with the distance corrected hyperopes who were able to recognize numbers having up to of blur in the multivergence hologram. When presented with a distant test chart in white light, both these groups were able to recognize large characters with around of blur.1 So, it appears that the presence of the number with vergence in the multivergence hologram is influencing the myopes to recognize numbers having only up to of vergence in the multivergence hologram. It is as if they are involuntarily focusing onto the number having vergence and are recognizing the number having vergence tolerating of blur in the limit. Whereas it appears that distance corrected hyperopes focus onto the number having 0 D vergence and recognize the number having vergence tolerating of blur in the limit. Essentially, it appears that an effect similar to the Mandelbaum effect manifested in the vision of the subjects. When presented with a multivergence target in a hologram which provides stimuli at various distances, myopes tend to focus on the near stimulus (number at 1-m distance) and hyperopes tend to focus on the distant stimulus (number at infinity). Perhaps distance corrected myopes are drawn by the Mandelbaum-like effect to focus on the number with vergence which would be close to their resting state of accommodation. Although the resting state of accommodation of hyperopes is known to be larger than that of myopes,6,7 distance corrected hyperopes tend to focus on the number with 0 D vergence in viewing through the multivergence hologram. This seems to suggest that the vision of hyperopes is influenced by their latent hyperopia in viewing through the multivergence target. We had observed this Mandelbaum-like effect in our earlier study too, with the multivergence target in a hologram having numbers as targets in the vergence range of to .10 In trying to measure the amplitude of accommodation of college age subjects using the multivergence hologram we found that distance corrected subjects could not accommodate to see some of the closer numbers which were well within the range of their clear vision, in spite of exercising their will. When presented with the stimulus of a near letter chart in white light close behind the hologram (at 40 cm from the subject’s eye), the accommodation of the subjects was triggered and they were able to read these numbers. It was very striking that without the near stimulus the young subjects could not recognize numbers of angular size around projected within their normal range of clear vision (at 20 to 25 cm from the eye). There is controversy in the literature regarding the existence and explanation of the Mandelbaum effect.11,12 Our observations with the multivergence hologram are consistent with Owen’s findings5 described earlier in this section and suggest that the Mandelbaum effect exists and manifests itself strongly under certain viewing conditions. Leibowitz and Owens13 have shown in the past that phenomena such as night myopia, empty field myopia, and instrument myopia correlate highly in magnitude to the dark focus. It would be interesting to measure the dark focus of individual subjects and see how it relates to their limiting blur. The hologram of a multivergence target with an extended negative and positive vergence range can be used to measure the refractive state of the eye.10 In this measurement, an uncorrected eye viewing a distant fixation target in white light is presented briefly (in flashes of about 1 s duration) with the multivergence hologram and the most positive number seen clearly by the subject gives a measure of his/her refractive error.10 When a spectacle corrected eye is presented with such a multivergence hologram in total darkness, we believe that the clearest number seen would give a measure of his/her dark focus. Looking more closely at the results of Experiment 2 with the logMAR hologram, a mean vision of 0.55 logMAR for the distance corrected subjects is much worse than the visual acuity that is obtained under white light illumination. The reduced visual acuity may be attributed to the coherent nature of the laser light illuminating the hologram.14 The range of the measured values of the visual acuity with the logMAR hologram is 0.48 in logMAR units. As we recruited subjects with vision better than in white light the expected range for the spread in the visual acuity is about 0.4 logMAR units (between and i.e., to ). If instrument myopia played a role in measuring vision using the logMAR hologram, the measured vision of all the subjects would be correlated to the age, as instrument myopia is an accommodation related phenomenon. However, the Pearson correlation coefficient between the age and the logMAR value of the vision for all the subjects was small (, , see Table 12). Interestingly, there was no correlation between the age and the logMAR value of the vision for myopes (, ) while the correlation between the age and the logMAR value of the vision for hyperopes was strong (, ). The negative sign for obtained for hyperopes implies that younger hyperopes had poorer vision in viewing through the logMAR hologram with their distance correction than the older hyperopes. It is known that when a distance correction is provided to hyperopes some latent accommodation remains in play. As the distance corrected vision through the logMAR hologram is worse for younger hyperopes as compared with the older hyperopes, this seems to suggest that the latent hyperopia is in play when hyperopic subjects view through the logMAR hologram. This is consistent with our initial findings reported in our earlier paper10 that it may be possible to get a measure of hyperopia without the intervention of latent accommodation using the multivergence hologram. Table 12The Pearson correlation coefficient between the age and vision, and the pupil size and vision for distance corrected subjects viewing through the logMAR hologram.
Table 12 also lists the Pearson correlation coefficient between the pupil size and the logMAR value for various refractive groups. A moderate level of negative correlation (, ) between the pupil size and the logMAR value for myopes implies that vision improves as the pupil size increases. This suggests a lack of blur in the vision of the distance corrected myopes viewing through the logMAR hologram. Similarly, a medium level of positive correlation between the pupil size and the logMAR value for hyperopes (, ) implies that vision decreases with an increase in pupil size. This implies that there is a presence of blur in the vision of distance corrected hyperopes which may be attributed to the latent accommodation not being in play. This is substantiated by the result for obtained when the four older hyperopes in the age range of 48 to 53 were excluded. The for the seven remaining younger hyperopes in the age range of 9 to 43 years turned out to be (). Perhaps, the difference between the visual acuity of a hyperope measured in white light and measured with the logMAR hologram would give an estimate of his/her latent hyperopia. We plan to pursue this in our next study. 5.ConclusionsThe results of the experiments described in this paper suggest that when distance corrected myopes and hyperopes are presented with a multivergence target in a hologram that contains images with negative and positive vergences, an effect similar to the Mandelbaum effect, affects the vision of the subjects. The results from the current study show that there is no difference in the mean logMAR values of the vision of various refractive groups when tested with a logMAR chart at infinity in a hologram. A spinoff from this study is the logMAR chart at infinity recorded in a hologram. With further experimentation and using larger characters it may be possible to standardize and calibrate the logMAR hologram to measure the visual acuity of myopes and to predict/estimate the latent hyperopia of hyperopes. It could be made compact, portable, and inexpensive by using a laser diode for illumination. In total darkness the multivergence hologram may prove to be useful in the measurement of the dark focus. AcknowledgmentsThis research was partly supported by the Australian PostGraduate Award which was granted to Nicholas Nguyen to carry out this work. ReferencesN. NguyenC. S. AvudainayagamK. V. Avudainayagam,
“An experimental investigation of the vision of hyperopes and myopes using a hologram,”
Biomed. Opt. Express, 3
(6), 1173
–1181
(2012). http://dx.doi.org/10.1364/BOE.3.001173 BOEICL 2156-7085 Google Scholar
A. Bagheriet al.,
“Optimal dosage of cyclopentolate 1% for complete cycloplegia: a randomized clinical trial,”
Eur. J. Ophthalmol., 17
(3), 294
–300
(2007). EJOOEL 1120-6721 Google Scholar
T. HugS. Olitsky,
“Dilation efficacy: is 1% cyclopentolate enough?,”
Optom. J. Am. Optom. Assoc., 78
(3), 119
–121
(2007). http://dx.doi.org/10.1016/j.optm.2006.06.018 JAOPBD 0003-0244 Google Scholar
J. Mandelbaum,
“An accommodation phenomenon,”
AMA Arch. Ophthalmol., 63
(6), 923
–926
(1960). http://dx.doi.org/10.1001/archopht.1960.00950020925005 AAOPAF 0096-6339 Google Scholar
D. A. Owens,
“The Mandelbaum effect: evidence for an accommodative bias towards intermediate viewing distances,”
J. Opt. Soc. Am., 69
(5), 646
–652
(1979). http://dx.doi.org/10.1364/JOSA.69.000646 JOSAAH 0030-3941 Google Scholar
N. A. McBrienM. Millodot,
“The relationship between tonic accommodation and refractive error,”
Invest. Ophthalmol. Visual Sci., 28
(6), 997
–1004
(1987). IOVSDA 0146-0404 Google Scholar
J. RosnerJ. Rosner,
“Relation between clinically measured tonic accommodation and refractive status in 6- to 14-year-old children,”
Optom. Vis. Sci., 66
(7), 436
–439
(1989). http://dx.doi.org/10.1097/00006324-198907000-00005 OVSCET 1040-5488 Google Scholar
R. J. Maddocket al.,
“Accommodation responses and refractive error,”
Invest. Ophthalmol. Visual Sci., 20
(3), 387
–391
(1981). IOVSDA 0146-0404 Google Scholar
M. TakashiT. Takashi,
“Relation between the dark focus of accommodation and refractive error—a cycloplegic study,”
Optom. Vis. Sci., 70
(4), 328
–331
(1993). http://dx.doi.org/10.1097/00006324-199304000-00012 OVSCET 1040-5488 Google Scholar
K. V. Avudainayagamet al.,
“Performance of the holographic multivergence target in the subjective measurement of spherical refractive error and amplitude of accommodation of the human eye,”
J. Opt. Soc. Am. A, 24
(10), 3037
–3044
(2007). http://dx.doi.org/10.1364/JOSAA.24.003037 JOAOD6 0740-3232 Google Scholar
R. L. StarkD. A. Atchison,
“Effect of an intervening screen on accommodation to a distant object,”
Clin. Exp. Optom., 81
(3), 119
–130
(1998). http://dx.doi.org/10.1111/cxo.1998.81.issue-3 0816-4622 Google Scholar
M. RosenfieldK. J. Ciuffreda,
“Effect of surround propinquity on the open-loop accommodative response,”
Invest. Ophthalmol. Visual Sci., 32
(1), 142
–147
(1991). IOVSDA 0146-0404 Google Scholar
H. W. LeibowitzD. A. Owens,
“Anomalous myopias and the intermediate dark focus of accommodation,”
Science, 189
(4203), 646
–648
(1975). http://dx.doi.org/10.1126/science.1162349 SCIEAS 0036-8075 Google Scholar
J. M. ArtigasA. Felipe,
“Effect of luminance on photopic visual acuity in the presence of laser speckle,”
J. Opt. Soc. Am. A, 5
(10), 1767
–1771
(1988). http://dx.doi.org/10.1364/JOSAA.5.001767 JOAOD6 0740-3232 Google Scholar
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||