|
|
1.IntroductionSelective removal of subgingival dental calculus is a preferred treatment method in nonsurgical periodontal therapy. While complete removal of calculus and disease-causing agents (i.e., oral bacteria) is of primary importance, leaving behind a hard tissue surface less prone to bacterial accumulation is also important. Grooves and craters resulting from conventional cleaning measures provide sites for future bacteria and calculus crystals to form and accumulate.1 Healthy cementum should be preserved to allow for the possibility of reattachment through fibroblasts.2,3 A weak attachment could lead to subsequent reoccurrence of periodontal problems. Conventional methods to remove calculus typically depend upon the experience of the clinician4,5 and other treatment factors.1 Unintentional damage can easily occur using hand instruments6 and power-driven scalers (e.g., ultrasonic and air-abrasion)7 causing grooves and/or excessive cementum removal. In addition, mechanical root scaling usually leaves behind a smear layer containing harmful bacteria, infected cementum, and calculus debris.8,9 A recent in vitro scanning electron microscope (SEM) study examined hard tissue surfaces following calculus removal with conventional treatments (e.g., hand instruments, ultrasonic scaling, and Er:YAG laser treatment) and found grooves and unintentional hard tissue removal.10 Currently, the Er:YAG laser ()11 is the only commercially available laser with significant experimental and clinical studies for dental hard tissue removal.1 Hard-tissue (enamel, dentin, and cementum) ablation at this wavelength relies on absorption by water,12 so calculus ablation is not selective. A review of several clinical studies13 and a recent meta-analysis14 concluded that the clinical outcome of calculus removal using the Er:YAG laser is similar to conventional mechanical debridement. The frequency-doubled Alexandrite (FDA) laser at can selectively remove plaque, caries, and calculus without damaging the underlying and surrounding hard tissue. The results of several studies investigating the FDA laser for selective removal are summarized in Ref. 15. The ablation mechanism is assumed to be based upon absorption by haemins (i.e., iron-containing porphyrins) into the Soret band.16,17 Iron-containing porphyrins are found in some oral bacteria in dental plaque and dental calculus.18,19 However, the inconsistent pulse shape and power output of the FDA laser has not allowed for more detailed studies. Recently, a frequency-doubled Ti:sapphire laser () was developed to allow for a more detailed analysis of dental calculus ablation in the near-ultraviolet (NUV: 300 to 400 nm).20 Compared with conventional calculus removal treatments, removal of dental calculus21,22 using this laser is complete and selective without any removal of pristine dental hard tissue.10,23 Mature extrinsic enamel stains are also selectively removed with this laser.24 For incident laser fluences close to the calculus ablation threshold (between 1 and ), ablation stalling is frequently encountered. Stalling is not observed at fluences well above the ablation threshold (6 to ). This paper uses a variety of experimental diagnostics to study the ablation mechanism of dental calculus at 400 nm and compare the results with predictions made by heuristic ablation models. Laser profilometry measures volume and depth of calculus ablated for different irradiation conditions. Blue-light microscopy and fluorescence spectroscopy identify photobleaching during calculus ablation. Together these diagnostics allow identification of a heuristic, modified ablation blow-off model to explain the experimental observations. Finally, the effect of tooth sterilization prior to laser irradiation is assessed by comparing removal rates of gamma-ray–sterilized and unsterilized calculus samples at the same incident fluence. All of this information is used to propose a mechanism for calculus ablation at 400 nm. 2.Heuristic Ablation Models2.1.Standard Blow-Off ModelIn the standard blow-off model, a common heuristic model is used to predict tissue ablation,25 Beer’s law is assumed to govern energy deposition into calculus. In this model, deposited energy densities exceeding the ablation threshold energy density, , cause calculus removal. The threshold energy density is typically a constant25,26 related to the enthalpy of ablation for calculus. The absorption coefficient, , is assumed to remain constant during irradiation and scattering is assumed to be negligible. For the standard blow-off model, is given by where is the incident fluence (in ) and is the fluence at depth . Ablation occurs over the etch depth if . Beyond the etch depth, tissue is not ablated but merely heated since the deposited energy density is below the ablation threshold. The fluence at the etch depth is the ablation threshold fluence and for the etch depth is found from Eq. (1) to be2.2.Modified Blow-Off ModelSince a photobleached surface layer is observed after 400-nm irradiation,20 a model that assumes the absorption coefficient to decrease during the laser pulse may be better suited for predicting calculus removal rates. Such a modified blow-off model was originally proposed for photoablation of polymethyl methacrylate in the deep ultraviolet.26 During photoablation, the number density of chromophores, , decreases as absorbed UV photons break chemical bonds and reduce absorption of subsequent photons.27,28 Permanent photochemical damage of the chromophores from photobleaching similarly decreases during laser irradiation. The derivation for the modified blow-off model is found in Ref. 26 where the approximate etch depth , for the fluences used in this paper, is determined to be where is Planck’s constant and is the laser frequency. The etch depth depends linearly on as opposed to the logarithmic dependence in Eq. (2) for the standard model. The full expression for Eq. (3) is found in Ref. 26. The chromophore number density is related to the absorption coefficient by where is the absorption cross section of the chromophore. The deposited energy density is approximately constant for and is given asEquation (4) indicates that the deposited energy is limited by the chromophore number density of the tissue within the etch depth. The deposited energy density for both blow-off models is plotted as a function of depth is based on the data in Table 1. A layer consisting of partially photobleached chromophores is located beyond the etch depth in Fig. 1(b). Table 1Absorption coefficients, threshold fluences, and chromophore number densities for the standard and modified blow-off models obtained from removal rates in Fig. 8.
Fig. 1Deposited energy density as a function of depth in calculus based upon the (a) standard and (b) modified blow-off models. The incident fluence is . The curves are based upon data in Table 1. In (a) and in (b) . 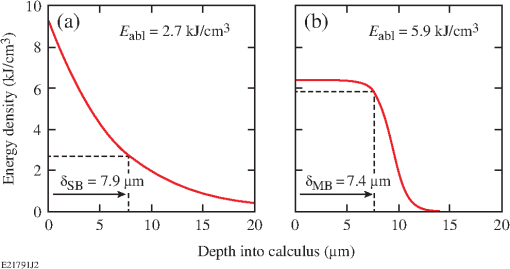 2.3.Volume Removal RatesThe etch depths in Eqs. (2) and (3) can be used to calculate volume removal rates for each blow-off model. Assuming an ’th-order super-Gaussian fluence distribution, we find with peak fluence and beam width . Substituting Eq. (5) into Eqs. (2) and (3) one obtains a radial distribution of the etch region. Scattering is assumed to be negligible compared with absorption. The volume removal rate is found by integrating over the entire volume irradiated at fluences . The volume removal rate per pulse for the standard blow-off model isThe volume removal rate predicted by the modified blow-off model is where is the energy efficiency for selective ablation used in Ref. 20 and is the gamma function. For the purposes of this study, , , , , and , resulting in and , where is in units of , is in units of , and is in units of .3.Materials and Methods3.1.Tooth SamplesTwenty extracted human teeth exhibiting calculus, equally divided between sub- and supragingival calculus, were obtained from the Department of Preventive and Restorative Dental Sciences, School of Dentistry at the University of California, San Francisco. They were sterilized with gamma radiation and stored at room temperature in a 0.1% thymol solution. Supragingival calculus was defined as being located on the anatomic crown (above the cementoenamel junction) whereas subgingival was defined as being located on the anatomic root (below the cementoenamel junction). Ten extracted, unsterilized human teeth with subgingival calculus were obtained from the Eastman Institute for Oral Health at the University of Rochester (Rochester, New York) and stored at room temperature in a saline solution. Calculus deposits on all of the teeth were of mixed coloration (e.g., yellow to dark brown). 3.2.Experimental SetupA frequency-doubled Ti:sapphire laser (400-nm wavelength, 60-ns pulse duration, 10-Hz repetition rate, and 25-mJ pulse energy) was developed for selective calculus ablation and has been described elsewhere.20 Laser radiation was coupled into a 600-μm-core-diameter optical fiber with a 1.8-mm-diameter tapered input (FVPE600660710/2M, Polymicro Technologies, Phoenix, Arizona) using a engineered diffuser (RPC Photonics, Rochester, New York) and an lens [Fig. 2(a)]. This fiber-coupling scheme, along with fiber coiling, efficiently mixes the many transverse fiber modes (thousands) creating a near top-hat envelope at the fiber output. This fiber output was then imaged onto the dental hard tissue using an objective resulting in a measured, -diameter, 10th-order super-Gaussian spot on the calculus surface21 after averaging over the underlying speckle pattern. This irradiation configuration was chosen to facilitate experimental observations. The peak fluence of each pulse was varied between 1.7 and () by varying the laser pulse energy. All tooth surfaces were irradiated at normal (perpendicular) incidence to the surface. (Similar ablation studies using oblique incidence were reported in Ref. 21.) Fig. 2(a) Experimental setup for tooth irradiation with the 400-nm laser and for blue-light microscopy. (b) Hard tissue fluorescence between 600 and 800 nm was excited at 400 nm and coupled into an optical fiber leading to a USB spectrometer. 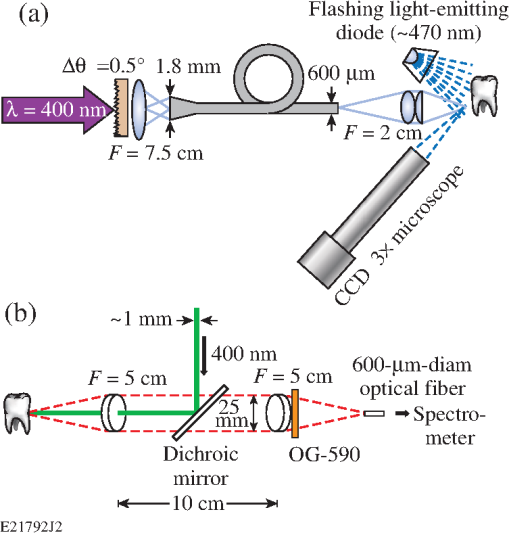 During laser irradiation, the tooth samples were sprayed with a water/air mixture at . The effect of this water spray on the intensity distribution of the irradiation laser at the tooth surface was reported in Ref. 20. After five laser pulses, excess water was gently blown off the tooth samples using an air spray to allow for the diagnostic imaging (i.e., laser profilometry and blue-light microscopy) described below. 3.3.Laser ProfilometryThe depth and volume of calculus removed was measured using a laser profilometer. A HeNe laser at (Model LHGR-0050, PMS Electro-Optics, Boulder, Colorado) was focused to a line onto the tooth surface using an -cylindrical lens and then scanned across the irradiated region before and after laser irradiation. The line was magnified (VMZ450i, Edmund Industrial Optics, Barrington, New Jersey) by imaging onto a charge-coupled device camera (TM-1020A-15CL, JAI, San Jose, California) oriented at 45 deg, resulting in an axial resolution of . The transverse resolution was . Depth-removal maps were found by taking the difference between three-dimensional (3-D) surface images taken before and after irradiation (as described in Ref. 21). Calculus removal rates were determined by irradiating in 5-pulse increments using a remotely operated shutter in the laser cavity. Single-pulse (S.P.) removal rates are calculated from the depth/volume removed by five laser pulses and dividing by the number of pulses, whereas the average removal rates are calculated from the total depth/volume removed. The uncertainty of the average removal rate was based on the uncertainty in the 3-D surface images. The main uncertainty arose from laser speckle and the high of the observation lens. 3.4.Blue-light MicroscopySince calculus is a strong absorber of blue light, microscopy with illumination in this wavelength range ( to 490 nm) was used to provide high contrast images between dental calculus and healthy hard tissue (enamel, dentin, and cementum). Different illumination wavelengths are compared in Fig. 3 where blue-light illumination was found to provide the best contrast between calculus and pristine hard tissues. Images of teeth before and after laser irradiation were taken with illumination from a flashing blue light-emitting diode (LED) using the same camera used in laser profilometry, as shown in Fig. 2(a). Identical images were obtained when illuminating with a 400-nm light source. Blue-light microscopy also serves to qualitatively distinguish unbleached from photobleached calculus, since the latter appears brighter under blue-light microscopy due to increased scattering and decreased absorption. Fig. 3Dental calculus (nonbleached: red arrow, photobleached: blue arrow) along the cementoenamel junction viewed with a microscope at illumination wavelengths in the range of (a) 450 to 490 nm, (b) 490 to 520 nm, (c) 612 to 640 nm, and (d) 570 to 880 nm. The light sources in (a) to (c) are flashing light-emitting diodes synchronized with the camera whereas (d) is a continuous broadband white-light source. The microscope was refocused in each image.  3.5.Fluorescence SpectroscopyFluorescence spectroscopy was used to compare the fluorescence of unbleached calculus with that of photobleached calculus and sound dental hard tissue. The fluorescence was excited with low pulse energy ( at 400 nm, 200 ns) over a 50-μm-beam spot. Fluorescence spectra were recorded between 600 and 800 nm using image relaying, an OG590 filter and a universal serial bus (USB) spectrometer (HR2000CG-UVNI, Ocean Optics, Dunedin, Florida) as shown in Fig. 2(b). In this spectral range, one can discriminate between dental hard tissue and calculus due to fluorescence from bacterial porphyrins between 615 and 725 nm29 found in plaque, caries, and dental calculus. At each measurement, 50 spectra were collected with a 10-s integration time, averaged, and smoothed by applying an spectral averaging filter. 3.6.Scanning Electron MicroscopySEM was used to obtain high-resolution images of laser-irradiated hard tissue surfaces and also to discriminate calculus from enamel, dentin, and cementum. The laser-treated areas were examined using an SEM (Zeiss-Auriga CrossBeam FIB-SEM, Carl Zeiss NTS, Peabody, Massachusetts) at the Institute of Optics, University of Rochester. The tooth surface topology was examined using an SE2 detector and 10-keV electron beam with a 30-μm aperture and working distance. The teeth were dried in a desiccator for at least 24 h. An -gold layer was subsequently sputtered onto the tooth surface. 4.ResultsBlue-light microscope images show nonsterilized subgingival calculus removed at [Figs. 4(a)–4(f)] within the irradiation beam (dashed red lines). After 30 pulses, the calculus is completely removed and the underlying cementum is reached [Fig. 4(f)]. No ablative stalling was observed, but irradiated calculus appears brighter compared with nonirradiated calculus, indicating a photobleached surface layer. Differential depth removal maps [Figs. 4(g)–4(k)] are shown below the microscope images. Average depth and volume removal rates for all nonsterilized calculus samples are and . Identical results are found for ablating-sterilized subgingival calculus21 at the same fluence and irradiation angle. Fig. 4Blue-light microscope images of nonsterilized subgingival calculus irradiated at (a) before and after (b) 5, (c) 10, (d) 15, (e) 20, and (f) 30 irradiation pulses. Differential removal maps from (g) 0 to 5, (h) 5 to 10, (i) 10 to 15, (j) 15 to 20, and (k) 20 to 30 irradiation pulses correspond to the above light microscope images. Red dashed circles outline the irradiation area. 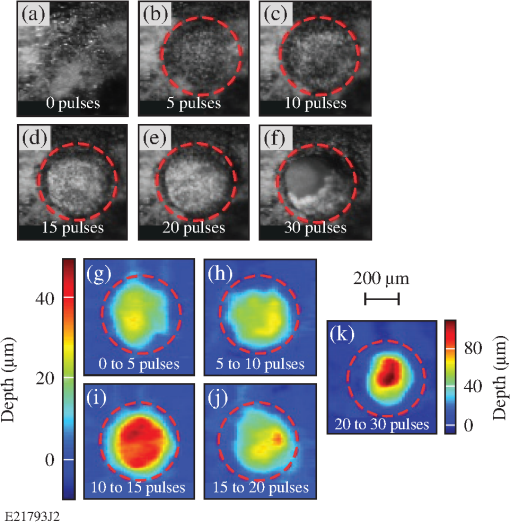 Subgingival calculus sterilized with gamma radiation is irradiated at for a total of 25 irradiation pulses (Fig. 5). Blue-light microscope images are shown in five-pulse increments [Figs. 5(a)–5(f)] where irradiated calculus is photobleached. Shadowing in the light microscope images in Figs. 5(e) and 5(f) is due to the steep angle of incidence of the LED illumination relative to the tooth surface. Differential depth removal maps are shown below the light microscope images in Figs. 5(g)–5(k). For this tooth sample, calculus is removed at a rate of and . Fig. 5Blue-light microscope images of sterilized subgingival calculus irradiated at (a) before and after (b) 5, (c) 10, (d) 15, (e) 20, and (f) 25 irradiation pulses. Differential removal maps from (g) 0 to 5, (h) 5 to 10, (i) 10 to 15, (j) 15 to 20, and (k) 20 to 25 irradiation pulses correspond to the above light microscope images. Red dashed circles outline the irradiation area. 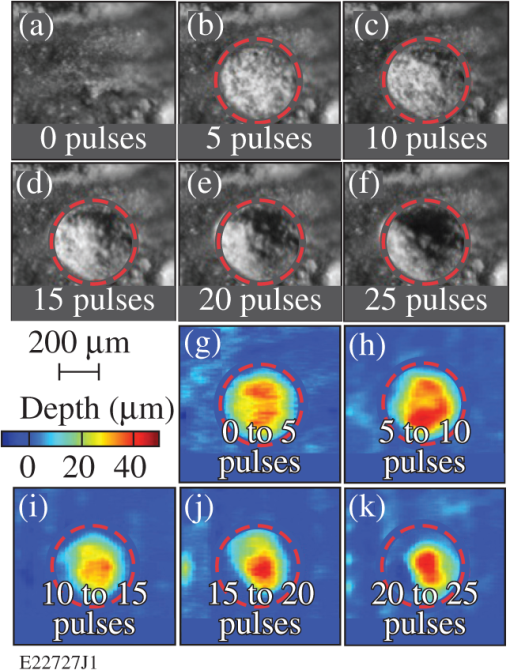 The blue-light microscope images before and after irradiation [Figs. 6(a) and 6(b)] indicate that a layer of calculus is removed but that a photobleached calculus surface layer remains [blue arrow in Fig. 6(b)]. Ablation stalls, and further irradiation at this fluence does not remove any additional calculus. Fig. 6Blue-light microscope images of supragingival calculus on enamel (a) before and (b) after 40 passes at and at using a -diameter, 6th-order super-Gaussian beam. This corresponds to superposed irradiation pulses per pass along the center on any given spot. The dashed yellow lines outline the irradiation path. (c) Fluorescence spectra of enamel, unbleached and photobleached calculus using a 400-nm excitation wavelength. (d) Normalized fluorescence spectra corresponding to (c). Colored arrows in (a) and (b) correspond to the spectra in (c) and (d) (i.e., red arrow: unbleached calculus, black arrow: enamel and blue arrow: photobleached calculus). 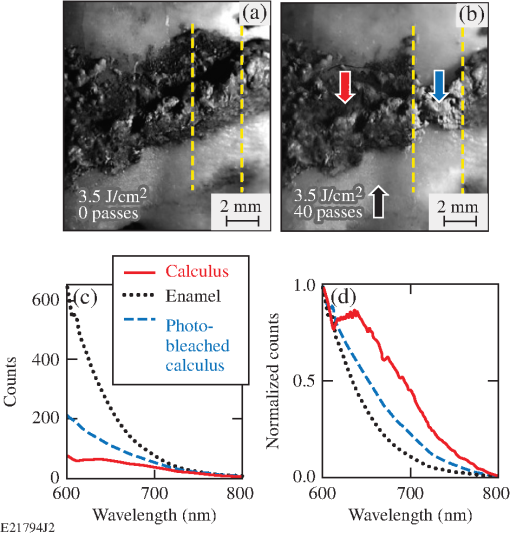 Fluorescence spectra between 600 and 800 nm, excited at 400 nm, of enamel (black arrow), nonirradiated calculus (red arrow), and irradiated calculus (blue arrow) in Fig. 6(b) are shown in Fig. 6(c). The fluorescence spectrum of irradiated calculus resembles the spectrum of enamel in shape, emitting more fluorescence photons than unbleached calculus [Fig. 6(c)]. Each spectrum is normalized in Fig. 6(d) to magnify the detail in spectra between 615 and 725 nm. Removing the OG590 filter in the fluorescence setup allowed measurement of the scattered/reflected signal at 400 nm. Photobleached calculus and enamel scattered twice as much 400-nm light into the collection optics as did unbleached calculus. The exact amount of 400-nm light scattered by photobleached calculus varies from tooth to tooth and can equal that for sound enamel. Laser-irradiated subgingival calculus is investigated under the SEM in Fig. 7(a). For comparison, the surface of nonlaser-irradiated calculus is observed under SEM in Fig. 7(b). Blue-light microscope images (not shown) of the irradiated calculus surface in Fig. 7(a) indicate that it is photobleached. Any change in the calculus surface roughness after laser ablation was below the resolution of the laser profilometer. Fig. 7SEM images of (a) laser-irradiated (, 25 pulses) and (b) nonlaser-irradiated gamma-ray-sterilized subgingival calculus. Red arrows in (a) and (b) indicate representative craters found in the calculus surface.  Average depth and volume removal rates for gamma-ray-sterilized sub- and supragingival calculus are plotted as a function of incident fluence in Fig. 8. Both removal rates increase linearly with increasing incident fluence and are indistinguishable (within the error bars) for sub- and supragingival calculus. The absolute error in depth and volume removal rates increases with fluence in Fig. 8 but the relative error actually decreases. Depth removal rates in Figs. 8(a) and 8(b) are fitted to Eqs. (2) and (3). The results from these fits are summarized in Table 1. The error bars render , , and indistinguishable for both types of calculus. The relevant tissue parameters in Table 1 are substituted into Eqs. (6) and (7) and plotted in Figs. 8(c) and 8(d) as predicted volume removal rates for sub- and supragingival calculus, respectively. The modified blow-off model overestimates the volume removal rate whereas the standard model underestimates it. Fig. 8Fluence-dependent depth removal rates for sterilized (a) subgingival and (b) supragingival calculus and corresponding volume removal rates (c) and (d). Short-dashed and solid lines correspond to fits using the standard and modified blow-off models, respectively. Black long-dashed lines in (c) and (d) are a linear regression through the data. 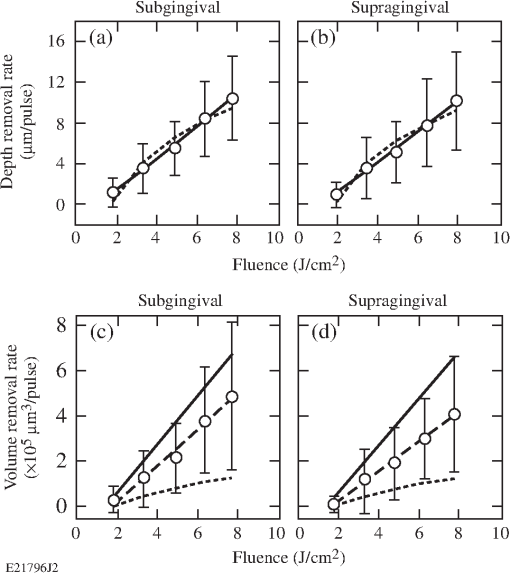 The S.P. depth and volume removal rates at for either subgingival [Figs. 9(a) and 9(c)] or supragingival [Figs. 9(b) and 9(d)] calculus sterilized with gamma radiation show similar trends with the number of incident pulses. The S.P. removal rates of sub and supragingival calculus at fluences from 3.5 to exhibit similar behavior. The change in ablated area for sub- and supragingival calculus [Figs. 9(e) and 9(f)] is found by dividing the S.P. volume removal rates by the S.P. depth removal rates in Fig. 9. The ablated area also decreases with increasing number of incident pulses. There is no discernable difference between the S.P. removal rates for sub- and supragingival calculus. Fig. 9Single-pulse (S.P.) removal rates for all gamma-ray-sterilized calculus samples irradiated at as a function of the number of incident pulses. The S.P. depth removal rates for (a) subgingival and (b) supragingival calculus. The S.P. volume removal rates for (c) subgingival and (d) supragingival calculus. The change in ablated area for (a) subgingival and (b) supragingival calculus. Trend lines through data are from a linear regression. Outliers in the S.P. removal rate data that skew the distribution were rejected according to Chauvenet’s criterion.30 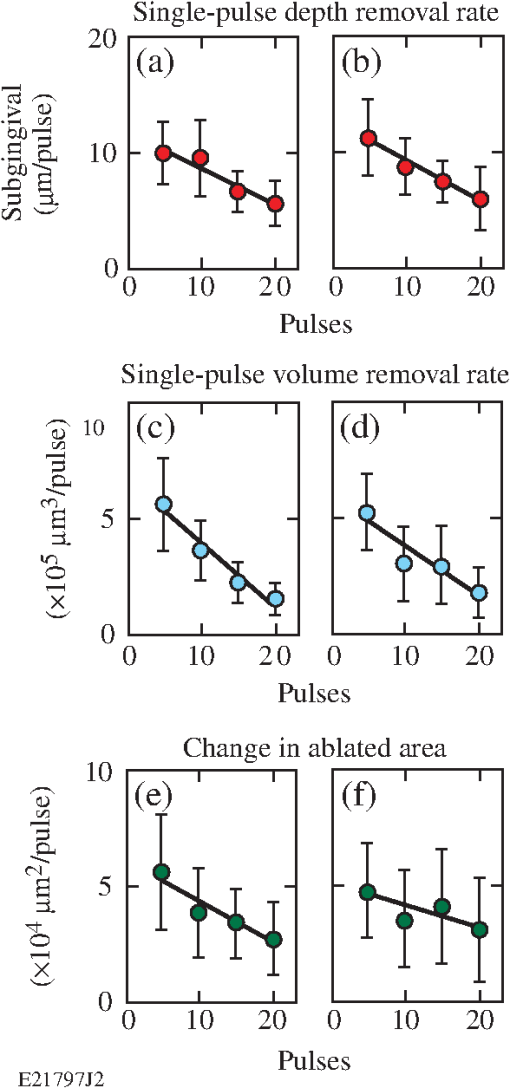 5.DiscussionThe properties (i.e., pulse energy, duration, and focal spot intensity distribution) of the 400-nm laser used in this study are extremely reproducible, causing shot-to-shot variations in ablation measurements to be attributable to the material heterogeneity of calculus itself. Thus, using the diagnostics outlined earlier allows for rather detailed inferences regarding the actual ablation mechanism. This contrasts with previous work using the 380-nm FDA laser31 whose poor reproducibility and characterization rendered it unsuitable for this kind of detailed study. However, the selective removal of oral bacteria, dental caries, and calculus by the 380-nm laser was summarized in Ref. 15 and was attributed to porphyrins endogenous to oral bacteria. In this study, blue-light microscopy clearly indicates photobleaching and reduced absorption on the calculus surface after laser irradiation (Figs. 4 and 5). For thick calculus layers and laser fluences less than this may lead to stalling before the entire calculus layer is removed [Figs. 6(a) and 6(b)]. Thus, photobleaching affects calculus ablation but does not necessarily prevent it. Fluorescence spectroscopy (Fig. 6) supports the interpretation of the blue-light microscope images of a photobleached calculus surface after laser irradiation. The absence of the porphyrin Soret band29,32,33 in the fluorescence spectrum of photobleached calculus [Fig. 6(d)] between 615 and 725 nm shows that endogenous porphyrins (e.g., protoporphyrin IX and coporphyrin) in oral bacteria (e.g., Prevotella intermedia, Prevotella nigrescens, and Prevotella melaninogenica) are the primary absorbers for 400-nm ablation. These porphyrins are permanently damaged (photobleached) in the vicinity of the irradiated surface and can no longer absorb 400-nm laser light. The observed fluorescence from enamel and photobleached calculus seen in Fig. 6 originates from the hard tissue matrix. Some remnant unbleached porphyrins within the photobleached surface layer likely give rise to the small differences observed in the enamel and photobleached calculus spectra. Oral bacteria are found throughout calculus34–37 and are typically lodged in the calculus pores (arrows in Fig. 7). The SEM images of irradiated surfaces [Fig. 7(a)] present empty pores in contrast to nonirradiated calculus [Fig. 7(b)]. These findings agree with the conclusions drawn from fluorescence spectroscopy and blue-light microscopy of photobleached surface layers. However, none of these diagnostics is able to determine the depth of this photobleached layer, which we henceforth call the depletion layer. This depletion layer also leads to the measured increase in reflection/scattering of 400-nm radiation compared with nonirradiated calculus and clearly affects ablation by subsequent laser pulses. The modified blow-off model appears well suited to explain calculus ablation at 400 nm while the standard blow-off model does not. The assumption of permanent chromophore depletion agrees with the results of blue-light microscopy, fluorescence spectroscopy and scattered laser light measurements. The model predicts a partially depleted layer of chromophores [Fig. 1(b)] with thickness beyond the etch depth after each laser pulse. The linear dependence of the average depth and volume removal rates with incident fluence (Fig. 8) also agrees with this model. The large error bars in Fig. 8 are attributed to tissue variations in absorption and/or the heterogeneity of the physical properties in calculus.21 The modified blow-off model readily agrees with most of the observations in Figs. 4–7. However, this model does not predict the ablation stalling seen in Fig. 6 or the reduction of ablation depth and volume with successive laser pulses in Fig. 9. This limitation is probably the result of neglecting scattering of laser light within dental calculus. These losses, especially within the depletion layer, can be significant due to multiple scattering, including broadening of the spot size. Calculus formation is known to be layered,38 most likely progressing from low chromophore number density (low-), Gram-positive bacteria39 on the calculus/tooth interface to high-, Gram-negative bacteria on the calculus surface.39–43 This gradual decrease in absorber density with depth and the concomitant increase in the depletion layer depth exacerbate the laser light losses ahead of the region where it may be effectively absorbed. This naturally leads to the decreasing removal rates with depth (Fig. 9) and potential stalling. This problem is compounded by the fact that the scattering length within dental hard tissue44 is not much longer than typical measured etch depths. (For this purpose, we have assumed scattering within calculus to be comparable to that in enamel.) The same reasoning also predicts that increasing the incident fluence and corresponding etch depths effectively prevents stalling before complete removal of the calculus layer. These conclusions agree with our observations that stalling occurs frequently close to the ablation threshold (1 to ) and is typically not observed for fluences . When stalling does occur, the intensity distribution of subsequent 400-nm-laser pulses will be broadened due to scattering within the depletion layer. Thermal effects in the underlying healthy tissue are not expected, as scattering dominates over absorption in pristine dental hard tissues at . Continued calculus ablation at 400 nm is assured if in the remaining surface layer throughout the laser treatment. Scattering, photobleaching, and decreasing chromophore density with depth into the calculus compete with this condition and can result in ablation stalling. However, stalling can effectively be prevented if the incident fluence and the corresponding etch depths are sufficiently high (). Since sound cementum and enamel are not ablated below 9 and , respectively,23 selective calculus ablation without stalling is assured for fluences of 6 to due to both deep etch depths and fewer incident laser pulses. Most ablation experiments in this study were carried out with gamma-ray-sterilized teeth. However, the measured ablation rates for sterilized and unsterilized teeth under otherwise identical conditions were essentially indistinguishable. Previous NUV ablation studies45 carried out at 380 nm reported ablation fluences of 1 to for effective calculus ablation using unsterilized teeth. Our comparison study eliminates the possibility that sterilization of the teeth significantly affects calculus ablation. We therefore suspect that the complicated nature of the temporal laser pulse shape in the 380-nm experiments (two successive, irregular 100-ns pulses within ) may account for the different reported relevant ablation fluences. 6.ConclusionCalculus ablation at 400 nm is best described by a modified blow-off model that is based on chromophore depletion (photobleaching). The results presented here strongly suggest that the relevant calculus chromophores are bacterial porphyrins, endogenous to plaque and dental calculus. A thin, surface layer of these chromophores becomes photobleached after each irradiation pulse. Tissue scattering within this photobleached layer exacerbated by a decreasing absorber (bacterial porphyrin) density with depth leads to decreasing removal rates with successive laser pulses and potential ablation stalling. However, stalling can be avoided by irradiating at incident fluences . AcknowledgmentsWe thank Dr. Georgios Romanos for contributing the nonsterilized tooth samples for this study. This work was supported by the U.S. Department of Energy Office of Inertial Confinement Fusion under Cooperative Agreement No. DE-FC52-08NA28302, the University of Rochester, and the New York State Energy Research and Development Authority. The support of DOE does not constitute an endorsement by DOE of the views expressed in this article. This work was also partially financially supported through a 2010 student grant from the American Society for Laser Medicine and Surgery (ASLMS). ReferencesS. Jepsenet al.,
“Calculus removal and the prevention of its formation,”
Periodontology 2000, 55
(1), 167
–188
(2011). http://dx.doi.org/10.1111/prd.2010.55.issue-1 0906-6713 Google Scholar
S. NymanJ. LindheT. Karring,
“Reattachment—New Attachment,”
Textbook of Clinical Periodontology, Munksgaard, Copenhagen
(1992). Google Scholar
P. RechmannT. Hennig,
“Lasers in periodontology—today and tomorrow,”
Med. Laser Appl., 16
(3), 223
–230
(2001). http://dx.doi.org/10.1078/1615-1615-00026 1615-1615 Google Scholar
H. T. BelliniJ. R. Johansen,
“Average time required for scaling and surgery in periodontal therapy,”
Acta Odontol. Scand., 31
(5), 283
–288
(1973). http://dx.doi.org/10.3109/00016357309002515 AOSCAQ 0001-6357 Google Scholar
W. K. Brayeret al.,
“Scaling and root planing effectiveness: the effect of root surface access and operator experience,”
J. Periodontol., 60
(1), 67
–72
(1989). http://dx.doi.org/10.1902/jop.1989.60.1.67 JOPRAJ 0022-3492 Google Scholar
J. Eberhardet al.,
“Efficacy of subgingival calculus removal with Er:YAG laser compared to mechanical debridement: an in situ study,”
J. Clin. Periodontol., 30
(6), 511
–518
(2003). http://dx.doi.org/10.1034/j.1600-051X.2003.00052.x JCPEDZ 0303-6979 Google Scholar
A. Aokiet al.,
“Lasers in nonsurgical periodontal therapy,”
Periodontology 2000, 36 59
–97
(2004). http://dx.doi.org/10.1111/prd.2004.36.issue-1 0906-6713 Google Scholar
A. M. Polsonet al.,
“The production of a root surface smear layer by instrumentation and its removal by citric acid,”
J. Periodontol., 55
(8), 443
–446
(1984). http://dx.doi.org/10.1902/jop.1984.55.8.443 JOPRAJ 0022-3492 Google Scholar
P. A. Adriaenset al.,
“Ultrastructural observations on bacterial invasion in cementum and radicular dentin or periodontally diseased human teeth,”
J. Periodontol., 59
(8), 493
–503
(1988). http://dx.doi.org/10.1902/jop.1988.59.8.493 JOPRAJ 0022-3492 Google Scholar
J. E. Schoenlyet al.,
“The efficacy of selective calculus ablation at 400 nm: comparison to conventional calculus removal methods,”
Proc. SPIE, 8566 85660E
(2013). http://dx.doi.org/10.1117/12.2011892 Google Scholar
L. J. Walsh,
“The current status of laser applications in dentistry,”
Aust. Dent. J., 48
(3), 146
–155
(2003). http://dx.doi.org/10.1111/j.1834-7819.2003.tb00025.x ADEJA2 0045-0421 Google Scholar
D. Fried,
“Laser processing of dental hard tissues,”
Proc. SPIE, 5713 259
–269
(2005). http://dx.doi.org/10.1117/12.598149 PSISDG 0277-786X Google Scholar
F. Schwarzet al.,
“Laser application in non-surgical periodontal therapy: a systematic review,”
J. Clin. Periodontol., 35
(Suppl. 8), 29
–44
(2008). http://dx.doi.org/10.1111/cpe.2008.35.issue-s8 JCPEDZ 0303-6979 Google Scholar
F. Sgolastraet al.,
“Efficacy of Er:YAG laser in the treatment of chronic periodontitis: systematic review and meta-analysis,”
Lasers Med. Sci., 27
(3), 661
–673
(2012). http://dx.doi.org/10.1007/s10103-011-0928-8 LMSCEZ 1435-604X Google Scholar
P. Rechmann,
“Dental laser research: selective ablation of caries, calculus, and microbial plaque. From the idea to the first in vivo investigation,”
Dent. Clin. North Am., 48
(4), 1077
–1104
(2004). http://dx.doi.org/10.1016/j.cden.2004.05.006 DCNAAC 0011-8532 Google Scholar
T. HennigP. RechmannB. Spengler,
“Caries selective ablations: regarding side effects,”
in Proc. 4th Int. Congr. Lasers Dent.,
143
–146
(1995). Google Scholar
T. E. BramantiS. C. Holt,
“Roles of porphyrins and host iron transport proteins in regulation of growth of Porphyromonas gingivalis W50,”
J. Bacteriol., 173
(22), 7330
–7339
(1991). JOBAAY 0021-9193 Google Scholar
P. RechmannT. HennigB. Spengler,
“Selective ablation of subgingival calculus,”
in Proc. 4th Int. Congr. Lasers Dent.,
159
–162
(1995). Google Scholar
J. E. SchoenlyW. SekaP. Rechmann,
“Investigation into the optimum beam shape and fluence for selective ablation of dental calculus at ,”
Lasers Surg. Med., 42
(1), 51
–61
(2010). http://dx.doi.org/10.1002/lsm.v42:1 LSMEDI 0196-8092 Google Scholar
J. E. SchoenlyW. D. SekaP. Rechmann,
“Near-ultraviolet removal rates for subgingival dental calculus at different irradiation angles,”
J. Biomed. Opt., 16
(7), 071404
(2011). http://dx.doi.org/10.1117/1.3564907 JBOPFO 1083-3668 Google Scholar
J. E. SchoenlyW. SekaP. Rechmann,
“Selective near-UV ablation of subgingival dental calculus: measurement of removal rates,”
Proc. SPIE, 7549 754906
(2010). http://dx.doi.org/10.1117/12.849336 Google Scholar
J. E. Schoenly,
“Selective ablation of dental calculus at 400 nm,”
209 Institute of Optics, University of Rochester, 2011). Google Scholar
J. E. Schoenlyet al.,
“Near-UV laser treatment of extrinsic dental enamel stains,”
Lasers Surg. Med., 44
(4), 339
–345
(2012). http://dx.doi.org/10.1002/lsm.v44.4 LSMEDI 0196-8092 Google Scholar
A. VogelV. Venugopalan,
“Mechanisms of pulsed laser ablation of biological tissues,”
Chem. Rev., 103
(5), 577
–644
(2003). http://dx.doi.org/10.1021/cr010379n CHREAY 0009-2665 Google Scholar
G. H. Pettit,
“The physics of ultraviolet laser ablation,”
Lasers in Medcine, 109
–129 CRC Press, Boca Raton
(2002). Google Scholar
R. Srinivasan,
“Ablation of polymers and biological tissue by ultraviolet lasers,”
Science, 234
(4776), 559
–565
(1986). http://dx.doi.org/10.1126/science.3764428 SCIEAS 0036-8075 Google Scholar
G. H. Pettitet al.,
“Transmission of polyimide during pulsed ultraviolet laser irradiation,”
Appl. Phys. A: Mater. Sci. Proces., 58
(6), 573
–579
(1994). http://dx.doi.org/10.1007/BF00348168 APAMFC 0947-8396 Google Scholar
W. BuchallaA. M. LennonT. Attin,
“Flourescence spectroscopy of dental calculus,”
J. Periondontal Res., 39
(5), 327
–332
(2004). http://dx.doi.org/10.1111/j.1600-0765.2004.00747.x JPDRAY 0022-3484 Google Scholar
J. R. Taylor, An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, University Science Books, Sausalito, California
(1997). Google Scholar
P. RechmannT. Hennig,
“Selective ablation of dental calculus with a frequency-doubled Alexandrite laser,”
Proc. SPIE, 2623 180
–188
(1996). http://dx.doi.org/10.1117/12.230326 PSISDG 0277-786X Google Scholar
Y. L. Qinet al.,
“Real-time detection of dental calculus by blue-LED-induced fluorescence spectroscopy,”
J. Photochem. Photobiol. B: Biol., 87 88
–94
(2007). http://dx.doi.org/10.1016/j.jphotobiol.2007.03.002 JPPBEG 1011-1344 Google Scholar
W. C. Dolowyet al.,
“Fluorescence of dental calculus from cats, dogs, and humans and of bacteria cultured from dental calculus,”
J. Vet. Dent., 12
(3), 105
–109
(1995). Google Scholar
B. T. K. Tanet al.,
“Study of bacterial viability within human supragingival dental calculus,”
J. Periodontol., 75
(1), 23
–29
(2004). http://dx.doi.org/10.1902/jop.2004.75.1.23 JOPRAJ 0022-3492 Google Scholar
H. E. Schroeder,
“Two different types of mineralization in early dental calculus,”
Helv. Odontol. Acta, 8 117
–127
(1964). HONAA4 0018-0211 Google Scholar
J. FriskoppL. Hammarstrom,
“A comparative scanning electron microscope study of supragingival and subgingival calculus,”
J. Periodontol., 51
(10), 553
–562
(1980). http://dx.doi.org/10.1902/jop.1980.51.10.553 JOPRAJ 0022-3492 Google Scholar
J. Friskopp,
“Ultrastructure of nondecalcified supragingival and subgingival calculus,”
J. Periodontol., 54
(9), 543
–550
(1983). http://dx.doi.org/10.1902/jop.1983.54.9.542 JOPRAJ 0022-3492 Google Scholar
D. J. White,
“Processes contributing to the formation of dental calculus,”
Biofouling, 4
(1), 209
–218
(1991). http://dx.doi.org/10.1080/08927019109378211 BFOUEC 0892-7014 Google Scholar
P. MarshM. V. Martin, Oral Microbiology, WrightBoston, Massachusetts,1999). Google Scholar
L. J. WalshF. Shakibaie,
“Ultraviolet-induced fluorescence: shedding new light on dental biofilms and dental caries,”
Aust. Dent. Practice, 56
–60
(2007). Google Scholar
N. S. Soukoset al.,
“Phototargeting oral black-pigmented bacteria,”
Antimicrob. Agents Chemother., 49
(4), 1391
–1396
(2005). http://dx.doi.org/10.1128/AAC.49.4.1391-1396.2005 AMACCQ 1098-6596 Google Scholar
S. S. Socranskyet al.,
“Microbial complexes in subgingival plaque,”
J. Clin. Periodontol., 25
(2), 134
–144
(1998). http://dx.doi.org/10.1111/cpe.1998.25.issue-2 JCPEDZ 0303-6979 Google Scholar
W. E. C. MooreL. V. H. Moore,
“The bacteria of periodontal disease,”
Periodontology 2000, 5
(1), 66
–77
(1994). http://dx.doi.org/10.1111/prd.1994.5.issue-1 0906-6713 Google Scholar
D. Friedet al.,
“Nature of light-scattering in dental enamel and dentin at visible and near-infrared wavelengths,”
Appl. Opt., 34
(7), 1278
–1285
(1995). http://dx.doi.org/10.1364/AO.34.001278 APOPAI 0003-6935 Google Scholar
P. RechmannT. Hennig,
“Selective ablation of sub- and supragingival calculus with a frequency-doubled Alexandrite laser,”
Proc. SPIE, 2394 203
–210
(1995). http://dx.doi.org/10.1117/12.207443 PSISDG 0277-786X Google Scholar
BiographyJoshua E. Schoenly is a laser applications engineer at IPG Photonics, Microsystems Division, located in Manchester, NH. He received his PhD in optics in 2011 from the University of Rochester while performing his research at the Laboratory for Laser Energetics. He performed his postdoctoral research at the University of Toronto prior to joining IPG Photonics. His industrial expertise is in the area of laser micromachining using excimer, DPSS, fiber, and ultrafast laser systems. Wolf Seka holds a PhD in physics from the University of Texas (Austin, 1965). Since 1976 he has been at the Laboratory for Laser Energetics (LLE), University of Rochester in Rochester, New York. He has worked, taught, and published in the fields of laser physics, laser fusion, and applications of laser in dentistry. He is currently a senior scientist at LLE and associate professor at The Institute of Optics. He is a member of SPIE. Peter Rechmann is at the University of California, San Francisco, Department of Preventive and Restorative Dental Sciences. He has been involved in clinical research on caries prevention, including the application of new oral care products, multiple laser/light-based diagnostic tools, and new delivery systems for caries preventive ingredients. He has also been involved in laboratory and clinical research using lasers in dentistry for the past 25 years. |
|||||||||||||||||||||||||||

