Robust estimation of cerebral hemodynamics in neonates using multilayered diffusion model for normal and oblique incidences

Idan Steinberg; Osnat Harbater; Israel Gannot

doi:10.1117/1.JBO.19.7.071406

6 March 2014 Robust estimation of cerebral hemodynamics in neonates using multilayered diffusion model for normal and oblique incidences

Idan Steinberg, Osnat Harbater, Israel Gannot

Author Affiliations +

Journal of Biomedical Optics, Vol. 19, Issue 7, 071406 (March 2014). https://doi.org/10.1117/1.JBO.19.7.071406

Abstract

The diffusion approximation is useful for many optical diagnostics modalities, such as near-infrared spectroscopy. However, the simple normal incidence, semi-infinite layer model may prove lacking in estimation of deep-tissue optical properties such as required for monitoring cerebral hemodynamics, especially in neonates. To answer this need, we present an analytical multilayered, oblique incidence diffusion model. Initially, the model equations are derived in vector-matrix form to facilitate fast and simple computation. Then, the spatiotemporal reflectance predicted by the model for a complex neonate head is compared with time-resolved Monte Carlo (TRMC) simulations under a wide range of physiologically feasible parameters. The high accuracy of the multilayer model is demonstrated in that the deviation from TRMC simulations is only a few percent even under the toughest conditions. We then turn to solve the inverse problem and estimate the oxygen saturation of deep brain tissues based on the temporal and spatial behaviors of the reflectance. Results indicate that temporal features of the reflectance are more sensitive to deep-layer optical parameters. The accuracy of estimation is shown to be more accurate and robust than the commonly used single-layer diffusion model. Finally, the limitations of such approaches are discussed thoroughly.

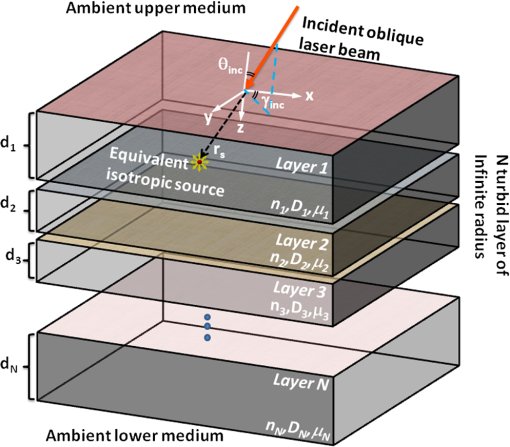
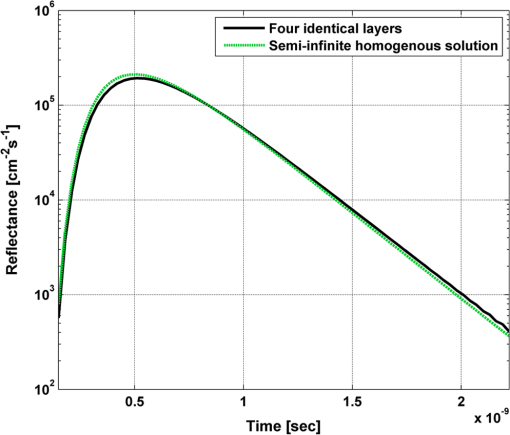
1. Introduction

Near-infrared spectroscopy (NIRS) measures tissue optical properties in the near-infrared wavelengths. Specifically, in the 650- to 1300-nm range known as the “tissue optical window,” the main chromophores are the oxygenated ( ${HbO}_{2}$ ) and nonoxygenated (Hb) hemoglobin.¹ Thus, NIRS is suitable for monitoring cerebral hemodynamics such as tissue oxygen saturation, especially in premature neonatal patients. These patients are at risk of suffering from hemodynamics instability, which has a profound effect on adverse neurodevelopment.²^,³ However, optical measurements of neonate and adult brains present great challenges. This is due to deliberate and nondeliberate changes in deep-tissue cerebral hemodynamic variables, which are masked by several superficial layers of highly turbid tissue such as the scalp and the skull. In addition, the complex multilayered geometry and diverse optical properties of the different tissues prohibit simple quantification techniques and necessitate multiple-wavelengths measurements.

Different types of methods are used for forward and inverse modeling in order to extract anatomical information and tissue optical parameters from the measurements performed in the clinic. The most simple and common technique is the Beer–Lambert law.⁴ In a typical time-resolved NIRS setup, the source and detector are placed with sufficient separation so the average photon path will sample the deep cerebral layers. The reflectance is measured as a function of time in response to a very short laser pulse.⁴ This method is subjected to some major constraints which greatly restrict its performance and applicability. In order to sample mainly the scarce photons which are backscattered from deep layers, large source-detector separations and large delays must be used. Thus, only a very small fraction (less than $10^{- 6}$ ) of the photons that are launched into the tissue are measured, causing significant degradation of the signal-to-noise ratio (SNR). Moreover, the forward model that is used provides only a crude estimation of the true absorption in deep layers. Although emphasizing the effect of deep layers over superficial ones, such a model is unable to truly separate the properties of different layers.

Stochastic Monte Carlo (MC) simulations for both time-resolved or steady state are considered to be the most accurate forward models available for macroscopic photon propagation in turbid media. Thus, they serve as a gold standard for comparison and validation of other techniques to be used as forward and inverse models in NIRS.⁵^–¹¹ The MC method may be used to solve the inverse problems but due to its stochastic nature, it is computationally intensive and requires time-consuming algorithms.¹² This is especially true when complex tissue geometries, large source-detector separations, and/or oblique incidence are present and require many millions of iterations to reduce the variance to an expectable limit. Scaling methods,¹³^,¹⁴ perturbation methods,¹⁵^–¹⁷ and hybrid diffusion-MC¹⁸^,¹⁹ methods are used in order to achieve some degree of acceleration of the simulations with minor losses in accuracy. Parallel computation and implementation of the MC on graphics processing units may reduce computation time significantly²⁰^,²¹ but are still uncommon in practice.

On the other hand, the diffusion approximation of the radiative transfer equation is considered to be quite accurate and a useful and simple approximation in regions where scattering dominates over absorption. This is the case in most biological tissues for wavelengths in the tissue optical window. This approximation tends to be more accurate when describing the propagation of photons far enough from the boundaries and the sources. Several analytical solutions for the diffusion equation, in both time-dependent and steady state,⁷^,⁸^,²² may be used for a single semi-infinite homogeneous medium. These are based on Green’s function solution in response to an isotropic point source in an infinite homogenous medium.²³ A common, single homogenous layer solution for the reflectance caused by a pencil beam source introduced by Patterson et al.²⁴ is commonly used in time-domain or frequency-domain NIRS.²⁵

For complex biological tissues such as the head, skin, muscles, and different internal organs, a single semi-infinite geometry is insufficient and a multilayer model is necessary. This is especially true for monitoring cerebral hemodynamics in neonates. A single-layer approximation, which is used in the literature for this application,²⁵^,²⁶ often causes significant deviations from the actual values due to the strong effect of the superficial layers such as scalp and skull.

To compensate the effect of multiple layers and to separate the effects of the layers of interest from the superficial ones, several approaches are taken. Numerical approaches which enable reconstruction of complex tissue geometry are usually based on the diffusion approximation to the radiative transport equation. These include finite element method, finite volume method, finite difference method, and boundary element method,²⁷ which all require significant computation time. Moreover, these require complex, accurate a priori anatomical information. Such data can only be acquired by computerized tomography or MRI scans which have obvious disadvantages that NIRS aims to avoid. Derivation of analytical solutions for a two-layered turbid medium using the diffusion equation has been introduced by several researchers both in time-domain and in steady state.²⁸^–³¹ Kienle et al.¹⁰ suggested an analytical solution which enables calculation of the reflectance from a two-layered turbid media having an infinitely thick second layer in the steady state at frequency and time domains. These analytical solutions have been used, and their accuracy was further tested against MC simulations¹⁰^,³²^,³³ and experimentally.¹⁰^,³⁴^,³⁵ Martelli et al.³⁶^–³⁸ introduced time-domain solutions for two and three layers. Das et al.³⁹ presented a solution incorporating a tilted interface and refractive index difference between two layers.

For multilayered media, Tualle et al.⁴⁰ investigated the asymptotic behavior of reflectance in scattering multilayered semi-infinite media in order to derive the optical properties of the deepest layer. Wang and Wang⁴¹ have also extended the solution of Kienle et al.¹⁰ for an $N$ -layered mismatched semi-infinite medium in the steady state and time domain and compared it with MC simulations. Recently, Liemert and Kienle have used a similar approach and developed a solution for an $N$ -layered turbid medium in both semi-infinite and finite. Their solutions are presented in steady state,⁴² time domain,⁴³ and frequency domain⁴³ and were compared with MC simulations. However, to the best of our knowledge, no general multilayered model was applied yet to the study of light propagation in neonate heads or for the estimation of the cerebral hemodynamics with NIRS.

Oblique incidence diffuse reflectance measurements have many advantages over normal incidence measurements. An oblique incidence setup can reduce detector saturation due to specular-reflected photons while ensuring collection of the diffusely reflected photons. These diffuse photons carry information from structures deep within the tissue, thus increasing their collection and the SNR. Oblique incidence is also advantageous in fluorescence measurements, since it enables selection of the depth of fluorescence origin by varying the angle of incidence.²⁶^,⁴⁴^,⁴⁵ Endoscopic probes, which are used in clinical applications, often use oblique incidence, and different configurations were designed for such purposes.⁴⁶ Measuring the reflectance in curvature geometry, such as neonate heads, may cause some artifacts⁴⁷ which could be reduced using oblique incidence.

Wang and Jacques⁴⁸ developed an oblique incidence reflectance method which measures the reduced scattering coefficient. This method was extended for determining both reduced scattering and absorption coefficients,¹¹ and the effect of tissue structures on the estimated coefficients was further investigated.⁴⁹^,⁵⁰ Spatially resolved oblique incidence diffused reflectance spectroscopy was used in vivo to discriminate melanoma and carcinoma skin cancers from benign and premalignant skin lesions.⁵¹ In these methods, only a single set of absorption and reduced scattering coefficients is estimated per wavelength, thus assuming a semi-infinite homogeneous turbid media. Currently, to the best of our knowledge, a method that combines oblique incidence with a multilayered model has not been presented.

Here, we introduce an analytical model for calculating the reflectance from a multilayered turbid media using normal or oblique incidence. Such a model differs from previous works as it is written in vector–matrix form to facilitate fast and simple computation in MATLAB® environment. In addition, it allows the simple integration of oblique incidence, complex beam shapes, or arbitrary temporal modulation. Both time-resolved and spatially resolved reflectance solutions are presented and compared with MC simulations. We then assessed the applicability of this model for monitoring cerebral hemodynamics in neonatal intensive care using NIRS. The accuracy is evaluated in different sets of absorption and scattering coefficients in multilayered media for synthetic tissue models and real-life neonate head models. The effects of changes in the optical coefficients in superficial and deep layers are tested and evaluated as well as the effects of normal or oblique incidence. Finally, we demonstrate the estimation of the deep-tissue oxygen saturation with spatiotemporal NIRS using the multilayered model and compare the estimated values to those estimated using the semi-infinite homogeneous model.⁸

2. Methods

2.1.

Theoretical Model

Presented here is a concise and rigorous mathematical development for the multilayered diffusion model. To this end, let us first consider the case of an incident pencil beam. Let the origin of a Cartesian coordinate system coincide with the beam incidence described in Fig. 1.

Fig. 1

Description of multilayer diffusion model’s geometry and notation.

Under the diffusion approximation in a $N$ -layered turbid medium, and for an incident pencil beam with azimuthal angle $γ_{inc}$ and polar angle $θ_{inc}$ , the photon fluence rate obeys a set of diffusion partial differential equations:

Eq. (1)

[\nabla^{2} - \frac{n_{i}}{c D_{i}} \frac{\partial}{\partial t} - \frac{μ_{ai}}{D_{i}}] ϕ_{i} (t; r) = - \frac{a_{i}^{'}}{D_{i}} δ [i - 1] δ (t) δ (r - r_{s}) i = 1, 2, \dots, N,

where

c

denotes the speed of light in vacuum, and the

δ [\cdot]

and

δ (\cdot)

denote the delta functions of Kronecker and Dirak, respectively.

ϕ_{i}

denotes the spatiotemporal fluence rate at the

i

’th layer, and

n_{i}

,

μ_{ai}

, and

μ_{si}^{'}

are the optical properties of the

i

’th layer: the (real) refractive index, optical absorption coefficient, and reduced scattering coefficient, respectively.

D_{i}

and

a_{i}^{'}

are the derived optical quantities: the optical diffusion coefficient given by

D_{i} = {[3 (μ_{ai} + μ_{si}^{'})]}^{- 1}

and the transport albedo defined as

a_{i}^{'} = μ_{si}^{'} / (μ_{ai} + μ_{si}^{'})

.

r_{s}

is the equivalent isotropic source position vector given by Snell’s law⁵²

Eq. (2)

r_{s} = (3 D_{1} n_{0} / n_{1}) {[\begin{matrix} \sin (θ_{inc}) \cos (γ_{inc}) & \sin (θ_{inc}) \sin (γ_{inc}) & \sqrt{n_{1}^{2} / n_{0}^{2} - \sin^{2} (θ_{inc})} \end{matrix}]}^{T},

where

n_{0}

is the refractive index of the ambient medium (usually assumed to be 1). The following boundary conditions (B.C.) are applied for each layer

Eq. (3)

\begin{array}{l} \lim_{x \to \infty} ϕ_{i} = \lim_{y \to \infty} ϕ_{i} = 0 & Fluence vanishes at infinite radius \\ {n_{i + 1}^{2} ϕ_{i} |}_{z = z_{i}} = {n_{i}^{2} ϕ_{i + 1} |}_{z = z_{i}} & Fresnel B.C. \\ {D_{i} \frac{\partial}{\partial z} ϕ_{i} |}_{z = z_{i}} = {D_{i + 1} \frac{\partial}{\partial z} ϕ_{i + 1} |}_{z = z_{i}} & Current density continuity \\ {ϕ_{1} |}_{z = - z_{bu}} = 0 & Extrapolated B.C. at upper interface \\ {ϕ_{N} |}_{z = z_{N} + z_{bl}} = 0 & Extrapolated B.C. at lower interface \end{array},

where

z_{i} = \sum_{n = 1}^{i} d_{n}

is the cumulative depth of the

i

’th layer, and

z_{bu}

and

z_{bl}

are the extrapolated boundary locations above and below the tissue, respectively. These can be computed by numerical integration of the Fresnel integrals presented by Haskell et al.²²

One should note that under these B.C.s, the fluence rate is time invariant and transversally shift invariant ( $x$ , $y$ coordinates) but not invariant to shifts at the longitudinal coordinate ( $z$ -coordinate). Consider the transverse spatiotemporal Fourier transform (TFT) defined with its inverse counterpart by

Eq. (4)

Φ (ω; k_{t}, z) \equiv \int_{t \in R} \int_{r_{t} \in R^{2}} ϕ (t; r_{t}, z) e^{- j (ω t - k_{t} \cdot r_{t})} d r_{t} d t r_{t} = {[\begin{matrix} x & y \end{matrix}]}^{T} ϕ (t; r_{t}, z) \equiv \frac{1}{{(2 π)}^{3}} \int_{ω \in R} \int_{k_{t} \in R^{2}} Φ (ω; k_{t}, z) e^{j (ω t - k_{t} \cdot r_{t})} d k_{t} d ω k_{t} = {[\begin{matrix} k_{x} & k_{y} \end{matrix}]}^{T},

where

j = \sqrt{- 1}

is the unit imaginary. Such transform will transform the set of diffusion equations into a set of a second-order, nonhomogeneous, ordinary differential equations

Eq. (5)

[\frac{\partial^{2}}{\partial z^{2}} - {| k_{t} |}^{2} - \frac{μ_{ai}}{D_{i}} + j \frac{ω n_{i}}{c D_{i}}] Φ_{i} (ω; k_{t}, z) = - \frac{a_{i}^{'}}{D_{i}} δ [i - 1] δ (z - r_{s z}) e^{- j k_{t} \cdot r_{st}},

where

r_{st}

is the transverse component of the isotropic source position vector. A note should be taken that the B.C.s are almost unaffected by this transform, as the longitudinal coordinate is unaltered. The frequency domain equations have a known solution

Eq. (6)

Φ_{i}^{H} (ω; k_{t}, z) = A_{i} (ω; k_{t}) e^{κ_{i} z} + B_{i} (ω; k_{t}) e^{- κ_{i} z} Φ_{1}^{P} (ω; k_{t}, z) = - \frac{a_{1}^{'}}{D_{1} κ_{1}} H (r_{s z} - z) \sin h [κ_{1} (r_{s z} - z)] e^{- j k_{t} \cdot r_{st}},

where

κ_{i}^{2} \equiv {| k_{t} |}^{2} + (μ_{ai} / D_{i}) - j (ω n_{i} / c D_{i})

is the square of the complex wavenumber, and

H (\cdot)

denotes the Heaviside step function. The superscripts

H

and

P

denote the homogeneous and particular solutions, respectively, such that

Φ_{i} (ω; k_{t}, z) = Φ_{i}^{H} (ω; k_{t}, z) + δ [i] Φ_{1}^{P} (ω; k_{t}, z)

. Such private solution is similar in form to the one presented by Kinele et al.¹⁰ The transverse functions

A_{i}

and

B_{i}

are to be defined by the various B.C.s. Considering the Fresnel and photon current density conditions and applying them on the solution given in Eq. (6), one can write the following matrix relation

Eq. (7)

[\begin{matrix} A_{i + 1} \\ B_{i + 1} \end{matrix}] = \frac{1}{2} [\begin{matrix} (\frac{D_{i} κ_{i}}{D_{i + 1} κ_{i + 1}} + \frac{n_{i + 1}^{2}}{n_{i}^{2}}) e^{- (κ_{i + 1} - κ_{i}) z_{i}} & - (\frac{D_{i} κ_{i}}{D_{i + 1} κ_{i + 1}} - \frac{n_{i + 1}^{2}}{n_{i}^{2}}) e^{- (κ_{i + 1} + κ_{i}) z_{i}} \\ - (\frac{D_{i} κ_{i}}{D_{i + 1} κ_{i + 1}} - \frac{n_{i + 1}^{2}}{n_{i}^{2}}) e^{(κ_{i + 1} + κ_{i}) z_{i}} & (\frac{D_{i} κ_{i}}{D_{i + 1} κ_{i + 1}} + \frac{n_{i + 1}^{2}}{n_{i}^{2}}) e^{(κ_{i + 1} - κ_{i}) z_{i}} \end{matrix}] [\begin{matrix} A_{i} \\ B_{i} \end{matrix}] .

Denoting the matrix described in Eq. (7) by $M^{(i)}$ , one can repeat this process to get the matrix relation (denoted by $M^{tot}$ ) between the first and last sets of transverse functions

Eq. (8)

[\begin{matrix} A_{N} \\ B_{N} \end{matrix}] = \binom{\underset{︸}{M^{(N - 1)} \dots M^{(3)} M^{(2)} M^{(1)}}}{M^{tot}} [\begin{matrix} A_{1} \\ B_{1} \end{matrix}] .

Applying the extrapolated B.C.s for the first and last layers yields a matrix equation with the following solution:

Eq. (9)

[\begin{matrix} A_{1} \\ B_{1} \end{matrix}] = \frac{a_{1}^{'}}{2 D_{1} κ_{1}} \frac{e^{- i k_{t} \cdot r_{st}} (e^{κ_{1} r_{s z}} - e^{- κ_{1} r_{s z}} e^{- 2 κ_{1} z_{b}})}{(M_{12}^{tot} + M_{22}^{tot} e^{- 2 κ_{N} z_{N}}) e^{- 2 κ_{1} z_{b}} - (M_{11}^{tot} + M_{21}^{tot} e^{- 2 κ_{N} z_{N}})} [\begin{matrix} M_{12}^{tot} + M_{22}^{tot} e^{- 2 κ_{N} z_{N}} \\ - M_{11}^{tot} - M_{21}^{tot} e^{- 2 κ_{N} z_{N}} \end{matrix}] .

Thus, the frequency-domain fluence rate may be calculated for all other layers by repeated application of Eq. (6). However, for the sole calculation of the reflectance, this is not required as it depends only on the fluence in the top layer.

To account for an arbitrary spatiotemporal beam shape, $I (t; r_{t})$ , one can compute the spatiotemporal fluence rate by

Eq. (10)

ϕ (t; r_{t}, z) = F^{- 1} {Φ (ω; k_{t}, z) F [I (t; r_{t})]},

where

F {\cdot}

and

F^{- 1} {\cdot}

denote the forward and inverse TFTs defined by Eq. (4). These can be easily and efficiently computed numerically by the FFT algorithm implemented in MATLAB and other environments.

Finally, the physical parameter commonly measured in practice is the spatiotemporal reflectance $R (t; r_{t})$ , which is related to the upper layer fluence for a refractive index of 1.4 by⁸

Eq. (11)

R (t; r_{t}) = {{0.118 ϕ_{1} (t; r_{t}, z) + 0.306 D_{1} \frac{\partial}{\partial z} ϕ_{1} (t; r_{t}, z)} |}_{z = 0} .

For other refractive indices, the reflectance may be calculated according to the general expression²²

Eq. (12)

R (t; r_{t}) = R_{eff} {{\frac{ϕ_{1} (t; r_{t}, z)}{4} + \frac{D_{1}}{2} \frac{\partial}{\partial z} ϕ_{1} (t; r_{t}, z)} |}_{z = 0},

where

R_{eff}

is the effective reflection coefficient, which may be calculated according to Haskell et al.²²

2.2.

Model Validation

The accuracy of the multilayered diffusion model was tested against ad hoc spatially resolved MC simulation [Monte Carlo multi-layered (MCML)]⁹ and oblique incidence time-resolved MC simulation written in MATLAB environment and based on the same principles as the MCML. This software was developed by L. V. Wang, S. L. Jacques for steady-state modeling of light transport in multi-layered tissue. These are considered to be the gold standard solutions for the radiative transfer equation. To simulate a scenario that resembles the actual anatomy of a neonate’s head, both the diffusion model and the MC simulations were tested on a head model composed of four layers—scalp, skull, gray matter, and white matter. The accuracy of the predicted reflectance was tested for a wide range of optical properties, such as the absorption and scattering of the gray and white matters, and for a different refractive index of the scalp and skull. The variation of these properties simulates variation in human anatomy and different oxygenation levels of the brain. The anatomical and optical properties which were chosen for each layer are based on previous reports for NIR light⁴⁷^,⁵³^,⁵⁴ and are summarized in Table 1. For each test, only one of the optical properties was varied, keeping the rest with their default values indicated in Table 1 by bold characters.

Table 1

Optical parameters of the different tissues used in the model.

Tissue type	Absorption coefficient, $μ_{ai}$ ( ${cm}^{- 1}$ )	Reduced scattering coefficient, $μ_{si}^{'}$ ( ${cm}^{- 1}$ )	Refractive index, $n_{i}$ (#)	Layer thickness, $d_{i}$ (cm)
Scalp	0.18	19.0	1.4 (matched) 1.55 (mismatched)	0.2
Skull	0.16	16.0	1.4 (matched) 1.55 (mismatched)	0.2
Gray matter	0.48 (High) 0.24 (Medium) 0.12 (Low)	10.0 (High) 5.0 (Low)	1.4	0.4
White matter	0.37 (High) 0.19 (Medium) 0.09 (Low)	10.0	1.4	2.0

In order to evaluate the error between the diffusion model and the MC simulations, the root mean square of the normalized deviation (RMSND) was calculated using the following relation:

Eq. (13)

RMSND (r_{t}) = \sqrt{〈 {[\frac{R_{MC} (t, r_{t}) - R_{Model} (t, r_{t})}{R_{MC} (t, r_{t}) + R_{Model} (t, r_{t})}]}^{2} 〉},

where

R_{MC}

and

R_{Model}

are the MC and diffusion [calculated using Eqs. (11) or (12)] spatiotemporal reflectances at a given point on the tissue surface, and

〈 \cdot 〉

denotes the time averaging.

2.3.

Estimation of Oxygenation Level

The most valuable clinical parameter monitored using NIRS is the tissue oxygen saturation ( ${StO}_{2}$ ). It is dependent on the concentrations of the nonoxygenated hemoglobin and oxygenated hemoglobin according to the following relation:

Eq. (14)

{StO}_{2} (%) = \frac{[{HbO}_{2}]}{[Hb] + [{HbO}_{2}]} \cdot 100,

where

[\cdot]

denotes the concentration of each analyte.

The absorption coefficients of the brain tissues in the NIR are dependent on several chromophores concentrations including mainly: water, ${HbO}_{2}$ , Hb, and the cytochrome ${aa}_{3}$ in its oxidized ( ${aa}_{3, oxi}$ ) and reduced ( ${aa}_{3, reduce}$ ) forms, whose oxidation state is affected by the ${StO}_{2}$ value. The water absorption can be ignored for wavelength up to 950 nm, since it is negligible compared with other chromophores.

Assuming that only these chromophores contribute to the brain tissue absorption, the absorption coefficient of the brain may be calculated according to the following equation:

Eq. (15)

μ_{a, brain}^{λ} = ε_{Hb}^{λ} [Hb] + ε_{{HbO}_{2}}^{λ} [{HbO}_{2}] + ε_{{aa}_{3, oxi}}^{λ} [{aa}_{3, oxi}] + ε_{{aa}_{3, reduce}}^{λ} [{aa}_{3, reduce}],

where

μ_{a, brain}

is the brain tissue absorption coefficient,

ε_{chromophore}

is the extinction coefficient, and the superscript

λ

denotes the wavelength.

The brain absorption coefficient was calculated for different oxygen saturation levels between 4% and 99%. The total concentration of cytochrome ${aa}_{3}$ was chosen to be 22 μmol, and the total hemoglobin concentration was chosen to be 65 μmol based on the literature.¹^,²⁶^,⁴⁷^,⁵⁵ The chosen wavelength was $λ = 700 nm$ , and the extinction coefficients of each chromophore were taken for this wavelength from literature.¹^,⁵⁶

A set of time-resolved MC simulations was used to estimate the performance of the multilayered diffusion model versus the semi-infinite homogeneous diffusion model of Kienle and Patterson.⁸ The simulation parameters were the same as presented in Table 1, apart from the absorption coefficient of the gray and white matters, which was calculated according to Eq. (15) for various levels of oxygen saturation from 4% to 99%. Normalized time-resolved reflectance curves were deduced from the simulations for a source-detector separation of 1.9 cm. A nonlinear least square curve-fitting algorithm⁵⁷^,⁵⁸ was used for fitting the time-resolved reflectance predicted by the single-layer and multilayer models. For the single-layer model, both the absorption and reduced scattering coefficients were estimated. For the multilayer model, the optical parameters of the superficial layers were assumed to be known. The estimated parameters were the gray and white matters’ absorption coefficients and the white matter scattering coefficient. In both cases, the brain tissue oxygen saturation levels were calculated based on the estimated absorption coefficients according to Eq. (15) and were compared with true values. The upper and lower limits used in the curve fitting represent oxygen saturation levels between 1% and 99%. The curve fitting was tested for different combinations of reduced scattering coefficient limits, initial guesses, and time ranges.

3. Results

3.1.

Comparison with Semi-Infinite Homogeneous Solution

In order to validate the accuracy of the multilayer model, it was first compared with the semi-infinite homogeneous solution of Kienle and Patterson.⁸ For this comparison, four identical layers were used for the multilayer model with the default optical parameters of the skull detailed in Table 1. The time-dependent reflectance was calculated using the multilayer diffusion analytical model according to Eq. (11). For the semi-infinite homogeneous model, the same parameters of the skull were chosen and the time-resolved reflectance was calculated according to the extrapolated B.C. solution presented by Kienle and Patterson.⁸ The time-resolved reflectance of both models was calculated in a radius of 1.9 cm, and the high correlation between both solutions is presented in Fig. 2. The RMSND between the two curves presented in Fig. 2 is 5.5%.

Fig. 2

Comparison between the time-resolved reflectance curves calculated using the multilayer diffusion model for four identical layers (solid line) and the semi-infinite homogeneous model (dashed line).

3.2.

Model Validation against MC Simulations

The diffusion approximation is known to be accurate in regions far from sources, since the ballistic photons are neglected and only the diffuse photons are taken into account.

In close proximity to the source, the portion of the ballistic photons is large compared with the diffused ones. Thus, the accuracy of the diffusion approximation increases with an increase of source-detector separation. This limitation is demonstrated in Fig. 3 where the time-resolved reflectance is presented for several distances from the incident light source, in the range of 1 to 2 cm, which is suitable for efficient sampling of photons propagating through brain tissue. The optical parameters for all three cases are identical and taken as the default values in Table 1. The time-dependent reflectance was calculated for each case using the diffusion analytical model according to Eq. (11). The intensity of reflectance is always displayed in logarithmic scale on all graphs to emphasize differences in both large and small scales between the MC simulation and the analytic calculation.

Fig. 3

Comparison between the time-resolved reflectance simulated by MC and calculated using the diffusion model for three distances from incident light. The MC simulations are presented using the circle, triangle, and asterisk symbols for a distance of 1, 1.4, and 1.8 cm, respectively. The diffusion model reflectance is presented in the dark dashed, solid, and light dashed lines for a distance of 1, 1.4, and 1.8 cm, respectively.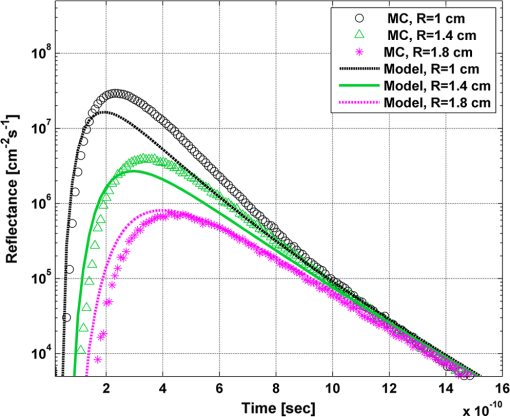

It is clear that the correlation between the diffusion model and the MC simulations increases with the increase in the distance from the source. In addition, even for the largest distance case, the model fails to accurately predict the MC reflectance at short times after the incident light pulse. This inaccuracy is again due to the larger portion of ballistic photons at short times compared with long times after incident pulse. The RMSND was calculated for the decaying part of the time-resolved reflectance of each case presented in Fig. 3 and was found to be 6.8%, 14.7%, and 22.7% for a distance of 1.8, 1.4, and 1 cm, respectively.

3.3.

Assessment of Model’s Accuracy for Different Optical Properties

The absorption coefficients of the gray and white matter are affected by the cerebral oxygenation and hemodynamics. In order to simulate these changes, several representative absorption coefficients were used for the gray and white matter in the head model. Three cases were tested—low, medium, and high brain absorption, as indicated in Table 1. Figure 4 demonstrates the effect of the brain absorption on the accuracy of the diffusion model compared with MC simulations at a distance of 1.9 cm from the incident light source. Only the decaying part of the time-resolved reflectance is presented due to the inaccuracy of the diffusion approximation in short times after the incidence, which is caused by the contribution of the ballistic photons to the reflectance.

Fig. 4

Comparison of the time-resolved reflectance as simulated by MC and calculated using the diffusion model for three cases: low, medium, and high brain absorption. The MC simulations are presented using the circle, triangle, and asterisk symbols for the cases of low, medium, and high absorption, respectively. The diffusion model reflectance is presented in the dark dashed, solid, and light dashed lines for the cases of low, medium, and high absorption, respectivley.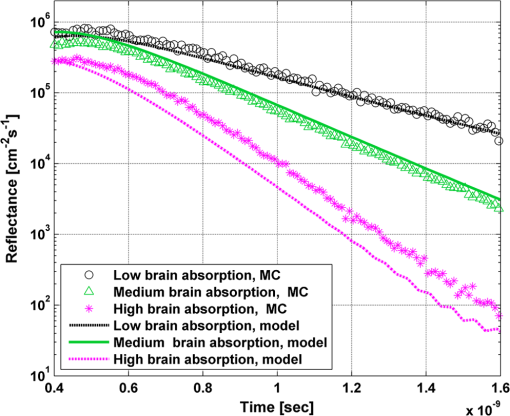

As evident from Fig. 4, the decay of the fluence rate is highly sensitive to absorption of the deep layer. For the case where low- and medium-absorption coefficients were used for the brain tissue, the model and the MC are highly correlated. However, for the high brain absorption case, the diffusion model is less accurate in predicting the reflectance although the time derivatives of the reflectance are very similar. This case presents some extremity where the absorption approaches its upper limit. The RMSND was calculated for the cases presented in Fig. 4. The RMSND for the decaying reflectance was 10.7%, 7.2%, and 35% for the low, medium, and high brain absorption cases, respectively. These results suggest that the correlation between the MC simulations and the diffusion model is rather high for a broad range of absorption coefficients. In many cases, these errors are comparable with measurement errors often encountered in clinical practice.

The influence of changes in the scattering coefficient was investigated as well. Previously reported reduced scattering coefficients for neonates in the NIR region⁴⁷^,⁵³^,⁵⁴ are in the range of 4 to $10 {cm}^{- 1}$ . The high scattering is often correlated with higher absorption (as both are dependent on the density). Thus, the combination of high or low scattering with high absorption was studied. Figure 5 displays the MC and the model’s time-dependent reflectance for low- and high-reduced scattering coefficients in the gray matter at a distance of 1.9 mm from incident light source.

Fig. 5

Comparison between the time-resolved reflectance simulated by MC and calculated using the diffusion model for two cases: low and high gray matter scatterings with high brain absorption in both cases at a distance of 1.9 cm from source. The MC simulations are represented using the triangle and circle symbols for the cases of low and high scattering, respectively. The diffusion model reflectance is represented in the solid and dashed lines for the cases of low and high scattering, respectively.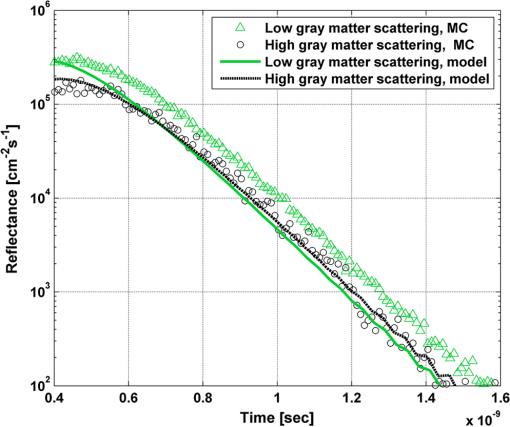

The correlation between the decaying reflectance of the model and the MC is shown to be stronger in the high gray matter scattering case than in the low scattering case. The RMSND for the decaying reflectance decreased from 35% in the low scattering case to 12% in the high scattering case.

Finally, the multilayered diffusion model takes into account the refractive index mismatch between layers. In order to test the influence of such an internal mismatch on the model’s accuracy, two cases were compared. In the first case, a refractive index of 1.4 was used for all four tissue layers and in the second case, a refractive index of 1.55 was used for the superficial layers (scalp and skull), while a refractive index of 1.4 was used for the brain tissue layers (gray and white matter).

Figure 6 demonstrates the high correlation between the decaying time-resolved reflectance of the model and the MC simulation, in both cases, at a distance of 1.8 cm from incident light source. The RMSND for the decaying reflectance presented in Fig. 6 is 7.9% for the refractive index matched case and 7.2% for the refractive index mismatched case.

Fig. 6

Comparison between the time-resolved reflectance simulated by MC and calculated using the diffusion model for two cases: refractive index matching and internal mismatching between layers ( $n_{scalp, skull} = 1.4$ or 1.55). The head model presented is the medium brain absorption with low gray matter scattering at a distance of 1.8 cm from incident source. The MC simulations are presented using the circle and triangle symbols for the cases of refractive index mismatching and matching, respectively. The diffusion model reflectance is presented in the dashed and solid lines for the cases of refractive index mismatching and matching, respectively.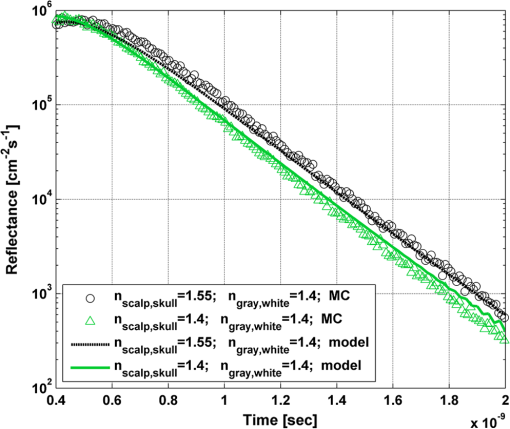

3.4.

Spatially Resolved Reflectance

The multilayered diffusion model provides a simple calculation of the spatially resolved reflectance for steady state or modulated illumination. The steady-state, spatially resolved reflectance from the MC simulations was compared with the diffusion model for two cases where both the scattering and absorption were changed: case A, medium brain absorption and low scattering, and case B, high brain absorption and high scattering.

The correlation between the reflectance simulated by MC and that calculated using the diffusion model was very high. However, there was a significant overlap between reflectance in the two cases and distinguishing between the cases was quite difficult. In order to enable distinguishing between the two cases, additional analysis was performed. Since our model provides us the spatially resolved reflectance as a function of both horizontal and vertical distances from incident light source, the reflectance along the horizontal coordinate was calculated for three fixed vertical positions: $x_{1} = 0.7 cm$ , $x_{2} = 1.2 cm$ , and $x_{3} = 1.6 cm$ . To be able to distinguish between the two cases, the following ratios were calculated: $R (x_{2}, y) / R (x_{1}, y)$ and $R (x_{3}, y) / R (x_{1}, y)$ . Figure 7 demonstrates these ratios for both the MC simulations and the analytical model.

Fig. 7

Comparison between the ratios of the spatially resolved reflectance in several vertical locations for two cases: Case A, medium brain absorption and small scattering, and Case B, large brain absorption and large scattering. The ratios presented are $R (x_{2} = 1.2 cm, y) / R (x_{1} = 0.7 cm, y)$ and $R (x_{3} = 1.6 cm, y) / R (x_{1} = 0.7 cm, y)$ . The ratios were calculated using both MC simulations (presented using the symbols) and the diffusion model (presented using the lines).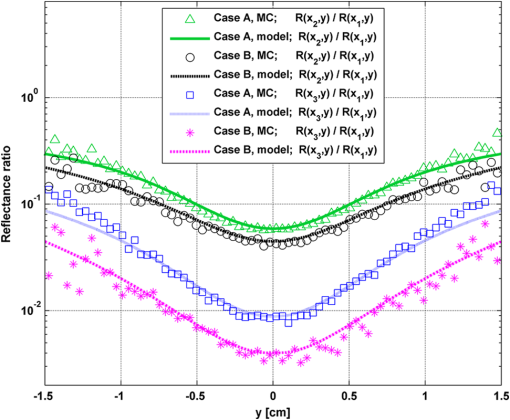

One can see that the MC simulation and analytical model predictions are highly correlated. For both reflectance ratios $R (x_{2}, y) / R (x_{1}, y)$ and $R (x_{3}, y) / R (x_{1}, y)$ , the difference between cases A and B is easily noticeable. However, these differences are accentuated in the time-resolved reflectance, and thus it is preferable to work with time-resolved or modulated (frequency-resolved) measurements. For comparison, Fig. 8 presents the time-resolved reflectance for both cases at a distance of 1.8 cm from the source. One can easily notice the profound effect that the two cases have on the decay rates of the fluence.

Fig. 8

Comparison between the time-resolved reflectance simulated by MC and calculated using the diffusion model for two cases: Case A, medium brain absorption and low scattering, and Case B, high brain absorption and high scattering. The simulations are presented using the triangle and circle symbols for cases A and B, respectively. The diffusion model reflectance is presented in the solid and dashed lines for cases A and B, respectively.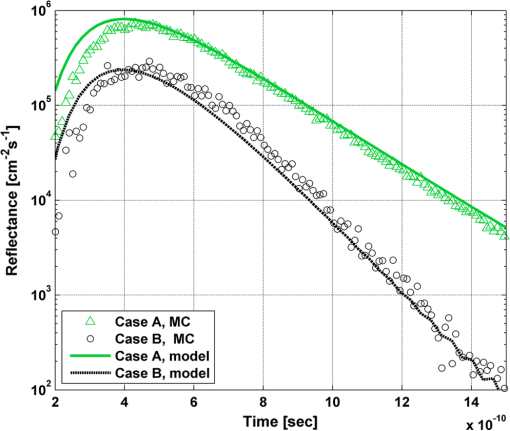

3.5.

Oblique Incidence

The spatially resolved reflectance is highly dependent on the angle of incidence. In most multilayered models, normal incidence is assumed. However, in the presented multilayered diffusion model, cases of oblique incidence were taken into account. The effect of oblique incidence on the fluence in the case of medium brain absorption is demonstrated for an incident angle of $θ_{inc} = 60 \deg$ and $γ_{inc} = 0 \deg$ . Figure 9 presents the fluence as a function of depth ( $z$ -axis) and $x$ -axis for different times after light incidence, for the oblique case (upper images) and normal incidence case (lower images). The offset of the isotropic source location from the $x$ -axis in the oblique incidence case is demonstrated. Notice that the depth of the isotropic source is also shifted compared with the normal incidence case due to the oblique incidence.

Fig. 9

The fluence rate in the case of medium brain absorption. (a and b) the fluence rate as a function of $(z, x)$ with $y = 0$ for an oblique incidence with $θ_{inc} = 60 \deg$ , and (c and d) for a normal incidence. The left figures are for $t = 0$ , and the right figures are for $t = 0.06 ns$ after light incidence.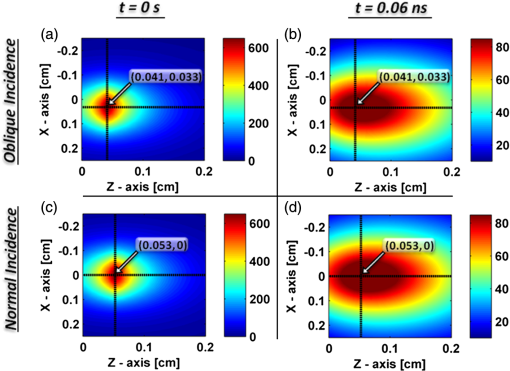

In order to emphasize the difference between the reflectance of oblique and normal incidences, the superficial layers of the head model were neglected and a simplified two-layered case of gray and white matter in an ambient cerebrospinal fluid was tested. The optical parameters of the layers are detailed in Table 2. The angle of incidence for the oblique case was chosen to be $θ_{inc} = 60 \deg$ and $γ_{inc} = 0 \deg$ . The refractive index of the ambient medium was similar to a watery medium, such as the cerebrospinal fluid, and was chosen to be $n_{0} = 1.33$ . Figure 10 compares the normal and oblique incidence spatially resolved reflectances as a function of the $y$ coordinate for $x = 1.2 cm$ . The correlation between the model and the MC is high for both cases, which are clearly distinguishable.

Table 2

Optical parameters of the layers used for normal and oblique incidences comparison.

Tissue type	Absorption coefficient $μ_{ai}$ ( ${cm}^{- 1}$ )	Reduced scattering coefficient $μ_{si}^{'}$ ( ${cm}^{- 1}$ )	Refractive index, $n_{i}$ (#)	Thickness, $d_{i}$ (cm)
Gray matter	0.12	4.0	1.4	0.4
White matter	0.09	10.0	1.4	2.0

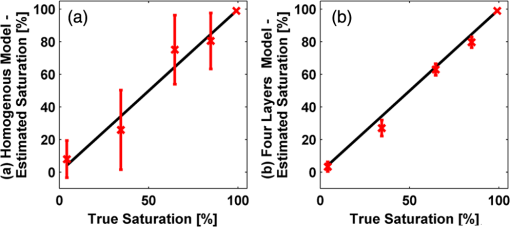
Fig. 10

Comparison between the spatially resolved reflectance simulated by MC and calculated using the diffusion model for two cases: normal and oblique incidences. The reflectance was calculated for a two-layer model, detailed in Table 2, at a location of $x = 1.2 cm$ . The MC simulations are presented using the triangle and circle symbols for the normal and oblique incidence cases, respectively. The diffusion model reflectance is presented in the solid and dashed lines for the normal and oblique cases, respectively.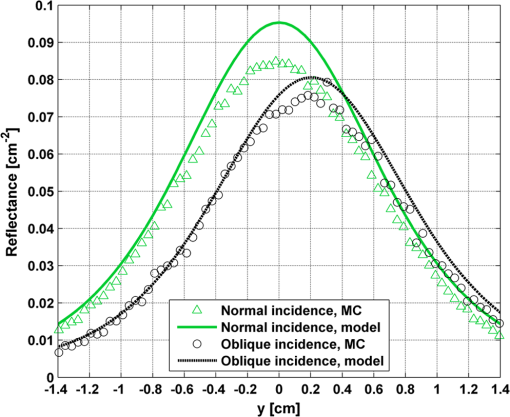

The spatial shift of the maximal intensity presented in Fig. 10, calculated by both the MC simulation and the diffusion model, is about 2 mm. Wang and Jacques⁴⁸ presented a formula for the spatial shift of the maximal intensity in case of oblique incidence. Adapting their formula to account for ambient media with nonunity refractive index yields

Eq. (16)

Δ x = 3 D_{1} \sin (θ_{inc}) n_{0} / n_{1} .

Calculation of the predicted shift using the above equation yields 1.95 mm, which is just shy of the accurate value.

3.6.

Estimation of the Oxygenation Saturation Level

Finally, the use of a semi-infinite homogeneous diffusion model was tested against the multilayer model in order to compare their accuracy in estimating the oxygenation saturation level in neonates. In clinical systems and applications, many parameters such as energy loss in the optical path and coupling efficiency may affect the measurement, therefore only uncalibrated curves are measureable. Thus, in order to make the comparison more realistic, the MC simulations, which provide reflectance in absolute units, were normalized at their maximal value. The curve fitting was then performed on the normalized MC curves and diffusion curves in order to avoid over-estimation of the algorithm performance compared with a true optical setup.

Using a nonlinear least square curve fitting, normalized MC time-resolved reflectance curves were fitted to normalized four-layer diffusion reflectance curves, assuming known optical properties of the superficial layers $(μ_{a}, μ_{s}, g, n)$ and the length of each layer. The curve fitting was tested in different combinations of reduced scattering coefficient limits, initial guesses, and time ranges. Variation in the initial guesses rarely changed the results of the curve fit in both models. However, the reduced scattering coefficient limits and mainly the variations of the time range of the curve did affect the fit results. For the case of the homogeneous model, the chosen time ranges adversely affected the accuracy of the estimated parameters, causing significant errors. On the other hand, the four-layer model was robust to changes in the data range, and the accuracy remained high.

The estimated oxygen saturation levels using the four-layer model and the homogeneous diffusion model were compared with the true oxygenation levels used in the MC simulations. Figure 11 presents the mean estimated saturation levels with 90% confidence intervals for the homogeneous model and the four-layer model [shown in Figs. 11(a) and 11(b), respectively]. The average error of all oxygen saturation levels estimated by the four-layered model was 3.8% with a maximum error of 12.4%. For the semi-infinite homogeneous model, the average error of all estimated saturation levels was 14.2% with a maximal error of 35%.

Fig. 11

Estimated saturation, using (a) the homogeneous model and (b) the four-layer model, versus the true saturation. The solid line represents the $1 ∶ 1$ ratio between the estimated and true saturation values. The stars represent the mean estimated values with 90% confidence intervals.

4. Discussion

This work describes the development and application of a multilayer model for light propagation in tissue based on the diffusion approximation. It was used for prediction of the spatiotemporal reflectance in response to normal or oblique excitation. The validity of this model was tested against MC simulations under various conditions. Finally, the proposed model was applied for NIRS, which monitors cerebral hemodynamics in neonates. The more realistic multilayer model was proven to be more accurate and robust to the choice of numerical scheme. This is in contrast to the simplistic semi-infinite homogeneous model used today.

The effects of changes in the various optical parameters of deep brain tissue on superficial reflectance were thoroughly studied and compared with gold-standard MC simulations. The model was found to be quite accurate as long as the assumptions of the diffusion approximation were respected. Typical RMSND values indicate less than 12% error in prediction of the spatiotemporal reflectance decay. This is true even for complex multilayered tissue with varying optical parameters and external and internal index mismatches. Even under the most difficult physiologically feasible scenario, in which the absorption is highest compared with the scattering, the typical error is 35%. Thus, this model is suitable to serve as a flexible, computationally light, forward solution for the estimation of optical parameters. It has advantages over the computationally heavy stochastic models such as time-resolved MC. Thus, this method can be easily implemented for the estimation of hemodynamic variables of clinical importance using spatiotemporal NIRS for neonates.

The estimation of the optical properties from the spatial distribution was also investigated. The effect of major changes in deep brain tissue on the spatial distribution of the diffusely reflected photons is almost nonexistent. Under such conditions, estimation of deep-tissue optical parameters is impossible unless some processing is performed to stress the effect of deeper layers. We demonstrated such a process by normalizing the spatial distribution along one dimension with respect to a parallel distribution closer to the equivalent isotropic source, as shown in Fig. 7. This process has successfully emphasized the spatial changes due to different optical properties of the deep layers. However, it seems less accurate than time-resolved measurements, as demonstrated in Fig. 8.

Reduction in the number of unknown optical parameters is possible by the use of oblique incidence, as demonstrated in Fig. 10. The work of Wang and Jacques⁴⁸ showed that for a single-infinite layer, if the refractive index of the superficial layer is known, then the optical diffusion coefficient can be simply deduced from the shift in the location of maximal reflectance. The model presented here, to the best of our knowledge, is the first to take into account oblique incidence in a multilayered diffusion model. Although a rigorous multilayer model is presented here, it is evident from Fig. 10 that this relation still holds provided that the depth of the superficial layer is sufficiently large compared with $l_{s}^{'}$ . In the example shown in Fig. 10, the depth of the superficial layer is 1.6 times $l_{s}^{'}$ and it is clearly evident that the estimation presented in Eq. (16) approximates well the results of both the MC and diffusion model. Another advantage of oblique incidence is evident when the detectors used for measuring the reflectance are not in contact with the tissue (such as in the case of cameras). The use of oblique incidence allows deflecting the intense specular Fresnel reflection away from the detector and avoiding saturation.

Finally, an inverse algorithm was applied in order to extract the brain oxygen saturation level using both the multilayered model and the commonly used semi-infinite homogeneous model. The estimated values using the homogeneous model were highly sensitive to the chosen curve-fitting conditions such as the reflectance time range on which the fit was performed. This caused high errors in the estimated oxygen saturation level, in some cases reaching 35%. However, the inverse algorithm applied on the multilayer model was robust to changes in the curve-fitting conditions and in all cases, the estimated saturation level was accurate with less than 12% error.

Although useful, the diffusion approach suffers from some apparent drawbacks which reflect from the results shown earlier. One of the major drawbacks of such a model is its inherent inaccuracy near the incident beam or the equivalent isotropic source. It is commonly accepted that at distances of 10 mean free paths ( $MFP \equiv 1 / μ_{s}^{'}$ ) from the isotropic source, the diffusion approximation becomes accurate. Since the superficial layers of the body such as skin, or the combined skin and scalp tissues for the head model presented here, are highly scattering, this restriction is not severe in most cases. For example, Fig. 3 demonstrates that at distances above 20 MFP ( $\sim 1 cm$ ), the RMSND is less than 20% and at distances above 30 MFP ( $\sim 1.6 cm$ ), the RMSND decreases below 10%. For neonates with thin scalp and skull tissues of 4 mm and more in thickness, a source-detector separation of 0.8 to 1.6 cm is required for covering the gray matter, and even larger separations are required in order to efficiently sample the white matter. These are large distances since the separation must be at least twice the depth of the tissue to be probed, thus the loss of accuracy in lower distances does not pose serious difficulties.

Another assumption which needs to be respected is that scattering should dominate absorption. The reduced albedo defined as $a^{'} = μ_{s}^{'} / (μ_{a} + μ_{s}^{'})$ should not fall below a certain value in order for the model results to be sufficiently accurate. This is well evident in Figs. 4 and 5. For high brain absorption, the reduced albedo is $\sim 0.9$ , which leads to some small discrepancies between the MC simulations and the diffusion approximation. For low and medium absorptions, the reduced albedos are $\sim 0.95$ and $\sim 0.97$ , respectively. In these cases, the matching between the MC simulation and analytical model is almost perfect. It is expected that for reduced albedos of 0.8 and below, the diffusion model will not be accurate enough. However, determination of the exact deterioration of performance as a function of the deterioration in the albedo is beyond the scope of this article and requires further investigation.

Additionally, the head model, which was used for this analysis, consists of the scalp, skull, gray matter, and white matter. A more realistic model should take into account also the cerebrospinal fluid layer, which is between the skull and the gray matter. The cerebrospinal fluid is known to be a clear medium with low scattering compared with absorption, and therefore the accuracy of the diffusion model in the presence of this layer may be decreased. However, since the thickness of this layer is very small compared with the gray and white matter, it may be combined with these layers⁴⁷ without significant loss of accuracy of the diffusion approximation.

To conclude, this work outlines the derivation and validation of a multilayer diffusion model for NIR monitoring of cerebral hemodynamics in neonates. It was demonstrated that even for complex media such as neonate heads, our approximated model is highly accurate and its predictions are very similar to those of the gold standard MC simulations. This model is robust and accurately coincides with any type of MC simulations—whether spatially resolved or temporally resolved, normal or oblique incidence, single or multiple layers. Since this model predicts the fluence accurately and much more rapidly compared with MC simulations, it may be used to solve inverse problems where the optical coefficients are to be estimated by iterating the forward solution proposed by this model. Finally, it was demonstrated on pure theoretical grounds that deep-tissue optical properties and consequently hemodynamics status can be estimated easily and accurately from the spatiotemporal reflectance curve using a quick and simple curve-fitting algorithm. This is even in the presence of unknown optical parameters of the superficial layers.

Acknowledgments

Idan Steinberg acknowledges the generous support of the Clore Israel Foundation and the Raymond & Beverly Sackler Institute for Biophysics at Tel Aviv University, Israel. Osnat Harbater acknowledges the support of the Israeli Ministry of Science and Technology—Women in science program.

References

1.

M. CopeD. Delpy, “System for long-term measurement of cerebral blood and tissue oxygenation on newborn infants by near infra-red transillumination,” Med. Biol. Eng. Comput., 26 (3), 289 –294 (1988). http://dx.doi.org/10.1007/BF02447083 MBECDY 0140-0118 Google Scholar

2.

N. Roche-Labarbeet al., “Noninvasive optical measures of CBV,

{StO}_{2}

, CBF index, and

{rCMRO}_{2}

in human premature neonates’ brains in the first six weeks of life,” Hum. Brain Mapp., 31 (3), 341 –352 (2010). http://dx.doi.org/10.1002/hbm.v31:3 HBRME7 1065-9471 Google Scholar

3.

K. D. LiemG. Greisen, “Monitoring of cerebral haemodynamics in newborn infants,” Early Hum. Dev., 86 (3), 155 –158 (2010). http://dx.doi.org/10.1016/j.earlhumdev.2010.01.029 EHDEDN 0378-3782 Google Scholar

4.

A. Torricelliet al., “Time domain functional NIRS imaging for human brain mapping,” NeuroImage, 85 (Part 1), 28 –50 (2013). http://dx.doi.org/10.1016/j.neuroimage.2013.05.106 NEIMEF 1053-8119 Google Scholar

5.

T. EruvM. Ben-DavidI. Gannot, “An alternative approach to analyze fluorescence lifetime images as a base for a tumor early diagnosis system,” IEEE J. Sel. Top. Quantum Electron., 14 (1), 98 (2008). http://dx.doi.org/10.1109/JSTQE.2007.913978 IJSQEN 1077-260X Google Scholar

6.

O. HarbaterM. Ben-DavidI. Gannot, “Fluorescence lifetime and depth estimation of a tumor site for functional imaging purposes,” IEEE J. Sel. Top. Quantum Electron., 16 (4), 981 –988 (2010). http://dx.doi.org/10.1109/JSTQE.2009.2033209 IJSQEN 1077-260X Google Scholar

7.

M. S. PattersonB. ChanceB.C. Wilson, “Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties,” Appl. Opt., 28 (12), 2331 –2336 (1989). http://dx.doi.org/10.1364/AO.28.002331 APOPAI 0003-6935 Google Scholar

8.

A. KienleM. S. Patterson, “Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium,” J. Opt. Soc. Am. A, 14 (1), 246 –254 (1997). http://dx.doi.org/10.1364/JOSAA.14.000246 JOAOD6 0740-3232 Google Scholar

9.

L. WangS. L. JacquesL. Zheng, “MCML—Monte Carlo modeling of light transport in multi-layered tissues,” Comput. Methods Programs Biomed., 47 (2), 131 (1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar

10.

A. Kienleet al., “Noninvasive determination of the optical properties of two-layered turbid media,” Appl. Opt., 37 (4), 779 (1998). http://dx.doi.org/10.1364/AO.37.000779 APOPAI 0003-6935 Google Scholar

11.

S.-P. Linet al., “Measurement of tissue optical properties by the use of oblique-incidence optical fiber reflectometry,” Appl. Opt., 36 (1), 136 –143 (1997). http://dx.doi.org/10.1364/AO.36.000136 APOPAI 0003-6935 Google Scholar

12.

C. ZhuQ. Liu, “Review of Monte Carlo modeling of light transport in tissues,” J. Biomed. Opt., 18 (5), 050902 (2013). http://dx.doi.org/10.1117/1.JBO.18.5.050902 JBOPFO 1083-3668 Google Scholar

13.

A. KienleM. S. Patterson, “Determination of the optical properties of turbid media from a single Monte Carlo simulation,” Phys. Med. Biol., 41 (10), 2221 (1996). http://dx.doi.org/10.1088/0031-9155/41/10/026 PHMBA7 0031-9155 Google Scholar

14.

R. Graaffet al., “Condensed Monte Carlo simulations for the description of light transport,” Appl. Opt., 32 (4), 426 (1993). http://dx.doi.org/10.1364/AO.32.000426 APOPAI 0003-6935 Google Scholar

15.

C. K. Hayakawaet al., “Perturbation Monte Carlo methods to solve inverse photon migration problems in heterogeneous tissues,” Opt. Lett., 26 (17), 1335 (2001). http://dx.doi.org/10.1364/OL.26.001335 OPLEDP 0146-9592 Google Scholar

16.

I. Seoet al., “Perturbation and differential Monte Carlo methods for measurement of optical properties in a layered epithelial tissue model,” J. Biomed. Opt., 12 (1), 014030 (2007). http://dx.doi.org/10.1117/1.2697735 JBOPFO 1083-3668 Google Scholar

17.

Y. P. KumarR. M. Vasu, “Reconstruction of optical properties of low-scattering tissue using derivative estimated through perturbation Monte-Carlo method,” J. Biomed. Opt., 9 (5), 1002 –1012 (2004). http://dx.doi.org/10.1117/1.1778733 JBOPFO 1083-3668 Google Scholar

18.

L. WangS. L. Jacques, “Hybrid model of Monte Carlo simulation and diffusion theory for light reflectance by turbid media,” J. Opt. Soc. Am. A, 10 (8), 1746 –1752 (1993). http://dx.doi.org/10.1364/JOSAA.10.001746 JOAOD6 0740-3232 Google Scholar

19.

T. HayashiY. KashioE. Okada, “Hybrid Monte Carlo-diffusion method for light propagation in tissue with a low-scattering region,” Appl. Opt., 42 (16), 2888 –2896 (2003). http://dx.doi.org/10.1364/AO.42.002888 APOPAI 0003-6935 Google Scholar

20.

E. AlerstamT. SvenssonS. Andersson-Engels, “Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration,” J. Biomed. Opt., 13 (6), 060504 (2008). http://dx.doi.org/10.1117/1.3041496 JBOPFO 1083-3668 Google Scholar

21.

Q. FangD. A. Boas, “Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units,” Opt. Express, 17 (22), 20178 (2009). http://dx.doi.org/10.1364/OE.17.020178 OPEXFF 1094-4087 Google Scholar

22.

R. C. Haskellet al., “Boundary conditions for the diffusion equation in radiative transfer,” J. Opt. Soc. Am. A, 11 (10), 2727 –2741 (1994). http://dx.doi.org/10.1364/JOSAA.11.002727 JOAOD6 0740-3232 Google Scholar

23.

A. Ishimaru, “Diffusion of a pulse in densely distributed scatterers,” J. Opt. Soc. Am., 68 (8), 1045 (1978). http://dx.doi.org/10.1364/JOSA.68.001045 JOSAAH 0030-3941 Google Scholar

24.

M. S. PattersonB. ChanceB. C. Wilson, “Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties,” Appl. Opt., 28 (12), 2331 –2336 (1989). http://dx.doi.org/10.1364/AO.28.002331 APOPAI 0003-6935 Google Scholar

25.

E. Ohmaeet al., “Cerebral hemodynamics evaluation by near-infrared time-resolved spectroscopy: correlation with simultaneous positron emission tomography measurements,” NeuroImage, 29 (3), 697 –705 (2006). http://dx.doi.org/10.1016/j.neuroimage.2005.08.008 NEIMEF 1053-8119 Google Scholar

26.

J. Zhaoet al., “In vivo determination of the optical properties of infant brain using frequency-domain near-infrared spectroscopy,” J. Biomed. Opt., 10 (2), 024028 (2005). http://dx.doi.org/10.1117/1.1891345 JBOPFO 1083-3668 Google Scholar

27.

A. GibsonJ. HebdenS. R. Arridge, “Recent advances in diffuse optical imaging,” Phys. Med. Biol., 50 (4), R1 (2005). http://dx.doi.org/10.1088/0031-9155/50/4/R01 PHMBA7 0031-9155 Google Scholar

28.

S. TakataniM. D. Graham, “Theoretical analysis of diffuse reflectance from a two-layer tissue model,” IEEE Trans. Biomed. Eng., BME-26 (12), 656 (1979). http://dx.doi.org/10.1109/TBME.1979.326455 IEBEAX 0018-9294 Google Scholar

29.

J. M. Schmittet al., “Multilayer model of photon diffusion in skin,” J. Opt. Soc. Am. A, 7 (11), 2141 (1990). http://dx.doi.org/10.1364/JOSAA.7.002141 JOAOD6 0740-3232 Google Scholar

30.

I. DayanS. HavlinG. H. Weiss, “Photon migration in a two-layer turbid medium a diffusion analysis,” J. Mod. Opt., 39 (7), 1567 (1992). http://dx.doi.org/10.1080/09500349214551581 JMOPEW 0950-0340 Google Scholar

31.

J.-M. Tualleet al., “Real-space Green’s function calculation for the solution of the diffusion equation in stratified turbid media,” J. Opt. Soc. Am. A, 17 (11), 2046 (2000). http://dx.doi.org/10.1364/JOSAA.17.002046 JOAOD6 0740-3232 Google Scholar

32.

G. AlexandrakisT. J. FarrellM. S. Patterson, “Accuracy of the diffusion approximation in determining the optical properties of a two-layer turbid medium,” Appl. Opt., 37 (31), 7401 (1998). http://dx.doi.org/10.1364/AO.37.007401 APOPAI 0003-6935 Google Scholar

33.

T. J. FarrellM. S. PattersonM. Essenpreis, “Influence of layered tissue architecture on estimates of tissue optical properties obtained from spatially resolved diffuse reflectometry,” Appl. Opt., 37 (10), 1958 (1998). http://dx.doi.org/10.1364/AO.37.001958 APOPAI 0003-6935 Google Scholar

34.

M. A. Franceschiniet al., “Influence of a superficial layer in the quantitative spectroscopic study of strongly scattering media,” Appl. Opt., 37 (31), 7447 (1998). http://dx.doi.org/10.1364/AO.37.007447 APOPAI 0003-6935 Google Scholar

35.

A. KienleT. Glanzmann, “In vivo determination of the optical properties of muscle with time-resolved reflectance using a layered model,” Phys. Med. Biol., 44 (11), 2689 (1999). http://dx.doi.org/10.1088/0031-9155/44/11/301 PHMBA7 0031-9155 Google Scholar

36.

F. MartelliS. Del BiancoG. Zaccanti, “Procedure for retrieving the optical properties of a two-layered medium from time-resolved reflectance measurements,” Opt. Lett., 28 (14), 1236 (2003). http://dx.doi.org/10.1364/OL.28.001236 OPLEDP 0146-9592 Google Scholar

37.

F. Martelliet al., “Analytical approximate solutions of the time-domain diffusion equation in layered slabs,” J. Opt. Soc. Am. A, 19 (1), 71 (2002). http://dx.doi.org/10.1364/JOSAA.19.000071 JOAOD6 0740-3232 Google Scholar

38.

F. Martelliet al., “Phantom validation and in vivo application of an inversion procedure for retrieving the optical properties of diffusive layered media from time-resolved reflectance measurements,” Opt. Lett., 29 (17), 2037 (2004). http://dx.doi.org/10.1364/OL.29.002037 OPLEDP 0146-9592 Google Scholar

39.

M. DasC. XuQ. Zhu, “Analytical solution for light propagation in a two-layer tissue structure with a tilted interface for breast imaging,” Appl. Opt., 45 (20), 5027 (2006). http://dx.doi.org/10.1364/AO.45.005027 APOPAI 0003-6935 Google Scholar

40.

J.-M. Tualleet al., “Asymptotic behavior and inverse problem in layered scattering media,” J. Opt. Soc. Am. A, 21 (1), 24 –34 (2004). http://dx.doi.org/10.1364/JOSAA.21.000024 JOAOD6 0740-3232 Google Scholar

41.

X. WangS. Wang, “Light transport model in an-layered mismatched tissue,” Waves Random Complex Media, 16 (2), 121 –135 (2006). http://dx.doi.org/10.1080/17455030600683321 1745-5030 Google Scholar

42.

A. LiemertA. Kienle, “Light diffusion in N-layered turbid media: steady-state domain,” J. Biomed. Opt., 15 (2), 025003 (2010). http://dx.doi.org/10.1117/1.3368685 JBOPFO 1083-3668 Google Scholar

43.

A. LiemertA. Kienle, “Light diffusion in N-layered turbid media: frequency and time domains,” J. Biomed. Opt., 15 (2), 025002 (2010). http://dx.doi.org/10.1117/1.3368682 JBOPFO 1083-3668 Google Scholar

44.

Q. LiuN. Ramanujam, “Experimental proof of the feasibility of using an angled fiber-optic probe for depth-sensitive fluorescence spectroscopy of turbid media,” Opt. Lett., 29 (17), 2034 –2036 (2004). http://dx.doi.org/10.1364/OL.29.002034 OPLEDP 0146-9592 Google Scholar

45.

T. J. PfeferA. AgrawalR. A. Drezek, “Oblique-incidence illumination and collection for depth-selective fluorescence spectroscopy,” J. Biomed. Opt., 10 (4), 044016 (2005). http://dx.doi.org/10.1117/1.1989308 JBOPFO 1083-3668 Google Scholar

46.

R. ReifO. A’AmarI. J. Bigio, “Analytical model of light reflectance for extraction of the optical properties in small volumes of turbid media,” Appl. Opt., 46 (29), 7317 –7328 (2007). http://dx.doi.org/10.1364/AO.46.007317 APOPAI 0003-6935 Google Scholar

47.

M. Dehaeset al., “Assessment of the frequency-domain multi-distance method to evaluate the brain optical properties: Monte Carlo simulations from neonate to adult,” Biomed. Opt. Express, 2 (3), 552 (2011). http://dx.doi.org/10.1364/BOE.2.000552 BOEICL 2156-7085 Google Scholar

48.

L. WangS. L. Jacques, “Use of a laser beam with an oblique angle of incidence to measure the reduced scattering coefficient of a turbid medium,” Appl. Opt., 34 (13), 2362 –2366 (1995). http://dx.doi.org/10.1364/AO.34.002362 APOPAI 0003-6935 Google Scholar

49.

G. Marquezet al., “Anisotropy in the absorption and scattering spectra of chicken breast tissue,” Appl. Opt., 37 (4), 798 –804 (1998). http://dx.doi.org/10.1364/AO.37.000798 APOPAI 0003-6935 Google Scholar

50.

J. Xiaet al., “Monitoring sarcomere structure changes in whole muscle using diffuse light reflectance,” J. Biomed. Opt., 11 (4), 040504 (2006). http://dx.doi.org/10.1117/1.2234278 JBOPFO 1083-3668 Google Scholar

51.

A. Garcia-Uribeet al., “In vivo diagnosis of melanoma and nonmelanoma skin cancer using oblique incidence diffuse reflectance spectrometry,” Cancer Res., 72 (11), 2738 –2745 (2012). http://dx.doi.org/10.1158/0008-5472.CAN-11-4027 CNREA8 0008-5472 Google Scholar

52.

S.-P. Linet al., “Measurement of tissue optical properties by the use of oblique-incidence optical fiber reflectometry,” Appl. Opt., 36 (1), 136 (1997). http://dx.doi.org/10.1364/AO.36.000136 APOPAI 0003-6935 Google Scholar

53.

P. van der ZeeM. EssenpreisD. T. Delpy, “Optical properties of brain tissue,” Proc. SPIE, 1888 454 –465 (1993). http://dx.doi.org/10.1117/12.154665 Google Scholar

54.

Y. FukuiY. AjichiE. Okada, “Monte Carlo prediction of near-infrared light propagation in realistic adult and neonatal head models,” Appl. Opt., 42 (16), 2881 –2887 (2003). http://dx.doi.org/10.1364/AO.42.002881 APOPAI 0003-6935 Google Scholar

55.

M. J. Purves, The Physiology of the Cerebral Circulation, Cambridge University Press, Cambridge (1972). Google Scholar

56.

S. J. Matcheret al., “Performance comparison of several published tissue near-infrared spectroscopy algorithms,” Anal. Biochem., 227 (1), 54 –68 (1995). http://dx.doi.org/10.1006/abio.1995.1252 ANBCA2 0003-2697 Google Scholar

57.

T. F. ColemanY. Li, “An interior trust region approach for nonlinear minimization subject to bounds,” SIAM J. Optim., 6 (2), 418 –445 (1996). http://dx.doi.org/10.1137/0806023 SJOPE8 1095-7189 Google Scholar

58.

T. F. ColemanY. Li, “On the convergence of interior-reflective Newton methods for nonlinear minimization subject to bounds,” Math. Programm., 67 (1–3), 189 –224 (1994). http://dx.doi.org/10.1007/BF01582221 0025-5610 Google Scholar

Biography

Idan Steinberg received his BSc and MSc in BME from Tel Aviv University, Israel. He is currently pursuing his PhD in BME at Tel Aviv University, focusing on developing multispectral photo-acoustic technique for evaluation of bone pathologies. He is the recipient of the Charles Clore and the Sackler’s biophysics scholarships. He has published several papers, a book chapter and has given several talks. He is the founder and acting president of the local SPIE student chapter.

Osnat Harbater received her BSc degree in biomedical engineering from the Technion—Israeli Institute of Technology, Israel in 2004 and her MSc degree in biomedical engineering in Tel-Aviv University, Israel in 2011. She is currently pursuing her PhD degree in biomedical engineering at Tel-Aviv University, Israel. Her research interests include photon propagation models in tissue, developing novel optical methods for diagnosing Alzheimer’s disease, monitoring cerebral hemodynamics and optical imaging modalities for additional medical applications.

Israel Gannot received his PhD from Tel-Aviv University in 1994. Between 1994 and 1997, he held a National Academy Sciences postdoctoral fellowship. Since 1997 he is a member of the Biomedical Engineering Department at Tel-Aviv University, where he served as a chair. Currently he is also a research professor at Johns Hopkins University. He is a fellow of SPIE, ASLMS, and AIMBE. He authored 60 papers, 90 proceeding papers, 7 book chapters, and 14 patents.

Citation Download Citation

Idan Steinberg, Osnat Harbater, and Israel Gannot "Robust estimation of cerebral hemodynamics in neonates using multilayered diffusion model for normal and oblique incidences," Journal of Biomedical Optics 19(7), 071406 (6 March 2014). https://doi.org/10.1117/1.JBO.19.7.071406

Published: 6 March 2014

Access the abstract

JOURNAL ARTICLE
13 PAGES

DOWNLOAD PAPER SAVE TO MY LIBRARY

GET CITATION

CITATIONS

Cited by 2 scholarly publications.

Explore citations on Lens.org

RIGHTS & PERMISSIONS

Get copyright permission Get copyright permission on Copyright Marketplace

KEYWORDS

Diffusion

Reflectivity

Absorption

Tissues

Scattering

Multilayers

Brain

1.

Introduction

2.

Methods

2.1.

Theoretical Model

Fig. 1

Eq. (1)

Eq. (2)

Eq. (3)

Eq. (4)

Eq. (5)

Eq. (6)

Eq. (7)

Eq. (8)

Eq. (9)

Eq. (10)

Eq. (11)

Eq. (12)

2.2.

Model Validation

Table 1

Eq. (13)

2.3.

Estimation of Oxygenation Level

Eq. (14)

Eq. (15)

3.

Results

3.1.

Comparison with Semi-Infinite Homogeneous Solution

Fig. 2

3.2.

Model Validation against MC Simulations

Fig. 3

3.3.

Assessment of Model’s Accuracy for Different Optical Properties

Fig. 4

Fig. 5

Fig. 6

3.4.

Spatially Resolved Reflectance

Fig. 7

Fig. 8

3.5.

Oblique Incidence

Fig. 9

Table 2

Fig. 10

Eq. (16)

3.6.

Estimation of the Oxygenation Saturation Level

Fig. 11

4.

Discussion

Acknowledgments

References

Biography

Show All Keywords

Keywords/Phrases

Search In:

Publication Years