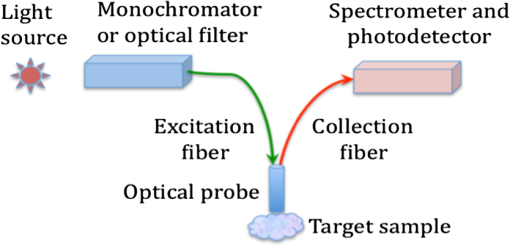
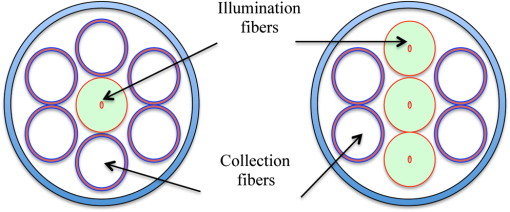
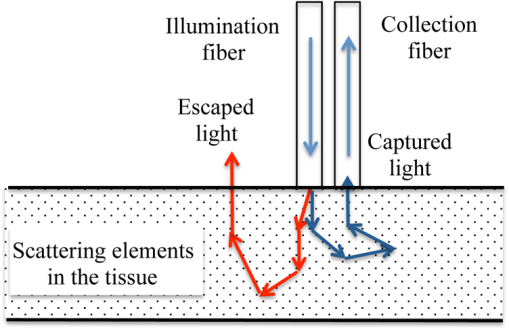
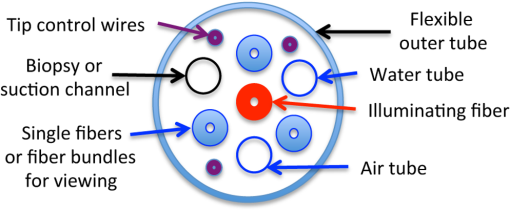
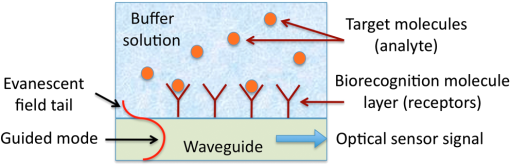
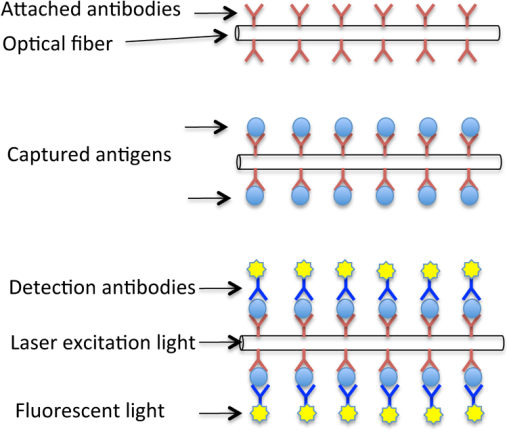
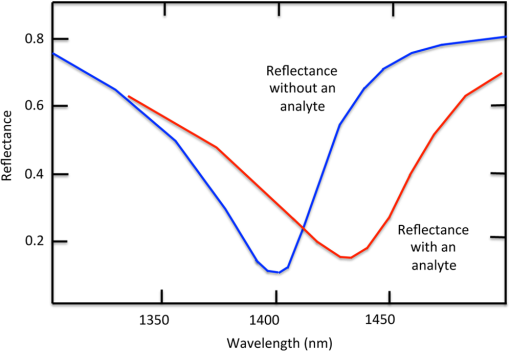
|
|
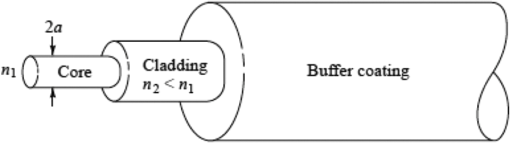
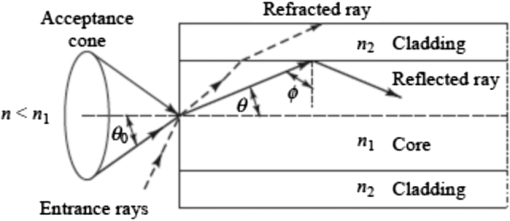
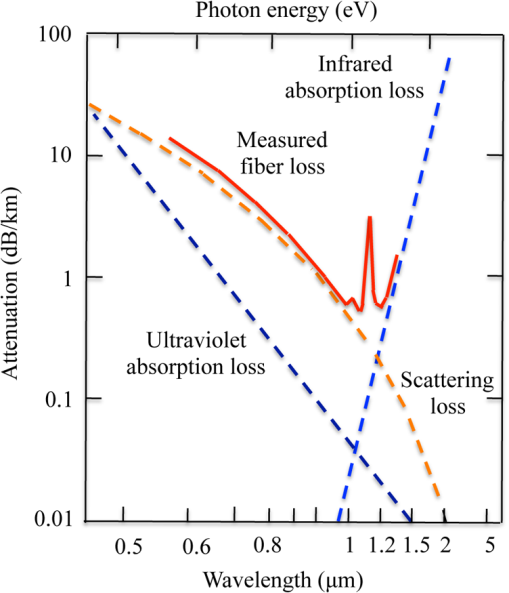
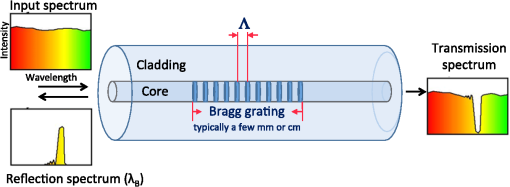
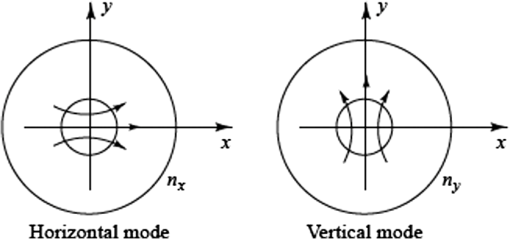
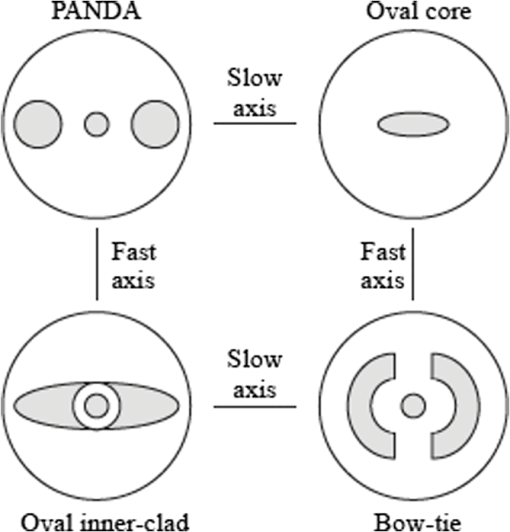
1.IntroductionIn recent years, there has been an extensive and rapidly growing use of photonics technology for basic life sciences research and for biomedical diagnosis, therapy, monitoring, and surgery.1–3 Among the numerous diverse applications are imaging, spectroscopy, endoscopy, tissue pathology, blood flow monitoring, light therapy, biosensing, biostimulation, laser surgery, dentistry, dermatology, and health status monitoring. Major challenges in biophotonics applications to life sciences include how to collect and transmit low-power (down to the nanowatt range) emitted light to a photodetector, how to deliver a wide range of optical power levels to a tissue area or section during different categories of therapeutic healthcare sessions, and how to access a diagnostic or treatment area within a living being with an optical detection probe or a radiant energy source in the least invasive manner. Depending on the application, all three of these factors may need to be addressed at the same time. The unique physical and light-transmission properties of optical fibers enable them to help resolve such implementation issues. Consequently, various types of optical fibers are finding widespread use in biophotonics instrumentation for life sciences related clinical and research applications. Each optical fiber structure has certain advantages and limitations for specific uses in different spectral bands. Therefore, it is essential that biophotonics researchers and implementers know which type of fiber is best suited for a certain application. This paper provides the background that is necessary to understand how optical fibers function, explains various categories of fibers, and illustrates how certain fibers are used for specific biophotonics implementations. To understand when and where to use specific optical fiber types, some background information is presented in Sec. 2 on why various lightwave bands in the ultraviolet, visible, and infrared regions are of interest for biomedical diagnostic and therapeutic implementations. Next, Sec. 3 discusses the fundamental principles for light guiding in conventional solid-core fibers. This discussion will be used as a basis for describing light guiding in other optical fiber structures. In addition, Sec. 3 also describes the optical fiber performance characteristics needed for specific spectral bands. With this background information, Sec. 4 then presents several categories of optical fiber structures and materials that are appropriate for use at different wavelengths. This discussion includes conventional and specialty multimode and single-mode solid-core fibers, double-clad fibers (DCFs), hard-clad silica (HCS) fibers, conventional hollow-core fibers, photonic crystal fibers (PCFs), polymer optical fibers (POFs), side-emitting and side-firing fibers, middle-infrared fibers, and optical fiber bundles. Included in this discussion are the fiber materials that are appropriate for use at different wavelengths. Finally, Sec. 5 describes some examples of optical fiber applications to various biomedical disciplines. 2.Biophotonics Spectral WindowsThis section describes the fundamental background as to why specific lightwave windows are needed to carry out various therapeutic and diagnostic biomedical photonics processes. Having this knowledge allows the selection of an optical fiber whose specification could meet the transmission criteria for carrying out a specific biomedical process. The interaction of light with biological tissues and fluids is a complex process because the constituent materials are optically inhomogeneous. Because diverse biological tissue components have different indices of refraction, the refractive index along some path through a given tissue volume can vary continuously or undergo abrupt changes at material boundaries, such as at flesh and blood vessel or bone interfaces. This spatial index variation gives rise to scattering, reflection, and refraction effects in the tissue.4–12 Thus, although light can penetrate several centimeters into a tissue, strong scattering of light can prevent observers from getting a clear image of tissue abnormalities beyond a few millimeters in depth. Light absorption is another important factor in the interaction of light with tissue, because the degree of absorption determines on how far light can penetrate into a specific tissue. Figure 1 shows the absorption coefficients for several major tissue components. These components include water ( of the body), whole blood, melanin, epidermis, and blood vessels. The wavelengths of interest span the spectral range from in the ultraviolet (UV) to in the infrared (IR). Fig. 1Absorption coefficients of water, hemoglobin (), melanin, and skin as a function of wavelength. 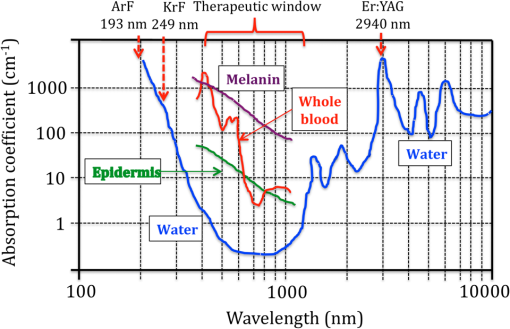 Most tissues exhibit comparatively low absorption in the spectral range that extends from 500 to , that is, from the orange region in the visible spectrum to the near-infrared (NIR). This wavelength band is popularly known as the therapeutic window or the diagnostic window because it enables viewing or treating tissue regions within a living body by optical means. Light absorption characteristics of tissue for regions outside the therapeutic window are important for implementing functions that depend on high optical power absorption, such as drilling, cutting, bonding, and ablation of tissue. A wide variety of optical sources can be used to carry out these functions.1,13–16 For example, as indicated in Fig. 1, UV light from ArF or KrF lasers emitting at wavelengths of 193 and 249 nm, respectively, is strongly absorbed in the surface of a tissue and, thus, can be used for many surgical applications. As an example, in the IR region, the 2940-nm light from an Er:YAG laser is strongly absorbed by osseous minerals, which makes optical sawing and drilling in bones and teeth possible. 3.Optical Fiber Structures and Performance CharacteristicsThis section discusses the fundamental principles for light guiding in conventional optical fibers. Here the term conventional refers to the structure of optical fibers that are widely used in telecom networks. This discussion will set a basis for describing light guiding in other optical fiber structures that are presented in Sec. 4. In addition, Sec. 3 also describes the performance characteristics needed for specific spectral regions, for example, optical signal attenuation, bending loss sensitivity, mechanical properties, and optical power-handling capabilities.17–23 3.1.Light Guiding Principles in Conventional Optical FibersAn optical fiber is a dielectric waveguide that operates at optical frequencies. This fiber waveguide is normally cylindrical in form. It confines electromagnetic energy in the form of light within its surfaces and guides the light in a direction parallel to its axis. The propagation of light along a waveguide can be described in terms of a set of guided electromagnetic waves called the modes of the waveguide. Each guided mode is a pattern of electric and magnetic field distributions that is repeated along the fiber at equal intervals. Only a certain discrete number of modes are capable of propagating along the waveguide. These modes are those electromagnetic waves that satisfy the homogeneous wave equation in the fiber and the boundary condition at the waveguide surfaces. Figure 2 shows a schematic of a conventional optical fiber, which consists of a cylindrical silica-based glass core surrounded by a glass cladding that has a slightly different composition.17–19 The core of diameter 2a has a refractive index and the cladding has a slightly lower refractive index . Surrounding these two layers is a polymer buffer coating that protects the fiber from mechanical and environmental effects. The refractive index of pure silica varies with wavelengths ranging from 1.453 at 850 nm to 1.445 at 1550 nm. By adding certain impurities, such as germanium dioxide (), to the silica during the fiber manufacturing process, the index can be slightly changed. This is done so that the refractive index of the cladding is slightly smaller than the index of the core (i.e., ). This condition is required so that light traveling in the core is totally internally reflected at the boundary with the cladding, which is the physical mechanism that guides light signals along a fiber. The variations in material and size of the conventional solid-core fiber structure dictate how a light signal is transmitted along a fiber and also influence how the fiber performance responds to environmental perturbations, such as stress, bending, and temperature variations. Variations in the material composition of the core give rise to two commonly used fiber types, as shown in Fig. 3. In the first case, the refractive index of the core is uniform throughout and undergoes an abrupt change (or step) at the cladding boundary. This is called a step-index fiber. In the second case, the core refractive index varies as a function of the radial distance from the center of the fiber. This type is a graded-index fiber. Fig. 3Comparison of conventional single-mode and multimode step-index and graded-index optical fibers. 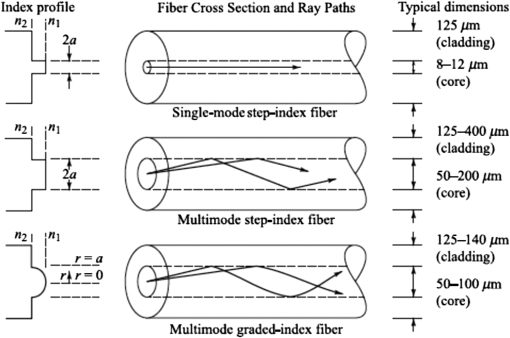 Both the step- and the graded-index fibers can be further divided into single-mode and multimode classes. As the name implies, a single-mode fiber (SMF) sustains only one mode of propagation, whereas a multimode fiber (MMF) contains many hundreds of modes. A few typical sizes of SMF and MMF are given in Fig. 3 to provide an idea of the dimensional scale. MMFs offer several advantages compared with SMFs. The larger core radii of MMFs make it easier to launch optical power into the fiber and to collect light emitted or reflected from a biological sample. SMFs are more advantageous when delivering a narrow light beam to a specific tissue area and also are needed for applications that deal with coherence effects between propagating light beams. The remainder of Sec. 3.1 describes the operational characteristics of step-index fibers, and Sec. 3.2 describes graded-index fiber structures. 3.1.1.Ray optics conceptsTo get an understanding of how light travels along a fiber, first consider the case when the core diameter is much larger than the wavelength of the light. For such a case, a simple geometric optics approach based on the concept of light rays can be used. Figure 4 shows a light ray entering the fiber core from a medium of refractive index , which is less than the index of the core. When the ray meets the fiber end face, it is refracted into the core and propagates at an angle , which is smaller than the entrance angle of that ray. Inside the core, the ray strikes the core-cladding interface at an angle relative to the normal to the surface. If the light ray strikes this interface at such an angle that it is totally internally reflected, the ray becomes confined to the core region and follows a zigzag path as it travels along the fiber. From Snell’s law, the minimum or critical angle that supports total internal reflection is given by Rays striking the core-cladding interface at angles less than will refract out of the core and be lost in the cladding as the dashed line shows. The condition of Eq. (1) can be related to the maximum entrance angle , which is called the acceptance angle , through the relationship where . Thus, those rays having entrance angles less than will be totally internally reflected at the core-cladding interface. Thus, defines an acceptance cone for an optical fiber. Rays outside of the acceptance cone, such as the ray shown by the dashed line in Fig. 4, will refract out of the core and be lost in the cladding.The critical angle also defines a parameter called the numerical aperture (NA), which is used to describe the light acceptance or gathering capability of fibers that have a core size much larger than a wavelength.5,17,18 This parameter defines the size of the acceptance cone shown in Fig. 4. NA is a dimensionless quantity that is less than unity, with values nominally ranging from 0.14 to 0.50. NA is given by The parameter is called the core-cladding index difference or simply the index difference. It is defined through the equation . Typical values of range from 1 to 3 percent for MMF and from 0.2 to 1.0 percent for SMF. Thus, since is much less than 1, the approximation on the right-hand side of Eq. (3) is valid. Because NA is related to the maximum acceptance angle, it is commonly used to describe the light acceptance or gathering capability of an MMF and to calculate the source-to-fiber optical power coupling efficiencies. The NA value is listed on vendor data sheets for fibers. 3.1.2.Modal conceptsAlthough the ray representation gives a general picture of light propagation along a fiber, mode theory is needed for a more detailed understanding of concepts such as mode coupling, dispersion, coherence or interference phenomena, and light propagation in single-mode and few-mode fibers. Figure 5 is a longitudinal cross-sectional view of an optical fiber that shows the field patterns of some of the lower-order transverse electric. The order of a mode is equal to the number of field zeroes across the guiding core. The plots show that the electric fields of the guided modes are not completely confined to the core but extend partially into the cladding. The fields vary harmonically in the core region of refractive index and decay exponentially in the cladding of refractive index . For low-order modes, the fields are tightly concentrated near the axis of an optical fiber with little penetration into the cladding region. Higher-order mode fields are distributed more toward the edges of the core and penetrate farther into the cladding. Fig. 5Electric field distributions of lower-order guided modes in an optical fiber (longitudinal cross-sectional view). 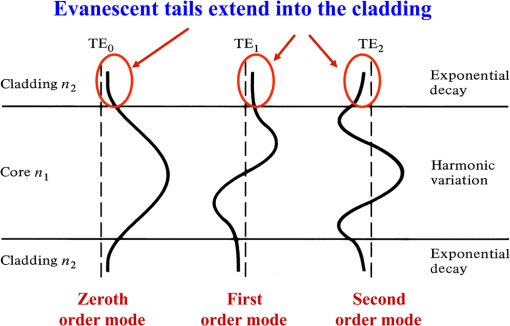 As the core radius shown in Fig. 2 is made progressively smaller, all modes except the fundamental mode shown in Fig. 5 will start getting cut off. A fiber in which only the fundamental mode can propagate is an SMF. An important parameter related to the cutoff condition is the number defined by where the approximation on the right-hand side comes from Eq. (3). This parameter is a dimensionless number that determines how many modes a fiber can support. Except for the lowest-order fundamental mode, each mode can exist only for values of that exceed the limiting value (with each mode having a different limit). The wavelength at which all higher-order modes are cut off is called the cutoff wavelength . For example, if and , then from Eq. (4), with , the cutoff wavelength is . That is, only the fundamental mode will propagate in the fiber for wavelengths . The fundamental mode has no cutoff and ceases to exist only when the core diameter is zero. This is the principle on which SMFs are based.The number can be also used to express the number of modes in a multimode step-index fiber when is large. For this case, an estimate of the total number of modes supported in such a fiber is Because the field of a guided mode extends partly into the cladding, as shown in Fig. 5, another quantity of interest for a step-index fiber is the fractional power flow in the core and cladding for a given mode. As the number approaches cutoff for any particular mode, more of the power of that mode is in the cladding. At the cutoff point, all the optical power of the mode resides in the cladding. For large values of far from cutoff, the fraction of the average optical power residing in the cladding can be estimated by where is the total optical power in the fiber.In an SMF, the geometric distribution of light in the propagating mode is needed when predicting the performance characteristics of these fibers, such as splice loss, bending loss, cutoff wavelength, and waveguide dispersion. Thus, a fundamental parameter of an SMF is the mode-field diameter (MFD), which can be determined from the mode-field distribution of the fundamental fiber mode.17,18,21 MFD is a function of the optical source wavelength, the core radius, and the refractive index profile of the fiber. MFD is analogous to the core diameter in an MMF, except that in an SMF, not all the light that propagates through the fiber is carried in the core. A standard technique to find MFD is to measure the far-field intensity distribution and then calculate the MFD using the Petermann II equation.17,18 where the parameter (with being called the spot size or the mode field radius) is the full width of the far-field distribution. For calculation simplicity, the exact field distribution can be fitted to a Gaussian function. where is the radius and is the field at zero radius, as shown in Fig. 6. Then MFD is given by the width of the optical power. The Gaussian pattern given in Eq. (8) is a good approximation for values of lying between 1.8 and 2.4, which designates the operational region of practical SMFs. An approximation of the relative spot size , which, for a step-index fiber, has an accuracy better than 1% in the range , is given byFig. 6Distribution of light in a single-mode fiber (SMF) above its cutoff wavelength. For a Gaussian distribution, the mode-field diameter is given by the width of the optical power. 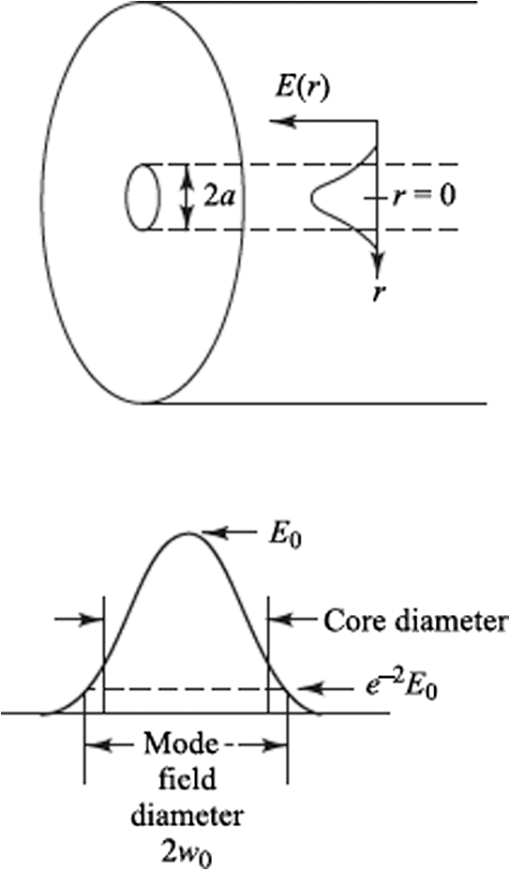 Manufacturers typically design an SMF to have values to prevent high cladding losses, but to avoid the possibility of having more than one mode in the fiber. 3.2.Graded-Index Optical Fibers3.2.1.Core index structureIn the graded-index fiber design, the core refractive index continuously decreases with an increasing radial distance from the center of the fiber but is generally constant in the cladding. The most commonly used construction for the refractive-index variation in the core is the power law relationship. Here, is the radial distance from the fiber axis, is the core radius, is the refractive index at the core axis, is the refractive index of the cladding, and the dimensionless parameter defines the shape of the index profile. The index difference for the graded-index fiber is given by The approximation on the right-hand side reduces this expression for to that of the step-index fiber. Thus, the same symbol is used in both cases. For , inside the core, Eq. (10) reduces to the step-index profile . 3.2.2.Graded-index numerical apertureDetermining the NA for graded-index fibers is more complex than for step-index fibers because it is a function of position across the core end face. This is in contrast to the step-index fiber, where NA is constant across the core. Geometrical optics considerations show that light incident on the fiber core at position will propagate as a guided mode only if it is within the local numerical aperture at that point. The local NA is defined as where the axial NA is defined asThus, the NA of a graded-index fiber decreases from NA(0) to zero as moves from the fiber axis to the core-cladding boundary. The number of bound modes in a graded-index fiber is Fiber manufacturers typically choose a parabolic refractive index profile given by . In this case, , which is half the number of modes supported by a step-index fiber (for which ) that has the same value. 3.2.3.Cutoff condition in graded-index fibersSimilar to step-index fibers, in order to eliminate intermodal dispersion, graded-index fibers can be designed as an SMF in which only the fundamental mode is allowed to propagate at the desired operational wavelength. An empirical expression of the parameter at which the second lowest-order mode is cut off for graded-index fibers has been shown to be17,18 Equation (15) shows that, in general, for a graded-index fiber, the value of decreases as the profile parameter increases. It also shows that the critical value of for the cutoff condition in parabolic graded-index fibers () is a factor of larger than for a similar-sized step-index fiber. Furthermore, from the definition of given by Eq. (4), the NA of a graded-index fiber is larger than that of a step-index fiber of comparable size. 3.3.Performance Characteristics of Generic Optical FibersWhen considering the type of fiber to use in a particular biophotonics system application, some performance characteristics that need to be taken into account are optical signal attenuation as a function of wavelength, optical power-handling capability, the degree of signal loss as the fiber is bent, and mechanical properties of the optical fiber. 3.3.1.Attenuation versus wavelengthAttenuation is due to absorption, scattering, and radiative losses of optical energy as light propagates along a fiber. For convenience of power-budget calculations, attenuation is measured in units of decibels per kilometer () or decibels per meter (). A variety of materials are used to make different types of optical fibers. The basic reason for providing such a selection is that each material type exhibits different light-attenuation characteristics in various spectral bands. For example, silica () glass is the principal material used to make conventional solid-core fibers for telecom applications. It has low losses in the 800- to 1600-nm region, but the loss is significantly higher at shorter and longer wavelengths. Thus, as Sec. 4 describes, other fiber types and/or materials are needed for biophotonics applications that use wavelengths outside of the telecom spectral band. 3.3.2.Bend-loss insensitivityAs described in Sec. 4.2.3, standard optical fibers exhibit radiative losses whenever the fiber is bent. For slight bends, this loss is negligible. However, as the radius of curvature decreases, the bending-induced loss exponentially increases and at a certain critical radius, the loss becomes extremely large. Specially designed fibers with an NA moderately higher than that in a conventional SMF are less sensitive to bending loss. Bend-insensitive fibers are commercially available to provide an optimum low bending loss performance at specific operating wavelengths, such as 820 or 1550 nm. These fibers are available with an cladding diameter as standard products. In addition to low bending losses, the smaller outer diameter of these fibers yields a much smaller coil volume compared with a standard cladding diameter when a length of this low-bend-loss fiber is coiled up within a miniature optoelectronic device package or in a compact biophotonics instrument. Section 4.2.3 presents more details on specialty optical fibers that are robust toward bending-induced power losses. Other fiber classes that exhibit low bending-induced losses include HCS fibers (see Sec. 4.4) and various types of PCFs (see Sec. 4.6). 3.3.3.Mechanical propertiesThere are a number of unique mechanical properties of optical fibers that make them attractive for biomedical applications. One important mechanical factor is that optical fibers consist of a thin highly flexible medium, which allows various minimally invasive medical treatments or diagnostic procedures to take place in a living body. As described in Sec. 5, these procedures can include endoscopy, bronchoscopy, cardiovascular surgery, and microsurgery. Several factors can affect the mechanical integrity of optical fibers used in biomedical environments.20–23 Among these effects are potential strength degradations due to repeated sterilization processes, long-term exposure to UV light, damage to fibers and connectors due to improper handling, and exposure to extremely high optical power levels. A second important mechanical characteristic is that by monitoring or sensing some intrinsic physical variation of an optical fiber, such as elongation or refractive index changes, one can create fiber sensors to measure many types of external physical parameter changes. For example, if the external parameter elongates the fiber or induces refractive index changes, this effect can modulate the intensity, phase, polarization, wavelength, or transit time of light in the fiber. The degree of light modulation is then a direct measure of changes in the external physical parameter. For biophotonics applications, the external physical parameters of interest include pressure, temperature, stress, strain, and the molecular composition of a liquid or gas surrounding the fiber. Section 5.8 gives some examples of these biosensor applications. 3.3.4.Optical power-handling capabilityAlthough in some biomedical photonics applications, such as imaging and fluorescence spectroscopy, the optical fibers carry power levels of , in other situations, the fibers must be able to transmit optical power levels of 10 W and higher. A principal application is laser surgery, which includes bone ablation, cardiovascular surgery, cosmetic surgery, dentistry, dermatology, eye surgery, and oncology surgery. Hard-clad silica optical fibers with fused silica cores that have very low contaminants are described in Sec. 4.4. These fibers are capable of conducting very high optical power from either a continuous wave (CW) or pulsed laser. Other fibers that are capable of transmitting high optical power levels include conventional hollow-core fibers (see Sec. 4.5), PCFs (see Sec. 4.6), and germanate () glass fibers (see Sec. 4.9). The challenge is the launching of high power levels into a fiber. Artifacts such as dust or scratches on the end face of the fiber can form absorption sites that generate high temperature levels at the fiber tip. In standard connectors where the fibers are glued into the connector housing, these high temperatures cause the surrounding epoxy to break down and give off gases. These gases burn onto the tip of the fiber, causing catastrophic damage to the fiber and the connector. To handle high power levels, various manufacturers have developed special fiber optic patch cords that have carefully prepared fiber end faces and specially designed fiber optic connectors that greatly reduce the susceptibility to thermal damage.22,23 4.Optical Fiber Types and Materials for Use in BiophotonicsThe optical power levels that have to be detected or transmitted in a biophotonics process can vary by ten orders of magnitude depending on the particular application. The detected light levels of interest can be in the nanowatt range for spectroscopic applications, whereas optical power being delivered to a biological specimen can be as high as several watts during light therapy sessions or during laser surgery. Consequently, certain fiber types need to be implemented for specific uses in different spectral bands. The basic fiber structures that can be used in biophotonics applications include conventional solid-core silica fibers, specialty solid-core fibers, DCFs, HCS fibers, conventional hollow-core fibers, PCFs, plastic fibers, side-emitting and side-firing fibers, middle-infrared fibers, and fiber bundles. This section describes the characteristics of these classes of fibers as they apply to biophotonics systems. 4.1.Conventional Optical FibersAs a result of extensive development work for telecom networks, conventional solid-core silica-based optical fibers are highly reliable and are available in a variety of core sizes. These fibers are used worldwide in telecom networks and in many biophotonics applications. Figure 7 shows the optical signal attenuation per kilometer for a standard -doped silica fiber as a function of wavelength and photon energy.17 The shape of the attenuation curve is due to three factors. Intrinsic material absorption due to electronic absorption bands causes high attenuations in the UV region for wavelengths . The Rayleigh scattering effect then starts to dominate the attenuation for wavelengths , but diminishes rapidly because of its behavior. Intrinsic absorption associated with atomic vibration bands in the basic fiber material increases with wavelength and is the dominant attenuation mechanism in the IR region above . As shown in Fig. 7, these attenuation mechanisms produce a low-loss region in silica fibers in the spectral range of 700 to 1600 nm, which matches the low-absorption biophotonics window illustrated in Fig. 1. The attenuation spike around 1400 nm is due to absorption by residual water ions in the silica material. Greatly reducing these ions during the manufacturing process results in a special low-water-content or low-water-peak fiber in which the attenuation spike has been greatly reduced. Conventional optical fibers fall into MMF and SMF categories. Because an SMF sustains only one mode of propagation, whereas MMFs contain many hundreds of modes, an MMF can carry more optical power than an SMF. However, an SMF is needed for applications that deal with coherence effects between propagating light beams. Commercially available MMF can be purchased with standard core diameters of 50, 62.5, 100, , or larger. As Sec. 5 describes, these MMFs are used in areas such as laser or light-emitting diode (LED) light delivery, biostimulation, optical fiber probes, and phototherapy. SMFs have core diameters around , the exact value depending on the wavelength of interest. Applications of SMFs include biomedical fiber sensors used in endoscopes or catheters, in imaging systems, such as optical coherence tomography (OCT) (see Sec. 5.2), and in healthcare sensor systems based on optical fiber sensors. 4.2.Specialty Solid-Core FibersSpecialty solid-core fibers are custom-designed for functions such as manipulating lightwave signals to achieve some type of optical signal-processing function, extending the spectral operating range of the fiber, or sensing variations of a physical parameter, such as temperature or pressure. Incorporation of such features into an optical fiber is achieved through either material or structural variations. For biophotonics applications, the main specialty fiber types are photosensitive fibers for creating internal gratings, fibers resistant to darkening from UV light, bend-loss-insensitive fibers for circuitous routes inside bodies, and polarization-preserving optical fibers for imaging and for fluorescence analyses in spectroscopic systems. 4.2.1.Photosensitive optical fiberA photosensitive fiber is designed so that its refractive index changes when it is exposed to UV light. For example, doping the fiber core material with germanium and boron ions may provide this sensitivity. The main application for such a fiber is to create a short fiber Bragg grating (FBG) in the fiber core, which is a periodic variation of the refractive index along the fiber axis.24–26 This index variation is illustrated in Fig. 8, where is the refractive index of the core of the fiber, is the index of the cladding, and is the period of the grating, that is, the spacing between the maxima of the index variations. If an incident optical wave at a wavelength (which is known as the Bragg wavelength) encounters a periodic variation in the refractive index along the direction of propagation, will be reflected back if the following condition is met: . Here, is the effective refractive index, which has a value falling between the refractive indices of the core and of the cladding. When a specific wavelength meets this condition, this wavelength will get reflected and all others will pass through. FBGs are available in a selection of Bragg wavelengths with spectral reflection bandwidths at a specific wavelength varying from a few picometers to tens of nanometers. As described in Sec. 5.9, an important biophotonics application of an FBG is to sense a variation in a physical parameter, such as temperature or pressure. For example, an external factor, such as strain, will slightly stretch the fiber. This stretching will lengthen the period of the FBG and, thus, will change the value of the specific reflected wavelength. Similarly, rises or drops in temperature will lengthen or shorten the value of , respectively, thereby changing the value of . 4.2.2.Fibers resistant to UV-induced darkeningConventional solid-core silica fibers are highly sensitive to UV light. The intrinsic attenuation is higher in the UV region compared to the visible and NIR spectra, and there are additional losses due to UV-absorbing material defects, which are created by high-energy UV photons. These additional UV-induced darkening losses are known as solarization and occur strongly at wavelengths . Thus, although newly manufactured conventional silica fibers offer low attenuation in the 214- to 254-nm range, upon exposure to an unfiltered deuterium lamp, the transmission of these fibers drops to of the original value within a few hours of continuous UV irradiation. Consequently, conventional silica optical fibers can be used only for applications above . However, recently, special glass material processing techniques, such as the use of pure silica fibers with a low water concentration, infusion of hydrogen into the silica core, or fluorine doping of the cladding, have resulted in fibers that exhibit lower UV sensitivity below 260 nm.27–29 When these types of fibers are exposed to UV light, the attenuation first increases rapidly and then stabilizes to an asymptotic value. The exact asymptotic value and the time to reach the plateau depend on the fiber type from specific manufacturers and on the UV wavelength. Shorter wavelengths result in higher attenuation changes and it takes longer to reach the asymptotic value. For example, Polymicro Technologies reported UV exposure test results from several of their fibers.27 Those tests consisted of launching light from a high-intensity deuterium lamp into a 2-m length of fiber for 4 h. The losses were measured at six different UV wavelengths ranging from 214 to 330 nm. The increase in attenuation and the time needed to reach loss equilibrium for the 2-m FBPI fiber® was as follows for 214, 254, and 330 nm wavelengths:
Solarization-resistant fibers are typically available with core diameters ranging from 50 to . When using these types of fibers, they should first be exposed to UV radiation for 5 min or more (depending on the desired wavelength being used) to establish a loss equilibrium. 4.2.3.Bend-loss-insensitive fiberIn many medical applications of optical fibers within a living body, the fibers need to follow a sinuous path with sharp bends through arteries that snake around bones and organs. Special attention must be paid to this situation, because standard optical fibers exhibit radiative losses whenever the fiber undergoes a bend with a finite radius of curvature. For slight bends, the radiative loss is negligible. However, as the radius of curvature decreases, the losses exponentially increase until at a certain critical radius the losses become extremely large. Thus, special bend-loss-insensitive fibers need to be used for certain implementations. The expansion of optical fiber links directly to homes and businesses has led the telecom industry to develop bend-loss-insensitive fibers that can tolerate numerous sharp bends for indoor installations at operating wavelengths between 960 and 1550 nm.30–32 These same types of fibers can also be used for medical applications. Such fibers have a moderately higher NA than in a standard telecom SMF. Increasing the NA reduces the sensitivity of the fiber to bending loss by confining the optical power more tightly within the core than in a conventional SMF. Bend-loss-insensitive fibers are commercially available from a variety of optical fiber manufacturers. These fibers are offered with either an 80- or a cladding diameter as standard products. The reduced-cladding fiber results in a 40% volume size compared with a cladding when a fiber length is coiled up within a miniature optoelectronic device package or in a biophotonics instrument. As an example, consider the the HI-1060 FLEX® fiber from Corning, Inc. (Corning, New York) designed for use in the 960- to 1665-nm range. This fiber has a lower single-mode cutoff wavelength (), a nominally 50% higher index difference value , and a 25% higher NA (0.20 versus 0.16) than other fibers. The higher NA of low-bend-loss fibers allows an improved coupling efficiency from laser diode sources and to planar waveguides. For a bend radius , the bending-induced loss is negligibly small. For fiber loops with a 10-mm bend radius, the bending loss is per loop across the entire 960- to 1665-nm operating range. A factor to keep in mind is that a mode-mismatch loss can be induced when interconnecting these fibers with standard SMFs due to the smaller MFD of low-bend-loss fibers. However, carefully made splices between these different fibers typically result in losses . 4.2.4.Polarization-maintaining fiberIn a conventional SMF, the fundamental mode consists of two independent orthogonal polarization modes.17,18 These modes may be arbitrarily chosen as the horizontal and vertical polarizations in the direction and direction, respectively, as shown in Fig. 9. In general, the electric field of the light propagating along the fiber is a linear superposition of these two polarization modes and depends on the polarization of the light at the launching point into the fiber. In ideal fibers with perfect rotational symmetry, the two modes are degenerate with equal propagation constants (, where and are the effective refractive indices along the and axes, respectively), and any polarization state injected into the fiber will propagate unchanged. In actual fibers, there are imperfections, such as asymmetrical lateral stresses, noncircular cores, and slight variations in refractive-index profiles. These imperfections break the circular symmetry of the ideal fiber and lift the degeneracy of the two modes. The modes then propagate with different phase velocities, and the difference between their effective refractive indices is called the fiber birefringence. If light is injected into the fiber so that both modes are excited, then one mode will be delayed in phase relative to the other as they propagate. When this phase difference is an integral multiple of , the two modes will beat at this point and the input polarization state will be reproduced. The length over which this beating occurs is the fiber beat length, . In conventional fibers, the small degrees of random imperfections in the core will cause the state of polarization to fluctuate as a light signal propagates through the fiber. In contrast, polarization-maintaining fibers have a special core design that preserves the state of polarization along the fiber with little or no coupling between the two modes. Figure 10 illustrates the cross-sectional geometry of four different polarization-maintaining fibers. The light circles represent the cladding and the dark areas are the core configurations. The goal in each design is to use stress-applying parts to create slow and fast axes in the core. Each of these axes will guide light at a different velocity. Crosstalk between the two axes is suppressed so that polarized light launched into either of the axes will maintain its state of polarization as it travels along the fiber. These fibers are used in special applications, such as fiber optic sensing and interferometry, where polarization preservation is essential.33,34 A further structural refinement uses the bow-tie geometry shown in Fig. 10 in order to create an extreme birefringence in a fiber. Such a birefringence allows one and only one polarization state of the fundamental mode to propagate with all other polarization modes being greatly suppressed. In these fibers, single-polarization guidance occurs in only a limited wavelength range of . Outside of that spectral range, either both of the polarization states or no light at all may be guided. These fibers are used in special fiber optic biosensing applications where it is desirable to monitor a single state of polarization. 4.3.Double-Clad FibersA DCF has found widespread use in constructing optical fiber lasers and now is being used in the medical field for imaging systems, such as endoscopy.35–38 More details on these applications are given in Secs. 5.3 and 5.4. As indicated in Fig. 11, a DCF consists of an inner cladding, an outer cladding, and a core region arranged concentrically. Typical dimensions of a commercially available DCF are a core diameter, an inner cladding diameter of , and an outer cladding with a diameter. Light transmission in the core region is single-mode, whereas in the inner cladding, it is multimode. The typical index of a DCF for biomedical applications is decreasingly cascaded from the core center to the cladding boundary. The integration of both single-mode and multimode transmissions allows using a single optical fiber for the delivery of the illumination light (using the single-mode core) and the collection of the tissue-reflected light (using the multimode inner cladding). 4.4.Hard-Clad Silica FibersA HCS optical fiber is a multimode design that consists of a silica glass core surrounded by a hard thin plastic cladding. The hard cladding increases fiber strength and reduces static fatigue in humid environments. These fibers also feature bend insensitivity, long-term reliability, ease of handling, and resistance to harsh chemicals.39,40 Core diameters of commercially available HCS fibers range from 200 to . Table 1 lists some performance parameters of three selected HCS fibers. A common HCS fiber for industrial and medical applications has a core diameter of and a cladding diameter of , which results in a very strong optical fiber with low attenuation ( at 820 nm), an NA of 0.39, negligible bending-induced loss for bend diameters , and an extremely high core-to-clad ratio to enable efficient light coupling into and out of the fiber. The fibers are available in both high and low content for operation in the UV, visible, and NIR regions. The mechanical, optical, and structural properties of HCS fibers are especially useful in applications like laser delivery, endoscopy, photodynamic therapy (PDT), and biosensing systems. Table 1General specifications of selected hard-clad silica (HCS) fibers.
4.5.Coated Hollow-Core FibersBecause a solid-core silica fiber exhibits tremendously high material absorption above , fibers that have a hollow core with an internal reflection coating provide one alternative solution for the delivery of mid-IR (2 to ) light to a localized site with a low transmission loss. Section 4.9 describes middle-IR fibers as another alternative for operation above . Examples of light sources operating above include () and Er:YAG () lasers, which have wide applications in urology, dentistry, otorhinolaryngology, and cosmetic surgery. In addition, hollow-core fibers are useful in the UV region, where silica-based fibers also exhibit high transmission losses. As shown in Fig. 12, a hollow-core fiber is composed of a glass tube with metal and dielectric layers deposited at the inner surface plus it has a protective jacket on the outside.41–47 In the fabrication process of these fibers, a layer of silver (Ag) is deposited on the inside of a glass tube, which then is covered with a thin dielectric film, such as silver iodide (AgI). Light is transmitted along the fiber through mirror-type reflections from this inner metallic layer. The thickness of the dielectric film (normally ) is selected to give a high reflectivity at a particular IR wavelength or a band of wavelengths. Tubes of other materials, such as plastic and metal, are also employed as hollow-core waveguides, but glass hollow-core fibers provide more flexibility and better performance. The bore sizes (diameters of the fiber hole) can range from 50 to . However, since the loss of all hollow-core fibers varies as , where is the bore radius, the more flexible smaller hollow-core fibers have higher losses. Compared to solid-core fibers, the optical damage threshold is higher in hollow-core fibers, there are no cladding modes, and there is no requirement for angle cleaving or antireflection coating at the fiber end to minimize laser feedback effects. To direct the light projecting from the hollow-core fiber into a certain direction, sealing caps with different shapes (e.g., cone and slanted-end) at the distal end of the fiber have been proposed and demonstrated by using a fusing and polishing technique.45 4.6.Photonic Crystal FibersA PCF differs from a conventional optical fiber in that the PCF has a geometric arrangement of air holes that run along the whole length of the fiber.48–52 A PCF is also referred to as a microstructured fiber or holey fiber. The core of the PCF can be solid or hollow as shown in Fig. 13 by the cross-sectional images of two typical PCF structures. This structural arrangement creates an internal microstructure, which offers another dimension of light control in the fiber. The arrangement, size, and spacing (known as the pitch) of the holes in the microstructure and the refractive index of its constituent material determine the light-guiding characteristics of a PCF. Depending on the PCF structure, light is guided along the fiber either by total internal reflection or by a bandgap effect. Fig. 13Sample structural arrangements of air holes in solid-core (a) and hollow-core (b) photonic crystal fiber (PCF).  The fact that the core can be made of pure silica gives the PCF a number of operational advantages over conventional fibers, which typically have a germanium-doped silica core. These advantages include very low losses, the ability to transmit high optical power levels, and a high resistance to darkening effects from nuclear radiation. The fibers can support single-mode operation over wavelengths ranging from 300 to . The mode field area of a PCF can be compared to the area of a conventional SMF. This allows the PCF to transmit high optical power levels without encountering the nonlinear effects exhibited by conventional fibers. For biophotonics applications, some hollow-core PCFs, such as the Kagome fiber, are promising substitutes for the hollow-core fiber mentioned in Sec. 4.5. These PCFs have a broadened transmission window for delivering middle-IR light with reduced transmission or bending loss.53,54 PCFs are also being used in optical fiber-based biosensors. Section 5.8 discusses a number of these biosensor applications. 4.7.Plastic Optical FibersPOFs are an alternative to glass optical fibers for applications such as biomedical sensors.55–61 POFs were first fabricated in the late 1960s, which makes them about the same age as silica fibers. However, compared to silica fibers, POFs did not become as popular due to factors such as high attenuation, immature fabrication techniques, and low temperature tolerance (). Most POFs are made of polymethylmethacrylate with a refractive index of , which is slightly higher than the index of silica. The size of a POF is normally larger than typical silica fibers, with diameters ranging up to 0.5 mm. In addition to POFs with large core diameters, currently both multimode and single-mode POFs with telecom core sizes are commercially available. The standard core sizes of a multimode POF include 50- and diameters, which are compatible with the core diameters of standard glass telecom MMFs. The development of single-mode POF structures enables the creation of FBGs inside plastic fibers, which, therefore, provides more possibilities for POF-based biosensing. Together with the advantages of low cost, inherent fracture resistance, low Young’s modulus, and biocompatibility, POF has become a viable alternative for silica fibers in biosensing. For example, some special fiber sensor designs, such as the exposed-core technique now being used in etched-core FBG sensors, were first realized by using polymer optical fibers.62–64 Although most POFs have a higher refractive index than silica, a single-mode perfluorinated POF with a refractive index of 1.34 has been fabricated.60 This low-index fiber has the potential for improvement in the performance of biosensors, because it results in a stronger optical coupling between a light signal and the surrounding biosensor analyte. Section 5.8 has more details on biosensors. 4.8.Side-Emitting and Side-Firing FibersIn most cases, the function of optical fibers is to transport light to its intended destination with as little optical power loss and signal distortion as possible. However, a different category of optical fiber that emits light along its entire length is finding increased biomedical applications.65–71 Such a side-emitting fiber or glowing fiber acts as an extended emitting optical source. These side-emitting fibers are widely available and their popular nonmedical applications include decorative lamps, submersible lighting, event lighting, and lighted signs. For medical use, wearable luminous fabric devices consisting of textiles imbedded with glowing fibers are being considered for use as a pulse oximeter and for inflammation and pain reduction, edema treatment, sunburn relief, and wound healing.67,68 Another embodiment for lateral emission of light is the side-firing fiber. As described in Sec. 5.1, this structure consists of an angled end face at the distal end of the fiber. This enables the light to be emitted almost perpendicular to the fiber axis. Uses of side-firing fibers for biomedical procedures include PDT, therapy for atrial fibrillation, treatment of prostate enlargements, and dental treatments.69–71 A variety of fiber materials and construction designs have been used to fabricate side-emitting fibers. Both plastic and silica fibers are available. One popular method of achieving the fiber glowing process is to add scattering materials into either the core or cladding of the fiber. This creates a side-emitting effect through the scattering of light from the fiber core into the cladding and then into the medium outside of the fiber. As Fig. 14 shows, one implementation of a side-emitting fiber is to attach a length of this type of fiber (e.g., 10 to 70 mm for short diffusers or 10 to 20 cm for long diffusers) to a longer delivery fiber (nominally 2 to 2.5 m), which runs from the laser to the side-emitting unit. As a result of scattering effects, the light intensity in a side-emitting fiber exponentially decreases with distance along the fiber. Therefore, the intensity of the side-emitted light will decrease as a function of distance along the fiber. If it is assumed that the side-emitting effect is much stronger than light absorption and other losses in the fiber, then the side-glowing radiation intensity, , that is emitted in any direction per steradian at a point located a distance from the input end of the diffuser is65,66 where is the input radiation intensity and is the side-scattering efficiency coefficient. Typical values of are 0.01 to .In many practical biomedical applications where the glowing fiber lengths are of the order of 10 or 20 cm, the effect of an exponential decrease in side-emitted light intensity may not be a major problem. However, there are two methods for creating a more uniform longitudinal distribution of the side-emitted light. One method is to simultaneously inject light into both ends of the fiber if it is possible to do so. In other applications, a reflector element attached to the distal end of the fiber can produce a relatively uniform emitted light distribution of the combined transmitted and reflected light if the fiber diffuser is not too long. 4.9.Middle-Infrared FibersA middle-IR, or simply an IR, optical fiber transmits light efficiently at wavelengths .72–81 Compared to conventional telecom silica fibers, IR fibers usually are more fragile and have larger refractive indices, lower melting or softening points, and greater thermal expansion. Typically, in biomedical photonics, IR fibers are used in lengths to 3 m for fiber optic sensors and optical power delivery applications. Based on the fiber material and structure used for their fabrication, IR fibers can be classified into glass, crystalline, PCFs, and hollow-core waveguide categories. This section describes glass and crystalline fiber classes. Hollow-core waveguides and PCFs are described in Secs. 4.5 and 4.6, respectively. Glass materials for IR fibers include heavy metal fluorides,72–74 fluoroindates,75 chalcogenides,76,77 and heavy metal germinates.78 Heavy metal fluoride glasses (HMFG) are the only materials that transmit light from UV to mid-IR without any absorption peak. These HMFG fibers are drawn from a preform using the same techniques as are used for silica fibers. Commercial HMFG fibers include (with attenuations of between 1.8 and ) and (with attenuations of between 1.8 and ). Such optical losses allow for practical short- and medium-length applications of a few meters. The reliability of HMFG fibers depends on protecting the fiber from moisture and on pretreatment of the preform to reduce surface crystallization. Thus, HMFG fibers are a good choice for the 1.5- to spectrum, which is increasingly used in medical applications. Chalcogenide glasses are based on the chalcogen elements sulfur, selenium, and tellurium together with the addition of other elements, such as germanium, arsenic, and antimony. These glasses are very stable, durable, and insensitive to moisture. Chalcogenide fibers are able to transmit longer wavelengths in the IR than fluoride glass fibers. Longer wavelengths are transmitted through the addition of heavier elements. All chalcogenide fibers have strong extrinsic absorption resulting from contaminants such as hydrogen. Although the losses of chalcogenides are generally higher than that of the fluoride glasses, these losses are still adequate for about 2-m transmissions in the spectral band ranging from 1.5 to . Some typical loss values are at the widely used 2.7- and wavelengths. The maximum losses for the three common chalcogenides are as follows: Applications of chalcogenide fibers include Er:YAG () and () laser power delivery, microscopy and spectroscopy analyses, and chemical sensing. glass fibers generally contain heavy metal oxides (for example, PbO, , and ) to shift the IR absorption edge to longer wavelengths. The advantage of fibers over HMFG fibers is that glass has a higher laser damage threshold and a higher glass transition temperature, making glass fibers more mechanically and thermally stable than, for example, tellurite glasses. glass has an attenuation of in the spectrum ranging from 1.0 to . A key application of fibers is for laser power delivery from the laser to a patient from Ho:YAG () or Er:YAG () lasers, where the fiber losses nominally are 0.25 and , respectively. These fibers can handle up to 20 W of power for medical procedures in dermatology, dentistry, ophthalmology, orthopedics, and general surgery. Crystalline IR fibers can transmit light at longer wavelengths than IR glasses, for example, transmission up to is possible.79–81 These fibers can be classified into single-crystal and polycrystalline fiber types. Although there are many varieties of halide crystals with excellent IR transmission features, only a few have been fabricated into optical fibers because most of the materials do not meet the required physical property specifications needed to make a durable fiber. Polycrystalline silver-halide fibers with AgBr cores and AgCl claddings have exhibited excellent crystalline IR fiber properties.78–81 There are several extrinsic absorption bands for Ag-halide fibers, for example, 3 and due to residual water ions. The attenuation of Ag-halide fibers is normally in the 5- to spectral band and 0.3 to at and can be as low as at this wavelength. 4.10.Optical Fiber BundlesTo achieve high throughput with flexible glass or plastic fibers, multiple fibers are often arranged in a bundle.81–83 Each fiber acts as an independent waveguide that enables light to be carried over long distances with minimal attenuation. A typical large fiber bundle array can consist of a few thousand to 100,000 individual fibers, with an overall bundle diameter of and an individual fiber diameter between 2 and . Such fiber bundles are mainly used for illumination purposes. In addition to flexibility, fiber bundles have other potential advantages in illumination systems: (1) illuminate multiple locations with one source by splitting the bundle into two or more branches, (2) merge light from several sources into a single output, and (3) integrate different specialty fibers into one bundle. For bundles with a large number of fibers, the arrangement of individual fibers inside the bundle normally randomly occurs during the manufacturing process. However, for certain biomedical applications, it is required to arrange a smaller number of fibers in specific patterns. Optical fibers can be bundled together in an aligned fashion such that the orientations of the fibers at both ends are identical. Such a fiber bundle is called a coherent fiber bundle or an ordered fiber bundle. Here the term coherent refers to the correlation between the spatial arrangement of the fibers at both ends and does not refer to the correlation of light signals. As a result of the matched fiber arrangements on both ends of the bundle, any pattern of illumination incident at the input end of the bundle is maintained and ultimately emerges from the output end. Figure 15 illustrates illumination and coherent fiber bundle configurations. As shown in Fig. 15(a), the optical fibers are randomly oriented on both ends in a bundle configuration that contains hundreds or thousands of fibers. Figure 15(b) shows one possibility of an ordered fiber arrangement in a bundle. In this hexagonal packaging scheme, the central fiber is used for illuminating a target tissue area and the surrounding fibers are used for fluorescent, reflected, or scattered light returning from the tissue. The discussions in Sec. 5 give further examples. Fig. 15(a) Randomly arranged fibers in a bundle containing many optical fibers. (b) Coherent bundle cable with identical arrangements of optical fibers on both ends. 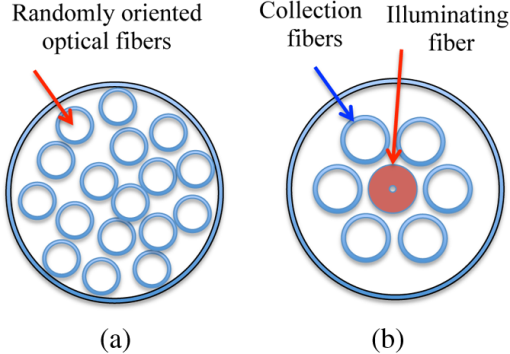 When using optical fiber bundles, there is a trade-off between high light collection efficiency and good image resolution. A large core diameter enables high light transmission but poor image resolution. A thicker cladding avoids crosstalk among individual fibers but limits light collection and image resolution because more of the light-emitting area is blocked when a thicker cladding is used. In practice, the core diameter of individual fibers is 10 to and the cladding thickness is to . Coherent fiber bundles are the key components in modern fiber optic endoscopes. Current sophisticated ear, nose, throat, and urological procedures utilize high-resolution flexible image bundles for image transfer. 5.Biomedical Applications of Optical FibersA major technology evolution of optical fibers was spawned by the telecom industry. The results in terms of material selections, diverse structures, coupling devices, wavelength-selective components, and the associated light sources and photodetectors have enabled a wide range of optical fiber applications to biomedicine. Optical fibers provide a thin and highly flexible medium for minimally invasive procedures to deliver light to diagnostic or treatment areas. In many cases, these areas are located in places within the body that are normally difficult to access. Through the use of optical fibers, thin (nominally 0.5 mm) and flexible medical diagnostic or treatment tools can be inserted directly through natural openings in the body or they can be inserted by means of a rigid structure, such as a needle through minor incisions or punctures in the skin, and guided to the tissue area of interest. This procedure greatly reduces the time spent in a clinic and lessens postoperative pain and discomfort compared to conventional techniques that do not involve optical fibers. In addition to delivering light to a localized area for medical diagnostics or treatment, optical fibers can be used in a feedback mode to collect light that is reflected, scattered, or fluorescently emitted from a tissue specimen and to transmit this light back to an analysis instrument, such as a viewing scope, a camera, or a spectrum analyzer. This section first describes fiber tip geometries used at the distal end. The tip configuration is an important consideration for efficient light delivery and collection in any biophotonics application. Subsequent subsections give examples of how optical fibers are being used in various biomedical research and clinical environments. This is not an exhaustive list, but serves as an introduction to a growing number of biomedical implementations. 5.1.Optical Fiber Biomedical ProbesOptical fibers are widely used as biomedical probes. An important factor to consider when using optical fiber probes for light delivery and collection functions is the tip geometry of the fiber at its distal end. The shape of the tip determines how the light emerging from the fiber is distributed on a tissue sample and also determines the light collection efficiency for viewing the irradiated tissue sample or examining scattered or fluorescing light emitted from the sample.84–96 When deciding on the geometry of an optical fiber tip, parameters that need to be evaluated include the sizes of the illumination and light-collection areas, the collection angle (related to the fiber NA), and the fiber diameter. Another important factor to keep in mind is that biological tissue has a multilayered characteristic from both compositional and functional viewpoints. Specific biological processes and diseases occur at different levels within this multilayered structure. Thus, when designing an optical fiber probe, it is necessary to ensure that the light that is aimed at the targeted biological process or disease penetrates the tissue down to the desired evaluation layer. A generic schematic of an optical fiber-based probe system is shown in Fig. 16. The excitation light can come from optical sources, such as a white light-emitting diode, a deuterium lamp, or a laser diode. Devices such as a dielectric spectral bandpass filter or a monochromator can be used to select a very narrow spectral width for delivery to a tissue sample. The transport fiber to the sample can be any of the fibers described in Sec. 4. If it is used, a return fiber can be selected to be an optical fiber bundle, an SMF, an MMF, a polarization-preserving fiber, a PCF, an IR fiber, or a DCF. In the case of a DCF, the light is typically delivered to the sample using the single-mode core of the fiber and the return path uses the large inner multimode cladding of the fiber for increased light collection efficiency. The photodetector that interprets the returned light can be an instrument such as a viewing scope, a photomultiplier tube (PMT), a charge-coupled device (CCD) camera, or an optical spectrum analyzer. A great number of fiber probe configurations have been analyzed, designed, and implemented. As Figs. 17(a) and 17(b) show, to distribute the light emerging from the fiber, the end face can be cleaved or polished flat or the exit surface can be polished at an angle relative to the fiber axis to deflect the light to the selected area. In other probe embodiments, a miniature lens can be formed or attached to the fiber end or a light-diffusing fiber segment can be attached (see Fig. 14). If the end face angle is equal to the critical angle for total internal reflection [Fig. 17(c)], then the light will leave the fiber through its side. This is the basis of the side-firing fiber. To increase the light illumination or collection efficiency, probe designs with two or more fibers are used. Figures 17(d) and 17(e) show two probe designs based on using either two flat-polished or beveled end faces. Fig. 17Examples of fiber distal end tips. (a) Flat-polished fiber. (b) Angle-polished fiber. (c) Side-emitting fiber. (d) Dual flat-polished fibers. (e) Dual angle-polished fibers. (Reproduced with permission from Ref. 84.) 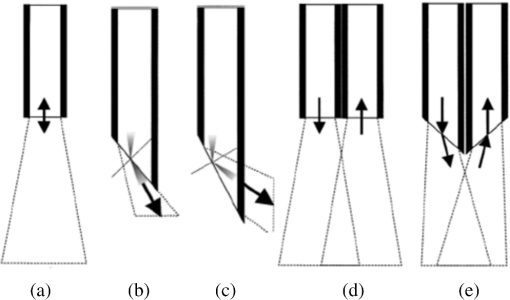 At the expense of having a larger probe, the efficiency can be increased by using more than two fibers for either or both of the illumination and collection functions. Figure 18 shows a classic example of hexagonal packing for a fiber probe. This arrangement enables the use of one or more fibers for illumination or fluorescence excitation with the remaining fibers used as the collection channels. Optionally, optical filters with different spectral pass bands can be deposited on the end faces of individual collection fibers. 5.2.Optical Coherence TomographyOptical imaging is playing an increasingly important role for the diagnosis of living cells and biological tissue. Among the successful medical imaging techniques, OCT has become an important and established noninvasive optical-based tissue diagnosis procedure.97–103 This section addresses three diverse areas of optical fiber uses in OCT. The first area is the use of single-mode silica fibers for transmitting the incident and reflected light in the OCT imaging process. The second application is the use of erbium-doped or ytterbium-doped optical fibers to construct wideband low-coherence fiber laser sources that enable high-resolution imaging. A third application is the use of various types of optical fibers to broaden the emission spectrum from commercially available femtosecond solid-state lasers for image-resolution enhancement. 5.2.1.OCT imaging processFrom the time it was developed for noninvasive imaging of biological tissue in the early 1990s, OCT has been successfully applied to many of the major human biomedical procedures for in vitro and in vivo imaging. As noted in Sec. 2, a biological window exists between and 1500 nm, where light can penetrate several millimeters into tissue. This is the operating region used for OCT, because light attenuation here is more dependent on scattering processes than on absorption processes. OCT performs ranging-based optical imaging in biological tissue due to the fact that a portion of the incident light is reflected by each interface whenever there is a change in refractive index in the biological tissue. Because the velocity of light is extremely high, low-coherence interferometry is utilized to measure the time delay of the reflected light. Low-coherence interferometry is performed using a Michelson-type interferometer. The use of optical fibers enables OCT systems to be compact and portable. Figure 19 shows the schematic of a basic optical fiber-based OCT system. The light from the broadband optical source is divided in half by an optical splitter or coupler and the two halves are sent to the reference arm and the sample arm separately through SMFs. Reflections from the reference arm mirror and from the sample are recombined by the optical coupler and sent to the detector. Because low-coherence light from a broadband source is used, constructive interference of the light only occurs when the optical path lengths are matched between the two arms of the interferometer. In order to achieve a high image resolution, it is necessary to use SMFs. By scanning across the face of the reference arm mirror, a single axial depth scan slice of reflection data is acquired from the sample. By slightly moving the position of the reference mirror, another scan slice is obtained at a different axial depth. Fig. 19A typical optical coherence tomography (OCT) imaging setup (reproduced with permission from Ref. 103). 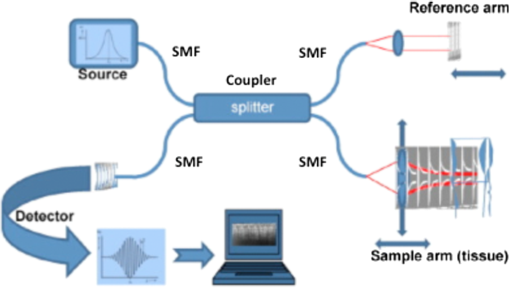 One important parameter for characterizing an OCT system is the imaging resolution. The axial resolution is determined by the coherence length of the source. Given that an OCT system uses a broadband probing light source with a center wavelength , the standard equation for the axial resolution is where is the optical fiber refractive index and is the spectral width of the probing source. Therefore, the axial resolution is directly proportional to the square of the source central wavelength and inversely proportional to the source spectral bandwidth. Thus, to achieve high axial resolution, optical sources with broad spectral bandwidths are desired. It is in the area of spectral broadening that various types of optical fibers are making a significant impact on OCT. Higher resolution could also be achieved by decreasing the center wavelength from the standard 1300-nm value. However, shorter wavelengths are more highly scattered in biological tissue, resulting in less imaging penetration.5.2.2.Fiber laser sources for OCTA variety of technologies have been considered in the quest to find an appropriate OCT light source.104–107 Many OCT systems utilize a superluminescent diode as a low-coherence light source. Superluminescent diodes are compact, have low electrical power requirements, and low noise. But their major limitation is low output powers that limit their use to slow image acquisition rates. The available spectral bandwidths are relatively narrow, limiting their imaging resolution to 10 to . More compact superluminescent optical fiber laser sources have also been developed and characterized for OCT applications. For example, in an ultrahigh-resolution, high-penetration-depth OCT setup, the use of an all-fiber supercontinuum source at 1700 nm was demonstrated.108 A Gaussian-like supercontinuum with a 358-nm bandwidth at a center wavelength of 1700 nm was generated by an ultrashort-pulse Er-doped fiber laser system. A longitudinal resolution of in tissue, with a sensitivity of 95 dB, was achieved. The 1700-nm supercontinuum source was generated by a normal-dispersion highly nonlinear fiber that was preceded by an Er-doped fiber to amplify the ultrashort pulse. A large-mode-area PCF was used for dispersion compensation of the high-power chirped pulse. As another example, an all-fiber 1300-nm ring laser source was demonstrated and proposed for a swept-source OCT system.109 5.2.3.Spectral broadening of solid-state laser outputAlternatively, short-pulse femtosecond solid-state lasers are attractive low-coherence sources for OCT. For example, the titanium:sapphire laser can produce not only broad spectral bandwidths for high-resolution imaging, but also high output powers for fast image acquisition. The ultrashort pulses from these lasers can be coupled into tapered, microstructured, or ultrahigh NA fiber to achieve even broader bandwidths and, hence, higher axial resolution imaging. Therefore, a third optical fiber application area for OCT is to spectrally broaden the femtosecond pulses from solid-state lasers.110–112 An early application of this technique was demonstrated by taking advantage of the high peak intensities associated with femtosecond pulse trains generated by an all solid-state Kerr-lens mode-locked Cr4+:forsterite laser source.110 In this scheme, using self-phase modulation in a dispersion-shifted SMF increased the spectral bandwidth of the source. OCT imaging with a resolution of and a dynamic range of 115 dB was achieved. In another work, a commercially available ultrahigh-NA fiber was adopted to widen the bandwidth of a mode-locked Ti:sapphire laser source to over 200 nm.111 The ultrahigh-NA fiber, which is a standard silica fiber with a nearly pure core, acts as a taper to enhance the nonlinear effect, but would not be fragile or difficult to fabricate. 5.3.Optical SpectroscopyA number of optical spectroscopic methodologies that make use of optical fiber technology are being used in research laboratories and medical clinics for rapid, accurate, and noninvasive detection and diagnosis of premalignant and malignant changes in tissue. In contrast to a standard biopsy that involves the removal of one or more tissue samples for later laboratory evaluation, optical spectroscopic methods eliminate this need for surgical removal of tissue. Instead, by using an optical probe placed on or near the surface of the tissue to be evaluated, an imaging system records some in vivo form of spectral analysis of the tissue. Depending on the method used, the diagnostic information obtained from the biological tissues can be at the biochemical, molecular structural, or physiological levels.113,114 Selections of optical fiber probe applications illustrated here from among the numerous optical spectroscopic methodologies are fluorescence spectroscopy,115,116 elastic scattering spectroscopy,117–119 diffuse correlation spectroscopy (DCS),120 and coherent anti-Stokes Raman scattering (CARS) spectroscopy.121 Each spectroscopic discipline is continuously adopting more sophisticated optical fiber-based systems for delivering probing light to an investigation site, for collecting fluorescence products or scattered imaging light, and for returning this light to photodetection and analysis instruments. 5.3.1.Fluorescence spectroscopyFluorescence spectroscopy instruments generally employ some variation of the generic probe system shown in Fig. 16. In such a setup, to be of analytical use, the wavelength of incident radiation needs to be selectable and the detector signal should be capable of precise spectral manipulation and presentation. Therefore, monochromators or spectrometers are provided for both the selection of the excitation light and the analysis of the emission from the sample. In a fluorescence process, photons from a UV or visible external source are sent by means of an optical fiber to a target area. There the photons can give up their energy to electrons in a molecule, thereby exciting these electrons from their ground state to higher electronic states. Fluorescence occurs when the excited electrons return to their initial state, thereby emitting a photon. The photon energy is equal to the difference in the excited and ground state electron energy. For a given instrument and environmental condition of the tissue being analyzed, the excitation and emission properties of a compound are fixed and can be used for identification and quantification of molecules and molecular processes. The key advantage of fluorescence spectroscopy in the diagnosis of tissue pathology is that the excitation or emission spectra are sensitive to the biochemical composition of the tissue. This feature is helpful in assessing whether the biochemical state of the tissue is normal or malignant. A proper fluorescence probe design is important for efficient transport and collection of photons, which ultimately helps in quantifying the resultant emissions and in understanding light-matter interaction. The fiber parameters that need to be taken into consideration include fiber core and cladding diameters, NA, and core-clad ratio. Numerous embodiments of multiple-fiber and single-fiber probes have been implemented for fiber-based fluorescence spectroscopy systems.86–90,122 One method for using a multiple-fiber probe is to couple the output of the light from the excitation monochromator into one arm of a bifurcated fiber bundle, which delivers the excitation light to the sample. The other arm of the bifurcated fiber bundle collects the emission light and couples the light to the emission monochromator. In another multiple-fiber embodiment, the excitation light can be guided to the tissue target through a large-core fiber (e.g., 400- or core diameter), while the collection and transmission of fluorescence emission can be realized by two or more collection fibers that are arranged circularly around the excitation fiber. An example schematic of a multifiber fluorescence spectroscopy probe87 is shown in Fig. 20. As the cross-section of the probe end shows, four collection fibers are symmetrically arranged around an excitation fiber. The core and cladding diameters of the excitation fiber are 200 and , respectively, and are 400 and , respectively, for the collection fibers. This particular probe was designed for immersion in a liquid. Fig. 20Schematic of an example fluorescence spectroscopy probe that uses one excitation fiber and four collection fibers (reproduced with permission from Ref. 87). 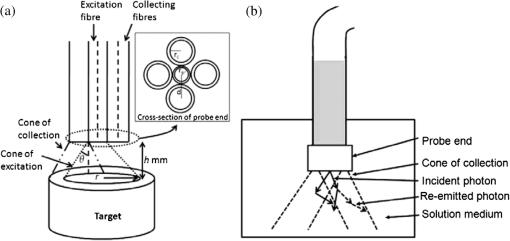 Currently, single-fiber probes are being used extensively for both in vitro and in vivo fluorescence research. The main configurations use MMFs, DCFs, or PCFs. In these applications, MMFs typically have core diameters of 200 to . NA of these MMFs ranges from 0.2 to 0.48, which corresponds to delivery and acceptance cone half-angles of 8 to 21 deg. A single-fiber probe consisting of a single optical fiber with a core diameter of allows for common illumination and light collection channels by means of a dichroic beam splitter arrangement. Figure 21 shows an example of a fluorescence spectroscopy application that uses a combination of SMF, DCF, and MMF.90 DCF had an inner core diameter of with an NA of 0.12. The inner cladding diameter was with an NA of 0.44 and the outer cladding diameter was . The function of the DCF is to enable simultaneous illumination of the sample and collection of the excitation emissions. A high level of excitation efficiency into the single-mode core of the DCF was achieved by sending 488-nm excitation light from an argon laser into a short SMF that was fusion-spliced to the DCF. The inner cladding layer of the DCF was used to collect the fluorescence signals emitted by the sample. At the receiving spectrometer, the fluorescent light collected by the DCF was coupled into a core diameter MMF by means of collimator lenses and . The neutral-density filter (ND) adjusted the intensity of the input beam, a bandpass filter (BP) removed the background noise of the laser, and a longpass filter (LP) blocked the fundamental excitation light that was elastically scattered back from the sample. Fig. 21Setup of a fluorescence spectroscopy system that uses SMF, DCF, and multimode fiber (reproduced with permission from Ref. 90). 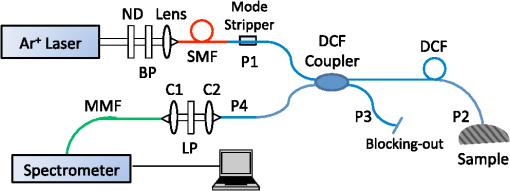 PCFs are also exploited to enhance the fluorescence emission. For example, in one experiment, a gold-coated side-polished D-shape microstructure optical fiber was employed to excite a surface plasmon, which could confine and amplify the leaky evanescent field from the fiber core. The plasmonic effect alone was found to provide an immediate fluorescence enhancement factor of two.122 5.3.2.Elastic scattering spectroscopyElastic scattering spectroscopy (ESS), which is also known as diffuse reflectance spectroscopy, is based on the elastic scattering of photons.117–119 In an elastic scattering process, photons hit tissue components and are scattered without experiencing a change in their energy, which means without a change in wavelength. The relative intensity of the backscattered light that can be collected by an optical fiber probe depends on the sizes and concentrations in the tissue of scattering components (e.g., nuclei, mitochondria, and connective tissue) and absorbing components (e.g., hemoglobin). Because the sizes and densities of these organelles change when the tissue becomes premalignant or malignant, the ESS process assists pathologists in diagnosing dysplasia. The scattered light may be detected by either the same fiber that is used for illumination or by a separate collection fiber. An example of an ESS optical fiber probe that uses separate illuminating and collecting fibers is shown in Fig. 22. A white light source is used in ESS in order to examine both the scattering and absorption properties of the tissue over a wide range of wavelengths. The optical probe passes through an endoscope channel and is placed in direct contact with tissue. A flash of white light illuminates a cylinder of tissue in diameter and nominally 1 mm deep. The backscattered signal is available for diagnosis within milliseconds. Note that only light that has undergone multiple scatterings can enter the collection fiber. 5.3.3.Diffuse correlation spectroscopyDCS is a continuous noninvasive technique that uses the time-averaged intensity autocorrelation function of a fluctuating diffusely reflected light signal to probe the flow of blood in thick or deep tissue vasculature, such as brain, muscle, and breast.120,123 This technique is also known as diffusing-wave spectroscopy. DCS operates in the 600- to 900-nm spectral range, where the relatively low tissue absorption enables deep penetration of light (see Fig. 1). This technique accounts for multiple scatterings of photons in thick tissues and quantifies blood flow in these tissues. The flow measurements are achieved by monitoring the speckle fluctuations of photons that are diffusely scattered by the movements of blood cells in the tissue. A typical DCS setup uses a laser that has a long coherence length, a single-photon-counting avalanche photodiode (APD) or a PMT as the photodetector, and a hardware autocorrelator. The schematic of the experimental setup that is shown in Fig. 23 is representative of an actual DCS measurement system. The purpose of the autocorrelator is to compute the autocorrelation function of the temporal fluctuation of the measured light intensity. To measure the blood flow, NIR light from the long-coherence-length laser is launched into the tissue through an MMF that has its distal end placed on the tissue surface. The light that is scattered through the tissue is collected by an SMF or a few-mode fiber that is placed a few millimeters or centimeters away from the source fiber. The observed temporal fluctuation of the light intensity in a single speckle area can be associated with the movements of the scattering components, which mainly are red blood cells in microvasculature. The blood flow can be quantified by calculating the decay of the light intensity, which is derived from the autocorrelation function results. Fig. 23Schematic of a representative experimental diffuse correlation spectroscopy setup (reproduced from Ref. 120). 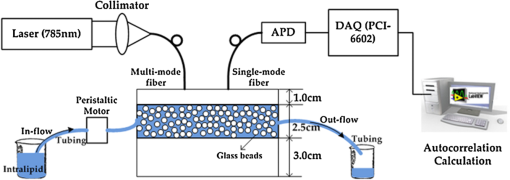 5.3.4.Raman spectroscopyRaman spectroscopy is a noninvasive, label-free biomedical optics tool that is used for evaluating the chemical composition of biological tissue samples. The compositional information is obtained by analyzing photons that have been inelastically scattered from the vibrational and rotational transitions in chemical bonds of the tissue sample, thereby providing detailed information about the biochemical composition of a sample. A number of variations have been investigated within this discipline, such as CARS, time-resolved spectroscopy, polarization modulation, and wavelength-modulated Raman spectroscopy.121,124,125 Miniaturized fiber-optic Raman probe designs have included a simple single fiber, two fibers with lenses for better sensitivity, and bifurcated coherent fiber bundles with integrated optical filtering modules. The applications include in vivo biomedical Raman spectroscopy for examining the bladder, the oral cavity, the larynx, the cervix, the lung, the breast, the colon, the esophagus, and the stomach. Figure 24 gives a general illustration of three Raman probe designs.121 In such probes, laser light emerging from an excitation fiber is scattered by the tissue and is then coupled into a collection fiber. Because only inelastically scattered photons are of interest in Raman spectroscopy, the elastically scattered photons are suppressed by longpass or notch filters. After emerging from the collection fibers, the inelastically scattered photons are dispersed in a spectrograph and registered by a CCD detector array. Fig. 24Three generic probe configurations used in Raman spectroscopy: (a) unfiltered single fiber, (b) two fibers with optical filters and a lens, and (c) fiber bundles with on-the-tip filters. BS, beamsplitter; LP, longpass; M, mirror; L, fiber coupling lens; EF, excitation fiber; CF, collection fiber; and BP, bandpass. (Reproduced with permission from Ref. 121.) 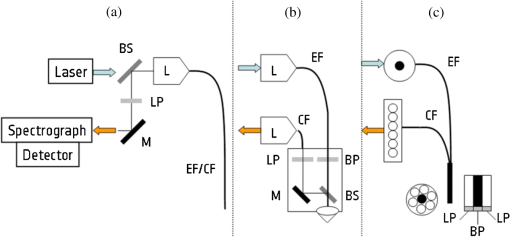 The simple probe configuration shown in Fig. 24(a) uses the same fiber for photon excitation and collection. Although this geometry offers a small, low-cost probe, its disadvantages include divergence of the beam at the distal end of the fiber and the generation of intense Raman signals within the core of the fiber, which interfere with the detection of photons below . The lens-based probe design shown in Fig. 24(b) offers better sensitivity owing to improved focusing of the light onto the tissue sample and its higher collection efficiency. This design suppresses the Raman signals that are generated in the excitation fiber and it enables detection of the entire desired 300- to wave-number range. The probe design illustrated in Fig. 24(c) offers further miniaturization because the optical longpass and bandpass filters are placed directly on the fiber ends and a fiber bundle that surrounds a central excitation fiber improves the Raman signal collection efficiency. 5.4.EndoscopyThe field of endoscopy deals with using a photonics-based instrument, called an endoscope, to look directly inside a hollow organ or body cavity for medical reasons. An endoscopic procedure is often called by names that depend on the body region being examined or treated, for example, laparoscopy for operations within the abdominal or pelvic cavities (also used for referring to minimally invasive surgery), rhinoscopy for examinations of the nasal cavity, arthroscopy for procedures involving joints, and bronchoscopy for visualizing the inside of the airways for diagnostic and therapeutic purposes. A diverse collection of endoscope designs have been progressively implemented to obtain finer details from biological tissues, such as acquiring images in various colors, obtaining greater depth resolution, or observing molecular or metabolic functions. Various advanced technologies are enabling these capabilities, for example, the development of new optical fiber types and miniaturized cameras. This section first discusses some endoscopic applications using different optical fiber designs, then gives examples of endoscopic or minimally invasive surgery, and concludes with a description of a recent technique called tethered capsule endomicroscopy. 5.4.1.Basic endoscopyA basic endoscope system consists of the following units:
An endoscope can also contain one or more additional channels to allow for the insertion of capillaries for specimen collection, manipulators for microsurgery, or additional optical fibers for therapy purposes. Traditionally, endoscopes have used a small flexible optical fiber bundle to transmit light to a diagnostic area and a coherent fiber bundle for image retrieval. Although the use of fiber bundles results in a noninvasive exploratory instrument, the number of individual fibers in the bundle and their characteristics limit the image resolution. In addition, the size and limited flexibility of the endoscope tube require patient sedation during use of the endoscope. Consequently, during the evolution to modern endoscopes, a replacement for the fiber bundle was sought using single optical fibers, such as SMF, MMF, DCF, or hollow-core PCF, to reduce the size and to increase the flexibility of endoscopes, thereby enabling safer, faster, and less expensive clinical procedures. In some endoscope designs, a single fiber is used for both delivery of the incident light and image transport. Other endoscope designs use a central fiber for illuminations and either another individual fiber or a circular array of fibers for image retrieval.126–131 A major limitation when using MMFs is the temporal variation of the modal distributions in the fiber, which can lead to image flickering. Actually this situation occurs in all imaging systems that employ MMFs both for the delivery and the collection of light. SMFs offer better resolution and a decrease in speckle noise compared with MMFs. Compared to conventional SMF and MMF, the DCF types described in Sec. 4.3 can support single-mode light transmission through the core for illumination of a target area and multimode image transfer (consisting of partially incoherent light reflected from the sample) through the inner cladding back to an imaging instrument. Thus, a DCF achieves high-resolution imaging, reduced speckle effects, and a large depth of field resulting from the larger collection diameter of the cladding. In conjunction with evaluating the potentials of using single fibers are innovative optical designs, miniature image scanning mechanisms, and specific molecular probes. The aims of the combined fiber plus technology advances are to provide images with various colors, more depth, and multiple dimensions in order to acquire greater biological details from tissue.132–134 5.4.2.Minimally invasive surgeryIn addition to inserting endoscopes through the natural openings in a body, endoscopic surgery or minimally invasive surgery is another branch of endoscopy. This is also referred to as laparoscopic surgery. In this surgical discipline, a small incision is made in the body through which an endoscope catheter is then inserted in order to diagnose and treat a medical condition.135,136 Optical fibers used for minimally invasive surgery need to be tolerant to tight bends. This characteristic allows the catheter to follow sinuous paths through veins and arteries and around organs and bones as it moves toward its destination. Another important parameter is the NA of the fiber. This characteristic influences how tightly the light is confined within the optical fiber core and dictates how much the fiber can be bent before optical bending loss becomes noticeable. A number of high-NA SMFs and MMFs are commercially available, some of which can be bent to diameters as small as 3 to 4 mm with minimum optical loss. The overall optical fiber size is a third important characteristic. Because the fibers are inside of space-constrained catheters, the outer fiber diameter should be as small as possible without sacrificing light transmission or mechanical durability. For this application, cladding-diameter SMFs and reduced-cladding MMFs are available from various suppliers. 5.4.3.Tethered capsule endomicroscopyThe use of a swallowable capsule that is tethered with an optical fiber link to a measurement instrument outside the body has enabled the use of high-resolution confocal microscopy techniques inside the body to diagnose and monitor diseases in the digestive tract. This technique is known as tethered capsule endomicroscopy and involves swallowing a nominally 7-mm-diameter rotating opto-mechanical capsule that captures cross-sectional microscopic images as it travels through the digestive tract. A variety of experimental configurations are described in the literature.137,138 Typically, the system consists of (1) an external control console containing a light source, a photodetector, and signal-processing elements, (2) a tether consisting of a drive shaft for manipulating the capsule, (c) a high-NA SMF encapsulated within the drive shaft, and (d) the rotatable capsule at the distal end that contains the viewing optics. 5.5.Fiber-Based Confocal MicroscopyConfocal microscopy is a well-established and widely used tool in cell biology because of its optical sectioning capability. This feature enables the analysis of morphologic changes in thick biologic tissue specimens with subcellular resolution. Traditionally, confocal microscopy was limited to in vitro studies of biopsy specimens and to in vivo analyses of easily accessible sites, such as the cornea, the skin, and lip and tongue areas, because it required large microscope objectives and relatively long image acquisition times. These limitations were overcome through the use of optical fiber technology.139,140 As one example, Fig. 26 shows a concept based on using a single optical fiber and a miniaturized microelectromechanical system (MEMS) scanning mirror.139 In this setup, 25 mW of linearly polarized 635-nm light from a laser diode (LD) was coupled through a bulk-optic polarizing beam splitter (PBS1) to a single-mode polarization-maintaining fiber for delivery to the tissue sample. At the distal end of this fiber, the beam was raster scanned on the sample by means of the MEMS scanner. The functions of the two PBS elements and the quarter-wave plate were to minimize the amplitudes of unwanted reflections in the optical path. The photodetector was an APD, which was connected to an image reconstruction and display unit. Fig. 26Example of a single-fiber confocal microscope system (reproduced with permission from Ref. 139). 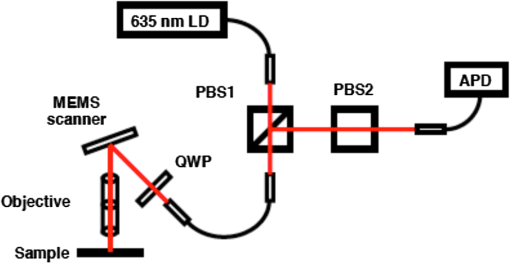 5.6.Optical Fibers in DentistryThe type of optical fiber used in dentistry depends on the specific application, such as tooth erosion studies, gum disease treatments, early dental caries detection, or ablation of hard dental tissues. An important reason for the use of optical fiber-based diagnostic and therapeutic dental tools is that the fibers allow noninvasive and nondestructive evaluation of dental tissues. The use of optical fibers also enables a wide range of optical power levels at different wavelengths to be delivered to specific viewing or treatment areas in an oral cavity.141–146 Conventional optical fibers can be used for procedures such as early dental caries detection, oral cavity and caries imaging, and discrimination of periodontitis and gingivitis from healthy gingiva. PCFs and conventional hollow-core fibers are commonly used for delivery of optical power from Nd:YAG, Er:YAG, and lasers for ablation of hard dental tissues. Figure 27 gives an example of a dental application of the fiber-based confocal microscope techniques discussed in Sec. 5.5. In this setup, 488-nm light is focused into an SMF for delivery to the probe. The three mirrors, the beam splitter, and an optical filter establish a path from the probe to a PMT for the 508-nm fluorescent signal emitted by the target tissue. Within the probe, the SMF is attached to a miniaturized tuning fork that is made to vibrate and rotate, thereby providing a two-dimensional scan of the laser beam on the tissue. The objective lens in the probe is used both to focus the excitation laser into the tissue and to collect the fluorescence signal for transmission to the PMT. Fig. 27Example of a confocal laser endomicroscope system for fluorescent imaging of the oral cavity (reproduced with permission from Ref. 145). 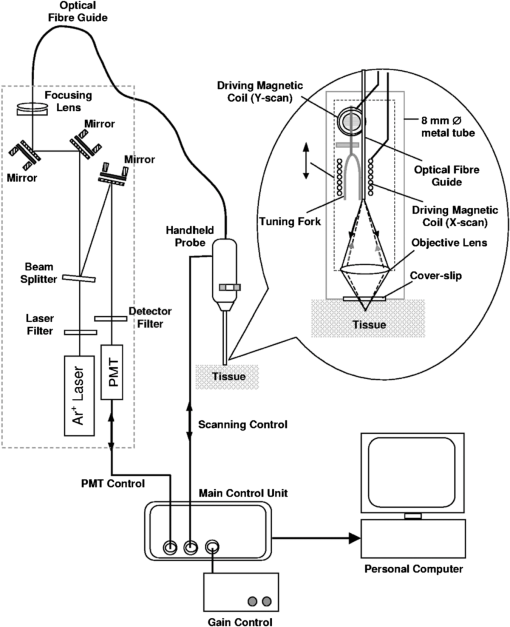 5.7.Photodynamic TherapyPDT is a treatment modality for diseases and cosmetic conditions ranging from acne to cancer that involve fast-growing or pathological cells or bacteria.147–151 Key uses of PDT include age-related macular degeneration, arteriosclerosis, Barrett’s syndrome, and cancer therapy. The PDT process uses laser light in conjunction with a light-sensitive drug that is administered before exposure to the light. The selected laser emits at a wavelength that corresponds to the absorption peaks of the photosensitive agent. The photosensitive agent accumulates in malignant cells and its role is to absorb the light energy, which then is transferred to these cells. The process of absorbing energy from the light results in the formation of singlet oxygen, which then causes chemical destruction of the tumor cells. Currently, the most commonly used light source is a laser diode that is selected to emit at the absorption wavelength of the photosensitive agent. Depending on the drug used, this wavelength can range from 620 to 760 nm, which is a region of high penetration depth into tissue (see Fig. 1). An advantage of using laser diode sources is that the light can be transmitted directly from the laser to an internal treatment site (such as the esophagus, the stomach or intestines, the urinary bladder, and the lungs) by means of optical fibers. The exit port of the fiber can be a flat or an angle-polished bare end or some type of diffuser that can be attached to the fiber tips for homogeneous spot or cylindrical light distribution. The diffuser could be a microlens or a short length of side-emitting fiber. In addition to using fibers to deliver the therapeutic light, optical fibers are also used to monitor the therapeutic light fluence, the concentration of the tumor sensitizer, and the oxygen levels produced by the PDT process. A wide range of optical fiber types can be used in PDT depending on the medical application and the desired light distribution pattern. Bare-ended fibers are typically silica glass fibers with large NAs (normally ) and core diameters ranging from 200 to . These fiber types allow the setting of a well-defined distance between the fiber end and the tissue being treated or examined and, thus, can enable precise irradiations to be administered or accurate values of tissue properties to be collected. As shown in Fig. 14, a cylindrical light diffuser is typically a plastic or a specially constructed glass side-emitting fiber that produces a radial light pattern, which is homogeneous along its entire length. Standard cylindrical diffuser fiber sections range from 10 to 70 mm in length, have a nominal core diameter of , an NA of 0.48, and a minimum bend radius of 10 mm. Their main uses are for intraluminal PDT, such as in arteries or veins, in the esophagus, in gastrointestinal tracts, in urinary tracts, or in bronchi in the lungs. The side-firing (or sideward irradiating) tip shown in Fig. 17(c) can be used with a needle (e.g., 0.5 to 0.9 mm diameter) for treating interstitial tumors. Intracavity or superficial tumors can be treated directly with light emerging from the end of a fiber with a core diameter ranging from 200 to . 5.8.Optical Fibers Used in Biomedical SensingNumerous embodiments of optical fiber structures using different materials and configurations have been investigated to form biosensors.5,152–159 A biophotonic detection process can involve the sensing of a change in a physical parameter, such as the refractive index of a material or optical power loss due to fiber movement or microbending. For example, an optical fiber-based device can be utilized to sense perturbations in the evanescent field of the propagating modes in an optical fiber. Technology platforms that have been examined for waveguide biosensors include various surface plasmon resonance (SPR) configurations, Mach-Zehnder and other interferometers, and photonic crystal-based devices. The attractions of such sensors are their small size, excellent integration capability, and relatively high sensitivity to detect analytes (substances being identified and measured). Figure 28 shows the basic operation of one type of fiber biosensor. This class of sensors uses absorbance measurements to detect any variations in the concentrations of substances of interest that absorb a specific wavelength of light. First, the fiber is coated with a biorecognition material that is referred to as an antibody. This antibody has the characteristic of being able to absorb or capture a specific analyte or antigen. The absorption process changes the effective refractive index of the fiber coating at a given wavelength of light. As noted in Fig. 5, because part of the energy of a propagating mode is in an evanescent field that travels in the cladding or coating, a change in the refractive index of the coating will cause a slight perturbation in the mode near the fiber-coating interface, which induces a variation in the optical power level in the fiber core. Now, the variation in the amount of light transmitted through the fiber at that wavelength can be related to the concentration of the absorbed analyte. This methodology has been developed for sensing conditions such as glucose levels, pH levels, oxygen levels, antibodies, and pressure. A variation on this class of antibody/antigen fiber sensor is shown in Fig. 29. The operational method is based on detecting fluorescence emitted from the addition of a detection antibody that can be made to bind to the absorbed antigen. The key characteristic of the detection antibody is that it will fluoresce at a specific excitation wavelength. In this sensor, first a fiber is coated with an antibody and then immersed in a medium containing antigens. Next a layer of the detection antibodies is attached to the captured antigens. Thereby, a sandwich structure is formed consisting of the basic antibody layer, the antigen layer, and the detecting antibody layer. After the detection antibody is attached to the antigen, a laser light is sent through the fiber, causing the detection antibody to fluoresce. The degree of fluorescence produced in this process is then a measure of the concentration of the antigen.160 As another example, Fig. 30 shows the operational scheme of an optical fiber-based glucose sensor that uses a fiber loop ringdown technique.161 First, glucose oxidase is deposited on the surface of a section of SMF ( long), which functions as the sensor head. When the coated sensor head is exposed to a glucose solution, the glucose oxidase reacts with the glucose and generates gluconic acid. This interaction results in a change in the refractive index around the surface of the sensor head. A measure of the glucose concentration is obtained by comparing the differences in the ringdown times before and during the exposure event. Fig. 30Concept of an evanescent-field fiber loop ringdown glucose sensor system (reproduced with permission from Ref. 161). 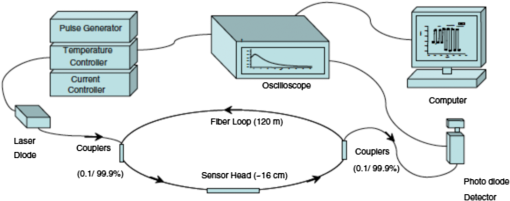 Some common optical fiber-based pressure sensors function by measuring variations in backreflected light, changes in light levels coupled between two fibers, or losses due to changes in microscopic bends in the fiber axis.162,163 The variations in the light intensities can then be directly correlated to changes in pressure. Two methods among many are shown in Fig. 31. In Fig. 31(a), light emerges from a fiber and is reflected back toward the fiber by a mirror or a diaphragm located at a distance from the end of the fiber. Part of the reflected light is partially captured by the same fiber core from which the light emerges and is transmitted back to a photodetector that senses the light intensity. If the pressure on the mirror or diaphragm increases or decreases, the distance will decrease or increase correspondingly. Thus, the reflected light captured by the fiber will increase or decrease, respectively. The variation of the light intensity at the photodetector, thus, is a measure of the change in pressure. In Fig. 31(b), light emerging from a fixed fiber is coupled into a second movable fiber separated a distance from the fixed fiber. The second fiber can move when there is a change in pressure, thus changing the distance between the two fiber ends. If the distance increases, then less light will be coupled into the second fiber and vice versa. Again, the variation of the light intensity at the photodetector is a measure of the change in pressure. Fig. 31Two examples of simple optical fiber-based pressure sensors: (a) reflecting mirror or diaphragm and (b) moving acceptor fiber. 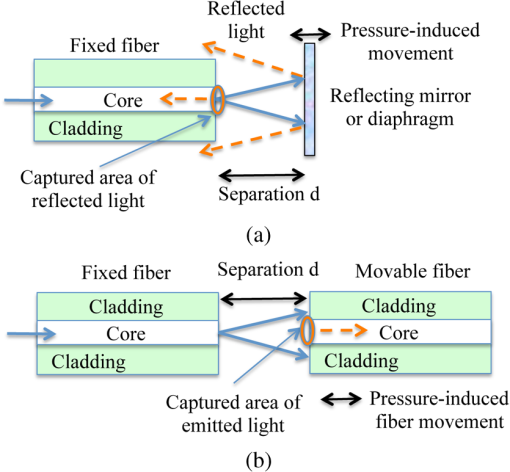 PCFs are being applied in several categories of biosensors. One reason is that the air holes in a PCF serve as natural chambers for a liquid sample to enter. This feature significantly reduces the volume of a sample that is typically required. The infiltration of liquid into the PCF can be realized by simply immersing the fiber end in the liquid.164–166 However, afterward if the liquid needs to be removed from the PCF, which often happens in multistep biochemical processes, vacuum or pressure needs to be applied to the fiber end. Different selective filling techniques have been reported using a UV polymer,167 a femtosecond laser,168 a focused ion beam,169 or even normal glue.170 The sensing principle for the analyte solution inside the PCF can be based on an FBG, interferometry, mode coupling, evanescent field monitoring, or observation of a bandgap shift. Another fiber sensor type that uses a PCF as the sensing element is based on intermodal interference between the forward-propagating core and the cladding modes in a PCF.171 The basic configuration of a two-beam interference method uses the core mode as the reference beam and the cladding modes as the sensing beam. An example of such a PCF-based interferometer is shown in Fig. 32. Here, a short length of PCF is sandwiched between input and output SMFs (such as the conventional industry standard G.652 fibers) to form an inline core-cladding intermodal interferometer. Different higher-order cladding modes can be excited in the PCF from the fundamental mode (called the mode) in the SMF by having abrupt fiber tapers formed at the interfaces between the PCF segment and the single-mode input and output fibers. Fig. 32Concept of an inline core-cladding intermodal interferometer based on the mode-field mismatch method (reproduced with permission from Ref. 171). 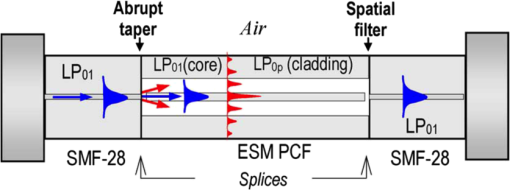 When light from a broadband source is sent through the device, the interference between the core and cladding modes in the PCF sensing section will result in a transmission-versus-wavelength interference pattern. Since the higher-order mode is a cladding mode of a glass-air waveguide, any change of the outer refractive index caused by immersion of the PCF sensing segment in a liquid will change the propagation constant of the higher-order mode and, consequently, will cause a shift in the interference fringes. Figure 33 illustrates an application of this method for the design of a compact and highly sensitive biosensor.172 In this design, conventional SMFs were arc-fusion spliced to both ends of an -long segment of PCF. The air-hole arrangement of the PCF is shown in Fig. 33(a). As shown in Fig. 33(b), the air holes were completely collapsed in the splice region and an air bubble was formed as a result of air being pushed out during the splicing process. As shown in Fig. 33(c), this air bubble acts as a diverging lens, which causes a substantial amount of light emerging from the SMF to be refracted toward the outer cladding of the PCF, thereby exciting the PCF cladding modes. Fig. 33Design of a compact and highly sensitive PCF-based biosensor with an internal air bubble lens (reproduced with permission from Ref. 172). 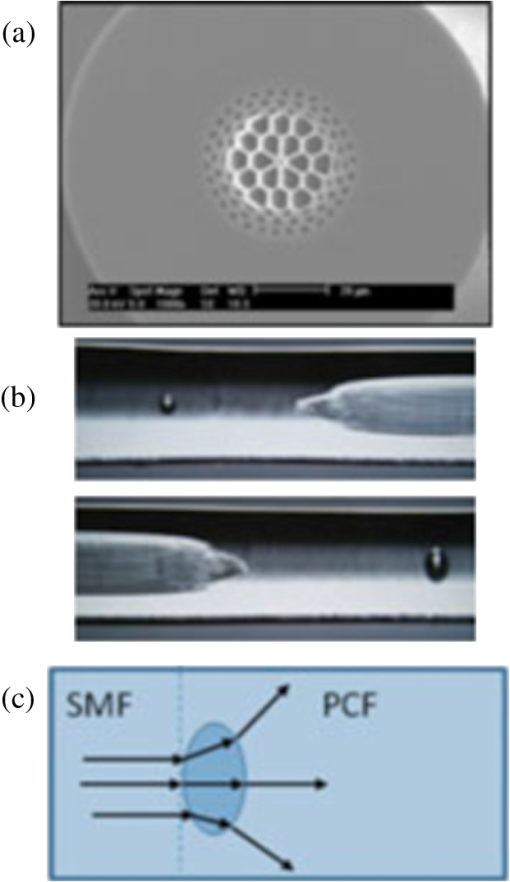 Sensitivities of up to 320 nm per relative index of refraction unit were demonstrated for this sensor for evaluating bulk liquids in the biosensing refractive index range of 1.33 to 1.34. The external bioaffinity sensing of biomolecules has been demonstrated with this device using biotin as the receptor and streptavidin as the analyte. 5.9.Health Status Diagnostics and MonitoringA highly successful precise wavelength selection component developed in the telecom industry is an FBG. As Sec. 4.2.1 describes, an FBG is a narrowband reflection-grating filter that is constructed within an optical fiber core. For biophotonics applications, an external force, such as a strain induced on the device by the weight of a person, will slightly stretch the fiber, thereby changing the length of the FBG and, thus, changing the reflected wavelength. To measure the induced strain, the FBG sensor is typically glued to or embedded in a specimen that responds to the external strain. The one precaution that needs to be taken when using such a sensor is to realize that the FBG is temperature sensitive. Thus, either the substrate on which the FBG is glued has to be temperature insensitive or some type of temperature compensating method has to be deployed along with the strain sensor. A wide selection of biosensor applications to diagnose or monitor the health status in a person has been realized using FBGs. Among these are the following:
More details for two of these examples are given below. Both applications used wavelength division multiplexing techniques for simultaneous querying of an array of FBG sensors along a single fiber line. 5.9.1.Smart-bed FBG systemOne implementation of an array of FBG sensors is a smart-bed system for healthcare applications. In this particular case, the smart-bed setup consisted of 12 FBG sensors with different Bragg wavelengths cascaded along a single fiber.175,176 The line of sensors was mounted on the surface of a bed to form a 3 by 4 matrix array, which then was covered by a standard mattress, as shown in Fig. 34. Each FBG sensor was specially packaged into an arc-shaped elastic bending beam using a carbon fiber reinforced plastic material, which ensures excellent sensitivity and good linear translation from a lateral force exerted on the apex of the sensor into axial strain of the FBG when a subject is on the bed. Thereby, patient movements and respiratory rates cause different pressures on individual FBG sensors, so that changes in the Bragg wavelength of specific FBG sensors allow the monitoring of both healthy and abnormal conditions of a patient. Fig. 34FBG bed sensor array for patient condition monitoring (reproduced with permission from Ref. 176).  5.9.2.Distributed FBG-based catheter sensorA second example of an FBG-based biosensor is a catheter that does distributed in vivo sensing of pressure in the gastrointestinal tract.181 The catheter was formed from a serial array of 12 FBG sensors that were fabricated into a continuous length of SMF. As shown in Fig. 35, each FBG was attached to a localized pressure-sensitive structure consisting of a rigid metallic substrate and a flexible diaphragm. Each FBG element was 3 mm long and had a full-width half-maximum spectral response of 0.6 nm for Bragg wavelengths spaced 1.3 nm apart in the 815- to 850-nm sensing range. The FBG sensor elements were spaced 10 mm apart, resulting in a catheter with a 12-cm sensing length. The device was designed to measure pressure changes between and , which adequately covers the range of pressures normally encountered in esophageal tracts. As shown in Fig. 35, a circulator was used to insert light from a broadband optical source into the sensor array. Optical signal variations returning from the sensor array reentered the circulator and were sent to an optical detector from the third port of the circulator. Fig. 35Data acquisition equipment to record pressure changes along the catheter. Inset: schematic of an FBG sensor (modified with permission from Ref. 181).  5.10.PhotorejuvenationIn addition to healthcare monitoring applications, optical fibers are also used in laser resurfacing or photorejuvenation for the treatment of certain skin conditions and for wrinkle removal. The dermatological conditions include skin atrophy, skin thickening, varicose veins, vascular lesions, unwanted hair, age spots, surgical and acne scars, and pigmented lesions. The photorejuvenation process uses intense pulses of light to ablate a skin area by inducing controlled wounds on the skin stimulating the skin to heal itself through the creation of new cells. Two lasers that have been historically used in free-space or direct-beam setups are the Er:YAG laser (emitting at 2940 nm) and the laser (emitting at ). To reduce the side-effects associated with large-area irradiation, techniques such as fractional lasers and fiber-coupled lasers have been introduced. In the fractional laser technique, the skin is irradiated with a dense array of pinpoints of light.183,184 This process leaves healthy skin between the ablated areas so that more rapid healing can take place. Transmitting laser light via an optical fiber allows a more precise delivery of this light to a localized skin area. The following are examples of fiber-coupled lasers, which are available for research on the basic cell photorejuvenation mechanisms185–188 and for clinical use.189–192 As discussed in Sec. 4, the particular optical fibers that are coupled to these light sources depend on the efficiency with which the fibers transmit light in the spectral emission region of the source.
5.11.Microscope-in-a-Needle ConceptA number of minimally invasive needle-based optical imaging techniques that use optical fibers are being investigated. One method is to perform confocal fluorescence microendoscopy or OCT by means of an optical fiber placed inside small-gauge needles for optical imaging within soft tissues or lesions.193–195 The basic technology goal is to put a microscope inside a standard hypodermic needle to enable three-dimensional (3-D) scanning. This technique enables surgeons to locate and diagnose very small tumor elements, thereby avoiding the need for more invasive surgery and allowing for a speedy patient recovery from the examination process. Figure 36 shows a prototype of an ultrathin 30-gauge needle ( in diameter) with an enclosed SMF. The distal elements consist of a section of a no-core fiber (NCF) and a section of a graded-index (GRIN) fiber that is spliced to the end of an SMF. Following the GRIN section is another section of NCF, which is polished at an angle of 45 deg using a fiber connector-polishing machine. This angled NCF allows side illumination and viewing. A laser-drilling method is used to create a window in the side of the needle. This structure creates an elliptical output beam that has a full-width half-maximum transverse resolution over a distance of in tissue of refractive index . The peak resolution was at 8.8 and in the - and -directions, respectively. Fig. 36Design and images of an ultrathin OCT probe. (a) Layout of the components. (b) Microscope image of the component assembly. (c) SEM image of the drilled hole. (d) Position of the hole in the needle. (Reproduced with permission from Ref. 194.) 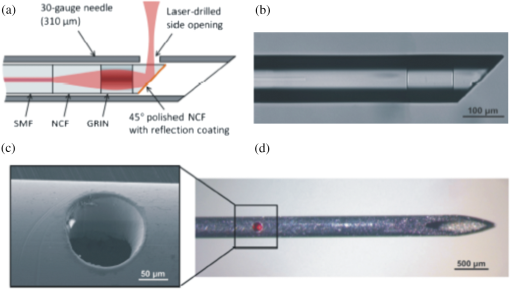 5.12.Lab-on-Fiber ConceptsThe recent joining of nanotechnology and optical fiber technology has led to the lab-on-fiber concept.196–199 In this currently evolving technology, major efforts include attaching patterned layers of nanoparticles either on the tip of a fiber or as a nanocoating over a Bragg grating written inside a microstructured optical fiber. When a patterned nanostructure is deposited on the tip of a standard optical fiber, localized surface plasmon resonances (LSPRs) can be excited by an illuminating optical wave because of a phase matching condition between the scattered waves and the modes supported by the nanostructure. Figure 37 shows an example in blue of the SPR wave associated with a nanostructure pattern for the condition when no analyte is covering the pattern on the end of a fiber. These LSPRs are very sensitive to the surrounding refractive index at the fiber tip. Thus, inserting the fiber tip into a fluid will cause the analyte liquid to cover the nanoparticle pattern. This action changes the refractive index of the nanolayer-fluid interface, thereby causing a wavelength shift in the LSPR peak due to a change in the phase matching condition, as shown by the red curve in Fig. 37. Thereby, highly sensitive physical, chemical, and biological sensing functions can be enabled. 6.SummaryThe extensive and rapid growth of photonics technology in the past two decades for basic life sciences research and for biomedical diagnosis, therapy, monitoring, and surgery has been greatly assisted through the use of diverse optical fibers. The unique operational characteristics of these fibers have been exploited to realize biomedical functions such as illumination, imaging, minimally invasive surgery, tissue ablation, biological sensing, biostimulation, and tissue diagnosis. Table 2 lists some of the major categories of optical fibers discussed in this review that are relevant to biomedical research and clinical practice. The biophotonics applications have been designated by the following three general categories with some basic examples:
Table 2Major categories of optical fibers and their applications to biomedical research and clinical practice.
Future developments in the applications of optical fibers to biomedicine are expected to see an increased use of FBG techniques for diagnostic and monitoring functions. The versatile characteristics of optical fibers coupled with nanoscale technology are now creating interest in advanced sensing and analysis technologies. Of particular interest are highly functional nanoprobes fabricated on the tips of optical fibers for nanoscale control and manipulation of light. Such probes form the basis of emerging lab-on-fiber devices for sophisticated sensing and analysis of physical, chemical, and biological tissue properties. The microscope-in-a-needle concept is another emerging technique for applying the unique characteristics of optical fibers to medical diagnosis. By enabling 3-D microscopic scanning resolution within a fiber probe, a fiber placed inside a standard hypodermic needle in principle should allow surgeons to locate very small tumor elements. Such a technique will potentially avoid the need for invasive diagnostic surgery. In addition, through the use of a DCF, stimulated emission depletion microscopy has been recently demonstrated to provide a robust way for high-resolution in vivo biomedical studies in a compact fiber-optical endoscopy system. ReferencesHandbook of Biophotonics (a) Vol. 1: Basics and Techniques, (b) Vol. 2: Photonics for Healthcare, Wiley-VCH, Weinheim, Germany
(2012). Google Scholar
Biomedical Photonics Handbook, 2nd ed.CRC Press, Boca Raton, Florida
(2014). Google Scholar
Handbook of Photonics for Biomedical Science, CRC Press, Boca Raton, Florida
(2010). Google Scholar
L. V. WangH. I. Wu, Biomedical Optics, Wiley, Hoboken, New Jersey
(2007). Google Scholar
Optical Fiber Sensor Technology: Fundamentals, Springer, New York
(2000). Google Scholar
D. L. Andrews, Biomedical Photonics, Spectroscopy, and Microscopy, Wiley, Hoboken, New Jersey
(2014). Google Scholar
K. Kulikov, Laser Interaction with Biological Material, Springer, New York
(2014). Google Scholar
Handbook of Biomedical Optics, CRC Press, Boca Raton, Florida
(2011). Google Scholar
S. L. Jacques,
“Optical properties of biological tissues: a review,”
Phys. Med. Biol., 58
(11), R37
–R61
(2013). http://dx.doi.org/10.1088/0031-9155/58/11/R37 PHMBA7 0031-9155 Google Scholar
W. F. CheongS. A. PrahlA. J. Welch,
“A review of the optical properties of biological tissues,”
IEEE J. Quantum Electron., 26
(5), 2166
–2185
(1990). http://dx.doi.org/10.1109/3.64354 IEJQA7 0018-9197 Google Scholar
J. MobleyT. V. Vo-DinhT. Tuchin,
“Optical properties of tissue,”
Biomedical Photonics Handbook, 23
–122 2nd ed.CRC Press, Boca Raton, Florida
(2014). Google Scholar
V. V. Tuchin,
“Light-tissue interactions,”
Biomedical Photonics Handbook, 123
–168 2nd ed.CRC Press, Boca Raton, Florida
(2014). Google Scholar
J. J. Anderset al.,
“In vitro and in vivo optimization of infrared laser treatment for injured peripheral nerves,”
Lasers Surg. Med., 46
(1), 34
–45
(2014). http://dx.doi.org/10.1002/lsm.v46.1 LSMEDI 0196-8092 Google Scholar
A. Mülleret al.,
“Diode laser based light sources for biomedical applications,”
Laser Photonics Rev., 7
(5), 605
–627
(2013). http://dx.doi.org/10.1002/lpor.2013.7.issue-5 LPRAB8 1863-8880 Google Scholar
Q. Penget al.,
“Lasers in medicine,”
Rep. Prog. Phys., 71
(5), 1
–28
(2008). http://dx.doi.org/10.1088/0034-4885/71/5/056701 RPPHAG 0034-4885 Google Scholar
R. RiesenbergA. Wutting,
“Light sources,”
Handbook of Biophotonics. Vol. 1: Basics and Techniques, 263
–295 Wiley-VCH, Weinheim
(2012). Google Scholar
G. Keiser, Optical Fiber Communications, 5th ed.McGraw-Hill, Singapore
(2015). Google Scholar
B. E. A. SalehM. C. Teich, Fundamentals of Photonics, 2nd ed.Wiley, Hoboken, New Jersey
(2007). Google Scholar
S. O. Kasap, Optoelectronics and Photonics: Principles and Practices, 2nd ed.Prentice-Hall, Englewood Cliffs, New Jersey
(2013). Google Scholar
A. A. Stolovet al.,
“Effects of sterilization methods on key properties of specialty optical fibers used in medical devices,”
Proc. SPIE, 8576 857606
(2013). http://dx.doi.org/10.1117/12.1000005 PSISDG 0277-786X Google Scholar
W. T. Andersonet al.,
“Mode-field diameter measurements for single-mode fibers with non-Gaussian field profiles,”
J. Lightwave Technol., 5
(2), 211
–217
(1987). http://dx.doi.org/10.1109/JLT.1987.1075501 JLTEDG 0733-8724 Google Scholar
S. T. JungD. H. ShinY. H. Lee,
“Near-field fiber tip to handle high input power more than 150 mW,”
Appl. Phys. Lett., 77
(17), 2638
–2640
(2000). http://dx.doi.org/10.1063/1.1320035 APPLAB 0003-6951 Google Scholar
M. De Rosaet al.,
“High-power performance of single-mode fiber-optic connectors,”
J. Lightwave Technol., 20
(5), 879
–885
(2002). http://dx.doi.org/10.1109/JLT.2002.1007944 JLTEDG 0733-8724 Google Scholar
J. AlbertL. Y. ShaoC. Caucheteu,
“Tilted fiber Bragg grating sensors,”
Laser Photonics Rev., 7
(1), 83
–108
(2013). http://dx.doi.org/10.1002/lpor.2013.7.issue-1 LPRAB8 1863-8880 Google Scholar
R. Kashyap, Fiber Bragg Gratings, 2nd ed.Academic Press, New York
(2010). Google Scholar
F. Berghmanset al.,
“Challenges in the fabrication of fibre Bragg gratings in silica and polymer microstructured optical fibres,”
Laser Photonics Rev., 8
(1), 27
–52
(2014). http://dx.doi.org/10.1002/lpor.201200103 LPRAB8 1863-8880 Google Scholar
T. Tichindelean,
“Silica-based fiber boosts broad-spectrum spectroscopy,”
Photonics Spectra, 47
(11), 60
–63
(2013). PHSAD3 0731-1230 Google Scholar
V. KhalilovJ. H. ShannonR. J. Timmerman,
“Improved deep UV fiber for medical and spectroscopy applications,”
Proc. SPIE, 8938 89380A
(2014). http://dx.doi.org/10.1117/12.2036397 PSISDG 0277-786X Google Scholar
T. Tobischet al.,
“Improvement of optical damage in specialty fiber at 266 nm wavelength,”
Proc. SPIE, 8938 89380G
(2014). http://dx.doi.org/10.1117/12.2041798 PSISDG 0277-786X Google Scholar
M. J. Liet al.,
“Ultra-low bending loss single-mode fiber for FTTH,”
J. Lightwave Technol., 27
(3), 376
–382
(2009). http://dx.doi.org/10.1109/JLT.2008.2010413 JLTEDG 0733-8724 Google Scholar
D. DonlagicB. LenardicS. Rehman,
“Bend insensitive multimode fibers with extreme bend loss tolerance and high bandwidth,”
Proc. SPIE, 8368 83680G
(2012). http://dx.doi.org/10.1117/12.921407 PSISDG 0277-786X Google Scholar
N. V. Wheeleret al.,
“Low-loss and low-bend-sensitivity mid-infrared guidance in a hollow-core–photonic-bandgap fiber,”
Opt. Lett., 39
(2), 295
–298
(2014). http://dx.doi.org/10.1364/OL.39.000295 OPLEDP 0146-9592 Google Scholar
S. L. JacquesJ. R. RomanK. Lee,
“Imaging superficial tissues with polarized light,”
Lasers Surg. Med., 26
(2), 119
–129
(2000). http://dx.doi.org/10.1002/(ISSN)1096-9101 LSMEDI 0196-8092 Google Scholar
V. V. TuchinL. WangD. A. Zimnyakov, Optical Polarization in Biomedical Applications, Springer, New York
(2006). Google Scholar
G. OhE. ChungS. H. Yun,
“Optical fibers for high-resolution in vivo microendoscopic fluorescence imaging,”
Opt. Fiber Technol., 19
(6), 760
–771
(2013). http://dx.doi.org/10.1016/j.yofte.2013.07.008 1068-5200 Google Scholar
S. Lemire-Renaudet al.,
“Double-clad fiber with a tapered end for confocal endomicroscopy,”
Biomed. Opt. Express, 2
(11), 2961
–2972
(2011). http://dx.doi.org/10.1364/BOE.2.002961 PSISDG 0277-786X Google Scholar
S. Y. Ryuet al.,
“The development of double clad fiber and double clad fiber coupler for fiber based biomedical imaging systems,”
J. Opt. Soc. Korea, 13
(3), 310
–315
(2009). http://dx.doi.org/10.3807/JOSK.2009.13.3.310 1226-4776 Google Scholar
S. Lianget al.,
“Intravascular atherosclerotic imaging with combined fluorescence and optical coherence tomography probe based on a double-clad fiber combiner,”
J. Biomed. Opt., 17
(7), 070501
(2012). http://dx.doi.org/10.1117/1.JBO.17.7.070501 JBOPFO 1083-3668 Google Scholar
B. J. SkutnikB. FoleyK. Moran,
“Hard plastic clad silica fibers for near UV applications,”
Proc. SPIE, 5691 23
–29
(2005). http://dx.doi.org/10.1117/12.591560 PSISDG 0277-786X Google Scholar
H. Podbielskaet al.,
“Optical properties of sol-gel fiber optic applicators for laser interstitial therapy,”
Laser Phys., 16
(5), 816
–826
(2006). http://dx.doi.org/10.1134/S1054660X06050124 LAPHEJ 1054-660X Google Scholar
J. A. Harrington,
“A review of IR transmitting, hollow waveguides,”
Fiber Integ. Opt., 19
(3), 211
–217
(2000). http://dx.doi.org/10.1080/01468030050058794 FOIOD2 0146-8030 Google Scholar
R. Kasaharaet al.,
“Transmission properties of infrared hollow fibers produced by drawing a glass-tube perform,”
Opt. Eng., 46
(2), 025001
(2007). http://dx.doi.org/10.1117/1.2710186 OPEGAR 0091-3286 Google Scholar
L. Moroniet al.,
“Polymer hollow fiber three-dimensional matrices with controllable cavity and shell thickness,”
Biomaterials, 27
(35), 5918
–5926
(2006). http://dx.doi.org/10.1016/j.biomaterials.2006.08.015 BIMADU 0142-9612 Google Scholar
P. Patimiscoet al.,
“Low-loss hollow waveguide fibers for mid-infrared quantum cascade laser sensing applications,”
Sensors, 13
(1), 1329
–1340
(2013). http://dx.doi.org/10.3390/s130101329 SNSRES 0746-9462 Google Scholar
T. WatanabeY. Matsuura,
“Side-firing sealing caps for hollow optical fibers,”
Lasers Surg. Med., 38
(8), 792
–797
(2006). http://dx.doi.org/10.1002/(ISSN)1096-9101 LSMEDI 0196-8092 Google Scholar
F. YuW. J. WadsworthJ. C. Knight,
“Low loss silica hollow core fibers for spectral region,”
Opt. Express, 20
(10), 11153
–11158
(2012). http://dx.doi.org/10.1364/OE.20.011153 OPEXFF 1094-4087 Google Scholar
C. M. BledtJ. A. HarringtonJ. M. Kriesel,
“Loss and modal properties of Ag/AgI hollow glass waveguides,”
Appl. Opt., 51
(16), 3114
–3119
(2012). http://dx.doi.org/10.1364/AO.51.003114 APOPAI 0003-6935 Google Scholar
P. St. J. Russell,
“Photonic crystal fibers,”
J. Lightwave Technol., 24
(12), 4729
–4749
(2006). http://dx.doi.org/10.1109/JLT.2006.885258 JLTEDG 0733-8724 Google Scholar
J. C. Knight,
“Photonic crystal fibres,”
Nature, 424
(6950), 847
–851
(2003). http://dx.doi.org/10.1038/nature01940 NATUAS 0028-0836 Google Scholar
M. Largeet al., Microstructured Polymer Optical Fibres, Springer, New York
(2008). Google Scholar
J. M. DudleyJ. R. Taylor,
“Ten years of nonlinear optics in photonic crystal fibre,”
Nat. Photonics, 3
(2), 85
–90
(2009). http://dx.doi.org/10.1038/nphoton.2008.285 1749-4885 Google Scholar
A. Argyros,
“Microstructured polymer optical fibers,”
J. Lightwave Technol., 27
(11), 1571
–1579
(2009). http://dx.doi.org/10.1109/JLT.2009.2020609 JLTEDG 0733-8724 Google Scholar
F. CounyF. BenabidP. S. Light,
“Large pitch kagome-structured hollow-core photonic crystal fiber,”
Opt. Lett., 31
(24), 3574
–3576
(2006). http://dx.doi.org/10.1364/OL.31.003574 OPLEDP 0146-9592 Google Scholar
P. Ghenucheet al.,
“Kagome hollow-core photonic crystal fiber probe for Raman spectroscopy,”
Opt. Lett., 37
(21), 4371
–4373
(2012). http://dx.doi.org/10.1364/OL.37.004371 OPLEDP 0146-9592 Google Scholar
J. ZubiaJ. Arrue,
“Plastic optical fibers: an introduction to their technological processes and applications,”
Opt. Fiber Technol., 7
(2), 101
–140
(2001). http://dx.doi.org/10.1006/ofte.2000.0355 1068-5200 Google Scholar
O. Ziemannet al., POF Handbook, 2nd ed.Springer, Berlin, Germany
(2008). Google Scholar
L. Bilroet al.,
“Optical sensors based on plastic fibers,”
Sensors, 12
(9), 12184
–12207
(2012). http://dx.doi.org/10.3390/s120912184 SNSRES 0746-9462 Google Scholar
Y. KoikeK. Koike,
“Progress in low-loss and high-bandwidth plastic optical fibers,”
J. Polym. Sci. B Polym. Phys., 49
(1), 2
–17
(2011). http://dx.doi.org/10.1002/polb.22170 JPLPAY 0887-6266 Google Scholar
Z. Xionget al.,
“Highly tunable Bragg gratings in single-mode polymer optical fibers,”
IEEE Photon. Technol. Lett., 11
(3), 352
–354
(1999). http://dx.doi.org/10.1109/68.748232 IPTLEL 1041-1135 Google Scholar
D. McCarthyet al.,
“Radiation dosimeter using an extrinsic fiber optic sensor,”
IEEE Sensors J., 14
(3), 673
–685
(2014). http://dx.doi.org/10.1109/JSEN.2013.2284857 ISJEAZ 1530-437X Google Scholar
M. RothmaierM. P. LuongF. Clemens,
“Textile pressure sensor made of flexible plastic optical fibers,”
Sensors, 8
(7), 4318
–4329
(2008). http://dx.doi.org/10.3390/s8074318 SNSRES 0746-9462 Google Scholar
A. N. Chryssiset al.,
“Detecting hybridization of DNA by highly sensitive evanescent field etched core fiber Bragg grating sensors,”
IEEE J. Sel. Topics Quantum Electron., 11
(4), 864
–872
(2005). http://dx.doi.org/10.1109/JSTQE.2005.857724 IJSQEN 1077-260X Google Scholar
S. S. Sainiet al.,
“Monolayer detection of biochemical agents using etched-core fiber Bragg grating sensors,”
IEEE Photon. Technol. Lett., 19
(18), 1341
–1343
(2007). http://dx.doi.org/10.1109/LPT.2007.902345 IPTLEL 1041-1135 Google Scholar
B. M. Cowieet al.,
“Fibre Bragg grating sensors for distributive tactile sensing,”
Meas. Sci. Technol., 18
(1), 138
–146
(2007). http://dx.doi.org/10.1088/0957-0233/18/1/017 MSTCEP 0957-0233 Google Scholar
J. Spiguliset al.,
“Glowing optical fiber designs and parameters,”
Proc. SPIE, 2967 231
–236
(1997). http://dx.doi.org/10.1117/12.266542 PSISDG 0277-786X Google Scholar
J. Spigulis,
“Side-emitting fibers brighten our world,”
Opt. Photonics News, 16
(10), 36
–39
(2005). http://dx.doi.org/10.1364/OPN.16.10.000034 OPPHEL 1047-6938 Google Scholar
J. ShenC. ChuiX. Tao,
“Luminous fabric devices for wearable low-level light therapy,”
Biomed. Opt. Express, 4
(12), 2925
–2937
(2013). http://dx.doi.org/10.1364/BOE.4.002925 BOEICL 2156-7085 Google Scholar
M. Krehelet al.,
“Development of a luminous textile for reflective pulse oximetry measurements,”
Biomed. Opt. Express, 5
(8), 2537
–2547
(2014). http://dx.doi.org/10.1364/BOE.5.002537 BOEICL 2156-7085 Google Scholar
I. Peshkoaet al.,
“Fiber photo-catheters for laser treatment of atrial fibrillation,”
Opt. Lasers Eng., 45
(4), 495
–502
(2007). http://dx.doi.org/10.1016/j.optlaseng.2006.10.003 OLENDN 0143-8166 Google Scholar
R. GeorgeL. J. Walsh,
“Performance assessment of novel side firing flexible optical fibers for dental applications,”
Lasers Surg. Med., 41
(3), 214
–221
(2009). http://dx.doi.org/10.1002/lsm.v41:3 LSMEDI 0196-8092 Google Scholar
R. Mishraet al.,
“Surface modification of polymer optical fibers for enhanced side emission behavior,”
Fibers Polym., 14
(9), 1468
–1471
(2013). http://dx.doi.org/10.1007/s12221-013-1468-6 FPIOA6 1229-9197 Google Scholar
J. A. Harrington, Infrared Fibers and Their Applications, SPIE Press, Bellingham, Washington
(2004). Google Scholar
D. C. TranG. H. SigelB. Bendow,
“Heavy metal fluoride glasses and fibers: a review,”
J. Lightwave Technol., 2
(5), 566
–586
(1984). http://dx.doi.org/10.1109/JLT.1984.1073661 JLTEDG 0733-8724 Google Scholar
M. Saad,
“Heavy metal fluoride glass fibers and their applications,”
Proc. SPIE, 8307 83070N
(2011). http://dx.doi.org/10.1117/12.915295 PSISDG 0277-786X Google Scholar
J. Beiet al.,
“Fabrication of extruded fluoroindate optical fibers,”
Opt. Mater. Express, 3
(3), 318
–328
(2013). http://dx.doi.org/10.1364/OME.3.000318 OMEPAX 2159-3930 Google Scholar
A. ZakeryS. R. Elliott,
“Optical properties and applications of chalcogenide glasses: a review,”
J. Non-Cryst. Solids, 330
(1–3), 1
–12
(2003). http://dx.doi.org/10.1016/j.jnoncrysol.2003.08.064 JNCSBJ 0022-3093 Google Scholar
B. J. EggletonB. Luther-DaviesK. Richardson,
“Chalcogenide photonics,”
Nat. Photonics, 5
(3), 141
–148
(2011). 1749-4885 Google Scholar
D. Lezalet al.,
“Heavy metal oxide glasses: preparation and physical properties,”
J. Non-Cryst. Solids, 284
(1–3), 288
–295
(2001). http://dx.doi.org/10.1016/S0022-3093(01)00425-2 JNCSBJ 0022-3093 Google Scholar
C. A. DaminA. J. Sommer,
“Characterization of silver halide fiber optics and hollow silica waveguides for use in the construction of a mid-infrared attenuated total reflection Fourier transform infrared (ATR FT-IR) spectroscopy probe,”
Appl. Spectrosc., 67
(11), 1252
–1263
(2013). http://dx.doi.org/10.1366/12-06935 APSPA4 0003-7028 Google Scholar
S. IsraeliA. Katzir,
“Attenuation, absorption, and scattering in silver halide crystals and fibers in the mid-infrared,”
J. Appl. Phys., 115
(2), 023104
(2014). http://dx.doi.org/10.1063/1.4861407 JAPIAU 0021-8979 Google Scholar
E. RaveA. Katzir,
“Ordered bundles of infrared transmitting silver halide fibers: attenuation, resolution and crosstalk in long and flexible bundles,”
Opt. Eng., 41
(7), 1467
–1468
(2002). http://dx.doi.org/10.1117/1.1485759 OPEGAR 0091-3286 Google Scholar
H. H. GorrisT. M. BlicharzD. R. Walt,
“Optical-fiber bundles,”
FEBS J., 274
(21), 5462
–5470
(2007). http://dx.doi.org/10.1111/j.1742-4658.2007.06078.x 1742-464X Google Scholar
J. D. EnderleJ. D. Bronzino,
“Biomedical optics and lasers,”
Introduction to Biomedical Engineering, 1112
–1173 3rd ed.Academic Press, Boston
(2012). Google Scholar
U. UtzingerR. R. Richards-Kortum,
“Fiber optic probes for biomedical optical spectroscopy,”
J. Biomed. Opt., 8
(1), 121
–147
(2003). http://dx.doi.org/10.1117/1.1528207 JBOPFO 1083-3668 Google Scholar
P. R. BargoS. A. PrahlS. L. Jacques,
“Optical properties effects upon the collection efficiency of optical fibers in different probe configurations,”
IEEE J. Sel. Topics Quantum Electron., 9
(2), 314
–321
(2003). http://dx.doi.org/10.1109/JSTQE.2003.811287 IJSQEN 1077-260X Google Scholar
T. J. Pfeferet al.,
“Multiple-fiber probe design for fluorescence spectroscopy in tissue,”
Appl. Opt., 41
(22), 4712
–4721
(2002). http://dx.doi.org/10.1364/AO.41.004712 APOPAI 0003-6935 Google Scholar
G. K. BhowmickN. GautamL. M. Gantayet,
“Design optimization of fiber optic probes for remote fluorescence spectroscopy,”
Opt. Commun., 282
(14), 2676
–2684
(2009). http://dx.doi.org/10.1016/j.optcom.2009.04.022 OPCOB8 0030-4018 Google Scholar
D. Lorenseret al.,
“Dual-modality needle probe for combined fluorescence imaging and three-dimensional optical coherence tomography,”
Opt. Lett., 38
(3), 266
–268
(2013). http://dx.doi.org/10.1364/OL.38.000266 OPLEDP 0146-9592 Google Scholar
R. Pashaie,
“Single optical fiber probe for fluorescence detection and optogenetic stimulation,”
IEEE Trans. Biomed. Eng., 60
(2), 268
–280
(2013). http://dx.doi.org/10.1109/TBME.2012.2221713 IEBEAX 0018-9294 Google Scholar
L. Wanget al.,
“Optical probe based on double-clad optical fiber for fluorescence spectroscopy,”
Opt. Express, 15
(26), 17681
–17689
(2007). http://dx.doi.org/10.1364/OE.15.017681 OPEXFF 1094-4087 Google Scholar
R. A. McLaughlinD. D. Sampson,
“Clinical applications of fiber-optic probes in optical coherence tomography,”
Opt. Fiber Technol., 16
(6), 467
–475
(2010). http://dx.doi.org/10.1016/j.yofte.2010.09.013 1068-5200 Google Scholar
P. GregorčičM. JezeršekJ. Možina,
“Optodynamic energy-conversion efficiency during an Er:YAG-laser-pulse delivery into a liquid through different fiber-tip geometries,”
J. Biomed. Opt., 17
(7), 075006
(2012). http://dx.doi.org/10.1117/1.JBO.17.7.075006 JBOPFO 1083-3668 Google Scholar
P. Svenmarkeret al.,
“Effects of probe geometry on transscleral diffuse optical spectroscopy,”
Biomed. Opt. Express, 2
(11), 3058
–3071
(2011). http://dx.doi.org/10.1364/BOE.2.003058 BOEICL 2156-7085 Google Scholar
I. Latkaet al.,
“Fiber optic probes for linear and nonlinear Raman applications—current trends and future development,”
Laser Photon. Rev., 7
(5), 698
–731
(2013). http://dx.doi.org/10.1002/lpor.2013.7.issue-5 1863-8880 Google Scholar
A. J. GomesV. Backman,
“Algorithm for automated selection of application-specific fiber-optic reflectance probes,”
J. Biomed. Opt., 18
(2), 027012
(2013). http://dx.doi.org/10.1117/1.JBO.18.2.027012 JBOPFO 1083-3668 Google Scholar
T. C. Hutchenset al.,
“Detachable fiber optic tips for use in thulium fiber laser lithotripsy,”
J. Biomed. Opt., 18
(3), 038001
(2013). http://dx.doi.org/10.1117/1.JBO.18.3.038001 JBOPFO 1083-3668 Google Scholar
S. A. Boppart,
“Optical coherence tomography: technology and applications for neuroimaging,”
Psychophysiology, 40
(4), 529
–541
(2003). http://dx.doi.org/10.1111/psyp.2003.40.issue-4 PSPHAF 0048-5772 Google Scholar
J. G. Fujimoto,
“Optical coherence tomography for ultrahigh resolution in vivo imaging,”
Nat. Biotechnol., 21
(11), 1361
–1367
(2003). http://dx.doi.org/10.1038/nbt892 NABIF9 1087-0156 Google Scholar
M. E. Brezinski, Optical Coherence Tomography, Academic, New York
(2007). Google Scholar
M. Wojtkowski,
“High-speed optical coherence tomography: basics and applications,”
Appl. Opt., 49
(16), D30
–D61
(2010). http://dx.doi.org/10.1364/AO.49.000D30 APOPAI 0003-6935 Google Scholar
Optical Coherence Tomography: A Clinical and Technical Update, Springer, Berlin
(2012). Google Scholar
A. Zysket al.,
“Optical coherence tomography: a review of clinical development from bench to bedside,”
J. Biomed. Opt., 12
(5), 051403
(2007). http://dx.doi.org/10.1117/1.2793736 JBOPFO 1083-3668 Google Scholar
E. C. C. Cauberget al.,
“A new generation of optical diagnostics for bladder cancer: technology, diagnostic accuracy, and future applications,”
Eur. Urol., 56
(2), 287
–297
(2009). http://dx.doi.org/10.1016/j.eururo.2009.02.033 EUURAV 0302-2838 Google Scholar
M. E. FermannI. Hartl,
“Ultrafast fibre lasers,”
Nat. Photonics, 7
(12), 868
–874
(2013). http://dx.doi.org/10.1038/nphoton.2013.280 1749-4885 Google Scholar
D. Zhuet al.,
“Broadband superluminescent diode-based ultrahigh resolution optical coherence tomography for ophthalmic imaging,”
J. Biomed. Opt., 16
(12), 126006
(2011). http://dx.doi.org/10.1117/1.3660314 JBOPFO 1083-3668 Google Scholar
C. XuF. W. Wise,
“Recent advances in fibre lasers for nonlinear microscopy,”
Nat. Photonics, 7
(11), 875
–882
(2013). http://dx.doi.org/10.1038/nphoton.2013.284 1749-4885 Google Scholar
W. Drexler,
“Ultrahigh-resolution optical coherence tomography,”
J. Biomed. Opt., 9
(1), 47
–74
(2004). http://dx.doi.org/10.1117/1.1629679 JBOPFO 1083-3668 Google Scholar
S. Ishidaet al.,
“Ultrahigh-resolution optical coherence tomography in region with fiber laser supercontinuum in low-water absorption samples,”
Appl. Phys. Exp., 4
(5), 52501
(2011). http://dx.doi.org/10.1143/APEX.4.052501 1882-0778 Google Scholar
M. A. Choma,
“Swept source optical coherence tomography using an all-fiber 1300-nm ring laser source,”
J. Biomed. Opt., 10
(4), 044009
(2005). http://dx.doi.org/10.1117/1.1961474 JBOPFO 1083-3668 Google Scholar
B. E. Boumaet al.,
“Self-phase-modulated Kerr-lens mode-locked Cr:forsterite laser source for optical coherence tomography,”
Opt. Lett., 21
(22), 1839
–1841
(1996). http://dx.doi.org/10.1364/OL.21.001839 OPLEDP 0146-9592 Google Scholar
D. L. MarksA. L. OldenburgJ. J. Reynolds,
“Study of an ultrahigh-numerical-aperture fiber continuum generation source for optical coherence tomography,”
Opt. Lett., 27
(22), 2010
–2012
(2002). http://dx.doi.org/10.1364/OL.27.002010 OPLEDP 0146-9592 Google Scholar
H. H. TuS. A. Boppart,
“Coherent fiber supercontinuum for biophotonics,”
Laser Photonics Rev., 7
(5), 628
–645
(2013). http://dx.doi.org/10.1002/lpor.2013.7.issue-5 LPRAB8 1863-8880 Google Scholar
R. Richards-KortumE. Sevick-Muraca,
“Quantitative optical spectroscopy for tissue diagnosis,”
Annu. Rev. Phys. Chem., 47
(1), 555
–606
(1996). http://dx.doi.org/10.1146/annurev.physchem.47.1.555 ARPLAP 0066-426X Google Scholar
A. Waxet al.,
“Optical spectroscopy of biological cells,”
Adv. Opt. Photonics, 4
(3), 322
–378
(2012). http://dx.doi.org/10.1364/AOP.4.000322 AOPAC7 1943-8206 Google Scholar
J. R. Lakowicz, Principles of Fluorescence Spectroscopy, 3rd ed.Springer, New York
(2006). Google Scholar
Fluorescence Spectroscopy and Microscopy: Methods and Protocols, Springer, New York
(2014). Google Scholar
J. R. MourantI. J. Bigio,
“Elastic scattering spectroscopy and diffuse reflection,”
Biomedical Photonics Handbook, 543
–564 CRC Press, Boca Raton, Florida
(2014). Google Scholar
K. W. CalabroI. J. Bigio,
“Influence of the phase function in generalized diffused reflectance models: review of current formalisms and novel observations,”
J. Biomed. Opt., 19
(7), 075005
(2014). http://dx.doi.org/10.1117/1.JBO.19.7.075005 JBOPFO 1083-3668 Google Scholar
B. Yuet al.,
“Diffuse reflectance spectroscopy of epithelial tissue with a smart fiber-optic probe,”
Biomed. Opt. Express, 5
(3), 675
–689
(2014). http://dx.doi.org/10.1364/BOE.5.000675 BOEICL 2156-7085 Google Scholar
J. Donget al.,
“Diffuse correlation spectroscopy with a fast Fourier transform-based software autocorrelator,”
J. Biomed. Opt., 17
(9), 097004
(2012). http://dx.doi.org/10.1117/1.JBO.17.9.097004 JBOPFO 1083-3668 Google Scholar
C. Krafftet al.,
“Raman and coherent anti-Stokes Raman scattering microspectroscopy for biomedical applications,”
J. Biomed. Opt., 17
(4), 040801
(2012). http://dx.doi.org/10.1117/1.JBO.17.4.040801 JBOPFO 1083-3668 Google Scholar
X. Yuet al.,
“Plasmonic enhanced fluorescence spectroscopy using side-polished microstructured optical fiber,”
Sens. Actuators B, 160
(1), 196
–201
(2011). http://dx.doi.org/10.1016/j.snb.2011.07.033 SABCEB 0925-4005 Google Scholar
Y. ShangK. GurleyG. Yu,
“Diffuse correlation spectroscopy (DCS) for assessment of tissue blood flow in skeletal muscle: recent progress,”
Anat. Physiol., 3
(2), 128
–135
(2013). Google Scholar
M. S. Bergholtet al.,
“Fiber-optic Raman spectroscopy probes gastric carcinogenesis in vivo at endoscopy,”
J. Biophotonics, 6
(1), 49
–59
(2013). http://dx.doi.org/10.1002/jbio.201200138 JBOIBX 1864-063X Google Scholar
Y. Huanget al.,
“Raman-assisted wavelength conversion in chalcogenide waveguides,”
IEEE J. Sel. Topics Quantum Electron., 18
(2), 646
–653
(2012). http://dx.doi.org/10.1109/JSTQE.2011.2128856 IJSQEN 1077-260X Google Scholar
S. J. Milleret al.,
“Targeted detection of murine colonic dysplasia in vivo with flexible multispectral scanning fiber endoscopy,”
J. Biomed. Opt., 17
(2), 021103
(2012). http://dx.doi.org/10.1117/1.JBO.17.2.021103 JBOPFO 1083-3668 Google Scholar
S. Lemire-Renaudet al.,
“Double-clad fiber coupler for endoscopy,”
Opt. Express, 18
(10), 9755
–9764
(2010). http://dx.doi.org/10.1364/OE.18.009755 OPEXFF 1094-4087 Google Scholar
R. Kiesslichet al.,
“Review paper: new imaging techniques and opportunities in endoscopy,”
Nat. Rev. Gastroenterol. Hepatol., 8
(10), 547
–553
(2011). http://dx.doi.org/10.1038/nrgastro.2011.152 NRGHA9 1759-5045 Google Scholar
S. F. ElahiT. D. Wang,
“Future and advances in endoscopy,”
J. Biophotonics, 4
(7–8), 471
–481
(2011). http://dx.doi.org/10.1002/jbio.v4.7/8 JBOIBX 1864-063X Google Scholar
V. SubramanianK. Ragunath,
“Advanced endoscopic imaging: a review of commercially available technologies,”
Clin. Gastroenterol. Hepatol., 12
(3), 368
–376
(2014). http://dx.doi.org/10.1016/j.cgh.2013.06.015 CGHLAW 1542-3565 Google Scholar
M. GuH. BaoH. Kang,
“Fibre-optical microendoscopy,”
J. Microsc., 254
(1), 13
–18
(2014). http://dx.doi.org/10.1111/jmi.2014.254.issue-1 JMICAR 0022-2720 Google Scholar
M. HughesP. GiataganasG. Z. Yang,
“Color reflectance fiber bundle endomicroscopy without back-reflections,”
J. Biomed. Opt., 19
(3), 030501
(2014). http://dx.doi.org/10.1117/1.JBO.19.3.030501 JBOPFO 1083-3668 Google Scholar
J. Mavadiaet al.,
“An all-fiber-optic endoscopy platform for simultaneous OCT and fluorescence imaging,”
Biomed. Opt. Express, 3
(11), 2851
–2859
(2012). http://dx.doi.org/10.1364/BOE.3.002851 BOEICL 2156-7085 Google Scholar
I. N. Papadopouloset al.,
“High-resolution, lensless endoscope based on digital scanning through a multimode optical fiber,”
Biomed. Opt. Express, 4
(2), 260
–270
(2013). http://dx.doi.org/10.1364/BOE.4.000260 BOEICL 2156-7085 Google Scholar
Minimally Invasive Spine Surgery, Springer, New York
(2014). Google Scholar
R. Autorinoet al.,
“Robot-assisted and laparoscopic repair of ureteropelvic junction obstruction: a systematic review and meta-analysis,”
Eur. Urol., 65
(2), 430
–452
(2014). http://dx.doi.org/10.1016/j.eururo.2013.06.053 EUURAV 0302-2838 Google Scholar
M. J. Goraet al.,
“Tethered capsule endomicroscopy enables less invasive imaging of gastrointestinal tract microstructure,”
Nat. Med., 19
(2), 238
–240
(2013). http://dx.doi.org/10.1038/nm.3052 1078-8956 Google Scholar
N. Tabatabaeiet al.,
“Tethered confocal endomicroscopy capsule for diagnosis and monitoring of eosinophilic esophagitis,”
Biomed. Opt. Express, 5
(1), 197
–207
(2014). http://dx.doi.org/10.1364/BOE.5.000197 BOEICL 2156-7085 Google Scholar
H. J. Shinet al.,
“Fiber-optic confocal microscope using a MEMS scanner and miniature objective lens,”
Opt. Express, 15
(15), 9113
–9122
(2007). http://dx.doi.org/10.1364/OE.15.009113 OPEXFF 1094-4087 Google Scholar
I. Ilevet al.,
“Simple fiber-optic confocal microscopy with nanoscale depth resolution beyond the diffraction barrier,”
Rev. Sci. Instrum., 78
(9), 093703
(2007). http://dx.doi.org/10.1063/1.2777173 RSINAK 0034-6748 Google Scholar
P. Lentonet al.,
“Imaging in vivo secondary caries and ex vivo dental biofilms using cross-polarization optical coherence tomography,”
Dent. Mater., 28
(7), 792
–800
(2012). http://dx.doi.org/10.1016/j.dental.2012.04.004 DEMAEP 0109-5641 Google Scholar
J. A. Rodrigueset al.,
“Light-emitting diode and laser fluorescence–based devices in detecting occlusal caries,”
J. Biomed. Opt., 16
(10), 107003
(2011). http://dx.doi.org/10.1117/1.3631796 JBOPFO 1083-3668 Google Scholar
J. S. Holtzmanet al.,
“Ability of optical coherence tomography to detect caries beneath commonly used dental sealants,”
Lasers Surg. Med., 42
(8), 752
–759
(2010). http://dx.doi.org/10.1002/lsm.20963 LSMEDI 0196-8092 Google Scholar
S. O. Konorovet al.,
“Laser ablation of dental tissues with picosecond pulses of radiation transmitted through a hollow-core photonic-crystal fiber,”
Appl. Opt., 43
(11), 2251
–2256
(2004). http://dx.doi.org/10.1364/AO.43.002251 APOPAI 0003-6935 Google Scholar
P. S. P. Thonget al.,
“Laser confocal endomicroscopy as a novel technique for fluorescence diagnostic imaging of the oral cavity,”
J. Biomed. Opt., 12
(1), 014007
(2007). http://dx.doi.org/10.1117/1.2710193 JBOPFO 1083-3668 Google Scholar
P. S. P. Thonget al.,
“Toward real-time virtual biopsy of oral lesions using confocal laser endomicroscopy interfaced with embedded computing,”
J. Biomed. Opt., 17
(5), 056009
(2012). http://dx.doi.org/10.1117/1.JBO.17.5.056009 JBOPFO 1083-3668 Google Scholar
M. R. HamblinP. Mroz, Advances in Photodynamic Therapy: Basic, Translational, and Clinical, Artech House, Norwood, Massachusetts
(2008). Google Scholar
Photodynamic Therapy: From Theory to Application, Springer, New York
(2014). Google Scholar
Z. WangN. Chocat,
“Fiber-optic technologies in laser-based therapeutics: threads for a cure,”
Curr. Pharm. Biotechnol., 11
(4), 384
–397
(2010). http://dx.doi.org/10.2174/138920110791233271 CPBUBP 1389-2010 Google Scholar
K. Svanberget al.,
“Photodynamic therapy: superficial and interstitial illumination,”
J. Biomed. Opt., 15
(4), 041502
(2010). http://dx.doi.org/10.1117/1.3466579 JBOPFO 1083-3668 Google Scholar
A. S. Garcezet al.,
“The use of optical fiber in endodontic photodynamic therapy,”
Lasers Med. Sci., 28
(1), 79
–85
(2013). http://dx.doi.org/10.1007/s10103-012-1073-8 LMSCEZ 1435-604X Google Scholar
X. D. WangO. F. Wolfbeis,
“Review: fiber-optic chemical sensors and biosensors (2008–2012),”
Anal. Chem., 85
(2), 487
–508
(2013). http://dx.doi.org/10.1021/ac303159b ANCHAM 0003-2700 Google Scholar
X. Fanet al.,
“Sensitive optical biosensors for unlabeled targets: a review,”
Anal. Chim. Acta, 620
(1–2), 8
–26
(2008). http://dx.doi.org/10.1016/j.aca.2008.05.022 ACACAM 0003-2670 Google Scholar
D. HoaA. G. KirkM. Tabrizian,
“Towards integrated and sensitive surface plasmon resonance biosensors: a review of recent progress,”
Biosens. Bioelectron., 23
(2), 151
–160
(2007). http://dx.doi.org/10.1016/j.bios.2007.07.001 BBIOE4 0956-5663 Google Scholar
A. S. Silvaet al.,
“Design and characterization of a wearable macrobending fiber optic sensor for human joint angle determination,”
Opt. Eng., 52
(12), 126106
(2013). http://dx.doi.org/10.1117/1.OE.52.12.126106 OPEGAR 0091-3286 Google Scholar
F. Taffoniet al.,
“Optical fiber-based MR-compatible sensors for medical applications: an overview,”
Sensors, 13
(10), 14105
–14120
(2013). http://dx.doi.org/10.3390/s131014105 SNSRES 0746-9462 Google Scholar
D. J. J. Huet al.,
“Long period grating cascaded to photonic crystal fiber modal interferometer for simultaneous measurement of temperature and refractive index,”
Opt. Lett., 37
(12), 2283
–2285
(2012). http://dx.doi.org/10.1364/OL.37.002283 OPLEDP 0146-9592 Google Scholar
H. QuM. Skorobogatiy,
“Resonant bio- and chemical sensors using low-refractive-index-contrast liquid-core Bragg fibers,”
Sens. Actuators B, 161
(1), 261
–268
(2012). http://dx.doi.org/10.1016/j.snb.2011.10.028 SABCEB 0925-4005 Google Scholar
L. C. L. ChinW. M. WhelanI. A. Vitkin,
“Optical fiber sensors for biomedical applications,”
Optical-Thermal Response of Laser-Irradiated Tissue, 661
–712 2nd ed.Springer, New York
(2011). Google Scholar
D. V. Lim,
“Detection of microorganisms and toxins with evanescent wave fiber-optic biosensors,”
Proc. IEEE, 91
(6), 902
–907
(2003). http://dx.doi.org/10.1109/JPROC.2003.813574 IEEPAD 0018-9219 Google Scholar
C. WangM. KayaC. Wang,
“Evanescent field-fiber loop ringdown glucose sensor,”
J. Biomed. Opt., 17
(3), 037004
(2012). http://dx.doi.org/10.1117/1.JBO.17.3.037004 JBOPFO 1083-3668 Google Scholar
P. Rorizet al.,
“Review of fiber-optic pressure sensors for biomedical and biomechanical applications,”
J. Biomed. Opt., 18
(5), 050903
(2013). http://dx.doi.org/10.1117/1.JBO.18.5.050903 JBOPFO 1083-3668 Google Scholar
Z. Chenet al.,
“Simultaneous measurement of breathing rate and heart rate using a microbend multimode fiber optic sensor,”
J. Biomed. Opt., 19
(5), 057001
(2014). http://dx.doi.org/10.1117/1.JBO.19.5.057001 JBOPFO 1083-3668 Google Scholar
X. D. FanI. M. White,
“Optofluidic microsystems for chemical and biological analysis,”
Nat. Photonics, 5
(10), 591
–597
(2011). http://dx.doi.org/10.1038/nphoton.2011.206 1749-4885 Google Scholar
X. Yanget al.,
“Direct molecule-specific glucose detection by Raman spectroscopy based on photonic crystal fiber,”
Anal. Bioanal. Chem., 402
(2), 687
–691
(2012). http://dx.doi.org/10.1007/s00216-011-5575-1 ABCNBP 1618-2642 Google Scholar
K. Milenkoet al.,
“Temperature sensitive photonic liquid crystal fiber modal interferometer,”
IEEE Photonics J., 4
(5), 1855
–1860
(2012). http://dx.doi.org/10.1109/JPHOT.2012.2215583 1943-0655 Google Scholar
Y. Y. HuangY. XuA. Yariv,
“Fabrication of functional microstructured optical fibers through a selective-filling technique,”
Appl. Phys. Lett., 85
(22), 5182
–5184
(2004). http://dx.doi.org/10.1063/1.1828593 APPLAB 0003-6951 Google Scholar
C. J. Hensleyet al.,
“Photonic band-gap fiber gas cell fabricated using femtosecond micromachining,”
Opt. Express, 15
(11), 6690
–6695
(2007). http://dx.doi.org/10.1364/OE.15.006690 OPEXFF 1094-4087 Google Scholar
C. Martelliet al.,
“Micromachining structured optical fibers using focused ion beam milling,”
Opt. Lett., 32
(11), 1575
–1577
(2007). http://dx.doi.org/10.1364/OL.32.001575 OPLEDP 0146-9592 Google Scholar
Y. Cuiet al.,
“Temperature sensor by using selectively filled photonic crystal fiber Sagnac interferometer,”
IEEE Photonics J., 4
(5), 1801
–1808
(2012). http://dx.doi.org/10.1109/JPHOT.2012.2217945 1943-0655 Google Scholar
W. J. Bocket al.,
“An inline core-cladding intermodal interferometer using a photonic crystal fiber,”
J. Lightwave Technol., 27
(17), 3933
–3939
(2009). http://dx.doi.org/10.1109/JLT.2009.2021282 JLTEDG 0733-8724 Google Scholar
D. J. J. Huet al.,
“Photonic crystal fiber-based interferometric biosensor for streptavidin and biotin detection,”
IEEE J. Sel. Topics Quantum Electron., 18
(4), 1293
–1297
(2012). http://dx.doi.org/10.1109/JSTQE.2011.2169492 IJSQEN 1077-260X Google Scholar
H. Ottevaereet al.,
“Dental composite resins: measuring the polymerization shrinkage using optical fiber Bragg grating sensors,”
Proc. SPIE, 8439 843903
(2012). http://dx.doi.org/10.1117/12.922127 PSISDG 0277-786X Google Scholar
C. Leitãoet al.,
“Development of a FBG probe for non-invasive carotid pulse waveform assessment,”
Proc. SPIE, 8427 84270J
(2012). http://dx.doi.org/10.1117/12.923560 PSISDG 0277-786X Google Scholar
J. Z. Haoet al.,
“FBG-based smart bed system for healthcare applications,”
Front. Optoelectron. China, 3
(1), 78
–83
(2010). Google Scholar
J. Haoet al.,
“An intelligent elderly healthcare monitoring system using fiber-based sensors,”
J. Chinese Inst. Eng., 33
(5), 653
–660
(2010). http://dx.doi.org/10.1080/02533839.2010.9671654 JCICAP 0368-1653 Google Scholar
L. Mohantyet al.,
“Fiber grating sensor for pressure mapping during total knee arthroplasty,”
Sens. Actuators A: Phys., 135
(2), 323
–328
(2007). http://dx.doi.org/10.1016/j.sna.2006.07.021 SAAPEB 0924-4247 Google Scholar
E. A. Al-FakihN. A. Abu OsmanF. R. M. Adikan,
“The use of fiber Bragg grating sensors in biomechanics and rehabilitation applications: the state-of-the-art and ongoing research topics,”
Sensors, 12
(10), 12890
–12926
(2012). http://dx.doi.org/10.3390/s121012890 SNSRES 0746-9462 Google Scholar
C. R. Dennisonet al.,
“An in-fiber Bragg grating sensor for contact force and stress measurements in articular joints,”
Meas. Sci. Technol, 21
(11), 115803
(2010). http://dx.doi.org/10.1088/0957-0233/21/11/115803 Google Scholar
G. T. Kanelloset al.,
“Two dimensional polymer-embedded quasidistributed FBG pressure sensor for biomedical applications,”
Opt. Express, 18
(1), 179
–186
(2010). http://dx.doi.org/10.1364/OE.18.000179 OPEXFF 1094-4087 Google Scholar
J. W. Arkwrightet al.,
“In-vivo demonstration of a high resolution optical fiber manometry catheter for diagnosis of in gastrointestinal motility disorder,”
Opt. Express, 17
(6), 4500
–4508
(2009). http://dx.doi.org/10.1364/OE.17.004500 OPEXFF 1094-4087 Google Scholar
A. Bhallaet al.,
“Shock absorption ability of laminate mouth guards in two different malocclusions using fiber Bragg grating (FBG) sensor,”
Dent. Traumatol., 29
(3), 218
–225
(2013). http://dx.doi.org/10.1111/edt.2013.29.issue-3 DTERB2 1600-4469 Google Scholar
M. H Gold,
“Update on fractional laser technology,”
J. Clin. Aesthet. Dermatol, 3
(1), 42
–50
(2010). DESUFE 1076-0512 Google Scholar
M. H. JihA. Kimyai-Asadi,
“Fractional photothermolysis: a review and update,”
Semin. Cutan. Med. Surg., 27
(1), 63
–71
(2008). http://dx.doi.org/10.1016/j.sder.2008.01.002 SCMSFR 1085-5629 Google Scholar
L. J. Boulnois,
“Photophysical processes in recent medical laser developments: a review,”
Lasers Med. Sci., 1
(1), 47
–66
(1986). http://dx.doi.org/10.1007/BF02030737 LMSCEZ 1435-604X Google Scholar
J. YaoB. LiuF. Qin,
“Rapid temperature jump by infrared diode laser irradiation for patch-clamp studies,”
Biophys J., 96
(9), 3611
–3619
(2009). http://dx.doi.org/10.1016/j.bpj.2009.02.016 BIOJAU 0006-3495 Google Scholar
M. G. Shapiroet al.,
“Infrared light excites cells by changing their electrical capacitance,”
Nat. Commun., 3
(3), 736
(2012). http://dx.doi.org/10.1038/ncomms1742 NCAOBW 2041-1723 Google Scholar
Q. Liuet al.,
“Exciting cell membranes with a blustering heat shock,”
Biophys. J., 106
(8), 1570
–1577
(2014). http://dx.doi.org/10.1016/j.bpj.2014.03.008 BIOJAU 0006-3495 Google Scholar
Z. Al-DujaitiC. C. Dierickx,
“Laser treatment of pigmented lesions,”
Laser Dermatology, 41
–64 2nd ed.Springer, Berlin
(2013). Google Scholar
L. Corcoset al.,
“The immediate effects of endovenous diode 808-nm laser in the greater saphenous vein: morphologic study and clinical implications,”
J. Vasc. Surg., 41
(6), 1018
–1024
(2005). Google Scholar
Y. C. Jung,
“Preliminary experience in facial and body contouring with 1444 nm micropulsed Nd:YAG laser-assisted lipolysis: a review of 24 cases,”
Laser Ther., 20
(1), 39
–46
(2011). http://dx.doi.org/10.5978/islsm.20.39 LATHE5 0898-5901 Google Scholar
D. Heoet al.,
“30-W Fiber-coupled laser-diode optical module for medical applications,”
J. Korean Phys. Soc., 59
(6), 3623
–3626
(2011). KPSJAS 0374-4884 Google Scholar
R. S. PillaiD. LorenserD. D. Sampson,
“Deep-tissue access with confocal fluorescence microendoscopy through hypodermic needles,”
Opt. Express, 19
(8), 7213
–7221
(2011). http://dx.doi.org/10.1364/OE.19.007213 OPEXFF 1094-4087 Google Scholar
X. Yanget al.,
“Imaging deep skeletal muscle structure using a high-sensitivity ultrathin side-viewing optical coherence tomography needle probe,”
Biomed. Opt. Express, 5
(1), 136
–148
(2014). http://dx.doi.org/10.1364/BOE.5.000136 BOEICL 2156-7085 Google Scholar
W. C. Kuoet al.,
“Real-time three-dimensional optical coherence tomography image-guided core-needle biopsy system,”
Biomed. Opt. Express, 3
(6), 1149
–1161
(2012). http://dx.doi.org/10.1364/BOE.3.001149 BOEICL 2156-7085 Google Scholar
M. ConsalesM. PiscoA. Cusano,
“Review: lab-on-fiber technology: a new avenue for optical nanosensors,”
Photonic Sens., 2
(4), 289
–314
(2012). http://dx.doi.org/10.1007/s13320-012-0095-y PSHEC2 2190-7439 Google Scholar
A. Ricciardiet al.,
“Lab-on-fiber devices as an all around platform for sensing,”
Opt. Fiber Technol., 19
(6), 772
–784
(2013). http://dx.doi.org/10.1016/j.yofte.2013.07.010 1068-5200 Google Scholar
G. Testaet al.,
“A hybrid silicon-PDMS optofluidic platform for sensing applications,”
Biomed. Opt. Express, 5
(2), 417
–426
(2014). http://dx.doi.org/10.1364/BOE.5.000417 BOEICL 2156-7085 Google Scholar
J. Albert,
“A lab on fiber,”
IEEE Spectr., 51
(4), 49
–53
(2014). http://dx.doi.org/10.1109/MSPEC.2014.6776305 IEESAM 0018-9235 Google Scholar
BiographyGerd Keiser is a research professor at Boston University and a professor and consultant at PhotonicsComm Solutions. He authored over 70 technical papers and wrote four books. He received his BA and MS degrees in physics from the University of Wisconsin Milwaukee and has a PhD in physics from Northeastern University. His professional interests are optical networking and biophotonics. He is an SPIE fellow, an IEEE life fellow, and an OSA fellow. Fei Xiong is a research assistant at the City University London working on the applications of optical fiber sensors. She received her PhD from Nanyang Technological University in Singapore, with a specialty in broadcast-enabling techniques and colorless light sources for wavelength-division-multiplexed passive optical networks. Ying Cui received her bachelor’s degree from Harbin Institute of Technology, Harbin, China. Currently, she is pursuing her PhD degree in the School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore. Her research interests include photonic crystal fiber design and fabrication and optical fiber sensing. Perry Ping Shum is a professor and the director of the Photonics Centre of Excellence at Nanyang Technological University in Singapore. He has published over 300 papers and had leadership roles in many international conferences. He received his BEng and PhD degrees from the University of Birmingham, United Kingdom. His research interests are optical communications, fiber technology, and fiber-based devices. He is an OSA and SPIE life member and an IEEE senior member. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||