|
|
1.IntroductionDiffuse optical tomography (DOT) is a modality of near-infrared spectroscopy (fNIRS) that provides three-dimensional (3-D) images of absorption changes in a semi-infinite volume. Recently, it has been applied in breast cancer imaging or optical mammography1–3 as well as in small animal imaging.4–6 The 3-D DOT has been proposed by various groups7–14 for imaging brain function. Used as a brain-imaging tool, DOT measures the changes in near-infrared light absorption in the cortex. It allows the operator to determine what functional changes are evoked in cerebral oxygenated () and deoxygenated hemoglobin (HbR) concentration in the cerebral blood flow during local brain activation. Due to the wavelength-dependent light attenuation, DOT usually employs two different wavelengths, each of them more sensitive to one of the main chromophores and HbR. Compared to fNIRS, DOT uses more light sources and detectors in a high-dense optical fiber grid, and allows many overlapping optical data channels with different source-detector distances to be recorded. Light, which is detected far away from the source, passes through the deeper tissue layers, allowing the separation of superficial layers from cerebral layers in a 3-D manner.15,16 Recovering the absorption coefficient inside the head from boundary measurements is a nonlinear problem, but it can be linearized if scattering () in the head is stable over time and the change in is small (perturbation approach). For image recovery, light propagation in the examined tissue needs to be modeled first. In tissue, where scattering dominates absorption and the propagation of light is close to isotropic, the diffusion equation can be applied for modeling. After discretization of the scanned volume (e.g., as a finite-element (FE) mesh), wavelength-specific optical properties are assigned to the elements (mesh nodes), and light propagation is modeled with respect to the positions of the optical fibers on the surface. Solving the forward problem results in a weight matrix that contains sensitivity values for all nodes in the reconstruction volume for all given light source and detector pairs. Reconstruction of DOT images requires inverting the forward mapping . This is an under-determined and ill-posed problem, since countless distributions of within the volume can explain the same surface measurement. Moreover, near-infrared light can pass skin and bone, but is highly attenuated with increasing depth, causing to be ill conditioned (or even singular), and the solution to the corresponding linear system to be prone to numerical instabilities. With a penetration depth of 3 to 4 cm, light can reach the cortex, but there is a vast sensitivity loss in the depth. This leads to a sparse matrix with very low sensitivity values in the largest fraction of the volume. Furthermore, small changes in optical properties at this depth have to be recovered from boundary measurements with nearby nodes that have a high sensitivity to superficial signals and are, therefore, sensitive to noise. Due to the ill-posed nature of the DOT inverse problem, a unique solution can only be obtained if the constraints are imposed on the distribution of the absorption coefficients. Moreover, since is ill-conditioned, a solution has to be found that optimally suppresses noise while still explaining the data. Many studies using DOT either add an additional regularization term to the model or eliminate the singular values smaller than a defined threshold from . Both methods overcome the problem of very small singular values of causing amplification of noise upon inversion. However, the choice of a regularization parameter (either the number of singular values maintained or the relative weight of the regularization term in the cost function) is often made ad hoc8,17–19 and lacks objective criteria. For researchers, it may be challenging to find an appropriate regularization parameter, since the measured data vary highly between the experiments, depending on the setup, imaging device, tissue properties, and noise level. Besides the problem of regularization, the distributed source localization methods such as minimum -norm estimate (MNE) and truncated singular value decomposition (tSVD) tend to yield blurry images rather than focused results. Therefore, a variety of sparse image reconstruction methods, such as -norm-based algorithms with , have been introduced in optical imaging.20–24 Other approaches to reconstruct the brain activation are provided by developments in electrophysiological dipole mapping. The inverse problem of electroencephalography (EEG) localizes the position of the active cerebral current source from the measured surface fields, and is comparable with the inverse problem of image reconstruction in DOT. The aim of this work is twofold. First, we show how the reconstruction quality in cerebral DOT depends on the amount of regularization chosen when distributed source localization methods (e.g., minimum norm estimates and tSVD) are used. We demonstrate the need for an independent parameter selection based on the features of the measurement data. To this end, we propose cross-validation (CV) for parameter selection. This yields high quality results and allows for an automatic data-driven determination. Second, we benchmark the outcome of seven image reconstruction methods which are:
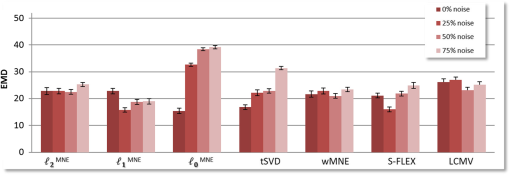
Our simulation mimics a cerebral DOT experiment. It provides a very realistic framework using an atlas-based five-layered head model in combination with real-world noise data, which are added to the simulated signals to take fiber distance-dependent noise levels. Rather than using transilluminated cylindrical (or breast tissue mimicking) geometries with one reconstructed sample point (e.g., to detect areas with different optical properties, such as tumors), we performed this study on a semi-infinite medium with a highly attenuated light sensitivity in deeper layers. Additionally, an enormous amount of data is being processed, as is typical for high-density cerebral DOT since it is used to record thousands of sample points in hundreds of optical data channels. 2.Methods2.1.Head Atlas and MeshingTo achieve a simulation setting which is close to a real measurement, we used the Montreal ICBM 2009a atlas, an unbiased nonlinear average of 152 anatomical MR images with voxel size,27,28 and corresponding tissue probability maps for cerebrospinal fluid, gray matter, and white matter.29 In order to obtain a five-compartment model including scalp and skull, we additionally segmented the ICBM2009a images using mathematical morphological operations.30 Based on this segmented brain atlas [see Fig. 1(a)], we used a masking and meshing software (Nirview)31 to create a 3-D tetrahedral mesh [Fig. 1(c)]. This mesh was used to calculate the photon transport, and thus provides the framework to simulate the cortical activation and to test the outcome of different reconstruction methods. Fig. 1(a) Segmented head atlas (ICBM 2009a, a nonlinear average of 152 MR images). From outer to inner layers: scalp, skull, cerebrospinal fluid, gray matter, white matter, (b) sketch of the optical fiber setup as used in the forward model (first nearest neighbor distance: 13 mm, (c) finite-element (FE) mesh of the left hemisphere with optical properties (), (d) example of the total sensitivity of determined from the unconstrained Jacobian . A cross section of the sensitivity volume is superimposed on the corresponding layer of the head model, (e) total sensitivity of the spatially constrained Jacobian : sensitivities for skull, scalp and CSF were set to zero. 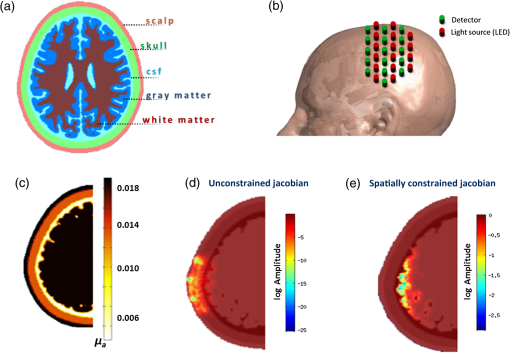 2.2.Forward Simulation and Spatial ConstraintsOptical fiber positions on the boundary of the FE mesh were chosen according to the setting of a previous real-world cerebral DOT experiment conducted under resting conditions [Fig. 1(b)]. Due to the use of registration landmarks from the EEG 10–20 reference system32 and known source-detector distances, the coordinates for each fiber were known. To model light propagation, we used the Nirfast software toolbox,33 a MATLAB®-based publicly available light modeling and reconstruction software. Nirfast applies the diffusion equation approximation, which is appropriate when scattering events dominate over absorption and the medium can be assumed to be an isotropic fluence field. One challenge in DOT is the sensitivity of the measurement to signals coming from noncortical regions. The specific wavelength is often contaminated with hemodynamic fluctuations from superficial veins in the scalp.34 On the other hand, the decrease in absorption from the HbR sensitive wavelength is highly correlated to the BOLD response in functional magnetic resonance imaging.35 For this simulation study, we use light model and data from the HbR sensitive wavelength of 760 nm. Optical properties and were assigned to each node of the FE mesh according to Strangman et al.36 The result of the simulated light propagation is a sensitivity/Jacobian matrix with dimensions , where is the number of measurements (optical data channels) and is the number of nodes in the reconstruction volume. describes the logarithmic relationship between changes in measured boundary data () that are caused by small changes of within the tissue for each channel-node combination, where Since the reconstruction volume was not entirely covered with the optode set, and since DOT has only a limited penetration depth of 3 to 4 cm, we constrained in order to reduce the result space and thus reduce the “degree of ill-posedness.” One criterion for the exclusion of nodes was their affiliation to the noncortical tissue. Nodes belonging to scalp, skull, or cerebrospinal fluid were discarded. To exclude “weak” channels with very low sensitivity (e.g., due to large source-detector separation), we calculated the vector norm for all rows of . Rows having a norm lower than 1% of the maximum value were discarded. The same procedure was performed for the mesh nodes, excluding nodes from the result space that had hardly been reached by any measuring channel. This step reduced the result space from 256 to 232 channels, and from 150,000 to 10,000 nodes. In the following, we refer to this reduced Jacobian as with the dimension of measuring channels and reconstruction nodes. Figure 1(d) depicts the total sensitivity of and Fig. 1(e) depicts , which is calculated as the sum of the sensitivity over all measurement pairs for all used nodes within the head volume. 2.3.Signal Generation and Noise ModelAs an input signal, we modeled a hemodynamic response function (hrf) for absorption changes at 760 nm peaking 5 s after stimulus onset,37 thereby mimicking a 400 s experiment with a stimulus duration of 20 s and an interstimulus interval of 20 s. This was necessary for testing the LCMV beamformer reconstruction method, which requires time-series data. Moreover, it allowed us to superimpose the artificial data with realistic noise of the same dimensionality obtained from the abovementioned resting-state recording. Detector readings were generated as follows. A sparse matrix with the dimension of was created, where is the number of “activated” nodes. Each column of labels one node by setting at a specific location , while all other nodes are set to “0.” The locations for these “activated” nodes were randomly chosen, but due to restrictions of the reduced Jacobian , all nodes were cortical. The specific sensitivity pattern in the activated node/nodes is defined by with having the dimensions , and the simulated DOT measurement defined by the matrix where the matrix hrf contains the activations of the simulated brain activity at the active nodes.We applied a realistic noise model for the purpose of testing different reconstruction algorithms under natural conditions. Most studies added white noise to the data to simulate the real measurements. In real life measurements, however, the noise is usually temporally and spatially correlated and is not normally distributed. We typically observe a higher increased noise level for larger source-detector separations than that for short distances. Second, the noise often has a high fraction of hemodynamic oscillations, which may interfere with the hemodynamic response and are sometimes hard to remove. Rather than applying a random noise term, we utilized data from a 10-min DOT experiment conducted under resting conditions as the noise model . For recording these resting-state data, we used a compact tomography imager that provides up to (NIRScoutX Tomography Imager, NIRx Medizintechnik, Berlin, Germany). This allowed us to achieve realistic simulation data with characteristic features of the real measurements. The setup for that resting-state experiment was the same as that of the simulation setup, so that fiber distances and orientations were preserved. We selected the rows of the noise matrix according to the choice of channels for , so that identical channels were used. Additionally, we took a subset of sampling/time points (columns) from , so that and had the same dimensions. Finally, and were normalized by their respective Frobenius norms in order to calibrate the artificial measurement and noise matrix. Given , and , where is the signal level with a value between 0 and 1, the noisy simulated measurement was constructed as According to the real measurements, we low pass-filtered (first-order Butterworth) the generated data with a cut-off frequency of 0.4 Hz to remove the cardiac signals. In Fig. 2(a), we see detector readings from the resting measurement for large, medium, and short source-detector separations, and the dependence of the noise level on the fiber distances. Figure 2(b) depicts examples of the generated signal for two different measurement channels, each with a signal strength of 50% (). Because of different locations and source-detector separations, the signal in the upper measurement is less dominated by noise compared to the second example in the lower graph. Fig. 2(a) Simulated DOT measurement with additive realistic noise recorded in resting condition using a compact tomography imager (NIRScoutX, NIRx, Medizintechnik, Germany). The noise level strongly depends on the source-detector separation, (b) two different measurement channels and generated signals with no noise (blue line) and with 50% noise (green line) added. The lower channel is noise dominated, since the signal generated is 100-fold smaller compared to the upper example. Due to different location and source-detector separations, noise has a different impact on the generated signal and may hamper the correct reconstruction. 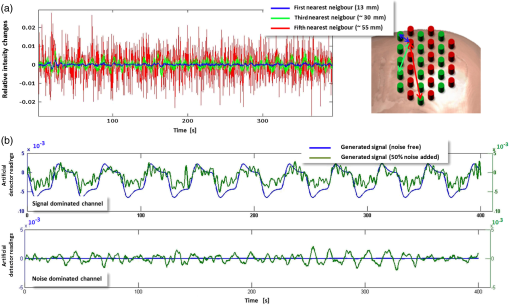 2.4.Image Reconstruction MethodsSince the number of measurements is much smaller than the number of reconstruction nodes, the linear system of Eq. (1) is heavily underdetermined, and a unique solution for can only be obtained under constraints on the absorption coefficient distribution. In order to find a solution which is neuro-physiologically plausible, these constraints should always encode valid prior assumptions on the properties of . Various such assumptions have been proposed in the literature on an EEG/MEG inverse problem, which has a similar mathematical structure. In the following paragraphs, we introduce the approaches tested. As in previous parts of the paper, we omit the dependence of and on time. Thus, unless stated otherwise, a separate reconstruction is performed for each time point (i.e., difference measurement). 2.4.1.Minimum -norm estimateA common way of constraining the brain source activity is to penalize its norm, thereby encoding a preference for the “least-active” (or, “least-complex”) brain state that gives rise to the measurement. In the simplest case, the complexity is measured using the norm. The minimum norm estimate (MNE) of the DOT inverse problem can be written as where adjusts the degree of regularization.38 The solution is obtained as where is a precomputable pseudoinverse matrix and is the identity matrix.2.4.2.Minimum -norm estimateIn the EEG/MEG literature, it is often noted that linear inverses (i.e., those employing -norm penalties) lead to blurred images of source activity, and are unable to simultaneously spatially separate the multiple active brain sites.26,39 As a remedy, estimation of the brain activation maps using -norm penalties is often suggested. Using -norm penalties leads to sparse solutions, i.e., activity maps, which are zero almost everywhere. Here, we consider a depth-weighted variant of the method proposed by Matsuura and Okabe.40 The minimum -norm solution is given by The weight matrix is chosen to be the same as in Eq. (14). The minimum of Eq. (8) is obtained using an iterative optimization algorithm. 2.4.3.Smoothed minimum -norm estimateThe method described in Ref. 41 has been applied to the cylindrical geometry for DOT in Ref. 21. It aims at a direct minimization of the -norm Thus, it searches for the solution with the smallest number of active voxels. Since this leads to a combinatorial optimization problem, a smooth approximation of the (discontinuous) -norm of a vector is considered, which leads to optimizing a sequence of certain continuous cost functions. The function, which approximates -norm, includes an additional parameter , which determines the quality of the approximation in terms of balancing smoothness and sparsity of the result. 2.4.4.Truncated singular value decompositionThe MNE solution Eq. (6) is defined for any positive regularization constant . The limit is called the Moore–Penrose (MP) pseudoinverse of . The MP solution is the source activity with the smallest -norm that exactly fulfills Eq. (1), whereas solutions for no longer perfectly explain the data. The computation of can be performed using the singular value decomposition (SVD) of , where is a diagonal matrix, are the singular values, is an orthogonal matrix with , and is an matrix with .The MP pseudoinverse of Eq. (10) can be equivalently written as Similarly, for , the SVD can be used to compute , and thus to solve Eq. (7). The formulation of in terms of , , and offers an alternative to regularizing the source activity using an -norm penalty. Given that , it is possible to compute a reduced-rank pseudoinverse using truncated matrices , , and , where the matrix and the matrix are obtained by selecting the first rows of and , respectively, and where is .Performing image reconstruction using corresponds to constraining the source estimate to lie within the -dimensional subspace of the brain, in which brain activity contributes most strongly to the sensors. 2.4.5.Weighted minimum norm estimateReconstructing activations only in those parts of the brain having a high impact on the measurements (as in tSVD) is reasonable, since doing so ensures that weak signal components (which might simply be noise) are not overinterpreted. However, one often wants to ensure that activations from different parts of the brain are equally likely to be detected. To this end, weighted minimum-norm estimates (wMNE) are employed. The idea here is to adjust the -norm penalty in Eq. (5) to compensate for the different gains activation foci have at the detector level depending on their depth. Formally, this is achieved by introducing a weight matrix in the penalty term: The solution of Eq. (14) is given by Here, we use a diagonal matrix and the entries of which are the diagonals of .39 2.4.6.Sparse basis field expansionsThe selection of active voxels by sparse inverses tends to be unstable and highly noise dependent. Moreover, the -norm penalty prevents multiple voxels with correlated activity to be jointly selected, which may lead to scattered solutions. To cope with these shortcomings, it has been suggested to replace sparsity in voxel domain by sparsity in a space of appropriately defined spatial basis functions.26 The basis function dictionary of the proposed S-FLEX (sparse basis field expansion) approach consists of Gaussian blobs of different widths centered at each voxel. Sparsifying the expansion coefficients corresponding to these blobs amounts to integrating the assumption that “plausible” activation maps are composed of a small number of blob-like activities, i.e., have a simple structure. Denoting the matrix of Gaussian basis functions by and the vector of corresponding expansion coefficients by , where is the number of blob widths, S-FLEX decomposes the estimated brain source activity into where is the weight matrix defined in the section above. S-FLEX minimizes the squared deviation from the data under an additional -norm constraint ensuring the sparsity of :The minimum of Eq. (17) is inserted into Eq. (16) to yield the estimated brain activation . Note that for , the S-FLEX solution coincides with the weighted minimum -norm solution Eq. (8). For a time series, S-FLEX jointly estimates the brain activations at all available time points under the assumption that a common set of spatial basis functions is active throughout the recording. To this end, coefficients corresponding to the same basis function but different time instants are grouped together and are jointly sparsified using a so-called -norm penalty.26 Note that without this technique, the sparsity pattern would jump from each reconstructed sample to the next, entirely obfuscating the temporal structure of the activations at the voxel level. We also use the technique of the minimum -norm approach. However, the minimum -norm approach, for which this problem also occurs, can not be extended to time-series data as easily. 2.4.7.Linearly constrained minimum variance beamformerIn contrast to the previously discussed techniques, beamforming is not only concerned with estimating activity across the entire brain at once, but a rather does the estimation separately for each node. To this end, the activity from each voxel is extracted by means of a designated linear spatial filter , which is optimized for the given data . The estimated brain activity is obtained as . The idea of the LCMV beamformer is to construct filters which let signals from a specific location pass with unit gain while suppressing all noise components.25 The optimal filter for location is obtained as the solution to the optimization problem where is the covariance matrix of the data taken across time, and is the gain vector for the -th voxel (the -th column of ). The solution is obtained asThe linear constraint ensures that brain activity from voxel (i.e., the signal of interest) is not damped, whereas the minimization of amounts to minimizing the overall (signal + noise) power of the projected data . In total, Eq. (19) maximizes the signal-to-noise ratio. However, this only holds if the source activity at different voxels is uncorrelated. If there is correlated activity, the estimation of (in particular, of the power of) the sources may be biased. 2.5.Reconstruction Quality Criterion: Earth Mover’s DistanceEach of the image reconstruction procedures resulted in a matrix with the dimension . To estimate the quality of the result, we calculated a general linear model in a sense of a linear regression for all reconstructed time courses with hrf as the regressor. Thus, for each voxel of the reconstruction volume, a -value was derived. All negative -values and those with a -value smaller than 20% of the maximum -value were eliminated. As a measure of overall reconstruction quality, we applied the Earth Mover’s Distance (EMD42) to the reconstruction results (-values) of all methods. The EMD calculates the minimal amount of energy that must be spent to transform one distribution into the other. Given the known locations (-coordinates) of the mesh nodes in a 3-D space, the EMD uses the Euclidean distance between all nodes as a ground metric to calculate the minimum costs of transforming the normalized histogram of -values into the normalized histogram of the simulated activations. Figure 3 shows an impression of a good reconstruction result with a low EMD [Figs. 3(b) and 3(c)] and a poor result [Fig. 3(d)] based on one simulated activation [Fig. 3(a)]. The advantage of the EMD is its ability to compare the overall distribution of the 3-D volumes. Unfortunately, solely looking at the EMD value gives no hint as to whether the result is blurry and/or dislocated. To gain additional information about the reconstruction quality in terms of the malpositioning of the activation, we additionally calculated the Euclidean distance between the simulated target and the maximum value of the result for the cases where only one spot was activated. Fig. 3Example for image reconstruction using tSVD and with different numbers of singular values used for inversion of . (a) Simulated target activation, (b) result using 30 used singular values for reconstruction (, best possible result), (c) result using (cross-validated) 60 singular values (), (d) result from reconstruction with 160 singular values (). 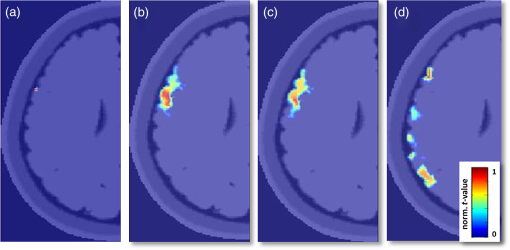 2.6.Automatic Determination of the Regularization Parameter Using Cross-ValidationDistributed inverses, such as MNE, MNE, MNE, tSVD, wMNE, and S-FLEX, directly estimate the source activity . This means that for an sensor time series, parameters have to be estimated, where . Under these circumstances, regularization is necessary (as outlined above), and the choice of the regularization parameter crucially affects whether the fitted model is too complex (overfitting the data), too simple (not explaining the relevant aspects of the data), or “just right.” Beamformers, on the other hand, are characterized by a low number of parameters. Therefore, the estimation is typically very stable. The LCMV beamformer in Eq. (19), for example, solves optimization problems (one for each voxel), each of which is concerned with the estimation of only a single -dimensional filter based on the covariance matrix of a dataset , where is the number of samples, and typically . The parameter of regularized models drives the estimated brain activation () away from the solution that explains the best measurement to a solution with “simpler” structure. As such, critically affects the shape of the chosen solution and the reconstruction accuracy. Therefore, choosing the “right” amount of regularization is very important. This choice should not be based on visual inspection or other subjective measures in order not to bias the later neurophysiological interpretation of the results. Rather, an automatic selection criterion is required. One way of assessing the quality of a regularized model is to measure how well it explains the unseen data which have not been used for estimating the model parameters. This can be done using CV. In -fold CV, the data are split into chunks. The model is fitted on chunks and evaluated on the remaining “test” chunk. This procedure is repeated for each choice of the regularization parameter and for each choice of the test chunk. The parameter that best explains the test data on average is selected is and used for training a final model based on the entire data available. In the distributed inverse source reconstruction, data folds are created by dividing the measurement channels into sets, and the performance criterion to be estimated is the squared loss at the “test” channels, i.e., , where and are the parts of and belonging to the test channels. For inverse methods estimating the brain activations as linear combinations of the data using some pseudoinverse (such as MNE, wMNE, and tSVD), an approximation to leave-one-out CV (i.e., -fold CV with ) can be carried out in the closed form. The so-called generalized CV score is given by where is the pseudoinverse constructed using the regularization parameter .43–45 The value of is calculated for every to be tested, and the parameter with the minimal score is used for reconstruction.One goal of this work is to show how the reconstruction quality alters when different regularization values are used for reconstruction. Methods that directly estimate are highly dependent on the choice of this parameter. To visualize this relationship, we first generated one target, then added 50% noise to the artificial measurement matrix, and finally reconstructed this specific activation using a wide range of values for . For every instance of this reconstruction result, the EMD was calculated. This procedure was repeated 50 times for MNE and wMNE. To test the same for tSVD, we proceed in the same manner except that we increased the number of singular values used for reconstruction, starting with the 10 highest and ending with using all (). 3.ResultsIn the following section, fisrt we show that the effectiveness of the proposed methods depend on the regularization parameter chosen (or in case of tSVD the number of singular values ). Second, we present simulation results that were achieved using the seven methods described above. We benchmark their performances in a realistic DOT simulation for one and two activated spots. 3.1.Reconstruction Quality Highly Depends on the Choice of the Regularization Parameter: an Almost Optimum Choice Can be Made without a User BiasTo visualize the impact of the chosen value for regularization, Fig. 3 depicts an example of reconstruction for tSVD, where the activation was recovered using different numbers of singular values for the inversion of . Figure 3(b) shows the best possible reconstruction result with the lowest EMD for this simulation [Fig. 3(a)]. The result that was achieved with the cross-validated number of singular values is shown in Fig. 3(c). Both parameters resolve the activation reasonably well with a correct location and little blur. The result obtained with 160 used singular values [Fig. 3(d)] leads to overfitting, which is evident from the high number of phantom activations. Figure 4 depicts multiple graphs, each representing one of the distributed reconstruction methods used. The red solid line shows the mean EMD for 50 different simulations and a wide range of values for (increasing number of singular values for tSVD, respectively). The red transparent area represents the standard error of the mean and the blue area represents the standard deviation. In all quality plots, we clearly see how EMD changes with different regularization parameters. We find a high EMD when very small or very high regularization values are chosen, rendering data that are either over or under fitted. Between them, we find a global minimum, which is indicated by the red dot representing the best possible EMD. Assuming that the location of this minimum would be known prior to reconstruction, this (, respectively) would be the first choice for parameter selection. However, in real-world experiments, the true location and extent of this activation is unknown and such a plot is not available. To overcome this challenge, this optimum is approximated by the CV as described in the section above. The blue dots in each subplot indicate the mean value for (, respectively), estimated using the CV and the respective mean EMD. In all three methods, the cross-validated value leads to results that are comparable in quality to the best possible result. The slight mismatch between the best possible and cross-validated results may be caused by the limited amount of data available. Fig. 4Depiction of the relation between regularization and reconstruction quality of three distributed reconstruction methods (noisy data, one activated spot). (a) Result for MNE. In each simulation run, the activation was reconstructed using 100 different regularization parameters. The red line depicts the average EMD for 50 simulation runs. The geometric mean of the best possible regularization value (red dot) and the same for the automatically detected (cross-validated) (blue dot) and their respective mean EMD. (b) Reconstruction quality for tSVD using an increasing number of singular values for reconstruction, (c) result for wMNE. 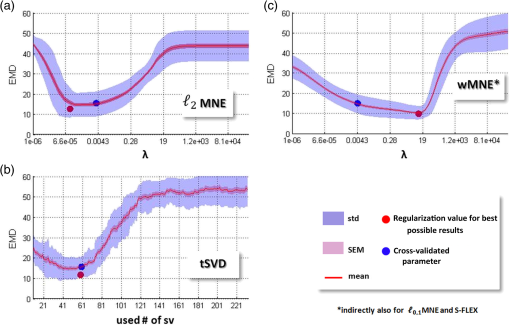 Please note that since MNE, MNE, and S-FLEX cannot be solved in the closed form and rely on numerical optimization, the calculation time for such a large number of variations was unreasonably high. Therefore, the results for these methods are not shown here. In practice, we choose the regularization strengths for these methods indirectly by selecting such that the data are explained to the same extent as it was explained by wMNE using a cross-validated . The LCMV beamformer is also omitted here, since it does not depend on the choice of a regularization parameter in the same way as do the other methods, as mentioned above. With respect to the reconstruction quality concerning different amplitudes of the simulated target, we calculated additional simulation, testing two more aspects. First, we reconstructed a target on a fixed location with two different amplitudes and a fixed regularization parameter (optimized for one of the simulations). Then, we reconstructed a target in a fixed location with different amplitudes and a variable regularization parameter. In both cases, the difference in amplitude heights in the most “active” voxels reflected the simulated difference. The reconstruction quality was almost identical. 3.2.Linearly Constrained Minimum Variance Beamforming Resolves Single Activation Spots BestThe second focus of this work is on benchmarking source reconstruction methods, among which are frequently used methods such as the recently proposed sparse algorithms and EEG-source localization methods. These methods are introduced below in the context of cerebral DOT with its semi-infinite geometry. Figure 5 gives an impression of the simulation and the reconstruction result for a single spot activation in a single case with the seven reviewed methods. For visualization, we show the transverse cross sections covering the area of the simulated activation. Fig. 5Exemplary reconstruction images for a single spot activation. (a) Transversal slices of the reconstruction volume with the simulated activation in column 6. The other columns depict transverse cross sections adjacent to the central layer ( direction, slice depth: 1 mm). (b) Reconstruction result for a 0% noise level. Each row represents the result from one particular reconstruction method. The number in the right column indicates the Earth Mover’s Distance (EMD) for this specific example. () 50% noise added to the data. 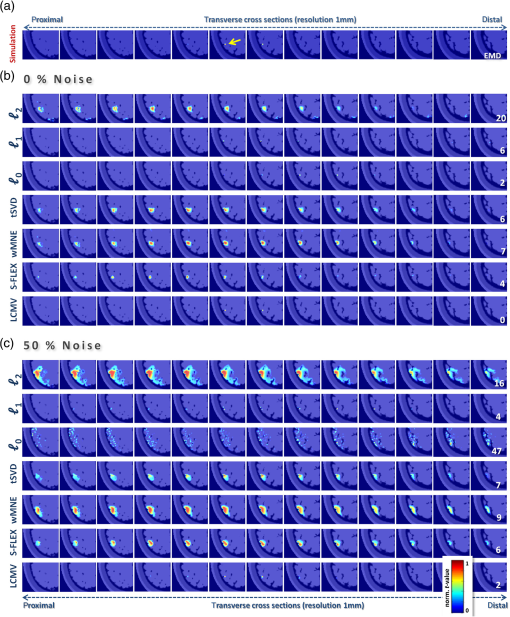 The arrow in Fig. 5(a) indicates the node that was set “active.” Rows 1 to 7 in Fig. 5(b) show the reconstructed images for all tested methods in a noise-free simulation. Within each row, the EMD between the simulation and the result is pointed out in the last column. Figure 5(c) shows the same simulation but with 50% noise in the data. For MNE, tSVD, and wMNE, we find a relatively good localization of the peak activation with slight blurring in the noise-free simulation. This blurring increases when noise is added to the data. Compared to MNE, wMNE shows an increased sparsity and a lower EMD. S-FLEX and MNE show small positioning errors in the noisy case and a focal result. In both noise levels, we find the ideal results for LCMV, with no displacement and a high focality. All the three latter methods appear to be rather insensitive to the applied noise level. MNE performs well in the noise-free case, but fails when noise is added to the data. For an overall comparison of all methods, the average EMD of 100 simulations with one activated spot and four different noise levels (0%, 25%, 50%, and 75%) can be found in Fig. 6(a) The respective mean Euclidean distance between simulation and maximum value of the reconstruction result can be found in Fig. 6(b). Fig. 6(a) Overall EMD statistics for single spot activation, four applied noise levels and all seven reconstruction methods, (b) averaged Euclidean distance between simulated target and maximum value of the result in mm for all methods and noise levels. Black bar indicates the standard error of mean. 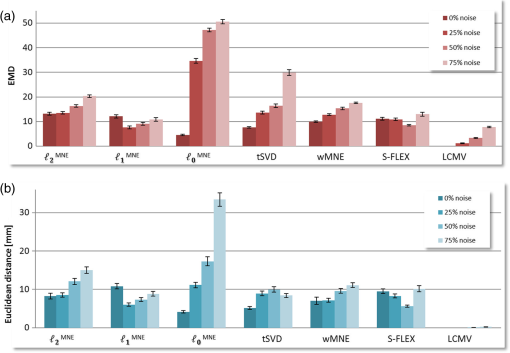 Similar to the single case, we find the best reconstruction at every noise level when LCMV is used. In almost all simulations, the beamformer achieves a correct positioning with minimal blurring even at the highest noise level. S-FLEX and MNE perform well and recover sparse results; however, their results are dislocated by a few millimeters. Interestingly, S-FLEX and MNE do not achieve their best EMD scores at the lowest noise levels with high signal levels [see Eq. (4)]. This may be due to the fact that, for efficiency reasons, the optimization for both methods is stopped after the data have been fitted with a goodness-of-fit of , where The data may be insufficiently fitted for very low noise levels. TSVD, MNE, and wMNE show a clear dependence on the noise level: with higher noise, the EMD increases. This can be especially observed in tSVD. However, although reaching a high EMD, tSVD still shows only a small positioning error (Euclidean distance) between the peak value of the reconstruction and the simulation [Fig. 6(b)]; within the highest noise level, the average Euclidean distance between the result and simulation is 8.3 mm (MNE: 15, wMNE: 11, LCMV: 0.2, S-FLEX: 10.1, and MNE: 8.8 mm). This implies that the main reason for a high EMD is a higher blur level rather than malpositioning; this blur could possibly be reduced by thresholding the result. The highest sensitivity to noise is found in MNE: beginning with low noise levels, the EMD and the positioning error dramatically increase. 3.3.Minimum -Norm Achieves Best Result When Two Spots Are ActiveWhen investigating a relatively small area of the brain, there is often only one spot of activation within the probe. However, there are approaches where larger areas or even the whole head are scanned. When the medium is larger, the possibility of including two or more areas with simultaneously fluctuating rhythms caused by a synchronic hemodynamic answer rises. We, therefore, simulated two additional areas with perfectly correlated activity in the brain. Recovering two (or more) activation foci in an algorithm is a challenge. TSVD, MNE, and wMNE show no significant differences in their EMD, which is attributable to the generally increased level of blur. That makes it harder to distinguish the quality using the EMD method. However, when looking at single cases with visualized reconstruction results (Fig. 7), we can see that all methods except the beamformer are capable of recovering both activations. Since MNE can reconstruct the sparser activation patches more clearly than the other methods, its performance is better, although again some slight positioning errors do occur. At lower noise levels, S-FLEX yields results comparable to those of MNE, but their quality decreases at the highest noise levels. MNE can almost perfectly recover both targets in a noise-free dataset, but fails again when noise is added. Due to reduced blur, wMNE shows a slight but not significant advantage over MNE, and with increased noise levels it also has a slight advantage over tSVD. Finally, it is obvious that the LCMV beamformer cannot resolve correlated activity at different brain sites, and, therefore, shows a greatly decreased performance. For a comparison see Fig. 8. Fig. 7Exemplary reconstruction images for two activations. (a) Simulated activation: two nodes in different locations were defined as “active” (indicated by the arrow), (b) reconstruction results for noise-free data and from seven different reconstruction algorithms, (c) results for noisy data (50%). Columns represent transverse cross sections of the reconstruction volume (-direction, slice depth: 1 mm).  3.4.Test on Experimental DataIt is always of interest to see how algorithms work with real data. However, it is difficult to estimate or compare the reconstruction quality with no objective reference. To get an impression of how the different algorithms work with real data, we added reconstruction results for a choice of reconstruction methods (LCMV, MNE, tSVD, and wMNE) for a finger tapping task (right hand tapping for 20 s followed by 20 s rest, 10-min duration). Activated areas were identified using a general linear model. In Fig. 9, we show the lateral view on the left hemisphere with colored areas indicating voxels with a significant (-values ) hemodynamic answer in the HbR time courses. Fig. 9Reconstruction result for a choice of methods [(a) LCMV, (b) MNE, (c) tSVD, (d) wMNE] and a finger tapping task of the right hand side. Lateral view on the left hemisphere. Colored areas indicate the voxels with a significant hemodynamic response in the HbR time courses due to the finger tapping (estimated with a GLM, -values ). 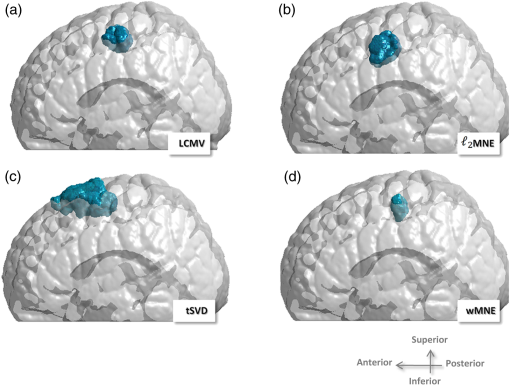 4.DiscussionWe conducted this simulation study to illustrate how image reconstruction methods depend on the regularization parameters chosen, and to benchmark a wide range of reconstruction procedures for cerebral DOT in a semi-infinite medium. To our knowledge, such an extensive study had not yet been performed. The implementation aimed at mimicking a very realistic environment for DOT measurements. However, assumptions of the nature of the used medium had to be made. For instance, the choice of optical properties to model light propagation in the head was intermediate values, since their true values alter and a variety of values have been reported46–48 Furthermore, Ref. 49 reported a decreasing scattering coefficient when looking at larger optode distances (reflecting deeper tissue), which is in contrast to the values used36 which assume an increasing value for . For a most realistic data generation, we added noise originating from a real-world experiment, including all the specific features such as hemodynamic fluctuations and fiber distance-dependent noise levels that can influence reconstruction quality. This allowed the generation of datasets to be recorded in psycho-physiological experiments, while at the same time allowing for a direct assessment of the reconstruction quality. In contrast to other studies,21,23 all methods were tested on a semi-infinite medium. This geometry can rely on back-reflected light only and there might be differences from the usually used circles or cylinders where light is applied from all sides. Since experimental setups and imaging devices vary between experiments and labs, parameters such as regularization values should be determined for every reconstruction in a data-dependent (and user independent) way. In this work, we demonstrated that CV is able to ascertain the degree of regularization required for a good balance between data and noise. It can be easily implemented within the reconstruction routine and leads to high-quality results by relying solely on the measurement and the Jacobian. CV is one of the most popular methods for model selection due to its high robustness and stability. Note, however, that CV assumes stationarity, independent, and identically distributed properties for the underlying data. In the setup of the present study, all assumptions are fulfilled: (1) even though different channels are left out, the reconstruction of the signal on the remaining channels follows the overall distribution without causing nonstationarity50 and (2) due to the low spatial range of NIRS, it can be safely assumed that the data are spatially independent. Linear methods, such as tSVD and MNE, are widely used in cerebral DOT and NIRS experiments or phantom studies, because they allow for fast or even real-time volumetric image reconstruction of time series. However, they often provide heavily blurred images in which the true activation may be indistinguishable. To overcome this drawback, sparse methods such as MNE or S-FLEX may be used. These methods prefer spatially focal results and they have proven able to distinguish multiple activation foci. They have provided good results regardless of the number of activated spots within a medium noise level. Besides the promising results for sparse methods, some other aspects may also hamper their applications. The most important is that they are nonlinear in the data. Thus, unlike the linear methods, they cannot be implemented as a multiplication of the data matrix with a precalculated pseudoinverse matrix, but rather require iterative optimization for each new data point or chunk. This makes these algorithms unsuitable for online use and even hard to apply to large data recordings, such as psycho-physiological experiments, at all. An increased number of measuring channels and/or a higher reconstruction resolution will dramatically increase the reconstruction time. In our setting, smooth source localization methods were superior to most of the sparse methods concerning the computational time. For a 400 s experiment (1360 sample points) with 225 data channels, a MNE and a wMNE need less than 10 s for reconstruction (including CV) and tSVD 96 s. Within the class of sparse methods, LCMV succeeds (3 min) over MNE (86 min), MNE (182 min), and S-FLEX (190 min). All calculations were performed with MATLAB R2011b (7.13), 64-bit (glnxa64) (The MathWorks, Inc., Natick, Massachusetts, USA) on an Intel Core i5-2500 (4x 3.3GHz), 32 GB RAM. As previously described, the complexity of the source localization problem, and thus the computational time, increases with a higher number of data channels. However, since for smooth (-norm penalized) methods, a data-independent pseudoinverse can be computed, the solution of these methods can be computed for a large number of samples in an almost negligible amount of time once that matrix is available. In contrast, sparse methods need to solve an optimization problem for each new sample/data segment, which leads to increased computational costs. As a further sparse method, we tested MNE, which failed to properly reconstruct the noisy data. In contrast to S-FLEX or MNE, the proposed implementation of MNE lacks the potential to treat a time series in its entirety. Since the inverse solution is recalculated for every time point, the sparsity patterns vary likewise. The performance could probably be improved if the activation is localized for one entire time series (rather than one sample at a time) with the constraint that identical voxels must be chosen for the whole time course, as was the case in implementing for S-FLEX or MNE. In addition to the distributed imaging approaches discussed above, we also introduced the LCMV beamformer, another reconstruction method used in the EEG field (although originally developed for radar arrays) which provides linear filters for transforming sensor measurements into source activations, and can be efficiently applied just like tSVD, MNE, and wMNE. Although LCMV provides a filter matrix the size of a pseudoinverse of , it technically does not provide a solution to the general forward equation. This means that certain parts of the measured data may not be explained at all, while the variance in other components may be accounted for many times in different voxels. The reason for this behavior lies in the beamformer’s property of separately modeling the activation at each voxel. Consequently, it shows excellent results when only one brain area is active or when multiple brain sites show uncorrelated activation, but it is unable to deal with correlated source signals. Furthermore, in contrast to all other methods, LCMV filters must be computed from a large amount of data. This prohibits the localization of single measurement samples and hampers straightforward online application. Its broad utilization in functional brain imaging experiments with potentially multiple correlated sources of activation has to be considered carefully in regard to paradigm, imaging setup, and the presumed area(s) of activation. Besides the implemented methods, a huge variety of other source localization algorithms exist. A few of them are mentioned here, such as the subspace preconditioned least-squares root,51 the generalized Tikhonov regularization (GTR), GTR in combination with the L-curve criterion (GTR-MLCC),52 -norm estimate (group lasso), (sparse group lasso),53 a total variation regularization,54 and a time-frequency mixed-norm estimate55 that uses time-frequency analysis for regularization. 5.ConclusionIn this work, we performed a highly realistic simulation of a functional brain imaging study with the cerebral DOT in humans on a semi-infinite medium with multiple highly attenuating layers. A choice of volumetric image reconstruction approaches were benchmarked including two recent methods for EEG source localization. We showed that linear reconstruction methods provide fast and adequate results. However, their accuracy can be increased by implementing sparse algorithms, albeit at the expense of computational time and effort. Using the framework presented, a robust system for cerebral DOT can be established and the necessary model parameters selected with the CV approach. We consider it now ready for broad usage in clinical studies, diagnosis, and general neuroscience research. Future studies will simultaneously investigate whole head multidistance optical tomography as well as multimodal image reconstruction using EEG and DOT in order to obtain a more robust reconstruction for complex sources. AcknowledgmentsThis work was supported by the German Ministry of Science and Education, BMBF, through the National Bernstein Network Computational Neuroscience, Bernstein Focus: Neurotechnology, No. 01GQ0850, Projects A1 and B3. Prof. Müller acknowledges funding by the World Class University Program through the National Research Foundation of Korea funded by the Ministry of Education, Science, and Technology, under grant R31-10008. We kindly thank Dr. Christoph Schmitz from NIRx Medizintechnik, Berlin, Germany for his advice and for providing the NIRScoutX Tomography Imager. We thank Catherine Aubel for copy editing the manuscript and the referees for their helpful comments. ReferencesD. R. Leffet al.,
“Diffuse optical imaging of the healthy and diseased breast: a systematic review,”
Breast Cancer Res. Treat., 108
(1), 9
–22
(2008). http://dx.doi.org/10.1007/s10549-007-9582-z BCTRD6 Google Scholar
S. NiokaB. Chance,
“Nir spectroscopic detection of breast cancer,”
Technol. Cancer Res. Treat., 4
(5), 497
–512
(2005). TCRTBS 1533-0346 Google Scholar
C. H. Schmitzet al.,
“Design and implementation of dynamic near-infrared optical tomographic imaging instrumentation for simultaneous dual-breast measurements,”
Appl. Opt., 44
(11), 2140
–2153
(2005). http://dx.doi.org/10.1364/AO.44.002140 APOPAI 0003-6935 Google Scholar
M. L. Flexmanet al.,
“Monitoring early tumor response to drug therapy with diffuse optical tomography,”
J. Biomed. Opt., 17
(1), 016014
(2012). http://dx.doi.org/10.1117/1.JBO.17.1.016014 JBOPFO 1083-3668 Google Scholar
E. LapointeJ. PichetteY. Bérubé-Lauzière,
“A multi-view time-domain non-contact diffuse optical tomography scanner with dual wavelength detection for intrinsic and fluorescence small animal imaging,”
Rev. Sci. Instrum., 83 063703
(2012). http://dx.doi.org/10.1063/1.4726016 RSINAK 0034-6748 Google Scholar
Y. Linet al.,
“Tumor characterization in small animals using magnetic resonance-guided dynamic contrast enhanced diffuse optical tomography,”
J. Biomed. Opt., 16
(10), 106015
(2011). http://dx.doi.org/10.1117/1.3643342 JBOPFO 1083-3668 Google Scholar
D. A. BoasA. M. Dale,
“Simulation study of magnetic resonance imaging-guided cortically constrained diffuse optical tomography of human brain function,”
Appl. Opt., 44
(10), 1957
–1968
(2005). http://dx.doi.org/10.1364/AO.44.001957 APOPAI 0003-6935 Google Scholar
H. Dehghaniet al.,
“Depth sensitivity and image reconstruction analysis of dense imaging arrays for mapping brain function with diffuse optical tomography,”
Appl. Opt., 48
(10), D137
–D143
(2009). http://dx.doi.org/10.1364/AO.48.00D137 APOPAI 0003-6935 Google Scholar
A. T. Eggebrechtet al.,
“A quantitative spatial comparison of high-density diffuse optical tomography and fMRI cortical mapping,”
Neuroimage, 61
(10), 1120
–1128
(2012). http://dx.doi.org/10.1016/j.neuroimage.2012.01.124 NEIMEF 1053-8119 Google Scholar
S. L. Ferradalet al.,
“Atlas-based head modeling and spatial normalization for high-density diffuse optical tomography: In vivo validation against fMRI,”
Neuroimage, 85 Pt 1 117
–126
(2014). http://dx.doi.org/10.1016/j.neuroimage.2013.03.069 NEIMEF 1053-8119 Google Scholar
C. Habermehlet al.,
“Somatosensory activation of two fingers can be discriminated with ultrahigh-density diffuse optical tomography,”
Neuroimage, 59
(4), 3201
–3211
(2012). http://dx.doi.org/10.1016/j.neuroimage.2011.11.062 NEIMEF 1053-8119 Google Scholar
J. W. JungO. K. LeeJ. C. Ye,
“Source localization approach for functional dot using music and fdr control,”
Opt. Express, 20
(6), 6267
–6285
(2012). http://dx.doi.org/10.1364/OE.20.006267 OPEXFF 1094-4087 Google Scholar
B. R. WhiteJ. P. Culver,
“Quantitative evaluation of high-density diffuse optical tomography: in vivo resolution and mapping performance,”
J. Biomed. Opt., 15
(2), 026006
(2010). http://dx.doi.org/10.1117/1.3368999 JBOPFO 1083-3668 Google Scholar
B. R. Whiteet al.,
“Resting-state functional connectivity in the human brain revealed with diffuse optical tomography,”
Neuroimage, 47
(1), 148
–56
(2009). http://dx.doi.org/10.1016/j.neuroimage.2009.03.058 NEIMEF 1053-8119 Google Scholar
R. L. Barbouret al.,
“Optical tomographic imaging of dynamic features of dense-scattering media,”
J. Opt. Soc. Am. A Opt. Image Sci. Vis., 18
(12), 3018
–3036
(2001). http://dx.doi.org/10.1364/JOSAA.18.003018 JOAOD6 1084-7529 Google Scholar
A. Bluestoneet al.,
“Three-dimensional optical tomography of hemodynamics in the human head,”
Opt. Express, 9
(6), 272
–86
(2001). http://dx.doi.org/10.1364/OE.9.000272 OPEXFF 1094-4087 Google Scholar
V. C. Kavuriet al.,
“Sparsity enhanced spatial resolution and depth localization in diffuse optical tomography,”
Biomed. Opt. Express, 3
(5), 943
–57
(2012). http://dx.doi.org/10.1364/BOE.3.000943 BOEICL 2156-7085 Google Scholar
H. Niuet al.,
“Comprehensive investigation of three-dimensional diffuse optical tomography with depth compensation algorithm,”
J. Biomed. Opt., 15
(4), 046005
(2010). http://dx.doi.org/10.1117/1.3462986 JBOPFO 1083-3668 Google Scholar
B. R. WhiteJ. P. Culver,
“Phase-encoded retinotopy as an evaluation of diffuse optical neuroimaging,”
Neuroimage, 49
(1), 568
–77
(2010). http://dx.doi.org/10.1016/j.neuroimage.2009.07.023 NEIMEF 1053-8119 Google Scholar
S. OkawaY. HoshiY. Yamada,
“Improvement of image quality of time-domain diffuse optical tomography with l sparsity regularization,”
Biomed. Opt. Express, 2
(12), 3334
–3348
(2011). http://dx.doi.org/10.1364/BOE.2.003334 BOEICL 2156-7085 Google Scholar
J. Prakashet al.,
“Sparse recovery methods hold promise for diffuse optical tomographic image reconstruction,”
IEEE J. Sel. Top. Quantum Electron., 20
(2), 74
–82
(2014). http://dx.doi.org/10.1109/JSTQE.2013.2278218 IJSQEN 1077-260X Google Scholar
C. B. ShawP. K. Yalavarthy,
“Prior image-constrained l(1)-norm-based reconstruction method for effective usage of structural information in diffuse optical tomography,”
Opt. Lett., 37
(20), 4353
–4355
(2012). http://dx.doi.org/10.1364/OL.37.004353 OPLEDP 0146-9592 Google Scholar
C. B. ShawP. K. Yalavarthy,
“Effective contrast recovery in rapid dynamic near-infrared diffuse optical tomography using l(1)-norm-based linear image reconstruction method,”
J. Biomed. Opt., 17
(8), 086009
(2012). http://dx.doi.org/10.1117/1.JBO.17.8.086009 JBOPFO 1083-3668 Google Scholar
M. SuzenA. GiannoulaT. Durduran,
“Compressed sensing in diffuse optical tomography,”
Opt. Express, 18
(23), 23676
–23690
(2010). http://dx.doi.org/10.1364/OE.18.023676 OPEXFF 1094-4087 Google Scholar
B. D. Van Veenet al.,
“Localization of brain electrical activity via linearly constrained minimum variance spatial filtering,”
IEEE Trans. Biomed. Eng., 44
(9), 867
–880
(1997). http://dx.doi.org/10.1109/10.623056 IEBEAX 0018-9294 Google Scholar
S. Haufeet al.,
“Large-scale eeg/meg source localization with spatial flexibility,”
Neuroimage, 54
(2), 851
–859
(2011). http://dx.doi.org/10.1016/j.neuroimage.2010.09.003 NEIMEF 1053-8119 Google Scholar
V. Fonovet al.,
“Unbiased average age-appropriate atlases for pediatric studies,”
Neuroimage, 54
(1), 313
–327
(2011). http://dx.doi.org/10.1016/j.neuroimage.2010.07.033 NEIMEF 1053-8119 Google Scholar
V. S. Fonovet al.,
“Unbiased nonlinear average age-appropriate brain templates from birth to adulthood,”
NeuroImage, 47
(Suppl. 1), S102
(2009). http://dx.doi.org/10.1016/S1053-8119(09)70884-5 NEIMEF 1053-8119 Google Scholar
D. Collinset al.,
“ANIMAL+INSECT: improved cortical structure segmentation,”
Lec. Notes Comput. Sci., 1613 210
–223
(1999). http://dx.doi.org/10.1007/3-540-48714-X LNCSD9 0302-9743 Google Scholar
B. DogdasD. W. ShattuckR. M. Leahy,
“Segmentation of skull and scalp in 3-d human mri using mathematical morphology,”
Hum. Brain Mapp., 26
(4), 273
–285
(2005). http://dx.doi.org/10.1002/(ISSN)1097-0193 HBRME7 1065-9471 Google Scholar
M. Jermynet al.,
“A user-enabling visual workflow for near-infrared light transport modeling in tissue,”
in Proc. Biomed. Opt., OSA Technical Digest,
BW1A. 7
(2012). Google Scholar
G. H. Klemet al.,
“The ten-twenty electrode system of the international federation. the international federation of clinical neurophysiology,”
Electroencephalogr. Clin. Neurophysiol. Suppl., 52 3
–6
(1999). EECSB3 0424-8155 Google Scholar
H. Dehghaniet al.,
“Near infrared optical tomography using nirfast: Algorithm for numerical model and image reconstruction,”
Commun. Numer Meth. Eng., 25
(6), 711
–732
(2008). http://dx.doi.org/10.1002/cnm.v25:6 CANMER 0748-8025 Google Scholar
E. Kirilinaet al.,
“The physiological origin of task-evoked systemic artefacts in functional near infrared spectroscopy,”
Neuroimage, 61
(1), 70
–81
(2012). http://dx.doi.org/10.1016/j.neuroimage.2012.02.074 NEIMEF 1053-8119 Google Scholar
J. Steinbrinket al.,
“Illuminating the bold signal: combined fMRI-fNIRS studies,”
Magn. Reson. Imaging, 24
(4), 495
–505
(2006). http://dx.doi.org/10.1016/j.mri.2005.12.034 MRIMDQ 0730-725X Google Scholar
G. StrangmanM. A. FranceschiniD. A. Boas,
“Factors affecting the accuracy of near-infrared spectroscopy concentration calculations for focal changes in oxygenation parameters,”
Neuroimage, 18
(4), 865
–79
(2003). http://dx.doi.org/10.1016/S1053-8119(03)00021-1 NEIMEF 1053-8119 Google Scholar
G. M. Boyntonet al.,
“Linear systems analysis of functional magnetic resonance imaging in human v1,”
J. Neurosci., 16
(13), 4207
–4221
(1996). JNRSDS 0270-6474 Google Scholar
M. S. HamalainenR. J. Ilmoniemi,
“Interpreting magnetic fields of the brain: minimum norm estimates,”
Med. Biol. Eng. Comput., 32
(1), 35
–42
(1994). http://dx.doi.org/10.1007/BF02512476 MBECDY 0140-0118 Google Scholar
S. Haufeet al.,
“Combining sparsity and rotational invariance in eeg/meg source reconstruction,”
Neuroimage, 42
(2), 726
–38
(2008). http://dx.doi.org/10.1016/j.neuroimage.2008.04.246 NEIMEF 1053-8119 Google Scholar
K. MatsuuraY. Okabe,
“Selective minimum-norm solution of the biomagnetic inverse problem,”
IEEE Trans. Biomed. Eng., 42
(6), 608
–615
(1995). http://dx.doi.org/10.1109/10.387200 IEBEAX 0018-9294 Google Scholar
H. MohimaniM. Babaie-ZadehC. Jutten,
“A fast approach for overcomplete sparse decomposition based on smoothed l0 norm,”
IEEE. Trans. Signal Process., 57
(1), 289
–301
(2009). http://dx.doi.org/10.1109/TSP.2008.2007606 ITPRED 1053-587X Google Scholar
Y. RubnerC. TomasiL. Guibas,
“A metric for distributions with applications to image databases,”
in Proc. IEEE Int. Conf. Computer Vision,
59
–66
(1998). Google Scholar
G. H. GolubM. HeathG. Wahba,
“Generalized cross-validation as a method for choosing a good ridge parameter,”
Technometrics, 21
(2), 215
–223
(1979). http://dx.doi.org/10.1080/00401706.1979.10489751 TCMTA2 0040-1706 Google Scholar
K. MuraseY. YamazakiS. Miyazaki,
“Deconvolution analysis of dynamic contrast-enhanced data based on singular value decomposition optimized by generalized cross validation,”
Magn. Reson. Med. Sci., 3
(4), 165
–175
(2004). http://dx.doi.org/10.2463/mrms.3.165 MRMSCT 1347-3182 Google Scholar
R. P. K. JagannathP. K. Yalavarthy,
“Minimal residual method provides optimal regularization parameter for diffuse optical tomography,”
J. Biomed. Opt., 17
(10), 106015
(2012). http://dx.doi.org/10.1117/1.JBO.17.10.106015 JBOPFO 1083-3668 Google Scholar
F. Bevilacquaet al.,
“In vivo local determination of tissue optical properties: applications to human brain,”
Appl. Opt., 38
(22), 4939
–4950
(1999). http://dx.doi.org/10.1364/AO.38.004939 APOPAI 0003-6935 Google Scholar
E. Okadaet al.,
“Theoretical and experimental investigation of near-infrared light propagation in a model of the adult head,”
Appl. Opt., 36
(1), 21
–31
(1997). http://dx.doi.org/10.1364/AO.36.000021 APOPAI 0003-6935 Google Scholar
A. Torricelliet al.,
“In vivo optical characterization of human tissues from 610 to 1010 nm by time-resolved reflectance spectroscopy,”
Phys. Med. Biol., 46
(8), 2227
–2237
(2001). http://dx.doi.org/10.1088/0031-9155/46/8/313 PHMBA7 0031-9155 Google Scholar
J. Choiet al.,
“Noninvasive determination of the optical properties of adult brain: near-infrared spectroscopy approach,”
J. Biomed. Opt., 9
(1), 221
–229
(2004). http://dx.doi.org/10.1117/1.1628242 JBOPFO 1083-3668 Google Scholar
M. SugiyamaM. KrauledatK. Müller,
“Covariate shift adaptation by importance weighted cross validation,”
J. Mach. Learn. Res., 8 985
–1005
(2007). 1532-4435 Google Scholar
M. JacobsenP. HansenM. Saunders,
“Subspace preconditioned lsqr for discrete ill-posed problems,”
BIT, 43
(5), 975
–989
(2003). http://dx.doi.org/10.1023/B:BITN.0000014547.88978.05 NBITAB 0006-3835 Google Scholar
M. S. Raveshet al.,
“Quantification of pulmonary microcirculation by dynamic contrast-enhanced magnetic resonance imaging: comparison of four regularization methods,”
Magn. Reson. Med., 69 188
–199
(2013). http://dx.doi.org/10.1002/mrm.24220 MRMEEN 0740-3194 Google Scholar
J. Montoya-Martinezet al.,
“Structured sparsity regularization approach to the eeg inverse problem,”
in Proc. 2012 Third Int. Workshop on Cognitive Information Processing (CIP),
1
–6
(2012). Google Scholar
W. Fan,
“Electrical impedance tomography for human lung reconstruction based on tv regularization algorithm,”
in Proc. 2012 Third Int. Conf. on Intelligent Control and Information Processing (ICICIP),
660
–663
(2012). Google Scholar
A. Gramfortet al.,
“Time-frequency mixed-norm estimates: sparse m/eeg imaging with non-stationary source activations,”
Neuroimage, 70 410
–422
(2013). http://dx.doi.org/10.1016/j.neuroimage.2012.12.051 NEIMEF 1053-8119 Google Scholar
BiographyChristina Habermehl is a PhD student at Charité University Hospital in Berlin. Her current research interests include functional near infrared spectroscopy, three-dimensional (3-D) imaging of brain function, and machine learning techniques. Klaus-Robert Müller has been a professor of computer science at Technische Universität Berlin since 2006; at the same time, he has been the director of the Bernstein Focus on Neurotechnology, Berlin. His research interests include intelligent data analysis, machine learning, signal processing, and brain–computer interfaces. In 2012, he was elected to be a member of the German National Academy of Sciences-Leopoldina. Stefan Haufe is a Marie-Curie postdoctoral fellow at Columbia University (with professor Paul Sajda). Before that, he was a postdoctoral researcher at the City College of New York (with professor Lucas Parra) and the Technische Universität Berlin (Professor Klaus-Robert Müller). He received his PhD degree in natural sciences in 2011 at TUB and his Diploma (master’s degree) in computer science from Martin-Luther Universität Halle-Wittenberg in 2005. |