|
|
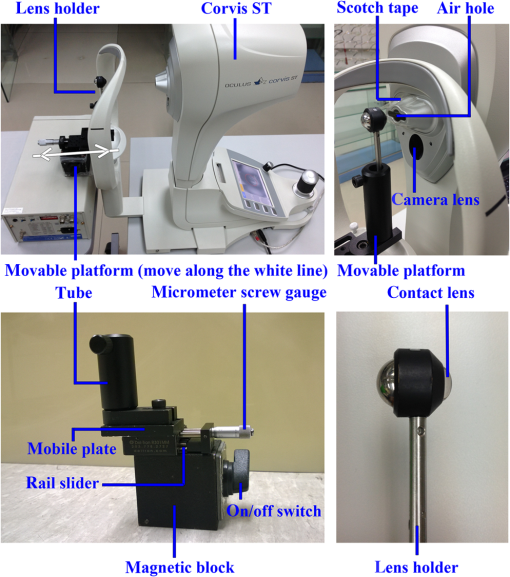
1.IntroductionAnterior segment imaging evolves rapidly in the field of ophthalmology. Early contact devices such as Ultrasound Biomicroscopy (P60 UBM, Paradigm Medical Industries Inc.) have proven meaningful to the ophthalmic diagnosis, but failed to become the part of routine clinical practice. Scanning Slit Topography (Orbscan IIz, Bausch & Lomb Inc.), as a noncontact device that achieved more extensive applicability. Major advantages of concomitant advancing devices are the noncontact nature of examination, a better repeatability, and a larger range of quantitative and qualitative information.1 Utilizing low-coherence interferometry, optical coherent tomography (OCT) achieves high-resolution anterior segment images by measuring the delay and intensity of light backscattered within biological tissue.2 Some commercial devices, such as the Visante OCT (Carl Zeiss Meditec Inc.) and the Slit-lamp OCT (Heidelberg Engineering Inc.), promise an axial resolution of . Other devices that adopt the Scheimpflug principle3 can also generate high-resolution slit images of the anterior segment of the eyeball. In a commercial instrument, the Pentacam (OCULUS Optikgeräte GmbH), the Scheimpflug camera is swiveling around the eye to capture a series of radially oriented images.4 However, these devices cannot generate any noncontact force onto the eye, so they can only evaluate the static characteristics of human eyes. The Ocular Response Analyzer (ORA, Reichert Technologies) integrates the air puff component to reveal the dynamic properties of the cornea in vivo.5 It evaluates the corneal hysteresis as the pressure difference derived in the inward and outward applanation events. Recent studies successfully combine the air puff function with more advanced spectral optical coherence tomography (sOCT) system.6–8 However, due to the limitation of techniques, both the commercial ORA and the new sOCT can only obtain the dynamic corneal parameters at a certain point of the cornea. The Corvis ST (OCULUS Optikgeräte GmbH, Wetzlar, Germany) is a compromise between the dynamic characteristics and the imaging range. It adopts a high-speed Scheimpflug camera to record the entire process of cornea deformation. In the clinical practice using the Corvis ST, a patient should place the chin on the chin rest and also attach the head console by the forehead. The patient is then asked to focus at the central red light-emitting diodes. In each measurement, the air puff component induces the indentation, so the cornea moves inward until reaching a point of highest concavity and then rebounds to its normal convex curvature. The camera within the Corvis ST takes 140 digital frames in 30 ms, which corresponds to the frame rate of 4300 frames per second. The image of each frame covers 8.5 mm horizontally of a single slit and has .9 Currently, the Corvis ST provides a number of dynamic-related parameters, including the deformation amplitude, the applanation length and velocity, the peak distance, apex radius, and intraocular pressure (IOP). It also measures the original central corneal thickness (CCT) and provides visualization of the continuous deformation of the cornea captured by the Scheimpflug camera. However, it does not provide definitive values of dynamic CCTs. Many studies only reported the good repeatability and its high correlation with ultrasound pachymetry in the measurement of stationary CCT.10 The measurement of CCT in a stationary status is widely accepted to be important to the diagnosis and follow-up of eye diseases and the refractive surgery. The CCT increases in the patients with cornea guttata received the dorzolamide therapy, and consequently needs monitoring.11,12 It also has significant value in discriminating eye diseases, such as keratoconus13,14 and glaucoma.15 The clinical evidence demonstrated an association between the CCT and the IOP measurement: a 10% difference in the CCT would result in a difference in the IOP,16 which was in consonance with the IOPs predicted by an advanced eye model considering the influence of corneal biomechanical properties.17 Except the IOP, recent studies reported dynamic-related parameters of the cornea measured with the ORA and the Corvis ST were widely dependent on the CCT.13,18 In comparison to the CCT at a stationary status, a rare clinical study concerned its dynamic changing during air puff indentation. This situation is due to the technical limitation rather than the needs, since no accessible way is provided for its measurement before the Corvis ST. Actually, the Covis ST visualizes the dynamic CCT, but cannot provide the definitive value. On the other hand, dynamic CCTs directly reveal the corneal deformation under certain air pressure, so it indicates the biomechanical properties of cornea to a large extent. It may contain many undiscovered important information for screening various eye diseases associated with collagen disorders or endothelial-based corneal dystrophies, such as keratoconus and cornea guttata. It may also identify the effect of corneal cross-linking in vivo, which both the Corvis ST and the ORA may not achieve at the current stage.13,19 In our previous study with the Corvis ST (OCULUS Optikgeräte GmbH), the directly measured CCT at highest concavity was found to be reduced by in 42 healthy subjects20 without considering the Scheimpflug distortion.21 The overall objective of our study is to predict the influence of Scheimpflug distortion on the CCT measurement, to propose a method to correct the distortion for dynamic CCTs, and to apply the method to study the CCT variation in clinical cases. The Scheimpflug principle has been applied to anterior segment imaging since the 1970s,22 but was not extensively utilized in clinical practice until 2005 when commercial instruments, such as the Pentacam, were introduced. An early study reported that the directly observed CCT was underestimated by in comparison with the true value.21,23 The authors corrected this error by using the ray tracing technique with a Basic program. An introduction to the theory of ray tracing and its computation implementation can be found in Ref. 24. With the advent of digital charge-coupled device (CCD) and the improvement of focus depth, more studies focused on the Scheimpflug distortion and provided more accurate measurement for different ocular components. Fink et al. reported their effort on the refractive correction for the cornea and eye lens in the digital CCD-recorded Scheimpflug photographs.25,26 It gave a numerical example to show that internal surfaces of the eye, such as the posterior corneal surface and the anterior lens surfaces, are far different from what it looks like in Scheimpflug imaging. The CCT is theoretically underestimated by in comparison with the true value. The study of Rosales and Marcos focused on the particular configuration of the commercial device Pentacam.27 They also applied the ray tracing technique and obtained the similar conclusion in artificial and human eyes. However, all these studies concerned the measurement and correction for a stationary eyeball without air puff indentation. In the present study, we investigated the measurement of dynamic CCTs with the Corvis ST and proposed a method to correct the Scheimpflug distortion. We considered the problem from a practical concern that the refractive index of cornea, the distance of cornea away from the lens, and the front curvature of cornea induced by air puff indentation may affect the CCT measurement. With the calibration for unit conversion in image length, from pixels to micrometers, the object–image curve derived theoretically can be applied to correct the Scheimpflug distortion in the CCT measurement. We conducted the experiment to verify a prediction concerning the measurement error induced by a different material refractive index. We also applied the proposed correction method to preliminarily investigate the CCT variation during air puff indentation. 2.Materials and Methods2.1.Optical Paths for Scheimpflug Imaging of the Corvis STIn a common photographic system, the camera lens and the image plane are parallel, so the plane of focus is parallel to the camera lens. Image sharpness can be controlled by a suitable focused distance. Scheimpflug principle demonstrates another geometric layout that promises a clear record.3 The condition is when the plane of camera lens and the image plane extended meet at a line through which the plane of focus also passes, the subject can be all in focus, although it is not parallel to the plane of the camera lens. In Scheimpflug imaging, the subject plane should rotate rather than move along the lens axis, when adjusting the focus. The axis of rotation is the intersection of the camera lens’s front focal plane and the plane through the center of the camera lens perpendicular to the image plane. This concept was documented in an early British patent.28 As per the principle, Corvis ST, like its precursor the Pentacam, substitutes a Scheimpflug camera for the slit-lamp camera of traditional anterior segment imaging devices in ophthalmology. Prior studies showed the three-dimensional optical path for Scheimpflug imaging.26,27 In the system of Corvis ST, the camera lens is placed to form an angle of 45 deg with the object plane according to the specification from the manufacturer. Figure 1 illustrates the two-dimensional optical path with more details. It will be used to deduce the correction formulas later in this section. Here the proportion of the measurement distance to the corneal thickness is exaggerated, so the geometrical relationship can be seen more clearly. The blue arcs denote the anterior and posterior surface of the cornea, while the green arc is the virtual image of the posterior surface. It should be noted that the camera lens is replaced by a pinhole and does not induce any scaling. This simplification works because the effective image can always be found ignoring the real optical magnification. The intrinsic reason behind is that the image distortion from scaling stays stationary in different tests and subjects, so it can be eliminated when calibrating the real length for each pixel of the photographic record. Fig. 1The optical paths of Scheimpflug imaging in the Corvis ST: (a) a cornea at the preindentation status and (b) a cornea at its highest concavity. 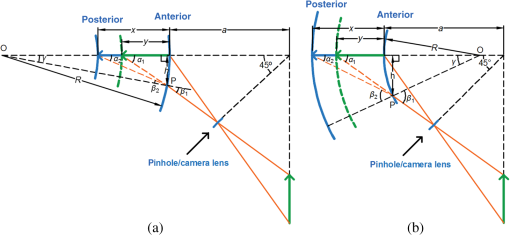 According to the optical path, a one-to-one correspondence can be observed between the real CCT and its image length, denoted as and , respectively. Ray tracing refers to a technique of generating an image by tracing the path of light.24 Figure 1 shows the imaginary light beams emanating from the anterior and the posterior surface of the cornea in orange. Consider the example of the light beam from the posterior surface. It forms an angle with the imaging plane. It refracts at the anterior surface of cornea, thus appearing as if it is coming from the light beam that forms angle with the imaging plane. It continues to propagate passing through a pinhole and, finally, projects onto the CCD. Figure 1(a) takes the cornea at its original status for an example; the relationship can be theoretically deduced between the object and image length . According to the configuration of the optical system, angle can be first calculated by where is two times the distance of the cornea away from the pinhole. It is true, since the distance is always much larger than the corneal thickness. Actually, the CCT of a human cornea thickness is at the level of ,16 while the distance is of the Corvis ST according to our measurement using a ruler. Due to a limited region concerned with the CCT measurement, the tip of anterior cornea surface can be regarded as nearly spherical. Supposing the known radius of , the refractive angle can be derived at the point P successively using Eqs. (2)–(4): where and are just the affiliated variables. Snell’s law tells the propagation of light at the refraction point, so the incident angle is given by where and are the refractive index of cornea and air. They are known in the literature. Applying the geometrical relationship again, can be obtained byAccordingly, the true CCT can be finally calculated from its image length A similar one-to-one correspondence can be found when the cornea is reversed by air puff indentation. When air puff indentation is performed, the cornea is deformed from convex to concave and then rebounds to its normal convex status. Ambrosio et al. show a graphical presentation of corneal deformation under air puff indentation with detected applanation moments in their study.9 The whole process can be regarded as the radius of curvature changes. Figure 1(b) shows the optical layout for the cornea reversed. The only difference is that the spherical center shifts from inside to outside of the eyeball, so some signs in Eqs. (2), (4), and (6) should be modified as follows: 2.2.Correcting the Distortion in Measuring the CCTThe essence of the CCT measurement is to estimate the real thickness from a raw photographic record. An intuitive-feasible approach is to conduct the calibration on standard samples and determine the effective length for each pixel of the photographic record. It can be analogical to reading a map in real life. If the distance between the two places is required, we can first measure the distance on the map and then calculate the real value using the scale of the map. Similarly, the estimated CCT can be calculated as the product of its pixel number and a total scaling factor. However, this method neglects the influence factors (the refractive index, the front curvature, and the measurement distance) differed from case to case. Here the method is proposed to better measure the CCT in two steps. When the CCT is estimated from a measured image length, the units of the image length can be either in micrometers for the image captured by the CCD or in pixels for the image displayed on the screen. There is only a proportional scaling factor between them. It is determined by the electronic display system of the Corvis ST, and is therefore irrelevant to the optical path in different cases. In the first step of measurement, the scaling factor is experimentally determined by a calibration conducted on the samples with known thickness. However, the influence factors affect when the object length of CCT is transformed to the image length, since they change the optical paths and require to be considered. Accordingly, correction procedures should be performed in the second step. A real thickness is obtained by following Eqs. (1)–(7), if the cornea is convex. When air ejects onto the cornea, it will move inward and become concave, so substitute Eqs. (8), (9), and (10) in Eqs. (2), (4), and (6) to estimate the CCT at a concave status. All codes are implemented in a custom-developed program using MATLAB® (Version R2013a, MathWorks Inc., Massachusetts). 2.3.Measuring the Scaling Factor for Unit ConvertingLike any other digital photographic system, the image projected onto the CCD is visualized on the display screen of a Corvis ST system. The calibration experiment described here aimed to find the invariable scaling factor, which calculates the image length in micrometers from the pixels read on the display screen or the exported image. Figure 2 shows the experimental setup for the calibration experiment. A piece of scotch tape seals the air hole to prevent the potential shift induced by air puff indentation for the tested samples. The base of the custom-made platform is a magnetic block with an on/off switch. It can be firmly fixed onto an iron surface. The rail slider is mounted on the base, so the mobile plate above can move along under the control of a micrometer screw gauge. A tube mount is attached to the mobile plate in order to fix the lens holder. When using the eye contact lens, it should be dampened to adhere to the head of lens holder. The rod side is then plugged into the tube mount. The eye contact lens is kept 7 mm away from the camera lens in the calibration experiment. Taking the advantage of the custom-made platform, the eye contact lens can be precisely moved, but it needs to be kept fixed in this calibration experiment. The ability of the custom-made platform for controlling the position will be used later in the experiment discussed in Sec. 2.5. Three customized hard contact lens and four human eyes were used to estimate the scaling factor. The contact lenses were made of polymethylmethacrylate (PMMA) with the refractive index () of 1.432. The thickness was measured by the thickness gauge (G. Nissel & Company Limited, United Kingdom), and the front curvature was measured by the Ophthalmometer OM-4 (Topcon Corporation, Tokyo, Japan) in the Optometry Clinic at the Hong Kong Polytechnic University. Two healthy human subjects were tested in the General Hospital of People’s Liberation Army (the Chinese PLA General Hospital, Beijing, China). Both the left and right eyes were included. The thickness and front curvature were measured in vivo by an OCT anterior segment scanner SS-1000 CASIA (TOMEY Corporation, Nagoya, Japan). Table 1 details the geometrical parameters of all seven samples. Table 1Geometrical parameters of the hard contact lens and human corneas.
Not considering the optical magnification, the effective image length of CCT in micrometers was derived from the true thickness measured with the theoretical object–image curve. It can also be measured manually in pixels on the display screen by the custom-developed program. The scaling factors were calculated in all cases and averaged for further applications. 2.4.Theoretical Simulations for the Influence FactorsTheoretical object–image curve of the CCT can predict measurement errors in the intuitive-feasible calibration aforementioned. This calibration actually assumes the scaling factor invariable from case to case for transforming image length in pixels to object length in micrometers. Accordingly, the factor can be determined experimentally and applied to each measurement. However, three factors may break this expectation: the refractive index, the front curvature, and the measurement distance. The simulation experiments here were designed to predict these influences. It should be noted that the simulation needs the inverse process, which calculates the image length from the real CCT. It cannot be directly obtained through Eqs. (1)–(10), but can be realized by interpolating29 the image–object curve derived from the forward process. A real experiment was additionally conducted to confirm the prediction concerning the refractive index later in Sec. 2.5. When investigating the influence of the refractive index, we simulated the materials of air (), human cornea (),30 and contact lens (). The front curvature was fixed to 7.5 mm, and the distance () between the sample and the camera lens was 7 mm. Another simulation imitated that a cornea moved toward the camera lens. The distances were set to be 5, 7, and 9 mm, while the front curvature was fixed to 7.5 mm. In the final simulation, the front curvature of a cornea varies from 7 mm at the convex status to the concave status of the same value, and the distance was set to 7 mm. It imitated the influence of the air puff indention, which changes the front curvature of cornea with time. All these simulations assumed that the intuitive-feasible calibration for determining the total scaling factor was conducted on a 550-um-thick cornea of the 7.5-mm front curvature measured 7 mm away from the lens. 2.5.Confirming the Prediction of the Refractive IndexA real experiment was conducted on the Corvis ST to confirm the prediction concerning the refractive index. It is that the human cornea should be adopted in the intuitive-feasible calibration; otherwise the sample with a different refractive index will induce errors in the CCT measurement. In the following experiment, the total scaling factors were measured for the material of air, the human cornea, and the PMMA material. And then the measurement errors can be calculated for a human cornea, assuming that the calibration was conducted in air or the hard contact lens made of PMMA. The custom-made platform was applied to carry the lens holder to move horizontally along the line connecting the sample and the camera lens. The hard contact lenses were initially tested at the distance of 7 mm and then moved away from the camera lens at regular intervals of 0.2 mm until the distance of 7.8 mm. The whole procedure was repeated five times. Just like the calibration experiment described in Sec. 2.3, a piece of scotch tape sealed the air hole to prevent the potential shift of the testing sample due to air puff indentation. The image data of four human corneas collected in Sec. 2.3 were also included for further analysis. Based on the data captured by the Corvis ST, we processed the collected images by the custom-developed program. On the images of hard eye contact lens, we manually recorded the apex of the anterior surface and the central thickness. Position records of the apex of the moving anterior surface were applied to calculate the total scaling factor in air, while the central thickness records were used to obtain that for PMMA. On the images of human corneas, the CCT were manually measured in pixels and averaged among five tests for calculating the total scaling factor in human cornea. Using the calibration result of air, human cornea, and PMMA, we calculated the CCT of a human cornea multiplying the total scaling factor by the measured pixel numbers. Consequently, we obtained the measurement errors that the refractive index induced. 2.6.Clinical ApplicationsOur previous study on the Corvis ST observed a thinning phenomenon with air puff indentation.20 Now the proposed method was applied to correct the Scheimpflug distortion, which aimed to confirm this thinning. Sixty cases of healthy human corneas included in the study were from 35 patients visiting the Chinese PLA General Hospital for the eye examination from 2012 August to 2013 October. Twelve cases were excluded, since eyelashes degraded image quality, which may interfere with the estimation of front curvature at highest concavity. All the examinations were conducted in accordance with the Declaration of Helsinki, and the experimental protocol received the approval from the institutional review board of the Chinese PLA General Hospital. The CCT of each case was measured three times on the first frame and the frame corresponding to highest concavity. It was manually recorded and averaged. These values of the pixel number gave the ratio of thinning without correction. Then the original CCT was calculated using the total scaling factor achieved in the intuitive-feasible calibration. The parameters of the calibration human cornea are as those in the simulation experiment (, , , ). The CCT at highest concavity was corrected with the curvature revealed by the Corvis ST at the measurement distance of 7 mm. The reasonableness of the approximation here will be presented in Sec. 4. Statistical analyses on corrected CCTs were performed in IBM SPSS Statistics (Version 20, IBM Corporation, New York, USA). Statistical significance was set at the 5% probability level. The CCT differences before and after air puff indentation were first checked for their normality through the Kolmogorov-Smirnov test.31 Then the paired test was conducted to compare their mean values. Besides, Pearson correlation was applied to examine the contribution of the original thickness to the CCT variation. Many literature references provide useful instructions for the statistical analysis.31,32 3.Experimental Results3.1.Scaling Factor for Unit ConversionIn each measurement, the Corvis ST captures the whole process of cornea movement at a rate of 4330 image frames per second and records a 140-frame video clip in 30 ms. The image of each frame covers 8.5 mm horizontally of a single slit and has .9 All the collected clips were exported and the related frames were selected for further analysis. The image length of any testing sample can be expressed both in pixels and in micrometers. We followed the protocol presented in Sec. 2.3 to experimentally derive the scaling factor for unit conversion. The average result of seven samples (three custom-made hard contact lens and four human corneas) manifested it to be in the Corvis ST, which means that each pixel in an exported image represents an image length of . This result was applied to estimate and correct the measurement error. 3.2.Measurement Errors Attributed to Different Influence FactorsFigure 3 provides the theoretical predictions on the images captured by the Corvis ST. They are simulated based on the proposed equations deduced in Sec. 2.1. Object–image curves for different materials are given in Fig. 3(a). The simulation result is consistent to our common sense that the image and object length is equal in air. As for the material with a higher refractive index, it is observed that the image length is much smaller than the object length. Fig. 3Theoretical predictions on the images captured by the Corvis ST: (a) object–image curve under different refractive indexes, (b) errors in the central corneal thickness (CCT) measurement related with the refractive index of calibrated samples, (c) errors in the CCT measurement at different measurement distances, and (d) errors in the CCT measurement with air puff indentation ( for the convex cornea and for the revised cornea under air puff indentation). 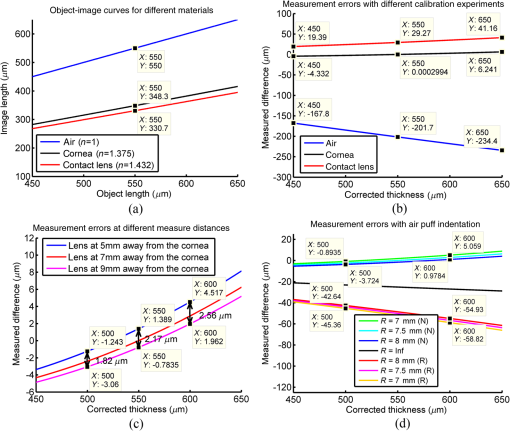 Further images demonstrate the influence of the refractive index, the measurement distance, and the front curvature on the CCT measurement. According to Fig. 3(b), measurement errors are positively correlated with the absolute value of the CCT. The measured value of a -thick human cornea is larger than its real value when the calibration is conducted on the contact lens, while it is underestimated by when the calibration is performed on a moving anterior surface of the contact lens in air. However, measurement errors can be confined to within the whole thickness range between 450 and , if human corneas are adopted in the calibration. Figure 3(c) shows the measurement errors of a human cornea deviating from the original measuring position in the calibration. The measurement error due to the measurement position is for a thick cornea. The value are 2.17 and for the CCT of 550 and , respectively. It is concluded that errors in a measurement are at the level of several micrometers, even if the testing cornea moves 2 mm away from the calibration position. According to our experience, the largest deviation would not exceed 0.5 mm; otherwise, the cornea would be out of the region of imaging and fail to be captured by the camera of Corvis ST. Figure 3(d) reveals the influence of air puff indention on the CCT measurement. The letters in parentheses denote the direction of corneal deformation. The letter N means the cornea is convex, and the letter R means the cornea is reversed under air puff indentation. The distance between the green line and the blue line shows only several micrometers error occurred due to the diversity of the front curvature of human corneas. However, when air puff indentation works and renders the cornea completely reversed, the measurement error could reach referred to a -thick human cornea. 3.3.Calibration Errors Related with the Refractive IndexFormer simulation results declared that a proper calibration could restrain the measurement errors of a stationary CCT to several micrometers. This conclusion will be further explained in Sec. 4. Here the experiment was performed to confirm the prediction concerning the refractive index shown in Fig. 3(b) that the CCT is underestimated with an improper calibration conducted on the moving anterior surface of contact lens in air, and it is overestimated by when the calibration is conducted on the contact lenses made of PMMA. We followed the experimental protocol presented in Sec. 2.5 to obtain the total scaling factor for the intuitive-feasible calibration. Among the three custom-made hard contact lenses, it was concluded that each pixel in the exported image represented for air and for contact lens, while the scaling factor was found to be among four human corneas. Accordingly, we calculated the measurement error of a -thick human cornea. It was found that the CCT was thicker based on the calibration of a moving anterior surface of contact lens in air and thinner based on the calibration of hard contact lens. Considering the pixel resolution of Corvis ST, which is for the human cornea without air puff indentation, the result was in accordance with our simulation, which predicted thicker and thinner. 3.4.Thinning Phenomena in Clinical ApplicationsThe proposed correction method was applied to confirm the thinning phenomenon observed in our previous study.20 It was observed that the CCT decreased by 7.6% of its original thickness when air puff indentation made the cornea totally reversed. After a correction, the CCT was found to increase by at highest concavity under air puff indentation, which was 2.5% of the original CCT. The corrected CCT was at the preindentation period and at highest concavity. Their differences in each case passed the Kolmogorov–Smirnov test for normality, and a significant difference was observed by the paired test (). Pearson correlation further found a weak positive correlation between the uncorrected variation of CCT and the stationary CCT (, ). However, no significant association was observed after the correction (, ). 4.DiscussionThe concept of scaling factors should be further clarified. Using the intuitive-feasible calibration, we may directly relate a real corneal thickness to its image length visualized on the screen. Accordingly, the scaling factor can be determined experimentally to transform the object length in micrometers to the image length in pixels. However, this procedure actually involves two steps of conversion. First, the cornea is projected onto the CCD of an optical system, which concerned the scaling factor to transform object length to image length. Second, the image captured by the CCD is visualized on a screen, which concerned the scaling factor to transform the image length from pixels to micrometers. The first conversion is influenced by the diversity of human corneas and the changeable experimental conditions, while the second only reflects the visualization for digital images, so it is invariable from case to case. Due to the first step, the axial pixel resolution of the corneal image captured by the Corvis ST is variable. The fundamental essence of the proposed correction method is to differentiate the two parts and derive the real total scaling factors in different cases. Simulated results from the theoretical analysis actually evinced an intriguing conclusion. The stationary CCT can be measured through the intuitive-feasible calibration without correcting the Scheimpflug distortion. The total scaling factor should be measured on the human cornea with the known CCT. This method simplifies the measurement of the stationary CCT. According to the simulation results shown in Figs. 3(b), 3(c), and 3(d), this method only induces the measurement error in the level of several micrometers. It is acceptable when we consider the pixel resolution of the Corvis ST, which makes each pixel present for human corneas. Even so, Fig. 3(b) visualizes a concomitant problem of the calibration. Errors in the CCT measurement are larger when the corneal thickness is away from the calibration point. Figures 3(c) and 3(d) show a similar tendency for the variation of the front curvature and the measurement distance. Since they are the simulation results of the proposed formulas, it reveals an inevitable defect of the intuitive-feasible calibration: the calibration error changes with the stationary CCT. On the other side, it is remarkable that the measurement error increases distinctly to dozens of micrometers when the air puff indentation completely reversed the cornea, indicating that we need to correct the Scheimpflug distortion for analyzing the dynamic changes of human corneas. The proposed method can correct the CCT with the influence from the front corneal curvature, the refractive index, and the measurement distance. It is applicable to correct not only for a reversed cornea, but also for the cornea diversity in different cases. Even so, the simplified calibration for the total scaling factor may be more convenient for measuring the stationary CCT, since no additional parameter is required to be measured. This calibration may not be performed in real life. We can imagine a human cornea with the known parameters and derive its image length from the object length. Combining the ratio with the scaling factor for unit conversion, we actually obtain the total scaling factor in the intuitive-feasible calibration. We expected the CCT variation occurring with air puff indentation. It may reflect the biomechanical properties of cornea, since an elastomer is deformed under pressure. According to our measurement, the of the original CCT was . It decreased by 7.6% at highest concavity before correction, and the result was approximately consistent with the observation in our previous study.20 After correction, the CCT increased by 2.5%. However, it is too rough to confirm that the CCT really increased by 2.5%, i.e., that a -thick cornea thickens by . We have reservations about this thickening phenomenon, considering the resolution of the Corvis ST is for human corneas. Moreover, the reason behind the phenomenon from the aspect of biomechanics is unclear. In this study, we corrected the Scheimpflug distortion for measuring dynamic CCTs, but there are still many technical obstacles to be overcome for finding the reason behind the phenomenon. If the thickening is true, we hypothesize the viscoelasticity33 may cause the phenomenon. As most biological materials, the cornea exhibits viscoelasticity.34 On the grounds of its elastic nature, it responds instantaneously to a stress. Meanwhile, to accommodate its viscous behavior, the strain decays with time. The corneal tissue may be accumulated within the central part under a prompt air puff indentation. Further studies should be conducted to have a better understanding about the dynamic indentation process of cornea using biomechanical analysis. In addition to the thickening phenomenon, a weak correlation was observed between the uncorrected variation and the original CCT in our clinical cases. It was consistent with the simulation result in Fig. 3(d), which shows an increasing tendency of thickness variation with the CCT without correction. It was remarkable that the proposed method eliminated the association by correcting the Scheimpflug distortion. An improper calibration increases the errors in the CCT measurement. The experimental result was consistent to the prediction roughly. Former studies indicated the difficulty in selecting the reference points for the CCT measurement with UBM due to the resolution.1 It is also the problem of the Corvis ST. According to our measurement, the Corvis ST presents each pixel as long for a human cornea, compromising the resolution by a high-speed camera. Fast moving cornea under air puff indentation blurred the image and worsened the problem. In addition, we actually did not correct the CCT at its preindentation status, but used the total scaling factor derived at an imaginary calibration point for estimation. This also contributed to the difference between the theoretical prediction and the experimental result. This study will especially benefit the analysis of dynamic changing corneas from two aspects. First, it demonstrated the reasonableness of performing an intuitive-feasible calibration for measuring the CCT at preindentation status. Second, the proposed correction method can be applied to correct dynamic CCT at any time, although the correction was only performed on the CCT at its highest concavity in this study. The difficulty is the dynamic estimation of the front curvature. Further study could integrate the achievement from cornea segmentation and curvature estimation to estimate the changing front curvature for measuring the dynamic CCTs. Another research focus can be the correction of the Scheimpflug distortion for other corneal parameters, especially the curvature map of posterior corneas. Although Corvis ST brings light to the dynamic analysis of cornea, we may still expect one day to improve the image quality and increase the shutter speed. 5.ConclusionsThe paper started from the optical path of Scheimpflug imaging in the Corvis ST and derived the formulas to predict the influence of three practical factors in the use of the Corvis ST. Applying these formulas, the Scheimpflug distortion can be corrected for the CCT measurement. The simulation results demonstrated that the stationary CCT can be measured through the intuitive-feasible calibration without correcting the Scheimpflug distortion. Compared to the pixel resolution of the Corvis ST, which reaches for human cornea, the maximal measurement error induced is . Even so, it should be considered that errors in the CCT measurement are larger when the corneal thickness is away from the calibration point. However, the simulation results also indicated the necessity to correct the distortion when the cornea is deformed under air pressure (the distortion suffers most at highest concavity). Otherwise, the measurement error of the CCT at highest concavity may reach several micrometers. Finally, the proposed method was adapted to study the CCT variation in clinical cases. The analysis result confirmed our previous observation that the seeming CCT observed by the Corvis ST at highest concavity was decreased. However, after correcting the distortion, the CCT at highest concavity is increased by 2.5%. We confirmed this variation is statistically significant, but have some reservations about this thickening phenomenon. It is observed that the proposed correction method eliminated the weak positive correlation between the CCT variation and its original value. AcknowledgmentsThis research was supported by the National Natural Science Foundation of China (11228411 and 81271052) and Hong Kong Polytechnic Joint PhD Scheme (G-UB58). ReferencesA. Konstantopoulos, P. Hossain and D. F. Anderson,
“Recent advances in ophthalmic anterior segment imaging: a new era for ophthalmic diagnosis?,”
Br. J. Ophthalmol., 91
(4), 551
–557
(2007). http://dx.doi.org/10.1136/bjo.2006.103408 BJOPAL 0007-1161 Google Scholar
J. G. Fujimoto et al.,
“Optical coherence tomography: an emerging technology for biomedical imaging and optical biopsy,”
Neoplasia, 2
(1), 9
–25
(2000). http://dx.doi.org/10.1038/sj.neo.7900071 1522-8002 Google Scholar
S. F. Ray, Applied Photographic Optics, 2nd ed.Focal Press, Oxford, United Kingdom
(1994). Google Scholar
R. Jain and S. P. S. Grewal,
“Pentacam: principle and clinical applications,”
J. Curr. Glaucoma Pract., 3
(2), 20
–32
(2009). http://dx.doi.org/10.5005/jp-journals-10008 0974-0333 Google Scholar
D. A. Luce,
“Determining in vivo biomechanical properties of the cornea with an ocular response analyzer,”
J. Cataract Refract. Surg., 31
(1), 156
–162
(2005). http://dx.doi.org/10.1016/j.jcrs.2004.10.044 JCSUEV 0886-3350 Google Scholar
L. K. Wang, Y. P. Huang and Y. P. Zheng,
“A miniaturized air jet indentation probe based on optical coherence tomography (OCT) for mechanical assessment of soft tissue,”
in Int. Tissue Elasticity Conference,
94
(2011). Google Scholar
D. Alonso-Caneiro et al.,
“Assessment of corneal dynamics with high-speed swept source optical coherence tomography combined with an air puff system,”
Opt. Express, 19
(15), 14188
–14199
(2011). http://dx.doi.org/10.1364/OE.19.014188 OPEXFF 1094-4087 Google Scholar
Y. P. Huang et al.,
“An optical coherence tomography (OCT)-based air jet indentation system for measuring the mechanical properties of soft tissues,”
Meas. Sci. Technol., 20
(1), 015805
(2009). http://dx.doi.org/10.1088/0957-0233/20/1/015805 MSTCEP 0957-0233 Google Scholar
R. AmbrosioJr. et al.,
“Dynamic ultra high speed Scheimpflug imaging for assessing corneal biomechanical properties,”
Rev. Bras. Oftalmol., 72
(2), 99
–102
(2013). http://dx.doi.org/10.1590/S0034-72802013000200005 RBOFA9 0034-7280 Google Scholar
L. Reznicek et al.,
“Evaluation of a novel Scheimpflug-based non-contact tonometer in healthy subjects and patients with ocular hypertension and glaucoma,”
Br. J. Ophthalmol., 97
(11), 1410
–1414
(2013). http://dx.doi.org/10.1136/bjophthalmol-2013-303400 BJOPAL 0007-1161 Google Scholar
M. G. Wirtitsch et al.,
“Effect of dorzolamide hydrochloride on central corneal thickness in humans with cornea guttata,”
Arch. Ophthalmol., 125
(10), 1345
–1350
(2007). http://dx.doi.org/10.1001/archopht.125.10.1345 AROPAW 0003-9950 Google Scholar
M. G. Wirtitsch et al.,
“Short-term effect of dorzolamide hydrochloride on central corneal thickness in humans with cornea guttata,”
Arch. Ophthalmol., 121
(5), 621
–625
(2003). http://dx.doi.org/10.1001/archopht.121.5.621 AROPAW 0003-9950 Google Scholar
S. Bak-Nielsen et al.,
“Dynamic Scheimpflug-based assessment of keratoconus and the effects of corneal cross-linking,”
J. Refract. Surg., 30
(6), 408
–414
(2014). http://dx.doi.org/10.3928/1081597X-20140513-02 JRSUEY 0883-0444 Google Scholar
S. Shah et al.,
“Assessment of the biomechanical properties of the cornea with the ocular response analyzer in normal and keratoconic eyes,”
Invest. Ophthalmol. Vis. Sci., 48
(7), 3026
–3031
(2007). http://dx.doi.org/10.1167/iovs.04-0694 IOVSDA 0146-0404 Google Scholar
L. W. Herndon, J. S. Weizer and S. S. Stinnett,
“Central corneal thickness as a risk factor for advanced glaucoma damage,”
Arch. Ophthalmol., 122
(1), 17
–21
(2004). http://dx.doi.org/10.1001/archopht.122.1.17 AROPAW 0003-9950 Google Scholar
M. J. Doughty and M. L. Zaman,
“Human corneal thickness and its impact on intraocular pressure measures: a review and meta-analysis approach,”
Surv. Ophthalmol., 44
(5), 367
–408
(2000). http://dx.doi.org/10.1016/S0039-6257(00)00110-7 SUOPAD 0039-6257 Google Scholar
J. Liu and C. J. Roberts,
“Influence of corneal biomechanical properties on intraocular pressure measurement: quantitative analysis,”
J. Cataract Refract. Surg., 31
(1), 146
–155
(2005). http://dx.doi.org/10.1016/j.jcrs.2004.09.031 JCSUEV 0886-3350 Google Scholar
A. Kotecha et al.,
“Biomechanical parameters of the cornea measured with the ocular response analyzer in normal eyes,”
BMC Ophthalmol., 14
(11),
(2014). http://dx.doi.org/10.1186/1471-2415-14-11 BOMPAC 1471-2415 Google Scholar
M. Gkika et al.,
“Evaluation of corneal hysteresis and corneal resistance factor after corneal cross-linking for keratoconus,”
Graefes Arch. Clin. Exp. Ophthalmol., 250
(4), 565
–573
(2012). http://dx.doi.org/10.1007/s00417-011-1897-0 GACODL 0721-832X Google Scholar
Y. Hon et al.,
“Corneal thinning during air puff indentation,”
in Annual Meeting of the Association for Research in Vision and Ophthalmology,
(2014). Google Scholar
T. Kampfer et al.,
“Improved biometry of the anterior eye segment,”
Ophthalmic Res., 21
(3), 239
–248
(1989). http://dx.doi.org/10.1159/000266815 OPRSAQ 0030-3747 Google Scholar
N. Brown,
“Slit-image photography and measurement of the eye,”
Med. Biol. Illus., 23
(4), 192
–203
(1973). Google Scholar
D. W. Richards, S. R. Russell and D. R. Anderson,
“A method for improved biometry of the anterior chamber with a Scheimpflug technique,”
Invest. Ophthalmol. Vis. Sci., 29
(12), 1826
–1835
(1988). IOVSDA 0146-0404 Google Scholar
A. S. Glassner, An Introduction to Ray Tracing, Morgan Kaufmann, Burlington, Massachusetts
(1989). Google Scholar
H. Huebscher et al.,
“Scheimpflug records without distortion—a mythos?,”
Ophthalmic Res., 31
(2), 134
–139
(1999). http://dx.doi.org/10.1159/000055525 OPRSAQ 0030-3747 Google Scholar
W. Fink,
“Refractive correction method for digital charge-coupled device-recorded Scheimpflug photographs by means of ray tracing,”
J. Biomed. Opt., 10
(2), 024003
(2005). http://dx.doi.org/10.1117/1.1899683 JBOPFO 1083-3668 Google Scholar
P. Rosales and S. Marcos,
“Pentacam Scheimpflug quantitative imaging of the crystalline lens and intraocular lens,”
J. Refract. Surg., 25
(5), 421
–428
(2009). http://dx.doi.org/10.3928/1081597X-20090422-04 JRSUEY 0883-0444 Google Scholar
T. Scheimpflug,
“Improved method and apparatus for the systematic alteration or distortion of plane pictures and images by means of lenses and mirrors for photography and for other purposes,”
(1904) http://www.trenholm.org/hmmerk/TSBP.pdf April 2015). Google Scholar
R. C. Gonzalez and R. E. Woods, Digital Image Processing, Publishing House of Electonics Industry, Beijing
(2006). Google Scholar
D. M. Maurice,
“The structure and transparency of the cornea,”
J. Physiol., 136
(2), 263
–286
(1957). http://dx.doi.org/10.1113/jphysiol.1957.sp005758 JPHYA7 0022-3751 Google Scholar
T. W. Kirkman,
“Statistics to use,”
(1996) www.physics.csbsju.edu/stats March 2015). Google Scholar
W. G. Hopkins,
“A new view of statistics,”
(2000) www.sportsci.org/resource/stats March 2015). Google Scholar
D. Gutierrez-Lemini, Engineering Viscoelasticity, Springer, Arlington, Texas
(2014). Google Scholar
A. Kotecha,
“What biomechanical properties of the cornea are relevant for the clinician?,”
Surv. Ophthalmol., 52
(6), S109
–S114
(2007). http://dx.doi.org/10.1016/j.survophthal.2007.08.004 SUOPAD 0039-6257 Google Scholar
BiographyTianjie Li is a postdoctoral fellow in the Biomedical Interdisciplinary Division of Biomedical Engineering at the Hong Kong Polytechnic University. She received her BS and PhD degrees from the Department of Electronic Engineering, Fudan University, China. Her research interests are in the areas of medical image processing and imaging. Within these fields, her current research focuses on Scheimpflug imaging for the anterior segment of the eyeball and elasticity measurement of muscles. Lei Tian is a project associate in the Interdisciplinary Division of Biomedical Engineering at the Hong Kong Polytechnic University. He received his MS and MD degrees from the Chinese PLA General Hospital, Beijing, China. He mainly works on research pertinent to corneal biomechanical properties. Like Wang is a project associate in the Interdisciplinary Division of Biomedical Engineering at the Hong Kong Polytechnic University. He received his BS and MS degrees from the Harbin Institute of Technology, China. He mainly works on biomechanical properties research by using optical and ultrasound methods. Ying Hon completed her BS degree in optometry from the Hong Kong Polytechnic University in 2009. She then worked as a research assistant for two years before pursuing a PhD program at the same university. She is currently a PhD candidate and her research topic is related to corneal biomechanics. Andrew K. C. Lam is an associate professor in the School of Optometry at the Hong Kong Polytechnic University. He completed his optometry training in Hong Kong, followed by obtaining his MPhil and PhD degrees from the Department of Optometry, University of Bradford, United Kingdom. He has been working on cornea-related studies, including corneal shape, orthokeratology, the influence of corneal parameters on tonometry, and corneal biomechanics. Yifei Huang is a professor of the Department of Ophthalmology, Chinese PLA General Hospital. He received his PhD/MD degree in ophthalmology from the Oxford Eye Institute. His current research focuses on the measurement of tissue biomechanical properties by different methods. Yuanyuan Wang is a professor of the Department of Electronic Engineering at Fudan University. After receiving his PhD degree in electronic engineering, he started his academic career in the fields of signal and image processing, and medical imaging. His recent work focuses on the development of computer-aided diagnosis systems, thermoacoustic tomography, and ultrafast ultrasound imaging. Yongping Zheng is an Ir professor of the Biomedical Interdisciplinary Division of Biomedical Engineering at the Hong Kong Polytechnic University. After he received his PhD degree, he started his career in the field of tissue elasticity measurement and imaging. His current research focuses on the measurement of tissue biomechanical properties by optical and ultrasound methods, three-dimensional ultrasound imaging, and remote health monitoring sensors and systems. |