|
|
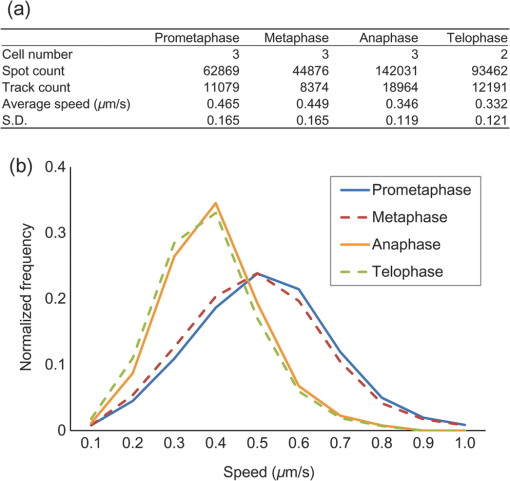
1.IntroductionThe nature of the actuating mechanism that drives the mitotic apparatus remains an important unresolved question despite extensive investigation in this field spanning more than a century. The concept of a mitotic apparatus was originally based on microscopy studies performed in the late 1800s.1,2 In early studies, images of cells and subcellular organelles were produced from fixed specimens. Such fixatives often introduced artifacts and consequently the existence of macromolecular structures within cells remained controversial. The first observation of a spindle apparatus within a living cell was made using polarizing light microscopy by Schmidt and Inoué.3–5 Inoué5 built an improved polarizing microscope that could image weakly birefringent materials and demonstrated for the first time the filamentous nature of the mitotic spindle within living cells using time-lapse imaging. Subsequently, Inoué and Sato et al.6,7 demonstrated that microtubules were the sole constituent of spindle fibers and established a basis for understanding how microtubule dynamics generate the forces for chromosome movement. The discovery and practical application of green fluorescent protein (GFP) by Shimomura8 and Chalfie9 as well as the development of color variations by Tsien10,11 has revolutionized the field of live imaging, by enabling the engineering and expression of chimeric fluorescent proteins in target cells (reviewed in Ref. 12). Microtubules are 25-nm diameter tubular polymers composed of two proteins, - and -tubulin. GFP-fused tubulin can be incorporated into microtubules without disrupting their function in many cell types, allowing the visualization of both cytoplasmic and spindle microtubules.13,14 In in vitro studies using purified proteins, microtubules exhibit repeated stochastic growth and shortening, a behavior referred to as “dynamic instability.”15,16 Visualization of microtubule behavior in living cells with GFP-tubulin or microinjected fluorescently labeled tubulin has proven that dynamic instability is a general property of microtubules and is fundamental in generating various cellular microtubule network patterns (reviewed in Refs. 1718.19.–20). However, owing to the performance limitations of fluorescence microscopes, the detection of discrete filaments has been limited to thinner regions of the cell, such as flattened membranous lamellipodia, or the imaging of small organisms such as yeasts, which only contain a few microtubule filaments. Although imaging methods such as poleward flux detection using photoactivatable fluorescent probes21 and fluorescent speckle microscopy22 have enabled the indirect observation of microtubule dynamics within the mitotic spindle, the direct observation of all the individual filaments within the spindle apparatus has never been achieved. We have previously generated a GFP fusion of the EB1 protein (EB1-GFP), which localizes to microtubule plus-ends [Fig. 1(a)],23,24 and demonstrated its utility as an analytical tool for the study of microtubule dynamics.25,26 Live-cell imaging revealed that EB1-GFP binds selectively to the growing ends of microtubules, forming a comet shape with a short axis diameter of approximately 25 nm and an anteroposteriorly elongated tail of up to 500 nm.23,25,27 EB1 functions as a hub, tethering microtubule ends to various subcellular structures generating an asymmetric filament network.17,28–30 Fluorescently tagged EB1 family proteins, including both EB1 and EB3, faithfully mark the growing portions of microtubules, even within the dense microtubule networks of the cell interior such as those found in columnar-shaped epithelial cells25 and neuronal filaments.31 Time-lapse imaging and tracking of EB1-GFP comets allows the generation of microtubule growth trajectories and the measurement of growth speed.32 However, until recently, image acquisition and analysis has been predominantly limited to a two-dimensional (2-D) plane, because the spatiotemporal resolution of conventional fluorescence microscopes is insufficient to follow the three-dimensional (3-D) motion of EB1-GFP comets that can move at several hundreds of nanometers per second. Fig. 1(a) Distribution of EB1-GFP in a mitotic HeLa cell at metaphase. HeLa cells (clone A1) stably expressing EB1-GFP (green) and H2B-TagRFP (magenta) were fixed and immunostained with an anti--tubulin antibody (red) to enable the position of microtubule ends to be identified. Images were collected with a LSM780 laser scanning confocal microscope. Examples of EB1-GFP comets at the ends of astral microtubules are indicated with arrowheads. Scale bar: . (b) An example of a lattice light-sheet (LLS) microscope image. The image was imported into Imaris 8 software and displayed in three-dimensional (3-D) space. The image was rotated horizontally about 90° from one direction (left) to another (right). At both angles, discrete EB1-GFP comets were visible at the tips of astral microtubules growing radially toward the cell cortex and within the spindle apparatus. Scale bars: . See also Video 1 (QuickTime, 8 MB) [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.1]. 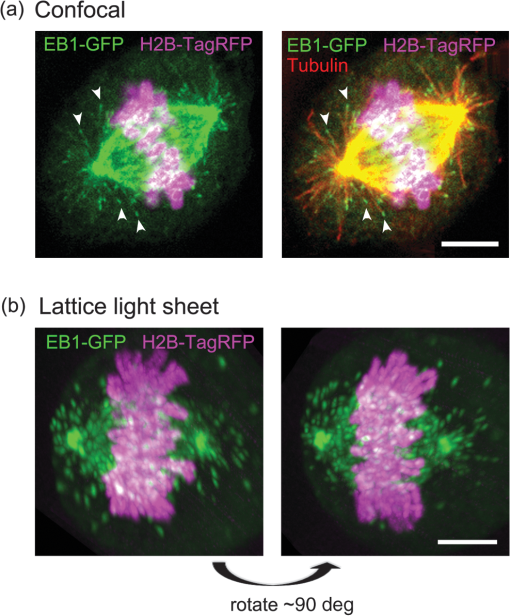 Recently, we succeeded in the 3-D tracking of EB1-GFP movement throughout the cell cytoplasm using the recently developed lattice light-sheet (LLS) microscope, which enables 3-D scanning at subsecond intervals with high-spatial resolution.33 This technology is an advanced type of light-sheet microscopy, which uses a separate excitation lens perpendicular to the wide-field detection lens to confine the illumination to the focal plane.34,35 In contrast to the conventional light sheet created with several-micron-thick Gaussian beams, the lattice light sheet is generated from a massive parallel array of nondiffracting light beams that mutually interfere to create an ultrathin light sheet extending over cellular dimensions.33,36 Spreading the excitation light across many foci greatly reduces the intensity at any single focus, and in turn, reduces fluorescence photobleaching and phototoxicity. This strategy allowed us to image whole cells for hundreds of volumes at subsecond intervals. LLS technology generates thousands of numerical data sets containing far more information than can be practically analyzed using conventional approaches. Therefore, automated computational strategies are required to extract biologically significant information in an efficient and reproducible manner. To analyze the 3-D motion of particles, automated object tracking methods by digital image processing have been developed and their application in biology is becoming popular.32,37 However, many challenges still exist regarding the interpretation of 3-D data. These challenges include the classification, selection, or grouping of objects of interest and the geometric presentation and interpretation of volumetric data. To this end, computational 3-D geometry and geometric modeling techniques are also necessary. In addition, the analysis of biological image data, which may be very noisy and is often multidimensional, requires improvement. Morita et al.38 established a computing system for the processing and visualization of large numbers of 3-D images, which can be offered through cloud-based platforms. Combining this system with mathematical computational techniques, we analyzed 3-D time-lapse images of EB1-GFP obtained with LLS microscopy to gain new insights into microtubule dynamics. Our analysis enabled both the microtubule growth speed and direction to be identified within the mitotic spindle apparatuses in 3-D. These observations support recent hypotheses emphasizing the important contribution of noncentrosomal microtubules, which cannot be detected using conventional light microscopy techniques, in spindle organization and chromosome segregation. The observations presented in this study push the limits of conventional microscopic analysis and demonstrate the power of this analysis framework, which we believe will be applicable and of benefit in a wide range of research fields. 2.Image Acquisition and Processing2.1.Image Acquisition of Cultured HeLa Cells by Lattice Light-Sheet MicroscopyTo analyze microtubule dynamics within the mitotic apparatus at high-spatiotemporal resolution, mitotic HeLa cells (clone A1)33 stably expressing EB1-GFP and histone H2B-TagRFP, markers for growing microtubule ends and chromatin, respectively, were observed by LLS microscopy [Fig. 1(b)]. HeLa cells have more than 60 chromosomes, in excess of the standard human chromosome number of 4639 and dense spindle microtubules, which makes detailed observation of the spindle apparatus difficult. When the performance of light microscopy is insufficient for analysis, sometimes large cell types such as the PtK1 rat kangaroo cell line, containing large spindles with fewer numbers of giant chromosomes, are selected for mitosis research.40,41 However, in solution-oriented science, we often need to observe smaller cells including cancer cells and differentiated/undifferentiated induced pluripotent stem (iPS) cells. Therefore, we used HeLa cells as a model to test our analysis capabilities. Cells were seeded on coverslips and maintained at 37°C throughout the observation period. Cells in mitosis were identified by the shape of their condensed chromosomes. Details of microscope optics, sample preparation, and imaging conditions have been previously described.33 For HeLa cell imaging, data were acquired in the dithered (faster) mode and deconvolved using an experimentally measured point spread function for each emission wavelength as previously described.33 All 3-D data sets acquired via sample scanning in the , , and (skewed) coordinate system were transformed (“deskewed”) to the more conventional , , and coordinates before visualization. The voxel size of images used in this study was . Dual- and single-color images were collected at 1.510- and 0.755-s intervals, respectively. 2.2.Image VisualizationImages were imported into Imaris 8 software (Bitplane, South Windsor, Connecticut). LLS microscopy provides a high-definition 3-D image that can be observed from any angle with similar resolving power,33 which is largely beyond the capabilities of conventional laser confocal fluorescence microscopes, enabling the discrimination of detailed structures in 3-D space within cells. Importantly, individual EB1-GFP comets were detectable even deep within the mitotic spindle apparatus [Fig. 1(b); Video 1], which is in sharp contrast to conventional confocal images in which the spindle structure appears as a single fluorescent mass [Fig. 1(a)]. LLS microscopy also provided a detailed view of the interaction of microtubule ends with the cell cortex. When an image of an anaphase cell was rotated and observed from the side, many EB1-GFP comets reaching the cell cortex were detected [Fig. 2; Videos 2 and 3]. In particular, at the basal cortex where the cell was attached to the substratum, EB1-GFP comets often ran along the plane of the surface [Fig. 2(c), arrowheads], which was in contrast to other regions, where the majority of EB1-GFP comets disappeared shortly after reaching the cortex [Fig. 2(b), arrows]. These observations suggest the nonuniform regulation of microtubule activity within different cortical regions of the cell. Observation of the detailed behavior of fine structures inside cells and the overall picture concurrently is a major advance in the whole-cell imaging by LLS microscopy because previously we were only able to observe cellular components from a fixed angle [optical axis direction ()] and in a limited area (due to the limitation of imaging speed) in live imaging. Fig. 2Observation of interactions between EB1-GFP comets and the cell cortex. (a) Side view of an anaphase cell. The plane of the coverslip ( direction) is indicated. (b) Superimposition of EB1-GFP trajectories generated by automated 3-D comet tracking. Arrows indicate trajectories that disappeared shortly after reaching the cortex. (c) Enlarged time-lapse images of the boxed area in (b). Some trajectories run along the basal cell cortex (white and yellow arrowheads). Time is shown in s:ms. Scale bars: (b), (c). Color bar: time (s:ms). See also Video 2 (QuickTime, 5.1 MB) and Video 3 (QuickTime, 9.9 MB). [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.2]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.3]. 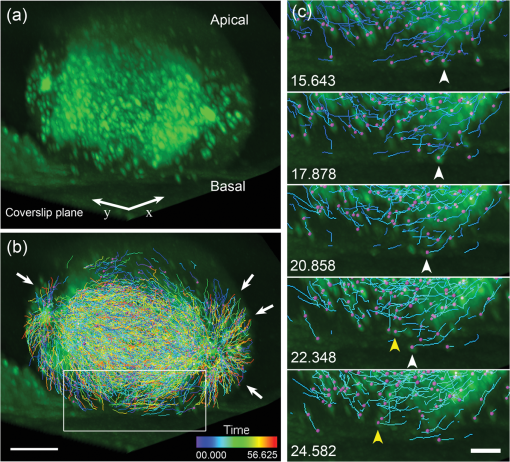 2.3.Image Preprocessing for Quantitative AnalysisFor the quantitative and statistical analysis of microtubule growth, especially inside spindles, we tried automated 3-D tracking of EB1-GFP comet movements throughout the cell using only single-channel images for GFP that were collected using the fastest acquisition mode. Subsequent analysis of EB1-GFP trajectory data in 3-D space enabled the quantification of microtubule growth within the cell. All images used were collected at 0.755-s intervals over a 56.625-s duration (75 frames) at different mitotic phases after nuclear membrane breakdown, i.e., during prometaphase, metaphase, anaphase, and telophase [for typical mitotic figures, see Fig. 5(a)]. Detailed procedures for image processing are described in the Appendix. 2.3.1.Drift correction of spindle positionWe performed several steps of image preprocessing to facilitate the high-precision tracking of EB1-GFP comets. First, we corrected for the movement of spindles. The spindle apparatus can serve as a useful frame of reference during cell division; however, it often rotates and changes orientation during division, which can reduce the accuracy of the positional measurements obtained for each EB1-GFP comet and can make interpretation of the results difficult. Consequently, in order to compare all datasets under a common reference frame, changes in the angular orientation of the spindle were compensated for using a drift correction method. The positions of the two centrosomes were automatically tracked and their displacements then used to correct for orientational and rotational drift for the whole data set using the Correct Drift function in Imaris software. As shown in Fig. 3(a) and Video 4, drift correction reduced changes in the positions of the spindle and chromosomes. Fig. 3Effects of drift correction. (a) Time-lapse images of a HeLa cell (clone A1) acquired with an LLS microscope (1.510-s interval, 50 frames) were imported into Imaris 8 software and displayed in 3-D space. The first frame is shown on the left. The middle and right panels show the maximum intensity projection (MIP) of all 50 frames. The spindle apparatus can often rotate in any direction in cells as shown in the middle panel. This rotational drift was corrected for by using the positions of the two centrosomes as a reference (right). Scale bar: . See also Video 4 (QuickTime, 8.2 MB) [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.4]. (b) Sum Slice projection (SSP) images generated from 30 frames of a metaphase cell before and after drift correction. After the drift correction, spots estimated to be kinetochore-associated EB1-GFP signals (arrowheads) and bundle of trajectories toward the kinetochores became visible. (c) Enlarged MIP images of astral EB1-GFP. MIP images of two-increment 11th to 31th time-lapse images (10 frames) of a metaphase cell before and after drift correction to observe the shape of an individual comet. The shape change of each comet was not evident, but the image was somewhat blurred after correction. (d) Comparison of EB1-GFP intensity profiles. The line profiles of two EB1-GFP comets ( width, shown in the left panels) were obtained and plotted in the right panel. The results are shown as relative intensity (right top) and normalized intensity standardized to the peak intensity (right bottom). The peak intensity was reduced by approximately 10% while the full width at half maximum of normalized intensity was increased by approximately 10% after drift correction. Scale bars: (a), (b), (c), (d). All the above images were created by capturing the Imaris screen view presenting objects in 3-D space. 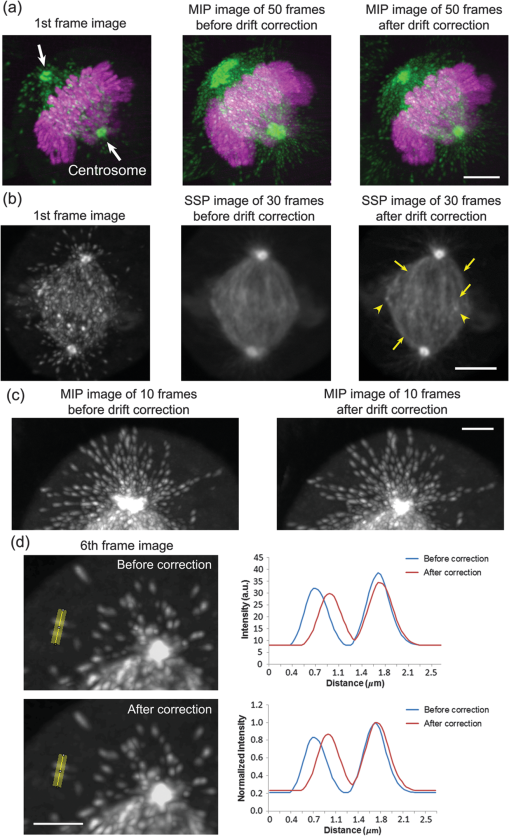 After drift correction, the repetitive appearance of EB1-GFP along the same trajectories toward kinetochores aided the visualization of the paths of growth of kinetochore microtubules in the Sum Slice projection (SSP) image [Fig. 3(b), arrows] and spots adjacent to the kinetochores [Fig. 3(b), arrowheads], which were observed in PtK1 cells.42 These observations indicate that fast 3-D scanning of mitotic HeLa cells by LLS microscopy faithfully captures common mitotic processes in a smaller cell type. In the drift corrected images, the change in shape of each EB1-GFP comet was not evident, but the images were blurred [Fig. 3(c)]. Therefore, we compared intensity profiles of isolated EB1-GFP comets and found that the peak intensity was reduced by approximately 10% while the full width at half maximum of normalized intensity was increased by approximately 10% in the drift corrected image [Fig. 3(d)], although we were not able to know what kind of method Imaris software applied. This may affect the EB1-GFP comet detection capability, especially for small, low-intensity comets. Nonetheless, we used the drift correction procedure because quantification of microtubule behavior (growth angle and position of EB1-GFP trajectories) is the main purpose of this study. It should be also noted that in the drift corrected images, information regarding the relative position of microtubule ends and cell cortex could not be retained. 2.3.2.Intensity equalization and signal enhancementWe performed two-step image quality improvement processing of the drift-corrected data to compensate for the effects of channel bleed-through and photobleaching. Only the signal from the green (EB1-GFP) channel from the dual-labeled HeLa cells was required for automated tracking. However, bleed-through from the red channel [Fig. 4(a)] as well as the time-dependent photo-bleaching of the signal in the green channel [Fig. 4(c)] were apparent from the analysis of image data. To reduce these unfavorable effects, images were subjected to both (1) intensity equalization and (2) small target enhancement by top-hat transformation, using VCAT5 software.38 (1) For intensity equalization, the intensity of a 3-D image at each time point was normalized using the average intensity value for the whole volume [Fig. 4(c)]. (2) To enhance EB1-GFP comet signals, we employed a top-hat transformation, an image processing technique for extracting small elements from images with a variable background.43 In acquired images, the area occupied by a single EB1-GFP comet ranged from in the case of a small comet to for the largest comets. We used opening radius in the plane and in the direction taking into account the 3-D voxel pitch (), and its effect is shown in Figs. 4(a) and 4(b); Videos 5 and 6. Fig. 4Effects of image preprocessing. After intensity equalization, the images were processed for image enhancement by top-hat transformation (opening radius in the plane and because the voxel pitch is ). An example of the resulting image (a) and a line profile [3 pixel line width, indicated with yellow lines in (a)] of signal intensity (b) are shown. Arrowheads in (a) indicate the bleed-through from the red channel labeling chromosomes. (c) Effect of intensity equalization and top-hat transformation on the 3-D volume intensity. Examples of a metaphase cell and a telophase cell are shown. Average intensities of 3-D volume at each time point before and after preprocessing are plotted. See also Videos 5 (QuickTime 3.3 MB) and 6 (QuickTime 3.1 MB) [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.5]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.6]. 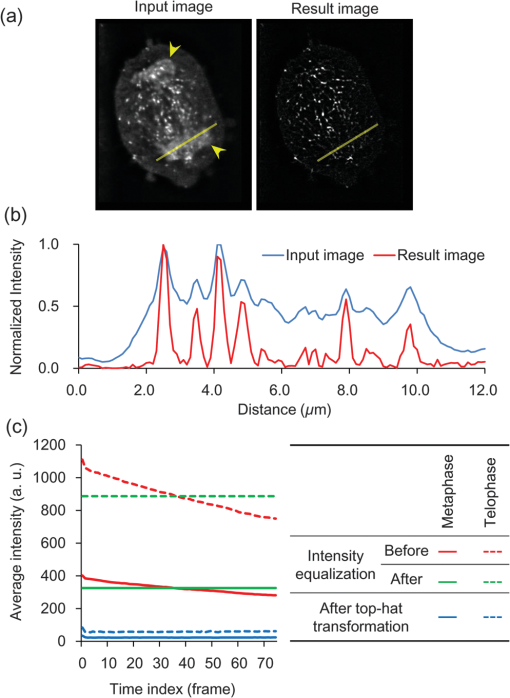 2.4.Automated tracking of EB1-GFP movementThe preprocessed images were imported into Imaris 8 software. EB1-GFP comets were automatically detected by local contrast mode and automated tracking was subsequently executed using the Autoregressive Motion algorithm, which predicts that the spot will move again the same distance and in the same direction. To eliminate possible tracking errors, several filter algorithms, including Max speed, track duration and straightness, were applied based on the assumption that microtubule growth is essentially straight with a variable, but limited elongation rate. We needed to adjust the parameters in different mitotic phases (for detailed procedures, see Appendix). Examples of the resultant trajectories are shown in Fig. 5(b) and Videos 7–12. Several cells in different mitotic phases [Fig. 5(a)] were analyzed, and a statistical summary of the distribution of microtubule track speeds for each phase are shown in Fig. 6. Consistent with our original observation using conventional 2-D timelapse imaging23 and previous observation by LLS microscopy, in which EB1-GFP comet speed was measured using different software,33 the population of fast-growing microtubules grew toward the prometaphase and metaphase where it peaked, then decreased gradually toward the telophase. Fig. 5Automated tracking of EB1-GFP comets. (a) Typical patterns of microtubule and chromosome organization at each indicated mitotic phase. HeLa cells (clone A1) were fixed and immunostained for microtubules and examined by confocal microscopy. Microtubule and histone H2B-TagRFP are shown in white and red, respectively. (b) Representative images of EB1-GFP trajectories in HeLa cells (clone A1) at different mitotic phases. The trajectories were generated by automated tracking. Results from the first 40 frames of a corrected 75-frame sequence are shown with a color code designating the moving speed. The color bar indicates the speed range for the instantaneous speed of EB1-GFP comets (0.3 to ). See also Videos 7–12 [QuickTime, 7.1 MB (7); 7.0 MB (8); 7.7 MB (9); 7.5 MB (10); 7.7 MB (11), 7.4 MB (12)] [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.7]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.8]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.9]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.10]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.11]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.12]. Scale bars: . 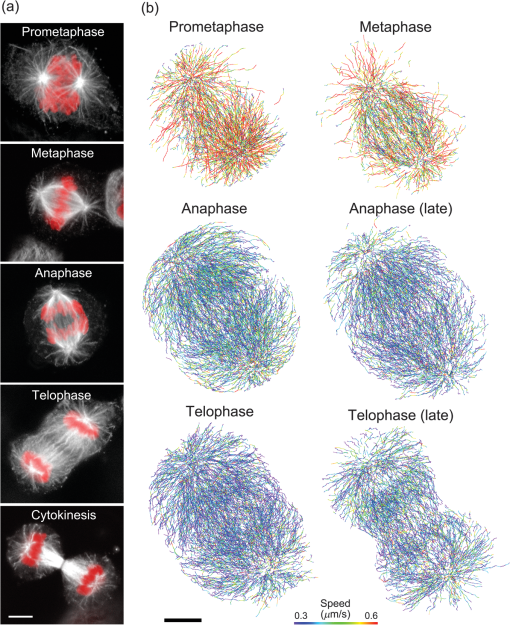 2.5.Analysis of Spatial Variations in Microtubule DynamicsThe dynamic and spatial properties of EB1-GFP trajectories were further analyzed by mathematical computing techniques and the calculated results were geometrically represented in 3-D space by developing a pipeline implemented in MATLAB® R2012a software (The Mathwork Inc., Natick, Massachusetts). 2.5.1.Classification of trajectories by growth speedFirst, mean travel speeds were grouped into intervals bins and displayed separately for each range [Fig. 7]. The trend showed a good correlation with the distribution of movement speeds plotted in Fig. 6, in which the high-speed population was largest in prometaphase and metaphase, with mean speeds decreasing toward telophase. An interesting feature that this presentation method highlights is the trend for trajectories with fast or slow migration speeds to be associated with particular regions of the cell. Fast trajectories often originated near the centrosomes, while slowly migrating ones tended to accumulate at the intercentrosome region, considering the slowly moving EB1-GFP comet traveling along microtubules associating with kinetochores. Because spindle microtubules exhibit poleward flux caused by their depolymerization at the minus ends,21 it is reasonable that a net movement of the comet is underestimated in the kinetochore fibers. In addition, it is possible that separation of the centrosome during anaphase/telophase affects measurement of the comet speed. In the data used, variations in the centrosome separation distance were less than during the observation period (56.625 s) (data not shown). Therefore, its effects are likely to be negligible. Fig. 7Subcellular distribution of EB1-GFP comet trajectories moving at different rates in each mitotic phase. Comet speed data were divided into 10 classes spanning the entire data range (0 to ). Data included in the 0.2 to range are shown. Each bin contains data equal to or more than the first threshold and less than the second threshold. Blue and red triangles indicate centrosomes. Color bar indicates the mean speed (). Cyan and yellow-green dots indicate the start and end position of trajectories, respectively. In this figure, trajectories initiated in the 1st to 30th frames are displayed. 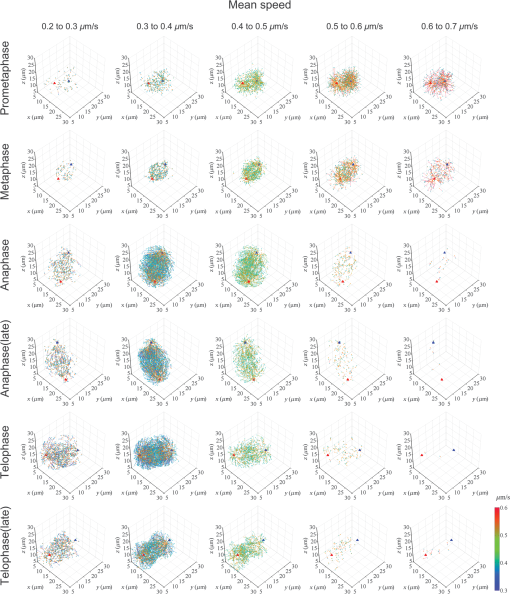 2.5.2.Analysis of growth angle and location of trajectoriesWe also measured the angle between the direction of EB1-GFP movement and the centrosomal axis [defined as the straight line between the two centrosomes; Fig. 8(a)]. The results for each cell are shown separately in this figure. The data clearly show that the distribution of growth trajectory angles was similar for cells in the same mitotic phase, while the overall distribution patterns were different among the different mitotic phases. The random orientation of trajectories observed in prometaphase shifted to a directional pattern, which was estimated to associate with the formation of spindle fibers or the spindle midzone at later stages. In the case of the prometaphase cells #2 and #3, a population of trajectories having shallower angles to the centrosomal axis started increasing, indicating that this cell was on the transition stage from prometaphase to metaphase. From an experimental validation perspective, these observations demonstrate the reproducibility achieved by our detection and automatic tracking. Fig. 8(a) Illustration of the method used to analyze the distribution of EB1-GFP trajectories in 3-D space. Spheres centered at centrosomes (red and blue triangles) and with radii equal to the intercentrosomal distance were generated and then divided into 10 spherical zones of equal radial length (top). The centrosomal axis is indicated with a blue line (bottom). The angle between each EB1-GFP comet trajectory and the centrosomal axis (yellow) was calculated. (b) The distribution of EB1-GFP comet trajectory angles was plotted according to their distance from the centrosome. The direction of the -axis (centrosomal axis) of one of the centrosomes was inverted by 180 deg and superimposed on another centrosome position to represent data from both centrosomes in a single coordinate. Each bin contains data equal to or more than the first threshold and less than the second threshold. The results from three different cells (two in the case of telophase) were plotted in line plots and histograms. 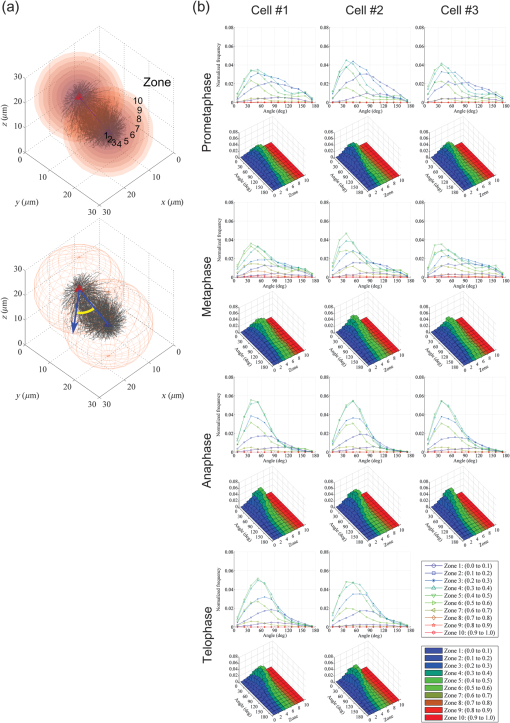 Next, we arranged EB1-GFP trajectories according to their subcellular location at prometaphase, metaphase, and anaphase (Fig. 9). Each EB1-GFP trajectory was assigned to one of 10 data bins according to the radial distance of its start position from the centrosome. The EB1-GFP trajectories of different data bins were then presented separately [Fig. 9(a)]. It can clearly be seen that many trajectories began their growth at positions located away from the centrosomes, an observation that is inconsistent with the established notion that the centrosome is the main microtubule nucleating structure. Notably, in the anaphase cell, large numbers of trajectories were aligned parallel with one another at the midpoint between the two centrosomes and most of their start points resided in zones 4 and 5 (an area between the centrosome and the midzone). It is possible that many of these were generated by regrowth from existing microtubules, and not by de novo nucleation, but that the gradual positional shift in the start points as mitosis progressed is clear [Figs. 9(b) and 9(c)], suggesting nucleation of microtubules at the noncentrosomal sites. Fig. 9(a) Trajectories of EB1-GFP comets grouped according to the position of the first track point are displayed separately for each indicated spherical zone [see Fig. 8(a)]. Representative results for cells in prometaphase, metaphase, and late anaphase are shown. Orange and cyan dots indicate start and end positions, respectively. The color bar indicates the mean speed (). The distribution of the start and end point positions of trajectories in cells shown in (a) are plotted according to their start position in the line graph in (b) and the histogram in (c). Each bin contains data equal to or more than the first threshold and less than the second threshold. 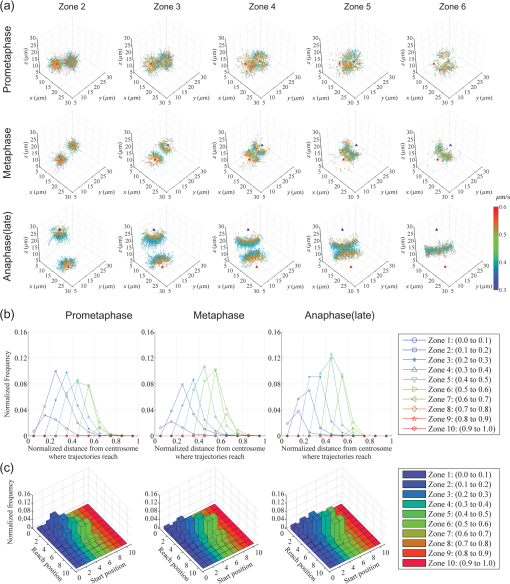 The EB1-GFP imaging alone cannot distinguish de novo nucleation from regrowth of existing microtubules, because it visualizes only the growing phase of microtubule dynamic instability. Therefore, to examine the above possibility further, we analyzed the angle of EB1-GFP comet movement relative to the centrosomal axis in vertical zones dividing the intercentrosomal space. If the angle of comet movement deviates from a line projected from the centrosome toward the comet position, this indicates that the microtubule is unlikely to have initiated from that centrosome (because microtubule outgrowth is essentially straight). Results shown in Fig. 10 indicate that a subpopulation of microtubules grew at an off-axis orientation, and support the possibility of noncentrosomal microtubule nucleation. Fig. 10(a) Illustration of the method used to analyze the distribution of EB1-GFP trajectories in 3-D space. The 3-D space was divided vertically and cylindrically about the centrosomal axis into 70 bins. The vertical zones and the cylindrical divisions were numbered as shown in (b). (c) In the green zone around the origin, trajectories initiated from the centrosome can take on any angle (green arrows). However, if the trajectory angle between EB1-GFP movement and the centrosomal axis is larger than 45 deg (red arrow) in the yellow-colored area, these microtubules are unlikely to originate from the centrosomes based on an assumption that microtubules grow in a straight line. (d) Representative results for cells in prometaphase, metaphase, anaphase, late anaphase, and telophase are shown in line plots grouped by division. Each bin contains data equal to or more than the first threshold and less than the second threshold. 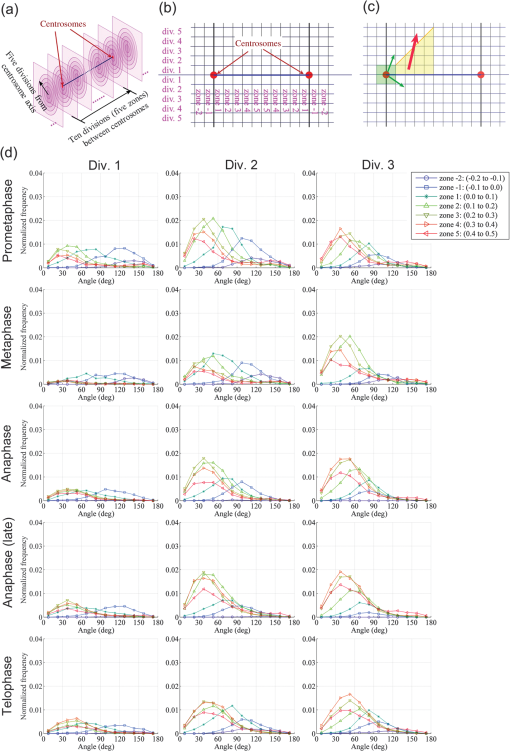 Recently a new model for interpolar microtubule assembly that is dependent upon augmin, a protein complex implicated in the nucleation of noncentrosomal microtubules, was proposed.44 In this model, a subset of microtubules in early anaphase is generated de novo around chromosomes in the interzone to generate central spindle microtubules that ensure completion of cytokinesis.44 Observations made in our study are consistent with this hypothesis. As this example shows, our study clearly demonstrates the applicability of our analytical strategy to a wide range of research areas that require precise 3-D information to understand more comprehensively the processes driving the actions of cellular machinery at the whole-cell level. 3.Summary and OutlookAfter more than 20 years since the discovery and practical application of GFP, the recent development of LLS microscopy now enables live whole-cell imaging in 3-D with high-spatial resolution and subsecond acquisition rates. On one hand, this technological advance greatly increases the potential of GFP as a subcellular fluorescent reporter, because it enables the movements of individual fluorescent proteins to be monitored throughout an entire cell with high spatiotemporal resolution. On the other hand, the enormous volume of multidimensional data provided by LLS microscopy represents a significant challenge because it contains complex information that cannot be analyzed using conventional methods that are mostly designed for 2-D platforms and often require substantial user interaction. Therefore, the introduction of computational techniques supporting automatic detection and geometric modeling is essential for interpreting these data. In this study, we imaged the motion of EB1-GFP in live mitotic HeLa cells to obtain 3-D trajectories of microtubule growth within the spindle apparatus using an LLS microscope. Image processing prior to automated tracking and mathematical computing allowed us to identify microtubule growth trajectories with different dynamic properties and to map their coordinates in 3-D space. As expected, the reconstructed 3-D displays revealed many microtubules started growing from regions near centrosomes and subsequently extended radially outward. These microtubules are also observable with conventional microscopes and are known as astral microtubules. However, an important observation was the existence of another group of microtubules that grew from a point distant from the centrosome. It has long been considered that centrosomes are the main microtubule nucleation sites. However, a pioneering in vitro reconstitution study45 and recent studies44–47 revealed that the centrosome itself is not critical for bipolar spindle formation and spindle microtubules can also be generated by noncentrosomal pathways; i.e., the chromatin-dependent pathway and the spindle microtubule-based microtubule generation mediated by augmin. These hypotheses were strongly supported by a later report describing the continued development of early mouse embryos in the absence of mature centrosomes until the 64-cell stage (early blastocyst).48 Studies such as this demonstrate that biological knowledge acquired through observations made with conventional microscopy techniques may overlook an unknown number of important phenomena. Therefore, as new technologies become available, we should extensively re-examine not only mitosis, but a variety of other fundamental biological processes, including cellular morphogenesis and polarization, differentiated/undifferentiated processes, and membrane/organelle trafficking, at spatiotemporal resolutions that permit a more detailed analysis of the molecular machinery of living cells. Our methods described here combined LLS microscopy with image processing and mathematical computing techniques, and our results demonstrated the great potential of this approach. However, before its application in the analysis of other novel molecular mechanisms, we need to improve our automated tracking and image processing techniques. Most importantly for our purpose, improved accuracy of EB1-GFP comet detection is critical. In the case of EB1-GFP detection, one effective way would be the expansion of a 2-D template matching method described by Matov et al.32 to 3-D space, using the average EB1-comet shape. In addition, because the automatic detection algorithm is sensitive to both specimen drift and variations in image intensity, methods that enable highly precise drift correction and image intensity equalization over time and in 3-D space are required for most applications. Changes in image intensity can be caused both by fluctuations in the excitation light intensity and by fluctuations in the distance of an object from the light source (i.e., depth within the specimen). Simple intensity equalization of a whole volume, such as that used in this study, is not sufficient for accurate and complete automatic detection. Indeed, some weak signals within the specimen that were furthermost from the light source or were most aberrated by the cell body were not detected by our analysis. We, therefore, need to develop a technique that can compensate for a three-dimensionally distributed intensity gradient within a specimen and optical heterogeneities within the specimen. Another factor that requires improvement is microscopes. Faster acquisition will improve the accuracy of object tracking. Limiting the scanning area can speed up the frame rate by several factors. This will also be highly beneficial for multicolor imaging. To improve the detection of objects at deeper regions, an adaptive optics system, which corrects for the blurring effects of emitted light distorted in the specimen in real time, is expected to bring an important improvement. In summary, once we have improved the computational analysis framework, its combined application with LLS microscopy will enable spatiotemporal information regarding the movements of fluorescent proteins within living specimens to be acquired with previously unobtainable precision. We, therefore, believe that this method of advanced imaging analysis will prove to be an invaluable research tool for a wide range of scientific fields in the future. AppendicesAppendix:Experimental ProceduresA1.HeLa Cell Culture and Conventional MicroscopyHeLa cells (clone A1) stably expressing EB1-GFP and H2B-TagRFP were previously described.28,33 For immunostaining of microtubules, cells were fixed and labeled with an anti-α-tubulin antibody (clone DM1A, Sigma) as previously described.28 Images of fixed cells were collected with a LSM780 laser scanning confocal microscope equipped with a , NA 1.40 oil immersion objective lens (Carl Zeiss). For performance comparisons with the LLS microscope that provides images with a voxel size of , confocal images were collected with an pixel pitch of in Fig. 1(a). A2.Image ProcessingGeneral image manipulation including stack image creation [maximum intensity projection (MIP) and SSP images] and movie editing was performed using ImageJ and QuickTime pro software. Each timelapse frame image, including a tracking result which is displayed in 3-D space on the Imaris window, was exported in conventional TIFF format and used for QuickTime movie creation. Cropping of 3-D regions of interest was performed using Imaris software. Image preprocessing for the automated tracking of EB1-GFP comets was performed using VCAT5 software,38 which was developed by the RIKEN Image Processing Research Team and is available from Ref. 49. A3.Imaris Settings for Particle TrackingA3.1.Spot detectionCentrosomes and EB1-GFP comet were detected by local contrast mode, one kind of watershed on the high-pass filtered image. Local contrast applies a Gaussian filter to estimate the intensity value of each voxel. Baseline subtraction is then performed by subtracting the variable background from every voxel in the image. A Gaussian kernel used in Imaris is a symmetric bell-shaped curve (excerpts from Imaris reference manual, the same hereinafter for the description of Imaris function). A3.2.Tracking of centrosome positionTo track centrosomes for the drift correction of the spindle position, we used the manual edit option. Objects identified by eye and selected manually were automatically tracked using Autoregressive Motion algorithm, which models the motion of each spot as an autoregressive AR1 process that looks back to one timepoint and predicts that the spot will move again the same distance and in the same direction, with the parameters described below:
As EB1-GFP accumulation to the centrosomes becomes weaker in the late mitotic phase, the estimated size needs to be adjusted. In the late telophase cell, small centrosomal signals were strongly affected by the appearance of new EB1-GFP comets and automatic tracking did not work appropriately. Therefore, the late telophase cell data was not subjected for drift correction, but in the telophase, the spindle position is relatively stationary. A3.3.Automated Tracking of EB1-GFP CometAutomated tracking of the EB1-GFP comet was performed using automatic creation mode. Automatically selected spots were tracked using the Autoregressive Motion algorithm using parameters below.
Imaris can automatically connect tracks with gaps. Although repeated growth and shrinking is the nature of microtubules, we did not use the gap filling option as there is no guarantee that separate tracks are attributed to the same filament. After automatic tracking, three types of filter were applied to limit the selection to those objects that meet the criteria. The descriptions of filters used are as follows:
The lower and upper threshold for each filter used in this study is shown below:
Figures showing data distribution and the effect of each filter under different parameter values are available at Ref. 50. After automated tracking, if necessary, apparent tracking errors were corrected using the manual edit option (deletion, creation, connection, and disconnection). Finally, if tracks in neighboring cells were mixed in the field of interest, these were manually removed. Because short tracks lasting less than three frames were removed during the filtering process, data from the first and last three frames were excluded from further statistical analysis. A4.Detailed Conditions for EB1-GFP Comet Tracking and Result Validation in Different Mitotic PhasesWe found that Imaris software detected EB1-GFP comets with a high accuracy even on the inside of anaphase/telophase spindles crowded with dense microtubules, but the accuracy of automated tracking varied according to mitotic phases; connection of each spot was prone to errors in prometaphase/metaphase cells compared with anaphase/telophase cells, probably because of the faster microtubule growth rate. It is also possible that lower background levels in anaphase/telophase cells, which could be caused by efficient incorporation of EB1-GFP into the thick microtubule filaments and consequent reduction of diffuse cytoplasmic pool generating background signals, has good effects on automated EB1-GFP comet detection. We needed to adjust the parameters and procedures in different mitotic phases. A4.1.Prometaphase and metaphase cellsAfter automatic detection and before applying filtering functions, when focusing only on astral microtubules, the detection of comets and tracking was almost perfect [Fig. 11(a), top; Videos 13 and 14]. In contrast, the inside of the spindle body spanning the intercentrosomal space appeared to contain a large quantity of possible pseudo-positive tracks showing random motion. To reduce the background and misconnection mainly attributed to background noise, filtering by max intensity of the spot was effective. However, the detection probability of astral EB1-GFP comets was decreased as the threshold value was elevated [Fig. 11(a), middle and bottom panels; Videos 15–18]. This is thought to be due to differences of background levels outside and inside of the spindle. In this study we used a higher intensity threshold to detect EB1-GFP comets in the inside of spindles, at the cost of astral EB1-GFP detection probability. Fig. 11Automated tracking with different intensity threshold values. To examine experimental conditions, a time-lapse LLS image containing 20 frames of a metaphase cell was used. (a) Comparison of the original image and tracking results obtained with different filtering conditions. Detected spots are indicated by magenta dots. The 1st frame and MIP image are shown for each condition. (b) The resulting trajectories obtained with a high stringent threshold still contain mistracks (arrows). Apparent mistracks identified by visual inspection were removed manually. (c) Summary of total number of spots and tracks detected under different filtering conditions. See also Videos 13–18 [QuickTime, 3.7 MB (13), 3.9 MB (14), 3.5 MB (15), 3.7 MB (16), 3.5 MB (17), 3.7 MB (18)] [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.13]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.14]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.15]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.16]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.17]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.18]. 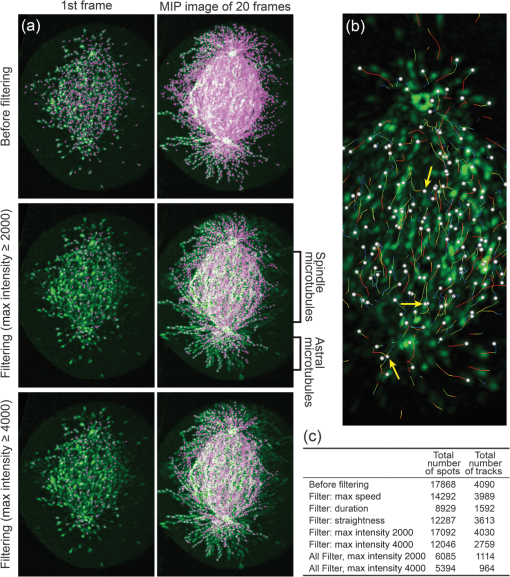 However, close inspection revealed that tracking errors still occurred inside spindles after filtering processes under high stringency conditions [Fig. 11(b)]. We could not further improve the accuracy by using the filtering functions currently available; therefore, apparent errors were edited manually. Because this study focused on microtubules in the “inside of spindles” rather than astral microtubules which can be observed with conventional microscopes, the trajectories of astral microtubules were not carefully edited. A4.2.Anaphase and telophase cellsBecause anaphase/telophase cells generate quite dense microtubules, it was almost impossible to discriminate individual trajectories by eye and to edit tracks manually on the inside of spindles in whole cell images [Fig. 12(a)]. Therefore, in the case of anaphase/telophase cells, fully automated tracking was performed, and the tracking accuracy was validated. To investigate the inside of the spindles, we computationally resliced an anaphase cell into an approximately thick segment passing through the centrosomes [Fig. 12(a), Videos 19 and 20]. Inside the spindles, each EB1-GFP comet was detected as a discrete spot and MIP image visualized the trajectories of EB1-GFP movement [Fig. 12(b)]. Projection images of spots detected and generated trajectories showed a good correlation with the MIP of the original image. Fig. 12Validation of the accuracy of automated EB1-GFP comet tracking in an anaphase cell. (a) Computational reslicing of whole cell volume. Using a plane clipping function of Imaris, areas to be shown were limited to an approximately width segment containing two centrosomes (yellow lines). Centrosomes are indicated with yellow triangles. The resliced image was then rotated 90 deg to be viewed from above. See also Video 19 (QuickTime, 8.6 MB). (b) Movement of EB1-GFP comets in the segment were visualized in a MIP image (left). Automatically detected spots (middle) and generated trajectories (right) are shown. Scale bars: . See also Video 20 (QuickTime, 8.4 MB). [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.19]. [URL: http://dx.doi.org/10.1117/1.JBO.20.10.101206.20]. (c) All trajectories initiated in the 1st to 8th frame and passing through the slice () were classified into seven categories shown in terms of validation of the tracking accuracy by visually comparing the original image and tracking result in 3-D presentation. “Correct” category contains trajectories that match with actual EB1-GFP movement. If the trajectory failed to connect more than three spots at the start or the end of detectable EB1-GFP track, it falls into the “start/disrupted in the middle” category, respectively (low intensity comets at the start/end are sometimes eliminated due to thresholding limit, not due to tracking failure). Jumping of a trajectory to a different EB1-GFP comet is often observed. If the orientation angle of trajectories before and after jumping is smaller than 90 deg, it falls into the “jump to different track in same direction” category, while others turning in the opposite direction fall into the “jump to different track in different direction” category. The “improper detection/connection” category contains apparently misdetected/misconnected trajectories. (d) Detection probability of EB1-GFP comet in the segment. An MIP image of the original image and detected spots in the 1st to 8th frame was generated to find spots moving processively (left). The boxed area in the left was enlarged in the middle. Tracks showing liner processive movement more than 3 frames were judged to be true signal (arrows). The detected and undetected trajectories were counted by visual inspection and the statistics result was shown in the right (; for aster, for spindle). Scale bars: (left), (middle). 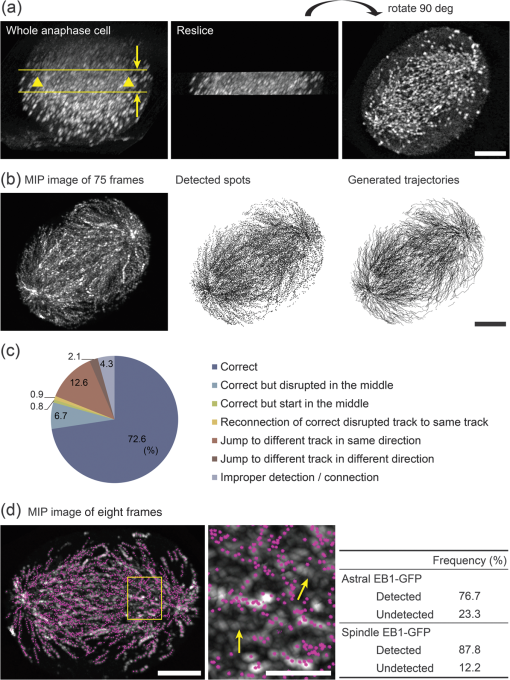 Next, false-positive detection was counted by comparing the original image with the tracking result. Trajectories were classified into seven categories as shown in Fig. 12(c). Visual inspection often identified tracks that jumped to a different trajectory. These errors contained switching both to a similar direction () and to the opposite direction. Direction change might affect analyses using information of the entire track length, such as the final reach distance and movement direction of the entire track. However, when only values of instantaneous EB1-GFP speed/movement were used for quantitative analysis of EB1-GFP behavior, track switching is not detrimental even if it turns to the opposite direction. We estimated the overall uncertainty of the tracking result was less than 10%, but when instantaneous values were used, the data retained a higher accuracy. In contrast, it was difficult to evaluate the exact frequency of false-negative detection. One reason for this was that we could not precisely distinguish true EB1-GFP comets from the granulated background pattern. In addition, because filtering processes remove a certain amount of true tracks, e.g., short-lived EB1-GFP tracks () and largely curved filaments (straightness ), which are indispensable for reducing possible misconnection, the false-negative analysis may not provide a direct indication of the quality of the automatic tracking function. To obtain information about the detection probability, we compared the MIP image of original picture with tracking patterns [Fig. 12(d)]. The MIP image allows us to find linearly processive spots that are estimated to be true EB1-GFP comet signals (arrows in the middle panel). As a result, in the aster and in the spindle, approximately 23% and 12% true signals, respectively, failed to be detected under the conditions used. A5.Mathematical Computing and Geometric RepresentationsMathematical computing and 3-D geometrical representation of the calculated results were performed by developing a pipeline implemented in MATLAB® R2012a software. A5.1.Notation
A5.2.Classification of trajectories by mean speed (Fig. 7)Each trajectory was classified according to its mean speed, . Mean speed, , was obtained as described below. Velocity of the EB1-GFP comet was calculated as: Mean speed, , of the EB1-GFP comet was defined as Each trajectory was divided into bins and trajectories with a mean speed within the 0.2 to (exclusive of ) range were plotted in Fig. 7. In this figure, only trajectories initiated in the 1st to 30th frames were shown. A5.3.Traveling direction of instantaneous EB1-GFP trajectoryDefinition of the centrosomal axisWe defined the straight line between the two centrosomes as the centrosomal axis [Fig. 8(a)], and derived the centrosomal axis vector as follows: A5.4.Traveling direction of all instantaneous EB1-GFP trajectories (Fig. 8)The angle between the direction of instantaneous EB1-GFP movement and the centrosomal axis () (3.2) was obtained for all trajectories and these angles were then grouped into 10 spherical zones of equal radial length that collectively spanned the intercentrosomal space [Fig. 8(a)]. The results were plotted in a line plot and histogram form that was normalized to the total number of EB1-GFP comet positions . The coordinate of one of sphere (centrosomes) was inverted horizontally and two data sets were drawn from the same origin. A5.5.Start and reach positions of EB1-GFP trajectories (Fig. 9)The start position and the reach position of each EB1-GFP trajectory was analyzed. The reach position was defined as the farthest point of a trajectory from the centrosome closest to that point. The results were grouped into spherical zones [Fig. 8(a)] on the basis of the start position or the reach position and were plotted as a line plot and histogram form that was normalized to the total trajectory number. A5.6.Traveling direction of instantaneous EB1-GFP movement in the specialized area (Fig. 10)The angle between the direction of EB1-GFP movement and the centrosomal axis was obtained for all positions of EB1-GFP comets in 70 spatial bins. First, the intercentrosomal was divided vertically into 10 equal zones, and an additional two zones were set at the outside of centrosomes [Fig. 10(a)]. Each zone was numbered symmetrically from the middle point (zone 5, 4, 3, 2, 1, , ) [Fig. 10(b)]. Next, the space was divided into five cylindrical zones around the centrosomal axis with the same intervals as the vertical zones [Fig. 10(a)]. Each division was numbered from the axis (div 1, 2, 3, 4, 5) [Fig. 10(b)]. Data were grouped into each bin with their start point and separately plotted by division in line plot form that was normalized to the total trajectory number. Only data from div. 1 to 3 of prometaphase, metaphase, anaphase, late anaphase, and telophase cells are shown in (d). AcknowledgmentsWe thank Dr. Philippe Roudot (Harvard Medical School, Danuser Lab) for valuable comments and suggestions. Our thanks are also due to Dr. Mika Toya (RIKEN Center for Developmental Biology), Dr. Tomoya Kitajima (RIKEN Center for Developmental Biology), and Ms. Masako Yamaguchi (Carl Zeiss Microscopy Co., Ltd.) for helpful suggestions, biological discussions, and helpful support using the Imaris software, respectively. We also thank Helen White (Janelia Research Campus) for the preparation of samples prior to LLS imaging. Y. M.-K. was supported by the Japan Society for the Promotion of Science–NEXT program LS128, the Takeda Science Foundation, Grants-in-Aid for Challenging Exploratory Research (Kakenhi No. 25650071), the Uehara Memorial Foundation, the Kurata Memorial Hitachi Science and Technology Foundation, and an intramural grant from the RIKEN Center for Life Science Technologies. ReferencesW. Flemming,
“Beitrage zur kenntnis der zelle und ihrer lebenserscheinungen,”
Archiv f. mikrosk. Anatomie, 16 302
–436 http://dx.doi.org/10.1007/BF02956386
(1879).
Google Scholar
E. B. Wilson, The Cell in Development and Inheritance, MacMillan, New York
(1896). Google Scholar
W. J. Schmidt, Bausteine des Tierkörpers in polarisiertem Lichte, Cohen, Bonn
(1924). Google Scholar
W. J. Schmidt,
“Doppelbrechung der Kernspindel und Zugfasertheorie der Chromosomenbewegung,”
Chromosoma, 1 253
–264 http://dx.doi.org/10.1007/BF01271634 CHROAU 1432-0886
(1939).
Google Scholar
S. Inoué,
“Polarization optical studies of the mitotic spindle. I. The demonstration of spindle fibers in living cells,”
Chromosoma, 5 487
–500 http://dx.doi.org/10.1007/BF01271498 CHROAU 1432-0886
(1953).
Google Scholar
S. Inoué and H. Sato,
“Cell motility by labile association of molecules. The nature of mitotic spindle fibers and their role in chromosome movement,”
J. Gen. Physiol., 50
(Suppl.), 259
–292 http://dx.doi.org/10.1085/jgp.50.6.259
(1967).
Google Scholar
H. Sato, G. W. Ellis and S. Inoué,
“Microtubular origin of mitotic spindle form birefringence. Demonstration of the applicability of Wiener’s equation,”
J. Cell Biol., 67 501
–517 http://dx.doi.org/10.1083/jcb.67.3.501
(1975).
Google Scholar
O. Shimomura, F. H. Johnson and Y. Saiga,
“Extraction, purification and properties of aequorin, a bioluminescent protein from the luminous hydromedusan, aequorea,”
J. Cell. Comp. Physiol., 59 223
–239 http://dx.doi.org/10.1002/jcp.1030590302 JCCPAY 0095-9898
(1962).
Google Scholar
M. Chalfie et al.,
“Green fluorescent protein as a marker for gene-expression,”
Science, 263 802
–805 http://dx.doi.org/10.1126/science.8303295 SCIEAS 0036-8075
(1994).
Google Scholar
N. C. Shaner et al.,
“Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein,”
Nat. Biotechnol., 22 1567
–1572 http://dx.doi.org/10.1038/nbt1037
(2004).
Google Scholar
R. Heim, D. C. Prasher and R. Y. Tsien,
“Wavelength mutations and posttranslational autoxidation of green fluorescent protein,”
Proc. Natl. Acad. Sci. U. S. A., 91 12501
–12504 http://dx.doi.org/10.1073/pnas.91.26.12501
(1994).
Google Scholar
R. Y. Tsien,
“The green fluorescent protein,”
Annu. Rev. Biochem., 67 509
–544 http://dx.doi.org/10.1146/annurev.biochem.67.1.509
(1998).
Google Scholar
N. M. Rusan et al.,
“Cell cycle-dependent changes in microtubule dynamics in living cells expressing green fluorescent protein-alpha tubulin,”
Mol. Biol. Cell, 12 971
–980 http://dx.doi.org/10.1091/mbc.12.4.971 MBCEEV 1059-1524
(2001).
Google Scholar
J. L. Carminati and T. Stearns,
“Microtubules orient the mitotic spindle in yeast through dynein-dependent interactions with the cell cortex,”
J. Cell Biol., 138 629
–641 http://dx.doi.org/10.1083/jcb.138.3.629
(1997).
Google Scholar
T. Horio and H. Hotani,
“Visualization of the dynamic instability of individual microtubules by dark-field microscopy,”
Nature, 321 605
–607 http://dx.doi.org/10.1038/321605a0
(1986).
Google Scholar
T. Mitchison and M. Kirschner,
“Dynamic instability of microtubule growth,”
Nature, 312 237
–242 http://dx.doi.org/10.1038/312237a0
(1984).
Google Scholar
Y. Mimori-Kiyosue,
“Shaping microtubules into diverse patterns: molecular connections for setting up both ends,”
Cytoskeleton, 68 603
–618 http://dx.doi.org/10.1002/cm.20540
(2011).
Google Scholar
O. C. Rodriguez et al.,
“Conserved microtubule-actin interactions in cell movement and morphogenesis,”
Nat. Cell Biol., 5 599
–609 http://dx.doi.org/10.1038/ncb0703-599 NCBIFN 1465-7392
(2003).
Google Scholar
J. Howard and A. A. Hyman,
“Dynamics and mechanics of the microtubule plus end,”
Nature, 422 753
–758 http://dx.doi.org/10.1038/nature01600
(2003).
Google Scholar
T. J. Mitchison and M. W. Kirschner,
“Properties of the kinetochore in vitro. II. Microtubule capture and ATP-dependent translocation,”
J. Cell Biol., 101 766
–777 http://dx.doi.org/10.1083/jcb.101.3.766
(1985).
Google Scholar
T. J. Mitchison,
“Polewards microtubule flux in the mitotic spindle: evidence from photoactivation of fluorescence,”
J. Cell Biol., 109 637
–652 http://dx.doi.org/10.1083/jcb.109.2.637
(1989).
Google Scholar
C. M. Waterman-Storer et al.,
“Fluorescent speckle microscopy, a method to visualize the dynamics of protein assemblies in living cells,”
Curr. Biol., 8 1227
–1230 http://dx.doi.org/10.1016/S0960-9822(07)00515-5 CUBLE2 0960-9822
(1998).
Google Scholar
Y. Mimori-Kiyosue, N. Shiina and S. Tsukita,
“The dynamic behavior of the APC-binding protein EB1 on the distal ends of microtubules,”
Curr. Biol., 10 865
–868 http://dx.doi.org/10.1016/S0960-9822(00)00600-X CUBLE2 0960-9822
(2000).
Google Scholar
E. E. Morrison et al.,
“EB1, a protein which interacts with the APC tumour suppressor, is associated with the microtubule cytoskeleton throughout the cell cycle,”
Oncogene, 17 3471
–3477 http://dx.doi.org/10.1038/sj.onc.1202247 ONCNES 0950-9232
(1998).
Google Scholar
A. Hotta et al.,
“Laminin-based cell adhesion anchors microtubule plus ends to the epithelial cell basal cortex through ,”
J. Cell Biol., 189 901
–917 http://dx.doi.org/10.1083/jcb.200910095
(2010).
Google Scholar
Y. Mimori-Kiyosue et al.,
“CLASP1 and CLASP2 bind to EB1 and regulate microtubule plus-end dynamics at the cell cortex,”
J. Cell Biol., 168 141
–153 http://dx.doi.org/10.1083/jcb.200405094
(2005).
Google Scholar
S. P. Maurer et al.,
“EBs recognize a nucleotide-dependent structural cap at growing microtubule ends,”
Cell, 149 371
–382 http://dx.doi.org/10.1016/j.cell.2012.02.049 CELLB5 0092-8674
(2012).
Google Scholar
S. Nakamura et al.,
“Dissecting the nanoscale distributions and functions of microtubule-end-binding proteins EB1 and ch-TOG in interphase HeLa cells,”
PLoS One, 7 e51442 http://dx.doi.org/10.1371/journal.pone.0051442 POLNCL 1932-6203
(2012).
Google Scholar
A. Akhmanova and M. O. Steinmetz,
“Tracking the ends: a dynamic protein network controls the fate of microtubule tips,”
Nat. Rev. Mol. Cell Biol., 9 309
–322 http://dx.doi.org/10.1038/nrm2369 NRMCBP 1471-0072
(2008).
Google Scholar
Y. Mimori-Kiyosue and S. Tsukita,
“‘Search-and-capture’ of microtubules through plus-end-binding proteins (+TIPs),”
J. Biochem., 134 321
–326 http://dx.doi.org/10.1093/jb/mvg148 JOBIAO 0021-924X
(2003).
Google Scholar
T. Stepanova et al.,
“Visualization of microtubule growth in cultured neurons via the use of EB3-GFP (end-binding protein 3-green fluorescent protein),”
J Neurosci., 23 2655
–2664
(2003).
Google Scholar
A. Matov et al.,
“Analysis of microtubule dynamic instability using a plus-end growth marker,”
Nat. Methods, 7 761
–U134 http://dx.doi.org/10.1038/nmeth.1493 1548-7091
(2010).
Google Scholar
B. C. Chen et al.,
“Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution,”
Science, 346 1257998 http://dx.doi.org/10.1126/science.1257998 SCIEAS 0036-8075
(2014).
Google Scholar
J. Huisken and D. Y. R. Stainier,
“Selective plane illumination microscopy techniques in developmental biology,”
Development, 136 1963
–1975 http://dx.doi.org/10.1242/dev.022426
(2009).
Google Scholar
J. Huisken et al.,
“Optical sectioning deep inside live embryos by selective plane illumination microscopy,”
Science, 305 1007
–1009 http://dx.doi.org/10.1126/science.1100035 SCIEAS 0036-8075
(2004).
Google Scholar
T. A. Planchon et al.,
“Rapid three-dimensional isotropic imaging of living cells using bessel beam plane illumination,”
Nat. Methods, 8 417
–423 http://dx.doi.org/10.1038/nmeth.1586 1548-7091
(2011).
Google Scholar
E. Meijering, O. Dzyubachyk and I. Smal,
“Methods for cell and particle tracking,”
Methods Enzymol., 504 183
–200 http://dx.doi.org/10.1016/B978-0-12-391857-4.00009-4 MENZAU 0076-6879
(2012).
Google Scholar
M. Morita et al.,
“Communication platform for image analysis and sharing in biology,”
Int. J. Networking Comput., 4 369
–391 http://dx.doi.org/10.15803/ijnc.4.2_369
(2014).
Google Scholar
J. J. Landry et al.,
“The genomic and transcriptomic landscape of a HeLa cell line,”
G3: Genes|Genomes|Genetics, 3 1213
–1224 http://dx.doi.org/10.1534/g3.113.005777
(2013).
Google Scholar
B. R. Brinkley and Jr. J. Cartwright,
“Ultrastructural analysis of mitotic spindle elongation in mammalian cells in vitro. Direct microtubule counts,”
J. Cell Biol., 50 416
–431 http://dx.doi.org/10.1083/jcb.50.2.416
(1971).
Google Scholar
U. Euteneuer and J. R. McIntosh,
“Structural polarity of kinetochore microtubules in PtK1 cells,”
J. Cell Biol., 89 338
–345 http://dx.doi.org/10.1083/jcb.89.2.338
(1981).
Google Scholar
J. S. Tirnauer et al.,
“EB1 targets to kinetochores with attached, polymerizing microtubules,”
Mol. Biol. Cell, 13 4308
–4316 http://dx.doi.org/10.1091/mbc.E02-04-0236 MBCEEV 1059-1524
(2002).
Google Scholar
R. C. Gonzalez and R. E. Woods, Digital Image Processing, 3rd ed.Prentice Hall, Upper Saddle River, New Jersey
(2007). Google Scholar
R. Uehara and G. Goshima,
“Functional central spindle assembly requires de novo microtubule generation in the interchromosomal region during anaphase,”
J. Cell Biol., 191 259
–267 http://dx.doi.org/10.1083/jcb.201004150
(2010).
Google Scholar
R. Heald et al.,
“Self-organization of microtubules into bipolar spindles around artificial chromosomes in Xenopus egg extracts,”
Nature, 382 420
–425 http://dx.doi.org/10.1038/382420a0
(1996).
Google Scholar
R. Uehara et al.,
“The augmin complex plays a critical role in spindle microtubule generation for mitotic progression and cytokinesis in human cells,”
Proc. Natl. Acad. Sci. U. S. A., 106 6998
–7003 http://dx.doi.org/10.1073/pnas.0901587106
(2009).
Google Scholar
G. Goshima et al.,
“Augmin: a protein complex required for centrosome-independent microtubule generation within the spindle,”
J. Cell Biol., 181 421
–429 http://dx.doi.org/10.1083/jcb.200711053
(2008).
Google Scholar
A. Courtois et al.,
“The transition from meiotic to mitotic spindle assembly is gradual during early mammalian development,”
J. Cell Biol., 198 357
–370 http://dx.doi.org/10.1083/jcb.201202135
(2012).
Google Scholar
Image Processig Research Team, Center for Advanced Photonics, RIKEN http://logistics.riken.jp/vcat/vcat/en
().
Google Scholar
BiographyNorio Yamashita received his PhD in precision engineering from The University of Tokyo, Tokyo, Japan in 2014. Currently, he is working as a postdoctoral researcher in RIKEN. His current research interests include 3-D internal structure microscopy, image-based 3-D shape analysis, and computation of geometry. Masahiko Morita received his doctor’s degree in media and governance from the Keio University, Japan, in March 2014. Currently, he is working at the RIKEN, focused on the development of a novel cloud computing system for biomedical images. Wesley R. Legant graduated summa cum laude from Washington University in St. Louis in 2006. Focusing on the development and application of new techniques to study cellular mechanosensing, he obtained his PhD in bioengineering from the University of Pennsylvania in 2012. In 2011, he was awarded a Whitaker International Fellowship at the Swiss Federal Institute of Technology in Zurich to investigate mechanical stresses transmission through extracellular matrix proteins. Since 2012, he has been developing new modalities of fluorescence microscopy as a post doctoral associate in Betzig’s group. Bi-Chang Chen received the BS and MS degrees from the Chemistry Department of the National Taiwan University, Taiwan. After two-year military service, he moved to University of Texas at Austin, USA, to complete his PhD degree in chemistry, where he studied the coherent anti-Stokes Raman imaging technique. He joined Betzig’s group in 2011 to develop lattice light-sheet microscopy. Currently, he is an assistant research fellow at the Research Center for Applied Science, Academia Sinica in Taiwan. He is interested in developing imaging platforms for live volume imaging. Eric Betzig obtained his BS in physics from Caltech, then moved to Cornell University in New York, earning his PhD in 1988, and worked on near-field optics—describing a method to break the diffraction barrier in light microscopy. In 1993, he imaged single fluorescent molecules under ambient conditions, and determined their positions to better than 1/40 of the wavelength of light. This led to the invention of the super-resolution technique PALM, which was the 2014 Nobel Prize-winning technology. Since 2005, he has been a group leader at Janelia. Hideo Yokota received his PhD degrees in precision engineering from The University of Tokyo, Tokyo, Japan in 1999. Currently, he is a team leader of the Image Processing Research Team at the RIKEN Center for Advanced Photonics. His goal is to develop original RIKEN data processing technology and multidimensional measurement technology in order to contribute to understanding biological phenomena, contributing especially to the fields of mathematical biology, bio-medical simulations, as well as medical diagnostic and treatment technology. Yuko Mimori-Kiyosue received her PhD from the Osaka University Graduate School of Engineering Science, Japan, in March 1995. After working in the field of structural biology with a helium-cooled cryo electron microscope, she joined the ERATO Tsukita Cell Axis Project from 1997 and studied cell biology using GFP technology, which led to the discovery of important cell axis regulators, “+TIPs.” Currently, she is a unit leader at the RIKEN Center for Life Science Technologies and is pursuing developmental cell biology research employing advanced imaging technologies. |