|
|
1.IntroductionPhotoacoustic tomography (PAT) is an emerging technique for in vivo imaging of soft biological tissue.1 This hybrid modality uses ultrasound to detect optical contrast, combining the high resolution of acoustic methods with the spectroscopic capability of optical imaging. To generate a PA image, a short laser pulse is shined into the object, the ultrasonic waves emitted following the heating of the tissue are measured, and an image of the absorbed optical energy field is recovered. Whereas purely optical methods suffer from poor spatial resolution, acoustic waves propagate with minimal scattering, and PAT can achieve resolution at depths of several centimeters. However, PA images provide only qualitative information about the tissue, and are not directly related to tissue morphology and functionality. The principal difficulty is that the PA image is the product of both the optical absorption coefficient (which is directly related to underlying tissue composition) and the light distribution (which is not). This severely restricts the range of applications for which PAT is suitable. Quantitative photoacoustic tomography (QPAT) aims to provide clinically valuable images of the optical absorption and scattering coefficients, or chromophore (light-absorbing molecules) concentrations from conventional PA images via an image reconstruction method.2,3 A model of light propagation is required to relate the absorbed optical energy to the light fluence and tissue parameters. The primary challenge of QPAT is solving the nonlinear imaging problem. In particular, recovering the scattering coefficient is especially difficult due to the weak dependence of the absorbed energy density on scattering. In this paper, we develop a method for solving the image reconstruction problem for QPAT by alternating reconstruction and segmentation steps in an automated iterative process. We introduce a probabilistic model that describes optical properties in terms of a limited number of optically distinct classes, which may correspond to tissues or chromophores. These are identified and characterized by a classification, or segmentation, algorithm. This approach allows for the use of information retrieved by the classification in the reconstruction stage and vice versa. The aim of the reconstruction is to choose solutions for which the image parameters take values close to a finite set of discrete points. The aim of the classification algorithm is to progressively improve the parametric optical model and correct for errors in the initial assumptions. Multinomial models have been employed previously in the related fields diffuse optical tomography4 and electrical impedance tomography.5 For QPAT, the main advantage is that this approach enables accurate recovery of both the absorption and scattering coefficients simultaneously. 2.Numerical Methods2.1.Quantitative Photoacoustic ImagingA conventional PAT image is proportional to the absorbed optical energy where is a position vector within the domain , and are the optical absorption and reduced scattering coefficients, is the optical fluence, and is the Grüneisen parameter. The Grüneisen parameter represents the efficiency with which the tissue converts heat into acoustic pressure, and is often taken to be the constant . The fluence is dependent on the optical parameters and illumination pattern in the whole domain. The problem of recovering the optical parameters from a conventional PAT image is known as the “quantitative” problem. The optical absorption is of particular interest because it is fundamentally related to underlying tissue physiology and functionality, and encodes clinically useful information such as tissue oxygenation levels and chromophore concentrations. Conversely, the absorbed energy density depends nontrivially on optical absorption and thus is not directly related to tissue morphology because it is distorted structurally and spectrally by the nonuniform light fluence.2.2.Diffusion Model of Light TransportIn order to recover the optical parameters , a model of light propagation within the tissue is required. For highly scattering media and those far from boundaries and sources, a low-order spherical harmonic approximation to the “radiative transfer equation” is suitable. The “diffusion approximation” is given by6 where is an isotropic source term and is the diffusion coefficient.We set Robin boundary conditions where accounts for the refractive index mismatch at the boundary.2.3.Minimization-Based Quantitative Photoacoustic Tomography ImagingIn this paper, we adopt a gradient-based minimization approach to image reconstruction. Typically, both and are unknown and need to be recovered simultaneously from the absorbed energy density. An objective function is defined, which measures the distance between the conventional PAT image and the data predicted by the model for the current estimates In order to treat the problem for a generic geometry, the finite element method is employed, whereby a weak formulation of the diffusion approximation [Eq. (2)] is considered. A discretization of the domain is defined, and the fluence and optical parameters are expressed in terms of the same piecewise-linear basis functions : for , where are nodal coefficients and .We assume that the data is the absorbed energy density , projected onto a particular basis , Choices for include:Substituting into the objective function [Eq. (4)] leads to the discrete form of the objective function If a single illumination source is used and both absorption and scattering are undetermined, the problem is ill posed.2 In this study, the nonuniqueness of the solution was removed by using multiple illumination patterns,7–9 thus the objective function must be summed over the number of sources. In the following, we have omitted this sum for ease of notation. Prior information regarding the solution can be included by adding a regularization term In the Bayesian framework, an image is obtained by maximizing the posterior probability of the parameters, given the data Under this interpretation, the regularization term is given by the negative log of the prior probability distribution2.4.Gradient CalculationsCox et al.10 have shown that, for the continuous case, the gradient of Eq. (4) with respect to at position is given by where the “adjoint” light field is the solution to the equationIn the following, we derive the expression for the gradient in the discrete case. The sampled forward model can be expressed as a vector where is a sparse matrix indexed by , where the support of the basis functions , , overlap. Taking the derivative of Eq. (6) with respect to , we have Using the expression for the absorbed energy density [Eq. (12)], where is a vector of zeros with a single 1 in position . Substituting into Eq. (13) gives The first term in Eq. (15) is where is given by a reordering of Note that while is symmetric, in general, is not.It remains to determine . The discrete form of the DA model [Eq. (2)] assumes the form11 where Taking the derivative of Eq. (18) with respect to the ’th coefficient of , where is given by the derivative of the system matrix. We define the adjoint field as the solution to the equation where is the adjoint source. Taking Equation (23) . Eq. (25), we obtain Substituting into Eq. (15) gives the expression for the derivative with respect to The derivative with respect to can be derived analogously where and . Note that calculation of the gradient requires only two runs of the forward model. The forward problem was solved using the Toast++ software package.11Choosing point-sampling gives simply . In this study, we chose piecewise-linear sampling , so we had and 3.Reconstruction-Classification Method for Quantitative Photoacoustic TomographyA reconstruction-classification scheme is devised, which enables the recovery and by approaching the image reconstruction and segmentation problems simultaneously. At each reconstruction step, we minimize a regularized objective function, where the regularization term is given by a mixture model. At each classification step, the result of the previous reconstruction step is employed to update the class parameters for the multinomial model. We alternate between reconstruction and classification steps for a fixed number of iterations (Fig. 1). 3.1.Mixture Model for andIn this section, we introduce a probability model for and , which encodes prior knowledge about the optical parameters and allows us to bias the solution of the imaging problem accordingly. We assume that an array of labels can be determined for each node, such that The labels constitute “hidden variables” on which the image parameters are dependent. For each class , a mean vector is defined, and the covariance of each class is described by matrix .We assume that if , the probability distribution for is given by a multivariate Gaussian distribution where indicates the set of class parameters .The prior probability distribution of the class properties is given by the conjugate prior to the Gaussian distribution. Prior information about the distribution of the class means or covariances can be encoded by choosing the parameters of the conjugate prior accordingly. Using a noninformative prior for the class means we have . The conjugate prior distribution for the covariance of a normal distribution is given by the normal inverse Wishart distribution (NIW): where is the dimension of the domain, indicates the number of degrees of freedom, and is a scaling matrix. If the prior is noninformative, then and , and the probability distribution of the class parameters becomes which is known as Jeffreys prior.The probability that the set of labels is assigned to the ’th node is given by a multinomial distribution where is the overall probability that a node is assigned to the ’th class. Therefore, the joint probability for is given by the product By marginalizing over all possible values of the indicator variables , a “mixture of Gaussians” model for the optical parameters is obtained Finally, for independent nodes, the prior of the image is given by3.1.1.Reconstruction stepThe objective function takes the form of Eq. (7), where at iteration of the reconstruction-classification algorithm, the regularization is given by Eqs. (9) and (39) where is a regularization parameter and is obtained by fixing the labels to the “maximum a posteriori” estimate, given the results of the previous iteration which is calculated in the classification step (see Sec. 3.1.2). The weighting matrix is the Cholesky decomposition of , where is a sparse matrix of which the ’th block along the diagonal is if the ’th element belongs to the ’th class.In order to sphere the solution space, that is, to render the space dimensionless, we performed a change of variables and , where is the initial guess for the optical parameters (in this study, we initialized to the homogeneous background). Given the size of the problem, we chose a gradient-based optimization method in order to reduce memory use and computational expense.12 The minimization was performed using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method,13 with a storage memory of six iterations. 3.1.2.ClassificationThe purpose of the classification step is to update the multinomial model using the result of the previous reconstruction step. First, the expected values of the labels are computed for the current class parameters and image (E-step). Then the model parameters are updated by maximizing the posterior probability (M-step)
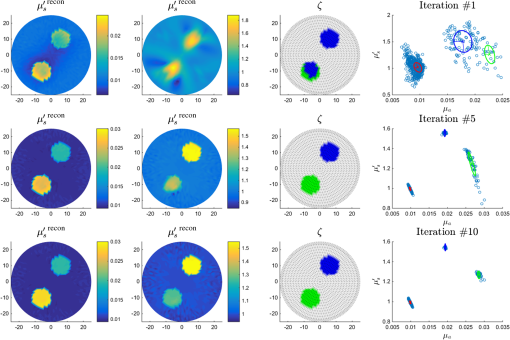
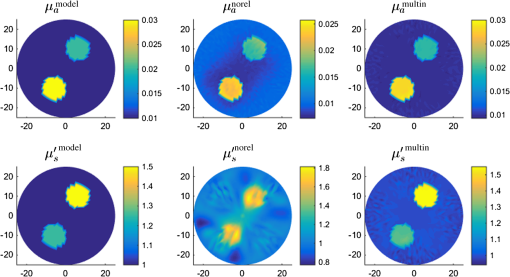
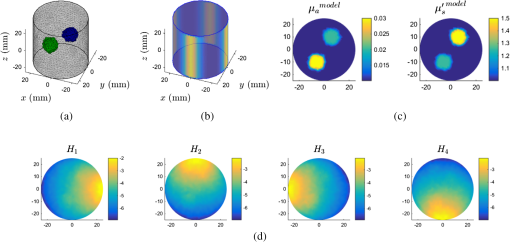
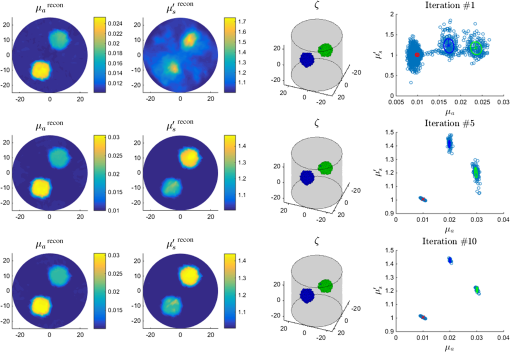
3.2.Class Means InitializationThe number of classes and the class means were initialized by automatically segmenting the result of the first reconstruction step and averaging over the segmented areas. To segment the image [e.g., see Fig. 2(a)], we looked at a binned histogram of the image of and chose the value for which the number of occurrences was highest [Fig. 2(c), column 1]. We found the first node index for which the value occurs, and identified the corresponding scattering value . Having chosen a covariance matrix , we computed a map of the multivariate normal probability of the images, with mean [Fig. 2(c), column 2]. A suitable choice for is the initial covariance of the classes. Then we selected a tolerance level at which to truncate the probability map, and selected all nodes with probability higher than the tolerance as belonging to the same class as node [Fig. 2(c), column 3]. We repeated this process on the remaining nodes until all nodes were classified. Thus, the number of classes was set to the number of iterations, and the average of the optical parameters over each class was used to initialize the class means [Fig. 2(b)]. Fig. 2Class initialization example: (a) original image of to which we apply the segmentation; (b) result of taking average image values over the segmented areas; (c) first column, histogram of occurrences of values of in the portion of the image requiring segmentation—value with highest number of occurrences is (indicated by a red cross); second column, probability density function with mean and covariance ; third column, labels identifying nodes with probability density higher than tolerance value ; each row corresponds to an iteration and a distinct class, so in this case, . 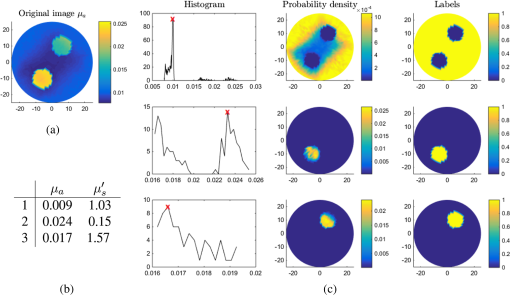 3.3.Visualization of the ResultsResults obtained using the reconstruction-classification method are displayed alongside scatter plots of the nodal values recovered in the two-dimensional (2-D) feature space [e.g., see Fig. 2(c), final column in 4]. The positions of the class means are identified by a cross, and the class covariances are represented by ellipses. These are color-coded by class, and are indicative of the clustering of image nodal values around the class means. 4.Results4.1.Two-Dimensional Validation and ReconstructionWe chose a numerical phantom defined on a 2-D circular mesh with 1331 nodes and radius 25 mm. Four illumination sources were placed on the boundary at angles 0, , , and . In all cases, the illumination profile was a normalized Gaussian with radius (distance from the center at which the profile drops to ) 6 mm. The background optical parameters were set to and . Two circular perturbations of radius 6 mm were added in positions (6 mm, 10 mm) and [Fig. 3(a)]. The values of the perturbations were , and , , respectively. The absorbed energy field was simulated for each illumination, and 1% white Gaussian noise was added [Fig. 3(b)]. The class covariances were initialized to where the first variable was the absorption and the second was the reduced scattering. The parameters of the Jeffreys prior were set to , for the background class and for the perturbation classes. The number of classes and optical parameters was initialized using the class means initialization method (Sec. 3.2) with and [Eq. (53)], and the labels were initialized to 1 for the background class and zero for all other classes. The tolerance of the L-BFGS algorithm was set to , and the total number of reconstruction-classification iterations was set to (Fig. 4). The regularization parameter was chosen by inspection. For comparison, images were reconstructed without introducing a prior (Fig. 5); the images were reconstructed by minimizing Eq. (6) using the L-BFGS method with .Fig. 3Two-dimensional (2-D) model: (a) circular mesh and (b) absorbed energy for each illumination pattern.  4.2.Three-Dimensional Validation and ReconstructionWe chose a three-dimensional (3-D) phantom analogous to the 2-D case, defined on a cylinder with 27,084 nodes, radius 25 mm, and height 25 mm. Two spherical inclusions of radius 6 mm were placed in (6, 10, and 0 mm) and (, , and 0 mm) [Fig. 6(a)]. Illumination sources were Gaussian in the -plane constant in the -axis, with radius 6 mm and length 25 mm [Figs. 6(b) and 6(c)]. PAT images were simulated for four illuminations at the cardinal points, and 1% noise was added to the absorbed energy [Fig. 6(d)]. The optical, covariance, and reconstruction parameters were set to the same values used in the 2-D case. The class initialization parameters were set to and . Images were reconstructed by performing 10 iterations of the reconstruction-classification method (Fig. 7). 5.Discussion5.1.Summary of FindingsWe applied the proposed reconstruction-classification algorithm to a 2-D numerical phantom with three tissues, a background, and two perturbations (Fig. 3). The optical absorption was recovered reliably within a small number of iterations, and the scattering was recovered with sufficient accuracy after approximately 10 iterations (Fig. 4). We compared the optical model with images obtained by the reconstruction-classification method and by a traditional reconstruction-only (no regularization) method (Fig. 5). We found that the reconstruction-classification method delivered superior image quality, particularly with regards to the scattering parameter. We applied the reconstruction-classification algorithm to a much larger 3-D problem (Fig. 6) and observed similar results (Fig. 7) as in the 2-D case. 5.2.Choice of ParametersThe parametric optical model and classification algorithm introduce a number of parameters that require tuning by the user. In addition to the regularization parameter, the parameters of the Jeffreys prior and and the initial guess of the class variances must be set before performing the classification. However, their significance is fairly intuitive, and with experience of a certain type of problem, the choice of parameters becomes natural. Visualizing the class covariance matrix as an ellipse, changing the value of varies its eccentricity, and changing varies the length of its axes. Further, given that in the first iteration the optical absorption is recovered with superior accuracy to the scattering, it is preferable to initialize the variance of the former to a smaller value than the latter, indicating greater confidence in the imaging solution. 5.3.Initialization of the Class MeansThe purpose of the means initialization scheme is to increase automation of the method so that minimum user intervention and no prior knowledge of the number of tissues or their optical properties is required. The algorithm simply performs a segmentation of the image, then takes averages over the segmented areas to initialize the class properties (Fig. 1). Alternative segmentation techniques could have been employed; however, the advantage of the proposed approach is that it directly exploits the mixture of Gaussians model to identify the tissues. Our choice to investigate a node with belonging to the bin with a maximum number of occurrences leads to the background tissue being identified first, followed by the perturbation tissues. The choice of the node index could have been randomized so that tissues would be identified in random order. This approach is equally valid; however, we found that in cases where tissue values were close together (such as after a single reconstruction-classification iteration), it was preferable to identify the largest classes first because the mean was estimated with greater accuracy for the classes with a larger number of samples. Further, for a given image and tolerance level, our choice renders the result of the segmentation process unique and reproducible. 5.4.Recovery of the ScatteringFrom the comparison with the reconstruction-only case with no regularization (Fig. 5), it is evident that the introduction of the parametric prior enables better recovery of the scattering. The inconsistency between the quality of the recovered absorption and scattering parameters in the nonregularized case is due to the weaker dependence of the latter on the absorbed energy density with respect to the former. This results in the scattering gradient being approximately an order of magnitude smaller than the absorption gradient. Although the problem can be mitigated by sphering the solution space, variations in the data due to the scattering often fall below the noise floor. In the reconstruction-classification case, typically the absorption is recovered with good accuracy within a small number of iterations. Thus, the absorption takes values very close to the class means (resulting in small clusters), and the variance along the direction converges to a small value. Given that the regularization term is weighted by the inverse of the covariance matrix, the dependence of the absorption gradient on the data becomes weaker at each iteration, until its magnitude is comparable or smaller to that of the scattering. In the iterations that follow, the descent of the data term of the objective function is primarily due to updates to the scattering, which converges to the correct values. 5.5.Computational DemandsComputational performance was found to be strongly dependent on the problem size. In the 2-D case with 1331 nodes (Fig. 4), the total reconstruction time (10 outer reconstruction-classification iterations) using MATLAB on a 16-processor PC with 128 GB RAM was only 77 s. In the 3-D case with 27,084 nodes (Fig. 7), the total reconstruction time increased linearly with the number of nodes and was approximately 3.7 h on the same workstation. The increase in computation time was mostly due to much longer processing times for the L-BFGS algorithm in the reconstruction step. 5.6.Experimental ApplicationIn experimental situations, prior information on tissue properties may be held, such as knowledge of the characteristic optical absorption and scattering spectra of chromophores of interest. These may be obtained from the literature15 or gained through tissue sample measurements. This information could be used in one of two ways. First, a library of typical chromophores could be used to initialize the class parameters instead of the proposed class means initialization method. The classification process could then perform the function of correcting for uncertainty, errors, or local variations in the real optical properties with respect to the prior information. Alternatively, it could be used to label the chromophores found by the segmentation process and identify these as certain tissues such as, e.g., “oxygenated blood” or “fat,” on the basis of the closeness of the recovered means to the characteristic properties. 5.7.Additional PriorsIn this study, we assumed independence between nodal values; however, the mixture of Gaussian models could be used in conjunction with a spatial prior. Knowledge of smoothness or sparsity properties of the solution could be employed to introduce a homogeneous spatial regularizer such as first-order Tikhonov16 or total variation.7,17 Knowledge of structural information, such as that provided by an alternative imaging method or anatomical library, could be exploited by introducing a spatially varying probability map for the optical properties. 6.ConclusionsIn this paper, we proposed a method for performing image reconstruction in QPAT. We introduced a parametric class model for the optical parameters and implemented a minimization-based reconstruction algorithm. We suggested an automated method by which to initialize the parameters of the class model and proposed a classification algorithm by which to progressively update and improve those parameters after each reconstruction step. We demonstrated though 2-D and 3-D numerical examples that the reconstruction-classification method allows for the simultaneous recovery of optical absorption and scattering. In particular, we found that this approach delivered superior accuracy in the recovery of the scattering with respect to traditional gradient-based reconstruction. ReferencesP. Beard,
“Biomedical photoacoustic imaging,”
Interface Focus, 1 602
–631
(2011). http://dx.doi.org/10.1098/rsfs.2011.0028 Google Scholar
B. Cox et al.,
“Quantitative spectroscopic photoacoustic imaging: a review,”
J. Biomed. Opt., 17 061202
(2012). http://dx.doi.org/10.1117/1.JBO.17.6.061202 JBOPFO 1083-3668 Google Scholar
H. Gao, S. Osher and H. Zhao,
“Quantitative photoacoustic tomography,”
Lect. Notes Math., 2035 131
–158
(2012). http://dx.doi.org/10.1007/978-3-642-22990-9_5 Google Scholar
P. Hiltunen, S. J. D. Prince and S. Arridge,
“A combined reconstruction-classification method for diffuse optical tomography,”
Phys. Med. Biol., 54 6457
–6476
(2009). http://dx.doi.org/10.1088/0031-9155/54/21/002 PHMBA7 0031-9155 Google Scholar
E. Malone et al.,
“A reconstruction-classification method for multifrequency electrical impedance tomography,”
IEEE Trans. Med. Imaging, 34
(7), 1486
–1497
(2015). http://dx.doi.org/10.1109/TMI.2015.2402661 ITMID4 0278-0062 Google Scholar
S. Arridge,
“Optical tomography in medical imaging,”
Inverse Prob., 15 R41
(1999). http://dx.doi.org/10.1088/0266-5611/15/2/022 INPEEY 0266-5611 Google Scholar
G. Bal and K. Ren,
“Multiple-source quantitative photoacoustic tomography in a diffusive regime,”
Inverse Prob., 27
(7),
(2011). http://dx.doi.org/10.1088/0266-5611/27/7/075003 INPEEY 0266-5611 Google Scholar
P. Shao, B. Cox and R. J. Zemp,
“Estimating optical absorption, scattering, and Grueneisen distributions with multiple-illumination photoacoustic tomography,”
Appl. Opt., 50
(19), 3145
–3154
(2011). http://dx.doi.org/10.1364/AO.50.003145 APOPAI 0003-6935 Google Scholar
H. Gao, J. Feng and L. Song,
“Limited-view multi-source quantitative photoacoustic tomography,”
Inverse Prob., 31
(6), 065004
(2015). http://dx.doi.org/10.1088/0266-5611/31/6/065004 INPEEY 0266-5611 Google Scholar
B. T. Cox, S. R. Arridge and P. C. Beard,
“Gradient-based quantitative photoacoustic image reconstruction for molecular imaging,”
Proc. SPIE, 6437 64371T
(2007). http://dx.doi.org/10.1117/12.700031 PSISDG 0277-786X Google Scholar
M. Schweiger and S. Arridge,
“The Toast++ software suite for forward and inverse modeling in optical tomography,”
J. Biomed. Opt., 19 040801
(2014). http://dx.doi.org/10.1117/1.JBO.19.4.040801 JBOPFO 1083-3668 Google Scholar
T. Saratoon et al.,
“3D quantitative photoacoustic tomography using the -Eddington approximation,”
Proc. SPIE, 8581 85810V
(2013). http://dx.doi.org/10.1117/12.2004105 PSISDG 0277-786X Google Scholar
J. Nocedal and S. Wright,
“Numerical optimization,”
Springer Series in Operations Research and Financial Engineering, Springer-Verlag, New York
(1999). Google Scholar
S. Prince, Computer Vision: Models, Learning, and Inference, Cambridge University Press, Cambridge, United Kingdom
(2012). Google Scholar
S. L. Jacques,
“Optical properties of biological tissues: a review,”
Phys. Med. Biol., 58 5007
–5008
(2013). http://dx.doi.org/10.1088/0031-9155/58/14/5007 PHMBA7 0031-9155 Google Scholar
T. Saratoon et al.,
“A gradient-based method for quantitative photoacoustic tomography using the radiative transfer equation,”
Inverse Prob., 29 075006
(2013). http://dx.doi.org/10.1088/0266-5611/29/7/075006 INPEEY 0266-5611 Google Scholar
T. Tarvainen et al.,
“Reconstructing absorption and scattering distributions in quantitative photoacoustic tomography,”
Inverse Prob., 28 084009
(2012). http://dx.doi.org/10.1088/0266-5611/28/8/084009 INPEEY 0266-5611 Google Scholar
|