|
|
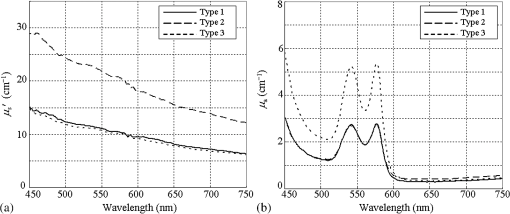
1.IntroductionAn imbalance in oxygen supply and demand causes hypoxia in solid tumor tissues, and tumor cells in chronic hypoxia show resistance to radiotherapy and chemotherapy, which leads to a poor prognosis for cancer patients.1–4 The treatment-resistant property of the tumor cells is a result of their adaptive response to the hypoxic environment by regulating oxygen-dependent gene expression. Recent studies have shown that hypoxia is also related to inflammation.5,6 Inflamed lesions can often become severely hypoxic, and the oxygen-dependent metabolism is also involved in inflammatory processes. Thus, detecting tissue hypoxia can provide useful information for detailed differential diagnosis and selection of therapeutic strategies of cancerous and inflammatory lesions. Since the hemoglobin oxygen saturation () varies with the dissolved oxygen concentration () in a tissue, and the absorption spectrum of the hemoglobin also varies with its , hemoglobin has often been used for optical measurements of tissue oxygen level. The tissue oximeter T-Stat (Spectros Co., Portola Valley) is a representative tool for measuring tissue .7 T-Stat has several types of probes and enables single-point measurement of tissue in vivo by illuminating tissue with white light and then analyzing the reflectance spectrum in the visible range. The performance of T-Stat has been validated by tissue-simulating phantom and animal experiments, and also by some human studies.7–9 Measurement of tissue oxygenation may provide useful information for endoscopic diagnosis, and there have been some clinical studies using T-Stat where the of gastrointestinal tissues was endoscopically measured.10,11 However, endoscopic application of spectroscopy-based oximetry has the following problems: (1) although oxygen concentration can be distributed heterogeneously in a cancerous lesion,12 single-point measurement cannot provide the spatial information; and (2) capturing images of many wavelengths for reflectance spectrum analysis is time-consuming, and the results are often blurred because the target tissue does not remain in a state of rest under endoscopic observation. Several studies have used the hyperspectral imaging method for in vivo optical imaging of distribution, using multiple images corresponding to different light wavelengths.13,14 However, very few studies have reported on imaging using a small number of wavelengths. As an application for a fundus camera, Nakamura et al.15 presented an imaging technique for human retinal vessels using only two wavelengths: 545 and 560 nm. However, this method focuses on the simple structure of the retinal tissue, where thick blood vessels sparsely exist near the surface. For endoscopic application, the imaging target should be thin vessels embedded in a tissue with strong light scattering. Nadeau et al.16 exploited the technique of spatial frequency domain imaging (SFDI) using three wavelengths of 658, 730, and 850 nm to visualize distribution of porcine kidneys. However, SFDI needs spatially modulated illumination in principle, and it is impractical to apply the technique to common forward-viewing endoscopes. We are currently developing an imaging technique for endoscopic application using a small number of wavelength ranges of light reflected from tissue, focusing on esophageal, gastric, and colorectal mucosa as the target tissues. We previously developed an imaging technique based on three wavelength ranges and applied it to a laser illumination endoscope system.17 Here, to argue for the application of imaging to clinical endoscopy, it is important to show that tissue can be obtained by a small number of wavelengths equivalently to a spectroscopy-based technique using many wavelengths. In this work, the physical principle of our method based on tissue optics is explained. We verified this method by observing tissue-simulating phantoms whose was controlled. 2.Principle of CalculationTo derive tissue using a small number of spectral bands, selection of the appropriate wavelength and bandwidth of each band is essential. The algorithm of our technique employs the following four wavelength ranges: two blues (narrow bands around 450 and 470 nm), green (broad band at 500–560 nm), and red (band around 620 nm). Figure 1 shows a comparison of these spectral bands [Fig. 1(c)] with the hemoglobin absorption spectra [Fig. 1(a)] and typical mucosal scattering coefficients [Fig. 1(b)]. Regarding the dependence of these spectral bands on the tissue optical parameters, the following properties are indicated: (1) since increases as the wavelength decreases, the 450 nm blue band is particularly sensitive to the scattering property; (2) since the 470 nm blue band corresponds to the point where the absorption gap of oxy- and deoxy-hemoglobin is locally wide, the reflectance at the 470 nm blue band is sensitive to ; (3) since the broad green band corresponds to the absorption peak, the reflectance at the green band is effectively sensitive to blood concentration; and (4) since the absorption at the red band is extremely small, the reflectance at the red band contains very little information about the tissue blood, and hence can be used as a reference standard. Fig. 1(a) of oxy- and deoxy-hemoglobins; (b) of typical gastrointestinal mucosae of esophagus,18 stomach,19 and colon;20 and (c) the four spectral bands used for this technique. The spectral bands are overlaid on the graphs in (a) and (b). For the hemoglobin values, we combined three literature values from Refs. 2122.–23 to fully match them with actual values.24 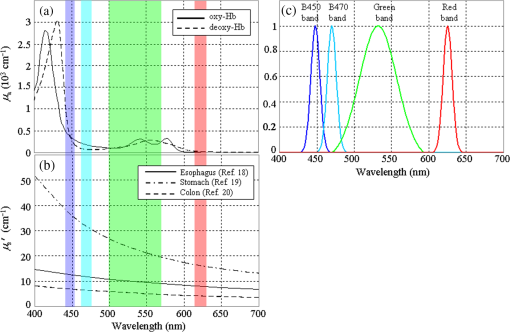 The algorithm for the calculation comprises the following steps: (1) obtain the diffuse reflectance of the observed tissue at the four spectral bands, (2) calculate the ratios of the reflectance at different wavelengths, and (3) transform the ratios into the tissue characteristics ( and blood concentration). The physical principle based on a simple model of tissue optics is described below. Optical properties of biological tissue are generally characterized by three quantities: the absorption coefficient , the scattering coefficient , and the anisotropy factor . Here, we consider a tissue as a homogeneous semi-infinite slab that is vertically irradiated by homogeneous illumination. Based on scale invariance arguments on this model, the total diffuse reflectance of the tissue depends on only the ratio , that , where is the reduced scattering coefficient.25 Since the hemoglobin is the dominant absorptive component in the gastrointestinal tissue, can be written as where is the volume fraction of the blood in the tissue; and , respectively, denote the absorption coefficient of the blood of and 0% [Fig. 1(a)]; and the is the oxygen saturation of the blood contained in the tissue. The reduced scattering coefficient of biological tissue is generally characterized by the exponential monotone decrease according to wavelength and can be modeled by the following equation with two parameters and :26 where is normalized by 500 nm. The parameter defines the overall strength of scattering, and determines the slope of decrease. Using these parametrizations and the dependence on the ratio of by the scale invariance property as mentioned above, the diffuse reflectance of the tissue can be described as a function where . is characterized by the three parameters , , and .Let , , , and be the obtained image signals corresponding to the four spectral bands. Here, each signal (, B470, G, and R) can be written as where is the illumination spectrum of each band [Fig. 1(c)], is the sensitivity of the image sensor, and is the arbitrary proportionality coefficient that depends on the distance between the tissue and the image acquisition system.To investigate the dependence of each signal on the three tissue parameters, we simulated the diffuse reflectance of the homogeneous tissue using the software package MCML,27 at various conditions of the parameters of , , and . The details of simulation conditions are described in Sec. 4.1.4. Figures 2(a)–2(c) show the simulated parameter dependence of each signal in the log scale. These results indicate the inverse dependence of and on [Fig. 2(a)], the large differences in the degree of dependence of each signal on (hence on ) [Fig. 2(b)], and the strong dependence of on . Based on the results, we consider the following three signal ratios in the log scale ( is canceled here): The simulated parameter dependence of each signal ratio is shown in Figs. 2(d)–2(f). These results shows the strong dependence of , , and on , , and , respectively.Fig. 2(a)–(c) Simulated dependences of the four signals and (d)–(f) the three signal ratios on the tissue parameters. For these simulations presented here, only one parameter was varied while the other two were fixed at the standard values, defined as , , , and . 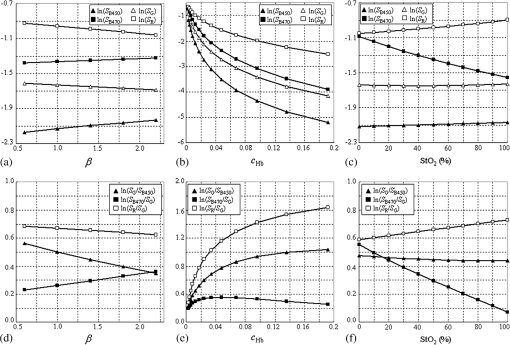 Note that the three signal ratios have markedly different dependences on the three tissue parameters. Each signal ratio does not depend on the single tissue parameter but on the three parameters simultaneously and nonlinearly. However, if we consider the three-dimensional (3-D) space spanned by , we can define nonlinear surfaces, each of which corresponds to the same value, and can be obtained separately from other two parameters. This is the principle of our technique. The details of the transformation method of into are described in Sec. 4.1.4. 3.Development of Imaging EndoscopeBased on the principle described in Sec. 2, we developed a prototype endoscope system for gastroenterological endoscopy that allowed us to obtain distribution images of tissue. As with the other types of our prototype systems,17,28 the light source of the system provided four bands of light: two blue narrow bands at 450 and 470 nm, a green broad band, and a red band [Fig. 1(c)]. Images were acquired with an RGB color CCD (same sensor as that mounted on EG590 endoscope, Fujifilm Co., Tokyo, Japan) mounted at the endoscope tip, and the image data were transmitted to the processor and saved on the hard disk of a computer that was connected to the processor. The illumination was switched sequentially among the four bands synchronized with the video frames at a rate of . Switching the illumination provided different spectroscopic images of the four colors at almost the same position on the object being observed unless the object moved quickly. The images were obtained at a rate of 7.5 frames/s in almost real time. The processing time from the data acquisition to display on the monitor was about 0.1 s. 4.Experiment4.1.Materials and Methods4.1.1.Ethics statementPrior to the study, the protocol of the experiment was reviewed and approved by the Fujifilm Imaging Technology Center. As for the human blood used in this experiment, it was confirmed by Kohjin Bio Co. Ltd. that the informed consent for its research usage had been obtained by the donor. 4.1.2.Tissue-simulating phantomsWe prepared tissue-simulating phantoms according to the following procedure.8 Precipitated erythrocytes (0.8 ml) were drawn from preserved human blood (Kohjin Bio Co., Ltd., Sakado, Japan). Then4 ml of saline was added to the erythrocytes, and the mixture was centrifuged at for 2.0 min. The supernatant was subsequently pipetted away. After the process was repeated twice, 20 ml of distilled water was added to hemolyze the erythrocytes completely over 15 min. The fluid was centrifuged again, and the fluid portion was extracted to obtain the hemoglobin solution. The concentration of this solution was measured by absorptiometry, and the solution was diluted to the target concentration. We prepared three types of phantoms, whose conditions are summarized in Table 1. We added Intralipid 10% solution as the light scatterer. A total of 125 ml of the phantom liquid was put into a 100-ml flask, and 0.6 g of sugar was added. The pH was then adjusted to 7.4 by adding NaOH. The temperature of the phantom was kept at 37°C by putting the flask into a thermostat bath. Table 1Conditions of tissue-simulating phantoms.
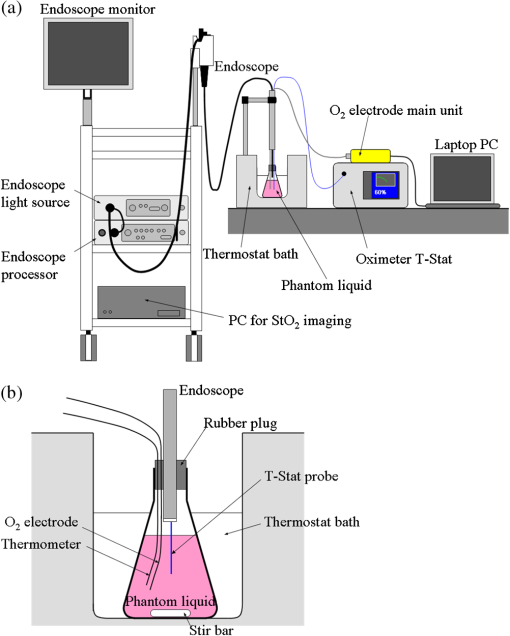
The following procedure was used for absorptiometric measurement of the hemoglobin concentration. Some of the hemoglobin solution was put into a glass cell, and the sample was illuminated by collimated light from a halogen lamp through a light diffuser. The spectra of the transmitted light of the sample and a blank cell were measured with a spectroradiometer SR-UL1 (Topcon Technohouse Co., Tokyo, Japan), and then the transmittance spectrum of the sample was obtained. The difference in the absorbance at wavelengths of 570 and 650 nm was compared with literature data of an oxy-hemoglobin solution of a fixed concentration, and then the concentration was derived. 4.1.3.Data and image acquisitionFigure 3 shows the experimental setup. The flask containing the liquid tissue-simulating phantom was fixed in the thermostat bath. The mouth of the flask was closed with a rubber plug with holes for probes and other devices. A flexible Clarke-type catheter microelectrode (RF CC1.R oxygen probe, Integra LifeSciences Co., Plainsboro) was used for measurement. The oxygen electrode was calibrated by measuring the current of the auxiliary calibration standard liquid according to the usage. The oxygen electrode, the auxiliary thermometer probe, and the tip of the endoscope were inserted into the flask through the holes of the rubber plug. The electrode and thermometer probe were immersed into the phantom. The tip of the endoscope was fixed 1 cm above the liquid level. Next, 0.3 g of dry yeast suspended in a small amount of the phantom liquid was put into the flask to gradually reduce the phantom . The holes of the rubber plug were sealed with oil-based nonhardenable putty to keep the phantom airproof. The endoscopic sensor probe of the T-Stat tissue oximeter was inserted into the phantom through the instrumental channel of the endoscope, and the probe tip was fixed approximately 3 cm below the liquid level. We monitored the phantom with T-Stat. The phantom was constantly stirred during the experiment except when the images were acquired with the endoscope. Since the endoscope illumination affected the measurement with T-Stat, we turned on the illumination only when we acquired images with the endoscope. The illumination of the T-Stat probe was dark enough at the phantom liquid level that it did not affect the endoscopic images. 4.1.4.Hemoglobin oxygen saturationWe derived the image using a set of consecutive frames of images corresponding to the four different bands of the illumination. Let , , , and be the obtained image signals corresponding to the four spectral bands at the same position. First, each signal of the phantom image was normalized by that of an image of the reflectance standard (WS-1-SL, Labsphere, Inc., North Sutton) to make the signal proportional to the reflectance of the phantom at the corresponding wavelength range. Next, we made three signal ratios in logarithmic form as given in Eq. (5), and then transformed the ratios into a value of using the numerical correspondence of the ratios and in the 3-D space of as described in Sec. 2. Performing this process for all the pixels provided the distribution image. The transformation of into was performed using a lookup table, which was based on the simulated diffuse reflectance by MCML. The conditions for the simulation are summarized in Table 2. The tissue thickness was set at 5 cm, which was thick enough to consider the tissue as semi-infinitely-deep for visible light. Using the parameters in Table 2, and were calculated by Eqs. (1) and (2), respectively. We calculated the total diffuse reflectance at each tissue condition in the wavelength range of 400 to 700 nm at 1 nm intervals, and then simulated the normalized image signals (, B470, G, and R) by the following equation using the sensor sensitivities and illumination spectra [corresponding to Eq. (4)] as where the summations over were performed at 1 nm steps. The three signal ratios were obtained by substituting Eq. (6) into in Eq. (5).Table 2Simulation conditions to obtain total diffuse reflectance by MCML.
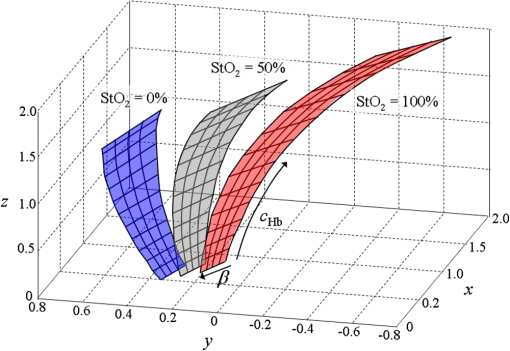
Next, we considered the distribution of points in the 3-D space. Here, a combination of three tissue parameters corresponded to each , and we found that if was fixed and the other two parameters were varied, the simulated distributed on a mildly curved surface. This curved surface defined the iso- surface for each value as presented in Fig. 4. Exploiting this property, we created the lookup table to transform into as follows. We approximated each surface by a third-degree polynomial of as and the determined coefficients were stored in the computer’s memory. Here, suppose that the obtained signal ratios by the experiment were . First, we calculated values by Eq. (7) for at 10% intervals, and searched for two consecutive values and at and , respectively, that satisfied . Then we obtained the obtained the corresponding value by a linear interpolation as4.1.5.Determination of optical propertiesThe optical properties of the phantom liquid were determined by the integrating sphere technique, using the same setup as described in Ref. 28. The phantom liquid was put into a custom-made planar glass cell with an inner spacing of 2 mm, and the total transmittance and diffuse reflectance of the 2-mm-thick liquid were measured using an integrating sphere and a spectrometer. The reduced scattering coefficient was determined by an inverse Monte Carlo technique.19 Here, we assumed a homogeneous, 2-mm-thick tissue model possessing the optical parameters of and , and calculated its and using the software package MCML. We performed the calculation for various and , and determined the optical parameters that reproduced the measured values with minimal errors. 4.2.Results4.2.1.StO2 imagesFigure 5 shows endoscopic images of the phantom liquid surface obtained at different conditions. We defined a region of interest on the phantom surface area for each image to eliminate inappropriate areas, such as specular reflection spots and the T-Stat probe. We then obtained the average value in the region of interest. Figure 6 shows the results of the phantom measurements, where measured with the endoscope and T-Stat are plotted against . The literature values of the hemoglobin dissociation curve are also presented. Here, the dissociation curve was created using the parameters of Ref. 22 at physiologic conditions. The endoscopic values agree with those from the literature within 10%. The raw T-Stat values disagreed in the range of and , where the literature becomes nearly 100% and 0%, respectively. The raw T-Stat tended to show constant values at these ranges. Hence, we normalized the T-Stat values so that their saturated values at high and low became 100% and 0%, respectively. The normalized values agree well with the endoscopic and literature values. Fig. 5Endoscopic images of the phantom liquid surface. Normal and pseudocolor images are juxtaposed for each level. The defined region of interest to calculate the average is indicated by a dashed closed curve on the image at (the region is common to all the images). 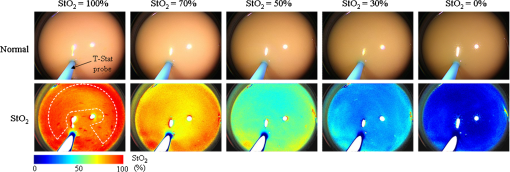 Fig. 6Relation of (endoscope and T-Stat) with (oxygen electrode) for each type of phantom. The hemoglobin dissociation curve at physiological conditions is also plotted (solid curve). The error bars show the standard deviations of the of the endoscope in the region as presented in Fig. 4: (a) type 1 (Intralipid: 0.7%, blood: 1.0%), (b) type 2 (Intralipid: 1.4%, blood: 1.0%), and (c) type 3 (Intralipid: 0.7%, blood: 2.0%). 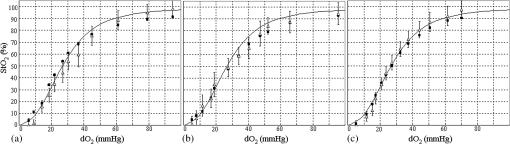 5.DiscussionIn this work, we measured the and of each phantom with the endoscope, T-Stat, and an oxygen electrode simultaneously. We prepared three phantoms with different hemoglobin and Intralipid concentrations (Table 1). The results showed values of both the endoscope and T-Stat plotted against obtained by the oxygen electrode reproduced the physiological hemoglobin dissociation curve, and thus indicated that our method of calculating using four spectral band signals was valid in the range of tissue optical properties measured in this experiment. In Sec. 2, we expressed the tissue reflectance [Eq. (3)] using three parameters, , , and , by assuming a semi-infinite homogeneous tissue model, and showed that the value can be obtained using the numerical correspondence of the ratios and in the 3-D space of the three signal ratios as defined in Eq. (5). Here, the parameter is the wavelength exponent of reduced scattering coefficient [Eq. (2)], which determines the degree of decrease of as the wavelength increases. According to some models based on the theory of Mie scattering, the exponent is closely related to the scatterer size in tissue.29–32 The value of is restricted theoretically and semiempirically in the range of . Scatterers of large sizes compared with the wavelength (e.g., cells and nuclei) give small values of , while smaller scatterers give large . The upper limit of corresponds to the case of Rayleigh scattering, where the scatter size is typically smaller than the wavelength of light by one order of magnitude (e.g., collagen and elastin fibrils). Therefore, different tissue structures or components can lead to different values of . Presently, we are going to apply our imaging technique to endoscopy of the esophagus, stomach, and colorectum. The tissue of the stomach and colorectum is glandular epithelium, where single-layer epithelial cells align along the intricate glandular pitted structure and cover the collagen-rich lamina propria, while the esophageal tissue is stratified squamous epithelium, where a thick flat layer of stratified epithelial cells covers the lamina propria. Considering the differences in structure and components of these organs, the value of should be changed depending on the tissue being observed. Our method may provide an appropriate value of for each organ by making use of the four spectral band signals. However, if we limit the target object to one organ and fix at an appropriate value corresponding to the optical properties of that organ, the can be obtained using only three spectral band signals (, , and ), namely the two signal ratios and in Eq. (5). In Ref. 17, we reported on a clinical study of imaging using a laser illumination endoscope system. The results showed that imaging could clearly distinguish neoplasia from non-neoplasia in the esophagus and colorectum. In that clinical study, was calculated using the three spectral bands of narrow 473 nm, broad green, and broad red, fixing a parameter corresponding to at an organ-dependent value according to the method explained above. In regard to this point, the endoscope system presented in this work, based on the four band signals, is more advantageous since it does not need to assume a fixed parameter , which leads to obtaining more precise values. Recently, several spectral endoscopic imaging techniques have been developed, such as narrow band imaging33–35 and blue laser imaging.36–39 Both techniques exploit narrow-band blue light to enhance the increase in abnormal microvessels in the superficial mucosa, which is one of the characteristic morphological features of cancerous lesions. The technique of imaging described in this work, however, does not focus on enhancing such morphological features of the tissue, but aims at realizing a new realm of endoscopic functional imaging through visualizing tissue oxygenation. To achieve functional imaging using spectral images in endoscopy, it is essential to acquire plural spectral band images with high-speed switching of illumination wavelengths synchronized with the video frames. For practical use, the number of wavelengths should be as few as possible. The technique of this work provides a practical system using only four spectral bands to realize imaging in endoscopy. Compared with the single-point measurement of T-Stat, our imaging endoscopy has an obvious benefit—it enables real-time observation of distribution in a broad area of tissue. It is expected that this technique will be applied clinically and contribute to more detailed differential diagnosis or defining lesion boundaries in endoscopy by exploiting the functional information of tissue oxygenation. ReferencesJ. M. Brown and W. R. Wilson,
“Exploiting tumour hypoxia in cancer treatment,”
Nature Rev. Cancer, 4 437
–447
(2004). http://dx.doi.org/10.1038/nrc1367 NRCAC4 1474-175X Google Scholar
P. Vaupel and A. Mayer,
“Hypoxia in cancer: significance and impact on clinical outcome,”
Cancer Metastasis Rev., 26
(2), 225
–239
(2007). http://dx.doi.org/10.1007/s10555-007-9055-1 Google Scholar
W. R. Wilson and M. P. Hay,
“Targeting hypoxia in cancer therapy,”
Nature Rev. Cancer, 11 393
–410
(2011). http://dx.doi.org/10.1038/nrc3064 NRCAC4 1474-175X Google Scholar
B. F. Jordan and P. Sonveaux,
“Targeting tumor perfusion and oxygenation to improve the outcome of anticancer therapy,”
Front. Phamacol., 3
(94), 1
–15
(2012). http://dx.doi.org/10.3389/fphar.2012.00094 Google Scholar
H. K. Eltzschig and P. Carmeliet,
“Hypoxia and inflammation,”
N. Engl. J. Med., 364
(7), 656
–665
(2011). http://dx.doi.org/10.1056/NEJMra0910283 NEJMAG 0028-4793 Google Scholar
S. P. Colgan and H. K. Eltzschig,
“Adenosine and hypoxia-inducible factor signaling in intestinal injury and recovery,”
Annu. Rev. Physiol., 74 153
–175
(2012). http://dx.doi.org/10.1146/annurev-physiol-020911-153230 ARPHAD 0066-4278 Google Scholar
D. A. Benaron et al.,
“Design of a visible-light spectroscopy clinical tissue oximeter,”
J. Biomed. Opt., 10
(4), 044005
(2005). http://dx.doi.org/10.1117/1.1979504 JBOPFO 1083-3668 Google Scholar
D. A. Benaron et al.,
“Continuous, noninvasive, and localized microvascular tissue oximetry using visible light spectroscopy,”
Anesthesiology, 100
(6), 1469
–1475
(2004). http://dx.doi.org/10.1097/00000542-200406000-00019 ANESAV 0003-3022 Google Scholar
S. Friedland et al.,
“Measurement of mucosal capillary hemoglobin oxygen saturation in the colon by reflectance spectrophotometry,”
Gastrointest. Endoscopy, 57
(4), 492
–497
(2003). http://dx.doi.org/10.1067/mge.2003.162 Google Scholar
P. G. Maxim et al.,
“Optical detection of tumors in vivo by visible light tissue oximetry,”
Technol. Cancer Res. Treat., 4
(3), 227
–234
(2005). http://dx.doi.org/10.1177/153303460500400301 Google Scholar
D. van Noord et al.,
“Endoscopic visible light spectroscopy: a new, minimally invasive technique to diagnose chronic GI ischemia,”
Gastrointest. Endoscopy, 73
(2), 291
–298
(2011). http://dx.doi.org/10.1016/j.gie.2010.10.025 Google Scholar
M. R. Junttila and F. J. de Sauvage,
“Influence of tumour micro-environment heterogeneity on therapeutic response,”
Nature, 501 346
–354
(2013). http://dx.doi.org/10.1038/nature12626 Google Scholar
B. S. Sorg et al.,
“Hyperspectral imaging of hemoglobin saturation in tumor microvasculature and tumor hypoxia development,”
J. Biomed. Opt., 10
(4), 044004
(2005). http://dx.doi.org/10.1117/1.2003369 JBOPFO 1083-3668 Google Scholar
K. J. Zuzak et al.,
“Visible reflectance hyperspectral imaging: characterization of a noninvasive in vivo system for detecting tissue perfusion,”
Anal. Chem., 74 2021
–2028
(2002). http://dx.doi.org/10.1021/ac011275f ANCHAM 0003-2700 Google Scholar
D. N. Nakamura et al.,
“Automated spectroscopic imaging of oxygen saturation in human retinal vessels,”
Proc. SPIE, 7163 71631N
(2009). http://dx.doi.org/10.1117/12.807537 PSISDG 0277-786X Google Scholar
K. P. Nadeau et al.,
“Quantitative assessment of renal arterial occlusion in a porcine model using spatial frequency domain imaging,”
Opt. Lett., 38
(18), 3566
–3569
(2013). http://dx.doi.org/10.1364/OL.38.003566 OPLEDP 0146-9592 Google Scholar
K. Kaneko et al.,
“Hypoxia imaging endoscopy equipped with laser light source from preclinical live animal study to first-in-human subject research,”
PLoS One, 9
(6), e99055
(2014). http://dx.doi.org/10.1371/journal.pone.0099055 POLNCL 1932-6203 Google Scholar
P. R. Bargo et al.,
“In vivo determination of optical properties of normal and tumor tissue with white light reflectance and an empirical light transport model during endoscopy,”
J. Biomed. Opt., 10
(3), 034018
(2005). http://dx.doi.org/10.1117/1.1921907 JBOPFO 1083-3668 Google Scholar
A. N. Bashkatov et al.,
“Optical properties of human stomach mucosa in the spectral range from 400 to 2000 nm: Prognosis for gastroenterology,”
Med. Laser Appl., 22
(2), 95
–104
(2007). http://dx.doi.org/10.1016/j.mla.2007.07.003 Google Scholar
H. Ao et al.,
“Thermal coagulation-induced changes of the optical properties of normal and adenomatous human colon tissues in vitro in the spectral range 400–1100 nm,”
Phys. Med. Biol., 53 2197
–2206
(2008). http://dx.doi.org/10.1088/0031-9155/53/8/013 PHMBA7 0031-9155 Google Scholar
S. Prahl,
“Optical absorption of hemoglobin,”
(2015) http://omlc.org/spectra/hemoglobin/ ( March ). 2015). Google Scholar
W. G. Zijlstra, A. Buursma and O. W. van Assendelft, Visible and Near Infrared Absorption Spectra of Human and Animal Haemoglobin, VSP BV, Netherlands
(2000). Google Scholar
O. W. van Assendelft, Spectrophotometry of Haemoglobin Derivatives, Royal Van Gorcum Ltd., Netherlands
(1970). Google Scholar
A. Amelink, T. Christiaanse and H. J. C. M. Sterenborg,
“Effect of hemoglobin extinction spectra on optical spectroscopic measurements of blood oxygen saturation,”
Opt. Lett., 34
(10), 1525
–1527
(2009). http://dx.doi.org/10.1364/OL.34.001525 OPLEDP 0146-9592 Google Scholar
G. Zonios and A. Dimou,
“Modeling diffuse reflectance from semi-infinite turbid media: application to the study of skin optical properties,”
Opt. Express, 14
(19), 8661
–8674
(2006). http://dx.doi.org/10.1364/OE.14.008661 OPEXFF 1094-4087 Google Scholar
S. L. Jacques,
“Optical properties of biological tissues: a review,”
Phys. Med. Biol., 58 R37
–R61
(2013). http://dx.doi.org/10.1088/0031-9155/58/11/R37 PHMBA7 0031-9155 Google Scholar
L. Wang, S. L. Jacquesa and L. Zheng,
“MCML—Monte Carlo modeling of light transport in multi-layered tissues,”
Comput. Methods Prog. Biomed., 47
(2), 131
–146
(1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar
H. Yamaguchi et al.,
“Quantitative study on appearance of microvessels in spectral endoscopic imaging,”
J. Biomed. Opt., 20
(3), 036005
(2015). http://dx.doi.org/10.1117/1.JBO.20.3.036005 JBOPFO 1083-3668 Google Scholar
J. R. Mourant et al.,
“Predictions and measurements of scattering and absorption over broad wavelength ranges in tissue phantoms,”
Appl. Opt., 36
(4), 949
–957
(1997). http://dx.doi.org/10.1364/AO.36.000949 APOPAI 0003-6935 Google Scholar
A. M. K. Nillson et al.,
“Changes in spectral shape of tissue optical properties in conjunction with laser-induced thermotherapy,”
Appl. Opt., 37
(7), 1256
–1267
(1998). http://dx.doi.org/10.1364/AO.37.001256 APOPAI 0003-6935 Google Scholar
M. Hunter et al.,
“Tissue self-affinity and polarized light scattering in the Born approximation: a new model for precancer detection,”
Phys. Rev. Lett., 97 138102
(2006). http://dx.doi.org/10.1103/PhysRevLett.97.138102 PRLTAO 0031-9007 Google Scholar
M. Xu and R. R. Alfano,
“Fractal mechanisms of light scattering in biological tissue and cells,”
Opt. Lett., 30
(22), 3051
–3053
(2005). http://dx.doi.org/10.1364/OL.30.003051 OPLEDP 0146-9592 Google Scholar
P. Lukes et al.,
“Narrow band imaging (NBI)—endoscopic method for detection of head and neck cancer,”
Endoscopy, 75
–87 InTech, Croatia
(2013). http://dx.doi.org/10.5772/52738 Google Scholar
V. Subramanian and K. Ragunath,
“Advanced endoscopic imaging: a review of commercially available technologies,”
Clin. Gastroenterol. Hepatol., 12
(3), 368
–376
(2014). http://dx.doi.org/10.1016/j.cgh.2013.06.015 Google Scholar
M. Song and T. L. Ang,
“Early detection of early gastric cancer using image-enhanced endoscopy: current trends,”
Gastrointest. Intervention, 3
(1), 1
–7
(2014). http://dx.doi.org/10.1016/j.gii.2014.02.005 Google Scholar
Y. Morimoto et al.,
“Development of a new generation endoscope system with lasers ‘LASEREO’,”
Fujifilm Res. Dev., 58 1
–6
(2013). Google Scholar
H. Osawa and H. Yamamoto,
“Present and future status of flexible spectral imaging color enhancement and blue laser imaging technology,”
Dig. Endoscopy, 26
(1), 105
–115
(2014). http://dx.doi.org/10.1111/den.12205 Google Scholar
N. Yoshida et al.,
“The ability of a novel blue laser imaging system for the diagnosis of invasion depth of colorectal neoplasms,”
J. Gastroenterol., 49 73
–80
(2014). http://dx.doi.org/10.1007/s00535-013-0772-7 Google Scholar
N. Yoshida et al.,
“Ability of a novel blue laser imaging system for the diagnosis of colorectal polyps,”
Dig. Endoscopy, 26
(2), 250
–258
(2014). http://dx.doi.org/10.1111/den.12127 Google Scholar
|