1.

Introduction

There is strong interest in developing high-resolution devices for internal in vivo imaging. These tools would aid medical doctors and researchers in diagnosing and understanding many medical ailments, such as cancer, with a less invasive method than current practice. Multiphoton imaging provides a useful tool for cellular imaging^1–6 and is widely used in brain⁶ and biological imaging.^1–4 Like confocal microscopy, multiphoton imaging provides optical sectioning, which is necessary for imaging within thick tissue samples.¹ The compatibility between multiphoton imaging and biology is well-known and a few endoscopic devices have been developed as a result.^7–10 Endoscopic devices for two-photon fluorescence (TPF) imaging generally utilize a single-mode fiber for pulse delivery with mechanical components encased in a probe at the fiber’s distal tip to enable point scanning.^8–10 The scanning mechanism significantly increases the size of the endoscope over that of the light-delivering fiber. Although these devices are a significant improvement over existing technologies, a more compact TPF endoscope remains a desired goal.

To meet this goal, endoscopes utilizing specialty fibers and optics without distal optics or mechanics are being pursued. For example, commercial confocal endoscopes (not multiphoton) utilize a multicore fiber (MCF) for small-diameter endoscopes.^11,12 These devices scan light through many cores of the fiber to sample the image at each core position at the distal end. The resolution of core-by-core scanning MCF endoscopes is limited by the core spacing,¹³ which must be kept sufficiently large to limit core-to-core coupling.^14,15 The resolution can be improved with a graded index (GRIN) lens that demagnifies the fiber facet; however, this improvement comes at the expense of a reduced field of view, and the resolution is still limited by core spacing. This GRIN lens arrangement was used in a previous implementation of TPF imaging through an MCF.⁷ More recently, MCFs have been utilized with wavefront shaping techniques to control the wavefront at the distal end.^13,16–18 These methods are similar to the methods recently deployed in step-index multimode fiber (MMF) imaging,^19–23 in which they create a focus at the distal end by properly selecting the wavefront at the proximal side. The key difference between these methods is that in MMFs, the modes provide the degrees of freedom in the light field control, whereas the fiber cores (and their modes) do in MCFs. With step-index MMFs, these methods are restricted with regard to multiphoton microscopy due to modal dispersion of a propagating ultrashort pulse. The temporal spread of the modes as they propagate through the fiber limits the number that can contribute to a focus spot recreation.²⁴ However, GRIN fibers exhibit significantly less modal dispersion, and we have recently demonstrated TPF imaging through one combined with a GRIN lens.²⁵ Using single-mode MCFs bypasses the restrictions imposed by modal dispersion, as well. Recently, a wavefront shaping method has been demonstrated with MCFs for multiphoton imaging.¹⁸ The system developed by Andresen et al.¹⁸ uses a custom-fabricated MCF comprised of 169 highly spaced, single-mode cores arranged in a hexagonal grid. With this fiber, the light field can be controlled with minimal core-to-core coupling. However, the large separation between periodically arranged cores resulted in a close spacing between diffraction orders at the focal plane, thus limiting the field of view and forcing a large working distance, which decreases resolution.^18,26

In this paper, we use wavefront shaping in conjunction with MCFs for TPF imaging, similar to Ref. 18. We utilize TPF imaging to enable optical sectioning in our lensless endoscope. However, to create the focus, we use coherence-gated digital phase conjugation (DPC), as we have done previously with a GRIN and step-indexed MMFs.^24,25 DPC compensates for core-to-core coupling²⁷ and allows for use of commercially available MCFs, which contain a large number (several thousand to 100,000) of densely packed cores arranged in a quasiperiodic array. The closely spaced cores spread the diffraction orders in the focal plane away from the desired focus, which allows for a larger field of view than possible with highly spaced core MCFs¹⁸ and also reduces the power distributed to the diffraction orders. Although the MCF used propagates a few modes at our experimental wavelength, we show that a single mode can be selected through modal dispersion in the fiber and coherence gating during hologram recording. We demonstrate that coherence-gated DPC allows for the selective propagation of individual modes and that the fundamental mode offers a better focusing performance when compared to the higher order mode. Finally, we construct TPF images by digital scanning of the phase-conjugated focus on the target object and fluorescence collection through the MCF to obtain images of fluorescently stained beads and cells.

2.

Coherence-Gated Digital Phase Conjugation

DPC of ultrashort pulses with fibers allows for precise selectivity of the phase-conjugated modes.²⁴ To perform DPC, a calibrating focus spot is created at the distal end of the fiber. After propagation through the fiber, the field is recorded at the proximal end using off-axis digital holography. The recorded field can then be phase conjugated digitally and coupled back into the fiber to recreate a focus spot at the original calibration focus. In the case of coherence-gated DPC, the two pulses recording the hologram must overlap in space and time at the detector array. One pulse emerges from the MCF and the other is a reference wave. In most commercially available MCFs, each core supports the propagation of only a few modes. An ultrashort pulse propagating in a core will couple into the linearly polarized (LP) modes, which temporally separate as a result of modal dispersion. During the hologram recording, the short coherence length of the high-bandwidth laser pulse coherence gates the recording process. This allows for time-sampling the pulse after propagation through the MCF, recording the field of a selected set of modes after propagation through the fiber.

To test coherence-gated DPC through an MCF, we use a commercially available fiber (Fujikura, FIGH-03-215S). This fiber has 3000 cores within a $190\text{-}\mu \mathrm{m}$ diameter. Individual cores have a numerical aperture (NA) of 0.34 and are $2.5\mu \mathrm{m}$ in diameter on average and spaced by $3.2\mu \mathrm{m}$ on average. These cores have a $V$ number of $\sim 3.4$ and support the ${\mathrm{LP}}_{01}$ and ${\mathrm{LP}}_{11}$ modes at 785-nm wavelength. These fibers are designed with a variation in core diameter to minimize core-to-core coupling.¹⁴ Notably, the smaller core spacing separates the diffraction orders in the far-field, which allows a wider field of view than possible with highly spaced core MCFs.¹⁷

The optical system used for coherence-gated DPC is shown in Fig. 1. The laser beam emitted from a Coherent Chameleon (3 W, 140 fs, operated at $\lambda =785\mathrm{nm}$) is collimated and split into reference and calibration arms. The power ratio between the two arms is selected depending on whether the system is in a hologram recording or readout configuration. For these experiments, a 30-cm length of MCF is mounted between two objectives separated by 28 cm, thus fixing the fiber with a slight curvature. Figure 1(a) shows the optical path during the hologram recording phase. To record a hologram, light travels through both the reference and calibration arms. The light in the calibration path is focused in front of the distal end of the fiber. After collection and transmission through the MCF, the light is imaged onto a CMOS detector (MV1-D1312IE-100-G2-12, Photonfocus) by an objective lens and a lens in a 4f configuration. The pulse that propagates through the reference path arrives concurrently on the CMOS and interferes with the calibration pulse. A delay line is placed in the reference path for tuning the temporal delay.

Fig. 1

The optical apparatus for DPC with an MCF. The optical apparatus in (a) hologram recording and (b) read out mode for focus spot recreation. (a) The beam is split into two parts: reference and calibration paths. The calibration path creates a focus spot at the distal end of the MCF. This beam interferes with the reference beam at the CMOS after propagation through the fiber. (b) The field recorded previously is phase conjugated and displayed on the SLM, which encodes the readout pulse before propagating through the MCF and recreating the focus spot. PBS, polarizing beam splitter; BS, beamsplitter; D, dichroic beamsplitter; 9:1, 90:10 (R:T) beamsplitter; Obj, objective lens; HWP, halfwave plate; L, lens; PMT, photomultiplier tube; and SLM, spatial light modulator.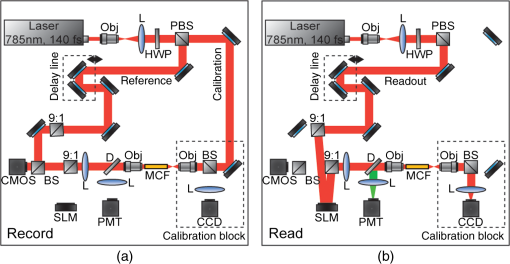

After recording, the phase of the field is extracted from the recorded hologram, phase conjugated, and displayed on the spatial light modulator (SLM, Pluto-NIR2, Holoeye). Figure 1(b) shows the optical path during the hologram readout. Two 90:10 beamsplitters (R:T) are used to read out the phase-conjugate hologram displayed on the SLM to minimize the beamsplitter losses of the phase-conjugated beam.²⁸ On the distal end of the fiber, the objective used to focus the calibration beam is used to capture the phase-conjugated light, which is then reimaged on a CCD (Point Grey Research, Chameleon 3) for examination.

Coherence-gated holography of the pulse allows an analysis of the temporal and spatial shapes of the transmitted pulse from each core. The coherence-gating reference pulse can be treated as a sampling window in time. However, its sampling window size is not determined by the pulse length, but by the coherence length of the source because the interference measurement is not sensitive to spectral phase (i.e., to chromatic dispersion, which broadens the pulse). In this way, it probes the temporal coherence function of the pulses emerging from each core. Because coherence-gated holography provides the coherence function across the fiber facet, it provides information about pulse transmission from individual cores.

The temporal profile of the coherence-gated output was measured by first-order cross correlation of the reference and the pulses transmitted through the MCF. To do this, the delay line was moved in $20\mu \mathrm{m}$ steps (133 fs), and a hologram was recorded at each position. Then, by integrating the power in the first diffraction order of the hologram’s Fourier transform, we measured the total power of the coherence-gated output from each core of the MCF at each step [Fig. 2(a)]. The temporal profile reveals that the light emerges from the MCF cores in two distinct LP modes: the ${\mathrm{LP}}_{01}$ and ${\mathrm{LP}}_{11}$. Figures 2(b) and 2(c) show the Fourier transforms of the hologram captured at ${\tau }_1=0.93ps$ and ${\tau }_2=7.2ps$, respectively. A comparison of the spatial frequency components encoded in the holograms shows distinct spatial frequency content in the two fields. After recovering the phase of the field, ${\tau }_1$ is clearly the ${\mathrm{LP}}_{01}$ mode of each core [Fig. 2(d)]. This is apparent in the quadratic phase, which encircles each core of the MCF at ${\tau }_1$, whereas the phase recovered at ${\tau }_2$ shows a phase image [Fig. 2(e)] corresponding to the higher order ${\mathrm{LP}}_{11}$ mode. The inset of Fig. 2(a) is a histogram showing the distribution of the times of the maximum power of the coherence function from each core during the ${\mathrm{LP}}_{01}$ mode arrival range. It contains 24 bins of 133 fs width.

Fig. 2

(a) The temporal profile of the total power of the coherence-gated output from the MCF. The inset shows a histogram of the delay times of the maximum power of the coherence function of the pulses from each core within the first 3.2 ps. (b) Fourier transform of the hologram captured at ${\tau }_1$, (c) Fourier transform of the hologram captured at ${\tau }_2$, (d) the phase reconstruction from (b), which shows quadratic phase patterns encircling individual cores indicating the ${\mathrm{LP}}_{01}$ mode, and (e) the phase reconstruction from (c) with the ${\mathrm{LP}}_{11}$ mode in each core.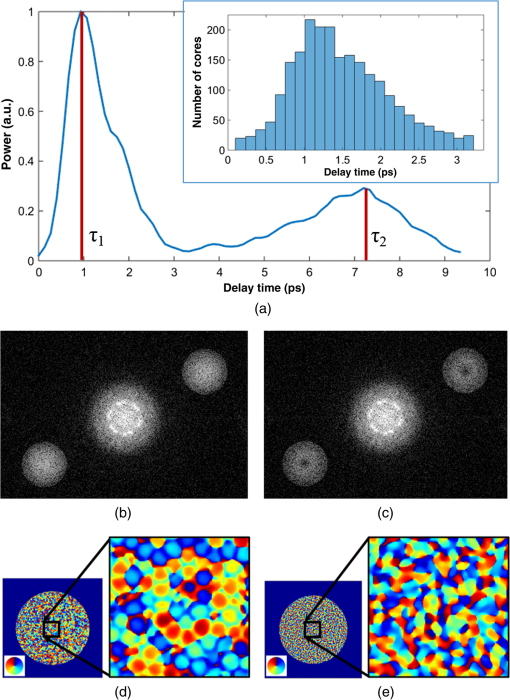

3.

Characterization of Digital Phase Conjugation Focused Ultrashort Pulses

The reconstructed focus spots obtained by DPC of the ${\mathrm{LP}}_{01}$ and the ${\mathrm{LP}}_{11}$ modes were characterized. This analysis revealed that the focus spot created from the DPC in an MCF behaves in two distinct ways depending on the LP mode used in the reconstruction.

3.1.

Focal Spot Contrast and Size

The calibration arm created a focus spot at $225\mu \mathrm{m}$ away from the MCF distal end. After phase conjugation, the measured signal in relation to the average of the background (e.g., signal-to-background ratio [SBR]) for a calibration focus transversely centered on the fiber was 130 for phase conjugation with the ${\mathrm{LP}}_{01}$ and 60 for the ${\mathrm{LP}}_{11}$ modes of the MCF cores. The full width at half maximum of the focus was $1.5\mu \mathrm{m}$ for the ${\mathrm{LP}}_{01}$ mode and $1.3\mu \mathrm{m}$ for the ${\mathrm{LP}}_{11}$ mode. Because the fundamental mode consists of light that effectively has a lower NA than higher-order modes, it is expected that the ${\mathrm{LP}}_{01}$ mode would create a larger focus spot than the ${\mathrm{LP}}_{11}$ mode.²⁹ We can use the measured spot sizes to calculate the effective NA (${\mathrm{NA}}_{\mathrm{eff}}$) to be 0.27 and 0.31 for the ${\mathrm{LP}}_{01}$ and ${\mathrm{LP}}_{11}$ modes, respectively. Figure 3(a) shows the focal plane with the phase-conjugated focus spot using the ${\mathrm{LP}}_{01}$ mode of the MCF cores at $225\mu \mathrm{m}$ from the MCF facet, in which the diffraction orders are not visible. After increasing the exposure time by 20 times [Fig. 3(b)], the background becomes visible, including the spatially spread diffraction orders surrounding the phase-conjugated focus at a lateral distance of $60\mu \mathrm{m}$. The focus is 28 times more intense than the brightest spot in the diffraction order.

Fig. 3

(a) The focus spot created by phase conjugating the ${\mathrm{LP}}_{01}$ mode of the MCF cores at $225\mu \mathrm{m}$ from the MCF facet. (b) The same focus spot with the exposure time increased $20\times$ to reveal the background, including the spread-out diffraction orders. The scale bars are $50\mu \mathrm{m}$.

3.2.

Modal Contribution to Focus Spot

The temporal profile of the total power of the coherence-gated phase-conjugated focus was analyzed at the distal end facet. An off-axis digital holography setup was built to enable this measurement. Figure 4 shows the temporal shape of the phase-conjugated pulse at the distal end of the fiber, measured in the same way as Fig. 2(a). When the ${\mathrm{LP}}_{01}$ mode was coherence gated [at ${\tau }_1$ in Fig. 2(a)] and phase conjugated, we measured that 88% of the optical power exiting the fiber arrived in the ${\mathrm{LP}}_{01}$ mode [Fig. 4(a)]. In fact, 70% of the core pulses arrive within 0.5 ps at the distal end [Fig. 4(a), inset]. The spread is a result of varying group delay in each core.³⁰ In contrast, 70% of the pulses arrive within 1.25 ps at the proximal end during the hologram recording phase [Fig. 2(a), inset]. When coherence gating the ${\mathrm{LP}}_{11}$ mode, some of the optical power after DPC coupled into the ${\mathrm{LP}}_{01}$ mode, but most, 62%, of the power propagated in the ${\mathrm{LP}}_{11}$ mode [Fig. 4(b)]. The loss of power could be attributed to slight misalignment or to phase-only wavefront modulation, which contributed to the lower focal spot SBR when using the ${\mathrm{LP}}_{11}$ mode. These results demonstrate the ability of DPC to control and couple the pulse directly into the ${\mathrm{LP}}_{01}$ mode. As mentioned above, slight variations in core properties cause a spread in group delay between cores.³⁰ Intercore group delay is not compensated by DPC, but coherence-gated DPC allows selective phase conjugation of pulses that have traveled with similar group delay. Thus, on the distal end, they arrive within a similar time frame. Of course, large differences in group delay between cores result in some cores not contributing to the phase conjugation. We estimate that only $\sim 50\%$ of the cores contribute to the formation of the pulsed wavefront at the focus spot resulting in a loss of peak intensity by a factor of 4.

Fig. 4

The temporal profile of the total power of the coherence-gated output from the distal end of the MCF after phase conjugation. (a) The pulse profile when phase conjugating the ${\mathrm{LP}}_{01}$ mode [at ${\tau }_1$ in Fig. 2(a)]. The inset shows a histogram of the distribution of the time point of peak intensity of the coherence function of the pulses from each core within the first 3.2 ps. (b) The profile when phase conjugating the ${\m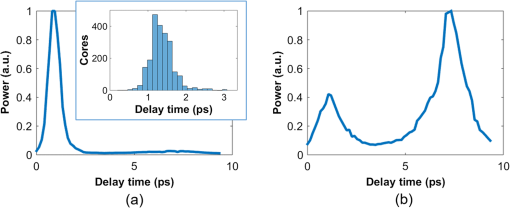athrm{LP}}_{11}$ mode [at ${\tau }_2$ in Fig. 2(b)].

4.

Digital Scanning and Field of View

TPF imaging through the MCF is enabled by scanning the focused femtosecond pulse across the object. This was implemented by recording and saving the phase conjugating hologram for each calibration focus spot in the sample plane. The distal end of the MCF was attached to a stage, which moved transversely in $1\mu \mathrm{m}$ increments. In this way, the focal spot position moved relative to the fiber facet. Once the holograms were saved in the computer memory, they were ready to be sequentially displayed on the SLM to scan a focus spot.

The field of view for imaging with this technique is limited by the angular spread of the phase-conjugated mode. As the focus spot transversely moves away from the center of the fiber, fewer cores can contribute to the focus spot and the aperture at the fiber facet shrinks and loses its circular shape, as shown already in DPC operation at large distances from the fiber facet.³² Furthermore, the hologram records the phase value from each individual core, which essentially discretizes the phase by sampling the quadratic phase field of the diverging calibration beam. When the quadratic phase is too strong, the core spacing undersamples the field, causing aliasing effects, and focusing into neighboring diffraction orders away from the desired focus.

The field of view was analyzed by simulating the spatial dependence of the focus intensity with the ${\mathrm{LP}}_{01}$ mode. To do this, the phase conjugating field at the distal facet of the MCF was modeled and propagated with a beam propagation simulation. The resulting focus intensities reveal the usable and optimal range for imaging. The core positions were modeled according to the experimentally measured positions of the MCF. We simulated the propagation of a monochromatic beam ($\lambda =785\mathrm{nm}$) from the MCF distal facet by a distance $z$ to reconstruct the focus spot. We selected the phase of the field at each core by sampling the phase of a spherical wave centered at the focus position. A phased-array pattern was then calculated using the radiation pattern of the ${\mathrm{LP}}_{01}$ mode centered at each core. Figure 5(a) shows an intensity map of the peak intensity of the focus radially ($\rho$) within a range of $\pm 100\mu \mathrm{m}$ and axially ($z$) from the fiber facet to $500\mu \mathrm{m}$. The simulation reveals a peak intensity hot spot located between 300 and $400\mu \mathrm{m}$ from the facet. This is the point where all the cores significantly contribute to the focus reconstruction corresponding to the ${\mathrm{NA}}_{\mathrm{eff}}$ of the phase conjugating mode. Also, creating a focus further from the facet minimizes the percentage of power in the diffraction orders. At $z=225\mu \mathrm{m}$, the simulation shows 15% of the total power in the focal spot, this value increases to 37% at $z=500\mu \mathrm{m}$. It is important to note that we expect lower percentages with a pulsed laser due to group delay variability between cores and mode coupling. Beyond the peak intensity hot spot, the focusing NA begins to decrease as the aperture diameter remains constant and $z$ increases, thus the increasing focus spot size decreases the intensity. Figure 5(b) shows the experimentally obtained intensity distribution of the DPC generated focus spot at $z=225\mu \mathrm{m}$. Figure 5(c) shows the profile of experimentally obtained focal spot intensities at $z=225\mu \mathrm{m}$ compared to the simulated intensity profile at that distance.

Fig. 5

(a) The relative intensity of a phase-conjugated focus spot at varying radial distance from fiber center ($\rho$) and distance from fiber facet ($z$). (b) The experimentally obtained intensity distribution of the DPC generated focus spot at $z=225\mu \mathrm{m}$. (c) The simulated intensity profile of the red dashed line shown in (a) compared with experimentally acquired intensity data, both correspond to 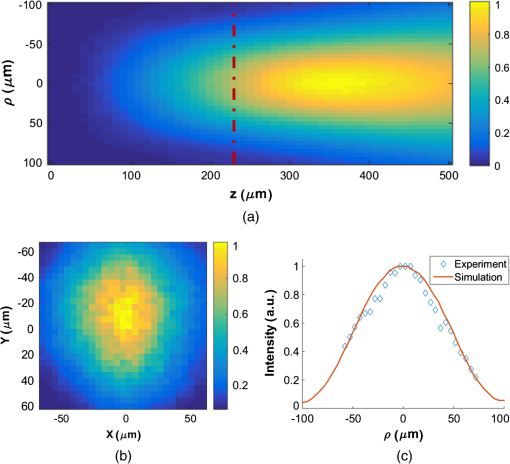$z=225\mu \mathrm{m}$.

5.

Two-Photon Fluorescence Imaging

In TPF microscopy, the signal detected from a voxel of a fluorescent object is proportional to $I^2$, where $I$ is the peak intensity of the excitation beam. In the experimental setup, the overall average optical power from the laser is reduced by a factor of almost 30 by the time it reaches the distal end of the fiber (2.8 W to 100 mW). This is mostly due to the diffraction efficiency of the SLM. In addition, only 1% of the transmitted power is concentrated on the $1.5\mu \mathrm{m}$ focused spot. This leads to an overall reduction by a factor of 3000 in the available peak intensity from the raw laser beam to the focused femtosecond pulse we obtain at the distal end of the fiber. Nevertheless, we obtain a peak intensity of $\sim 1.6\times {10}^9\mathrm{W}/{\mathrm{cm}}^2$ with a 390-fs pulse. We used these pulses to demonstrate TPF imaging and optical sectioning through the MCF by imaging a three-dimensional (3-D) sample of $1\mu \mathrm{m}$ polystyrene beads stained with Rhodamine 6G mounted in polydimethylsiloxane (PDMS). An $80\times 80\mu {\mathrm{m}}^2$ focal plane was calibrated with $1\mu \mathrm{m}$ steps between focus spots. An imaging plane at $z=225\mu \mathrm{m}$ was selected for optimal fluorescence collection. We measured the collection efficiency of the MCF for the fluorescence signal to be 20% collection and transmission of light within the fiber NA. With the ${\mathrm{LP}}_{01}$ phase conjugating holograms saved, the sample was placed in the focal plane and the saved holograms were sequentially projected to scan the focal spot. The holograms were projected by the SLM at a 7-Hz rate. The central focus spot had 1-mW average power. For detection, the excited TPF signal collected by the MCF is deflected by a dichroic mirror (700-nm longpass) to a photomultiplier tube detector (Hamamatsu, H11526-20-NN) [Fig. 1(b)]. For simplicity in this initial demonstration, the axial scan was performed in four planes by moving the fiber in $\mathrm{\Delta }z=10\mu \mathrm{m}$ steps. The obtained image (Fig. 6) shows slices of the high-resolution, high-contrast TPF image. The $Y\text{-}Z$ and $X\text{-}Z$ slices of the image demonstrate axial sectioning, with a depth of field determined by the ${\mathrm{NA}}_{\mathrm{eff}}$ of the ${\mathrm{LP}}_{01}$ mode, in this case, $\sim 16\mu \mathrm{m}$.¹ The $Y\text{-}Z$ and $X\text{-}Z$ slices in Fig. 6 were obtained by interpolation of the four data points using the software ImageJ.

Fig. 6

Two-photon fluorescent image of $1\mu \mathrm{m}$ polystyrene beads stained with Rhodamine 6G dispersed in PDMS. The image was acquired using DPC with the MCF to sequentially create $80\times 80$ focus spots spaced by $1\mu \mathrm{m}$. These were scanned at four axial planes separated by $10\mu \mathrm{m}$. The fluorescence detection was performed at the proximal side of the MCF. Power in focus: 1 mW at image center. Pixel dwell time: 140 ms. The scale bar is 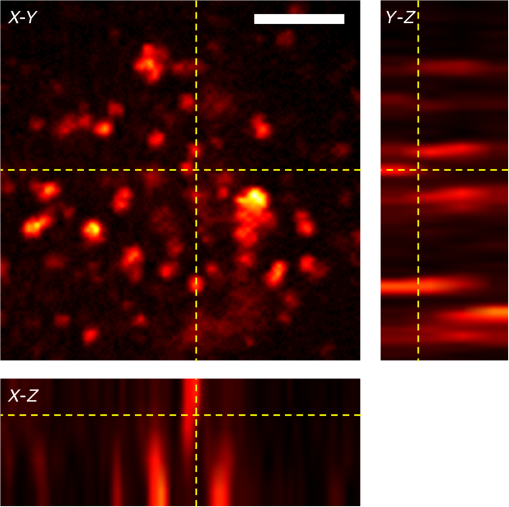$20\mu \mathrm{m}$.

To further demonstrate TPF imaging through the MCF, we imaged clustered cells. We prepared human colon carcinoma (HCT 116) cells by staining them with Rhodamine 6G and mounting them on a microscope slide under a cover slide. The cell clusters provided a good object to test the resolvability of individual cells with the resolution provided by the MCF. Figures 7(a) and 7(b) show a highly dense clustering of HCT 116 cells. In the TPF image, individual cells are clearly distinguishable. Figures 7(c) and 7(d) show a less-dense clustering of cells, in which the TPF image shows individual cells and good agreement with the white light, widefield image.

Fig. 7

(a) and (c) Two-photon fluorescent image of HCT 116 cells stained with Rhodamine 6G. The images were acquired using DPC with the MCF to sequentially create $80\times 80$ focus spots spaced by $1\mu \mathrm{m}$. The fluorescence detection was performed at the proximal side of the MCF. Power in focus: 1 mW at image center. Pixel dwell time: 140 ms. (b) and (d) The corresponding white light, widefield images of the cells. The scale bars are $20\mu \mathrm{m}$.

6.

Discussion and Conclusion

We have presented wavefront shaping for focusing ultrashort pulses through commercially available MCFs. In this paper, we utilized DPC for the wavefront calibration and focusing. DPC allows for a single-shot calibration for focusing to a single point at the distal end of the fiber. DPC focusing with the MCF yielded SBR of $\sim 130$, which was sufficient for TPF imaging through the MCF. It should be noted that the image was formed despite the suboptimal collection efficiency of the MCF, a result of the cores covering only $\sim 33\%$ of the fiber facet. To overcome this problem, Andresen et al.¹⁷ designed a double-clad fiber to increase the collection efficiency of their MCF endoscope. Of course, implementing a similar approach for increased light collection efficiency would require a custom designed fiber. Furthermore, in this implementation, we did not include any chromatic dispersion compensation because of the relatively short length of the fiber. Although, we could expect further improvement in the excited TPF signal by prechirping the pulse.

The commercially available MCFs allowed for an imaging field of view and resolution currently not possible with highly spaced core MCFs. The small core diameters propagate only a few modes, thus limiting modal dispersion. Additionally, we have shown that the commercially available MCFs provide benefits due to their quasiperiodic and high-density core arrangement. Specifically, these offer an increased field of view due to the suppression and spreading of the diffraction orders. To understand what limits the field of view, we simulated focusing at different axial and radial distances and found that the optimal focusing distance is determined by the distance at which the mode ${\mathrm{NA}}_{\mathrm{eff}}$ and MCF diameters allow for focal spot contribution from all cores. This is in contrast to MMFs and confocal use of MCFs, which operate optimally near the distal end facet. We also explored the unique characteristics of coherence-gated DPC with the fundamental ${\mathrm{LP}}_{01}$ mode and the higher order ${\mathrm{LP}}_{11}$ mode. We found that when phase conjugating the ${\mathrm{LP}}_{01}$ mode of the MCF that most of the energy stayed in the ${\mathrm{LP}}_{01}$ after propagating through the fiber. The MCF length that we used had a minimal spread in intercore group delay. Further lengthening the fiber would increase the delay between cores and reduce the number of cores participating in the phase conjugation. On the other hand, a shorter fiber would increase the number of cores contributing and would increase the focal spot power.

Future work on the multiphoton MCF endoscope should enable dual mode imaging and high speed scanning. Traditionally, MCFs have been used for widefield endoscopic imaging. Combining a widefield imaging modality with TPF imaging would provide a powerful tool for endoscopic use. Also, in a previous paper,²⁷ we showed that the ${\mathrm{LP}}_{01}$ mode exhibits a large scan range when a linear phase gradient is applied to the DPC hologram. This “memory effect” ability could be utilized to increase the imaging speed with high speed galvo-mirror scanning within a single calibration point, or with high speed digital mirror SLMs.³³ It should be noted that the DPC process through the MCF is sensitive to bending, although significantly less than MMFs.²⁷ This sensitivity would confine the use of the endoscope to a rigid housing, while research progresses on a solution to the bending problem. With the current prospects, the MCF endoscope shows potential use in high-resolution, TPF imaging inside difficult to reach spaces, such as in cochlear, retinal, or brain imaging.

In conclusion, we have demonstrated lensless focusing of ultrashort pulses through a commercially available MCF for TPF imaging. We characterized the focusing of ultrashort pulses through an MCF using coherence-gated DPC. Importantly, we showed that DPC can put most phase-conjugated power back into the coherence-gated mode. Thus, implying that coherence-gated DPC can overcome the limits of modal dispersion. Finally, we demonstrated optical sectioning with TPF imaging on a 3-D matrix of dispersed fluorescent beads and we also showed cellular imaging through the MCF. These results indicate the potential of high-density MCFs for integration into high-resolution TPF endoscope imaging.