|
|
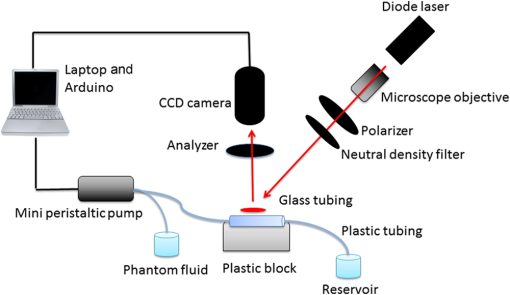
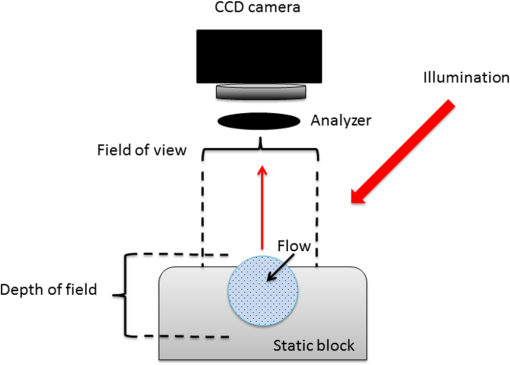
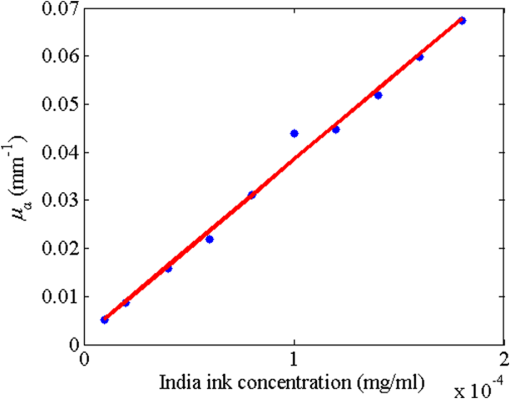
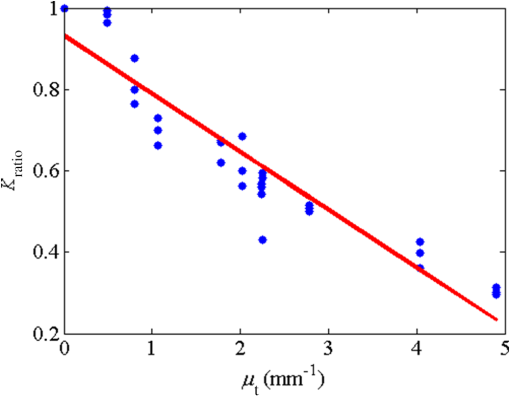
1.IntroductionLaser speckle contrast imaging (LSCI) is a low cost and noninvasive method used to monitor blood perfusion and blood flow.1–3 This method has a wide field of view, and it is efficient and simple for full-field monitoring. The simplicity of LSCI along with its high spatial and temporal resolution allows it to be used as a powerful tool to measure, monitor, and investigate living processes in near real-time. The concept behind this method lies in the mathematical relationship between moving particles (i.e., red blood cells) in the object space (i.e., the blood vessel) and the translating or “boiling” speckles in the image plane. When there is motion in the object space, the intensity of speckles in the image space fluctuates over time. It is these time-varying speckles in the image space that encode the motion in the object space. In time varying, or dynamic, speckle patterns, the speckle is blurred during the finite camera integration time, and the spatial variation, or contrast, in intensity is thereby decreased. Contrast in LSCI is typically defined as where is the mean intensity of a small window ( in this work)4 of pixels centered at location , and is the standard deviation of the intensity over the same window.1 In practice, this window is slid on a pixel-by-pixel basis over the entire speckle image yielding a final spatial contrast image. In LSCI, the contrast of the speckle images is lower in regions displaying motion relative to static regions. For a polarized speckle pattern, , yielding an expected value of .1–3 It should be noted that this expectation, however, has its own statistical distribution.4 When there is motion in the scattering particles, the shifting back-scattered waves coming from the moving particles will cause a temporal variation in the speckle intensity. This fluctuation results in a blur of the speckle pattern, and thereby, a reduction in .In a previous publication,5 using arguments from mass transport theory, it was demonstrated that the contrast values calculated in LSCI are sensitive to the sum of diffusive flux and advective flux in the circulation. In that paper,5 we argued that the diffusion with drift equation6 adequately describes the physical phenomena to which LSCI is ultimately sensitive. The steady-state diffusion with drift equation can be written without any loss of generality in one-dimension as where is the total flux, the first term on the right side (RHS) of Eq. (2); , describes the diffusional flux; , a component of and the second term on the right side of Eq. (2), , describes the advective flux, , and is the product of the velocity, , of the fluid and the concentration, [], of the scatterers suspended in it. The term, , describes ordered motion of the particles and the dynamic behavior of the individual particles is unique to the individual scatterers, whereas the term describes random motion of the particles and the behavior of an individual scatterer is representative of the scatterer population as a whole.7 These two behaviors independently describe the two extreme, limiting behaviors of particle motion in a fluid, and their associated correlation functions have been used to relate the observed speckle contrast to the motion of the scattering particles.1–3Khaksari and Kirkpatrick5 demonstrated a clear negative, linear relationship between both the and [] components of advective flux and that LSCI was approximately equally sensitive to both terms. Changes in particle concentration, [], manifest as changes in the scattering coefficient, , of the fluid. A key conclusion from this study is that changes in red blood cell concentration, i.e., changes in hematocrit, which result in a change in the scattering coefficient of the blood, may appear as changes in velocity in LSCI and vice versa. However, a change in hematocrit also results in a change in the absorption coefficient, , due to changes in the amount of hemoglobin present in the observation volume. The confounding effect of changes in absorption was not considered in Khaksari and Kirkpatrick.5 Changes in observed speckle contrast in LSCI due to changes in hematocrit8 or directly due to changes in and in phantom materials have been described by others in the literature;9 however, a systematic study of the combined effects of absorption and scattering on the observed contrast values in LSCI has yet to be reported. Hematocrit, i.e., the percentage of red blood cells in whole blood, typically ranges between 38.8% and 50% for men and 39.4% and 44.5% for women in the systemic circulation.10 However, even beyond these wide normal ranges, the hematocrit level of blood varies both naturally and under various pathological conditions. There are regional differences in hematocrit levels. For example, there is ∼ a threefold variation in hematocrit between the capillary circulation and the systemic circulation.11 Age and certain diseases such as anemia, leukemia, diarrhea, and colon cancer can also change hematocrit level. A different level of hematocrit reflects a difference in the number of red blood cells, which function as both absorbers and scatters in LSCI. Our motivation to examine the effects of optical properties on contrast imaging arises from the fact that different levels of hematocrit may influence contrast via a change in optical properties. The practical question, then, reduces to: How do differences in optical properties, due to changes in hematocrit, effect the calculated contrast in LSCI? Furthermore, if LSCI is to be used to evaluate blood flow over a time course, or between individuals, does relative hematocrit that manifests as different and need to be considered in the interpretation of the results? In the present work, we investigate how the optical properties of the scattering and absorption media influence speckle contrast imaging results. In order to examine this issue, LSCI was performed on a series of flowing solutions with different reduced scattering and absorption coefficients. The hypothesis is that changing the volume fraction of scatterers and absorbers changes the reduced scattering coefficient and absorption coefficient resulting in a change in contrast. The goal of this study is to quantitatively examine the effects of optical properties on LSCI. 2.Materials and Methods2.1.Laser Speckle Contrast Imaging SystemAn LSCI system was designed and constructed specifically to examine the effects of the optical properties of the moving fluid on contrast values (Fig. 1). The system was essentially identical to the one used in Khaksari and Kirkpatrick.5 A polarized 660-nm diode laser (B&W Tek, Newark, Delaware) was used to illuminate a section of glass tubing with an outer diameter of 2 mm and an inner diameter of 1.5 mm resting on top of a grooved plastic base. The illuminated region was in length. The glass tube, which served as our imaging window, rested in the groove. The glass tube was attached to a segment of rubber tubing that ran from the fluid phantom reservoir and through a miniperistaltic pump (Instech Laboratories, Plymouth Meeting, Pennsylvania, model P625) that controlled the flow velocity. The miniperistaltic pump was controlled by an Arduino microcontroller. A MATLAB® GUI controlled the imaging CCD camera (Point Grey, Dragonfly, Vancouver, British Columbia, Canada) and the pump and also calculated and saved contrast images in near real-time. 2.2.Liquid PhantomsWe used an added-absorber method to generate our flow phantoms. We initially created purely scattering phantoms in the same fashion as was done in Khaksari and Kirkpatrick5 by mixing calcium aluminum borosilicate glass microspheres (LUXSIL Cosmetic Microspheres, Potters Industries, Inc., Malvern, Pennsylvania) with de-ionized (DI) water. The microspheres were polydisperse in terms of diameter, ranging between 9 and , which is close to the diameter of red blood cells. The microspheres had mass density of , which, being close to that of water, minimized settling. Using a Mie calculator,12 the appropriate microsphere concentration was calculated using Mie theory to approximate the scattering coefficient of whole blood at various hematocrit levels.11 For these calculations, we assumed that the microspheres were pure scatterers and that . These assumptions were made to more readily separate the combined effects of absorption and scattering. Furthermore, the absorption coefficient of the glass microspheres is negligible compared to the scattering coefficient at the wavelength of light employed, so the assumption is valid. Once the necessary concentrations of microspheres needed to create samples that approximate the scattering properties of whole blood were calculated, the flow phantoms were made by adding the calculated amount of microspheres to DI water. Ten solution phantoms of different scatterer concentrations were made using the results from the Mie calculations. Scattering coefficients of the fluid phantoms were confirmed via ballistic transmission measurements. A modified version of the Lambert–Beer law was used to calculate the scattering coefficient. Equations (3) and (4) summarize the approach where is the scattering coefficient, is the absorption coefficient, and z is the linear path length through the sample. The samples were contained in cuvettes with 1 cm internal width (). is the intensity of the ballistically transmitted beam when pure DI water was used as the sample in place of a scattering phantom. Since of the DI water and the scattering samples were measured in the same cuvette and the ratio between the intensities, was calculated, the intensity loss due to the cuvette wall was eliminated from the calculations.To calculate the reduced scattering coefficient, , we assumed scattering anisotropy of from the Mie calculations and Because the microsphere powder was polydisperse in terms of diameter, ranging between 9 and , with a mean size of , according to the manufacturer, but with an unknown size probability distribution, Mie calculations were performed assuming monodispersions of 9.0, 11.7, and . The scattering coefficients calculated via Mie theory were compared to the values generated via the ballistic transmission experiments in order to better characterize the scattering behavior of the fluid phantoms. The effect of varying on LSCI was also of interest in this study. Thus, a series of absorbing liquid phantoms was constructed. An “added-absorber” approach was followed in making these phantoms. Empirically determined volumes of India ink were added to the purely scattering phantoms and pure DI water. Using ballistic transmission again, and with a priori knowledge of the scattering coefficient of the sample, the absorption coefficient was estimated as Equation (6) calculates the total attenuation coefficient (). By rearrangement, then, Ultimately, an matrix of phantom solutions with each element of the matrix having a unique combination of , , and therefore was developed. The initial sample in this matrix was pure DI water (), and the last sample has the largest concentration of microspheres and India ink ().2.3.Laser Speckle Contrast Imaging MeasurementsEach fluid phantom was imaged with the LSCI system described above at a uniform velocity. Figure 2 shows the cross-section of the sample preparation we used in the LSCI setup. As can be seen in the figure, the moving and static parts are in the same depth of field (flow is coming out of the page, toward the reader). The camera lens (100 mm macrozoom) was fixed at , which resulted in relatively large speckles (see below) and an extended depth of field. During the experiments, all experimental parameters were held constant with the exception of the optical properties of the moving fluid, which varied by sample. The flow velocity was held constant at . The camera integration time was 6 ms and held constant for all the experiments. Images were acquired at a frame rate of . Thus, the only varying parameters were the optical properties of the fluid phantom used. An important parameter in an LSCI experiment is the relative size of the speckles versus camera pixel size.13 The minimum speckle size (in pixels), , was determined by calculating the power spectral density of the raw speckle images [Figs. 3(a) and 3(b)] and applying Eq. (8) Fig. 3(a) A laser speckle pattern, (b) power spectral density of the speckle pattern shown in (a). The diameter of the bright central region is inversely proportional to the minimum speckle size in the speckle pattern. 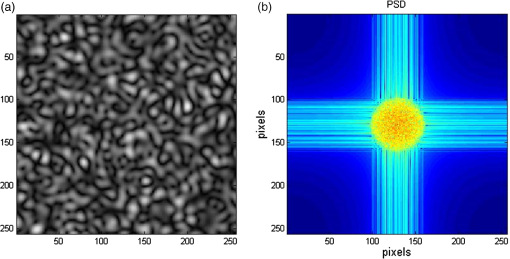 In LSCI, unlike other speckle techniques, such as diffusing wave spectroscopy, the minimum speckle size should not match the camera pixel size but must be greater than two times of camera pixel pitch to meet the spatial Nyquist criteria.13 In these experiments, the minimum speckle size was set to 2.72 times the pixel size (). The minimum speckle size in the image plane was, therefore . It was also ensured that the speckle size relative to the size of the sliding window used in the contrast calculations () was appropriate to account for the local statistics of the calculated contrast.4 For image collection, the laser was set slightly off-axis to avoid specular reflection. A video of 100 frames was recorded with the CCD camera for each sample. The experiment was repeated three times for each sample. In the end, 300 frames of raw speckle and 300 contrast images were recorded for each sample. The 300 frames were then averaged to create an “average” contrast image. The ratio between the dynamic (fluid) region and the static region () of the contrast images was calculated for all of the images. Similar to above, an matrix was created of values. This matrix demonstrated the change in contrast that resulted from the change in the optical properties of the fluid phantoms. The numerical values of lay between 0 and 1.0, since the contrast is always lower in the fluid (dynamic) region of the contrast image Variations in ambient light,14 the normal statistics of local speckle contrast,4 and experimental variation lead to small changes in between experiments.3.Results3.1.Phantom CharacterizationThe scattering coefficients for 10 different sample concentrations of microspheres (plus pure DI water) was measured and by assuming , the reduced scattering coefficient of the samples was estimated. By increasing the number of scatterers, the reduced scattering coefficient increased in a linear fashion. Figure 4 shows the phantom’s reduced scattering coefficients and the relationship between the concentration of scatterers and the reduced scattering coefficient. Because the microspheres were polydisperse with an unknown size distribution, Fig. 4 also displays the results of Mie scattering simulations for the minimum, maximum, and mean sizes of the spheres as reported by the manufacturer. It is seen that the polydisperse mixtures displayed overall scattering behavior similar to that of a monodisperse system of spheres. Microsphere concentration [] ranged from () to (), and the reduced scattering coefficient of the samples ranged from 0.48 to . A linear regression through the experimental data yielded the following relationship: By adding measured amounts of India ink to the sample with the highest concentration of microspheres (), we determined the absorption coefficient at 10 different India ink concentrations via ballistic transmission measurements of and using Eq. (7). Absorption coefficient values of the phantoms used in our study ranged from . Figure 5 shows the linear relationship between India ink concentration and the measured absorption coefficient ; ).Fig. 4Mie calculations predicting the reduced scattering coefficient for glass spherical particles of 9.0, 10.5, 11.7, and diameters (dashed lines, red dashed lines online). Reduced scattering coefficient as determined by ballistic transmission data points is shown for the fluid phantoms (dots) along with the best-fit line in a least-squares sense. The polydisperse microsphere phantoms behaved approximately as a monodisperse system made of glass microspheres. (; .) 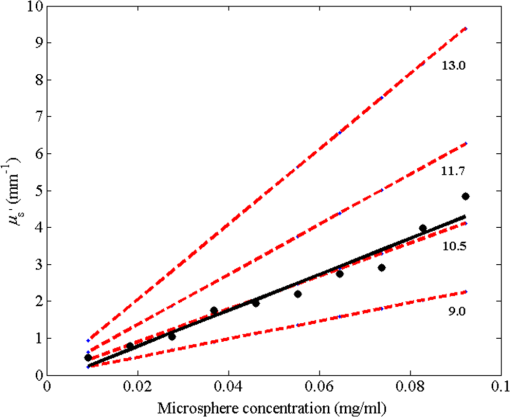 3.2.Contrast ImagingThe main goal of this investigation was to examine the combined effects of scattering and absorption on the contrast in LSCI images. As discussed above, the experiments were run for the 121 phantoms with unique combinations of reduced scattering and absorption coefficients. Accordingly, within the matrix, the absorption coefficient changed when moving along the rows and the reduced scattering coefficient changed moving along the columns. Values of were obtained from this matrix, and the contrast ratios for the different combinations of optical properties were plotted. Figure 6 shows an example LSCI images from the matrix. The tubing that contained fluid phantom flowed runs from the lower left to the upper right and the resulting low-contrast area is readily observed in the images. The triangular regions to the right and left of the tube are the “static” plastic block. The relationship between and was found to be linear. An increase the concentration of scatterers [], which manifested as an increase in resulted in a decrease in .5 The results are plotted in Fig. 7, where is plotted as a function of for 11 different values of . All the linear fits were statistically significant (-test, ); the slopes, , of the best fit lines ranged between ; and there was no significant difference between the slopes (-test, ). The mean slope was . Figure 8 plots the -intercepts () of the regression lines shown in Fig. 7 as a function of absorption coefficient, . This plot reveals a linear reduction in with an increase in in our experiments (; ). As will be discussed below, this reduction in contrast is due to the attenuation of the light reaching the static scattering block below the moving fluid and, thus, reducing the influence of these static scatterers on the overall contrast. Others8,9 have observed an increase in contrast with an increase in absorption; however, in their experiments, there was no underlying layer of static scatterers and their scattering mediums were optically semi-infinite or close to it. Fig. 6A representative LSCI image. The fluid motion was in the low contrast region flowing from lower left to upper right of the image. The surrounding higher contrast triangular areas are the static plastic block.  Fig. 7Plot of versus at 10 different values of . All slopes were statistically significant (-test, ) and there was no statistically significant difference between the slopes (-test, ). The mean slope was . Absorption coefficient is lowest for the top line and highest for the bottom line. 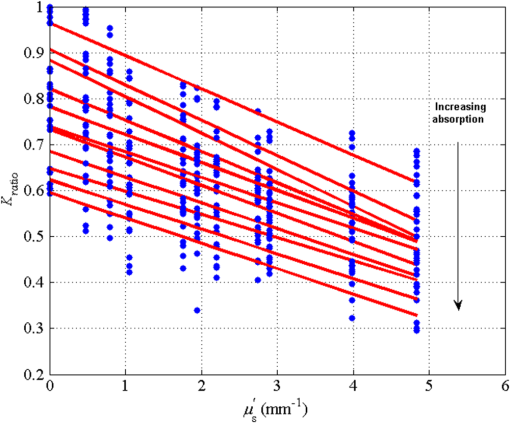 Fig. 8Plot of the -intercepts () of Fig. 7 as a function of respective absorption coefficients. An increase in absorption resulted in a linear decrease in in these experiments due to reducing the influence of the underlying static scatterers. (; ). 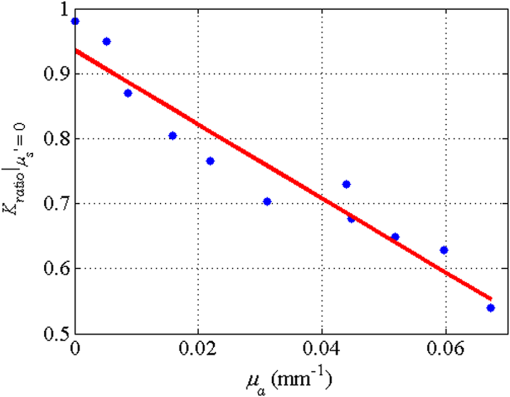 Thus, with an increase in absorption coefficient, decreased. This trend is shown for the fluid phantoms with 11 different reduced scattering coefficients in Fig. 9. All the linear fits were statistically significant (-test, ); the slopes, , of the best fit lines ranged between ; and there was no significant difference between the slopes (-test, ). The mean slope was . Figure 10 plots the -intercepts of these regression lines as a function of the corresponding reduced scattering coefficients. This plot reveals a linear reduction in with an increase in in our experiments [; ]. By combining the scattering and absorption data, the influence of total attenuation coefficient, , on was assessed. As expected from the results presented above, there was a linear decrease in with an increase in . Figure 11 shows the results of the versus for the samples that were along the major axis of the scattering—absorption phantom matrix. The equation describing the least-square fit was ; . The slope is statistically significant (-test, ). Fig. 9Plot of versus at 10 different values of . All slopes were statistically significant (-test, ), and there was no statistically significant difference between the slopes (-test, ). The mean slope . Scattering coefficient is lowest for the top line and highest for the bottom line.  Fig. 10Plot of the -intercepts () of Fig. 7 as a function of respective reduced scattering coefficients. An increase in scattering resulted in a linear decrease in . (; ). 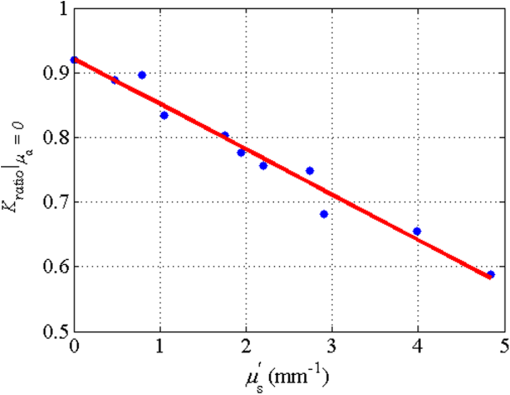 4.ConclusionsWe have demonstrated a linear decrease in speckle contrast, , with an increase in reduced scattering coefficient. This decrease in contrast with an increase in was independent of absorption as quantified by the absorption coefficient, . It is important to note that the parameter of real interest is not the scattering coefficient, per se, but the concentration of scatterers, [], in the imaging volume. A change in [] manifests as a linear change in .5 Likewise, in this study, contrast decreased linearly as absorption increased. Others8,9 have reported an increase in contrast as absorption increases. At initial glance, it may appear that these results are contradictory. However, this is not the case; indeed, the results presented here are entirely consistent with what has been reported in the literature previously. The effect of increasing absorption is to decrease the number of (deep) scattering events. In previous publications, the fluid phantoms were relatively deep and the entire imaging volume was populated by dynamic scatterers. Thus, by adding absorbers, the number of dynamic scattering events was reduced, resulting in an increase in contrast. In the present situation, the addition of absorbers accomplished the same thing: a decrease in the number of deep scattering events. However, in our case, the deep scatterers were static, coming from the fixed plastic block underneath the glass tube that served as our imaging window. Thus, the absorbers decreased the number of static scattering events, and thereby the influence of these static scattering events was reduced, resulting in decreased contrast values. Recently, Kazmi et al.,8 focusing entirely on scattering, concluded that LSCI is sensitive to the product of speed and a dimensional term that is proportional to vessel diameter. In the Introduction to this paper, and in our prior work,5 it was argued that LSCI is sensitive to advective flux. These two conclusions are, again, entirely consistent with each other. Recall from above that advective flux, is the second term on the right side of the diffusion with drift equation. Rewriting Eq. (2),5 andThus, Khaksari and Kirkpatrick5 concluded that LSCI is sensitive to the product of velocity (assuming direction is known) and scatterer concentration. Note that advective flux as defined by Eq. (12) is related to the total mass flux across a plane perpendicular to the direction of flow via where is the internal cross-sectional area of the tube or vessel containing the flow, is the total flux, and the dot over the variable explicitly indicates the time derivative. It assumed that diffusional flux = 0 and . To be consistent with the conclusions of Kazmi et al.,8 Eq. (13) can be rewritten in terms of diameter where is the diameter of the vessel. By substitution, thenThus total mass flux is given by Eq. (15), assuming that diffusional flux = 0. In the case where diffusional flux does not equal 0.0 (likely in most practical LSCI applications), then the total mass flux is given as Equations (15) and (16), then, show the consistency between the present results, the results of Khaksari and Kirkpatrick,5 and the results of Kazmi et al.8 That is, in terms of mass flux, LSCI is sensitive to the product of velocity (or speed if direction is not known explicitly), particle concentration, and a factor that is proportional to diameter squared.The present paper is certainly not the first paper to demonstrate that speckle contrast changes as a function of the amount of scattering or absorption present;5,8,9 however, this is the first systematic study that systematically evaluated the combined effects of scattering and absorption on contrast values. Furthermore, the present paper demonstrates that by viewing LSCI in terms of mass transport, consistency between earlier studies and the present one can be achieved. Specifically, we demonstrate that both scattering and absorption have linear effects on contrast values. Contrast values decrease linearly with an increase in scattering, regardless of absorption. An increase in absorption serves to reduce the number of deep scattering events observed. Thus, depending if the “deep” scatterers are dynamic or static, contrast values can either increase or decrease with increased absorption. ReferencesA. F. Fercher and J. D. Briers,
“Flow visualization by means of single-exposure speckle photography,”
Opt. Commun., 37
(5), 326
–330
(1981). http://dx.doi.org/10.1016/0030-4018(81)90428-4 OPCOB8 0030-4018 Google Scholar
D. A. Boas and A. K. Dunn,
“Laser speckle contrast imaging in biomedicine,”
J. Biomed. Opt., 15
(1), 011109
(2010). http://dx.doi.org/10.1117/1.3285504 JBOPFO 1083-3668 Google Scholar
D. Briers et al.,
“Laser speckle contrast imaging: theoretical and practical limitations,”
J. Biomed. Opt., 18
(6), 066018
(2013). http://dx.doi.org/10.1117/1.JBO.18.6.066018 JBOPFO 1083-3668 Google Scholar
D. D. Duncan, S. J. Kirkpatrick and R. K. Wang,
“Statistics of local speckle contrast,”
J. Opt. Soc. Am. A, 25
(1), 9
–15
(2008). http://dx.doi.org/10.1364/JOSAA.25.000009 JOAOD6 0740-3232 Google Scholar
K. Khaksari and S. J. Kirkpatrick,
“Laser speckle contrast imaging is sensitive to advective flux,”
J. Biomed. Opt., 21
(7), 076001
(2016). http://dx.doi.org/10.1117/1.JBO.21.7.076001 JBOPFO 1083-3668 Google Scholar
H. C. Berg, Random Walks in Biology, Princeton University Press, Princeton, New Jersey
(1983). Google Scholar
D. D. Duncan and S. J. Kirkpatrick,
“Can laser speckle flowmetry be made a quantitative tool?,”
J. Opt. Soc. Am., 25
(8), 2088
–2094
(2008). http://dx.doi.org/10.1364/JOSAA.25.002088 Google Scholar
S. M. Kazmi et al.,
“Flux or speed? Examining speckle contrast imaging of vascular flows,”
Biomed. Opt. Express, 6
(7), 2588
–2608
(2015). http://dx.doi.org/10.1364/BOE.6.002588 Google Scholar
A Mazhar et al.,
“Laser speckle imaging in the frequency domain,”
Biomed. Opt. Express, 2
(6), 1553
–1563
(2011). http://dx.doi.org/10.1364/BOE.2.001553 Google Scholar
J. F. Murray,
“Systemic circulation,”
Ann. Rev. Physiol., 26 389
–420
(1964). http://dx.doi.org/10.1146/annurev.ph.26.030164.002133 Google Scholar
D. J. Pine et al.,
“Diffusing-wave spectroscopy: dynamic light scattering in the multiple scattering limit,”
J. Phys., 51
(27), 2101
–2127
(1990). http://dx.doi.org/10.1051/jphys:0199000510180210100 Google Scholar
S. J. Kirkpatrick, D. D. Duncan and E. M. Wells-Gray,
“Detrimental effects of speckle-pixel size matching in laser speckle contrast imaging,”
Opt. Lett., 33
(24), 2886
–2888
(2008). http://dx.doi.org/10.1364/OL.33.002886 OPLEDP 0146-9592 Google Scholar
M. A. Kirby, K. Khaksari and S. J. Kirkpatrick,
“Assessment of incident intensity on laser speckle contrast imaging using a nematic liquid crystal spatial light modulator,”
J. Biomed. Opt., 21
(3), 036001
(2016). http://dx.doi.org/10.1117/1.JBO.21.3.036001 Google Scholar
|