|
|
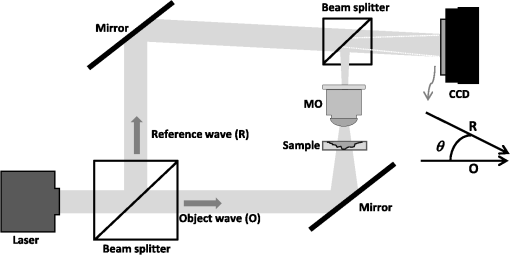
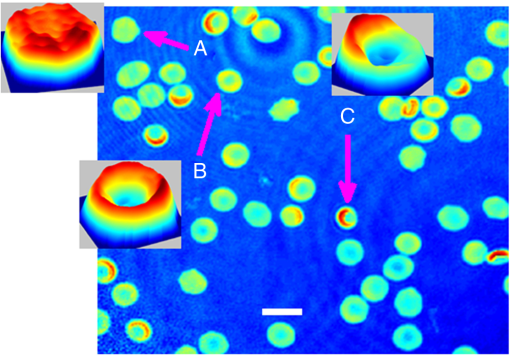
1.IntroductionHuman blood contains different type of cells; however, red blood cells (RBC) or erythrocyte are the most abundant cell type. RBC contains hemoglobin, which binds to either oxygen or carbon dioxide. This allows oxygen to be transported to tissues and organs and carbon dioxide to be taken away during microcirculation. The biconcave shape of the erythrocyte is extremely important in the functionality of RBCs. It allows the membrane to have a high surface area to volume (SAV) ratio facilitating large reversible elastic deformation of the RBC while squeezing through the tiny capillaries.1–3 According to its importance, it has drawn considerable attentions into the pathology research in the clinical relevant blood diseases. Pathological disorders can modify RBCs and lead to significant alterations in its original shape.4 The consequences of modified RBC often are observed as clinical symptoms ranges from obstruction of capillaries and restriction of blood flow to tissues to necrosis and organ critical damages.4–9 Also, counting cell types in the blood sample is another important task for investigating clinical status, which can be evaluated by well-known methods such as complete blood count or RBC distribution width, which are part of cytometry field. Because an automated cell counter samples and counts so many cells, the results are reliable in most of the cases.10 However, certain abnormal cells in the blood may not be identified correctly, requiring manual review and identification of any abnormal RBCs the instrument could not categorize. This information can be very helpful regarding identifying the cause of a patient’s anemia. Abnormal increase or decrease in RBC counts as revealed in a complete RBC count may indicate that you have an underlying medical condition that calls for further evaluation. In the case of RBC, biconcaves are a substantial type in a healthy person, but there are other RBCs types with the different percentage varying between healthy and unhealthy persons. It has been shown that the percentages of different types of RBCs will be distinct according to the RBC diseases type.10 Accordingly, it is essential to measure the percentage of each RBC type in a blood sample consists of multiple RBCs for diagnosis and drug testing subjects. Typically, the diagnosing is performed by a human expert, and it shows some drawbacks, such as time-cost consuming and inaccuracy. Generally, experts visualize the sample in the images through a microscope based on their subjective knowledge from the viewpoint of intensity, morphology, texture, and so on based features. Usually, small-scale differences in the features are overlooked by human eyes especially for the border-line diagnostic scenario. However, the situation has changed completely by the emergence of automatic classification algorithms. These techniques have been applied to problems in biology and have shown promising results for automatic recognition and classification of various micro-organisms.11,12 Among the classification methods, the pattern recognition neural network (PRNN) has been suggested in nonlinear classification problems, such as RBC classification and counting.13–15 The fundamental benefit of artificial neural network (ANN) is nothing, but it does not use any mathematical model since ANN learns from data sets and identifies patterns in a sequence of input and output data without any previous assumptions about their type and interrelations. Also, ANN eliminates the drawbacks of the conventional methods by extracting the wanted information using the input data. In conventional RBC classification problems, the experts deal with two-dimensional (2-D) erythrocyte images obtained by conventional microscopes and cameras.13,16–19 These methods generally have good performance but most of them have a significant number of features since they need to discriminate groups by utilizing 2-D features. However, in the case of RBC, which is transparent or semitransparent, we cannot take advantage of conventional intensity-based microscopes. Therefore, we believe that to obtain a satisfied level of accuracy, the classification and recognition should also take into account the three-dimensional (3-D) shape of RBCs. Among the techniques that can provide 3-D images of transparent or semitransparent cells, digital holographic microscopy (DHM) has shown promising results.20–24 Also, the DHM technique has been utilized in the classification of RBC using 2-D and 3-D features since DHM can provide quantitative phase image.25–27 In studying RBC, DHM enables the measurement of 3-D features, such as mean corpuscular volume, surface area, SAV ratio, functionality factor, sphericity index, and sphericity coefficients.28,29 Chemical parameters of MCH and MCHSD can also be obtained due to DHM. Accordingly, we believe that any automated RBC classification that can distinguish different RBC types accurately should take into accounts the benefits of DHM imaging technique. In this study, four main types of RBC shapes, biconcave (doughnut shape), flat discs, stomatocyte, and echinospherocyte are interested RBCs for the quantitative determination of the percentage of RBC types in multiple human RBCs. The reason for differentiating doughnut-shaped and flat-disc RBCs is that it can help in the applications of separating old cells versus young cells. It has been shown that during the stages of biconcave-echinocyte transformation in so-called storage lesion, biconcave cells become flat discs (loss of ATP results in a stiffer cytoskeleton that pulls the bilayer) after a few weeks of storage in blood bank.29–34 Transfusion of these old samples might have critical consequences according to the previous studies.35,36 At first, RBCs are visualized by off-axis DHM and the quantitative phase images are reconstructed by the numerical algorithm.37,38 Then, single RBCs are extracted from images with multiple RBCs using the watershed algorithm.39 At the next step, following 2-D features of projected surface area (PSA), perimeter, radius, elongation, and PSA to perimeter rate are extracted. In this paper, we have ignored extracting 2-D features related to the inner section of RBC, unlike the previous method proposed by Refs. 25, 26, since flat-disc and echinospherocyte RBCs do not have the inner section. Also, volume, surface area, SAV ratio, average RBC thickness, sphericity index, sphericity coefficient and functionality factors, and MCH and MCH surface density (chemical properties of RBC) are extracted from single RBCs. The latter feature-set is related to the morphological and biochemical properties of RBC 3-D profile. Along with the 3-D features, two new features related to the ring section of RBC are introduced. These features add significant information to the classification model and increase the discrimination power of the classifier. Then, each feature set is fed into PRNN, separately, and the classification results are compared using 10-fold cross validation (CV) technique. Since we are involved in a classification model with nonlinear decision boundary, we have decided to use PRNN strategy. In PRNN, the training algorithm is Bayesian regulation back-propagation, which updates the weights according to Levenberg–Marquardt optimization technique and the activation function for midlevel layers is hyperbolic tangent sigmoid. Finally, to propose the best feature set, concerning both 2-D and 3-D features, sequential forward feature selection (SFFS) is utilized here. It has been shown that the best performance of a classification model can be achieved by selecting the most informative features and remove noisy ones that are either redundant or irrelevant.40 Indeed, reducing the number of features can shorten training time, reduce the complexity of classifier, and simplify the model for interpretation goals. SFFS technique tries to select a subset of variables that best predict the data by sequentially selecting features until there is no improvement in the prediction. In this paper, we have extracted 108 biconcave RBCs from a healthy sample stored for 1 day in the blood bank, 106 samples of stomatocyte shape from a sample with predominantly of stomato cells, 38 samples of flat-disc shape, and 71 samples of echinospherocyte shape for training and testing PRNN. Flat-disc and echinospherocyte cells are extracted from RBC samples stored in the blood bank for 40 days and 57 days, respectively. Performance comparison is evaluated by calculating misclassification rate of 10-fold CV technique. It is often claimed that leave-one-out-cross-validation (LOOCV) has higher variance than -fold CV, and that it is because the training sets in LOOCV have more overlap. This makes the estimates from different folds more dependent than in the -fold CV and, hence, increases the overall variance.41 Our experimental results demonstrate that the PRNN trained by 3-D features gives a good performance in classifying and counting RBCs in multiple human RBCs in an automated manner in comparisons with the 2-D features. In addition, we introduce the best set of features that combines 2-D and 3-D features to improve the RBCs classification accuracy. We believe that the final feature set evaluated with the presented neural network classification strategy can provide better discrimination results. This paper is organized as follows. Section 2 explains the general scheme of the off-axis DHM to image RBCs and RBCs preparation. Section 3 explains 2-D and 3-D features extracted in this research and gives a short review about them. In Sec. 4, we will focus on designing the PRNN and counting different RBCs in multiple RBCs, automatically. The experimental results and discussions are provided in Sec. 5. Finally, the conclusion is presented in Sec. 6. 2.Off-Axis Digital Holographic Microscopy and RBC Preparation2.1.Off-Axis Digital Holographic MicroscopyFigure 1 shows the off-axis DHM based on the Mach–Zehnder interferometer geometry.42 In this optical setup, light from a coherent source (HeNe laser diode source ) is split into reference and object beams by a beam splitter. The object beam is transmitted through the RBC sample and magnified by a NA microscope objective and interferes with the reference beam. The interference patterns between the diffracted object beam and the reference beam are recorded onto a CCD camera. The reconstruction of the RBC wavefront is obtained from the recorded hologram by using the numerical algorithm described in Refs. 37 and 38. After reconstructing RBC phase images, single RBCs are extracted by the maker-controlled watershed segmentation algorithm.39 Figure 2 shows a reconstructed phase image of a sample consisting of biconcave, flat-disc, and stomatocyte shape RBCs. This image shows that in a single sample it is possible to see RBC with different morphologies. 2.2.RBC PreparationThe RBCs of healthy laboratory personnel were obtained through the Laboratoire Suisse d’ Analyse Du Dopage, CHUV and stored at 4°C during the storage period. The DHM measurements were performed several days after the blood was collected from the laboratory personnel. A total of 100 to of RBC stock solution was suspended in a high-efficiency particulate air (HEPA) buffer at 0.2% hematocrit for predominantly stomatocyte and discocyte-shaped RBCs while at a concentration of for predominantly echinocyte-shaped RBCs. A total of of the erythrocyte suspension was diluted to of the HEPA buffer and introduced into the experimental chamber, including two cover slips separated by spacers 1.2 mm thick. The cells were incubated for 30 min at a temperature of 37°C before mounting on the chamber on the DHM stage. All experiments were performed at room temperature (22°C). 3.Feature Extraction3.1.Two-Dimensional FeaturesAfter segmentation step and extracting many single RBCs, features can be extracted. We first start with 2-D features. Following features are extracted in 2-D case. Elongation of the RBC is a measure of the ratio of width to length for oblong RBCs. It can be computed from the chain code by summing the number of each type of elements 0 to 7 and combining 0 and 4, 1 and 5, 2 and 6, and 3 and 7.16 Average and STD values of the above features are in the agreement with previously reported values (data not shown here).25,26 3.2.Three-Dimensional FeaturesSince some 3-D features require thickness of the RBC, we first need to convert phase image into thickness image. Accordingly, the thickness value for each pixel of with phase value in a phase image can be expressed as28,29 where is the phase value in radians, and the refractive index of RBCs, , has been measured with a dual-wavelength DHM. Here, is 1.396 with no significant difference among groups of RBCs. The index of refraction of the HEPA medium, , is 1.3334. Surface area is another important property and has the main contribution in different 3-D features. Generally speaking, the surface area of the RBC is the surface area of the membrane mesh plus PSA. The method in this paper splits and divides RBC surfaces into smaller regular areas (triangles here) and adds these smaller areas to give the entire surface area. Understandably, the accuracy of such a calculation is dependent on the smaller area chosen.293-D features listed in Table 1 are extracted in this paper. We only give a short description of the eight features related to the morphological properties of RBC, but interested readers can refer to Refs. 28 and 29 for the detail of each feature. Regarding the calculation of three features (F9-F11), we obtained many points over the ring section of RBC by applying two techniques. First, we estimate the ring section (blue triangles in Fig. 3) by calculating the radius of a circle having the area of the projection of RBC on plane (the ring is around three-fourth of the RBC radius). Then, we update the position of each point on estimated ring (blue triangles) by finding the thickest point in a neighbor (red stars in Fig. 3). From now on we name the red stars as RPs. The single green point shows the center of RBC regarding the calculation of sphericity coefficient. In this study, we have decided to obtain 30 RP points. The reason is that the total number of points on the ring section for the stomatocyte RBCs is between 90 and 120 points according to our calculation. Also, since we are looking at a neighborhood around the blue triangles to find the point on the ring (red stars), there is high possibility of overlapping between red stars. For example, Fig. 4 shows the position of red stars and blue triangles when we increase the number of points. We can see that by increasing the number of red stars many of them overlap. Table 13-D features descriptions.
Fig. 33-D representation of four RBC categories and points on the ring section. (a) A typical biconcave sample, (b) a flat disc with center raised, (c) a stomatocyte RBC, and (d) a spherocyte RBC.  Fig. 43-D representation of RBC ring section with red stars and blue triangles on it. (a) Number of points is 60 and (b) number of points is 600. 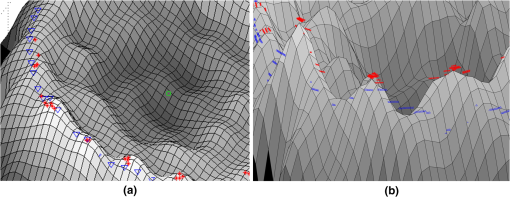 We believe that earlier 3-D features can distinguish among different RBCs since they are related to the 3-D profile of RBC. The statistic -test using two-sample Kolmogorov–Smirnov test revealed that some of these features are independent (data not shown). Table 2 shows average and STD values of each feature for each RBC type. Table 23-D features (mean±STD).
4.Pattern Recognition Neural NetworkANNs are highly simplified mathematical models of biological neural networks having the ability to learn and provide meaningful solutions to the problems with high-level complexity and nonlinearity. The ANN approach is faster compared to its conventional techniques, robust in noisy environments, and can solve a wide range of problems. Due to the advantages, ANNs have been used in numerous applications.13–15 A typical ANN is presented in Fig. 5. An important application of neural networks is pattern recognition that can be implemented by using a feed-forward neural network with a specific training function and specific function in the output layer. During training, the network is trained to associate outputs with input patterns. When the network is used, it identifies the input pattern and tries to output the associated output pattern. Fig. 5Feed-forward ANN configuration with five input nodes, two output nodes, and two hidden layers. 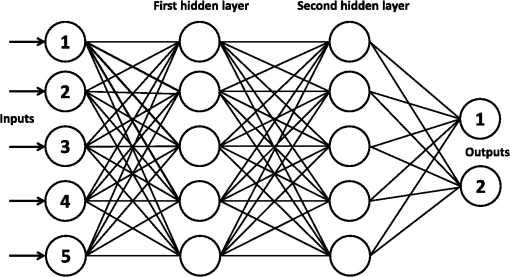 The information processing in the ANN strategy starts from the input layer to the hidden layer (from one hidden layer to another one if there are more than one) and from the last hidden layer to the output layer. A synaptic weight is assigned to each link to represent the relative connection strength of two nodes at both ends in predicting the input-output relationship. (the output) of any node , is given as where is the connection weight, denotes the ’th input of node , is the number inputs to node , and is the bias value. Function or so-called activation function determines the response of a node to the total input signal that is received. Generally, the activation function for hidden layer in PRNN is hyperbolic tangent sigmoid transfer function due to the following advantages: (1) it limits the range of data to values between and 1. This function is almost linear near the mean. It is smooth and has monotonic nonlinearity property at both extremes, (2) it remains differentiable everywhere and the sign of the derivative is unaffected by the normalization. Generally, the differentiable requirement is needed for hidden layers and hyperbolic tangent sigmoid transfer function is often recommended as being more balanced, (3) the 0 for hyperbolic tangent sigmoid transfer function is at the fastest point (highest gradient or gain) and not a trap, (4) the hyperbolic tangent sigmoid transfer function suit the output layer to the competitive outputs of softmax function, (5) since it can be estimated by it can be implemented faster in MATLAB®.For output layer in PRNN, the activation function is softmax transfer function (normalized exponential) that can be interpretable as posterior probabilities for a categorical target variable. It is highly desirable for those outputs to lie between zero and one and to sum to one. The purpose of the softmax activation function is to enforce these constraints on the outputs. Let the input to each output unit be , , where is the number of classes. Then the softmax output is According to Eq. (3), sum of all “”s is equal to unity and can be interpreted as the posterior probability for the final decision. The training algorithm updates the weight and bias values according to Levenberg–Marquardt optimization. It minimizes a combination of squared errors and weights and then determines the correct combination so as to produce a network that generalizes well (Bayesian regularization).435.Experimental Results and DiscussionIn this experiment, 108 RBCs are labeled as biconcaves, 106 RBCs labeled as stomatocytes, 38 RBCs are labeled as flat-disc, and 71 RBCs labeled as echinospherocytes. Four samples of each group are shown in Fig. 6. Simulations are all executed on a 64-bit Windows 7 computer with a 3.60-GHz Intel Core i7-4790 CPU, 8 GB RAM, and 8 cores. The performance of the classification model is assessed by utilizing 10-fold CV check. Put it simply, the data set is divided into 10 subsets, and the test is repeated 10 times. Each time, one of the 10 subsets is used as the test set and the other 9 subsets are put together to form a training set. Then, the average misclassification error across all 10 trials can show the overall misclassification error. PRNN consists of one input, output layer, and three hidden layers. Number of neurons in each hidden layer is 5, 10, and 5, respectively. Neuron numbers are obtained by trial-and-error technique. All the simulations codes are implemented in MATLAB® 2014. Fig. 6Samples of each RBC group used in this research: (a) four samples of flat disks, (b) four samples of stomatocyte morphology, (c) four samples of biconcave RBC, and (d) four samples of spheroechinocyte RBC. 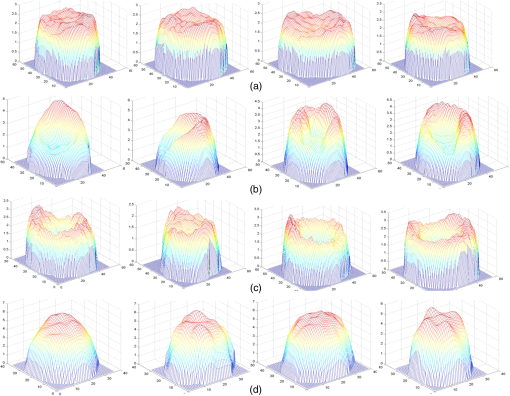 5.1.Comparison Between 2-D and 3-D FeaturesIn the case of 2-D features (Table 3), 10-fold CV revealed that the total misclassification rate is significantly high. In detail, misclassification of each group is: flat-disc 64%, stomatocyte 13.4%, biconcave 32.3%, and echinospherocyte are 4.2%. Only echinospherocyte RBCs can be accurately classified by taking into account 2-D features while other categories have significant error. According to the confusion matrix, PRNN confuses between biconcaves and flat-discs by using 2-D features (data not shown). In contrast, 3-D features explained in Table 1 generate more accurate and interesting results. According to the results of 10-fold CV, misclassification rates are 0%, 1.6%, 3.2%, and 0% for flat-disc, stomatocyte, biconcave, and echinospherocyte RBCs, respectively. Table 4 shows the classification error for 2-D and 3-D features. It is noted that the presented neural network classification strategy was used to evaluate the discrimination power of the feature set based on 3-D morphological properties of RBC against 2-D features. The classification results obtained with the neural network demonstrate that the 3-D features can be more effective in RBC classification than the 2-D features. Table 32-D feature descriptions.
Table 4Misclassification results of 2-D and 3-D features.
In another experiment, we evaluated the normalized mutual information between each feature in 2-D and 3-D features.40 In the case of 2-D features, it turns out, as shown in Table 5, that there is big mutual information among some features. Mutual information is the amount of information that two features share. If the mutual information between the two features is large (small), the two features are closely (not closely) related. If the mutual information becomes zero, the two features are independent. For example, 2-D-F1 has significant mutual information with features 2-D-F2, 2-D-F4, 2-D-F5, and 2-D-F6 (see first row of Table 5). Therefore, this feature is statistically redundant and cannot add significant information. Table 5Normalized mutual information between 2-D features.
5.2.Combining 2-D and 3-D Features and Select the Best Feature-SetWe believe that the best classification model should take into account not only 3-D features but also 2-D features. However, it is worth mentioning that not any feature can add significant information to the classification model. Therefore, we believe that the performance of any classification model can be enhanced by taking advantages of feature selection (FS) strategy. In FS, we seek to find the best set of the features that has the strongest ability (or strong) to distinguish each class. Generally speaking, FS preserves the original features intact; features deemed unimportant/irrelevant/redundant are simply eliminated from further consideration while selecting only those features that significantly contribute to the classification problem. Therefore, FS can reduce the number of features (variables) of the classification problem and make the model simpler (or less complex) and shorten training time.40 We also implemented FS in this research by using SFFS technique. Generally speaking, in SFFS features are sequentially added to an empty candidate set until the addition of further features does not decrease the criterion. It has two components of an objective function, called the criterion, and a sequential search algorithm. In former, common criteria are misclassification rate for classification objects (similar in this paper) and mean squared error for regression models. A sequential forward search algorithm adds features from a candidate subset while evaluating the criterion. Since an exhaustive comparison of the criterion value at all subsets of an -feature data set is typically infeasible (sometimes feasible but time-consuming), sequential searches grow the candidate set. It turns out that the following features of average RBC thickness (3-D-F1), top view surface (TVS) area volume ratio (3-D-F4), sphericity coefficient (3-D-F9), the upper side of the ring divided by lower side of the ring (3-D-F11), and perimeter (2-D-F2) can better classify multiple RBCs in this research. Our experimental results also show that adding more features does not add significant discrimination ability to the final classification model. As it has been mentioned earlier, SFFS is responsible for adding or removing features from the final feature set. One component of SFFS is the objective function, which here is the misclassification rate. SFFS starts from an empty set and add features one by one to the set and evaluates the misclassification rate. If there is a significant change in the objective function (misclassification rate) then the feature can be added to the final feature set (see Table 6). Table 6Misclassification rate after adding each feature to the feature set.
According to Table 6 after adding the 7th and 8th features, the misclassification rate never changes. It means that they have no contribution to the final feature set. Adding the 6th feature decreases the misclassification rate marginally but we still did not consider it as part of the feature set since we wanted to keep the final feature set as small as possible (only five features). Figure 7 shows the data distribution RBCs for each selected feature. We can see that the distribution of average RBC thickness of echinospherocyte RBCs has almost no overlap with other distributions [Fig. 7(a)]. Table 7 shows misclassification rate of the final feature-set and PRNN approach. Fig. 7Data distribution of the best feature set. (a) Average thickness value. (b) Sphericity coefficient. (c) Upper side of the ring/lower side of the ring. (d) Top view surface area volume ratio. (e) Perimeter. 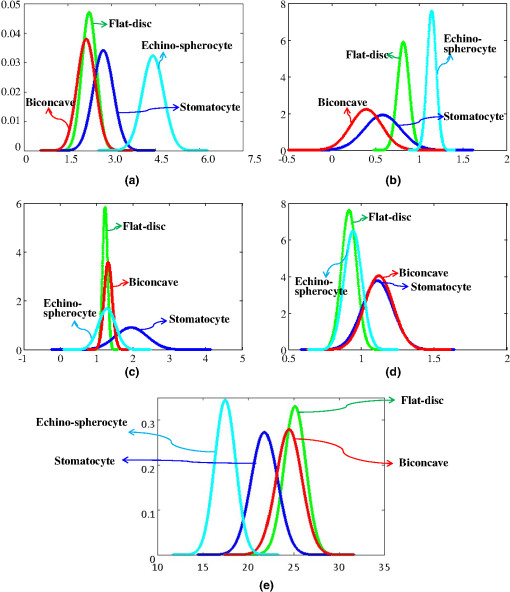 Table 7Misclassification results for the best feature set obtained by sequential features selection technique.
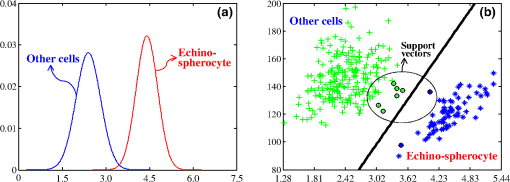
The confusion matrix of the test set shows that PRNN sometimes confuses stomatocytes and echinospherocytes because there are cases in which RBC has a morphology similar to both stomatocyte and echinospherocytes (see Fig. 8). According to Fig. 8, we can see that RBC is similar to both stomatocyte and echinospherocytes morphology and posterior probability for belonging to stomatocyte and echinospherocyte categories are 0.33 and 0.66, respectively. Even for a human examiner, it can be difficult to put it in the correct category. Fig. 8An RBC sample that confuses neural network, resembles both stomato and spherocyte. (a) 3-D representation and (b) representation on plane. 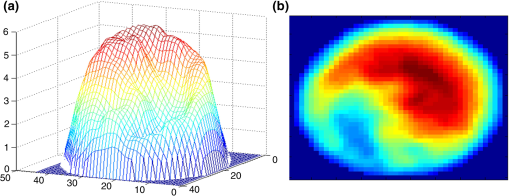 In another experiment, we tried to count different types of RBCs in five quantitative phase images with multiple RBCs. Images are inspected visually by the human inspector and then results are presented. In Fig. 9(a) stomatocyte RBCs are dominant (flat discs 0/80, stomatocytes 58/80, biconcave 8/80, and echinospherocyte 14/80) and in other images biconcave RBCs [Fig. 9(b) has following flat discs 2/27, stomatocytes 5/27, biconcave 20/27, and echinospherocyte 0/27] and echinospherocytes are dominant [Fig. 9(c) shows RBC types of flat-disc 0/49, stomatocytes 5/49, biconcaves 6/49, and echinospherocytes 38/49, and Fig. 9(d) shows RBC types of flat-disc 0/63, stomatocytes 3/63, biconcaves 1/63, and echinospherocytes 59/63]. Figure 9(e) shows an image with 40 days storage time with many flat-disc RBCs (flat-disc: 16/36, stomatocytes: 7/36, biconcaves: 5/36, and echinospherocytes: 8/36). The numbers in parenthesis show the number of each morphology obtained by the human inspector. At first, each image is segmented into many RBCs since feature extraction should be applied at the single cell level. Then, the percentage of the different types of RBCs in the RBC phase images is calculated (see Fig. 9). As expected, the classifier showed that at the first sample stomatocyte RBCs are dominant. In contrast, in the second and fifth figures biconcave and flat-disc RBCs are the major types. Third and fourth figures illustrate that echinospherocytes are dominant RBCs. Although there is a small error in counting nondominant RBCs, the main and important thing is counting and reporting the dominant type for further investigation. Fig. 9Five RBC samples and counting results. (a) Flat-disc: 0%, stomatocytes: 76.2% (61/80), biconcave: 11.25% (9/80), and echinospherocyte: 10% (8/80). (b) Flat-disc: 7.40% (2/27), stomatocytes: 18.51% (5/27), biconcave: 74.07% (20/27), and echinospherocyte: 0%. (c) Flat-disc: 0%, stomatocytes: 12.24% (6/49), biconcave: 10.2% (5/49), and echinospherocyte: 77.55% (38/49). (d) Flat-disc: 0%, stomatocytes: 7.94% (5/63), biconcave: 1.59% (1/63), and echinospherocyte: 90.4% (57/63). (e) Flat-disc: 47.22% (17/36), stomatocytes: 25% (9/36), biconcave: 19.5.2% (7/36), and echinospherocyte: 8.3% (3/36). 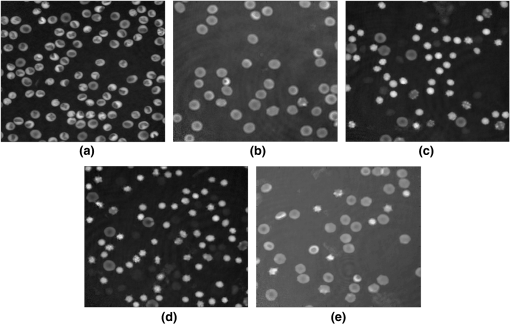 According to the results, the proposed feature set and classifier can automatically count and categorize different types of RBCs in human RBCs by taking advantages of 2-D and 3-D profiles of RBC. The classifier is helpful to assess RBC-related abnormality since the ratio of the different types of RBCs is associated with certain types of diseases. There are some disadvantages in using NN technology regarding the classification such as there is no formula for the number of nodes and hidden layers. Generally, these numbers in the network are problem dependent and are decided by the trial-and-error method. We believe that DHM, by providing the quantitative phase images, allows for doing different analysis especially classification goals. For example, someone can easily classify echino-echino-spherocyte from the rest of cells easily by using a conventional binary support vector machine (SVM) classifier and one or two features. Figure 10(a), e.g., shows the density of average cell thickness of echinospherocytes against other RBCs. Any binary classifier can be used to separate these two groups. Figure 10(b) shows the scattering of two groups based on average thickness (AT) value and surface area, and an SVM classifier with its boundary region. 6.ConclusionsAutomatic classification of different types of RBCs in human RBC is a challenging and important problem for pathological diagnosis. In particular, as far as RBCs are concerned, classification based on their 3-D profile is highly relevant. Another issue is that since demands on laboratories are ever increasing and funding and staffing levels are generally below the desired level, the implementation of a system that shortens staff time, cost-effective, and noninvasive is greatly desired. In this paper, we have presented and assessed the use of PRNN applied to the 2-D and 3-D features of RBCs obtained through DHM in order to categorize and count biconcave, stomatocyte, flat-disc, and echinostomatocyte RBCs in an RBC sample with multiple types. Six 2-D features and 13 3-D features have been extracted and classification results are compared right after. Our experimental results show that the 3-D features have more useful information in RBC classification. In addition, FS shows that average RBC thickness, TVS area volume ratio, sphericity coefficient, the upper side of the ring divided by lower side of the ring, and RBC perimeter can better classify RBCs into the desired categories. The experimental results and the performance imply that the final feature set can help in classifying and counting RBCs, which is substantially important in analyzing RBC abnormality and shape-related diseases. AcknowledgmentsThis work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), which is funded by the Ministry of Science, ICT & Future Planning (NRF-2015K1A1A2029224) and the research funds from Chosun University, 2016. ReferencesP. Canham,
“The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell,”
J. Theor. Biol., 26 61
–81
(1970). http://dx.doi.org/10.1016/S0022-5193(70)80032-7 JTBIAP 0022-5193 Google Scholar
C. Uzoigwe,
“The human erythrocyte has developed the biconcave disc shape to optimise the flow properties of the blood in the large vessels,”
Med. Hypotheses, 67 1159
–1163
(2006). http://dx.doi.org/10.1016/j.mehy.2004.11.047 MEHYDY 0306-9877 Google Scholar
Z. Tu,
“Geometry of membranes,”
J. Geom. Symmetry Phys., 24 45
–75
(2011). Google Scholar
M. Bessis, R. Weed and P. Leblond, Red Cell Shape, Physiology, Pathology Ultrastructure, Springer, New York
(1973). Google Scholar
Y. Kim et al.,
“Profiling individual human red blood cells using common-path diffraction optical tomography,”
Sci. Rep., 4 6659
(2014). http://dx.doi.org/10.1038/srep06659 SRCEC3 2045-2322 Google Scholar
C. Aubron et al.,
“Age of red blood cells and transfusion in critically ill patients,”
Ann. Intensive Care, 3 2
–11
(2013). http://dx.doi.org/10.1186/2110-5820-3-2 Google Scholar
D. Triulzi and M. Yazer,
“Clinical studies of the effect of blood storage on patient outcomes,”
Transfus. Apheresis Sci., 43 95
–106
(2010). http://dx.doi.org/10.1016/j.transci.2010.05.013 Google Scholar
G. Bosman et al.,
“Erythrocyte ageing in vivo and in vitro: structural aspects and implications for transfusion,”
Transfus Med., 18 335
–347
(2008). http://dx.doi.org/10.1111/tme.2008.18.issue-6 Google Scholar
Y. Park et al.,
“Metabolic remodeling of the human red blood cell membrane,”
Proc. Natl. Acad. Sci. U. S. A., 107 1289
–1294
(2010). http://dx.doi.org/10.1073/pnas.0910785107 Google Scholar
M. Buttarello and M. Plebani,
“Automated blood cell counts,”
Am. J. Clin. Pathol., 130 104
–116
(2008). http://dx.doi.org/10.1309/EK3C7CTDKNVPXVTN AJCPAI 0002-9173 Google Scholar
I. Moon et al.,
“Automated three dimensional identification and tracking of micro/nano biological organisms by computational holographic microscopy,”
Proc. IEEE, 97 990
–1010
(2009). http://dx.doi.org/10.1109/JPROC.2009.2017563 IEEPAD 0018-9219 Google Scholar
J. Collakova et al.,
“Coherence-controlled holographic microscopy enabled recognition of necrosis as the mechanism of cancer cells death after exposure to cytopathic turbid emulsion,”
J. Biomed. Opt., 20 111213
(2015). http://dx.doi.org/10.1117/1.JBO.20.11.111213 JBOPFO 1083-3668 Google Scholar
R. Marabini and J. Carazo,
“Pattern recognition and classification of images of biological macromolecules using artificial neural networks,”
Biophys. J., 66 1804
–1814
(1994). http://dx.doi.org/10.1016/S0006-3495(94)80974-9 BIOJAU 0006-3495 Google Scholar
A. Khashman,
“IBCIS: intelligent blood cell identification system,”
Progr. Nat. Sci., 18 1309
–1314
(2008). http://dx.doi.org/10.1016/j.pnsc.2008.03.026 Google Scholar
M. Veluchamy, K. Perumal and T. Ponuchamy,
“Feature extraction and classification of blood cells using artificial neural network,”
Am. J. Appl. Sci., 9 615
–619
(2012). http://dx.doi.org/10.3844/ajassp.2012.615.619 Google Scholar
J. Bacus and J. Weens,
“An automated method of differential red blood cell classification with application to the diagnostics of anemia,”
J. Histochem. Cytochem., 25 614
–632
(1977). http://dx.doi.org/10.1177/25.7.330716 JHCYAS 0022-1554 Google Scholar
L. Wheeless et al.,
“Classification of red blood cells as normal, sickle, or other abnormal, using a single image analysis feature,”
Cytometry, 17 159
–166
(1994). http://dx.doi.org/10.1002/(ISSN)1097-0320 CYTODQ 0196-4763 Google Scholar
P. Rakshita and K. Bhowmik,
“Detection of abnormal findings in human RBC in diagnosing sickle cell anaemia using image processing,”
Proc. Technol., 10 28
–36
(2013). http://dx.doi.org/10.1016/j.protcy.2013.12.333 Google Scholar
H. Lee and Y. Chen,
“Cell morphology based classification for red cells in blood smear images,”
Pattern Recognit. Lett., 49 155
–161
(2014). http://dx.doi.org/10.1016/j.patrec.2014.06.010 PRLEDG 0167-8655 Google Scholar
F. Dubois et al.,
“Digital holographic microscopy for the three-dimensional dynamic analysis of in vitro cancer cell migration,”
J. Biomed. Opt., 11 054032
(2006). http://dx.doi.org/10.1117/1.2357174 JBOPFO 1083-3668 Google Scholar
P. Marquet, C. Depeursinge and P. Magistretti,
“Review of quantitative phase-digital holographic microscopy: promising novel imaging technique to resolve neuronal network activity and identify cellular biomarkers of psychiatric disorders,”
Neurophotonics, 1 020901
(2014). http://dx.doi.org/10.1117/1.NPh.1.2.020901 Google Scholar
B. Rappaz et al.,
“Comparative study of human erythrocytes by digital holographic microscopy, confocal microscopy, and impedance volume analyzer,”
Cytometry A, 73 895
–903
(2008). http://dx.doi.org/10.1002/cyto.a.v73a:10 Google Scholar
Y. Li et al.,
“Digital holographic microscopy for longitudinal volumetric imaging of growth and treatment response in three-dimensional tumor models,”
J. Biomed. Opt., 19 116001
(2014). http://dx.doi.org/10.1117/1.JBO.19.11.116001 JBOPFO 1083-3668 Google Scholar
X. Yu et al.,
“Four-dimensional motility tracking of biological cells by digital holographic microscopy,”
J. Biomed. Opt., 19 045001
(2014). http://dx.doi.org/10.1117/1.JBO.19.4.045001 JBOPFO 1083-3668 Google Scholar
F. Yi, I. Moon and B. Javidi,
“Cell morphology-based classification of red blood cells using holographic imaging informatics,”
Biomed. Opt. Express, 7 2385
–2399
(2016). http://dx.doi.org/10.1364/BOE.7.002385 BOEICL 2156-7085 Google Scholar
F. Yi, I. Moon and Y. H. Lee,
“Three-dimensional counting of morphologically normal human red blood cells via digital holographic microscopy,”
J. Biomed. Opt., 20 016005
(2015). http://dx.doi.org/10.1117/1.JBO.20.1.016005 JBOPFO 1083-3668 Google Scholar
R. Liu et al.,
“Recognition and classification of red blood cells using digital holographic microscopy and data clustering with discriminant analysis,”
J. Opt. Soc. Am. A, 28 1204
–1210
(2011). http://dx.doi.org/10.1364/JOSAA.28.001204 JOAOD6 0740-3232 Google Scholar
I. Moon et al.,
“Automated quantitative analysis of 3D morphology and mean corpuscular hemoglobin in human red blood cells stored in different periods,”
Opt. Express, 21 30947
–30957
(2013). http://dx.doi.org/10.1364/OE.21.030947 OPEXFF 1094-4087 Google Scholar
K. Jaferzadeh and I. Moon,
“Quantitative investigation of red blood cell three-dimensional geometric and chemical changes in the storage lesion using digital holographic microscopy,”
J. Biomed. Opt., 20 111218
(2015). http://dx.doi.org/10.1117/1.JBO.20.11.111218 JBOPFO 1083-3668 Google Scholar
W. Reinhart and S. Chien,
“Red cell rheology in stomatocyte-echinocyte transformation: roles of cell geometry and cell shape,”
Blood, 67 1110
–1118
(1986). BLOOAW 0006-4971 Google Scholar
L. Gerald, M. Wortis and R. Mukhopadhyay,
“Stomatocyte-discocyte echinocyte sequence of the human red blood cell: evidence for the bilayer-couple hypothesis from membrane mechanics,”
Proc. Natl. Acad. Sci. U. S. A., 99 4457
–4461
(2002). http://dx.doi.org/10.1073/pnas.202617299 Google Scholar
J. Laurie, D. Wyncoll and C. Harrison,
“New versus old blood—the debate continues,”
Crit. Care, 14 130
(2010). http://dx.doi.org/10.1186/cc8878 Google Scholar
D. Kor, C. Van Buskirk and O. Gajic,
“Red blood cell storage lesion,”
Bosn J. Basic Med. Sci., 9 21
–27
(2009). Google Scholar
R. Card,
“Red cell membrane changes during storage,”
Transf. Med. Rev., 2 40
–47
(1998). http://dx.doi.org/10.1016/S0887-7963(88)70030-9 TMEREU 0887-7963 Google Scholar
C. Koch et al.,
“Duration of red-cell storage and complications after cardiac surgery,”
N. Engl. J. Med., 358 1229
–1239
(2008). http://dx.doi.org/10.1056/NEJMoa070403 Google Scholar
G. Bosman et al.,
“Erythrocyte ageing in vivo and in vitro: structural aspects and implications for transfusion,”
Transf. Med., 18 335
–347
(2008). http://dx.doi.org/10.1111/tme.2008.18.issue-6 TMEREU 0887-7963 Google Scholar
E. Cuche, P. Marquet and C. Depeursinge,
“Simultaneous amplitude and quantitative phase contrast microscopy by numerical reconstruction of Fresnel off-axis holograms,”
Appl. Opt., 38 6994
–7001
(1999). http://dx.doi.org/10.1364/AO.38.006994 APOPAI 0003-6935 Google Scholar
T. Colomb et al.,
“Automatic procedure for aberration compensation in digital holographic microscopy and application to specimen shape compensation,”
Appl. Opt., 45 851
–863
(2006). http://dx.doi.org/10.1364/AO.45.000851 APOPAI 0003-6935 Google Scholar
F. Yi et al.,
“Automated segmentation of multiple red blood cells with digital holographic microscopy,”
J. Biomed. Opt., 18 026006
(2013). http://dx.doi.org/10.1117/1.JBO.18.2.026006 JBOPFO 1083-3668 Google Scholar
G. Forman,
“An extensive empirical study of feature selection metrics for text classification,”
J. Mach. Learn. Res., 3 1289
–1305
(2003). Google Scholar
Y. Bengio and Y. Grandvalet,
“No unbiased estimator of the variance of K-fold cross-validation,”
J. Mach. Learn. Res., 5 1089
–1105
(2004). Google Scholar
P. Marquet et al.,
“Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy,”
Opt. Lett., 30 468
–470
(2005). http://dx.doi.org/10.1364/OL.30.000468 OPLEDP 0146-9592 Google Scholar
J. David and C. MacKay,
“Bayesian interpolation,”
Neural Comput., 4 415
–447
(1992). http://dx.doi.org/10.1162/neco.1992.4.3.415 NEUCEB 0899-7667 Google Scholar
BiographyKeyvan Jaferzadeh is a PhD student in the Computer Engineering Department at Chosun University. He received his BS degree in software engineering and MS degrees in mechatronic engineering in 2006 and 2010, respectively. His current research interests include image processing, digital holography, image compression, and machine vision. Inkyu Moon received his BS degree in electronics engineering from SungKyunKwan University in Korea in 1996 and his PhD in electrical and computer engineering from the University of Connecticut in the United States in 2007. He joined Chosun University in Korea in 2009 and is currently a professor at the School of Computer Engineering. His research interests include digital holography, biomedical imaging, and optical information processing. He is member of IEEE, OSA, and SPIE. |