|
|
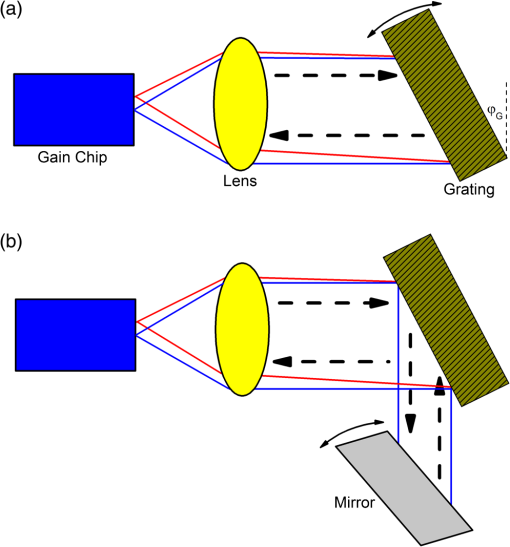
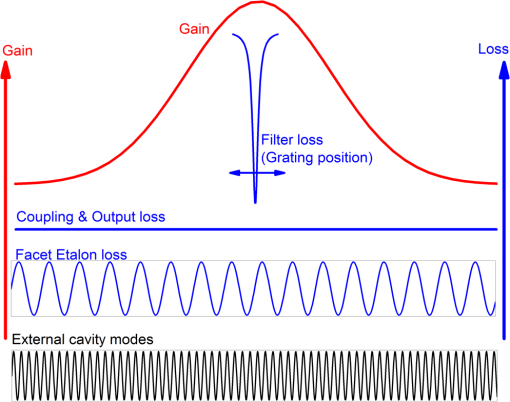
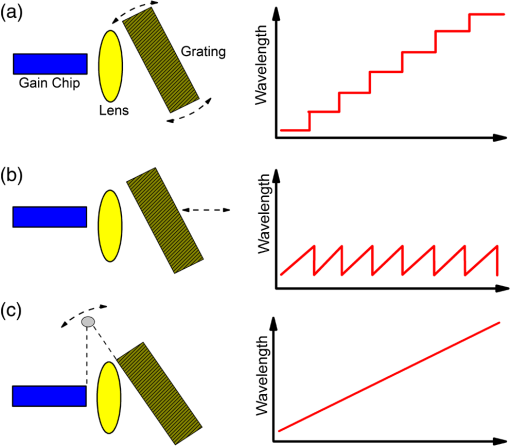
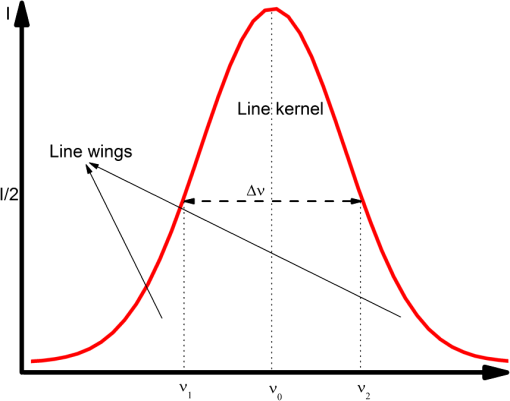
1.IntroductionTechnologies for clinical diagnoses and monitoring are always needed for discriminating patients from healthy subjects. To identify diseases and to monitor therapy and/or the progression of diseases, most used methods—such as biopsy, computer tomography, magnetic resonance imaging, endoscopy, and blood analysis—are time-consuming, expensive, invasive, painful, stressful, and difficult to perform. Therefore, noninvasive tools are needed to monitor the diseases in their early stages and to holistically measure the physiological status of patients. There are different potential noninvasive techniques, such as breath, nail, hair, mucus, saliva, sweat, and/or tear analysis. Among them, the detection of volatile organic compounds (VOCs) present in breath at trace concentrations with an acceptable accuracy and precision is most promising. This method may provide noninvasive, point-of-care (PoC), easily repeatable, painless, and real-time diagnosis of a number of disease states and therefore is preferable. Breath biomarkers can be analyzed either after administration of a drug or substrate or without any prior administration of a chemical. A number of breath molecules have been detected and quantified so far using the different methods, such as proton transfer reaction mass spectrometry (PTR-MS), selected ion flow tube mass spectrometry (SIFT-MS), gas chromatography-mass spectrometry (GC-MS), e-noses, and laser-based sensors. Laser spectroscopic detection techniques—such as tunable diode laser absorption spectroscopy (TDLAS), cavity-enhanced absorption spectroscopy (CEAS), integrated cavity output spectroscopy (ICOS), cavity ringdown spectroscopy (CRDS), photoacoustic spectroscopy (PAS), quartz-enhanced photoacoustic spectroscopy (QEPAS), cavity leak-out spectroscopy, and optical frequency comb cavity-enhanced absorption spectroscopy—provide the features of high-sensitivity, high-selectivity, low costs, real-time measurements, and PoC function. Therefore, these methods are candidates for performing accurate breath diagnostics in hospitals. To identify and quantify the molecules in breath, narrow linewidth (), mode-hop-free (1 to ) wavelength-tunable, single-mode light sources are needed. These features can be obtained using external cavity lasers (ECLs). ECL-based spectroscopic techniques may become very suitable for monitoring diseases by analyzing exhaled breath air samples. Many review papers about breath analysis using laser-based techniques have been published. Ciaffoni et al.1 focused on the current status of volatile sulfur compounds sensing via laser absorption spectroscopy. The review article of Wang and Sahay2 is related to breath analysis of almost all of the biomarkers that have been analyzed in actual human breath using high-sensitivity laser spectroscopic techniques. Wojtas et al.3 presented recent advances in human breath analysis using optical methods. Risby and Tittel4 reviewed the current status of mid-infrared quantum and interband cascade lasers for clinical breath analysis. The review article of Bielecki et al.5 presented an overview on high-sensitivity laser absorption spectroscopic techniques used for trace gas detection. Mid-infrared spectroscopic sensing techniques were reviewed for potential application in breath diagnostics.6 In the review paper,7 techniques such as mass spectrometry-based (GC-MS, PTR-MS, SIFT-MS), laser absorption spectroscopy-based (CRDS and TDLAS), and other spectroscopic techniques for breath analysis applications were compared in terms of advantages/disadvantages, versatilities and plausibility to be transformed in clinical applications. McCurdy et al.8 summarized some of the recent advances in laser absorption spectroscopy based on semiconductor lasers and optical detection techniques for clinically relevant exhaled gas analysis in breath, specifically molecular biomarkers such as nitric oxide, ammonia, carbon monoxide, ethane, carbonyl sulfide, formaldehyde, and acetone. Regarding the issues above mentioned, the present review article focuses on the latest status of breath analysis using the ECL-based methods. The article is structured as follows: first, we will explain the respiratory system and breath sampling. The absorption of electromagnetic waves by breath molecules is discussed next. The latest developments and functional principle of ECLs are described in detail as well. Finally, the laser-based techniques used for breath analysis and limitations of breath analysis are presented in detail. Regarding this content, the present review article differentiates itself from previous reviews related to the laser-based breath analysis. 2.Respiratory SystemThe lung is primarily responsible for gas exchange between the atmosphere and the blood. The molecules present in blood can diffuse into the alveoli and subsequently appear in the exhaled breath. Transport of metabolites from the blood to the exhaled breath air can make it possible to utilize breath analysis as a noninvasive diagnostic tool. Low and high blood-soluble gases present in the breath air:9 Gases with low blood-solubility like oxygen () and carbon dioxide () exchange in the alveoli. For these gases, there is a simple relationship between the breath and blood, which depends predominately on two factors: the blood solubility of the gas () and the distribution of ventilation-to-perfusion in all gas exchange units. Gas exchange of high blood-soluble gases like ethanol () takes place in the airways, and there is a more complex relationship between end-exhaled breath measurement and blood. Airway gas exchange is related to multiple factors, such as airway temperature, bronchial blood flow, and blood–air partition coefficient. Soluble gases with a blood:air partition coefficient less than 10 () exchange almost solely with the alveoli, whereas gases with a blood:air partition coefficient greater than 100 () exchange almost exclusively with the airways. Gases in between these two extremes () exchange partially with the airways and partially with the alveoli.9,10 Figure 1 shows expirograms in which gases that exchange in the alveoli and those that exchange in the airways can be seen: phase 1 shows that the anatomic dead space empties. When fresh air is inhaled, low blood-soluble gases in the blood are transfered into the inspired air entering the alveoli. This action continues throughout the entire breathing cycle (inspiration and expiration). When the air is exhaled, molecules present in the conducting airways exit the lung first (phase 1). The airways take part in the gas exchange. Therefore, phase 1 does not exist in the expirogram for gases that exchange completely in the airways (e.g., ethanol). Therefore, an anatomical dead space cannot be given for such gases. For these gases, the end-exhaled breath concentration is always less than that in the alveoli. Phase 2 represents the transition from air residing in the dead space to alveolar air containing high partial pressures of gas. Phase 3 corresponds to air from the alveoli for low soluble gases and airways for high soluble gases. Alveolar air is expired via the conducting airways (phase 3). Molecules with high blood solubility are absorbed from the tissue and mucus lining the airway wall. In contrast to low blood-soluble gases, therefore, these gases present in large concentrations in the airway tissue and mucus for a given partial pressure. The partial pressure of soluble gas in the end-exhaled breath is always less than that in the alveoli due to the absorption–desorption process, which is the major mechanism of pulmonary gas exchange for any gas with a blood–air partition coefficient greater than 100.10 Fig. 1Phases of an expirogram from a low blood-soluble gas that exchanges in the alveoli (red line) and from a high blood-soluble gas that exchanges in the airways (blue line).9 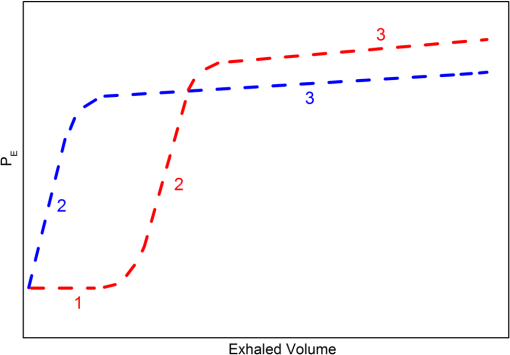 3.Breath SamplingBreath sampling procedures are threefold: alveolar, dead-space, and mixed sampling. Dead space air contains the first 150 mL of expiration air, and here no gas exchange takes place. Alveolar breath is the part of exhaled air coming after the dead-space air, whereas end-tidal air is the last fraction of expired air. Alveolar gas exchange is dependent on ventilation, pulmonary perfusion, and the blood:air partition.10 The term “end-exhaled breath” should be utilized for highly blood soluble VOCs, whereas the term “alveolar breath” may be used for low blood-soluble compounds. It is often tacitly assumed that end-tidal air will reflect the alveolar concentration , which is related to the concentration of the VOC in mixed venous blood , the substance-specific blood:gas partition coefficient , alveolar ventilation , and cardiac output :11,12 where states the diffusion equilibrium between alveoli and capillaries, describes the volume of VOC per unit time that arrives to the alveoli, and describes the blood volume, which is pumped by the heart.In mixed sampling, total breath (alveolar + dead space) is collected. Concentrations of endogenous VOCs in alveolar air are two to three times higher than those found in mixed expiratory samples because there is no dilution by dead space gas.13 There may be discrepancies between the true alveolar breath and the measured levels of water-soluble VOCs because their concentrations may be diluted on their way (a dilution effect). A single breath or multiple breath cycles can be applied for breath sampling.14 Breaths may considerably change from each other. The alveolar gas sample may not be represented by the composition of a single breath. Therefore, multiple breaths may be preferable. 4.Absorption of Electromagnetic Waves by MoleculesAnalysis of the breath molecules using laser-based methods is based on the absorption of electromagnetic waves by molecules under investigation. Therefore, we will explain the absorption phenomena in this section. The overall excited energy of a molecule is a sum of the electronic (), vibrational (), and rotational transitions () energy: Rotational spectra originate from the transitions between rotation levels of a given vibration level in an electronic state [Fig. 2(a)]. In this process, only the rotational quantum number () changes. These spectra lie in the spectral range from the microwave to the far infrared. The rotational–vibrational spectra consist of the transitions from rotation levels of a vibration level to rotation levels of another vibration level in the same electronic state [Fig. 2(b)]. The rotation and vibration () quantum number change in these transitions. These spectra lie in the infrared spectral region. Electronic spectra consist of the transitions between the rotation levels of different vibration levels of an electronic state and rotation or vibration levels of another electronic level [Fig. 2(c)]. There are changes in all three quantum numbers (, , and electronic quantum number). These spectra lie in the near-infrared or visible range or in the UV range. Fig. 2Electronic, vibrational, and rotational quantum states and corresponding transitions: (a) rotational transition, (b) rotational–vibrational transition, and (c) electronic transition. 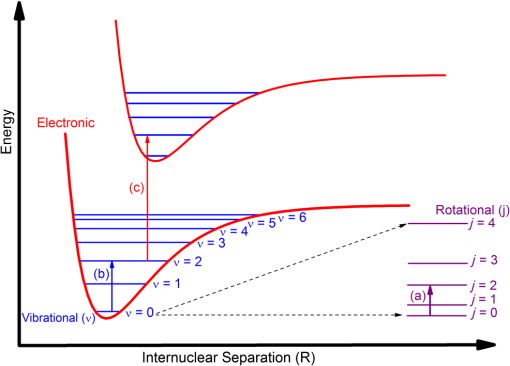 The number of normal vibrations of a molecule is given as where is the number of internal degrees of freedom. For water molecules, is equal to 3: there are three modes of normal vibrations (Fig. 3). Transitions from the ground state to the first excited state are known as fundamental transitions (e.g., 0,0,0 → 1,0,0). There are also other transition types: harmonic transitions (overtones) from the ground state (e.g., 0,0,0 → 2,0,0), combination transitions from the ground state (e.g., 0,0,0 → 1,2,1), harmonic transitions between excited states only (e.g., 1,0,0 → 3,0,0), and combination transitions between excited states only (e.g., 1,2,0 → 2,3,1).Fig. 3Normal vibration modes of a water molecule and its characteristic ground and first excited vibrational energy levels. 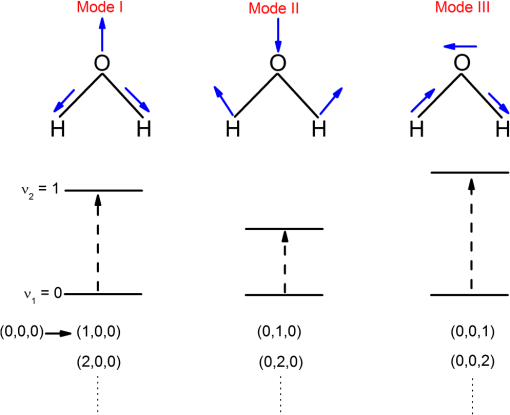 The ratio of the transmitted intensity and initial intensity of laser beam transmitting through an absorbing medium at a particular frequency is given using the Beer–Lambert equation: or where is absorption coefficient, is lineshape function, is total pressure of the medium, is mole fraction of the absorbing species, is pathlength, is the number-density of the absorbing species, and () is linestrength, which is defined as the total absorption per molecule. The linestrength of an absorption transition depends on the population in the lower quantum state, which is a function of the Boltzmann fraction, and the probability of the transition.15 The linestrength for a transition normalized to the total number density is expressed (in cgs units) by16 where and are the number density of molecules in the states and , respectively, with their corresponding statistical weights and , denotes the Planck constant, is the transition dipole moment, and (in ) is the frequency of the transition. In the case of thermal equilibrium of the system at temperature , the equation above can be rearranged using the Maxwell–Boltzmann distribution law (SI units): with the energy of the lower state and the total internal partition function . The equation for is analogue. This leads to a form of (in cm/molecule), which accords with the notation of the HITRAN database: where is the abundance. Since the linestrength in HITRAN is defined for the reference temperature , must be corrected using the tabulated values , , , and :16 where is in units of []. For units of [], the following temperature scaling can be used:15The conversion between and is given as follows:15 A typical lineshape of an isolated absorption line is centered at and has a linewidth . The absorption line can be broadened due to natural broadening, Doppler broadening, and collision broadening. The homogeneous natural and collision broadening result in Lorentzian line shapes, whereas the Doppler broadening gives rise to a Gaussian line profile. The natural linewidth is determined by the lifetimes of the energy states ( and ): The linewidth can be broadened due to the Doppler effect. The distribution of random velocities of molecules in gas is described by the Maxwellian velocity distribution function. Each velocity group gives rise to its own Doppler shift. The Doppler broadening is given by15 with Doppler halfwidth [full-width at half-maximum (FWHM)]:The perturbations that shorten energy level lifetimes cause collisional broadening. The linewidth broadening occurs due to the Heisenberg uncertainty principle; shortening the energy level lifetime results in greater uncertainty of the energy of molecule, and thus the absorption lineshape becomes broader. The lineshape for collisional broadening takes the form of a Lorentzian function:15 with collision halfwidth (FWHM): where is the mass of molecule, is the diameter of molecule, and is the pressure of gas.At low pressure, the near-Gaussian line shape is obtained because thermal motion is the dominant broadening mechanism. The line shape becomes near-Lorentzian with the increasing pressure. When the Doppler contribution can be neglected (), the line shape can be considered pure Lorentzian. In the case of , a pure Gaussian line shape is received. Molecular ro-vibrational transitions exhibit pressure broadened FWHM of () at low pressures and () at atmospheric pressure, where Doppler widths of 30 … 90 MHz () at room temperature are typically observed for molecular transitions in the infrared.16 When the condition is fulfilled (between 5 and 100 Torr for most lightweight gases), the line shape will be a combination of the Gaussian and Lorentzian, which is known as Voigt profile. 5.External Cavity Diode LasersDifferent methods can be utilized to realize a wavelength-tunable single-mode operation: tunable lasers, tunable dye lasers, tunable solid-state lasers, tunable excimer lasers, nonlinear optical frequency conversion lasers, tunable free-electron lasers, and tunable external cavity semiconductor lasers. Within the framework of this work, the focus will only be on the tunable external cavity semiconductor lasers (ECLs). Further information on the other tunable lasers can be found in, e.g., Ref. 17. Grating-coupled ECLs can be realized in Littrow or Littman configurations.18 In the Litrow configuration [Fig. 4(a)], there are a gain chip, a lens (or a parabolic mirror), and a diffraction grating. The gain chip serves as the gain medium for ECL setup. The lens (or parabolic mirror) is used to collimate the beam emitted from the gain chip. The collimated beam is diffracted by a grating. The first order of the diffracted beam is fed back into the gain medium. The wavelength is tuned by rotating the grating. Because two optical components (mirror or lens and grating) are used, the alignment is easy and the feedback is strong. In the Littman configuration [Fig. 4(b)], a mirror is added to the setup. The diffracted beam is sent back to the grating by a mirror and diffracted again. Finally, the beam reaches to the gain chip and it is amplified. The tuning is usually achieved by rotating the mirror. Because of the double pass of the beam on the grating, the optical feedback strength is reduced. However, the Littman setup has an advantage of the increased wavelength selectivity. Generally, the Littrow setup is preferable for maximizing the tuning range. To optimize the optical feedback, the incident beam and first order of the diffracted beam have to be colinear. The directions of the various orders of the diffracted beam with respect to the normal are determined by where is the angle of the incident beam, is the angle of the diffracted beam of the , order, is the period of the grating, and is the wavelength. The wave whose wavelength satisfies the condition: is selected by the grating and is amplified. For the other wavelengths, it can be written as follows: where is the angle between incident and diffracted beam [see Fig. 4(a)] and is defined asFinally, the wave, which makes an angle , is focalized on the facet at a distance: where is the focal length of the lens.The reflectivity of the facet inside the external cavity setup is very important for a properly operating ECL. This reflectivity should be as low as possible to effectively suppress the Fabry–Perot modes of the gain chip, so a pure single mode can be selected and amplified. The reflectivity of the outcoupling facet of the gain chip can be reduced by various ways, such as the tilted gain stripes, the buried facets, and the antireflection (AR) coating. The tilting of the waveguide decreases in the internal Fresnel reflection from the facet and therefore increases the losses.19,20 In the case of buried facets, a semi-insulating material between the end of the guide and the facet, which reduces the coupling of the beam back into the active region, is utilized.21 When a facet is AR-coated, a phase shift of and, therefore, an optical path difference of occur after the reflection in the optical thick medium. The reduction of the reflectivity of the AR-coated facet is achieved by the destructive interference between the waves reflected from the front and rear sides of the layer. The reflectivity reduction causes a decrease in the competition between the modes of the small cavity (gain chip) and of the large cavity (ECL) for oscillation. This situation leads to enhancement of the coupling efficiency to the EC, to increased output power of the ECL, and to enlarged coarse/fine tuning range and the range of the stable operating region. 5.1.Wavelength SelectionTuning mechanism of an ECL can be explained by considering a sketch for the gain and losses in the ECL setups (Fig. 5).17 As one can see in Fig. 5, there are three loss mechanisms: (1) Filter loss due to the wavelength selectivity property of the wavelength selective element (e.g., grating), (2) coupling and output loss between the guided waves in the gain chip and vacuum in ECL, and (3) facet etalon loss, which is modulated at the period of the internal Fabry Perot mode spacing . The facet etalon loss is caused by the interference between the reflections from facets. The injection current is controlled to tune the gain profile of the gain chip and the internal cavity mode frequency. To vary the external mode frequency, the grating can be rotated and/or the EC length can be changed by applying the voltage to a piezoelectric transducer controlling the grating position. For a perfect operation of the ECLs, the facet etalon loss ripple should be weak and the bandwidth of the wavelength selective element loss should be narrow compared with the period of the ripple. The bandwidth of the grating can be estimated by the following equation: where is the wavelength, is the diameter of the collimated laser beam, and is the incident angle of the beam. Only the EC mode, which is the closest to the loss minimum of the wavelength selective element, can oscillate. The other modes see higher losses and cannot be amplified. Tuning to the next EC mode can be achieved by varying the loss minimum of the wavelength selective element. In the case of the grating-coupled ECLs in Littrow configuration, this variation occurs by rotating the grating [Fig. 6(a)] and/or changing the cavity length [Fig. 6(b)]. A strong facet etalon loss and a wider bandwidth of the wavelength-selective element loss lead to tuning with EC mode jumps approximately equal to . This discontinuity is called “tuning gap” [Figs. 6(a) and 6(b)]. The shift in the external mode frequency exceeding half the free spectral range of the external cavity gives rise to mode hops. At this point, the adjacent external mode has moved closer to the peak of the internal mode, and the laser oscillation hops to this new mode.22 To achieve the tuning without any gap (tuning on the EC mode, mode-hop-free tuning) [Fig. 6(c)], there are different methods: (1) the injection current, the grating angle, and/or the external cavity length should be simultaneously controlled;23 (2) the grating has to be mounted on a pivot arm, which is rotated about an axis lying near the intersection of the grating and laser output facet plane;24 and (3) an electro-optically tunable single-mode ECL has to be built.255.2.Spectral Tuning CharacteristicsTo consider the gain chip and the ECL as a combined laser system with a compound cavity, the intracavity facet should have a low reflectivity, and the coherence length should be longer than the distance from the gain chip to the grating. The tuning range is limited by the gain bandwidth of the used gain chip that is an inherent characteristic of the gain medium. The separation between the FP and EC modes must be larger than the bandwidth of the grating for a single-mode operation. This can be achieved, for instance, using an appropriate AR coating. The theoretically reachable tuning range of an ECL for wavelength is given by26 and, equivalently, the frequency tuning range: where is the emission wavelength, is the FWHM of the modal gain spectrum, is the photon energy at the gain maximum, is the apex of the modal gain spectrum, is the Planck constant, is the chip length, is the first-order efficiency of the grating, and is the lens transmission. The relative tuning is given by , where is the center wavelength and and are the shortest and the largest achievable wavelengths, respectively, in the ECLs. From these equations, one can conclude that the following should be considered to increase the tuning range: a gain chip with a broad gain bandwidth should be used in an ECL setup, and reflectivity from the facet inside the ECL should be decreased by one of the methods mentioned above. In Table 1, some ECLs reported in the spectral range between 1.0 and are listed.Table 1Some ECLs in the spectral range between 1 and 11 μm.
Note: RT, room temperature; nRT, near room temperature; FR, free running; FS, frequency stabilized; NS, not stated. 5.3.LinewidthThe laser linewidth (FWHM of the lineshape) describes the spectral purity of a laser (Fig. 7). The linewidth of a semiconductor laser is given by the Schawlow–Townes formula modified by Henry (Ref. 37 and references therein): where is the lasing frequency, is the total losses of the cavity, is the mirror losses of the output facet, is the output power, is the FWHM of the cavity resonance, and are the populations of the upper and lower states of the laser transition at threshold, respectively, and is the linewidth enhancement factor introduced by Henry. The imaginary () and real parts () of the refractive index change during the relaxation oscillations of the field intensity. Varying of the imaginary part of the index causes the gain to change, whereas the change in the real part of the refractive index gives rise to an additional phase shift. Therefore, the laser linewidth is broadened by a factor () compared with the Schawlow–Townes linewidth. The lower energy level of semiconductor lasers is not empty, which is different from most other lasers. As laser photons in the valence band may reradiate by spontaneous emission, phase fluctuations of the laser field increase. This is another phenomenon that leads to the linewidth broadening of semiconductor lasers.Loh et al.38 investigated experimentally the influence of the grating reflectivity, grating resolution, and AR coating on the intrinsic linewidth of a grating-coupled ECL. They found that the linewidths are little affected by the presence of an AR coating on the diode facet and that the grating resolution has a larger effect on the linewidth than the grating reflectivity.38 The laser linewidth can be determined using several methods, such as optical cavity measurements,29 heterodyne measurements,37 homodyne/heterodyne interferometry using a long interferometer delay,39 measurements from the frequency noise power spectral density,40 measurements from root-mean-square frequency deviation,41 and saturation spectroscopy.42 Tkach and Chraplyvy43 reported that there are five distinct regimes of feedback effects, with well-defined transitions between them as a function of feedback power ratio. At the lowest levels of feedback down to (regime I), linewidth narrowing or broadening is observed depending on the phase of the feedback. Regime II is seen at a feedback level (up to around ), which depends on the distance to the external reflector, and frequency splitting of the mode and mode hopping are observed. Regime III is found at a level (about to ), which does not depend on the distance to the reflection. In this regime, the mode hopping is suppressed, and the laser is observed to operate on a single narrow line. Regime IV starts at and is independent from the distance to the reflection. In this regime, line broadening is observed due to the coherence collapse effect. Relaxation oscillation sidebands that present in each mode in the optical spectrum increase in strength giving rise to the line broadening. Consequently, coherence time decreases. Regime V is independent of distance too and observed at the highest levels of feedback (usually greater than ). AR coating of output facet is needed to achieve this regime. In this regime, the operation of the laser occurs on a single longitudinal mode with narrow linewidth for all phases of the feedback and the laser is relatively insensitive to additional external optical perturbations.43 5.4.Frequency StabilizationThere are different noise sources, which can affect on the laser’s linewidth: (1) fundamental noises (white, shot, and thermal noises): the intrinsic Lorentzian linewidth can be reduced using optical feedback44 and (2) flicker () noises and technical noises (noises from the laser driver, piezo drift, mechanical vibrations, temperature fluctuations, acoustic noises, air pressure fluctuations). These noise sources broaden the laser linewidth. This Gaussian linewidth can be measured using the methods given above. For reduction of these noises, with other word, stabilization of a laser’s frequency over time and consequently narrowing the linewidth of laser, there are different stabilization techniques, such as side-of-fringe stabilization,45 on-peak-locking, Paul–Drever–Hall (PDH) method.46 Using these techniques, the sub-kHz-linewidth47 and sub-Hz-linewidth48 ECLs have been reported. 5.5.Rate EquationsA set of rate equations can describe the time evolution of the photon flux and the electronic populations of the upper and lower states of the radiative transition . Yang et al.26 conducted rate equations analysis of EC quantum cascade lasers. They considered a four-level quantum cascade laser structure. The EC system was simplified to an effective system with both the internal cavity and the EC having the same cavity length . To consider the longer round-trip time of the EC, they used the effective speed of light introduced by Maulini.49 The EC can be simplified to have an effective cavity length of but with a reduced speed of light , where , and are the round-trip times of the internal cavity and the EC, respectively. The rate equations then are given by26,49,50 where is the injection current density, is the unit charge, and are the sheet carrier density of upper laser level 3 and lower laser level 2, represents the nonradiative scattering lifetime from level to level (, , 2, 3), , , is the spontaneous emission time (calculated to be ), is the fraction of the spontaneous light emitted in the lasing mode, is the photon flux density (per unit length per second) generated by the laser chip facets, is the photon flux density for a certain mode selected by the external cavity, and represent the total losses corresponding to the frequencies of FP mode and the EC mode, and denote the values of the gain cross-section corresponding to the frequencies of FP mode and the EC mode and are determined by26 where is the matrix dipole element of the optical transition, is the optical confinement factor of the laser, is the free-space permittivity, is the period length of the QCL, is the emission wavelength, is the FWHM of the gain spectrum, is the lasing frequency, and is the Planck constant.6.External Cavity Laser-Based Techniques for Breath AnalysisThe ECL-based techniques can be effectively used for the detection and quantification of breath VOCs at concentrations ranging from parts per million by volume (ppmv) to the parts per trillion (pptv) level. The laser sources should have high sensitivity and selectivity for breath molecule sensing. For selectivity, an absorption line that is free of interference from other species in gas mixture should be used. For the best sensitivity, a strong molecular absorption line should be chosen. To achieve a higher signal-to-noise ratio (SNR), either the noise levels should be decreased and/or the signal should be enhanced. For decreasing the noise levels, there are different methods, such as wavelength/frequency modulation spectroscopy. The signal can be further increased by obtaining an effective long pathlength using multipass cells or cavity enhancement methods. ECL-based spectroscopic detection techniques, such as multipass cell absorption method (MCAB), CRDS, CEAS, ICOS, PAS, and QEPAS, provide the features of high-sensitivity, high-selectivity, low costs, real-time measurements, and PoC function. Furthermore, laser-based techniques can be implemented without the need for radioactive labels. Therefore, these methods are candidates for performing accurate breath diagnostics in hospitals. In Table 2, some important breath molecules, detection wavelength, detection limit, and methods are summarized. Table 2Some important breath molecules, detection wavelengths, detection limits, and methods.
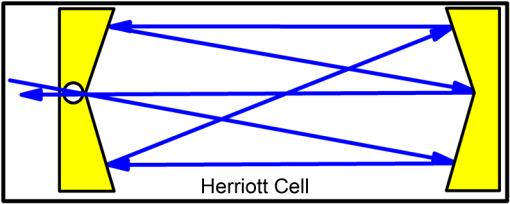
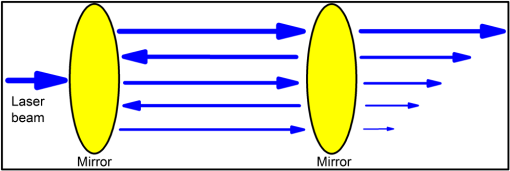
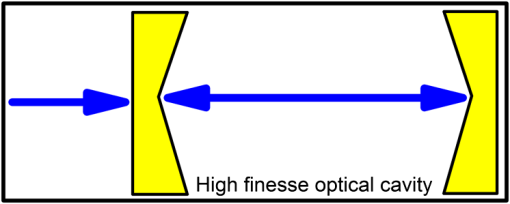
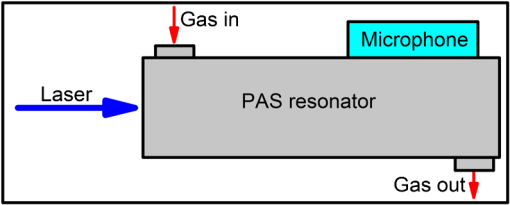
Note: CRDS, cavity ringdown spectroscopy; CEAS, cavity-enhanced absorption spectroscopy; (QE)PAS, (quartz-enhanced) photoacoustic absorption spectroscopy; MPAS, multipass absorption spectroscopy; WMS, wavelength modulation spectroscopy. 6.1.Multipass Absorption SpectroscopyIn the MCAB,75 the absorption signal can be enhanced via longer optical pathlengths using optical multipass cells. There are four types of multipass cells most commonly applied: White cells,76,77 Herriott cells,78 Chernin cells,79 and astigmatic mirror multipass cells.80 Beer–Lambert law of linear absorption is used to determine the absorption coefficient : where is transmitted intensity of the radiation after a distance through the medium, is initial intensity of the radiation, is effective path-length, is absorption cross-section of the absorbing species, is molecular concentration (the number density of the absorbing species), is linestrength (i.e., the total absorption per molecule) of the absorbing species at temperature , is line shape function for the particular absorption line.Using Eq. (33), the absolute number density can be calculated by integrating the absorption coefficient: The Herriott cell consists of two mirrors (Fig. 8). The input mirror has a small hole. A laser beam is injected into a Herriott cell through the hole and it is reflected multiple times between the two mirrors. The light path might be lengthened 10 or 100 times inside the cell. The laser beam leaving the cell through the same or the other hole reaches the detector. The sensors employing a multipass gas cell have been reported for many trace gases, such as acetaldehyde,51 ethane,61 formaldehyde,67 and methane.71,72 6.2.Cavity Ringdown SpectroscopyCRDS81 is based on the observation of the decay rate of a laser beam stored in an optical cavity formed from ultra-high reflective mirrors (Fig. 9) and is first demonstrated by O’Keefe and Deacon.82 In this case, the absorption coefficient is determined using the following equation: where and are the ringdown time without and with the absorbing gas present, is the light velocity.A laser beam, which is coupled into the optical cavity, is reflected back and forth inside the cavity. When beam is reflected every time, a small fraction of this light leaks out of the cavity. Many trace gases, such as acetone,52 carbon dioxide,57 ethanol,63 isoprene,70 and nitric oxide,73,74 have been analyzed using the CRDS technique. 6.3.Integrated Cavity Absorption Spectroscopy and Cavity-Enhanced Absorption SpectroscopyICOS83 and CEAS84 are the same method. ICOS is used in the context of pulsed excitation, and CEAS is used in the context of continuous-wave cavity excitation. This method is based on analyzing the intensity of light transmitted through a high finesse optical cavity as a function of wavelength (Fig. 10). To reduce the noise levels and therefore to improve the detection limit, the laser beam can be coupled into the optical cavity at a small angle with respect to the cavity axis or away from the central axis of the optical cavity. This is known as “off-axis alignment,” which has advantage over on-axis alignment: it is almost insensitive to vibrations. In the case of ICOS and CEAS, Eq. (36) is applied to extract the absorption coefficient: where is mirror reflectivity and is the distance between mirrors.The gases—such as acetone,53 ammonia,54 carbon monoxide,54 carbonyl sulfide,60 and ethane60—have been analyzed using the ICOS or CEAS techniques. 6.4.Photoacoustic Spectroscopy and Quartz-Enhanced Photoacoustic SpectroscopyIn the PAS,85 the acoustic waves resulting from the absorption of radiation (photoacoustic effect) are detected and analyzed using a sensitive microphone (Fig. 11). The PAS response to optical absorption is given by Eq. (37): where is the absorption coefficient per unit concentration of the target species, is the concentration of the target species, is the optical power, is the PA sound frequency, is the resonator cross-section area, and is a constant describing the microphone transfer function and other system parameters. Usually, PA resonators are designed for values in the 500 to 4000 Hz range and have factors of to 200.86Another approach to photoacoustic detection of trace gases is QEPAS,86,87 which utilizes a quartz tuning fork (QTF) as a sharply resonant acoustic transducer. The QTF is a piezoelectric element. To further increase the QEPAS signal, a microresonator can be added to the QEPAS sensor system.88 Also, to achieve the best QEPAS detection sensitivity and selectivity, it is important to choose the optimum operating pressure for a QEPAS sensor system. The PAS- or QEPAS-based sensors have been used for the detection of many gases, such as ammonia,55,56 carbonyl disulfide,58 carbon monoxide,59 ethanol,62 ethylene,64–66 and hydrogen sulfide.68,69 7.Breath BiomarkersOwing to its noninvasiveness, ease of use, easy repeatability, and painlessness, breath analysis has attracted considerable attention for scientific and clinical studies. Until now, many studies have demonstrated that the human breath air contains more than 1000 different molecules.2,89 The matrix of exhaled breath air is much less complicated compared to serum or urine. A few atmospheric molecules in % concentration (, , , ), inorganic gases (e.g., NO, , and CO), VOCs at the levels of parts per million (ppm), parts per billion (ppb), or parts per trillion (ppt) (e.g., , , ), and nonvolatile substances measured in breath condensate (e.g., isoprostanes, cytokines, leukotrienes) have been found to be present in exhaled human breath (Table 3). Spectral fingerprints of these molecules span from the UV to the IR spectral regions. The mixture is exhaled at temperatures between 34°C and 37°C while relative humidity may range from 91% to 96% in oral exhalations and from 82% to 85% in nasal exhalations.90 The mixture of exhaled breath air varies from person to person both quantitatively and qualitatively.91 Analysis of some VOCs, which present in everyone, can provide a safe method for studying human metabolism, detecting diseases, clinical diagnosis, therapeutic monitoring, and investigation of potential adverse effects of new drug therapy. In Table 4, some important breath molecules, concentration, physiological basis, and related diseases are summarized. The 872 breath VOCs from apparently healthy humans have been reported in the review article of de Lacy Costello et al.89 Table 3Main breath molecules.3
Table 4Some important breath molecules, concentration, physiological basis, and related diseases.
8.Limitations of Breath AnalysisIt has been known for a long time that the smell of exhaled breath is an indicator for diseases.122 The work of Pauling et al., in which hundreds of VOCs were determined in normal human breath at the levels of parts per billion (ppb) or lower, has been accepted as the beginning of the modern breath analysis. In spite of the long investigation time, this method has not yet been introduced as a standard tool into clinical diagnosis. Very few diseases are actually diagnosed using exhaled breath air analysis; for example, breath urea analysis. There are several potential confounders and issues blocking the introduction of breath analysis into clinical applications. To widely use the breath test for more specific diseases in hospitals, the following issues should be addressed:123–125
To address all these issues and to move breath analysis forward, collaboration among optical engineers, experts in breath analysis, clinicians, and spectroscopists is required. 9.Conclusion and OutlookSeveral issues should be addressed for advances in the field of breath monitoring and for widespread usage of this method as a routine clinical tool. Breath analysis has not yet been used in hospitals as a clinical tool due to lack of generally accepted evaluation criteria for data. Multiple potential confounders, such as interference from other molecules, smoking and alcohol consumption, dermal absorption, inhalation from the ambient air, and so on, should be carefully considered when performing measurements of breath biomarkers. Breath research may be performed as (1) exploratory research (the discovery of new breath molecules, e.g., breath markers for chronic kidney disease), (2) focused research (the in-depth evaluation of a molecule whose biochemistry is already well-understood, e.g., breath acetone), and (3) breath condensate (the analysis of nonvolatile molecules).123 Breath analyses conducted by the techniques, such as GC-MS, SIFT-MS, and PTR-MS, are still in laboratory research. The development of inexpensive, real-time, portable breath monitors is a key factor in the advancement of breath tests. Such devices should be moved from laboratory research to commercial reality. Laser-based spectroscopic instruments are a good candidate for this field. The current laser-based methods are not satisfactory for medical applications as routine diagnostics tool. Technologies in laser physics and optical engineering should be further improved. The development of absorption spectroscopy instruments with lasers may provide certain advantages for sensitive examination of not only small molecules but also heavy molecules with relatively broad spectral structures. The issue of spectral interferences can be eliminated using single-mode tunable laser. Another type of interference, which should be considered, is biointerferences; for instance, ammonia is a biomarker for both asthma and chronic kidney diseases. This challenging field requires the extensive interdisciplinary collaborations. The availability of a cheap breath analyzer can even enable patients to measure their own biomarker levels at home. This situation can result in performing more large cross-sectional and longitudinal in-depth studies with many data points, instead of making just small pilot studies limiting the gain of widespread usage of breath analysis. One may expect that the issues mentioned in the present manuscript may be soon addressed and breath analysis may be introduced into clinical practice. DisclosuresThe author has no relevant financial interests and no other potential conflicts of interest to disclose. ReferencesL. Ciaffoni, R. Peverall and G. A. D. Ritchie,
“Laser spectroscopy on volatile sulfur compounds: possibilities for breath analysis,”
J. Breath Res., 5 024002
(2011). http://dx.doi.org/10.1088/1752-7155/5/2/024002 Google Scholar
C. Wang and P. Sahay,
“Breath analysis using laser spectroscopic techniques: breath biomarkers, spectral fingerprints, and detection limits,”
Sensors, 9 8230
–8262
(2009). http://dx.doi.org/10.3390/s91008230 SNSRES 0746-9462 Google Scholar
J. Wojtas et al.,
“Ultrasensitive laser spectroscopy for breath analysis,”
Opto-Electron. Rev., 20 26
–39
(2012). http://dx.doi.org/10.2478/s11772-012-0011-4 OELREM 1230-3402 Google Scholar
T. H. Risby and F. K. Tittel,
“Current status of mid-infrared quantum and interband cascade lasers for clinical breath analysis,”
Opt. Eng., 49 111123
(2010). http://dx.doi.org/10.1117/1.3498768 Google Scholar
Z. Bielecki et al.,
“Application of quantum cascade lasers to trace gas detection,”
Bull. Pol. Acad. Sci. Tech. Sci., 63 515
–525
(2015). http://dx.doi.org/10.1515/bpasts-2015-0059 Google Scholar
S. S. Kim et al.,
“Potential and challenges for mid-infrared sensors in breath diagnostics,”
IEEE Sens. J., 10 145
–158
(2010). http://dx.doi.org/10.1109/JSEN.2009.2033940 ISJEAZ 1530-437X Google Scholar
K. K. Chow, M. Short and H. Zeng,
“A comparison of spectroscopic techniques for human breath analysis,”
Biomed. Spectrosc. Imaging, 1 339
–353
(2012). http://dx.doi.org/10.3233/BSI-120029 Google Scholar
M. R. McCurdy et al.,
“Recent advances of laser-spectroscopy-based techniques for applications in breath analysis,”
J. Breath Res., 1 014001
(2007). http://dx.doi.org/10.1088/1752-7155/1/1/014001 Google Scholar
J. C. Anderson and M. P. Hlastala,
“Breath tests and airway gas exchange,”
Pulm. Pharmacol. Ther., 20 112
–117
(2007). http://dx.doi.org/10.1016/j.pupt.2005.12.002 Google Scholar
J. C. Anderson, A. L. Babb and M. P. Hlastala,
“Modeling soluble gas exchange in the airways and alveoli,”
Ann. Biomed. Eng., 31 1402
–1422
(2003). http://dx.doi.org/10.1114/1.1630600 ABMECF 0090-6964 Google Scholar
L. E. Farhi,
“Elimination of inert gas by the lung,”
Respir. Physiol., 3 1
–11
(1967). http://dx.doi.org/10.1016/0034-5687(67)90018-7 Google Scholar
J. King et al.,
“A mathematical model for breath gas analysis of volatile organic compounds with special emphasis on acetone,”
J. Math. Biol., 63 959
–999
(2011). http://dx.doi.org/10.1007/s00285-010-0398-9 JMBLAJ 0303-6812 Google Scholar
W. Miekisch, J. K. Schubert and G. F. E. Noeldge-Schomburg,
“Diagnostic potential of breath analysis—focus on volatile organic compounds,”
Clin. Chim. Acta, 347 25
–39
(2004). http://dx.doi.org/10.1016/j.cccn.2004.04.023 CCATAR 0009-8981 Google Scholar
M. E. O’Hara et al.,
“Development of a protocol to measure volatile organic compounds in human breath: a comparison of rebreathing and on-line single exhalations using proton transfer reaction mass spectrometry,”
Physiol. Meas., 29 309
–330
(2008). http://dx.doi.org/10.1088/0967-3334/29/3/003 PMEAE3 0967-3334 Google Scholar
M. E. Webber,
“Diode laser measurements of and for combustion and bioreactor applications,”
Stanford University,
(2001). Google Scholar
S. Welzel,
“New enhanced sensitivity infrared laser spectroscopy techniques applied to reactive plasmas and trace gas detection,”
Ernst-Moritz-Arndt Universität Greifswald,
(2009). Google Scholar
Tunable Lasers Handbook (Optics and Photonics), Eastman Kodak Company, Rochester, New York
(1995). Google Scholar
M. G. Littman and H. J. Metcalf,
“Spectrally narrow pulsed dye laser without beam expander,”
Appl. Opt., 17 2224
–2227
(1978). http://dx.doi.org/10.1364/AO.17.002224 APOPAI 0003-6935 Google Scholar
D. R. Scifres, W. Streifer and R. D. Burnham,
“GaAs/GaAlAs diode lasers with angled pumping stripes,”
IEEE J. Quantum Electron., 14 223
–227
(1978). http://dx.doi.org/10.1109/JQE.1978.1069780 Google Scholar
M. C. Robbins, J. Buus and D. J. Robbins,
“Analysis of antireflection coatings on angled facet semiconductor laser amplifiers,”
Electron. Lett., 26 381
(1990). http://dx.doi.org/10.1049/el:19900248 ELLEAK 0013-5194 Google Scholar
N. K. Dutta et al.,
“Fabrication and performance characteristics of buried-facet optical amplifiers,”
J. Appl. Phys., 67 3943
–3947
(1990). http://dx.doi.org/10.1063/1.345003 JAPIAU 0021-8979 Google Scholar
S. Dutta, D. S. Elliott and Y. P. Chen,
“Mode-hop-free tuning over 135 GHz of external cavity diode lasers without antireflection coating,”
Appl. Phys. B, 106 629
–633
(2012). http://dx.doi.org/10.1007/s00340-011-4841-4 Google Scholar
A. T. Schremer and C. L. Tang,
“External-cavity semiconductor laser with 1000 GHz continuous piezoelectric tuning range,”
IEEE Photonics Technol. Lett., 2 3
–5
(1990). http://dx.doi.org/10.1109/68.47023 IPTLEL 1041-1135 Google Scholar
F. Favre and D. Le Guen,
“82 nm of continuous tunability for an external cavity semiconductor laser,”
Electron. Lett., 27 183
–184
(1991). http://dx.doi.org/10.1049/el:19910117 Google Scholar
L. Levin,
“Mode-hop-free electro-optically tuned diode laser,”
Opt. Lett., 27 237
(2002). http://dx.doi.org/10.1364/OL.27.000237 OPLEDP 0146-9592 Google Scholar
Q. K. Yang et al.,
“Rate equations analysis of external-cavity quantum cascade lasers,”
J. Appl. Phys., 107 043109
(2010). http://dx.doi.org/10.1063/1.3309764 Google Scholar
I. Bayrakli,
“Frequency stabilization at the sub-kilohertz level of an external cavity diode laser,”
Appl. Opt., 55 2463
–2466
(2016). Google Scholar
I. Bayrakli,
“Actively frequency-stabilized external cavity diode laser with a linewidth of 2.9 kHz,”
Opt. Quantum Electron., 48 1
–8
(2016). http://dx.doi.org/10.1007/s11082-015-0305-0 OQELDI 0306-8919 Google Scholar
I. Bayrakli and H. Akman,
“Ultrasensitive, real-time analysis of biomarkers in breath using tunable external cavity laser and off-axis cavity enhanced absorption spectroscopy,”
J. Biomed. Opt., 20
(3), 037001
(2015). http://dx.doi.org/10.1117/1.JBO.20.3.037001 JBOPFO 1083-3668 Google Scholar
S. Bennetts et al.,
“External cavity diode lasers with 5 kHz linewidth and 200 nm tuning range at and methods for linewidth measurement,”
Opt. Express, 22 10642
–10654
(2014). http://dx.doi.org/10.1364/OE.22.010642 OPEXFF 1094-4087 Google Scholar
S. Tan et al.,
“Low-threshold, high SMSR tunable external cavity quantum cascade laser around ,”
Opt. Quantum Electron., 45 1147
–1155
(2013). http://dx.doi.org/10.1007/s11082-013-9731-z OQELDI 0306-8919 Google Scholar
G. Wysocki et al.,
“Widely tunable mode-hop free external cavity quantum cascade laser for high resolution spectroscopic applications,”
Appl. Phys. B, 81 769
–777
(2005). http://dx.doi.org/10.1007/s00340-005-1965-4 Google Scholar
T. Dougakiuchi et al.,
“Broadband tuning of external cavity dual-upper-state quantum-cascade lasers in continuous wave operation,”
Appl. Phys Express, 4 102101
(2011). http://dx.doi.org/10.1143/APEX.4.102101 APEPC4 1882-0778 Google Scholar
R. Maulini et al.,
“External cavity quantum-cascade laser tunable from 8.2 to using a gain element with a heterogeneous cascade,”
Appl. Phys. Lett., 88 201113
(2006). http://dx.doi.org/10.1063/1.2205183 APPLAB 0003-6951 Google Scholar
A. Hugi et al.,
“External cavity quantum cascade laser tunable from 7.6 to ,”
Appl. Phys. Lett., 95 061103
(2009). http://dx.doi.org/10.1063/1.3193539 APPLAB 0003-6951 Google Scholar
A. Wittmann et al.,
“Heterogeneous high-performance quantum-cascade laser sources for broad-band tuning,”
IEEE J. Quantum Electron., 44 11
(2008). http://dx.doi.org/10.1109/JQE.2008.2001928 IEJQA7 0018-9197 Google Scholar
R. Maulini et al.,
“Continuous-wave operation of a broadly tunable thermoelectrically cooled external cavity quantum-cascade laser,”
Opt. Lett., 30 2584
(2005). http://dx.doi.org/10.1364/OL.30.002584 OPLEDP 0146-9592 Google Scholar
H. Loh et al.,
“Influence of grating parameters on the linewidths of external-cavity diode lasers,”
Appl. Opt., 45 9191
–9197
(2006). http://dx.doi.org/10.1364/AO.45.009191 APOPAI 0003-6935 Google Scholar
T. Okoshi, K. Kikuchi and A. Nakayama,
“Novel method for high resolution measurement of laser output spectrum,”
Electron. Lett., 16 630
–631
(1980). http://dx.doi.org/10.1049/el:19800437 ELLEAK 0013-5194 Google Scholar
G. Di Domenico, S. Schilt and P. Thomann,
“Simple approach to the relation between laser frequency noise and laser line shape,”
Appl. Opt., 49 4801
–4807
(2010). http://dx.doi.org/10.1364/AO.49.004801 APOPAI 0003-6935 Google Scholar
D. S. Elliott, R. Rajarshi and S. J. Smith,
“Extracavity laser band-shape and bandwidth modification,”
Phys. Rev. A, 26 12
–18
(1982). http://dx.doi.org/10.1103/PhysRevA.26.12 Google Scholar
N. Mukherjee et al.,
“Linewidth measurement of external grating cavity quantum cascade laser using saturation spectroscopy,”
Appl. Phys. Lett., 92 111116
(2008). http://dx.doi.org/10.1063/1.2901038 APPLAB 0003-6951 Google Scholar
R. W. Tkach and A. R. Chraplyvy,
“Regimes of feedback effects in distributed feedback laser,”
J. Lightwave Technol., 4 1655
–1661
(1986). http://dx.doi.org/10.1109/JLT.1986.1074666 JLTEDG 0733-8724 Google Scholar
P. Samutpraphoot et al.,
“Passive intrinsic-linewidth narrowing of ultraviolet extended-cavity diode laser by weak optical feedback,”
Opt. Express, 22 11592
–11599
(2014). http://dx.doi.org/10.1364/OE.22.011592 OPEXFF 1094-4087 Google Scholar
M. Kourogi and M. Ohtsu,
“Novel optical frequency discriminator for FM noise reduction of semiconductor lasers,”
Opt. Commun., 81 204
–208
(1991). http://dx.doi.org/10.1016/0030-4018(91)90639-U OPCOB8 0030-4018 Google Scholar
R. W. P. Drever et al.,
“Laser phase and frequency stabilization using an optical resonator,”
Appl. Phys. B, 31 97
–105
(1983). http://dx.doi.org/10.1007/BF00702605 Google Scholar
Y. Zhao et al.,
“100-Hz linewidth diode laser with external optical feedback,”
IEEE Photonics Technol. Lett., 24 1795
–1798
(2012). http://dx.doi.org/10.1109/LPT.2012.2214029 IPTLEL 1041-1135 Google Scholar
S. Hirata et al.,
“Sub-hertz-linewidth diode laser stabilized to an ultralow-drift high-finesse optical cavity,”
Appl. Phys. Express, 7 022705
(2014). http://dx.doi.org/10.7567/APEX.7.022705 APEPC4 1882-0778 Google Scholar
R. Maulini,
“Broadly tunable mid-infrared quantum cascade lasers for spectroscopic applications,”
Université de Neuchâtel,
(2006). Google Scholar
J. Faist et al., Semiconductors and Semimetals Quantum Cascade Laser, 66 Academic Press, San Diego
(2000). Google Scholar
P. C. Kamat et al.,
“Measurement of acetaldehyde in exhaled breath using a laser absorption spectrometer,”
Appl. Opt., 46 3969
–3975
(2007). http://dx.doi.org/10.1364/AO.46.003969 APOPAI 0003-6935 Google Scholar
M. Sun et al.,
“A fully integrated standalone portable cavity ringdown breath acetone analyzer,”
Rev. Sci. Instrum., 86 095003
(2015). http://dx.doi.org/10.1063/1.4930121 RSINAK 0034-6748 Google Scholar
L. Ciaffoni et al.,
“Demonstration of a mid-infrared cavity enhanced absorption spectrometer for breath acetone detection,”
Anal. Chem., 85 846
–850
(2013). http://dx.doi.org/10.1021/ac3031465 ANCHAM 0003-2700 Google Scholar
M. J. Thorpe et al.,
“Cavity-enhanced optical frequency comb spectroscopy: application to human breath analysis,”
Opt. Express, 16 2387
–2397
(2008). http://dx.doi.org/10.1364/OE.16.002387 OPEXFF 1094-4087 Google Scholar
A. A. Kosterev and F. K. Tittel,
“Ammonia detection by use of quartz-enhanced photoacoustic spectroscopy with a near-IR telecommunication diode laser,”
Appl. Opt., 43 6213
–6217
(2004). http://dx.doi.org/10.1364/AO.43.006213 APOPAI 0003-6935 Google Scholar
R. Lewicki et al.,
“Real time ammonia detection in exhaled human breath using a distributed feedback quantum cascade laser based sensor,”
Proc. SPIE, 7945 79450K
(2011). http://dx.doi.org/10.1117/12.874887 PSISDG 0277-786X Google Scholar
E. R. Crosson et al.,
“Stable isotope ratios using cavity ring-down spectroscopy: determination of 13C/12C for carbon dioxide in human breath,”
Anal. Chem., 74 2003
–2007
(2002). http://dx.doi.org/10.1021/ac025511d ANCHAM 0003-2700 Google Scholar
J. P. Waclawek, H. Moser and B. Lendl,
“Compact quantum cascade laser based quartz-enhanced photoacoustic spectroscopy sensor system for detection of carbon disulfide,”
Opt. Express, 24 6559
–6571
(2016). http://dx.doi.org/10.1364/OE.24.006559 OPEXFF 1094-4087 Google Scholar
M. Yufei et al.,
“Sensitive detection of carbon monoxide based on a QEPAS sensor with a fiber-coupled antimonide diode laser,”
J. Opt., 17 055401
(2015). http://dx.doi.org/10.1088/2040-8978/17/5/055401 JOOPDB 0150-536X Google Scholar
J. Wojtas,
“Application of cavity enhanced absorption spectroscopy to the detection of nitric oxide, carbonyl sulphide, and ethane-breath biomarkers of serious diseases,”
Sensors, 15 14356
–14369
(2015). http://dx.doi.org/10.3390/s150614356 SNSRES 0746-9462 Google Scholar
C. Li et al.,
“Compact TDLAS based optical sensor for ppb-level ethane detection by use of a room-temperature CW interband cascade laser,”
Sens. Actuators B, 232 188
–194
(2016). http://dx.doi.org/10.1016/j.snb.2016.03.141 SABCEB 0925-4005 Google Scholar
I. R. Ivascu et al.,
“ laser photoacoustic measurements of ethanol absorption coefficients within infrared region of ,”
Spectrochim. Acta Part A, 163 115
–119
(2016). http://dx.doi.org/10.1016/j.saa.2016.03.038 Google Scholar
S. Zhou, Y. Han and B. Li,
“Simultaneous detection of ethanol, ether and acetone by mid-infrared cavity ring-down spectroscopy at ,”
Appl. Phys. B, 122 187
(2016). http://dx.doi.org/10.1007/s00340-016-6465-1 Google Scholar
M. Navas, A. Jiménez and A. Asuero,
“Human biomarkers in breath by photoacoustic spectroscopy,”
Clin. Chim. Acta, 413 1171
–1178
(2012). http://dx.doi.org/10.1016/j.cca.2012.04.008 CCATAR 0009-8981 Google Scholar
R. Cernat et al.,
“Laser photoacoustic spectroscopy method for measurements of trace gas concentration from human breath,”
Rom. Rep. Phys., 62 610
–616
(2010). RORPED 1221-1451 Google Scholar
Z. Wang, J. Geng and W. Ren,
“Quartz-enhanced photoacoustic spectroscopy (QEPAS) detection of the ν 7 band of ethylene at low pressure with interference analysis,”
Appl. Spectrosc., 1
–8
(2017). http://dx.doi.org/10.1177/0003702817690406 APSPA4 0003-7028 Google Scholar
W. Ren, L. Luo and F. K. Tittel,
“Sensitive detection of formaldehyde using an interband cascade laser near ,”
Sens. Actuators, B, 221 1062
–1068
(2015). http://dx.doi.org/10.1016/j.snb.2015.07.078 Google Scholar
A. Szabo et al.,
“In situ and wide range quantification of hydrogen sulfide in industrial gases by means of photoacoustic spectroscopy,”
Meas. Sci. Technol., 24 065501
(2013). http://dx.doi.org/10.1088/0957-0233/24/6/065501 Google Scholar
S. Viciani et al.,
“A quartz-enhanced photoacoustic sensor for trace-gas detection at ,”
Appl. Phys. B, 119 21
–27
(2015). http://dx.doi.org/10.1007/s00340-014-5991-y Google Scholar
P. Sahay, S. Scherrer and C. Wang,
“Measurements of the weak UV absorptions of isoprene and acetone at 261–275 nm using cavity ringdown spectroscopy for evaluation of a potential portable ringdown breath analyzer,”
Sensors, 13 8170
–8187
(2013). http://dx.doi.org/10.3390/s130708170 SNSRES 0746-9462 Google Scholar
J. Mikolajczyk et al.,
“System of optoelectronic sensors for breath analysis,”
Metrol. Meas. Syst., 23 481
–489
(2016). Google Scholar
L. Dong et al.,
“Compact sensor system based on a continuous-wave, low power consumption, room temperature interband cascade laser,”
Appl. Phys. Lett., 108 011106
(2016). http://dx.doi.org/10.1063/1.4939452 APPLAB 0003-6951 Google Scholar
A. A. Kosterev et al.,
“Cavity ringdown spectroscopic detection of nitric oxide with a continuous-wave quantum-cascade laser,”
Appl. Opt., 40 5522
–5529
(2001). http://dx.doi.org/10.1364/AO.40.005522 APOPAI 0003-6935 Google Scholar
B. W. M. Moeskops, S. M. Cristescu and F. J. M. Harren,
“Sub-part-per-billion monitoring of nitric oxide by use of wavelength modulation spectroscopy in combination with a thermoelectrically cooled, continuous-wave quantum cascade laser,”
Opt. Lett., 31 823
–825
(2006). http://dx.doi.org/10.1364/OL.31.000823 OPLEDP 0146-9592 Google Scholar
D. S. Baer et al.,
“Multiplexed diode-laser sensor system for simultaneous , , and temperature measurements,”
Opt. Lett., 19 1900
–1902
(1994). http://dx.doi.org/10.1364/OL.19.001900 OPLEDP 0146-9592 Google Scholar
R. G. Pilston and J. U. White,
“A long path gas absorption cell,”
J. Opt. Soc. Am., 44 572
–573
(1954). http://dx.doi.org/10.1364/JOSA.44.000572 JOSAAH 0030-3941 Google Scholar
J. U. White,
“Long optical paths of large aperture,”
J. Opt. Soc. Am., 32 285
–288
(1942). http://dx.doi.org/10.1364/JOSA.32.000285 JOSAAH 0030-3941 Google Scholar
D. Herriott, H. Kogelnik and R. Kompfner,
“Off-axis paths in spherical mirror interferometers,”
Appl. Opt., 3 523
–526
(1964). http://dx.doi.org/10.1364/AO.3.000523 APOPAI 0003-6935 Google Scholar
S. M. Chernin and E. G. Barskaya,
“Optical multi-pass matrix systems,”
Appl. Opt., 30 51
–58
(1991). http://dx.doi.org/10.1364/AO.30.000051 APOPAI 0003-6935 Google Scholar
J. B. McManus, P. L. Kebabian and M. S. Zahniser,
“Astigmatic mirror multi-pass absorption cells for long-path length spectroscopy,”
Appl. Opt., 34 3336
(1995). http://dx.doi.org/10.1364/AO.34.003336 APOPAI 0003-6935 Google Scholar
M. Mazurenka et al.,
“Cavity ring-down and cavity enhanced spectroscopy using diode lasers,”
Ann. Rep. Prog. Chem. Sect. C: Phys. Chem., 101 100
–142
(2005). http://dx.doi.org/10.1039/b408909j Google Scholar
A. O’Keefe and D. A. G. Deacon,
“Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources,”
Rev. Sci. Instrum., 59 2544
–2551
(1988). http://dx.doi.org/10.1063/1.1139895 RSINAK 0034-6748 Google Scholar
A. O’Keefe,
“Integrated cavity output analysis of ultra-weak absorption,”
Chem. Phys. Lett., 293 331
–336
(1998). http://dx.doi.org/10.1016/S0009-2614(98)00785-4 CHPLBC 0009-2614 Google Scholar
R. Engeln et al.,
“Cavity enhanced absorption and cavity enhanced magnetic rotation spectroscopy,”
Rev. Sci. Instrum., 69 3763
–3769
(1998). http://dx.doi.org/10.1063/1.1149176 RSINAK 0034-6748 Google Scholar
D. Hofstetter et al.,
“Photoacoustic spectroscopy with quantum cascade distributed-feedback lasers,”
Opt. Lett., 26 887
–889
(2001). http://dx.doi.org/10.1364/OL.26.000887 OPLEDP 0146-9592 Google Scholar
A. A. Kosterev and F. K. Tittel,
“Applications of quartz tuning forks in spectroscopic gas sensing,”
Rev. Sci. Instrum., 76 043105
(2005). http://dx.doi.org/10.1063/1.1884196 RSINAK 0034-6748 Google Scholar
A. A. Kosterev et al.,
“Quartz-enhanced photoacoustic spectroscopy,”
Opt. Lett., 27 1902
–1904
(2002). http://dx.doi.org/10.1364/OL.27.001902 OPLEDP 0146-9592 Google Scholar
P. Patimisco et al.,
“Quartz-enhanced photoacoustic spectroscopy: a review,”
Sensors, 14 6165
–6206
(2014). http://dx.doi.org/10.3390/s140406165 SNSRES 0746-9462 Google Scholar
B. de Lacy Costello et al.,
“A review of the volatiles from the healthy human body,”
J. Breath Res., 8 014001
(2014). http://dx.doi.org/10.1088/1752-7155/8/1/014001 Google Scholar
T. Hibbard and A. J. Killard,
“Breath ammonia analysis: clinical application and measurement,”
Crit. Rev. Anal. Chem., 41 21
–35
(2011). http://dx.doi.org/10.1080/10408347.2011.521729 CCACBB 1040-8347 Google Scholar
P. Gouma and M. Stanacevic,
“Selective nanosensor array microsystem for exhaled breath analysis,”
Procedia Eng., 25 1557
–1560
(2011). http://dx.doi.org/10.1016/j.proeng.2011.12.385 Google Scholar
L. D. Bos et al.,
“Exhaled breath metabolomics as a noninvasive diagnostic tool for acute respiratory distress syndrome,”
Eur. Respir. J., 44 188
–197
(2014). http://dx.doi.org/10.1183/09031936.00005614 Google Scholar
C. Wang, A. Mbi and M. Shepherd,
“A study on breath acetone in diabetic patients using a cavity ringdown breath analyzer: exploring correlations of breath acetone with blood glucose and glycohemoglobin A1C,”
IEEE Sens. J., 10 54
–63
(2010). http://dx.doi.org/10.1109/JSEN.2009.2035730 Google Scholar
I. Bayrakli, A. Turkmen and M. C. Kockar,
“Examination of feasibility of using breath ammonia analysis based on off-axis cavity-enhanced absorption spectroscopy with external cavity diode laser for non-invasive real-time diagnosis of Helicobacter pylori,”
Appl. Spectrosc., 70 1269
–1277
(2016). http://dx.doi.org/10.1177/0003702816654052 APSPA4 0003-7028 Google Scholar
I. Bayrakli et al.,
“Applications of external cavity diode laser-based technique to non-invasive clinical diagnosis using expired breath ammonia analysis: chronic kidney disease, epilepsy,”
J. Biomed. Opt., 21 087004
(2016). http://dx.doi.org/10.1117/1.JBO.21.8.087004 JBOPFO 1083-3668 Google Scholar
A. Amano et al.,
“Monitoring ammonia to assess halitosis,”
Oral Surg. Oral Med. Oral Pathol., 94 692
–696
(2002). http://dx.doi.org/10.1067/moe.2002.126911 Google Scholar
G. Song et al.,
“Quantitative breath analysis of volatile organic compounds of lung cancer patients,”
Lung Cancer, 67 227
–231
(2010). http://dx.doi.org/10.1016/j.lungcan.2009.03.029 Google Scholar
R. H. Eggers et al.,
“A methodological analysis of the -urea breath test for detection of Helicobacter pylori infections: high sensitivity and specificity within 30 min using 75 mg of -urea,”
Eur. J. Gastroenterol. Hepatol., 2 437
–444
(1990). EJGHES 0954-691X Google Scholar
M. Phillips,
“Detection of carbon disulfide in breath and air: a possible new risk factor for coronary artery disease,”
Int. Arch. Occup. Environ. Health, 64 119
–123
(1992). http://dx.doi.org/10.1007/BF00381479 IAEHDW Google Scholar
M. A. Kamboures et al.,
“Breath sulfides and pulmonary function in cystic fibrosis,”
Proc. Natl Acad. Sci. U. S. A., 102 15762
–15767
(2005). http://dx.doi.org/10.1073/pnas.0507263102 Google Scholar
K. Zayasu et al.,
“Increased carbon monoxide in exhaled air of asthmatic patients,”
Am. J. Respir. Crit. Care Med., 156 1140
–1143
(1997). http://dx.doi.org/10.1164/ajrccm.156.4.96-08056 AJCMED 1073-449X Google Scholar
M. Yamaya et al.,
“Increased carbon monoxide in exhaled air of subjects with upper respiratory tract infections,”
Am. J. Respir. Crit. Care Med., 158 311
–314
(1998). http://dx.doi.org/10.1164/ajrccm.158.1.9711066 AJCMED 1073-449X Google Scholar
S. S. Sehnert et al.,
“Breath biomarkers for detection of human liver diseases: preliminary study,”
Biomarkers, 7 174
–187
(2002). http://dx.doi.org/10.1080/13547500110118184 Google Scholar
K. A. Cope et al.,
“Abnormal exhaled ethane concentrations in scleroderma,”
Biomarkers, 11 70
–84
(2006). http://dx.doi.org/10.1080/13547500500515046 Google Scholar
P. Paredi, S. A. Kharitonov and P. J. Barnes,
“Elevation of exhaled ethane concentration in asthma,”
Am. J. Respir. Crit. Care Med., 162 1450
–1454
(2000). http://dx.doi.org/10.1164/ajrccm.162.4.2003064 AJCMED 1073-449X Google Scholar
H. Amal et al.,
“Breath testing as potential colorectal cancer screening tool,”
Int. J. Cancer, 138 229
–236
(2016). http://dx.doi.org/10.1002/ijc.29701 Google Scholar
C. Popa, M. Petrus and A. M. Bratu,
“Ammonia and ethylene biomarkers in the respiration of the people with schizophrenia using photoacoustic spectroscopy,”
J. Biomed. Opt., 20 057006
(2015). http://dx.doi.org/10.1117/1.JBO.20.5.057006 JBOPFO 1083-3668 Google Scholar
C. Popa et al.,
“The level of ethylene biomarker in the renal failure of elderly patients analyzed by photoacoustic spectroscopy,”
Laser Phys., 23 125701
(2013). http://dx.doi.org/10.1088/1054-660X/23/12/125701 LAPHEJ 1054-660X Google Scholar
A. Wehinger et al.,
“Lung cancer detection by proton transfer reaction mass-spectrometric analysis of human breath gas,”
Int. J. Mass Spectrom., 265 49
–59
(2007). http://dx.doi.org/10.1016/j.ijms.2007.05.012 IMSPF8 1387-3806 Google Scholar
F. J. Gilchrist et al.,
“Hydrogen cyanide concentrations in the breath of adult cystic fibrosis patients with and without Pseudomonas aeruginosa infection,”
J. Breath Res., 7 026010
(2013). http://dx.doi.org/10.1088/1752-7155/7/2/026010 Google Scholar
M. Whiteman et al.,
“The novel neuromodulator hydrogen sulfide: an endogenous peroxynitrite ‘scavenger’?,”
J. Neurochem., 90 765
–768
(2004). http://dx.doi.org/10.1111/j.1471-4159.2004.02617.x JONRA9 0022-3042 Google Scholar
T. Karl et al.,
“Human breath isoprene and its relation to blood cholesterol levels: new measurements and modeling,”
J. Appl. Physiol., 91 762
–770
(2001). Google Scholar
L. Le Marchand et al.,
“Use of breath hydrogen and methane as markers of colonic fermentation in epidemiologic studies: circadian patterns of excretion,”
Environ. Health Perspect., 98 199
–202
(1992). http://dx.doi.org/10.1289/ehp.9298199 EVHPAZ 0091-6765 Google Scholar
W. Filipiak et al.,
“Characterization of volatile metabolites taken up by or released from Streptococcus pneumoniae and Haemophilus influenzae by using GC-MS,”
Microbiology, 158 3044
–3053
(2012). http://dx.doi.org/10.1099/mic.0.062687-0 MIBLAO 0026-2617 Google Scholar
R. F. del Rio et al.,
“Volatile biomarkers in breath associated with liver cirrhosis—comparisons of pre- and post-liver transplant breath samples,”
EBioMedicine, 2 1243
–1250
(2015). http://dx.doi.org/10.1016/j.ebiom.2015.07.027 Google Scholar
M. Hongying et al.,
“Analysis of human breath samples of lung cancer patients and healthy controls with solid-phase microextraction (SPME) and flow-modulated comprehensive two-dimensional gas chromatography (GC × GC),”
Anal. Methods, 6 6841
–6849
(2014). http://dx.doi.org/10.1039/C4AY01220H AMNEGX 1759-9679 Google Scholar
B. J. Novak et al.,
“Exhaled methyl nitrate as a noninvasive marker of hyperglycemia in type 1 diabetes,”
Proc. Natl. Acad. Sci. U. S. A., 104 15613
–15618
(2007). http://dx.doi.org/10.1073/pnas.0706533104 Google Scholar
C. O. Olopade et al.,
“Exhaled pentane and nitric oxide levels in patients with obstructive sleep apnea,”
Chest, 111 1500
–1504
(1997). http://dx.doi.org/10.1378/chest.111.6.1500 CHETBF 0012-3692 Google Scholar
S. A. Kharitonov and P. J. Barnes,
“Nitric oxide, nitrotyrosine, and nitric oxide modulators in asthma and chronic obstructive pulmonary disease,”
Curr. Allergy Asthma Rep., 3 121
–129
(2003). http://dx.doi.org/10.1007/s11882-003-0024-7 Google Scholar
S. A. Kharitonov and P. J. Barnes,
“Nitric oxide in exhaled air is a new marker of airway inflammation,”
Monaldi. Arch. Chest Dis., 51 533
–537
(1996). Google Scholar
M. A. Birrell et al.,
“Utility of exhaled nitric oxide as a noninvasive biomarker of lung inflammation in a disease model,”
Eur. Respir. J., 28 1236
–1244
(2006). http://dx.doi.org/10.1183/09031936.00048506 Google Scholar
J. Huh, D. Yi and B. Gam, Korea Traditional Medicine Book, Nae Yi Won, Seoul, Korea
(1613). Google Scholar
T. H. Risby and S. F. Solga,
“Current status of clinical breath analysis,”
Appl. Phys. B, 85 421
–426
(2006). http://dx.doi.org/10.1007/s00340-006-2280-4 Google Scholar
W. Cao and Y. Duan,
“Current status of methods and techniques for breath analysis,”
Crit. Rev. Anal. Chem., 37 3
–13
(2007). http://dx.doi.org/10.1080/10408340600976499 CCACBB 1040-8347 Google Scholar
W. Miekisch, J. Herbig and J. K. Schubert,
“Data interpretation in breath biomarker research: pitfalls and directions,”
J. Breath Res., 6 036007
(2012). http://dx.doi.org/10.1088/1752-7155/6/3/036007 Google Scholar
M. Phillips,
“Method for he collection and assay of volatile organic compounds in breath,”
Anal. Biochem., 247 272
–278
(1997). http://dx.doi.org/10.1006/abio.1997.2069 Google Scholar
T. H. Risby and S. S. Sehnert,
“Clinical application of breath biomarkers of oxidative stress status,”
Free Radical Biol. Med., 27 1182
–1192
(1999). http://dx.doi.org/10.1016/S0891-5849(99)00212-9 Google Scholar
A. T. Society,
“Recommendations for standardized procedures for the online and offline measurement of exhaled lower respiratory nitric oxide and nasal nitric oxide in adults and children-1999,”
Am. J. Respir. Crit. Care Med., 160 2104
–2117
(1999). http://dx.doi.org/10.1164/ajrccm.160.6.ats8-99 AJCMED 1073-449X Google Scholar
A. T. Society,
“ATS/ERS Recommendations for standardized procedures for the online and offline measurement of exhaled lower respiratory nitric oxide and nasal nitric oxide, 2005,”
Am. J. Respir. Crit. Care Med., 171 912
–930
(2005). http://dx.doi.org/10.1164/rccm.200406-710ST AJCMED 1073-449X Google Scholar
B. Buszewski et al.,
“Human exhaled air analytics: biomarkers of diseases,”
Biomed. Chromatogr., 21 553
–566
(2007). http://dx.doi.org/10.1002/(ISSN)1099-0801 BICHE2 0269-3879 Google Scholar
R. Schubert et al.,
“Metabolic monitoring and assessment of anaerobic threshold by means of breath biomarkers,”
Metabolomics, 8 1069
–1080
(2012). http://dx.doi.org/10.1007/s11306-012-0408-6 Google Scholar
BiographyIsmail Bayrakli is an associate professor at Suleyman Demirel University. He received his MSc degree in 2005 and his PhD in physics in 2008 from Technical University of Berlin and Humboldt University, Berlin, Germany. His research interests include tunable single- and double-mode diode lasers, ultra-sensitive and ultra-resolution laser-based biomedical sensors, and breath analysis. |