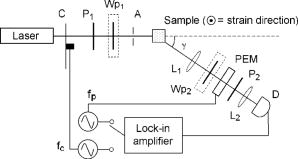
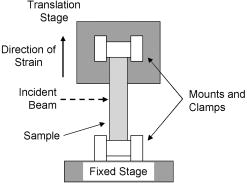
1.

Introduction

Recently, there has been increased interest in using polarized light for the assessment of biological tissues, due to the noninvasive nature of light-tissue interactions and the wealth of information potentially available. The field of traditional polarimetry is well established in clear media, but the multiple scattering and resulting light depolarization hinder the application of these techniques for the examination of turbid media such as biological tissue. However, many biological tissue constituents interact with polarized light, including collagen, muscle fibers, keratin, retina, and glucose.¹ Thus, if the depolarization effects of multiple scattering can be minimized or accounted for, polarized light can potentially serve as a sensitive probe of the state of tissue and its constituents. ^{2, 3, 4, 5, 6}

The use of polarized light for determining the concentrations of optically active molecules such as glucose is currently being explored.^{7, 8} A tremendous need exists for a noninvasive glucose monitor for diabetics to increase the frequency of monitoring and better guide treatments, thus preventing or delaying the long-term complications due to the disease. A variety of optical methods have been proposed for blood glucose monitoring including near-IR spectroscopy,⁹ optical coherence tomography¹⁰ (OCT), Raman spectroscopy,¹¹ photoacoustic techniques,¹² and fluorescence techniques.¹³ While some of these techniques are approaching acceptable levels of accuracy in vivo, none have yet been approved for clinical use. Polarized light offers another potential method by exploiting changes in polarization caused by glucose, which result from its optical activity, and induced changes in the scattering properties due to the rise in refractive index with additional glucose.¹⁴ Accordingly, we are investigating the potential to determine concentrations of optically active molecules such as glucose in scattering media in an effort to develop a suitable methodology to predict blood glucose levels in vivo.^{8, 14, 15}

To aid in the investigation of polarized light propagation in turbid media such as biological tissue, accurate modeling is enormously useful for gaining physical insight, designing and optimizing experiments, and analyzing measured data. The use of electromagnetic theory with Maxwell’s equations is the most rigorous and best-suited method for polarimetric analysis; however, solving Maxwell’s equations for polarized light propagation in turbid media is impractical.¹⁶ Light propagation through scattering media can in principle be modeled through transport theory; however, transport theory and its simplified variant, the diffusion equation, are both intensity-based techniques, and hence typically neglect polarization.^{17, 18} A more general and robust approach is the Monte Carlo technique. The first Monte Carlo models were developed for intensity calculations only and neglected polarization, the most commonly used being that developed by Wang ¹⁹ More recently, a number of implementations have incorporated polarization into their Monte Carlo models. ^{20, 21, 22, 23, 24, 25} Currently, the Monte Carlo technique is the most general approach to simulate polarized light propagation in scattering media, although long computation times are often required to generate statistically meaningful results.

However, most current Monte Carlo models for polarized light propagation do not fully simulate all the polarization-influencing effects of tissue. To better model the propagation of polarized light in biological tissue, effects such as optical activity due to chiral molecules (e.g., glucose and proteins), and linear birefringence due to anisotropic tissue structures (e.g., collagen and muscle), must be incorporated into the model in the presence of scattering. This is particularly important for glucose polarimetry, as many biological tissues at accessible anatomical sites (skin, muscle) have anisotropic (birefringent) properties. A number of tissue Monte Carlo models have included either optical activity or birefringence alone.^{26, 27, 28} However, none have included both these properties simultaneously in turbid media. This is primarily due to the difficulty in formulating the combined (simultaneous) effect for both these optical effects in the presence of scattering; however, as will be discussed, this task can be accomplished through the Jones $N$ -matrix formalism. In this paper, we extend the Jones $N$ -matrix formalism to model simultaneous birefringence and optical activity in the presence of depolarization phenomena. In addition, no Monte Carlo models that have incorporated birefringence have been experimentally validated due to the difficulty in creating phantoms with controllable birefringence. As we also discuss, this can be achieved through the use of strain-induced birefringence in hydrogel polymers.

The outline of this paper is as follows. First, optical activity and birefringence are reviewed and the Monte Carlo formalism for modeling the combined effect in turbid media is presented. As this work extends an existing clear media formalsim, we focus primarily on the additions to the formalism applicable to multiply scattering samples. Second, the experimental system and methods of analysis as well as the optical phantoms used in the validation experiments are described in detail. Third, the results of the validation experiments are presented and shown to correlate well with the extended polarization-sensitive Monte Carlo model predictions; in addition, the observed physical polarization phenomena are interpreted and discussed.

2.

Basic Polarization-Sensitive Monte Carlo Formalism

This paper extends the Monte Carlo algorithm developed and validated by Côté and Vitkin.²⁹ Source code (ANSI $\mathrm{C}++$ ) is available for free download from the Internet.³⁰ A brief summary of the formalism is given in the following; further details on the calculations and validation are available.^{29, 30}

It is assumed in this algorithm that scattering events occur independently and have no coherence effects. Medium domains through which the photons propagate are specified by a set of surface elements defined by two vectors and a normal vector pointing outward. The position, propagation direction, and polarization of each photon are initialized and modified as the photon propagates through the sample. The photon’s polarization, with respect to a set of arbitrary orthonormal axes ${\widehat{\mathbf{e}}}_{\perp }$ and ${\widehat{\mathbf{e}}}_{\parallel }$ defining its reference frame, is represented as a four element Stokes vector³¹ $\mathbf{S}$ . The first element $I$ represents the intensity of the light beam, the second element $Q$ represents the linear polarization at 0 and $90\mathrm{deg}$ , the third element $U$ represents the linear polarization at 45 and $135\mathrm{deg}$ , and the fourth element $V$ represents the circular polarization. Polarization effects are applied to the Stokes vector using a $4\times 4$ Mueller matrix³¹ $\mathsf{M}$ .

The photon propagates in the sample between scattering events a distance sampled from the probability distribution $\exp (-{\mu }_{t}d)$ , where the extinction coefficient ${\mu }_t$ is the sum of the absorption ${\mu }_a$ and scattering ${\mu }_s$ coefficients, and $d$ is the distance traveled by the photon. On encountering a scattering event, a scattering plane and angle are statistically sampled based on the polarization state of the photon and the Mueller matrix of the scatterer. The photon’s reference frame is first expressed in the scattering plane and then transformed through multiplication by a Mueller matrix calculated through Mie scattering theory.³² On encountering a domain interface, the probability of either reflection or transmission is calculated. The Stokes vector and propagation direction of the photon are then modified according to either the reflection or transmission. If the photon is transmitted through the interface, the Stokes vector of the photon is recorded for that surface element. As no interference effects are considered, the final Stokes vector values are computed as the sum of all the appropriate photon subpopulations exiting the sample.

2.1.

Birefringence and Optical Activity Extension

The Monte Carlo algorithm was extended to include the effects of optical activity and birefringence to better model biological tissue. An overview of these properties and the practical implications of modeling their effects are given in the following section.

Optical activity arises from either individual molecules exhibiting chirality (handedness) such as glucose in solution, or from a chiral structure of the material as in the case of quartz crystals. Optical activity results in a rotation of the plane of linearly polarized light. This rotation arises from the difference in the refractive indices for left and right circularly polarized light, due to either the molecular or structural asymmetry. When considering optical active molecules in solution the induced rotation through an angle $\alpha$ is given by

Eq. 1

$$\alpha ={\left[\alpha \right]}_{\lambda }^{T}LC,$$

where $[\alpha {]}_{\lambda }^T$ is the rotatory power of the molecule usually given in $\mathrm{deg}\mathrm{ml}{\mathrm{g}}^{-1}{\mathrm{dm}}^{-1}$ $(1\mathrm{dm}=10\mathrm{cm})$ and dependent on the temperature $T$ and wavelength $\lambda$ of the light, $L$ is the photon path length through the medium, and $C$ is the concentration of the optically active molecules. Strictly speaking, Eq. 1 is valid only for clear media, as scattering results in an ambiguity in $L$ ; however, this ambiguity can be accounted for if Eq. 1 is applied to individual photons between scattering events, using the distance between scattering events $d$ in place of $L$ . Typical rotations due to optical active molecules in tissue (proteins and other biological molecules) are of the order of fractions of a degree per centimeter. In our formalism, optical activity is specified as a rotation $\chi$ in degrees per centimeter where $\chi =[\alpha {]}_{\lambda }^{T}C$ and $\alpha =\chi d$ . This rotation can then be applied to individual photons as they propagate between scattering events through multiplication of the Mueller matrix for a rotator.

Linear birefringence arises from a directional anisotropy in the refractive index of the medium through which the light is propagating. The axis along which the refractive index differs from that along other directions is referred to as the extraordinary axis. Axes perpendicular to the extraordinary axis along which the refractive index is uniform are referred as ordinary axes. The refractive indices along the extraordinary and ordinary axes are referred to as $n_e$ and $n_o$ , respectively. This anisotropy in refractive indices $\mathrm{\Delta }n=n_e-n_o$ leads to a difference in the phase speeds for light polarized parallel and perpendicular to the direction of the extraordinary axis and results in a retardation of parallel and perpendicular linear polarization components. In this formalism, we assume that the medium is uniaxial (the refractive index differs along only one axis) and that the direction of the axis and difference in refractive indices is constant throughout the sample. In addition, we assume that anisotropies in the refractive index of the medium have no effect on the phase function of the scattering events and no effect on reflections and transmissions from interfaces. Birefringence (and optical activity) is (are) assumed to only influence the polarization of photons as they move between scattering events. These assumptions are reasonable given the fact that typical birefringence values in biological tissue are small, typically $\mathrm{\Delta }n<1\times {10}^{-2}$ , and the resulting effects on the statistically sampled scattering phase function and Fresnel coefficient are small. Birefringence is specified in our current formulation by a vector defining the extraordinary axis $\mathbf{b}$ , the extraordinary refractive index $n_e$ , and the ordinary refractive index $n_o$ .

As the photon propagates between scattering events, the difference in refractive indices seen by the photon depends on the propagation direction with respect to the extraordinary axis. The refractive index with the maximum difference from $n_o$ as seen by the photon referred to as $n\left(\theta \right)$ , can be expressed as

Eq. 2

$$n\left(\theta \right)=\frac{n_o{n}_e}{{(n_e^2{\cos }^2\theta +n_o^2{\sin }^2\theta )}^{1∕2}},$$

where $\theta$ is the angle between the photon’s propagation direction ${\widehat{\mathit{e}}}_{\mathrm{prop}}$ and the extraordinary axis³³ $\mathbf{b}$ . The difference in refractive indices seen by the photon is then given by

Eq. 3

$$\mathrm{\Delta }n=n\left(\theta \right)-n_o.$$

This refractive index difference results in the retardation of orthogonal linear polarization states. As the photon moves, its polarization states along the ordinary and extraordinary axes undergo retardation $\delta$ given by

Eq. 4

$$\delta =\mathrm{\Delta }n\frac{2\pi d}{\lambda },$$

where $d$ is the distance traveled by the photon between scattering events, and $\lambda$ is the wavelength of the light in vacuum. However, to apply the Mueller matrix for a retarder to the Stokes vector of the photon, the photon’s reference frame must first be rotated so that ${\widehat{\mathbf{e}}}_{\parallel }$ is parallel to the axis of maximal refractive index difference ${\mathbf{b}}^{\prime }$ . The axis ${\mathbf{b}}^{\prime }$ is first found by rotating the extraordinary axis by an angle $90\mathrm{deg}-\theta$ around a second axis defined by $\mathbf{b}\times {\widehat{\mathbf{e}}}_{\mathrm{prop}}$ , as shown Fig. 1 . The photon’s reference frame is then rotated by an angle $\beta$ so that ${\widehat{\mathbf{e}}}_{\parallel }$ is parallel to ${\mathbf{b}}^{\prime }$ . After this rotation of the reference frame, the Stokes vector of the photon is now expressed such that the calculated retardation from Eq. 4 can be applied to this Stokes vector through the multiplication of the Mueller matrix for a retarder.

Fig. 1

Schematic of manipulations required so that ${\widehat{\mathbf{e}}}_{\parallel }$ in the photon’s reference frame is parallel to the rotated extraordinary axis ${\mathbf{b}}^{\prime }$ . This is required so that the Mueller or Jones matrix for birefringence can be expressed only in terms of the retardation $\delta$ experienced by the photon; otherwise angular dependencies would also be present. The plane is defined by the photon’s reference frame ( ${\widehat{\mathbf{e}}}_{\perp }$ and ${\widehat{\mathbf{e}}}_{\parallel }$ ), $\theta$ is the angle between the photon’s propagation direction ${\widehat{\mathbf{e}}}_{\mathrm{prop}}$ and the extraordinary axis $\mathbf{b}$ , and $\beta$ is the angle between the direction of maximal refractive index difference 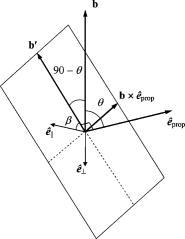${\mathbf{b}}^{\prime }$ and ${\widehat{\mathbf{e}}}_{\parallel }$ .

3.

Experimental Methods and Materials

As described, the Monte Carlo model was extended to include birefringence and optical activity. However, it is of paramount importance to ensure that the model correctly simulates what occurs physically through experimental validation. This is particularly challenging for polarization-sensitive Monte Carlo development research and, unfortunately, is sometimes neglected. The following section describes the experimental system and phantoms used for the validation experiments.

3.1.

Stokes Polarimeter

To perform the validation experiments, polarimetric measurements were made using the experimental setup shown in Fig. 2 , which has been slightly modified from that described in a previous publication.³⁷ Unpolarized light at $632.8\mathrm{nm}$ from a $\mathrm{HeNe}$ laser (Research Electro-Optics, LHRR-120M) first passes through a mechanical chopper operating at a frequency $f_c=500\mathrm{Hz}$ , then through a polarizer with its pass-axis at $0\mathrm{deg}$ (horizontal), and finally through a removable quarter-wave plate placed before the sample with its fast axis at $45\mathrm{deg}$ . The removable quarter-wave plate causes the light incident on the sample to be either circularly polarized when in place or linearly polarized when removed. The detection optics begin with another removable quarter wave plate at $-45\mathrm{deg}$ , when in place allowing for the measurement of the Stokes parameters $Q$ and $U$ (linear polarization), and when removed allowing for the measurement of the Stokes parameter $V$ (circular polarization). Sample-scattered light then passes through a photoelastic modulator (PEM, Hinds Instruments IS-90 operating at $f_p=50\mathrm{kHz}$ ) with its fast axis at $0\mathrm{deg}$ , and its retardation modulated according to the sinusoidal function ${\delta }_{\mathrm{PEM}}\left(t\right)={\delta }_o\sin {\omega }_{p}t$ , where ${\omega }_p=2\pi f_p$ , and ${\delta }_o$ is the user-specified amplitude of maximum retardation. The light finally passes through an analyzer orientated at $45\mathrm{deg}$ and the resulting modulated intensity of the light is measured by an avalanche photodiode (APD) detector (Hamamatsu, C5460). The detection arm of the setup is mounted on a rotatable platform to enable angularly $\left(\gamma \right)$ resolved measurements of light scattered by the sample. A pair of lenses in the detection optics is used to give a detection area of $1{\mathrm{mm}}^2$ (circular area) on the sample and an acceptance angle of $14\mathrm{deg}$ for light scattered by the sample. The detected signal is sent to a lock-in amplifier (Stanford Research Systems, SR830) with the reference input of the amplifier toggled between the signals from the chopper and PEM controllers. The Stokes parameters of the light scattered from the sample can be calculated from the first harmonic of the signal at the chopper frequency $V_{1f_c}$ and the first and second harmonics of the signal at the PEM frequencies $V_{1f_p}$ and $V_{2f_p}$ , respectively. As is shown in a previous publication,³⁷ the Stokes parameters normalized by the intensity of the light ( $q=Q∕I$ , $u=U∕I$ , and $v=V∕I$ ) can be extracted as follows. With the detection quarter-wave plate $\left(W_{p_2}\right)$ in place (linear detection), $q$ and $u$ are found from

Eq. 16

$$q=\frac{V_{1f_p}}{\sqrt{2}{J}_1\left({\delta }_o\right)V_{1f_c}},$$

Eq. 17

$$u=\frac{V_{2f_p}}{\sqrt{2}{J}_2\left({\delta }_o\right)V_{1f_c}},$$

where $J_1$ $\left({\delta }_o\right)$ and $J_2$ $\left({\delta }_o\right)$ are first- and second-order Bessel functions of the first kind evaluated at the amplitude of retardation ${\delta }_o$ of the PEM. With the detection quarter-wave plate $\left(W_{p_2}\right)$ removed (circular detection), $v$ is found from

Eq. 18

$$v=\frac{V_{1f_p}}{\sqrt{2}{J}_1\left({\delta }_o\right)V_{1f_c}}.$$

Based on the calculated Stokes parameters the fraction of linear polarization ${\beta }_L$ and the fraction of circular polarization ${\beta }_C$ can be calculated as

Eq. 19

$${\beta }_L={(q^2+u^2)}^{1∕2},$$

Eq. 20

$${\beta }_C=v.$$

Fig. 2

Schematic of Stokes polarimeter used for experimental measurements: $C$ , mechanical chopper; $P_1$ and $P_2$ , polarizers; $W_{p_1}$ and $W_{p_2}$ , removable quarter-wave plates; $A$ , aperture; $L_1$ and $L_2$ , lenses; PEM, photoelastic modulator; $D$ , photodetector; $f_c$ and $f_p$ modulation frequencies of mechanical chopper and PEM, respectively.

3.2.

Polyacrylamide Phantoms

To validate the developed Monte Carlo model, optical phantoms exhibiting controllable scattering, linear birefringence, and optical activity are required. The creation of phantoms with controllable scattering is easily accomplished through the addition of polystyrene mircospheres or Intralipid, and optical activity can be controlled through the addition of known amounts of chiral molecules such as glucose or sucrose. However, the problem of creating controllable birefringence is somewhat more difficult and has not been previously demonstrated for turbid tissue phantoms. For this study, strain-induced birefringence in a polymer hydrogel was used to create controllable linearly birefringent phantoms. Specifically, polyacrylamide was strained through extension to create birefringence along the direction of strain. This creation of birefringence through strain is also referred to as mechanical birefringence and is a result of the normally isotropic arrangement of the polymer molecules becoming anisotropic along the direction of the applied strain. In other words, the long polymer chains become aligned along the direction of strain and result in a higher refractive index along this direction. In the developed phantoms, scattering is produced through the addition of polystyrene microspheres, and optical activity in induced with the addition of sucrose.

The polyacrylamide phantoms were fabricated using a formulation adapted from Suroweic.³⁸ The polymerization of acrylamide was carried out using ammonium persulfate as the initiator, $\mathrm{N},{\mathrm{N}}^{\prime }$ methylenebisacylamide as a cross-linking agent, and tetramethylethylenediamine as the catalyst. The exothermic polymerization process was completed several minutes after the addition of the catalyst. The phantoms were polymerized in plastic molds with dimensions $1\times 1\times 4\mathrm{cm}$ , removed from the molds after $24\mathrm{h}$ and stored at 4°C until used. The density of polyacrylamide is ${\rho }_o=1.01\mathrm{g}∕{\mathrm{cm}}^3$ and the refractive index was measured through refractometry (Abbe refractometer model 2WAJ) to be approximately 1.393 at $633\mathrm{nm}$ . Polystyrene microspheres (refractive index $n_s=1.59$ , density $\rho =1.05\mathrm{g}∕{\mathrm{cm}}^3$ , radius $r=0.7\mathrm{\mu }\mathrm{m}$ ) were added to the samples prior to polymerization as scattering particles. The scattering efficiency and anisotropy of these particles in polyacrylamide was calculated from Mie theory and found to be $Q_{\mathrm{scat}}=2.72$ and $g=0.95$ , respectively, at $632.8\mathrm{nm}$ . Based on the weight fraction $f_w$ of added microspheres, the scattering coefficient is calculated as

Eq. 21

$${\mu }_s=\frac{3Q_{\mathrm{scat}}{f}_w{\rho }_o}{4r\rho }.$$

Two sets of phantoms were created with scattering coefficients of 30 and $60{\mathrm{cm}}^{-1}$ . A measured mass of sucrose was also added to some samples prior to polymerization to create phantoms with a known concentration of sucrose and, through Eq. 1, a known optical activity. Sucrose was used as an optically active molecule rather than glucose, because a reducing sugar such as glucose will interfere with the polymerization process. The addition of sucrose raises the refractive index of polyacrylamide by 0.026 per molar, requiring a recalculation of the scattering efficiency and scattering coefficients.³⁹ A third set of samples was created with $1\mathrm{M}$ of sucrose and, based on the recalculation of the scattering efficiency as $Q_{\mathrm{scat}}=2.22$ and the anisotropy as $g=0.96$ at $632.8\mathrm{nm}$ , with a scattering coefficient of $60{\mathrm{cm}}^{-1}$ .

To apply controllable strain to produce linear birefringence, the phantoms were glued on both ends to plastic holders and clamped at one end to fixed mount and at the other to a linear translation stage (Fig. 3 ). The phantoms were stretched to induce birefringence along the direction of strain. To determine the magnitude of the induced birefringence with phantom extension, measurements were taken using the polarimeter with clear samples (no added microspheres or sucrose) strained vertically ( $90\mathrm{deg}$ to the lab bench) and input right circularly polarized light (input quarter-wave plate in place). Based on the measured Stokes parameters $u$ and $v$ , the retardation was calculated as

Eq. 22

$$\delta ={\tan }^{-1}\left(\frac{u}{v}\right),$$

or using Eqs. 17, 18 as

Eq. 23

$$\delta ={\tan }^{-1}\left[\frac{J_1\left({\delta }_o\right)V_{2f_p}}{J_2\left({\delta }_o\right)V_{1f_p}}\right].$$

Fig. 3

Diagram of mounting system used to strain phantoms to induce birefringence. The phantoms are strained vertically in the laboratory reference frame, producing an extraordinary axis along this direction.

4.

Results and Discussion

The induced retardation with extension (strain) is shown in Fig. 4a and can be seen to increase linearly. The small nonzero retardation at zero extension is due to small amounts of strain on the sample present when clamped to the mount and translation stage. From the measured retardation, one is able to calculate the difference in refractive indices from Eq. 3; however, the contraction (reduction in width) of the phantom due to the extension must be taken into account as this effectively reduces the path length through the sample. This contraction was estimated from the Poission ratio for polyacrylamide (the ratio of fractional change in width to fractional change in length⁴⁰), which was estimated from unpublished reports and verified with measurements to be 0.33. Practically, this means that the sample width decreases from $1\mathrm{cm}$ (no strain) to $0.95\mathrm{cm}$ at maximum strain level ( $6\mathrm{mm}$ extension). This contraction was then taken into account when calculating the difference in refractive indices using Eq. 3. Figure 4b shows the difference in refractive indices corrected for contraction with extension of the polyacrylamide samples. The variability seen in the measurements is due to slight differences in mounting of the samples, slight differences between batches of samples, and small inhomogeneities in the birefringence of the samples. Overall, however, variability in batches is not significant and the samples appear homogeneous as measurements where made in varying vertical positions. In addition, the induced birefringence was examined spatially with crossed polarizers and was seen to be reasonably uniform. Based on these methods, we were able to produce phantoms with controllable scattering, birefringence, and optical activity and use the calculated physical parameters of these phantoms as input into the Monte Carlo model for validation.

Fig. 4

Measurements in the forward direction $(\gamma =0\mathrm{deg})$ through clear media of induced (a) retardation $\delta$ and (b) birefringence $\mathrm{\Delta }n$ with phantom extension (strain). The birefringence values were corrected for lateral contraction due to extension so that they can be used in Monte Carlo simulations. The unstrained length of the samples is 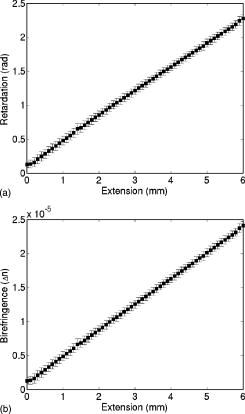$4\mathrm{cm}$ .

The first set of Monte Carlo calculations and experiments involved validation of birefringence in the presence of scattering (no sucrose). The second set of calculations and experiments involved validation of both birefringence and optical activity (i.e., staining of samples and added sucrose) in the presence of scattering. In both cases, Monte Carlo simulations were run with input parameters matching those present physically in the fabricated phantoms, as calculated from the previously described methods. The photon collection geometry mimics that present experimentally with a detection area of $1{\mathrm{mm}}^2$ (rectangular area now as opposed to the circular experimental area) and an acceptance angle of $20\mathrm{deg}$ (slightly larger than that employed experimentally).

Figures 5 and 6 show the experimentally measured and Monte Carlo calculated normalized Stokes parameters for two sets of samples with scattering coefficients of 30 and $60{\mathrm{cm}}^{-1}$ , respectively, as a function of strain-induced birefringence. Measurements and calculated values are shown for both the forward and lateral detection geometries ( $\gamma =0\mathrm{deg}$ and $\gamma =90\mathrm{deg}$ in Fig. 2) with input right circularly polarized light (quarter-wave plate before the sample in place, as shown in Fig. 2). Input circularly polarized light is used as it eliminates the requirement for alignment of the sample’s extraordinary axis with the input light’s polarization to achieve the maximum effect from the birefringence. In both cases, the measurements and calculations were performed in the center of the sample faces. The samples were strained vertically (refer to Fig. 3), creating a vertical extraordinary axis as the induced retardation varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ). All Monte Carlo simulations were run with ${10}^8$ photons to achieve reasonably low statistical uncertainties in the calculated values. The experimental values plotted are the average from measurements on five samples. In isotropic turbid media (no birefringence) the effect of scattering on the polarization of the light in both the forward and lateral directions is a depolarization of the incident circularly polarized light. As one would expect, higher scattering coefficients result in greater depolarization. The effect of birefringence on the polarization becomes evident with increasing birefringence as a continuous change from the input right circularly polarized light to linear polarized light at $45\mathrm{deg}$ (Stokes parameter $U$ ). This is due to the retardation of orthogonal polarization states parallel and perpendicular to the extraordinary axis in the vertical direction. As this retardation increases with strain, the polarization begins to transfer from circular to linear polarization. The sample is in a sense acting as a turbid variable wave plate with its extraordinary axis in the vertical direction changing the polarization from circular to linear and depolarizing the light. The change from circular to linear polarization occurs more rapidly with increasing birefringence in the forward direction than in the lateral. This is likely a result of the longer optical path length of light that propagates directly through the sample, in comparison to that which is scattered and exits from the side of the samples. From Monte Carlo simulations, the average photon path length for light exiting in the lateral direction $(\gamma =90\mathrm{deg})$ was 1.042 and $1.362\mathrm{cm}$ for 30 and $60{\mathrm{cm}}^{-1}$ , respectively, versus 1.174 and $1.753\mathrm{cm}$ for 30 and $60{\mathrm{cm}}^{-1}$ , respectively, for light exiting the samples in the forward direction $(\gamma =0\mathrm{deg})$ . The longer path length results in more retardation of the light, as seen in Eq. 4, and a larger change from circular to linear polarization. Close agreement can be seen between the Monte Carlo calculations and experimental results, indicating that the model correctly simulates the effect of linear birefringence in the presence of scattering. The calculated root mean square error (RMSE) between experimental and Monte Carlo calculations was 0.025 for $60{\mathrm{cm}}^{-1}$ and 0.058 for $30{\mathrm{cm}}^{-1}$ . The slightly larger disagreement present between the calculations and measurements at $30{\mathrm{cm}}^{-1}$ is likely caused by a greater variability in the magnitude of strain-induced birefringence between samples due to either variation in the mounting of the samples or in the fabrication process. To our knowledge, this is the first experimental validation of a polarization-sensitive Monte Carlo model for turbid media incorporating birefringence.

Fig. 5

Experimental measurements (symbols) and Monte Carlo calculations (lines) of the normalized Stokes parameters $q$ (squares and solid line), $u$ (triangles and dotted line), and $v$ (circles and dashed line) in the (a) forward $(\gamma =0\mathrm{deg})$ and (b) lateral $(\gamma =90\mathrm{deg})$ detection geometries with input circularly polarized light and a scattering coefficient of $60{\mathrm{cm}}^{-1}$ . Birefringence is varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ). Experimental values are the means of measurements on five samples.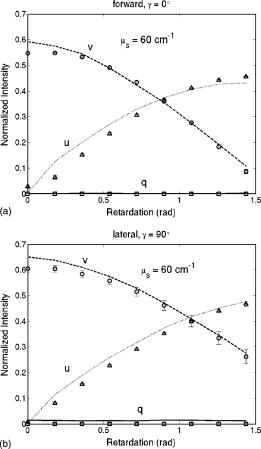

Fig. 6

Experimental measurements (symbols) and Monte Carlo calculations (lines) of the normalized Stokes parameters $q$ (squares and solid line), $u$ (triangles and dotted line), and $v$ (circles and dashed line) in the (a) forward $(\gamma =0\mathrm{deg})$ and (b) lateral $(\gamma =90\mathrm{deg})$ detection geometries with input circularly polarized light and a scattering coefficient of $30{\mathrm{cm}}^{-1}$ . Birefringence is varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ). Experimental values are the means of measurements on five samples.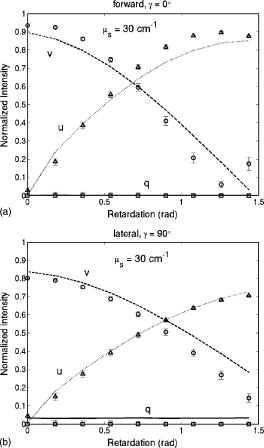

Monte Carlo simulations and experimental measurements were then undertaken with turbid samples exhibiting both birefringence and optical activity. As previously mentioned, the magnitude of chirality-induced optical rotation in biological tissue is low, of the order of tens to hundreds of millidegrees per centimeter. This small effect is superimposed on the relatively large retardations (of the order of $180\mathrm{deg}∕\mathrm{cm}$ ) caused by linear birefringence due to structural proteins and the large depolarization due to scattering. Accordingly, the effect of optical chirality/rotation on the polarization of light in biological tissue is significantly lower than that of scattering or birefringence. Figure 7 shows the normalized Stokes parameters from Monte Carlo simulations run with increasing magnitudes of optical activity. As before, the calculated values were in the forward and lateral geometries, the input light was circularly polarized, and the induced retardation was varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ). The magnitudes of optical activity were $\chi =0\mathrm{deg}{\mathrm{cm}}^{-1}$ , $\chi =0.8194\mathrm{deg}{\mathrm{cm}}^{-1}$ , and $\chi =8.194\mathrm{deg}{\mathrm{cm}}^{-1}$ corresponding to 0, 1, and $10\mathrm{M}$ concentrations of glucose respectively (note that optical activity due to glucose was used in these calculations). The index-matching effect of chiral molecules has been ignored in these simulations to focus on the effects of birefringence and optical activity alone. Often changes in polarization are due to significant changes in the scattering properties.^{14, 37} As seen, the effect of optical activity is small and generally only evident at a $10\mathrm{M}$ glucose concentration, more that 1000 times greater than physiological levels. The difference caused by this large amount of added glucose (at least if the refractive index-matching effect is ignored), in fact, approaches the noise threshold for these calculations in the case of all Stokes parameters except $q$ . The primary effect of optical activity is an increase in the normalized Stokes parameter $q$ with increasing birefringence. This increase results from the interplay of several mechanisms. Optical activity has no measurable effect on circularly polarized light, as rotating the plane of circularly polarized light introduces only a global phase shift, which is normally not detectable. Therefore, the effect of optical activity is evident only as the input light is retarded and transferred from the input circularly polarization to linearly polarization. As the light becomes linearly polarized at $45\mathrm{deg}$ (Stokes parameter $U$ ) due to the increasing birefringence, the plane of linear polarization is rotated due to the optical activity. This manifests as a small reduction in the normalized Stokes parameter $u$ and an increase in the normalized Stokes parameter $q$ . The reduction in $u$ is small and difficult to see in the plots; however, the increase in $q$ due to rotation can be seen. This increase is not due to increasing rotation with increasing birefringence but is due to the increase in the fraction of linear polarization associated with the increasing birefringence. In other words, the total amount of linear polarization increases with increasing birefringence, and as a result so do the chirality-induced changes in both $q$ and $u$ . We also see that $q$ increases more rapidly in the forward direction than in the lateral direction. As was described for birefringence, this may also be due to the larger path length traversed by light in the forward direction, producing a larger retardation and higher fraction of linear polarization. The longer path length also results in more optical rotation due to glucose chirality, thus also resulting in a larger value of $q$ in the forward direction.

Fig. 7

Monte Carlo calculations with optical activity $\chi =0\mathrm{deg}{\mathrm{cm}}^{-1}$ (dashed lines), $\chi =0.8194\mathrm{deg}{\mathrm{cm}}^{-1}$ (solid lines), and $\chi =8.194\mathrm{deg}{\mathrm{cm}}^{-1}$ (dotted lines) corresponding to 0, 1, and $10\mathrm{M}$ glucose concentrations, respectively. The normalized Stokes parameters are plotted in the (a) forward $(\gamma =0\mathrm{deg})$ and (b) lateral $(\gamma =90\mathrm{deg})$ detection geometries with input circularly polarized light and a fixed scattering coefficient of $60{\mathrm{cm}}^{-1}$ for all glucose concentrations. Birefringence is varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ). Only a small chirality-induced change in $q$ is apparent.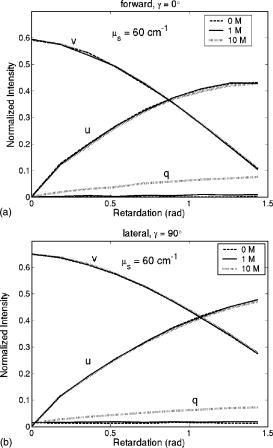

To validate these Monte Carlo model predictions with both birefringence and optical activity, calculations and measurements were compared for samples with $1\mathrm{M}$ of sucrose $(\chi =1.965\mathrm{deg}{\mathrm{cm}}^{-1})$ , the retardation varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ), and a scattering coefficient of $60{\mathrm{cm}}^{-1}$ (the refractive index-matching effect of sucrose was taken into account in calculation of the required weight fraction $f_w$ of microspheres). Results for input circularly polarized light and forward detection direction $(\gamma =0\mathrm{deg})$ are shown in Fig. 8 . In contrast to the previous calculations, the index-matching effect of sucrose was now taken into account. Figure 8 shows the change in the normalized Stokes parameter $q$ $\left(\mathrm{\Delta }q\right)$ with increasing birefringence both with and without added sucrose. The increase in $q$ from the induced optical rotation with increasing birefringence, as seen in the previous Monte Carlo simulations, is also evident. The calculated and measured values of $\mathrm{\Delta }q$ with no added sucrose are also plotted to demonstrate the effect of optical activity. Close agreement is seen between the calculations and experimental measurements, thus indicating that the model correctly simulates the effects of birefringence, optical activity, and scattering on the polarization of light. To our knowledge this is the first polarization-sensitive model to incorporate all three effects and the first, albeit limited, validation of such a model.

Fig. 8

Experimental measurements and Monte Carlo calculations of the change in the normalized Stokes parameter $q$ with optical activity (solid lines and squares) and without optical activity (dotted lines and circles) in the forward $(\gamma =0\mathrm{deg})$ detection geometry with input circularly polarized light and a fixed scattering coefficient of $60{\mathrm{cm}}^{-1}$ . Birefringence is varied from $\delta =0$ to $1.4364\mathrm{rad}$ ( $\mathrm{\Delta }n=0$ to $1.628\times {10}^{-5}$ ) and the magnitude of optical activity is $\chi =1.965\mathrm{deg}{\mathrm{cm}}^{-1}$ , corresponding to a $1\mathrm{M}$ sucrose concentration.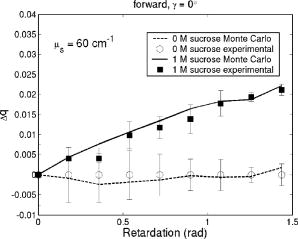

This upgraded model will be used to investigate the potential for polarized-light-based detection of glucose in biological media. In the current validation study, incident circularly polarized light was used in all simulations and experiments, however, in future work incident linearly polarized light with varying orientations with respect to the direction of birefringence will be investigated. This will be done to test the ability to quantify optical activity in the presence of birefringence. Linearly rather than circularly polarized light may prove to be superior for measuring chirality-induced optical activity as the effects of optical activity are generally more pronounced. Current results with input circularly polarized light demonstrate that the effects of optical activity can be quantified (change in $q$ ), however, this was done with knowledge of the direction of birefringence and with uniform birefringence through the sample. Future work will investigate the ability to quantify the effects of optical activity in nonuniform birefringent media without prior knowledge of the direction of birefringence using both the Monte Carlo model and polyacrylamide phantoms. The spatial and angular dependence of polarization effects in turbid chiral media will also be examined in the presence of birefringence. Finally, this upgraded model will also be used to explore the use of spectroscopic polarimetry and chemometric analysis to extract the rotation only due to glucose from that of other chiral species present in tissue.

5.

Conclusions

We demonstrate an experimentally validated Monte Carlo model for polarized light propagation in birefringent, optically active, turbid media. Birefringence and optical activity are two common phenomena in biological tissue; therefore the upgraded Monte Carlo model now more accurately simulates the interactions of polarized light in tissue. This is particularly important in the context of turbid polarimetry for glucose detection, as biological tissues are anisotropic, thus exhibiting linear birefringence. The problem of combining the effects of birefringence and optical activity in scattering media is resolved through use of the Jones $N$ -matrix formalism, giving the Mueller matrix for the combined effect that can be applied to photons as they propagate between scattering events. This formalism also enables the incorporation of other scattering-independent optical polarization effects such as circular or linear dichroism. To validate this extended model, polarimetric measurements on light scattered by polyacrylamide phantoms with strain-induced birefringence and sucrose-induced optical activity were compared to Monte Carlo calculations with similar parameters. The results show close agreement between experimental measurements and Monte Carlo calculations, providing strong evidence for the validity of the model. To our knowledge, this is the first polarization-sensitive Monte Carlo model to incorporate the effects of both birefringence and optical activity in scattering media, and the corresponding first validation studies.