|
|
|
Red blood cells (RBCs) lack nuclei and major organelles, and thus provide a convenient model for studying the dynamical properties of cells and the cytoskeleton. AFM has emerged as a high-resolution technique for structural analysis of minimally fixed erythrocytes.1 Although quantitative, AFM samples one single point at a time, requires contact, and is technically limited when applied to soft structures such as membranes of mammalian cells. RBC “flickering”—spontaneous membrane fluctuations—was first observed more than a century ago. These submicron motions are characterized by membrane displacements that take place at the millisecond scale or less. Significant progress has been made in modeling this phenomenon and connecting mechanical properties of the cell to the statistical properties of these fluctuations. 2, 3, 4, 5 It has been suggested that thermal excitation does not entirely explain these motions and that a deterministic component exists that may in fact accomplish certain physiological tasks, such as improving cell flexibility and filterability.2, 6 More recently, based on theoretical modeling and simulation, it has been suggested that the thermal fluctuations of the membrane regulate protein mobility.7 Experimental work on quantifying such intrinsic cellular fluctuations has been limited, due to the lack of noninvasive imaging techniques for quantifying nanoscale membrane fluctuations. Phase contrast microscopy has been used to study spatially-resolved RBC fluctuations.2, 8 However, the relationship between the detected intensity and the cell thickness is nonlinear; thus, the phase contrast technique is essentially restricted to qualitative investigations. Reflection interference contrast (RIC) microscopy was developed to quantify the thermally-induced fluctuations of the erythrocyte membrane.9 As with phase contrast, RIC is quantitative only in certain limiting situations.10 In point dark field microscopy, undulations of the cell are quantified by detecting the displacements of the cell edge.11 This technique was used to demonstrate the effect of adenosine tri-phosphate (ATP) on RBC membrane dynamics, but it allows only for point measurements and is not suitable for studying subtle, spatial behavior of fluctuations. Recently, quantitative phase imaging has been shown to have direct applicability in studying RBC structure and dynamics.12, 13, 14 Fourier phase microscopy (FPM) has been developed in our laboratory as a highly sensitive quantitative phase imaging technique with high transverse resolution.15 Due to its subnanometer path-length stability over many hours, FPM is very well suited for studying slow (seconds to days) phenomena in cell biology. In particular, this measurement technique is ideal for quantifying nanoscale RBC structure and fluctuations, as the cells can be assumed to be optically homogeneous, i.e., the local phase shift produced by the cells is linearly proportional to their thickness.10 The FPM experimental arrangement is described in detail elsewhere.15 The technique is based on describing image formation as an interference phenomenon and combines phase-contrast microscopy and phase-shifting interferometry. The phase shifting and data acquisition are synchronized and fully controllable by a computer. The FPM acquisition rate is limited by the refresh rate of the liquid crystal modulator, which is 7 to .15 Thus the technique allows the study of nanoscale structure and slow (minutes) dynamics of live RBCs with high-transverse resolution and subnanometer path-length sensitivity over long periods of time. Fresh human blood sandwiched between two cover slips was directly imaged by FPM, using a objective. For the illumination wavelength used , we assumed the cells to be characterized by a constant refractive index and the surrounding plasma by .16 The quantitative phase image retrieved, , was transformed to provide the thickness profile of red blood cells, . Figure 1 shows a map retrieved from an entire whole blood smear, where the normal discoid shape of the cells is clearly resolved in a quantitative manner. In order to study the low-frequency dynamics of live cells, we acquired full-field phase images for at a repetition rate of . The stability of the technique against the inherent phase noise was established by measuring the path-length fluctuations associated with a region containing no cells [indicated by the rectangular region in Fig. 1a]. Figure 1b shows the histogram of path-length standard deviations associated with the pixels in this region. Remarkably, the average standard deviation has a value of , without performing time-averaging. The only other technique that can achieve such remarkable -axis displacement sensitivity is AFM. However FPM, being a full-field, noncontact, preparation-free technique, provides unique advantages for live cell studies. Fig. 1(a) FPM image of a whole blood smear (red scale). The color bar indicates the cell thickness in microns (color online only). (b) Histogram of optical path-length standard deviation associated with pixels in the rectangular area indicated in (a). 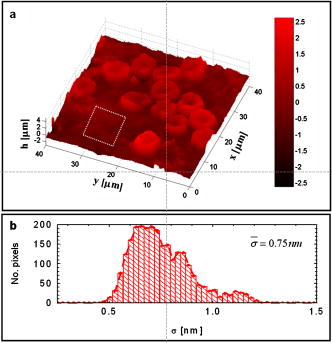 For analysis of cell dynamics, individual cells were segmented from the background using a computer routine developed in-house. Typically, cells exhibit transverse motion of the order of a micron or less. These translational movements were suppressed by tracking the cell centroid. Thus, time series of individual cell fluctuations were obtained over the period of observation. These datasets contain detailed four-dimensional information about the cell dynamics. Figure 2b shows the temporal fluctuations of the cell displacement associated with the points indicated in Fig. 2a. Water transport through the membrane due to osmolarity instability can potentially modify the cell optical path length and, thus, introduce errors in the fluctuation measurement.17 In order to demonstrate that the signals shown in Fig. 2b are free from such effects, we measured temporal fluctuations of the average cell thickness [solid curve in Fig. 2b]. The fact that this curve is essentially flat demonstrates that, overall, there are no volume changes associated with the cell and the path-length fluctuations are due to membrane displacements. Remarkably, moving from the center of the cell toward the rim, the fluctuations appear to be characterized by a progressively increasing standard deviation. In addition, the time-varying traces extracted exhibit clear periodic components, with various dominant frequencies. The spatially-resolved temporal autocorrelation function is defined as Thus, the power spectrum of the fluctuations in each point of the image is simply obtained by Fourier transforming the autocorrelation function,In order to characterize the cell fluctuations in a spatially-resolved manner, the entire cell was mapped out in terms of the average frequency of fluctuation ,Figure 2c shows this map and suggests that the cell can be divided into areas of independent dynamics with different average oscillation frequencies. These results may be due to specific biochemical domains within the cytoskeleton or plasma membrane (e.g., lipid rafts). Figure 2d depicts the average frequency map associated with the rectangular background area shown in Fig. 1a. This map is essentially uniform and demonstrates that the frequency map of Fig. 2c is directly related to the dynamic motion of the cell membrane. Such low-frequency cell dynamics may be related to active (ATP-assisted) processes within the cell. Similarly, although within different frequency ranges, recent studies involving and interference microscopy18 identified unexpected distinct modes of fluctuations in bacteria and neurons, respectively. This type of nanometer scale cellular dynamics should be highly relevant in understanding the processes that regulate cell metabolism. Quantifying membrane fluctuations should also provide information about the mechanical properties of the membrane-cytoskeleton ensemble.Fig. 2(a) Spatially-resolved dynamics of the cell. (b) Temporal cell thickness fluctuations associated with the selected points indicated in (a); the corresponding standard deviations are indicated. Similar data is obtained for every point in the image (not shown). The solid line shows the fluctuation of the average cell thickness (shifted down by , to inhance visibility). (c) Whole cell map of the average fluctuation frequency, calculated from the measured power spectrum of membrane fluctuations. The color bar indicates the mean frequency in inverse minutes (color online only). High values at the cell edges are due to transverse motions. High values in the center of the cell indicate high-frequency dynamic domains. (d) Average frequency map of the region indicated in Fig. 1a. 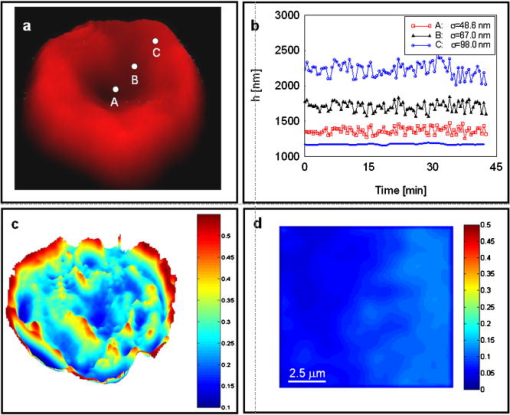 In summary, we measured noncontact, spatially-resolved, quantitative nanoscale red blood cell membrane fluctuations. The results demonstrate the existence of low-frequency fluctuations across the cells, which develop in isolated subdomains. These motions may be caused by nonrandom sources, such as metabolic processes within the cell. To our knowledge, this type of slow cell membrane dynamics has been reported here for the first time. Current work in our laboratory is directed toward understanding the effect of ATP to the possibly deterministic membrane motion. AcknowledgmentsThis work was carried out at the MIT Laser Biomedical Research Center, supported by NIH P41 RR 02594 and partially by Hamamatsu Photonics K.K. ReferencesR. Nowakowski,
P. Luckham, and
P. Winlove,
“Imaging erythrocytes under physiological conditions by atomic force microscopy,”
Biochim. Biophys. Acta, 1514 170
–176
(2001). 0006-3002 Google Scholar
F. Brochard and
J. F. Lennon,
“Frequency spectrum of the flicker phenomenon in erythrocytes,”
J. Phys. (Paris), 36 1035
–1047
(1975). 0302-0738 Google Scholar
R. Lipowski and
M. Girardet,
“Shape fluctuations of polymerized or solidlike membranes,”
Phys. Rev. Lett., 65 2893
–2896
(1990). https://doi.org/10.1103/PhysRevLett.65.2893 0031-9007 Google Scholar
N. Gov,
“Membrane undulations driven by force fluctuations of active proteins,”
Phys. Rev. Lett., 93 268104
(2004). https://doi.org/10.1103/PhysRevLett.93.268104 0031-9007 Google Scholar
N. S. Gov and
S. A. Safran,
“Red blood cell membrane fluctuations and shape controlled by ATP-induced cytoskeletal defects,”
Biophys. J., 88 1859
–1874
(2005). https://doi.org/10.1529/biophysj.104.045328 0006-3495 Google Scholar
S. Tuvia,
S. Levin, and
R. Korenstein,
“Correlation between local cell-membrane displacements and filterability of human red-blood-cells,”
FEBS Lett., 304 32
–36
(1992). https://doi.org/10.1016/0014-5793(92)80583-3 0014-5793 Google Scholar
F. L. Brown,
“Regulation of protein mobility via thermal membrane undulations,”
Biophys. J., 84 842
–853
(2003). 0006-3495 Google Scholar
K. Zeman,
E. H., and
E. Sackman,
“Bending undulations and elasticity of the erythrocyte membrane: effects of cell-shape and membrane organization,”
Eur. Biophys. J., 18 203
–219
(1990). https://doi.org/10.1007/BF00183373 0175-7571 Google Scholar
A. Zilker,
H. Engelhardt, and
E. Sackmann,
“Dynamic reflection interference contrast (RIC) microscopy—a new method to study surface excitations of cells and to measure membrane bending elastic-moduli,”
J. Phys. (Paris), 48 2139
–2151
(1987). 0302-0738 Google Scholar
A. Zilker,
M. Ziegler, and
E. Sackmann,
“Spectral-analysis of erythrocyte flickering in the 0.3-4-mu-M-1 regime by microinterferometry combined with fast image-processing,”
Phys. Rev. A, 46 7998
–8002
(1992). https://doi.org/10.1103/PhysRevA.46.7998 1050-2947 Google Scholar
S. Levin and
R. Korenstein,
“Membrane fluctuations in erythrocytes are linked to Mgatp-dependent dynamic assembly of the membrane skeleton,”
Biophys. J., 60 733
–737
(1991). 0006-3495 Google Scholar
T. Ikeda,
G. Popescu,
R. R. Dasari, and
M. S. Feld,
“Hilbert phase microscopy for investigating fast dynamics in transparent systems,”
Opt. Lett., 30 1165
–1168
(2005). https://doi.org/10.1364/OL.30.001165 0146-9592 Google Scholar
G. Popescu,
T. Ikeda,
C. A. Best,
K. Badizadegan,
R. R. Dasari, and
M. S. Feld,
“Erythrocyte structure and dynamics quantified by Hilbert phase microscopy,”
J. Biomed. Opt., 10 060503
(2005). https://doi.org/10.1117/1.2149847 1083-3668 Google Scholar
G. Popescu,
T. Ikeda,
R. R. Dasari, and
M. S. Feld,
“Diffraction phase microscopy for quantifying cell structure and dynamics,”
Opt. Lett., 31 775
–777
(2006). 0146-9592 Google Scholar
G. Popescu,
L. P. Deflores,
J. C. Vaughan,
K. Badizadegan,
H. Iwai,
R. R. Dasari, and
M. S. Feld,
“Fourier phase microscopy for investigation of biological structures and dynamics,”
Opt. Lett., 29 2503
–2505
(2004). https://doi.org/10.1364/OL.29.002503 0146-9592 Google Scholar
M. Hammer,
D. Schweitzer,
B. Michel,
E. Thamm, and
A. Kolb,
“Single scattering by red blood cells,”
Appl. Opt., 37 7410
–7418
(1998). 0003-6935 Google Scholar
B. Rappaz,
P. Marquet,
E. Cuche,
Y. Emery,
C. Depeursinge, and
P. J. Magistretti,
“Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy,”
Opt. Express, 13 9361
–9373
(2005). https://doi.org/10.1364/OPEX.13.009361 1094-4087 Google Scholar
O. V. Sosnovtseva,
A. N. Pavlov,
N. A. Brazhe,
A. R. Brazhe,
L. A. Erokhova,
G. V. Maksimov, and
E. Mosekilde,
“Interference microscopy under double-wavelet analysis: a new approach to studying cell dynamics,”
Phys. Rev. Lett., 94 218103
(2005). https://doi.org/10.1103/PhysRevLett.94.218103 0031-9007 Google Scholar
|

