|
|
1.IntroductionMost biological tissues are optically anisotropic turbid media, containing fibrous microstructures and birefringence optical polarization effects.1–3 It is important to mimic and interpret the structural and optical anisotropies using polarized scattering models or phantoms for tissue characterization.4–7 There have been many polarized scattering models for biological tissues.8 Wang et al. presented a sphere birefringence model, which contains spherical particles randomly suspended in linearly birefringent media.9 He and Yun et al. proposed a sphere-cylinder scattering model (SCSM) to characterize the anisotropic scattering property of fibrous tissues, such as skeletal muscles.10,11 Furthermore, Du et al. extended the SCSM to the sphere-cylinder birefringence model (SCBM) by introducing birefringence to the medium between scatterers.12 In a previous study, we examined the tissue anisotropy contributed by both the scattering of cylindrical scatterers and the birefringent media using Mueller matrix polar decomposition.13 Lately, it has been noticed that there exists intrinsic birefringence on intracellular microtubules, microfilaments, and other fibrous scatterers in tissues.14 Recently, in a study on the microstructures of textiles, Peng et al. proposed a birefringent cylinder scattering model, in which the textile fibers have different refractive indices in the axial and radial directions; a corresponding Monte Carlo simulation was also reported for textile fibers randomly distributed in the plane.15 In this article, we extend further the SCBM to include the intrinsic birefringence on the cylindrical scatterers of arbitrary spatial distributions. We also developed a new Monte Carlo simulation program to calculate the effects of well-ordered birefringent fibers to mimic the structure of biological tissues.16 After verifying the validity of the new anisotropic tissue model and the Monte Carlo simulation program, we then analyzed the contributions of the well-ordered birefringent cylinders to the retardance obtained from Mueller matrix polar decomposition. We present the comparison of polarization characterization for the birefringent cylinders model and the model of nonbirefringent cylinders with birefringence medium between them. The study will help us to understand and mimic the polarization behavior of photons in complicated tissues and explain the optical anisotropy and characteristic features of tissues based on polarized photon scattering measurements. 2.Theory2.1.Polarized Photon Scattering at a Inhomogeneous Birefringent CylinderWe have developed a SCSM and a SCBM to describe tissue anisotropy.11,12 We assumed that the small spheres and infinite cylinders are embedded in the medium of linear birefringence. When photons transport through the media, they will be scattered by the spherical and cylindrical scatterers. We extended the SCBM by replacing the nonbirefringent cylinders with birefringent ones. Peng’s calculation of single scattering for birefringent cylinders is referenced in this paper, but we corrected a mistake in Eq. (9), and the dielectric coefficient and permeability are replaced with refractive index, consistent with our previous notations.11 We can establish a coordinate system shown below in Fig. 1. The refractive index of birefringent cylinders can be written as axisymmetric tensors where , , and are the transverse and axial unit vectors.Then, we can write the internal electromagnetic field quantities in the form Subscript expresses the transverse plane, which is perpendicular to the axis. According to these, Maxwell’s equation can be expressed as17,18 where , , , and are quadratic functions of , and is a differentiating operator. By using plane wave expansion method, we can solve Eq. (3) to get internal electromagnetic field quantities and , and get and . Using the continuity conditions on the boundary, we can get scattered field (parallel component and perpendicular component ) where and represent the radial and axial distances in the cylindrical coordinates, is the radius of the cylinder, is the refractive index and is the wave impedance of the ambient medium, is the wave number, is the angle between the direction of incident light and the direction of cylinder, and is the azimuth angle of the scattered light on the scattering cone. is the Bessel function, and , respectively, expressing the first and second kind of Hankel function.From the above formulas, we can get Mueller matrix and its elements as follows19 2.2.Validity for Single Scattering ProcessIn the present model, scattering by a birefringent cylinders with equal axial and radial refractive indices should be equivalent to a nonbirefringent cylinders studied in our previous work.11 Hence, we test the validity of the new model and the new simulation program by checking if the scattering behavior of birefringent cylinders with equal axial and radial refractive indices coincides with the situation that the cylinder scatters without the birefringence. Figure 2 shows the Mueller matrix elements as functions of the azimuth angle for a single scattering of a birefringent cylinder with the different axial and radial refractive indices marked by solid black line, and a birefringent cylinder with same axial and radial refractive indices marked by dotted black line. All are calculated using our newly developed program. The Mueller matrix elements of nonbirefringent cylinder calculated with our previous program are shown as the red dotted line completely overlapping with the dotted black line,11 which confirms the validity of the developed program for birefringent cylinders. In Fig. 2, Mueller matrix except for (, ) are all normalized by . And is normalized by , . Fig. 2Single scattering Mueller matrix of a birefringent cylinder with the different axial and radial refractive indices of 1.57 and 1.53 (solid black lines), and a birefringent cylinder (dotted black lines) with the same axial and radial refractive indices of 1.57. Calculations for a nonbirefringent cylinder with the refractive index of 1.57 are shown as the red dotted lines, which overlap completely with the dotted black lines. The incident angle of light is and the diameter of the cylinder is 1.5 μm. The abscissa is azimuth 0–180 deg. 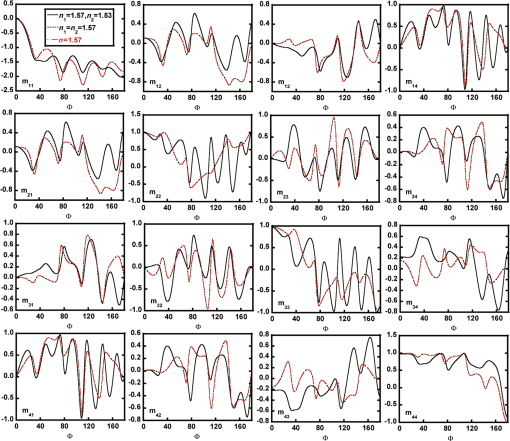 Figure 2 shows that the Mueller matrix elements for single scattering by a birefringent cylinder are clearly different from those by a nonbirefringent cylinder. To examine the polarization features of fibrous tissue microstructures, contributions by the intrinsic birefringence on the cylinders need to be considered. 3.Samples and ExperimentsFor further verification of our Monte Carlo program for birefringent cylinders and demonstration of the influence of birefringent cylinders on polarization measurements, we present the simulation and experimental results of forward scattering Mueller matrix of nonbirefringent and birefringent cylinders, respectively. In the experiments, we prepare two samples by winding either well-aligned nonbirefringent glass fibers or birefringent silk fibers around small frames.20 The experimental setup has been used in a previous study for forward scattering Mueller matrix measurements.5 Before the experiments, we measured air and a polarizer as the standard samples, and the calibration errors can be estimated at about 5%.13 Figure 3(a) represents the experimental result for the silk sample, and Fig. 3(c) is for the glass fiber sample. Earlier studies have shown that the silk fibers contain fibrous substructures of 1.5-μm diameter,5 and the refractive indices along radial and axial directions are 1.53 and 1.57.20 The glass fibers have a refractive index of 1.547 and about 10 μm in diameter (observed by SEM).13,20 The corresponding simulation results of birefringent and nonbirefringent cylinders are shown in Figs. 3(b) and 3(d) with the scattering coefficient and the other parameters the same as the experimental conditions; the wavelength in the simulation is 633 nm. Figures 3(a)–3(d) show very good agreement between experiments and simulations and confirm the validity of the scattering model and the corresponding Monte Carlo simulation program for scattering medium containing orderly arranged birefringent cylinders. Fig. 3Experimental and simulation results of forward scattering Mueller matrix. (a) and (b) are experimental and simulated results of birefringent cylinders (well-aligned silk fiber). (c) and (d) are experimental and simulated results of nonbirefringent cylinders (well-aligned glass fiber). 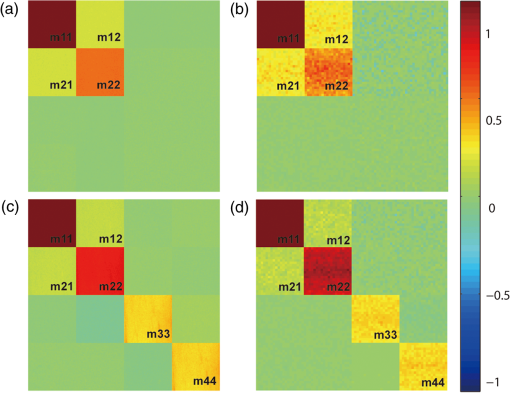 It can be seen from Fig. 3, for both the well-aligned nonbirefringent or birefringent cylinders, and are nearly equal, and is significantly bigger than the other polarization dependent elements. For the Mueller matrix elements and , however, they are different for the birefringent and nonbirefringent cylinders, probably due to the intrinsic birefringence on cylindrical scatters. Considering the possible small fluctuation of arrangement and size for cylinders during the preparation of experimental phantoms, the slight differences between experiments and simulations are possibly due to the uncertainty of the simulation approximation. Further simulations with different parameters in the model show that the effects on the Mueller matrix elements due to the birefringence in the cylindrical scatterers are complicated and sensitive to the diameter and refractive indices of the cylinders. 4.Results and DiscussionThe Mueller matrix can characterize polarization properties of a sample. There are several other methods to decompose Mueller matrix; in a previous work,13 we used the Lu-Chipman Mueller matrix polar decomposition method to “decompose” a Mueller matrix into three constituent “basic” matrices, representing depolarization (), retardance (), and diattenuation ().21 From Eq. (10), we can see that the value of Mueller matrix elements depends on various factors, but we focus on the relationship between Mueller matrix and intrinsic birefringence of cylindrical scatterers. By Monte Carlo simulations, we examine how the birefringent cylinders affect the retardance () for an anisotropic sample. We simulate Mueller matrix images using different birefringence values of the cylinders, evaluate the retardance (), depolarization (), and diattenuation () pixel by pixel using Mueller matrix polar decomposition, and then calculate their mean values. Figure 4 shows the retardance () from the simulated data as functions of the radial and axial refractive indices difference and diameters of the cylinders. The diameters of the cylinders are from 0.6 to 2 μm, and the values of birefringence are from 0 to ; the thickness of the medium is 1 cm. Figures 4(a)–4(c), respectively, represent three cases of different scattering coefficients, , , . It can be seen that the contributions by the birefringent cylinders to the retardance strongly depend on their diameter and density. For , the retardance decreases as the diameter of the cylinders increases and increases as the scattering coefficient increases, as found in the previous work.13 There is a good positive linear relationship between and the intrinsic birefringence of the cylinders, which appear to be very similar to the effects due to the birefringent medium between scatterers.13 The slope of the retardance-birefringence curves is shown in Fig. 4, which represents how sensitively the retardance varies with the birefringence on the cylinder, and also increases with the diameter of the birefringent cylinders and the scattering coefficient. We extract the values of slopes of the curves by linear function fitting. We plot in Figs. 5(a) and 5(c) these slopes as functions of the diameter and scattering coefficient of the birefringent cylinders. After a normalized transformation of abscissa axis by , Figs. 5(a) and 5(c) change into Figs. 5(b) and 5(d); there is a clear positive and approximately linear correlation between the slope and the product of cylinder diameter and density. Fig. 4The relationship between the birefringence of the cylinders and the retardance . Different curves represent different diameters of birefringent cylinders, (a)–(c) represent different scattering coefficients of the sample. 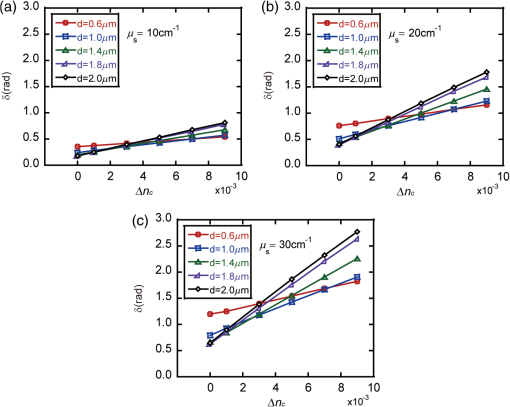 Fig. 5Slopes extracted from Figs 4(a)–4(c), (a) and (c) represent the relationship between the diameter and scattering coefficient and , (b) and (d) represent the relationship between the product of diameter and scattering coefficient and . 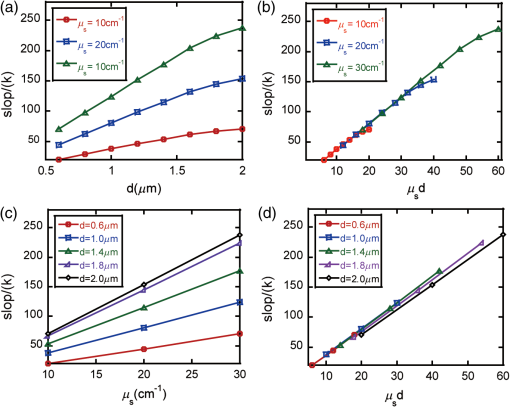 In addition, we did some investigation about depolarization () and diattenuation () in the birefringent cylinders model. We can find that, compared with the retardance, and just have a small fluctuation with the birefringence on the birefringent cylinders. In the previous study,13 we have analyzed the contributions of retardance by the nonbirefringent cylinders with the birefringent medium between scatterers. According to our previous research work, Fig. 6 shows as functions of the medium birefringence in the cylinder-birefringence sample. The retardance increases linearly with the birefringence of the ambient medium and decreases with the diameter of the cylinders. Here, we compare two types of birefringence, respectively, in the birefringent cylinders and the cylinder-birefringence sample. For the birefringent-cylinder scattering samples (Figs. 4 and 5), the diameter of the cylinders plays an important role on the retardance. However, for the cylinder-birefringence model, the birefringent medium surrounding the nonbirefringent cylinder is the major source of the total retardance. Fig. 6Change in the birefringence of the medium surrounding the nonbirefringent cylinder. The diameters of the cylinder were 1.0, 1.4, and 2.0 μm, and the scatter coefficient is ; the birefringence of the ambient medium varies from 0 to . 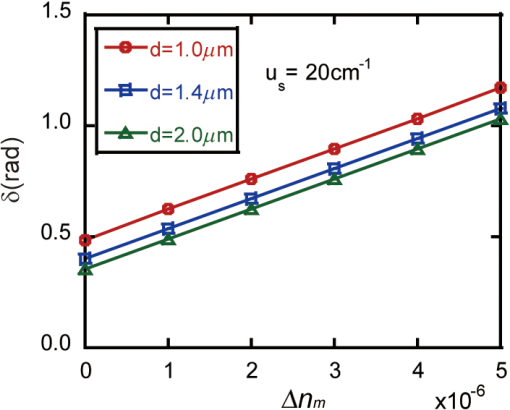 In Fig. 6, the well-aligned nonbirefringent cylinders are in parallel to the birefringence axis of the birefringent medium, where the range is set to a smaller scale to ensure stays in the range of 0 to . The scattering coefficient of cylinders affects only the initial value of the retardance, but not the slope of the curve. For the birefringent medium, the retardance can be written as , where is the projection along the direction of the moving distance between two successive scattering events, is the birefringence of the medium, is the average refractive index, and is the wavelength of light. If we set the same birefringence parameter as Fig. 6, the coefficient is nearly equal to the slope of curves in Fig. 6, which is around . By contrast, in the birefringent cylinders samples, the slope of the curves shown in Fig. 5 is only on the order of magnitude of , indicating that the intrinsic birefringence of cylindrical scatterers has weaker influence on the total retardance than the birefringence of the ambient medium. 5.ConclusionWe established an anisotropic scattering model including birefringent cylinders with different refractive indices along the radial and axial directions and developed the corresponding Monte Carlo simulation program. The validity of simulation program is tested by experiments using well-aligned nonbirefringent and birefringent cylinders. The present study shows that the retardance due to scattering of well-ordered birefringent cylinders comes from two sources: scattering by nonbirefringent cylinders and an additional part associated with the intrinsic birefringence on cylinders. Moreover, the retardance increases linearly with and almost linearly with the diameter of the birefringent cylinder. We also compare the influence of the birefringent cylinders on the retardance with our previous cylinder-birefringence model. For the same birefringence, the birefringent cylinders usually contribute much less to the retardance than the birefringent medium. AcknowledgmentsWe acknowledge financial support from the National Natural Science Foundation of China (NSFC) Grant Nos. 11174178, 61205199, and 11374179. ReferencesK. S. Saladin, Anatomy and Physiology, Watnick, New York
(2010). Google Scholar
A. F. HuxleyR. Niedergerke,
“Measurement of the striations of isolated muscle fibers with the interference microscope,”
J. Physiol., 144
(3), 403
–425
(1958). JPHYA7 0022-3751 Google Scholar
J. J. Pasquesiet al.,
“In vivo detection of exercised-induced ultrastructural changes in genetically-altered murine skeletal muscle using polarization-sensitive optical coherence tomography,”
Opt. Express, 14
(4), 1547
–1556
(2006). http://dx.doi.org/10.1364/OE.14.001547 OPEXFF 1094-4087 Google Scholar
S. N. Savenkovet al.,
“Light transmission in inhomogeneous birefringent medium as a function of propagation and observation angles,”
J. Quant. Spectrosc. Radiat. Transfer, 110
(14), 1441
–1447
(2009). http://dx.doi.org/10.1016/j.jqsrt.2009.01.009 JQSRAE 0022-4073 Google Scholar
H. Heet al.,
“Application of sphere-cylinder scattering model to skeletal muscle,”
Opt. Express, 18
(14), 15104
–15112
(2010). http://dx.doi.org/10.1364/OE.18.015104 OPEXFF 1094-4087 Google Scholar
M. F. G. WoodX. GuoI. A. Vitkin,
“Polarized light propagation in multiply scattering media exhibiting both linear birefringence and optical activity: Monte Carlo model and experimental methodology,”
J. Biomed. Opt., 12
(1), 014029
(2007). http://dx.doi.org/10.1117/1.2434980 JBOPFO 1083-3668 Google Scholar
A. Pierangeloet al.,
“Polarimetric imaging of uterine cervix: a case study,”
Opt. Express, 21
(12), 14120
–14130
(2013). http://dx.doi.org/10.1364/OE.21.014120 OPEXFF 1094-4087 Google Scholar
N. GhoshM. F. G. WoodI. A. Vitkin,
“Mueller matrix decomposition for extraction of individual polarization parameters from complex turbid media exhibiting multiple scattering, optical activity, and linear birefringence,”
J. Biomed. Opt., 13
(4), 044036
(2008). http://dx.doi.org/10.1117/1.2960934 JBOPFO 1083-3668 Google Scholar
X. WangL. V. Wang,
“Propagation of polarized light in birefringent turbid media: a Monte Carlo study,”
J. Biomed. Opt., 7
(3), 279
–290
(2002). http://dx.doi.org/10.1117/1.1483315 JBOPFO 1083-3668 Google Scholar
H. Heet al.,
“Two-dimensional backscattering Mueller matrix of sphere-cylinder scattering medium,”
Opt. Lett., 35
(14), 2323
–2325
(2010). http://dx.doi.org/10.1364/OL.35.002323 OPLEDP 0146-9592 Google Scholar
T. Yunet al.,
“Monte Carlo simulation of polarized photon scattering in anisotropic media,”
Opt. Express, 17
(19), 16590
–16602
(2009). http://dx.doi.org/10.1364/OE.17.016590 OPEXFF 1094-4087 Google Scholar
E. Duet al.,
“Two-dimensional backscattering Mueller matrix of sphere-cylinder birefringence media,”
J. Biomed. Opt., 17
(12), 126016
(2012). http://dx.doi.org/10.1117/1.JBO.17.12.126016 JBOPFO 1083-3668 Google Scholar
Y. Guoet al.,
“A study on forward scattering Mueller matrix decomposition in anisotropic medium,”
Opt. Express, 21
(15), 18361
–18370
(2013). http://dx.doi.org/10.1364/OE.21.018361 OPEXFF 1094-4087 Google Scholar
M. ShribakR. Oldenbourg,
“Techniques for fast and sensitive measurements of two-dimensional birefringence distributions,”
Appl. Opt., 42
(16), 3009
–3017
(2003). http://dx.doi.org/10.1364/AO.42.003009 APOPAI 0003-6935 Google Scholar
B. PengT. DingP. Wang,
“Propagation of polarized light through textile material,”
Appl. Opt., 51
(26), 6325
–6334
(2012). http://dx.doi.org/10.1364/AO.51.006325 APOPAI 0003-6935 Google Scholar
V. V. TuchinL. V. WangD. A. Zimnyakov,
“Tissue structure and optical models,”
Optical Polarization in Biomedical Applications, 7
–28 Springer, New York
(2006). Google Scholar
J. C. Monzon,
“Three-dimensional scattering an infinite homogeneous anisotropic circular a spectral approach,”
IEEE Trans. Antennas Propag., 35 670
–682
(1987). http://dx.doi.org/10.1109/TAP.1987.1144159 IETPAK 0018-926X Google Scholar
X. B. WuK. Yasumoto,
“Three-dimensional scattering by an infinite homogeneous anisotropic circular cylinder: an analytical solution,”
J. Appl. Phys., 82 1996
–2003
(1997). http://dx.doi.org/10.1063/1.366009 JAPIAU 0021-8979 Google Scholar
C. F. BohrenD. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley & Sons, New York
(1983). Google Scholar
Textile Physics, 2nd ed.Donghua Press, Shanghai
(2009). Google Scholar
S. Y. LuR. A. Chipman,
“Interpretation of Mueller matrix based on polar decomposition,”
J. Opt. Soc. Am. A, 13
(5), 1106
–1113
(1996). http://dx.doi.org/10.1364/JOSAA.13.001106 JOAOD6 0740-3232 Google Scholar
|