|
|
1.IntroductionRecently, with the development of fluorescent probes and reporter technologies, rapid advancement has been achieved in the fluorescent imaging of turbid media.1,2 Fluorescent imaging methods based on fluorescent probes allow the noninvasive visualization of biological processes at the cellular and molecular levels, providing a next-generation tool for molecular imaging. Fluorescence tomographic methods employing a near-infrared spectral window of 700 to 900 nm as a new and promising imaging modality can three-dimensionally resolve the fluorescence distribution in vivo, enabling applications in small-animal research and preclinical diagnostics.3–10 However, it is well known that most biological tissues comprise turbid media with a high optical scattering in the infrared spectral window,1 in which the diffusion-like behavior of the excitation and fluorescent photons in turbid media presents a considerable challenge for the quantitative accuracy of fluorescence tomographic imaging. An accurate and effective photon propagation model for the excitation-to-emission conversion and the transport of the fluorescence is essential for a fluorescence tomographic method to meet this challenge. The development of new excitation and fluorescent light propagation models that are more accurate and computationally efficient will improve the quantitative accuracy of fluorescence tomographic imaging. Thus, the fluorescence model attracts unprecedented attention for the excitation-to-emission conversion and the transport of the fluorescence in turbid media. The present models for the excitation-to-emission conversion and the transport of the fluorescence in turbid media are derived from the radiative transport equations (RTEs),11,12 including the simple analytical model,13 diffusion approximation model,14–19 and Monte Carlo (MC) model.20–27 The analytical model can be applied only in relatively simple configurations, such as the slab model with homogeneous media. The diffusion approximation model is widely used because it can be performed quickly compared with the other methods, such as the RTEs and MC. However, the diffusion approximation has several limitations: it is inadequate in the case of nonscattering media, inaccurate near the boundary within the mean free path, and inappropriate in the case of highly absorbent tissues.17 The MC model can solve the RTEs without the limitations of complex geometries and optical properties. Theoretically, MC solutions can be obtained for any desired accuracy, and thus, the MC model is widely recognized as the gold standard for its superior accuracy and versatility.16,23 However, the accuracy is proportional to , where is the number of photons propagating. Thus, relative errors less than a few tenths of a percent require the propagation of substantial numbers of photons ( to ) and large amounts of computing time. This is especially true for the MC models of the fluorescence, such as the standard fluorescence MC model,28 because the probability of the excitation-to-emission conversion of the fluorescence is far lower, and a far longer computation time is required to obtain statistically reliable results for the fluorescence photons. Especially for fluorescence-based in vivo tomography, changing any of the input parameters requires a new simulation, resulting in a large computational load. To overcome this problem, the adjoint fluorescence MC (afMC)27,29 model and the perturbation fluorescence MC (pfMC) model25,29–33 are developed as fluorescence MC techniques that are more feasible for application in fluorescence-based tomography. The afMC model is built on the basis of the Born approximation and assumes that the source and detector are interchangeable, i.e., equivalent, which is difficult to satisfy for a free-space configuration because of the large difference between the light sources and photodetectors, i.e., pixels on a charge-coupled device (CCD). The pfMC model assumes that the fluorescence photons are launched anisotropically, rather than isotropically, and are calculated along the path histories of the excitation light using the Beer-Lambert law. Owing to these assumptions, the afMC and pfMC models are accuracy-limited in quantitative fluorescence calculation, especially for high fluorophore concentrations or complex fluorophore distributions. The pfMC model is more accurate than the afMC model in media with a high heterogeneity and scattering if there are sufficient photons for the MC simulation, because the assumption of the equivalence between the sources and detectors decreases the accuracy of the afMC model, restricting the model’s application in free-space fluorescence molecular tomography.29 The efficiency of the afMC model is also very low in fluorescence diffuse optical tomography (FDOT) if there are a large number of detectors, equal to the number of MC simulations required.29 On the basis of integral forms of the transport equations for a fluorescence MC model, we present a decoupled fluorescence MC (dfMC) model for the direct computation of the fluorescence in turbid media. By decoupling the excitation-to-emission conversion and transport process of the fluorescence from the path probability density function and associating the corresponding parameters involving the fluorescence process with the weight function, the sampling path of the fluorescence photons becomes identical to that of the excitation light, and the fluorescence statistical quantities are unbiased. Using the path histories of the exciting photons and the corresponding new weight function, we can compute the fluorescence distribution directly. This paper is structured as follows. Section 2 describes the theoretical derivation of the dfMC model from the RTEs; we analyze the dfMC model by comparing it with the pfMC model. Then, we introduce the implementation of the dfMC model in the programming language C and the acceleration of the MC simulation by graphic processing unit (GPU) clusters. Section 3 describes two groups of phantom experiments to verify the accuracy of the dfMC model. Section 4 describes the results of the phantom experiments by comparing them with those of the dfMC and pfMC simulations, and we discuss the influence of the optical parameters on the accuracy. Last, we look ahead to the future development of the dfMC model. 2.Methods2.1.Theoretical ModelAs illustrated in Fig. 1, we use the following definitions for biological tissues. The volume denotes the nonfluorescence zone, and denotes the fluorescence zone. In the excitation light state, the optical parameters are , , in and . In the fluorescent light state, the optical parameters are , , in and . The specific absorption coefficient of the fluorophore is , and the quantum yield is . Here, we assume that the optical property in is not affected by fluorophore. The total attenuation is then , . Fig. 1Mechanism of excitation-to-emission conversion and transport in media. Excitation and emission are indicated by green and red segments, respectively. The sequence is an arbitrary state sequence that represents a type of photon path from the source to the detector through collisions. 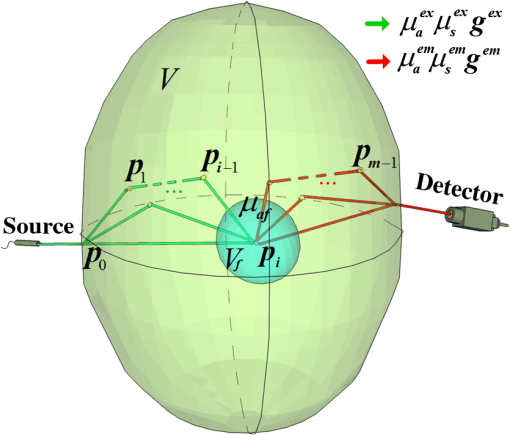 We define as an arbitrary state sequence of the photon propagation in the media, including the state of the excitation and emission photons generated in the fluorescence zone, where the state is a six-dimensional vector comprising the spatial coordinate vector as the position and the unit direction vector as the direction of motion. We assume that and are two arbitrary adjacent states from and that is before within the sequence. The RTE can be written in the appropriate integral forms for the excitation and fluorescence light.34 The RTE for the excitation light is given by Here, is the probability density of excitation light at state , which consists of two parts. is the source of excitation light at state . is the excitation photons scattering to state from other states. Once fluorescence light is generated, its propagation can be modeled using another RTE: Here, is the probability densities for the photon emission at a position along the direction , which consists of two parts. is the fluorescence photons generated at state . is the fluorescence photons scattering to state from other states. The kernel , which describes the state transitions from to , can be factored into the product of the transport kernel and the collision kernel , having the form . The transport kernel is given by , which describes the probability density of the photon flights between neighboring collisions. Here, is the length variable along toward . The collision kernel describes the photon collision interactions, comprising the probability of scattering at as well as the angular deflection of the photon if a scattering collision occurs. Here, is the anisotropic scattering phase function that prescribes the probability density for the scattering from the direction to , which is typically the Henyey-Greenstein phase function. The special kernel describes the generation of a fluorescence photon, including the probability of a direct scattering flight from to and the transformation from an excitation photon to a fluorescence photon at . Here, describes the transformation from an excitation photon to an emitting fluorescence photon. The function is the isotropic scattering phase function, equals to . Also, . Let denote the probability density of a photon scattering from to through collisions with optical parameters , , , as described below: According to Eqs. (1)–(3), has the following series solution: To employ the path of the excitation light to calculate the fluorescence , the fluorescence emission from state to must be transformed into the scattering of excitation photons. We use the following transformation to decouple the excitation-to-emission process of the fluorescence from the special kernel describing the generation of fluorescence photons: where . From Eq. (5), we can see that the fluorescence photons of the state excited by the excitation photons of state are proportional to the excitation photons of state scattered from the state . The transformation can maintain energy conservation. This means the excited fluorescence photons can be equivalent to the scattered excitation photons by the equivalent transformation. In addition, the transport of the fluorescence photons from to can be changed into that of excitation light, yielding the following transformation:From Eq. (6), we can see that the fluorescence photons of the state scattered from the state are proportional to the excitation photons of the state scattered from state . The transformation maintains energy conservation. This denotes that the fluorescence photons can propagate from to state in media with the kernel of excitation photons by multiplying a corresponding proportion. This also means that the propagation of fluorescence photons can be equivalent to that of the excitation photons by the equivalent transformation. Using the conversions of Eqs. (5) and (6), we transform Eq. (4) as follows: With a known detector function , in the MC simulation, virtual detectors are placed on the surface of the object. Thus, is the three-dimensional impulse function . The fluorescence statistical quantity collected on the detector is determined as Derived from the RTE method, we obtain the form of the fluorescence statistical quantity . is a multiple integral form. MC is preferred as the most accurate method of solving the integral problem. MC methods have been widely applied in varying types of physical problems. Historically, the MC methods have first been successfully used to solve particle transport problems.34,35 This is still one of the areas of most extensive use at present. On the basis of the principle of the MC method, in the fluorescence MC simulation, the probability density function and the weight function are constructed to solve the fluorescence statistical quantity . With and have the following forms: Here, is the weight function of an excitation photon, and equals . The product of and , which represents the probability that an excitation photon is transported from the laser source to through collisions in turbid media, is then converted to a fluorescence photon and transported to the detector through collisions in the media. Apparently, if we set the path sampling function to that of the excitation light, the path of the fluorescence photon is identical to that of the excitation photon. Therefore, along the paths sampled by Eq. (9), the fluorescence statistical quantities can be calculated using the new weight function determined by Eq. (10). The new weight function of the fluorescence photon is associated with the specific absorption coefficients of the fluorophores at all scattering positions of the photon path in the fluorescence zone. We store the path information of the excitation photons, including the scattering length and factors , at every scattering position and calculate the fluorescence weight according to Eq. (10). For most biological tissues, the excitation and emission wavelengths differ by only a few tens of nanometers. Therefore, we can simplify the weight function by assuming that and .25 Thus, the simplified form of Eq. (10) is Equation (11) indicates that the accuracy of the dfMC model is primarily influenced by the scattering coefficient and the specific absorption coefficient of the fluorophore . This is because the sampling of the path histories is primarily affected by the scattering coefficient and the probability of the fluorescence excitation is primarily affected by the specific absorption coefficient of the fluorophore . The derived formulation of Eq. (11) clearly differs from that of the pfMC model. The pfMC model is derived on the basis of the Born approximation.36 In the pfMC model, all fluorescence photon bundles are generated anisotropically and propagate to the detectors along the path of the excitation photons.25 The weight of the fluorescence bundle is calculated on the basis of the Beer-Lambert law:25,36 On the basis of Eqs. (8)–(10), the statistical quantity of fluorescence obtained by the dfMC model is unbiased. However, compared with the dfMC model, the weight expression Eq. (12) of the pfMC model makes the quantity of fluorescence biased. Therefore, the dfMC model is theoretically more accurate than the pfMC model. 2.2.Code Implementation and SimulationsThe generation and propagation of fluorescence photons in turbid media are illustrated in Fig. 1. A point laser source is located at the surface of the turbid media, and the photons are collected at the CCD detectors, which are placed opposite the source. The media is dissected into a spatial voxel grid. Each of the voxel has defined optical parameters. The dfMC modeling consists of two parts: the white MC (wMC), in which a large number of path histories are generated when excitation photons are simulated in background media without fluorophores, and the calculation of the fluorescence weight based on the path histories. Herein, the wMC code is developed, essentially following the concepts of Monte Carlo modeling of light transport in multi-layered tissues, Monte Carlo modeling of photon migration in voxelized media, and Monte Carlo eXtreme.37–39 In the wMC model, the photon packets are launched into the media from the position of the laser source. The scattering length is given by , and the absorption of the photons in the media occurs along the path histories, with a weight attenuated by . According to Eqs. (9) and (10), the scattering length , scattering factor , and index of the voxel in the spatial grid are stored along the path histories of the excitation photon packets in the media. Using the three quantities recorded on the path history and the spatial distribution of the fluorophores, the fluorescence detected by the CCD can be calculated using Eq. (10). The path histories can be repeatedly used for fluorescence calculations with different distributions of fluorophores. The wMC is also time-consuming, as these histories contain a great amount of information, and a large amount of hard-disk storage space is needed. Thus, a fast implementation of the wMC is essential for practical applications. This problem is solved using GPU clusters:39 we build a wMC simulation based on GPU clusters with a compute unified device architecture and MPICH2 (a high-performance and widely portable implementation of the MPI standard). The parallel acceleration is primarily achieved using multinodes, multi-GPUs, and multiprocessing units in the GPU.39–41 The frame is implemented in the programming language C. We simultaneously launch a given number of threads, each simulating a sequence of the photon migration process. The allocation of the threads is determined according to the hardware and length of the path histories. In each thread, a series of photon packets propagates within the media to produce a sequence of scattering histories and weights in media until it exits the media. The tasks of the MC simulation are allocated to every GPU in each node, depending on the number of GPUs in each node, as determined by the Open MP and MPICH2. The path histories are separately obtained in each GPU and each node. The process of the MC simulation is briefly summarized as follows.
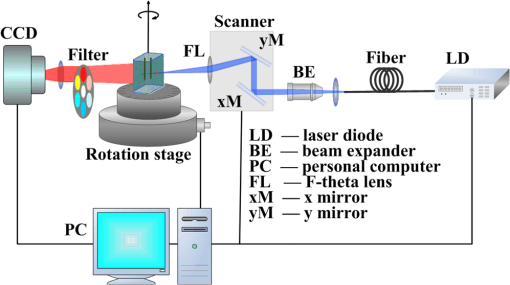
The path histories are generated and stored separately in each node. The distribution of the fluorescence at the CCD can also be calculated in each node, and then the distributions from each node are summed using the GPU clusters. Parallel computing accelerates the wMC simulation and the reading and writing of the path historical data, which expedites the calculation of the fluorescence using the path histories. In order to further accelerate the wMC, a two-step method40 is used to increase the efficient photons, i.e., those reaching the detectors. This method comprises two steps. In the first step, the seeds of a random number, which make the photons reach the detectors, can be obtained using a fast wMC modeling without storing the path histories. These seeds are stored in memory. In the second step, using the stored seeds, a new wMC simulation is conducted to determine and store the path histories of the efficient photons. In wMC, the main time consumption is the storage of path histories. On the basis of the two-step method, only the path histories of efficient photons are stored, which greatly accelerates the speed of MC simulation. 3.Experimental Validations and Comparisons3.1.Experimental Setup and PhantomWe test the accuracy through phantom experiments with different fluorescent concentrations and turbid media. Figure 2 presents a sketch of the experimental system developed in our lab.42 A 748-nm continuous-wave diode laser (BWF1, B&W Tek, USA) is employed as an excitation source. The excitation source is adjusted by fast raster scanning with a dual-axis galvanometric scanner (Nutfield XLR8) to obtain the correct incident position and angle, and the two-dimensional projections are collected by an electron-multiplying CCD (DU-897, Andor, UK). The filters, having a center wavelength of 775 nm and a full width at half maximum of 46 nm (FF01-775/46-25, Semrock, USA), are placed inside a filter wheel and used to select the emission wavelengths. A rotation stage (ADRS -100, Aerotech, USA) fixed at the center of the system holds the imaging object. Here, the rotation stage is used to adjust the imaging object for obtaining projections of any view. The experiment data are collected in a single computer, which is shown in Fig. 2. All the data are processed in special GPU clusters (configuration in every node: Intel Core(TM) i7-2600 CPU; 8 cores, 16 G memory, NVIDIA GeForce GTX 670). The experiments are conducted with a phantom comprising a transparent glass box (5.5 cm in length, 3.0 cm in width, and 4.2 cm in height) filled with Intralipid (Sichuan Kelun Pharmaceutical Co. Ltd 25%), which can be diluted to adjust the scattering coefficient. Two smaller transparent glass tubes filled with DiR-BOA (1,1′-dioctadecyl-3,3,3′,3′-tetramethylindotricarbocyanine iodide bisoleate, a lipid-anchored near-infrared fluorophore; ex. 748 nm, em. 780 nm) are employed as fluorescent targets, designed to simulate multifluorophores in biological tissue. The configuration of the phantom together with the two targets is shown in Fig. 3(a). Fig. 3(a) Configuration of phantom together with two fluorescent targets and direction of source. (b) Voxel subdivision of fluorescence phantom. 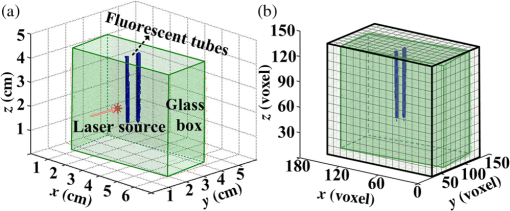 In order to quantitatively verify the accuracy of the proposed dfMC model, two groups of experiments are designed. In group 1, phantoms with different scattering coefficients are prepared. Intralipid is diluted to 10, 6, and 2%, respectively, by adding 95% ethanol. These are then poured into three glass boxes, respectively. The small tubes in the three boxes are injected with the raw solution of DiR-BOA.43 In group 2, phantoms with different specific absorption coefficients of the fluorophores are prepared. Three glass boxes are filled with a 10% Intralipid solution. The small tubes in the three glass boxes are then injected with Dir-BOA, diluted to 20, 60, and 100%, respectively. The optical properties of Intralipid and Dir-BOA are determined by their concentrations, which are measured by a spectrophotometer (Lamda 950, PerkinElmer, USA). In detail, we use the spectrophotometer to measure the reflectivity and transmissivity, and use the adding-doubling method to calculate the optical coefficient from the measured data. Tables 1 and 2 summarize the optical properties of the phantoms in the two groups. Because the absorption coefficient of the raw solution of Intralipid is very small, we set the fluorescence quantum yield as 1 and the absorption coefficient and anisotropy factor of the turbid media as and 0.9, respectively.44 Table 1List of optical parameters of phantom in group 1.
Table 2List of optical parameters of phantom in group 2.
3.2.ResultsThe phantom is dissected into voxels according to the computed tomography data.42 The size of each voxel is 0.0348 cm. As shown in Fig. 3(b), there are in the model. The position and direction of the laser source are shown in Fig. 3(a). In order to retain the precision of the MC simulation, a large number of photon packets must be simulated to obtain simulation results with an adequate signal-to-noise ratio. Here, photons are simulated in the wMC simulation. The accuracy of the dfMC model is affected by the optical parameters of the turbid media. According to Eq. (11), the path histories in the turbid media are mainly affected by the scattering coefficient; the probability of the fluorescence excitation is affected by the specific absorption coefficient of the fluorophores. In contrast, the influence of the difference in the absorption coefficient between the excitation light and fluorescence light on the accuracy of the dfMC model can be neglected if there are enough photons. This is because the fluorescence statistical quantity of the dfMC model is unbiased. First, we verify the accuracy of the path histories of the excitation photons by comparing the spatial distribution of the excitation light intensity on the CCD detectors between the wMC simulations and phantom experiments for three different scattering coefficients. Figures 4(a1)–4(a3), 4(b1)–4(b3), and 4(c1)–4(c3) compare the normalized intensity of the excitation light between the wMC and phantom experiments at scattering coefficients of 44.1, 129.8, and , respectively. Figures 4(a3), 4(b3), and 4(c3) indicate the contour lines of the excitation light. Fig. 4Comparisons of excitation light intensity on CCD detectors between white Monte Carlo (wMC) simulations and phantom experiments with (a1) to (a3) , (b1) to (b3) , and (c1) to (c3) ; (a3), (b3), and (c3) indicate contour lines of excitation light intensity. 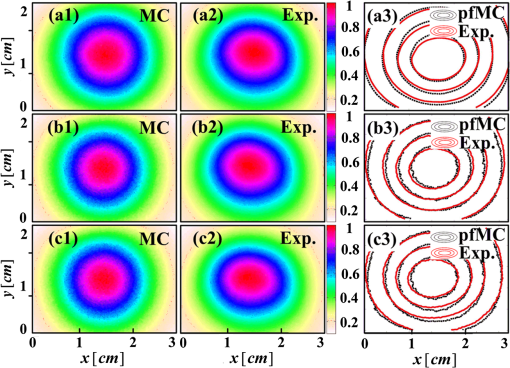 Next, we evaluate the effects of the scattering coefficients of the media and the specific absorption coefficients of the fluorophores on the dfMC model’s accuracy. We compare the spatial distributions of the fluorescence intensity on the CCD detectors calculated by the dfMC model, the pfMC model,32 and experimental measurements. Figures 5(a1)–5(a3), 5(b1)–5(b3), and 5(c1)–5(c3) indicate the intensity of fluorescence light on the CCD detectors with scattering coefficients of 44.1, 129.8, and , respectively, and fluorescent-specific absorption coefficients of . Figures 5(a4) and 5(a5), 5(b4) and 5(b5), and 5(c4) and 5(c5) compare the calculated and experimental contour lines of the fluorescence intensity. Figures 6(a1)–6(a3), 6(b1)–6(b3), and 6(c1)–6(c3) indicate the intensity of the fluorescence light on the CCD detectors calculated by the dfMC model, pfMC model, and phantom experiments with specific fluorophore absorption coefficients of 0.2, 0.6, and , respectively. Figures 6(a4) and 6(a5), 6(b4) and 6(b5), and 6(c4) and 6(c5) compare the calculated and experimental contour lines of the fluorescence intensity. Fig. 5Comparisons of fluorescence intensity on CCD detectors among perturbation fluorescence Monte Carlo (pfMC) model, decoupled fluorescence Monte Carlo (dfMC) model, and phantom experiments with (a1) to (a3) , (b1) to (b3) , and (c1) to (c3) ; (a4) to (a5), (b4) to (b5), and (c4) to (c5) indicate contour lines of fluorescence intensity calculated by pfMC model, dfMC model, and phantom experiments. 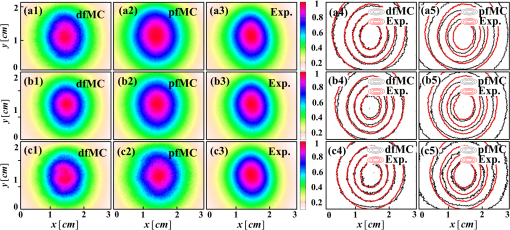 Fig. 6Comparisons of fluorescence intensity on CCD detectors among dfMC model, pfMC model, and phantom experiments with (a1) to (a3) , (b1) to (b3) , and (c1) to (c3) ; (a4) to (a5), (b4) to (b5), and (c4) to (c5) indicate contour lines of fluorescence intensity calculated by dfMC model, pfMC model, and phantom experiments.  We report the statistical results comprising the standard deviation of the relative errors of the fluorescence intensity on the CCD detectors. Figures 7(a) and 7(b) indicate the standard deviation of the relative errors of the fluorescence intensity between the dfMC model and pfMC model toward phantom experiments for different scattering coefficients of the media and different specific absorption coefficients of fluorophores, respectively. Fig. 7(a) Statistical errors of fluorescence intensity on CCD detectors calculated by dfMC model and pfMC model toward phantom experiments for , 129.8, and . (b) Statistical errors of fluorescence intensity on CCD detectors calculated by dfMC model and pfMC model toward phantom experiments for , 0.6, and . 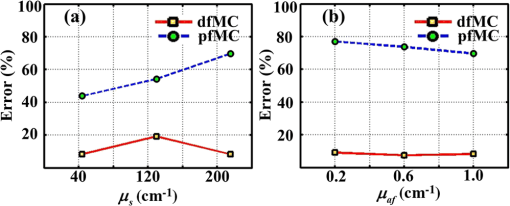 4.Discussion and ConclusionsTheoretically, the accuracy of the dfMC model is mainly affected by the scattering coefficient and the specific absorption coefficients in the media. The scattering coefficient has a great influence on the sampling of the path histories. Also, the specific absorption coefficient determines the probability of the fluorescence excitation. Both of these affect the calculation of the fluorescence signal and introduce some statistical noise. Before the verification of the dfMC model, we must confirm the accuracy of the path histories of the excitation photons generated in the media in the wMC simulation. In Fig. 4, we determine the accuracy through the comparison of the intensity of the excitation light on the CCD between the wMC simulation and experimental measurements. It can be seen that the wMC simulations agree well with the experiments with respect to the shape of the intensity distribution as well as their relative amplitudes for different scattering coefficients. The excellent agreement of the intensity distribution between the wMC simulations and phantom experiments verifies the accuracy of the wMC simulations, which also indicates the validity of the path histories in the white MC simulations. This is because the MC method is a statistical method that is suitable for solving problems of particle transport, such as nuclear physics. In the diffuse optical field, the MC method has been widely developed, e.g., MCMV and MCX.38,39 The MC method is called the gold standard.23 In order to determine whether the accuracy of the dfMC model and pfMC model are affected by the optical parameters of the media, such as the scattering coefficients and specific absorption coefficients, we compare the intensity of the fluorescence light on the CCD among the dfMC model, the pfMC model, and experimental measurements under different scattering coefficients and different specific absorption coefficients. As indicated by Fig. 5, when the scattering coefficient changes from 44.1 to , the intensity of the fluorescence light calculated by the dfMC model exhibits a better agreement with the experimental measurements than that calculated by the pfMC model. Similarly, Fig. 6 shows that when the specific absorption coefficients of the fluorophores change from 0.2 to , the intensity of the fluorescence light calculated by the dfMC model exhibits a better agreement with the experimental measurement than that calculated by the pfMC model. These results suggest that the dfMC model can be quite accurate over a wide range of scattering coefficients and specific absorption coefficients of fluorophores. This is because the dfMC model is directly derived from the RTEs.11–12 Also, the dfMC ensures that the fluorescence statistical quantities are unbiased, which means that the dfMC model can be as accurate as the RTEs if there are sufficient simulated photons. The discrepancies between the dfMC simulations and measurements mainly arise from statistical and measurement noise. In contrast, the results suggest that the accuracy of the pfMC model is easily affected by the scattering coefficients and specific absorption coefficients. This is because the fluorescence statistical quantities of the pfMC model are biased and, therefore, easily influenced by the optical parameters. The discrepancies between the pfMC model and measurements always exist, even in the absence of statistical and measurement noise. Thus, the errors of the pfMC model cannot be eliminated completely by increasing the number of simulated photons. The dfMC model is more accurate than the afMC model. The fluorescence statistical quantities of the afMC model are also biased, because the afMC model relies on the Born approximation and the equivalence between the sources and detectors. These assumptions can cause serious errors in some situations, especially in biological tissues. The differences among the dfMC model, pfMC model, and experimental measurements are further studied by examining the trends of the errors with changes in the optical parameters. As shown in Fig. 7, the standard deviations of the relative errors of the fluorescence intensity calculated by the dfMC model toward the phantom experiments are . However, the standard deviations of the relative errors of the fluorescence intensity calculated by the pfMC model toward the phantom experiments are . These results clearly indicate that the accuracy of the dfMC model fluctuates slightly with the scattering and specific absorption coefficients of fluorophores, and it is more accurate than the pfMC model for the same number of simulated photons. The errors of the dfMC model comprise the statistical and measurement noise and have no relation to the optical parameters, because the fluorescence statistical quantities of the dfMC model are unbiased. Thus, the standard deviations of the relative errors are very small if there are sufficient photons for the MC simulation. However, the errors of the pfMC model are influenced by the optical parameters in tissues apart from the statistical and measurement noise, as the fluorescence statistical quantities of the pfMC model are biased. The deviation of the pfMC model increases as the heterogeneity and scattering coefficients increase in tissues. Also, the accuracy increases as the specific absorption coefficients increase because the probability of the fluorescence excitation is influenced by the specific absorption coefficients. In the present dfMC model, we neglect the second excitation of the fluorophores because the probability of the second excitation is very small in most situations. This is widely accepted by researchers for solving the forward and inverse problems of FDOT.25,29 However, the resorption of the fluorescence photons by the fluorophores is considered in the dfMC model. Thus, the accuracy of the dfMC model is not affected by the number or volume of fluorophores. Our efforts to develop an efficient and accurate fluorescence MC model were motivated by FDOT. Because the dfMC model is derived from the RTEs and the fluorescence statistical quantities are unbiased, the accuracy of the dfMC model is restricted only by the statistical noise. Thus, the accuracy of the dfMC model can be improved by increasing the photons for the wMC simulation. However, this will increase the simulation time. In order to solve this problem, two schemes are used to improve the efficiency of the dfMC model. The first is to accelerate the wMC simulation, which can be achieved using GPU clusters. With sufficient GPUs in the cluster, considerable time can be saved for the fluorescence modeling. The second is to increase the proportion of the effective photons to the total number of simulated photons using a two-step method,40 wherein the effective photons are defined as those reaching the detectors. We employed these strategies to greatly improve the efficiency of the dfMC model for the fluorescence calculation without reducing its accuracy. In the present paper, we described a decoupled fluorescence MC model for the direct computation of the fluorescence in turbid media, along with its implementation and validation for phantom experiments. The dfMC model is derived from the RTEs and has an unbiased fluorescence statistical quantity. It can be very accurate in calculating the fluorescence signal on detectors and is also very efficient. Therefore, the dfMC model is suitable for solving the forward and inverse problems of FDOT. In the future, the dfMC model can be expanded into a time-domain fluorescence model,45 and its efficiency can be further improved by combining with other methods, such as the controlled MC, whereby the direction of the scattering is set toward the detectors.46 In addition, the dfMC model can expand its utility by incorporating the second excitation of fluorophores. The dfMC model has great potential for application in fluorescence-based in vivo tomography. AcknowledgmentsThis project is supported by the National Major Scientific Research Program of China (No. 2011CB910401), National Key Technology R&D Program (Grant No. 2012BAI23B02), Science Fund for Creative Research Group (Grant No. 61121004), and National Natural Science Fund (Grant No. 61078072). ReferencesV. Ntziachristos,
“Going deeper than microscopy: the optical imaging frontier in biology,”
Nat. Methods, 7 603
–614
(2010). http://dx.doi.org/10.1038/nmeth.1483 1548-7091 Google Scholar
D. E. Sosnoviket al.,
“Fluorescence tomography and magnetic resonance imaging of myocardial macrophage infiltration in infarcted myocardium in vivo,”
Circ. Res., 115 1384
–1391
(2007). http://dx.doi.org/10.1161/CIRCULATIONAHA.106.663351 CIRUAL 0009-7330 Google Scholar
J. Halleret al.,
“Visualization of pulmonary inflammation using noninvasive fluorescence molecular imaging,”
J. Appl. Phys., 104 795
–802
(2008). http://dx.doi.org/10.1152/japplphysiol.00959.2007 JAPIAU 0021-8979 Google Scholar
M. Nahrendorfet al.,
“Dual channel optical tomographic imaging of leukocyte pecruitment and protease activity in the healing myocardial infarct,”
Circ. Res., 100 1218
–1225
(2007). http://dx.doi.org/10.1161/01.RES.0000265064.46075.31 CIRUAL 0009-7330 Google Scholar
X. Montetet al.,
“Tomographic fluorescence imaging of tumor vascular volume in mice,”
Radiology, 242 751
–758
(2007). http://dx.doi.org/10.1148/radiol.2423052065 RADLAX 0033-8419 Google Scholar
V. Josserandet al.,
“In vivo mice lung tumor follow-up with fluorescence diffuse optical tomography,”
J. Biomed. Opt., 13 011008
(2008). http://dx.doi.org/10.1117/1.2884505 JBOPFO 1083-3668 Google Scholar
A. Aleet al.,
“FMT-XCT: in vivo animal studies with hybrid fluorescence molecular tomography-x-ray computed tomography,”
Nat. Methods, 9 615
–620
(2012). http://dx.doi.org/10.1038/nmeth.2014 1548-7091 Google Scholar
V. Ntziachristoset al.,
“Fluorescence molecular tomography resolves protease activity in vivo,”
Nat. Med., 8 757
–761
(2002). http://dx.doi.org/10.1038/nm729 1078-8956 Google Scholar
R. WeisslederV. Ntziachristos,
“Shedding light onto live molecular targets,”
Nat. Med., 9 123
–128
(2003). http://dx.doi.org/10.1038/nm0103-123 1078-8956 Google Scholar
H. F. Minogueet al.,
“Noninvasive molecular imaging of c-Myc activation in living mice,”
Proc. Natl. Acad. Sci. U. S. A., 107 15892
–15897
(2010). http://dx.doi.org/10.1073/pnas.1007443107 PNASA6 0027-8424 Google Scholar
L. D. MontejoA. D. KloseA. H. Hielscher,
“Implementation of the equation of radiative transfer on block-structured grids for modeling light propagation in tissue,”
Biomed. Opt. Express, 1 861
–878
(2010). http://dx.doi.org/10.1364/BOE.1.000861 BOEICL 2156-7085 Google Scholar
H. K. Kimet al.,
“PDE-constrained multispectral imaging of tissue chromophores with the equation of radiative transfer,”
Biomed. Opt. Express, 1 812
–824
(2010). http://dx.doi.org/10.1364/BOE.1.000812 BOEICL 2156-7085 Google Scholar
J. WuM. S. FeldR. P. Rava,
“Analytical model for extracting intrinsic fluorescence in turbid media,”
Appl. Opt., 32 3585
–3595
(1993). http://dx.doi.org/10.1364/AO.32.003585 APOPAI 0003-6935 Google Scholar
W. Xieet al.,
“L1 regularization for restraining artifacts in FMT reconstruction images with limited measurements,”
Opt. Lett., 39 4148
–4151
(2014). http://dx.doi.org/10.1364/OL.39.004148 OPLEDP 0146-9592 Google Scholar
A. Corluet al.,
“Three-dimensional in vivo fluorescence diffuse optical tomography of breast cancer in humans,”
Opt. Express, 15 6696
–6716
(2007). http://dx.doi.org/10.1364/OE.15.006696 OPEXFF 1094-4087 Google Scholar
L. V. WangH. Wu, Biomedical Optics: Principles and Imaging, John Wiley & Sons, Hoboken
(2007). Google Scholar
K. M. YooF. LiuR. R. Alfano,
“When does the diffusion approximation fail to describe photon transport in random media?,”
Phys. Rev. Lett., 65 2610
–2211
(1990). http://dx.doi.org/10.1103/PhysRevLett.65.2210 PRLTAO 0031-9007 Google Scholar
T. Correiaet al.,
“Quantitative fluorescence diffuse optical tomography in the presence of heterogeneities,”
Opt. Lett., 38 1903
–1905
(2013). http://dx.doi.org/10.1364/OL.38.001903 OPLEDP 0146-9592 Google Scholar
X. Songet al.,
“Reconstruction for free-space fluorescence tomography using a novel hybrid adaptive finite element algorithm,”
Opt. Express, 15 18300
–18317
(2007). http://dx.doi.org/10.1364/OE.15.018300 OPEXFF 1094-4087 Google Scholar
C. ZhuQ. Liu,
“Review of Monte Carlo modeling of light transport in tissues,”
J. Biomed. Opt., 18 050902
(2013). http://dx.doi.org/10.1117/1.JBO.18.5.050902 JBOPFO 1083-3668 Google Scholar
K. VishwanathM. A. Mycek,
“Time-resolved photon migration in bi-layered tissue models,”
Opt. Express, 13 7466
–7482
(2005). http://dx.doi.org/10.1364/OPEX.13.007466 OPEXFF 1094-4087 Google Scholar
E. Péryet al.,
“Monte Carlo modeling of multilayer phantoms with multiple fluorophores: simulation algorithm and experimental validation,”
Biomed. Opt. Express, 14 024048
(2009). http://dx.doi.org/10.1117/1.3122368 BOEICL 2156-7085 Google Scholar
J. Swartlinget al.,
“Accelerated Monte Carlo models to simulate fluorescence spectra from layered tissues,”
J. Opt. Soc. Am. A, 20 714
–727
(2003). http://dx.doi.org/10.1364/JOSAA.20.000714 JOAOD6 0740-3232 Google Scholar
G. Maet al.,
“Comparison of simplified Monte Carlo simulation and diffusion approximation for the fluorescence signal from phantoms with typical mouse tissue optical properties,”
Appl. Opt., 46 1686
–1692
(2007). http://dx.doi.org/10.1364/AO.46.001686 APOPAI 0003-6935 Google Scholar
A. Liebertet al.,
“Monte Carlo algorithm for efficient simulation of time-resolved fluorescence in layered turbid media,”
Opt. Express, 16 13188
–13202
(2008). http://dx.doi.org/10.1364/OE.16.013188 OPEXFF 1094-4087 Google Scholar
J. Lakowicz, Principles of Fluorescence Spectroscopy, 3rd ed.Springer, New York
(2006). Google Scholar
A. T. N. Kumar,
“Direct Monte Carlo computation of time-resolved fluorescence in heterogeneous turbid media,”
Opt. Lett., 37
(22), 4783
–4785
(2012). http://dx.doi.org/10.1364/OL.37.004783 OPLEDP 0146-9592 Google Scholar
A. J. Welchet al.,
“Propagation of fluorescent light,”
Lasers Surg. Med., 21 166
–178
(1997). http://dx.doi.org/10.1002/(ISSN)1096-9101 LSMEDI 0196-8092 Google Scholar
J. ChenX. Intes,
“Comparison of Monte Carlo methods for fluorescence molecular tomography-computational efficiency,”
Med. Phys., 38 5788
–5798
(2011). http://dx.doi.org/10.1118/1.3641827 MPHYA6 0094-2405 Google Scholar
P. K. Yalavarthyet al.,
“Experimental investigation of perturbation Monte-Carlo based derivative estimation for imaging low-scattering tissue,”
Opt. Express, 13 985
–997
(2005). http://dx.doi.org/10.1364/OPEX.13.000985 OPEXFF 1094-4087 Google Scholar
C. K. Hayakawaet al.,
“Perturbation Monte Carlo methods to solve inverse photon migration problems in heterogeneous tissues,”
Opt. Lett., 26 1335
–1337
(2001). http://dx.doi.org/10.1364/OL.26.001335 OPLEDP 0146-9592 Google Scholar
A. Sassaroli,
“Fast perturbation Monte Carlo method for photon migration in heterogeneous turbid media,”
Opt. Lett., 36 2095
–2097
(2011). http://dx.doi.org/10.1364/OL.36.002095 OPLEDP 0146-9592 Google Scholar
J. ChenX. Intes,
“Time-gated perturbation Monte Carlo for whole body functional imaging in small animals,”
Opt. Express, 17 19566
–19579
(2009). http://dx.doi.org/10.1364/OE.17.019566 OPEXFF 1094-4087 Google Scholar
P. L’EcuyerA. B. Owen, Monte Carlo and Quasi-Monte Carlo Methods 2008, Springer-Verlag, Berlin
(2009). Google Scholar
I. LuxL. Koblinger, Monte Carlo Particle Transport Methods: Neutron and Photon Calculations, CRC Press, Boca Raton
(1991). Google Scholar
A. T. Kumaret al.,
“Time resolved fluorescence tomography of turbid media based on lifetime contrast,”
Opt. Express, 14 12255
–12270
(2006). http://dx.doi.org/10.1364/OE.14.012255 OPEXFF 1094-4087 Google Scholar
L. V. WangS. L. JacquesL. Zheng,
“MCML–Monte Carlo modeling of light transport in multi-layered tissues,”
Comput. Methods Prog. Biomed., 47
(2), 131
–146
(1995). http://dx.doi.org/10.1016/0169-2607(95)01640-F CMPBEK 0169-2607 Google Scholar
Q. LuoT. LiH. Gong,
“MCVM: Monte Carlo modeling of photon migration in voxelized media,”
J. Innov. Opt. Health Sci., 3 91
–102
(2010). http://dx.doi.org/10.1142/S1793545810000927 JIOHAA 1793-5458 Google Scholar
Q. FangD. A. Boas,
“Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units,”
Opt. Express, 17 20178
–20190
(2009). http://dx.doi.org/10.1364/OE.17.020178 OPEXFF 1094-4087 Google Scholar
F. CaiS. He,
“Using graphics processing units to accelerate perturbation Monte Carlo simulation in a turbid medium,”
J. Biomed. Opt., 17 040502
(2012). http://dx.doi.org/10.1117/1.JBO.17.4.040502 JBOPFO 1083-3668 Google Scholar
N. Renet al.,
“GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues,”
Opt. Express, 18 6811
–6823
(2010). http://dx.doi.org/10.1364/OE.18.006811 OPEXFF 1094-4087 Google Scholar
X. Yanget al.,
“Combined system of fluorescence diffuse optical tomography and micro-computed tomography for small animal imaging,”
Rev. Sci. Instrum., 81 054304
(2010). http://dx.doi.org/10.1063/1.3422252 RSINAK 0034-6748 Google Scholar
Z. Zhanget al.,
“Biomimetic nanocarrier for direct cytosolic drug delivery,”
Angew. Chem. Int. Ed. Engl., 48 9171
–9175
(2009). http://dx.doi.org/10.1002/anie.v48:48 ACIEAY 0570-0833 Google Scholar
V. Ntziachristos,
“Fluorescence molecular imaging,”
Annu. Rev. Biomed. Eng., 8 1
–33
(2006). http://dx.doi.org/10.1146/annurev.bioeng.8.061505.095831 ARBEF7 1523-9829 Google Scholar
A. T. Kumaret al.,
“A time domain fluorescence tomography system for small animal imaging,”
IEEE Trans. Med. Imaging, 27 1152
–1163
(2008). http://dx.doi.org/10.1109/TMI.2008.918341 ITMID4 0278-0062 Google Scholar
N. Chen,
“Controlled Monte Carlo method for light propagation in tissue of semi-infinite geometry,”
Appl. Opt., 46 1597
–1603
(2007). http://dx.doi.org/10.1364/AO.46.001597 APOPAI 0003-6935 Google Scholar
|